Geum.ru

Моу «Краснослободская средняя общеобразовательная школа №2»

Вид материалаРешение

Содержание


Совокупность команд, которые могут (в принципе) быть выполнены исполнителем, называется
Второй способ (формальный)
Слайды 9, 10,11
Подобный материал:
МОУ «Краснослободская средняя общеобразовательная школа №2»





Подготовила учитель

математики-информатики Белякова И.Н.


План (слайд 2)

1. Понятие алгоритма

2. Свойства алгоритма

3. Исполнитель, система команд исполнителя

4. Способы исполнения алгоритма

5. Виды записи алгоритмов

6. Базовые алгоритмические структуры


  1. СЛАЙД 3



Человек ежедневно встречается с множеством задач - от самых простых и хорошо известных до очень сложных. Для многих задач существуют определенные правила (инструкции, предписания), объясняющие исполнителю, как решать данную задачу. Эти правила человек может изучить заранее или сформулировать сам в процессе решения задачи. Чем точнее и понятнее будут описаны правила решения задач, тем быстрее человек овладеет ими и будет эффективнее их применять.

Решение многих задач человек может передавать техническим устройствам – автоматам, ЭВМ, роботам. Применение таких технических устройств предъявляет очень строгие требования к точности описания правил и последовательности выполнения действий. Поэтому разрабатываются специальные языки для четкого и строгого описания различных правил.

В математике для решения типовых задач мы используем определенные правила, описывающие последовательности действий.

Например, правила сложения дробных чисел, решения квадратных уравнений и т. Для решения задачи надо знать, что дано, что следует получить, какие действия, и в каком порядке следует для этого выполнить.


Алгоритм – предписание (указание) исполнителю совершить последовательность действий, выполнив которые он получит нужный результат.


Название "алгоритм" произошло от латинской формы имени величайшего среднеазиатского математика Мухаммеда ибн Муса аль-Хорезми (Alhorithmi), жившего в 783—850 гг. В своей книге "Об индийском счете" он изложил правила записи натуральных чисел с помощью арабских цифр и правила действий над ними "столбиком", знакомые теперь каждому школьнику. В XII веке эта книга была переведена на латынь и получила широкое распространение в Европе.

СЛАЙД 4




Пример 1.

В повседневной жизни нам часто приходится пользоваться алгоритмами, не подозревая об этом. Если Вы идете домой, то не обращаете внимания, какие ориентиры, какие действия Вы выполняете, все Вам давно знакомо. Но если нужно обучить другого или объяснить кому-то, как добраться до Вашего дома, Вы будете по шагам, детально рассказывать маршрут, включая номер дома, подъезд, квартиру.


Пример 2.

Подготавливаясь к празднику, мы также действуем по алгоритму. Первым делом мы определяем круг гостей. Затем определяем место и время проведения праздника, составляется меню. Подготавливается программа проведения праздника, и т.д.

Пример 3.

К литературе тоже применимо понятие алгоритма. Например, при написании сочинение мы соблюдаем определенный порядок. Прежде всего, мы выбираем и обдумываем тему сочинения. Затем определяем ведущую мысль, которую мы будем развивать и доказывать. Вспоминаем и отбираем тот материал, который понадобиться для подтверждения этой мысли, в отобранном материале выделяем главное. Подбираем примеры, факты, цитаты, подтверждающие наши мысли. Чтобы четко раскрыть тему, составляем план и, работая над текстом сочинения, следуем намеченному плану. Окончив сочинение, прочитываем написанное, проверяем содержание, последовательность изложения, грамотность. Переписываем работу «набело». Еще раз проверяем написанное, в частности, смотрим, нет ли описок и пропусков букв.

СЛАЙД 5




Правильно составленный алгоритм обладает следующими свойствами:
  1. Понятность, ясность
  2. Определенность, точность
  3. Дискретность
  4. Правильность
  5. Результативность
  6. Массовость
  7. Эффективность


Понятность – означает представление алгоритма в доступном для исполнителя виде. Каждая команда и весь алгоритм в целом изложены ясно и не вызывают сомнений.


Определенность – это свойство тесно связано с предыдущим. Алгоритм должен быть представлен так, чтобы все действия определялись и понимались однозначно. Предписание, понятное разным исполнителям, после реализации каждым из них давало бы один и тот же результат при одних и тех же данных. Кроме того, исполнителю должно быть ясно, какое из предписаний должно выполнятся на следующем шаге.


Дискретность (прерывность, раздельность) – представление алгоритма в виде последовательности отдельных, независимых друг от друга команд. При необходимости, это свойство дает возможность включить в алгоритм дополнительные промежуточные действия. Только выполнив предыдущее действие, можно перейти к следующему.


Правильность – это способность алгоритма обеспечить получение именно того результата, который требуется постановкой задачи. Неправильность может объясняться неполнотой наших представлений о свойствах объекта или упущением в решении. Доказательство правильности алгоритма – один из самых трудных этапов тестирования. Задача часто делится на блоки, и правильность доказывается для каждого блока, хотя такая проверка не является полной. На практике чаще всего судят о правильности алгоритма по результатам исполнения программы параллельно со счетом «вручную».


Результативность означает, что при любых допустимых исходных данных и точном выполнении всех предписаний алгоритма вычислительный процесс должен через конечное число шагов остановиться и выдать искомый результат. Но это требование может не учитывать реальных условий, поэтому иногда говорят о “потенциальной” (а не реальной) выполнимости алгоритма.


Массовость означает, что алгоритм является решением задачи в общем виде, т.е. алгоритм может быть применен не только к единственным исходным данным, но и к целому классу похожих задач. Результат исполнения алгоритма не зависит от конкретного исполнителя, от времени и места его исполнения. При точном и правильном выполнении всех команд будет получен верный ожидаемый результат.


Эффективность – это свойство не одного алгоритма, а нескольких. Для решения одной задачи могут быть предложены разные алгоритмы. Предположим, что они правильны и выполнимы. Для применения следует выбрать тот из них, который по определенному критерию предпочтительнее. В зависимости от заданного критерия, предпочтение отдается тому или другому алгоритму, и он определяется как эффективный.

СЛАЙД 6




В виде алгоритма можно представить выполнение любого задания, к примеру проведение экспериментов по физике и химии, приготовление какого – либо блюда, поход за покупками и т.д.

Примеры алгоритмов показывают, алгоритм состоит из отдельных указаний выполнить некоторое законченное действие. Каждое такое указание называется командой.

Команды алгоритма выполняются одна за другой. На каждом шаге исполнения алгоритма исполнителю точно известно, какая команда должна выполняться следующей.

Каждый алгоритм строится в расчете на некоторого исполнителя.


Исполнитель - это тот, кто выполняет заданную последовательность действий. Им может быть человек, компьютер, любое животное, механизм, электрический прибор.


Для того, чтобы исполнитель мог решить задачу по заданному алгоритму, необходимо, чтобы он был в состоянии выполнить каждое действие, предписываемое командами алгоритма.

Совокупность команд, которые могут (в принципе) быть выполнены исполнителем, называется системой команд исполнителя.

СЛАЙД 7




Среди математиков популярна притча, ярко иллюстрирующая алгоритмический способ мышления.

Вопрос. Имеется плита, спички, водопровод, чайник. Как вскипятить чай?

Ответ:

1) из водопровода налить в чайник воду;

2) спичкой зажечь газ;

3) поставить чайник на газ;

4) ждать несколько минут.

Вопрос. А если в чайнике уже есть вода и газ уже горит?

Ответ. Выключить газ, вылить воду, и мы сведем задачу к предыдущей, решение которой уже есть.


Притча, при всей своей нелепости, имеет следующий смысл: выявление закономерностей при решении задачи; сведение задачи к другой, решение которой известно.

Возможно, способ будет не самым коротким, но задача будет решена с гарантией.


Построение алгоритма для решения задачи из какой–либо области требует от человека глубоких знаний в этой области, бывает связано с тщательным анализом поставленной задачи, сложными, иногда очень громоздкими рассуждениями. На поиски алгоритма решения некоторых задач ученые затрачивают многие годы. Но когда алгоритм создан, решение задачи по готовому алгоритму уже не требует каких–либо рассуждений и сводится только к строгому выполнению команд алгоритма. В этом случае исполнение алгоритма можно поручить не человеку, а машине. Это положение и лежит в основе работы автоматических устройств.

Неформальное исполнение алгоритма – осознанное исполнение, при котором исполнитель понимает смысл задания, выбирает самый эффективный метод его выполнения, ориентируясь на желаемый результат.


Формальное исполнение алгоритма – это исполнение алгоритма, при котором исполнитель может не вникать в смысл того, что он делает, и вместе с тем получить нужный результат. Он отвлекается от содержания поставленной задачи и только выполняет действия в указанной последовательности, не раздумывая.

Это очень важная особенность алгоритмов. Наличие алгоритма формализовало процесс, исключило рассуждения.

СЛАЙД 8




Пример решения задачи

Найти площадь прямоугольного треугольника, если известен катет а и гипотенуза с.

Первый способ (неформальный)

Он основан на том, что мы знаем из курса геометрии формулу

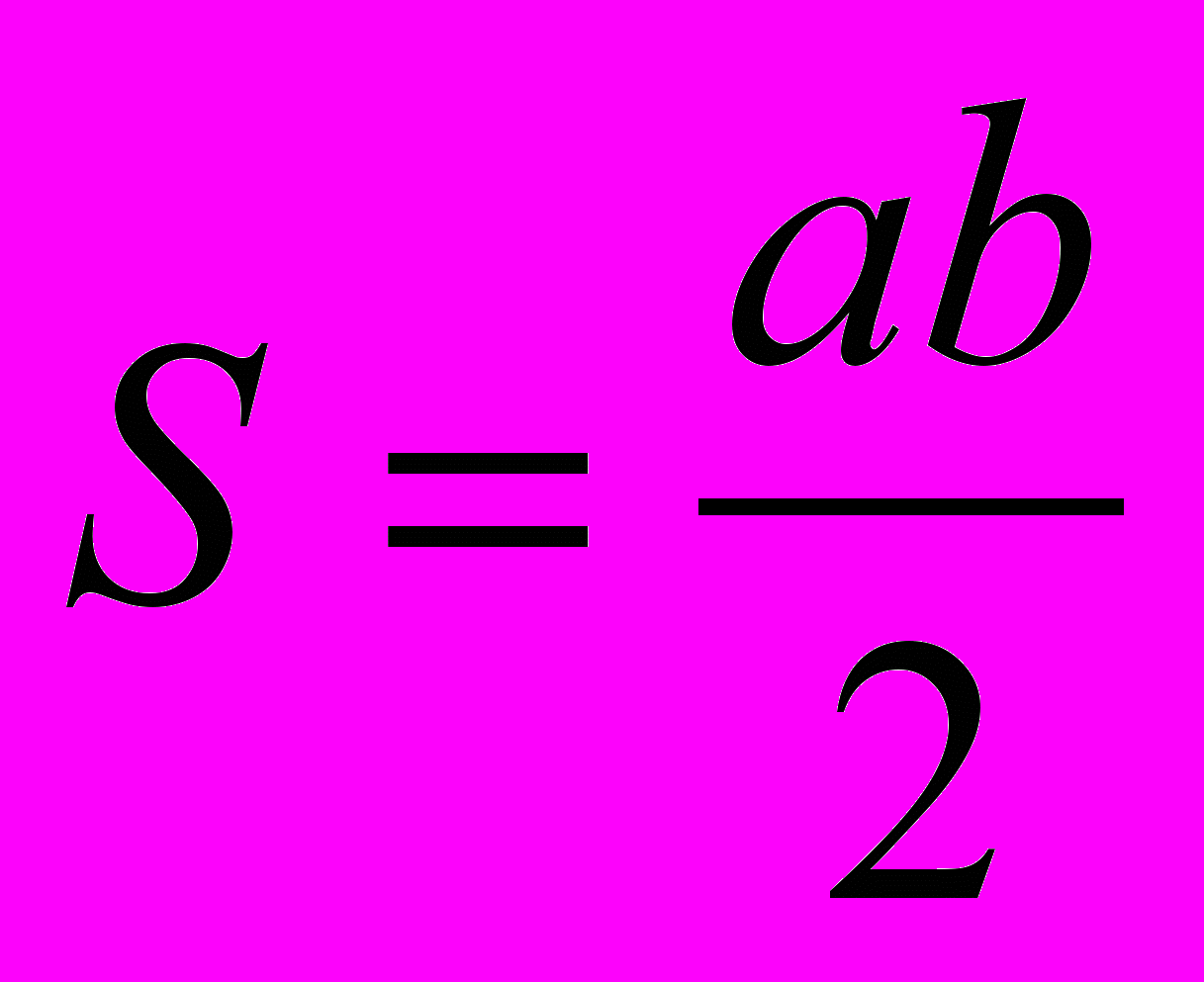
и теорему Пифагора а2+b2=c2. Вычисления сводятся к подстановке в формулу


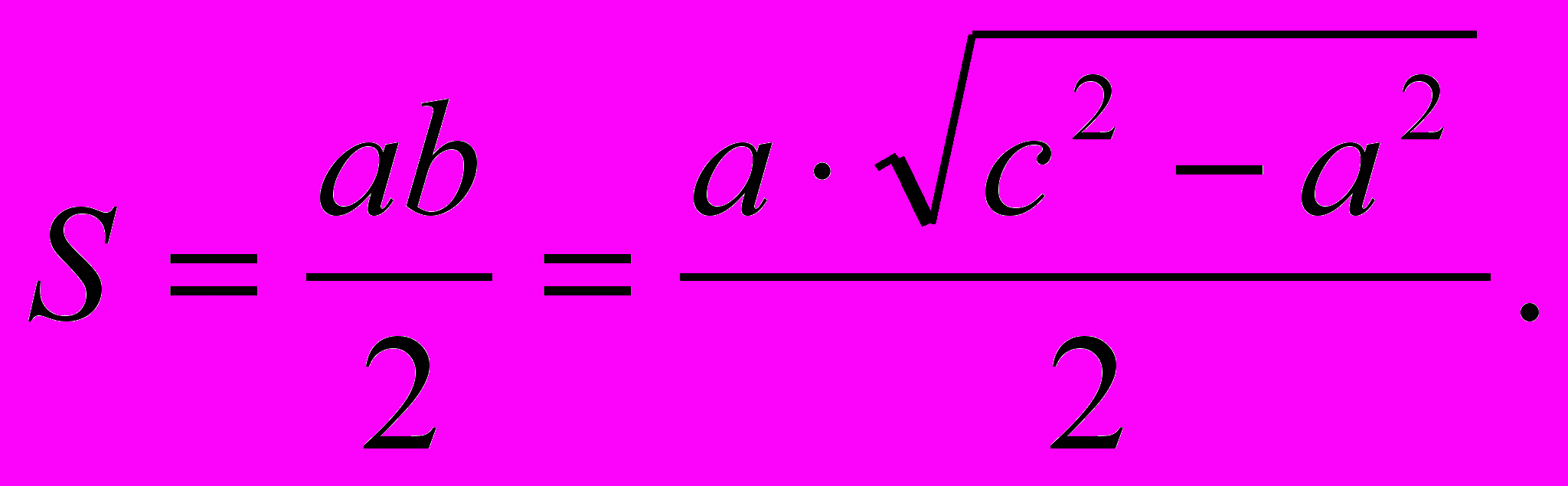
Второй способ (формальный)

Он для тех, кто не изучал или забыл геометрию. Тому проще ничего не объяснять, а просто дать последовательность действий, которая приведет к нужному результату:

1) получить разность с–а;

2) получить сумму с+а;

3) перемножить результаты 1 и 2 шага;

4) взять корень из результата 3 шага;

5) умножить результат 4 шага на а;

6) поделить результат 5 шага на 2;

7) записать ответ.

СЛАЙДЫ 9, 10,11




    • Словесно-формульная запись. Этот способ основан на задании предписаний о выполнении конкретных действий в определенной последовательности с использованием математических формул и словесных пояснений. Формулы в сочетании с правилами их написания представляют собой, по существу, своеобразный алгоритмический язык, применяемый для задания вычислительных алгоритмов. Этот способ общепринят при описании математических выкладок, доказательств теорем.



    • На алгоритмическом языке. Для разных областей деятельности человека созданы условные сокращения терминов, правила расположения записей относительно друг друга и другие условности. В результате запись приобретает краткий и сжатый вид, понятный специалисту. Это и есть алгоритмический язык.



    • Графическая форма записи (в виде блок-схемы). При графическом представлении алгоритм изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий. Такое графическое представление называется схемой алгоритма или блок-схемой. В блок-схеме каждому типу действий (вводу исходных данных, вычислению значений выражений, проверке условий, управлению повторением действий, окончанию обработки и т.п.) соответствует геометрическая фигура, представленная в виде блочного символа.



СЛАЙД 12


Алгоритмы можно представлять как некоторые структуры, состоящие из отдельных базовых элементов (т.е. основных). Естественно, что при таком подходе к алгоритмам изучение основных принципов их конструирования должно начинаться с изучения этих базовых элементов.

Логическая структура любого алгоритма может быть представлена комбинацией трех базовых структур: линейной, разветвляющейся, циклической. Характерной особенностью базовых структур является наличие в них одного входа и одного выхода.

    • Линейная.

Это самая простая из структур. Она образуется последовательностью действий, следующих одно за другим:


действие 1



действие 2




…………….

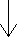действие n

    • Разветвление

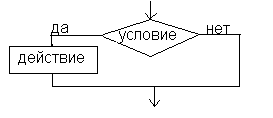
Обеспечивает в зависимости от результата проверки условия (да или нет) выбор одного из альтернативных путей работы алгоритма. Каждый из путей ведет к общему выходу, так что работа алгоритма будет продолжаться независимо от того, какой путь будет выбран. Структура разветвление существует в двух основных вариантах:


1. если—то—иначе (полная форма) 2.если—то (неполная форма)




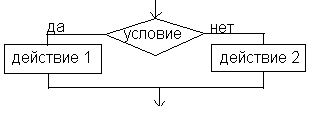
    • Циклическая.

О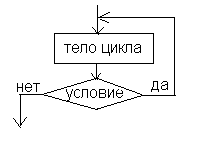беспечивает многократное выполнение некоторой совокупности действий, которая называется телом цикла. Основные разновидности циклов представлены в таблице:


Цикл по схеме пока. Предписывает выполнять тело цикла до тех пор,

пока выполняется условие, записанное после слова пока.




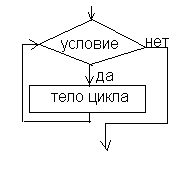
Цикл по схеме до





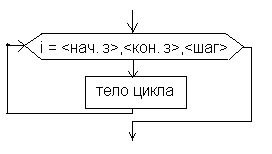
Цикл с параметром (цикл для). Предписывает выполнять тело цикла для всех значений некоторой переменной (параметра цикла) в заданном диапазоне.


    • Блочные символы соединяются линиями переходов, определяющими очередность выполнения действий. В таблице приведены наиболее часто употребляемые символы.




Название символа
  Обозначение

и пример заполнения  

Пояснение

Процесс


Вычислительное действие или
последовательность действий

Решение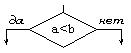


Проверка условий

Модификация


Начало цикла

Предопределенный процесс


Вычисления по подпрограмме, стандартной подпрограмме

Ввод-вывод


Ввод-вывод в общем виде

Пуск-останов


Начало, конец алгоритма, вход и выход в подпрограмму

Документ


Вывод результатов на печать

Блок "процесс" применяется для обозначения действия или последовательности действий, изменяющих значение, форму представления или размещения данных. Для улучшения наглядности схемы несколько отдельных блоков обработки можно объединять в один блок. Представление отдельных операций достаточно свободно.

Блок "решение" используется для обозначения переходов управления по условию. В каждом блоке "решение" должны быть указаны вопрос, условие или сравнение, которые он определяет.

Блок "модификация" используется для организации циклических конструкций. (Слово модификация означает видоизменение, преобразование). Внутри блока записывается параметр цикла, для которого указываются его начальное значение, граничное условие и шаг изменения значения параметра для каждого повторения.

Блок "предопределенный процесс" используется для указания обращений к вспомогательным алгоритмам, существующим автономно в виде некоторых самостоятельных модулей, и для обращений к библиотечным подпрограммам.