Нформаційні системи І моделювання

Вид материала

Содержание

Материал и результаты исследований. Энергетическая и физическая модель ЭТМП.
Феноменологические уравнения преобразований энергии в ЭТМП.
Таблица 1 - Соотношение потоков и сил для систем феноменологических уравнений ДМ и ТМ

Подобный материал:

ІНФОРМАЦІЙНІ СИСТЕМИ І МОДЕЛЮВАННЯ

УДК 621.314.262:536.7.001.57

МОДЕЛЬ ЭЛЕКТРОТЕПЛОМЕХАНИЧЕСКОГО ПРЕОБРАЗОВАТЕЛЯ КАК СИСТЕМЫ С НЕРАВНОВЕСНЫМИ ТЕРМОДИНАМИЧЕСКИМИ ПРОЦЕССАМИ ПРЕОБРАЗОВАНИЯ ЭНЕРГИИ

Заблодский Н.Н.

Донбасский государственный технический университет

Введение. Электротепломеханические преобразователи (ЭТМП) и системы на их основе, относящиеся к новому классу электромеханических преобразователей энергии, дают возможность создавать энерго- и ресурсосберегающие технологии в различных отраслях промышленности 1, 2, 3. Поскольку в ЭТПМ оптимизации подлежат, строго говоря одновременно три процесса преобразования энергии (электрической – в механическую, электрической – в тепловую и механической – в тепловую), необходим поиск новых подходов, раскрывающих взаимное влияние указанных процессов и формирующих содержание управляющих воздействий. Известны исследования процессов электромеханического преобразования методами линейной термодинамики неравновесных процессов 4. Однако они касаются электроприводов постоянного тока и не затрагивают преобразований в тепловую энергию.

Цель работы – разработка физической и математической моделей ЭТМП как системы с неравновесными термодинамическими процессами преобразования энергии.

Материал и результаты исследований.

Энергетическая и физическая модель ЭТМП.

В рамках термодинамики неравновесных процессов (ТДНП) любой преобразователь свободной энергии может быть представлен «черным ящиком», который преобразует свободную энергию на входе в выходную свободную энергию. Общая энергетическая схема ЭТМП показана на рис. 1.

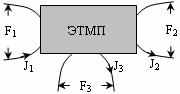
Рисунок 1 - Общая энергетическая схема ЭТМП

Потоки J₁, J₂, J₃ представляют собой, соответственно, скорости поступления электрической, отвода механической и тепловой энергий. Каждый поток J_i является функцией не только своей собственной термодинамической силы, но и остальных сил системы F_i и дополнительных факторов a_i. К числу последних могут быть отнесены перенапряжения в электрической сети, изменения производительности, резкие изменения нагрузки и условий теплообмена ротора ЭТМП.

Если рассматривать ЭТМП в непосредственной близости к состоянию равновесия, то уравнения потоков и функция производства энтропии могут быть представлены следующими выражениями:

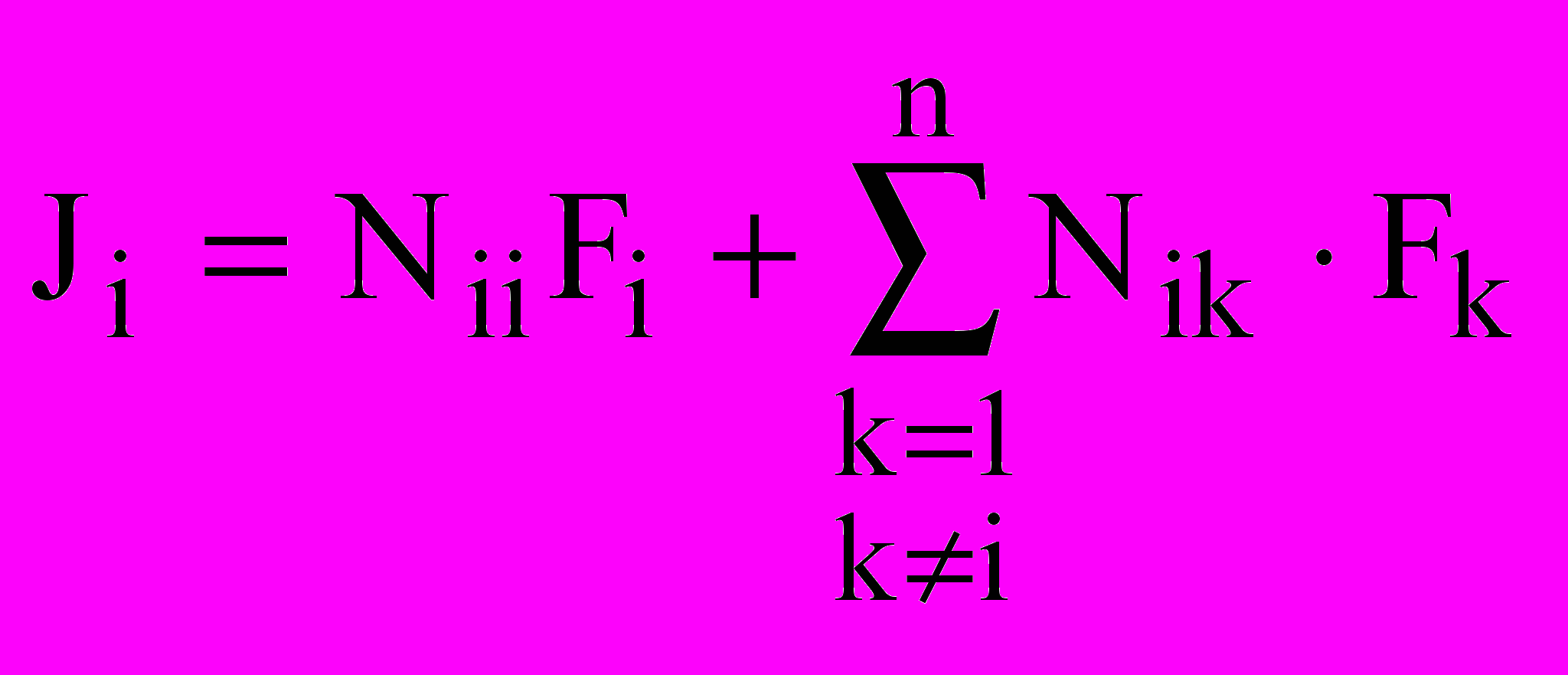, (1)

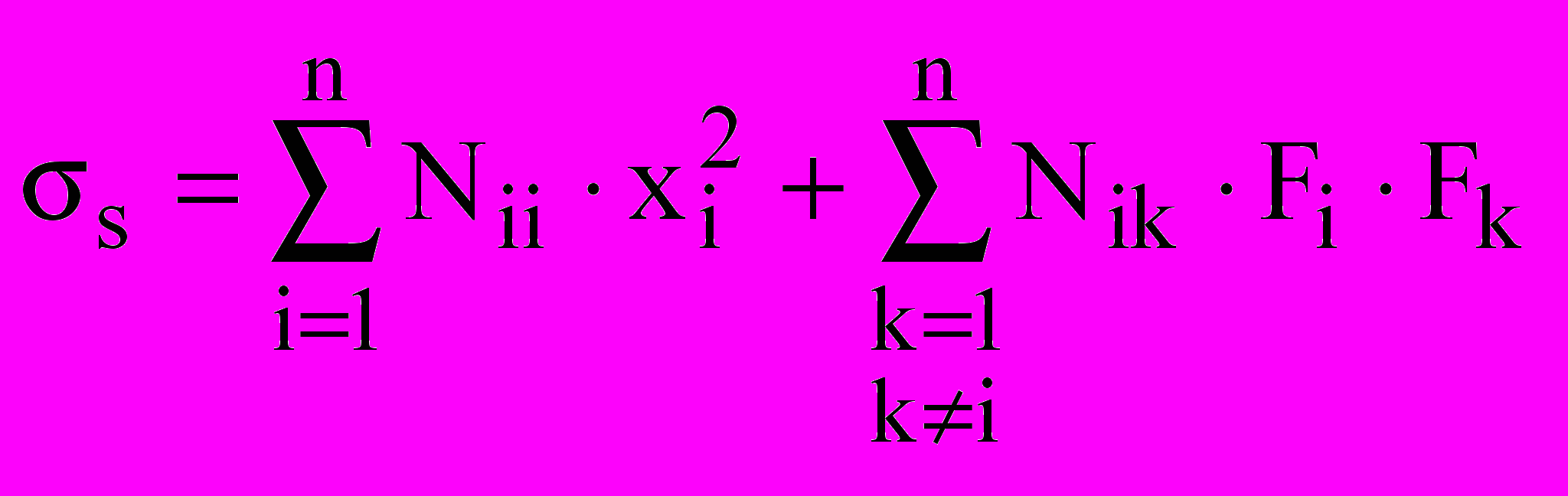, (2)

где

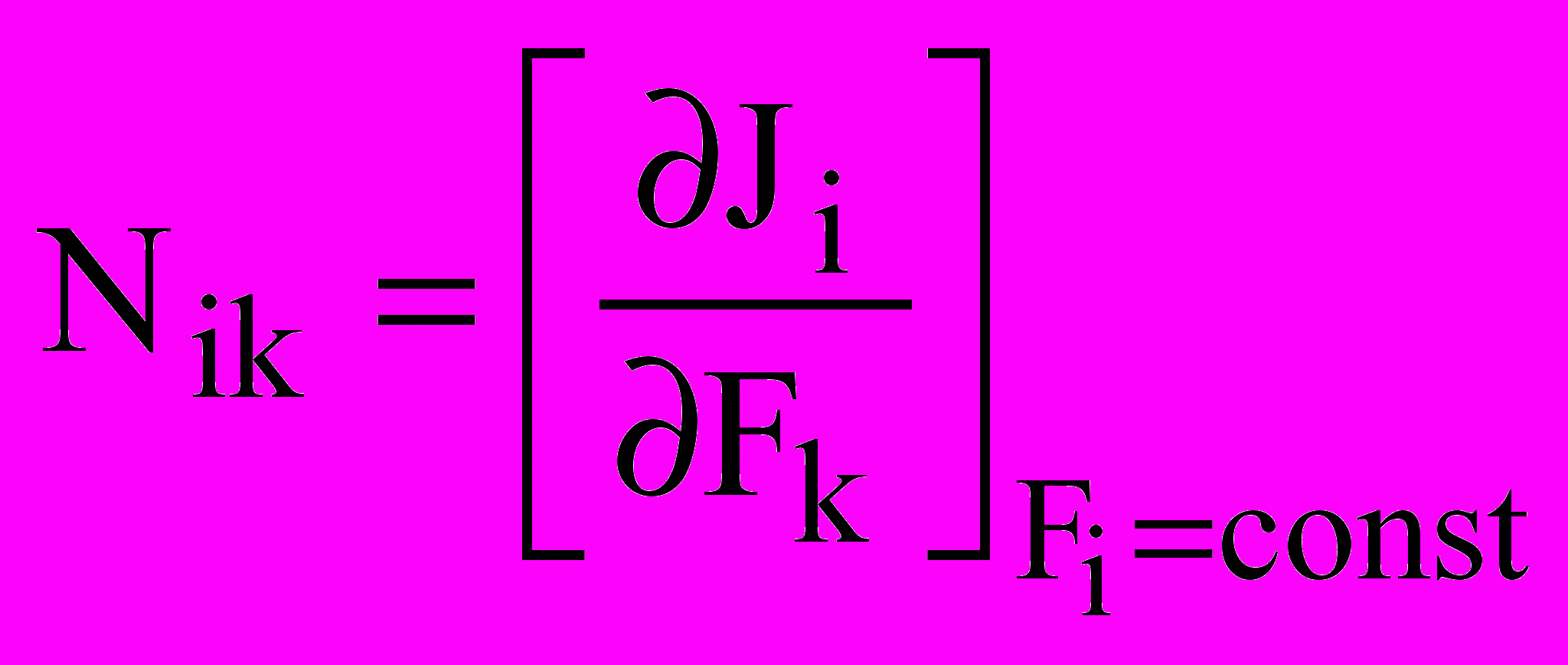– феноменологические коэффициенты, указывающие на степень термодинамического сопряжения в системе сил.

При рассматриваемых условиях применим принцип Онсагера, согласно которому N_ik = N_ki, т.е. вблизи состояния равновесия при отсутствии внешнего магнитного поля и вращения системы в целом линейная зависимость любого потока J_i от любой силы F_к совпадает с аналогичной зависимостью потока J_k от силы F_i. Чтобы исключить явления срыва термодинамического сопряжения, которое может наступать при одновременном возрастании коэффициентов N_iiи N_ik, вводится так называемая степень сопряжения . Кроме того, для универсального представления результатов в рамках ТДНП введены нормированные величины: феноменологическая стехиометрия Z и отношение действующих сил . Для случая действия в преобразователе энергии двух сил и двух потоков, связь между ними подчинена следующим выражениям:

. (3)

Соответствующие нормированные величины для указанных соотношений следующие: степень сопряжения выходного процесса с входным

; феноменологическая стехиометрия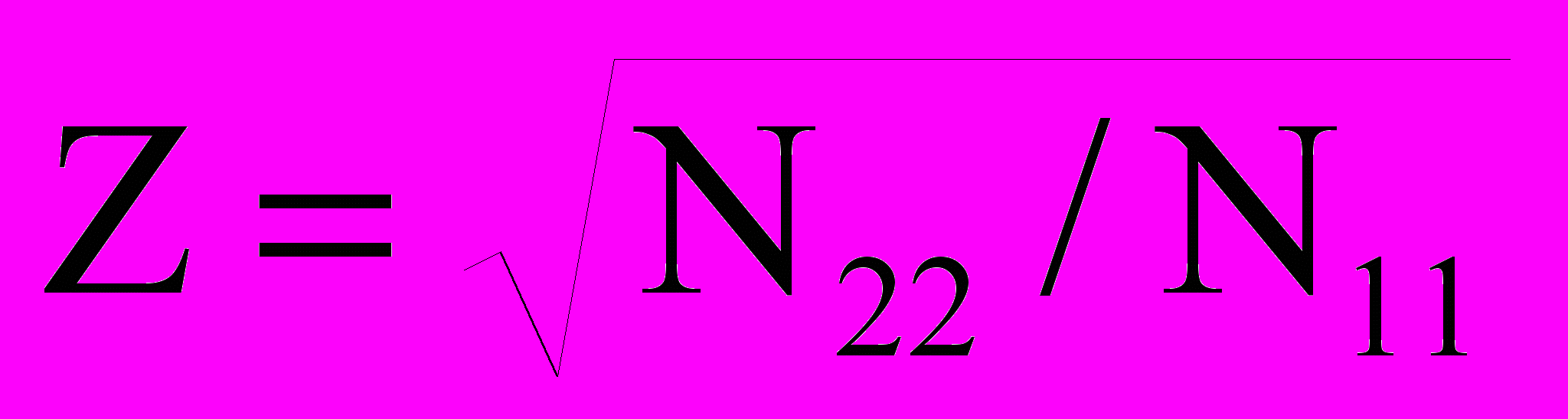

; отношение сил

.

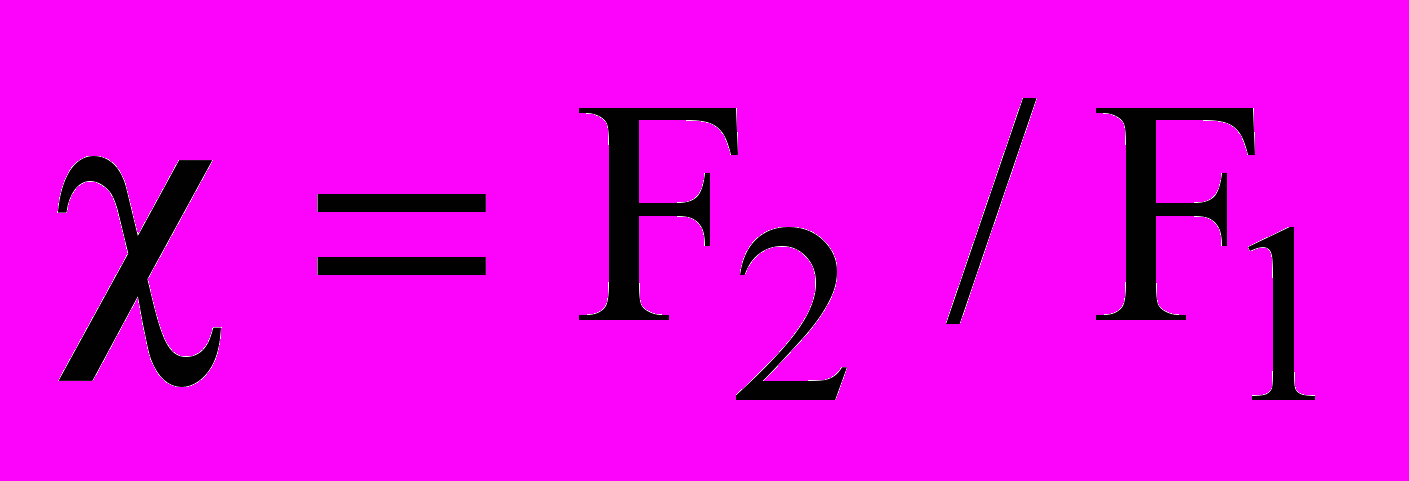Такое представление преобразований энергии справедливо для стационарного режима работы обычных асинхронных двигателей. Но функциональное и структурное построение ЭТМП предусматривает работу одного из его модулей в режиме противовключения, когда определенная доля механической энергии двигательного модуля (ДМ), передаваемая на общий массивный ротор, преобразуется тормозным модулем (ТМ) в тепловую энергию.

На рис. 2 представлена физическая модель роторной части шнекового ЭТМП, где электрические параметры стали массивного ротора показаны в

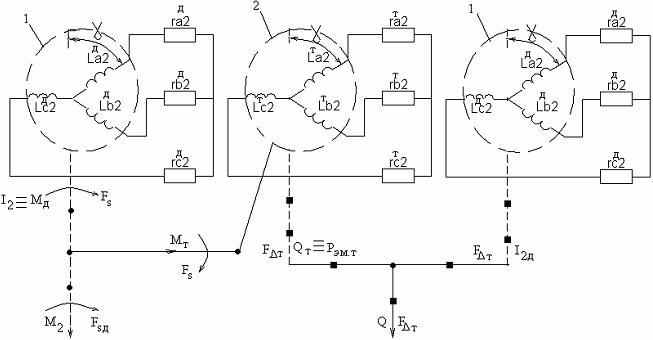
Рисунок 2 - Физическая модель роторной части ЭТМП

виде эквивалентных обмоток

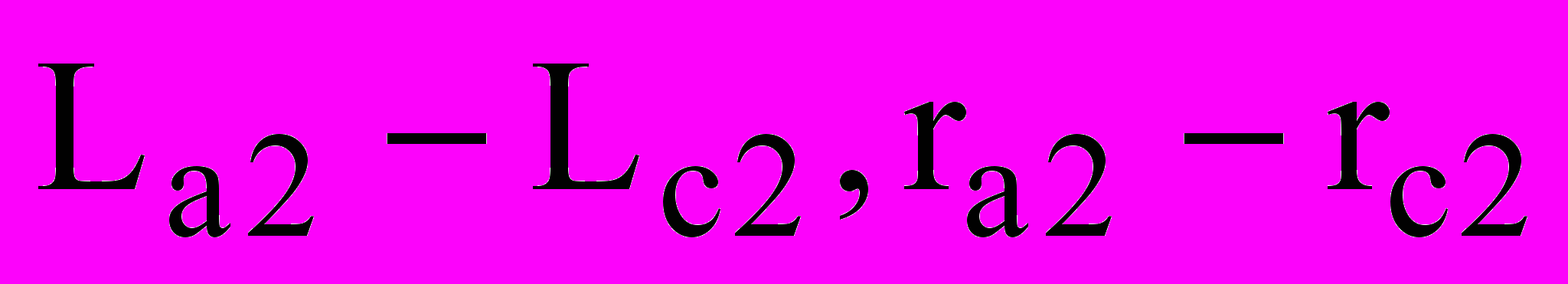соответственно для ДМ и ТМ.

Общий массивный ротор разделен по длине на два участка, соответствующих зонам электромагнитного действия статора ДМ (зона 1), работающего в двигательном режиме, и ТМ (зона 2), работающего в режиме электромагнитного торможения (противовключения). При этом зона 1 ротора, статорная и роторная обмотки ДМ показаны дважды, поскольку ДМ осуществляет преобразование электрической энергии и в механическую, и в тепловую энергию.

Действующие потоки энергии представлены следующим перечнем:

J_1д = I_1д - ток статора ДМ;

J_1т = I_1т - ток статора ТМ;

J_2д = I^/_2т≡ М_i - ток главной цепи Т-образной схемы замещения ДМ, пропорциональной электромагнитному моменту;

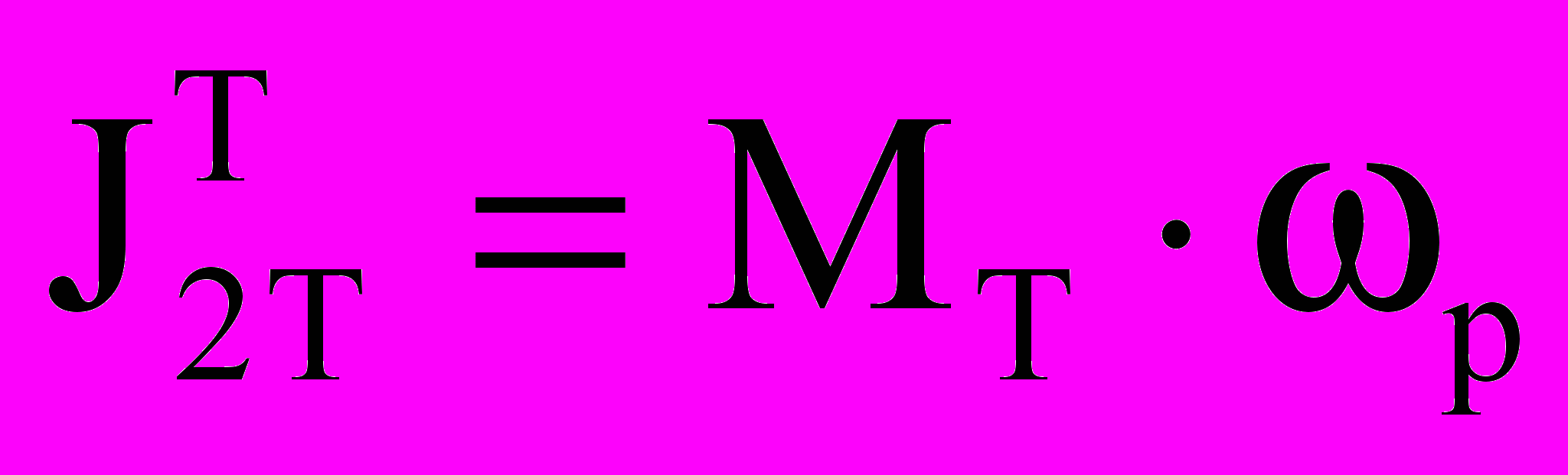- составляющая полной механической мощности ДМ, передаваемая механическим путем ТМ;

- нагрузка ЭТМП. В установившемся режиме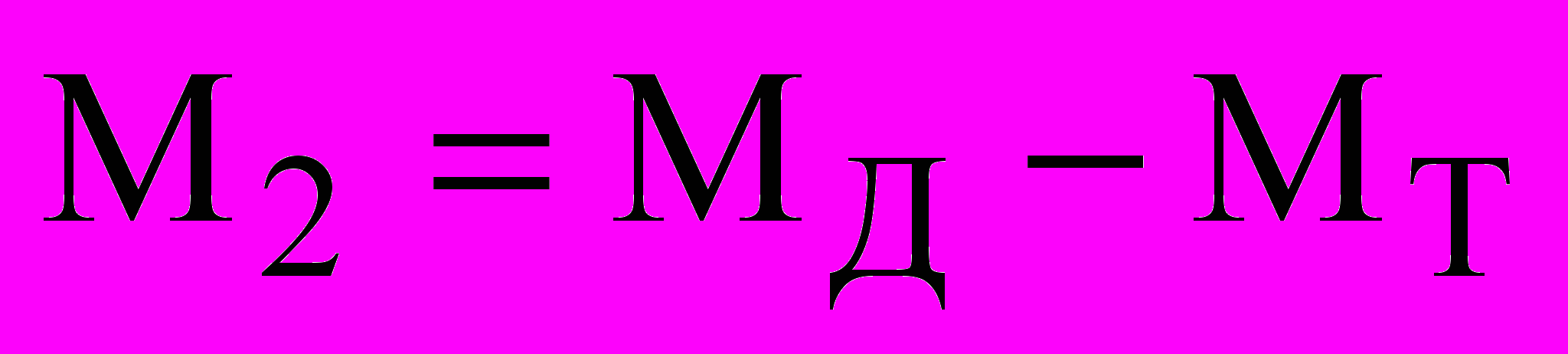

.

Для упрощения картины распределения потоков энергии момент холостого хода ЭТМП учтен в составляющей М_т.

J₃ = Q - тепловой поток ротора ЭТМП;

J₃_д = I^//_2Д - ток главной цепи Г-образной схемы замещения;

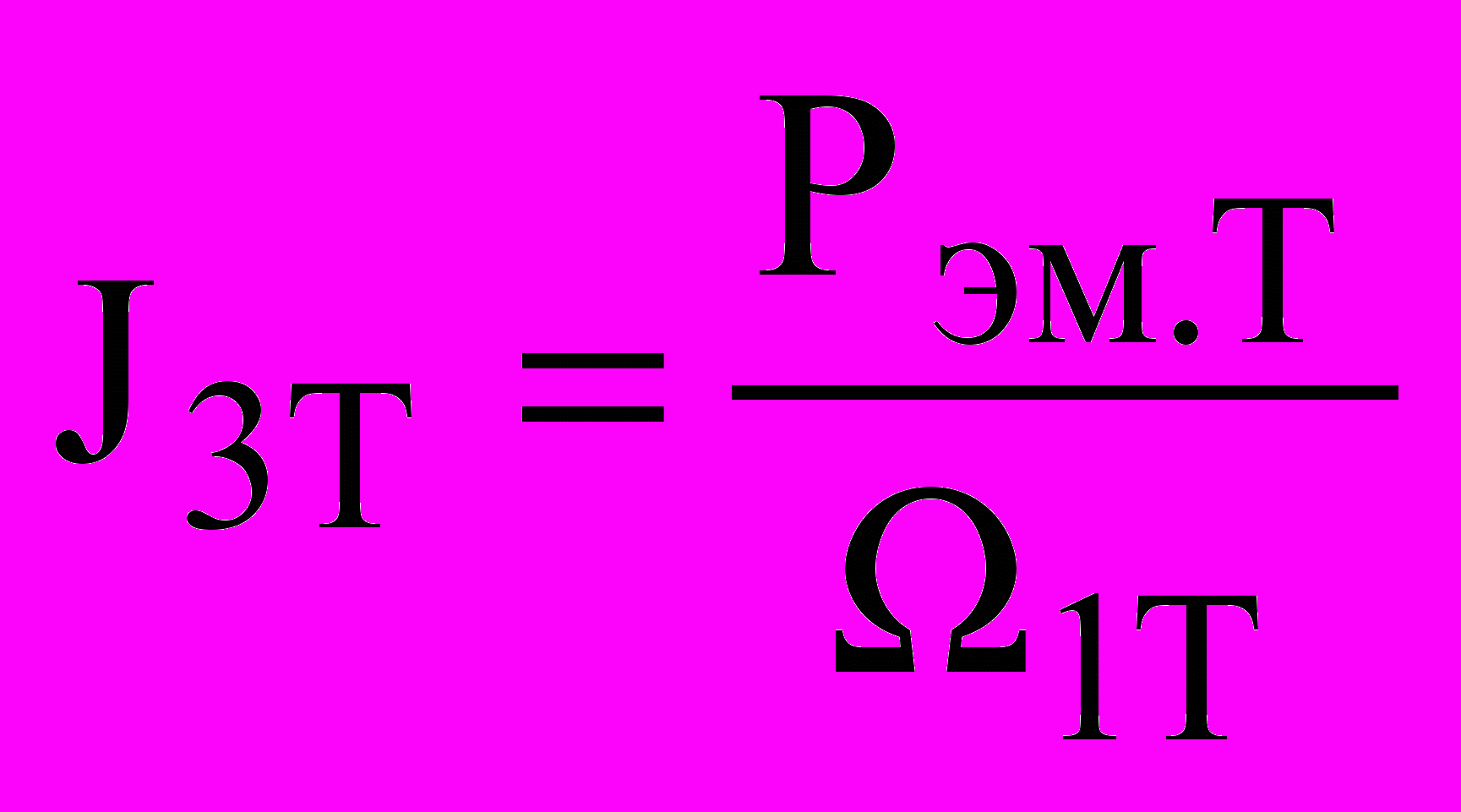- электромагнитная мощность тормозного модуля, отнесенная к синхронной угловой скорости ТМ.

Распределение термодинамических сил можно представить следующим образом:

F₁ = U_1ф - фазное напряжение статорной обмотки;

F₂ = F_s - сила воздействия скольжения на потоки ДМ ЭТМП;

F₃ = F_Δ_Т - сила температурного воздействия на потоки ДМ ЭТМП, зависящая от разности температур массивного ротора и перерабатываемого материала.

Феноменологические уравнения преобразований энергии в ЭТМП.

Математическая модель ДМ ЭТМП в общем виде представлена системой феноменологических уравнений:

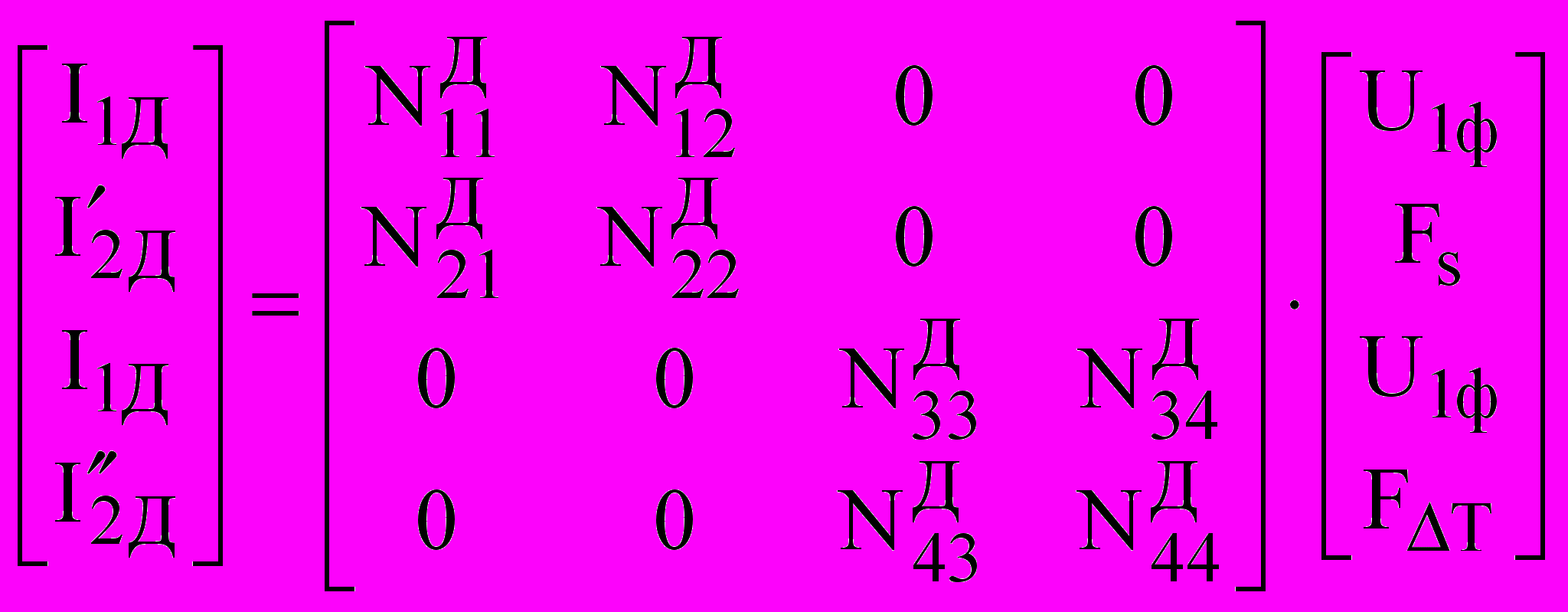, (4)

где N^Д₁₁, N^Д₁₂, N^Д₂₁, N^Д₂₂ - феноменологические коэффициенты процесса преобразования электрической энергии в механическую для ДМ; N^Д₃₃, N^Д₃₄, N^Д₄₃, N^Д₄₄ - феноменологические коэффициенты процесса преобразования электрической энергии в тепловую.

Диссипативная функция указанных преобразований энергии в ДМ имеет вид:

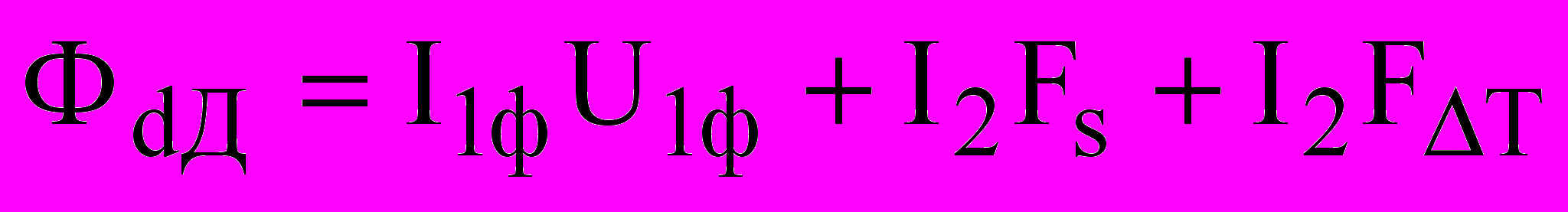. (5)

Введем параметры при s = 1, I^//₂ = 1 , взятые из опыта короткого замыкания при номинальном токе статора  6.

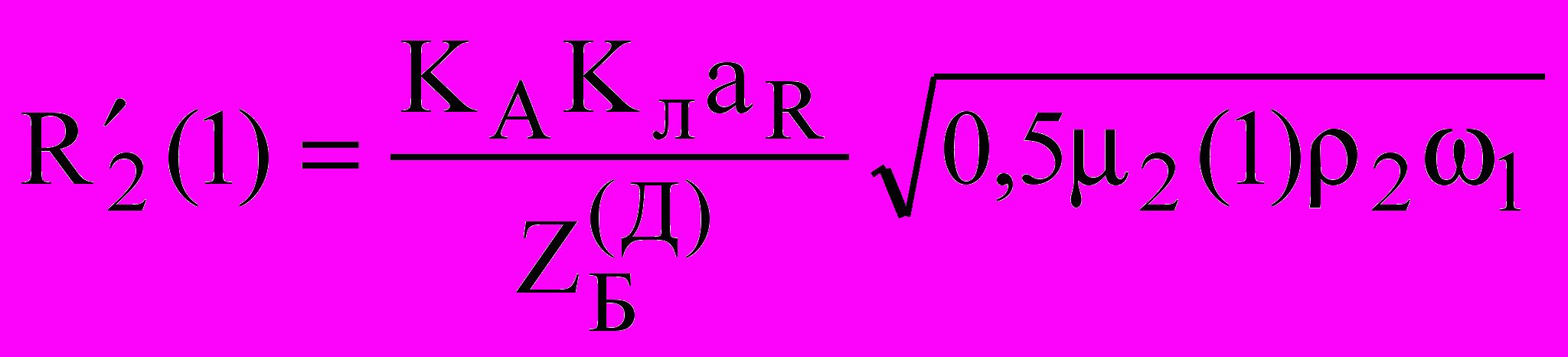, (6)

, (7)

где

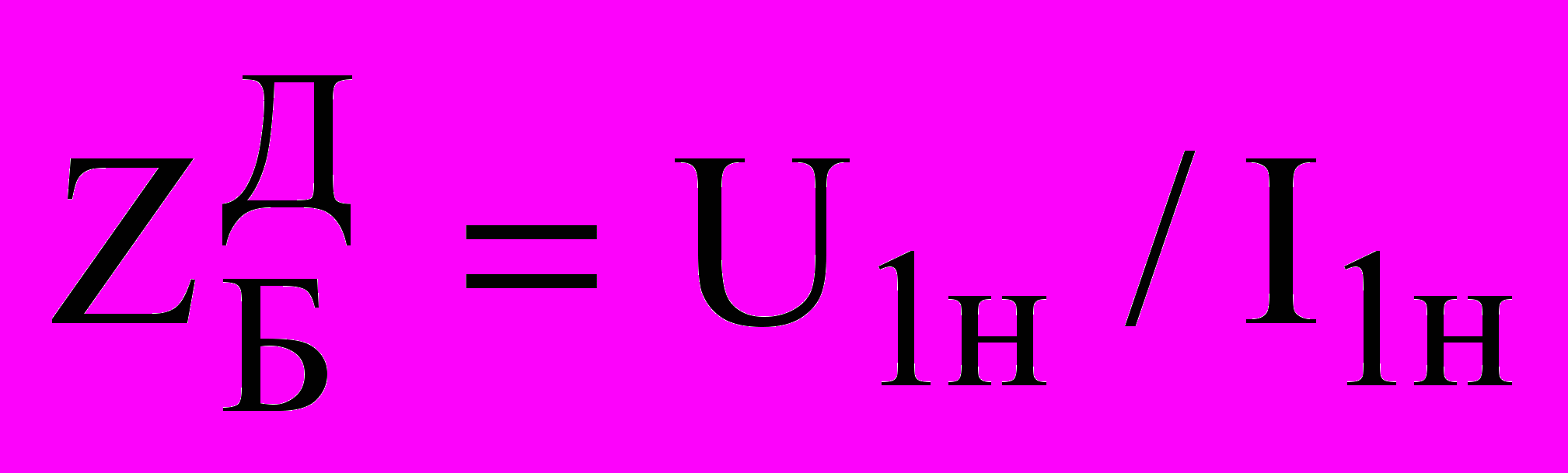– базисный импеданс статора ДМ;

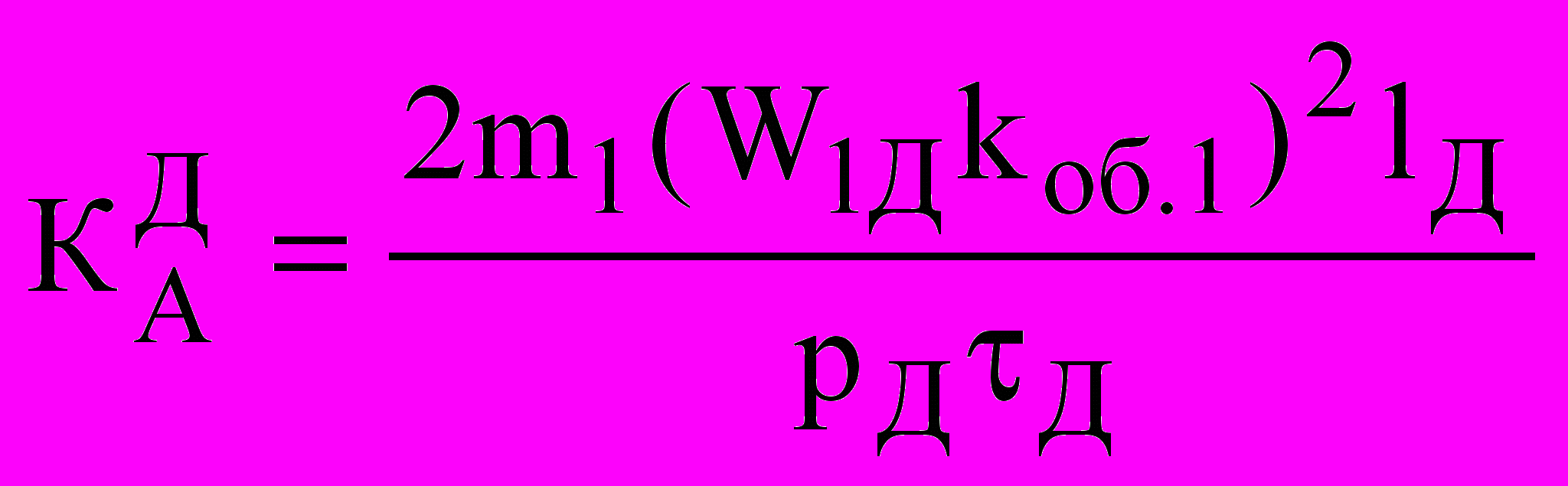- коэффициент приведения удельных параметров к системе полных сопротивлений статора;

- коэффициент конечной длины участка ротора, соответствующего ДМ; a_R = 1,4  6; a_x = 0,6a_R - коэффициенты, учитывающие изменение магнитной проницаемости и гистерезис; ₂(1) - магнитная проницаемость, определяемая по основной кривой намагничивания материала ротора при соотношении поверхностной тангенциальной напряженности магнитного поля на поверхности ротора и амплитуды номинальной линейной нагрузки статора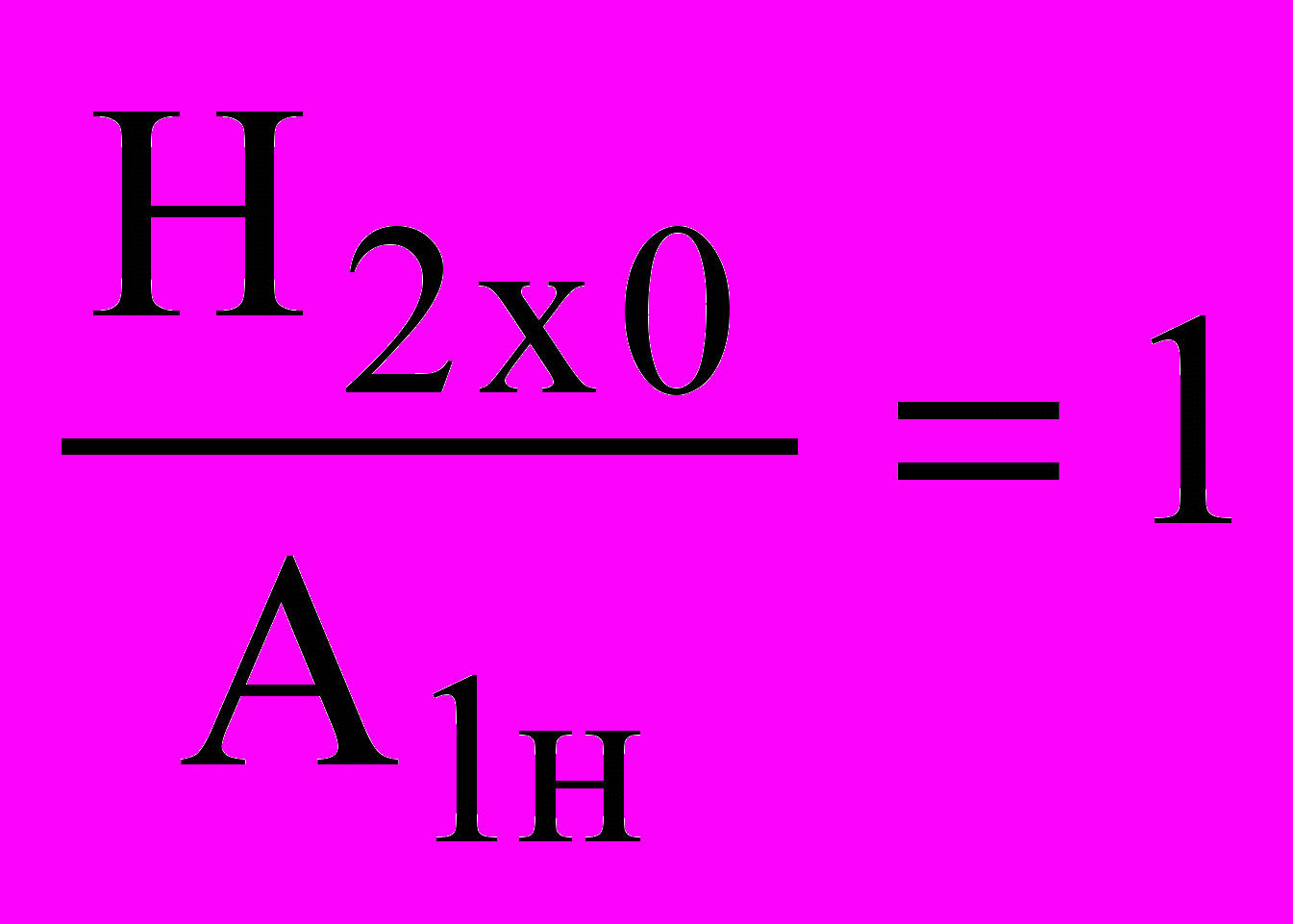

.

Тогда, значения параметров главной цепи, например, Г-образной схемы замещения, зависящие от скольжения находим по формулам:

, (8)

, (9)

где

.

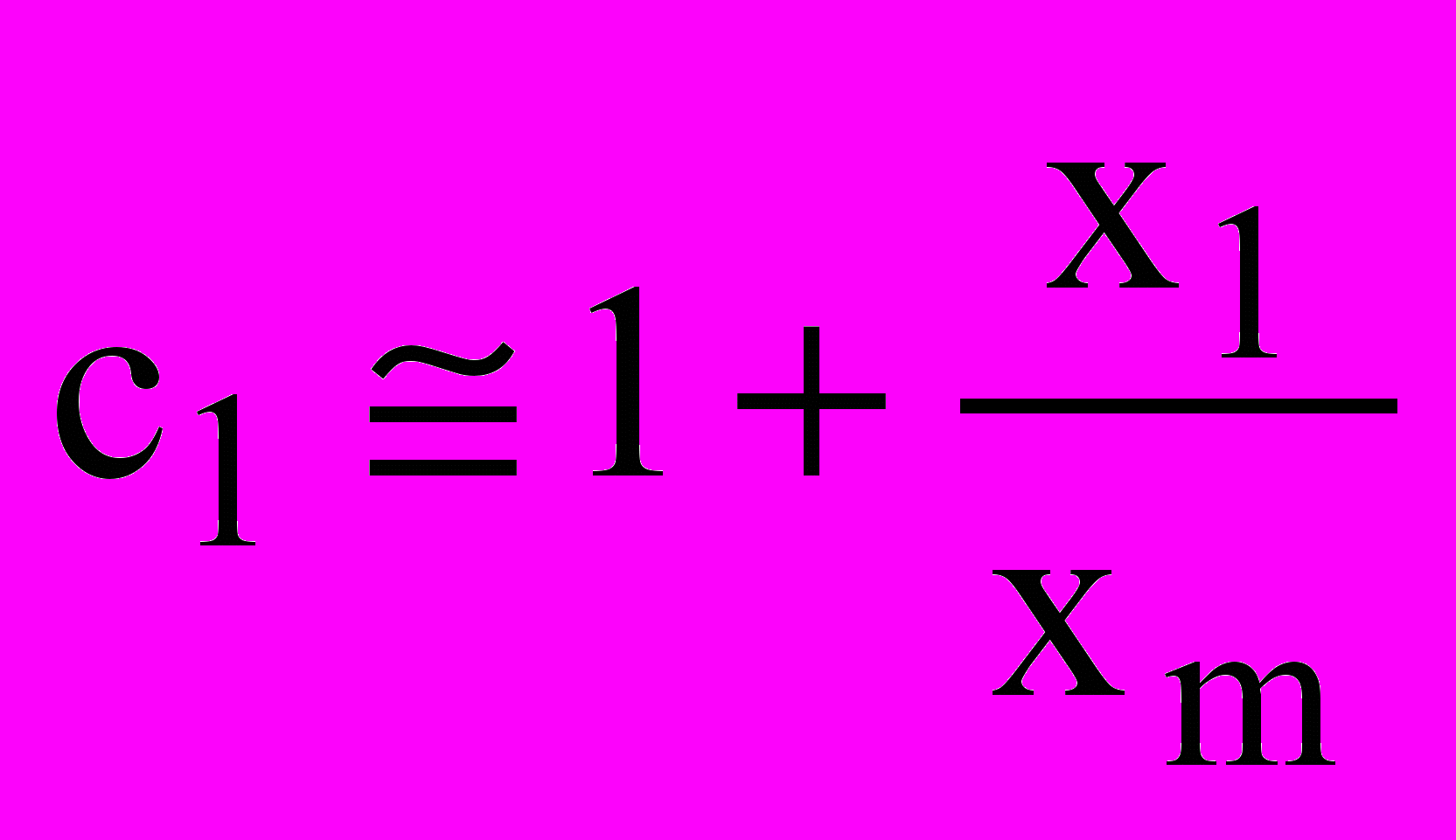Результаты моделирования и экспериментальных испытаний опытных образцов ЭТМП, а также других типов асинхронных машин с массивным ротором указывают на характерную особенность, заключающуюся в том, что в рабочем диапазоне скольжений 0,8 < s_p < 1 значение первичного и вторичного токов меняется незначительно. Это обстоятельство позволяет в выражении (8) принять в первом приближении текущее значение вторичного тока I^//_2Д = К_п_i, где К_п_i – кратность пускового тока ЭТМП.

Далее в феноменологических уравнениях используем именно относительные значения электрических величин.

В области достаточно сильного поверхностного эффекта, т.е. в области больших скольжений, различие между вторичными параметрами, получаемыми из волновой и традиционной схем замещения, несущественно  6.

Используя Т-образную схему замещения ДМ феноменологические уравнения преобразования электрической энергии в механическую можно представить в виде

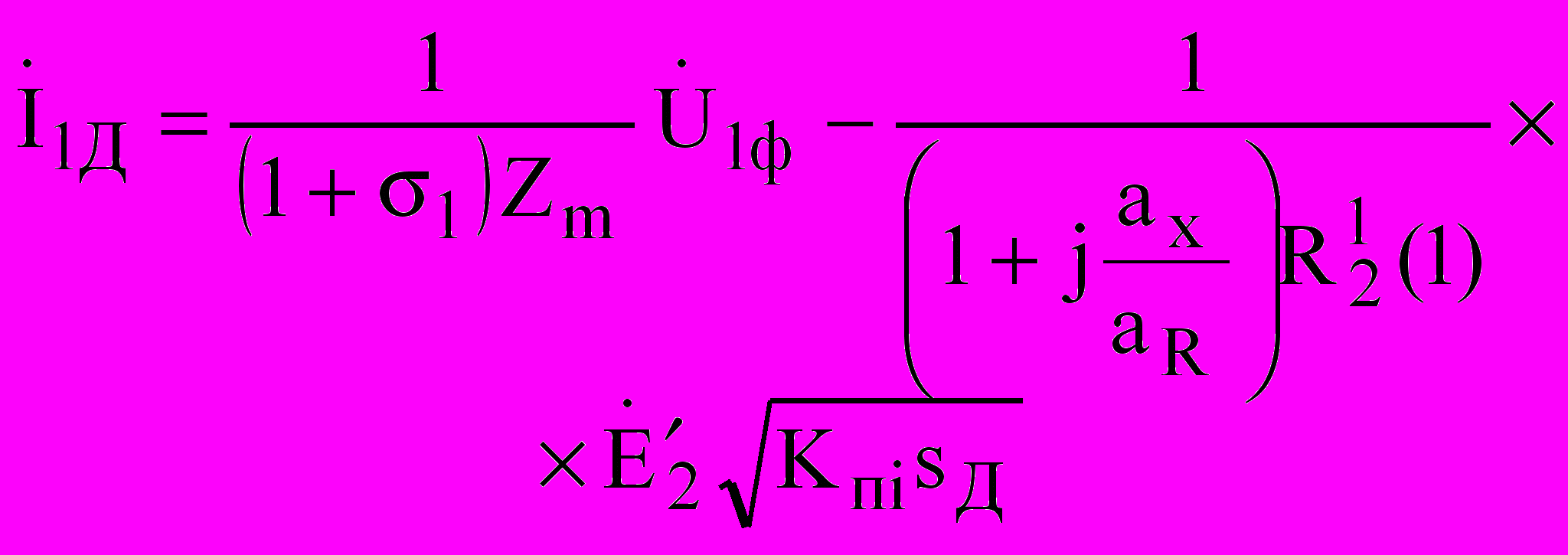, (10)

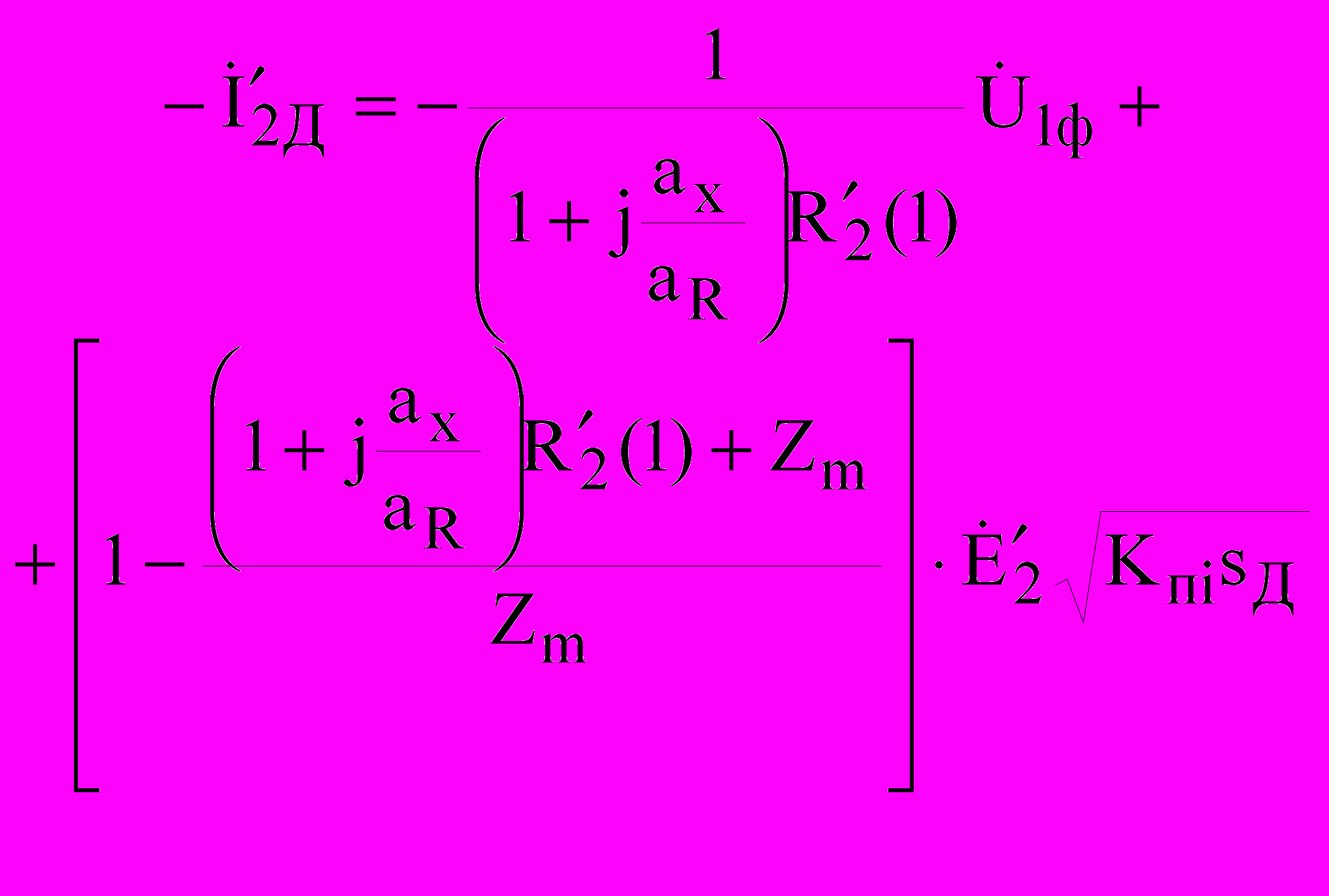, (11)

где

– фазное напряжение в о.е.;

- коэффициент рассеяния обмотки статора ДМ; s - текущее скольжение ДМ.

Представленная система уравнений справедлива для диапазона больших скольжений. В области малых скольжений, когда глубина проникновения поля превышает радиальные размеры ротора,

, где I__p – составляющая тока холостого хода, которая идет на создание МДС ротора. Величина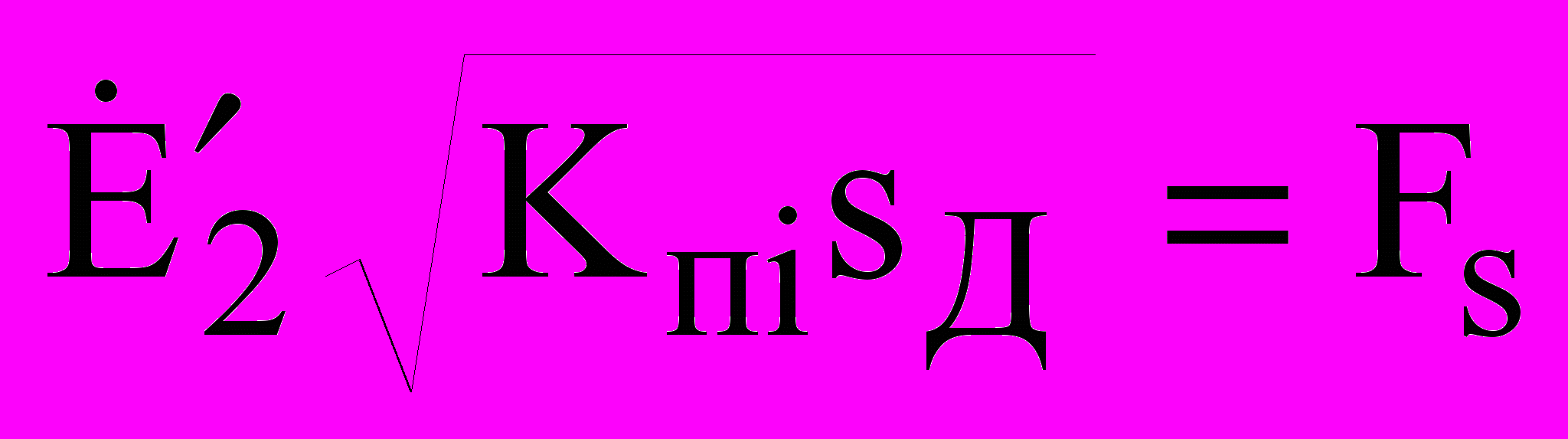

– сила воздействия скольжения s_Д ДМ на потоки I_1Д и

.

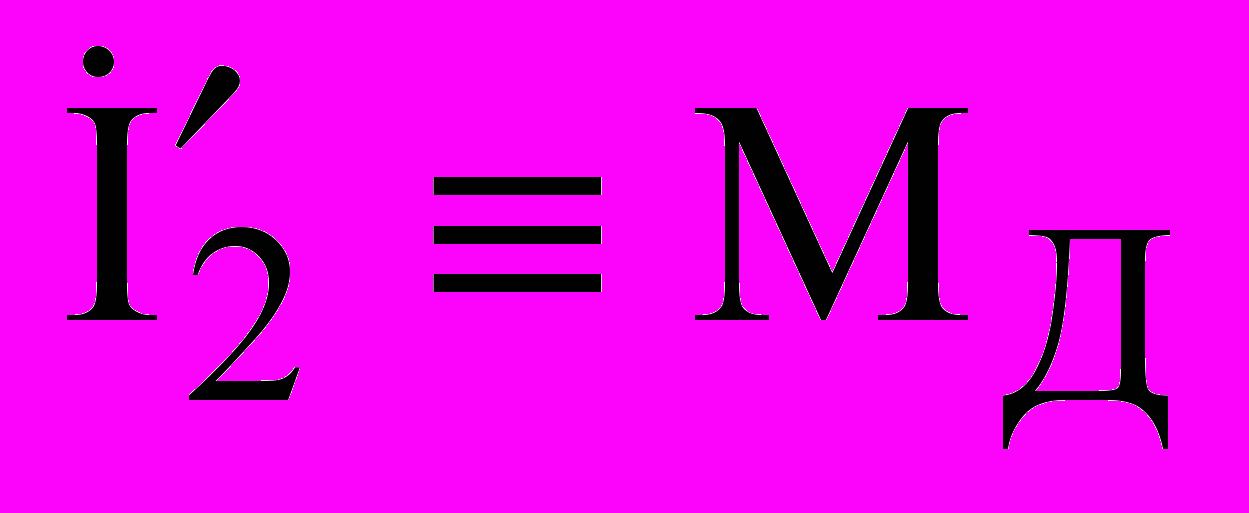Феноменологические уравнения процесса преобразования электрической энергии в тепловую удобно формировать, базируясь на соотношениях величин в Г-образной схеме замещения

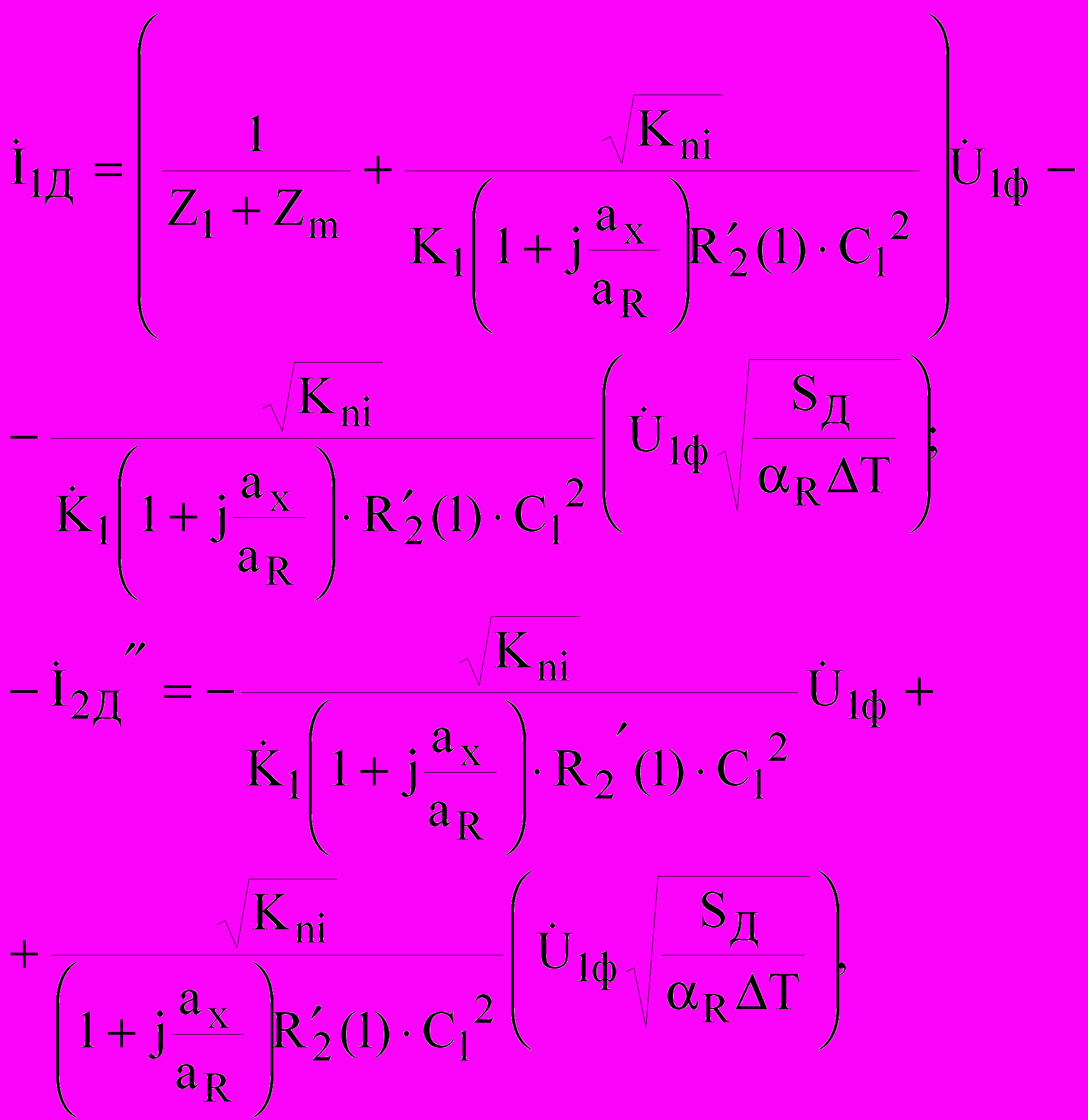(12)

где

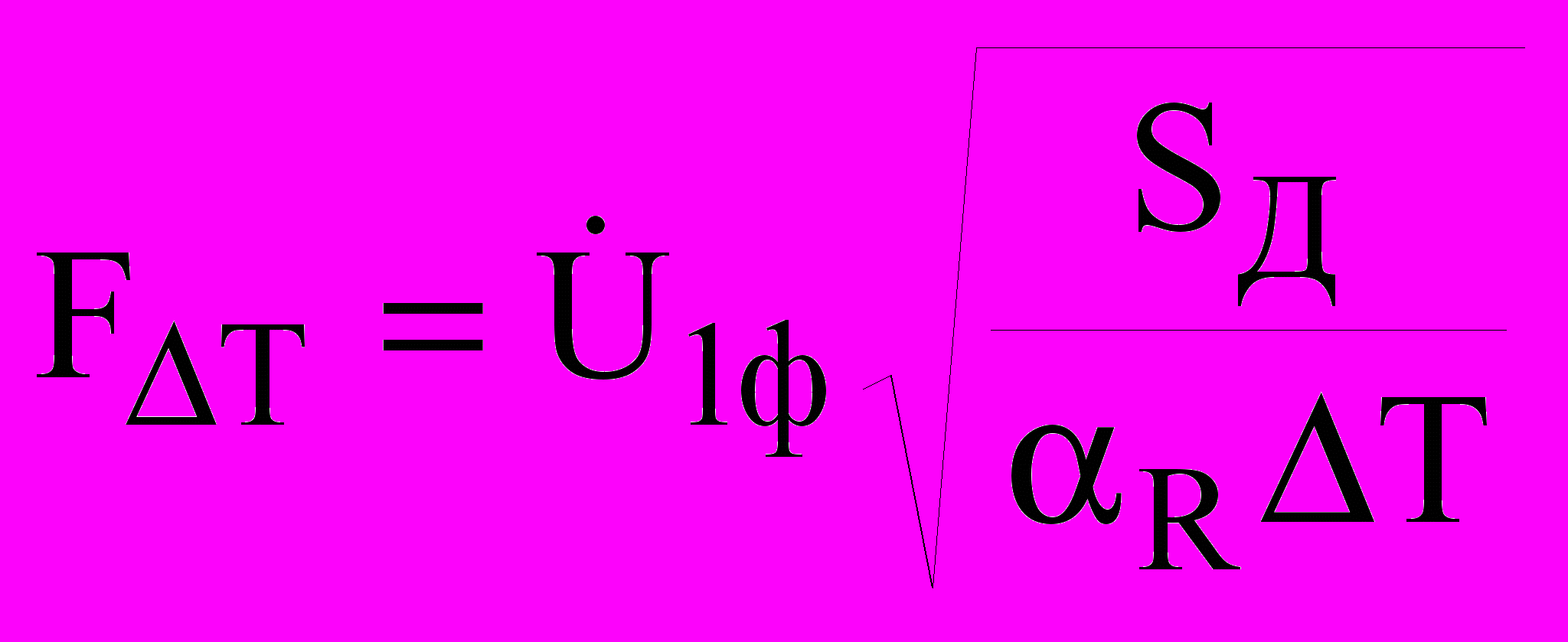– сила температурного воздействия на потоки; _R - положительный температурный коэффициент активного сопротивления массивного ротора. Для ротора из Ст.3 _R= 0,006.

Ввиду малости относительных значений R₁ и X₁статорной обмотки в уравнениях (12), влияние указанных параметров учтено поправочным комплексным коэффициентом

.

Электромагнитные параметры и токи ТМ зависят от значений скольжения s_т, соответствующего режиму электромагнитного торможения:

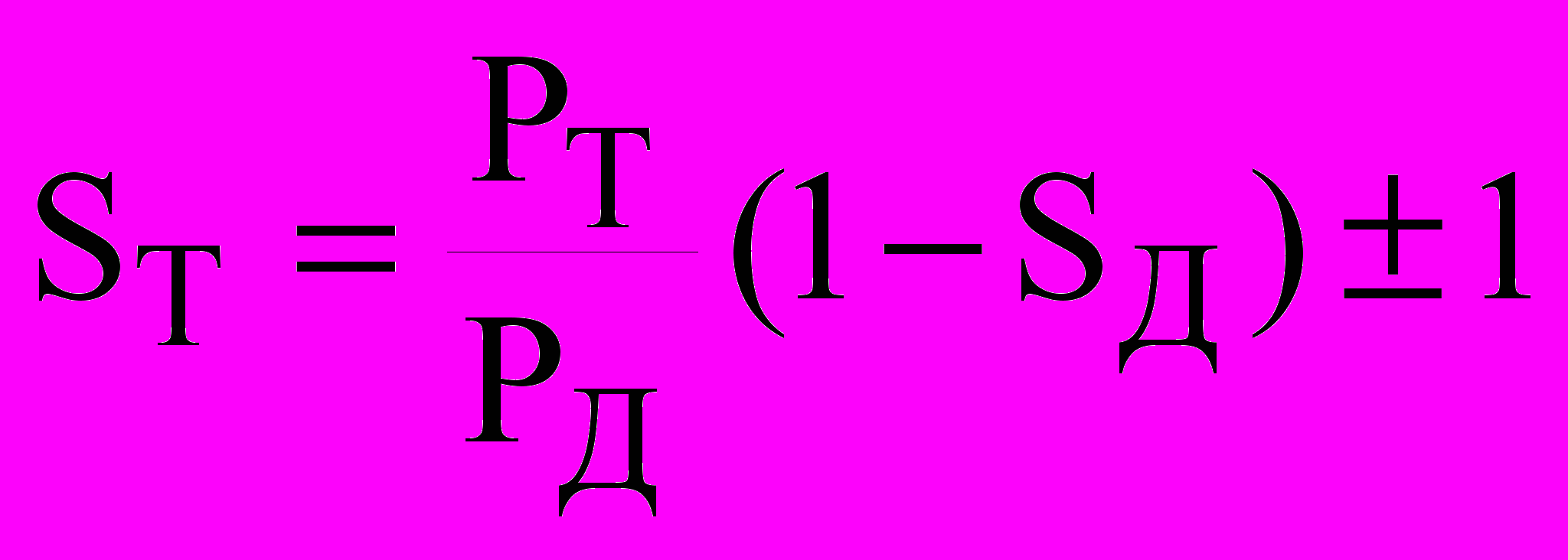, (13)

где р_Д, р_Т – соответственно число пар полюсов ДМ и ТМ. Знак «+» соответствует встречному, а «-» согласному вращению магнитных полей ДМ и ТМ.

Феноменологические уравнения преобразований электрической и механической энергии в тепловую, происходящие в ТМ, представляются следующей системой уравнений.

Преобразование «электрическая – тепловая энергия»:

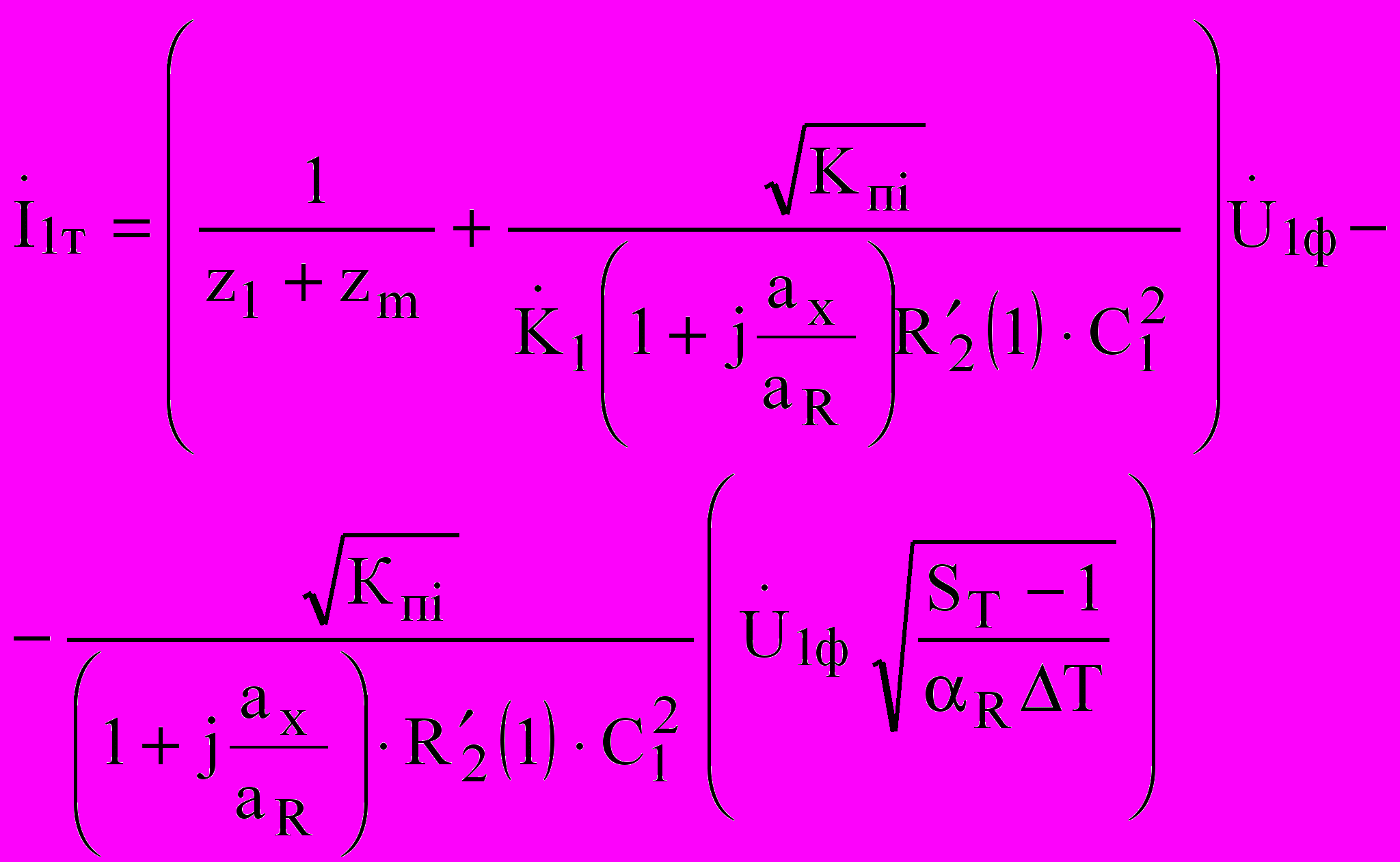,(14)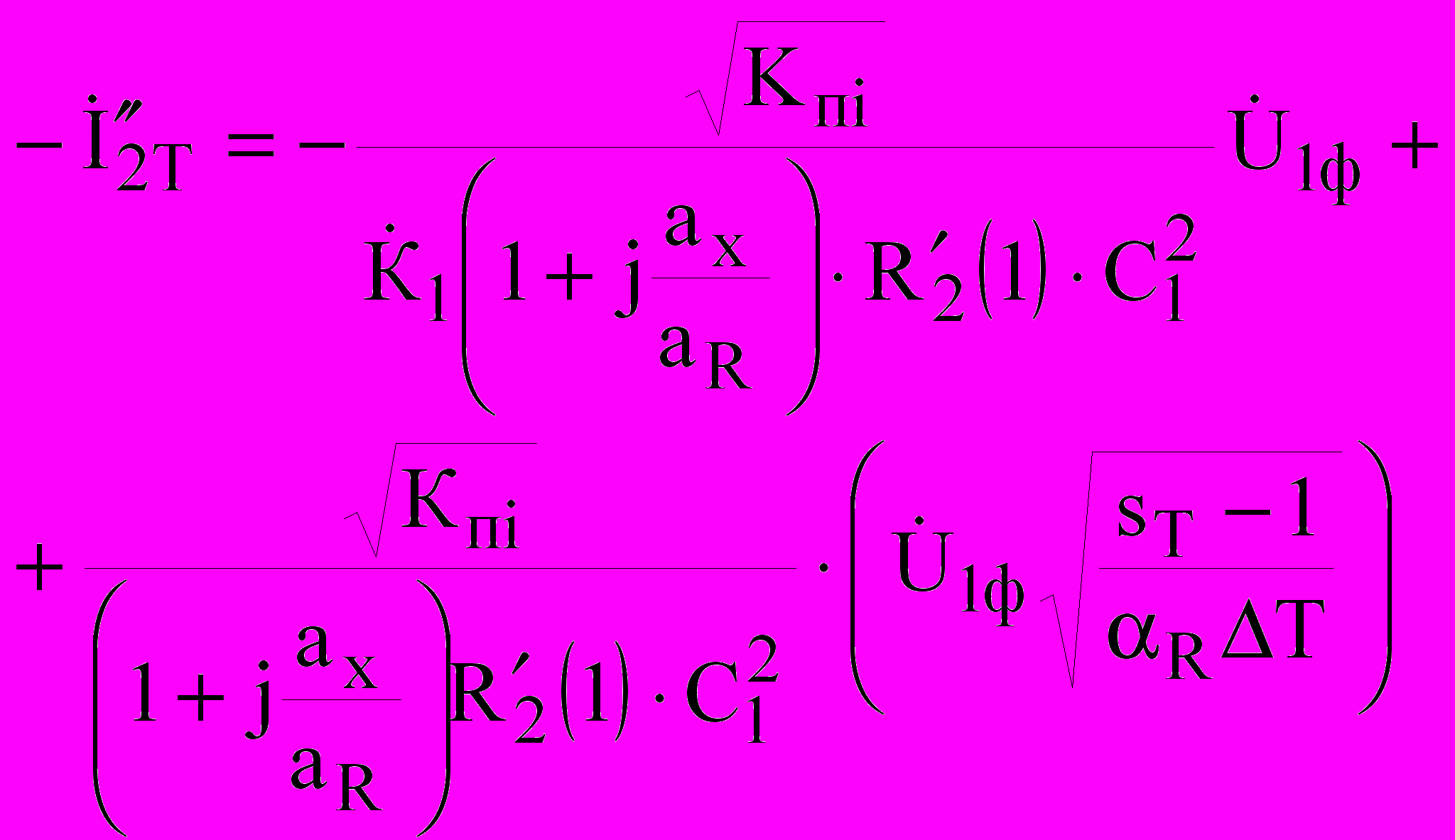

. (15)

Преобразование «механическая – тепловая энергия»:

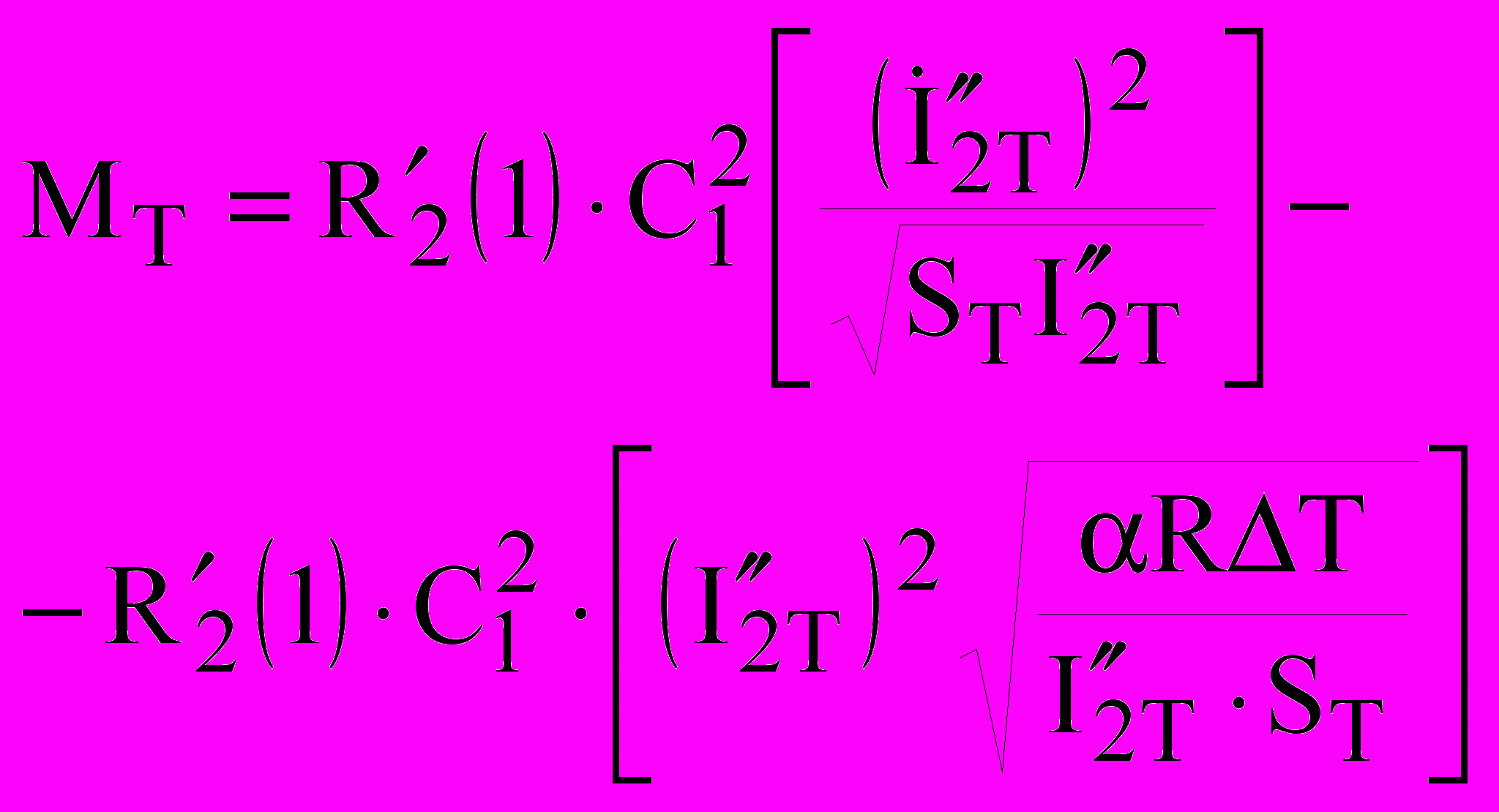, (16)

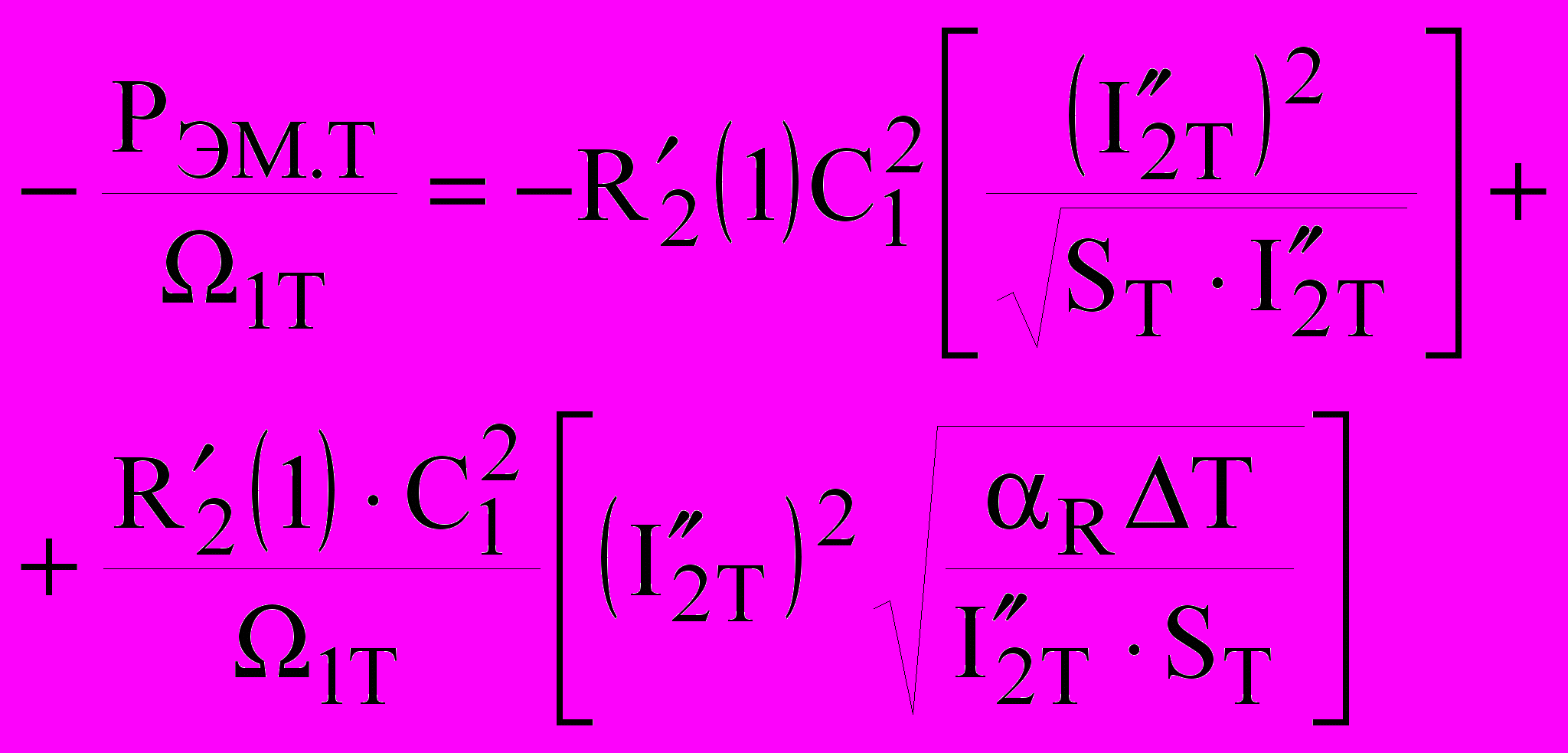. (17)

где М_т – механический момент вращения ротора ТМ. В режиме, близком к равновесному термодинамическому состоянию М_т уравновешивается тормозным электромагнитным моментом;

– эквивалентное значение силы механического воздействия ДМ на ТМ;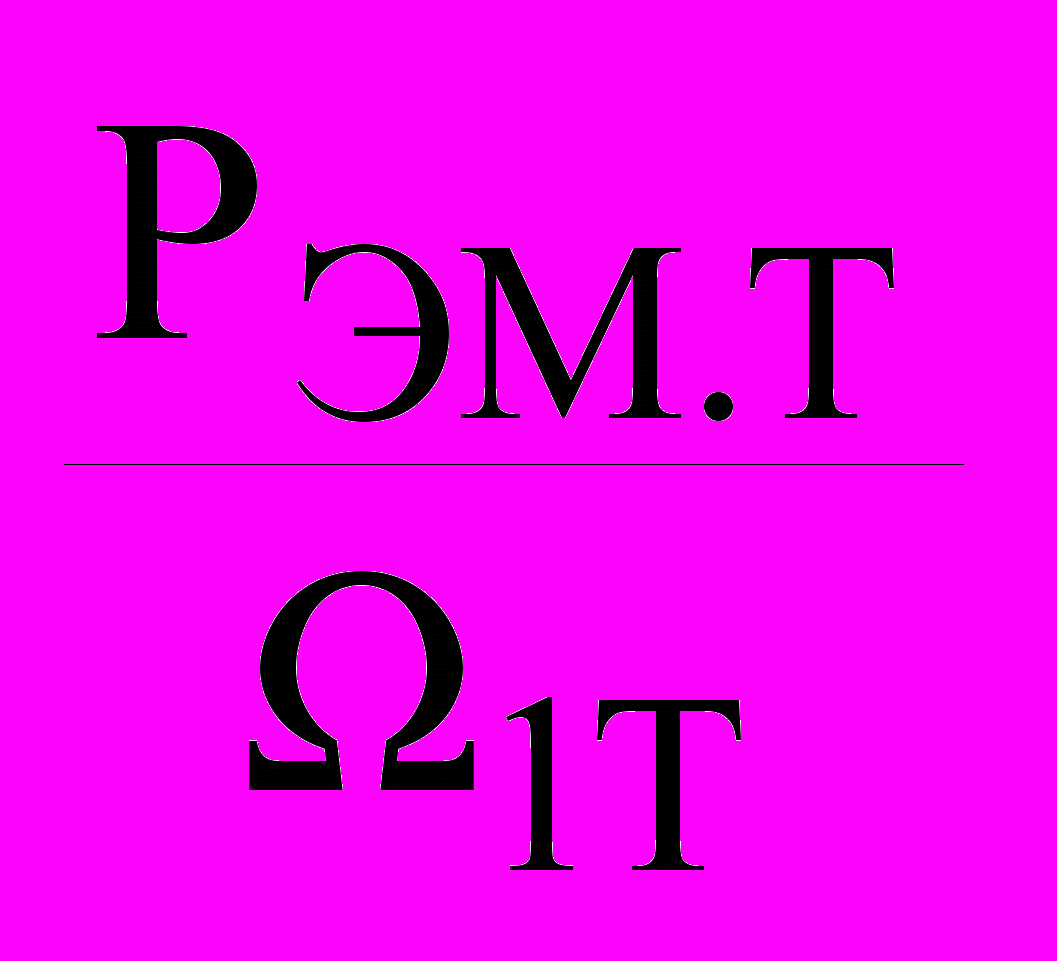

- электромагнитная мощность, отнесенная к угловой синхронной скорости ТМ;

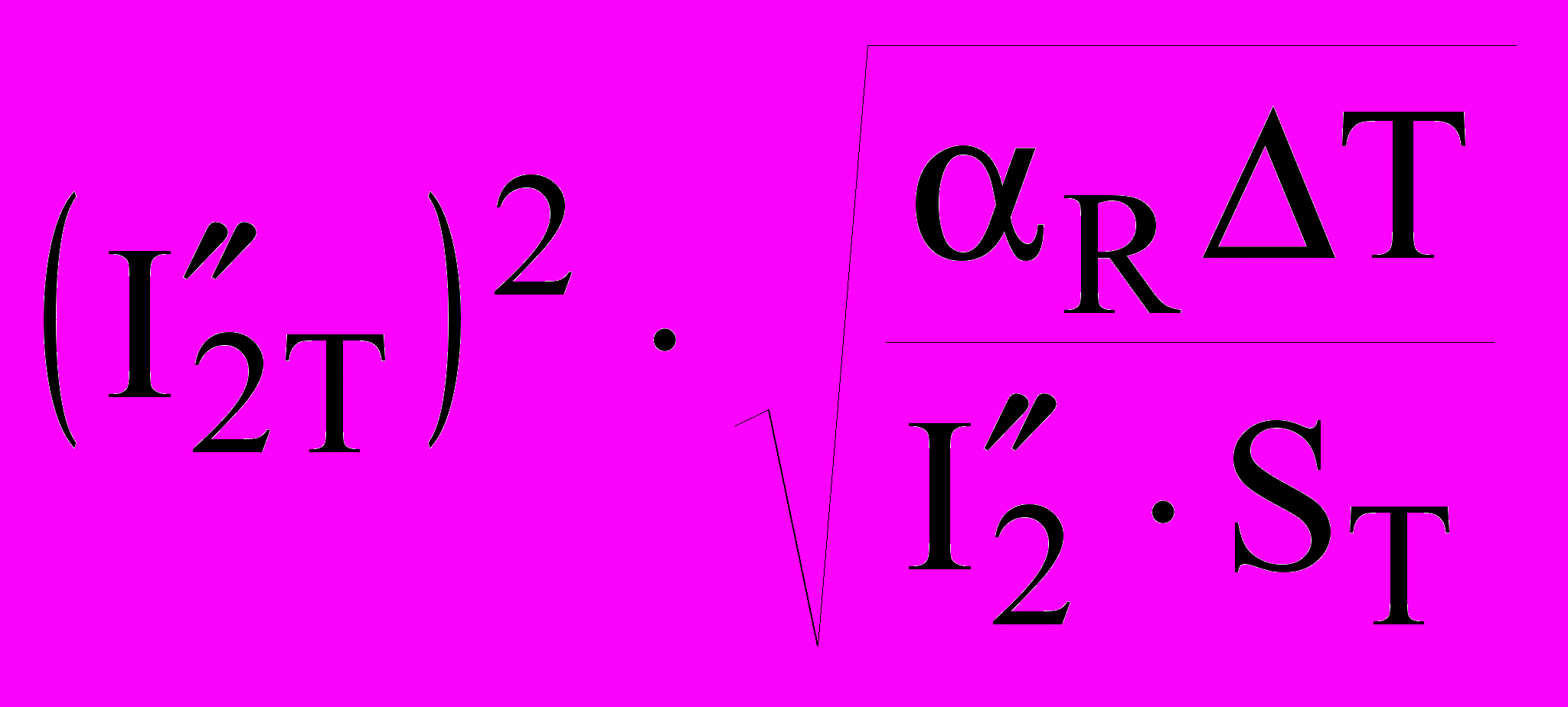- сила температурного воздействия на потоки М_т и Р_ЭМ.Т/_1Т .

Закон регулирования тепловой и механической мощности ЭТМП, который определяется технологическим режимом переработки материалов и смесей, может формироваться на основе анализа феноменологических уравнений и нормированных величин , Z, .

В дальнейшем будем отмечать индексами «i» и «о» величины соответственно на входе и выходе ЭТМП.

Начнем с анализа феноменологических коэффициентов. Чем более отрицательно значение N_io = N_oi по сравнению со значениями других коэффициентов, тем выше степень влияния силы на входе F_i, вызывающей поток на выходе. Вместе с тем, при более отрицательных значениях N_io увеличивается степень ингибирования (приглушения) входного потока силой на выходе F_о.

Это говорит о том, что коэффициент N_io в любом из уравнений связан со степенью сопряжения друг с другом входного и выходного процессов. Но увеличение – N_io не всегда соответствует сильному сопряжению. При одновременном росте в одинаковой степени всех коэффициентов (N_ii, N_oo и -N_i_о) входной и выходной потоки возрастают в той же самой степени. При этом уже нельзя говорить об изменении сопряжения между двумя потоками. Как указывалось ранее, для исключения подобного явления, так называемая степень термодинамического сопряжения  определяется как коэффициент N_io, нормированный на коэффициенты N_ii и N_oo:

.

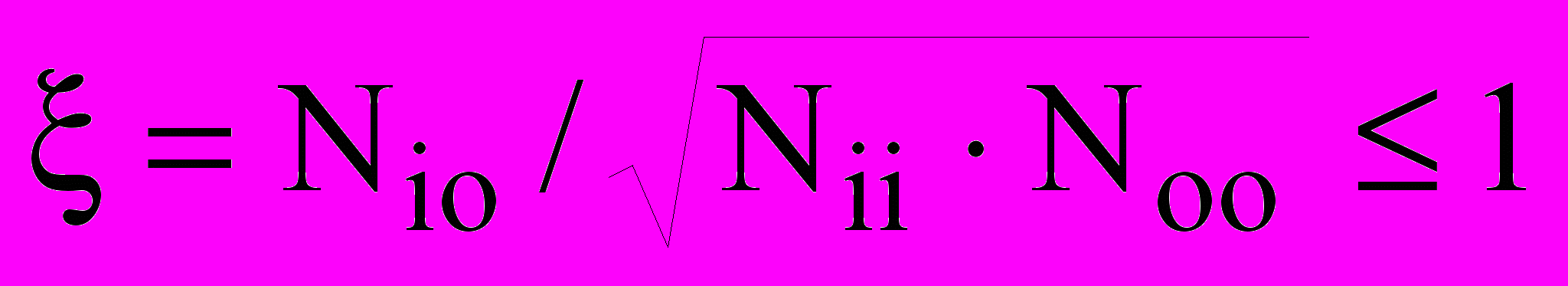Термин «термодинамическое сопряжение» означает, что существует физический процесс, сопрягающий два процесса, которые в противном случае не могли бы быть сопряжены друг с другом. В нашем случае таким процессом является однонаправленный электромагнитный процесс.

Очевидно, что каждый поток вызывается своей сопряженной силой. Но возможность термодинамического сопряжения означает, что на данный поток может также влиять любая из имеющихся в системе сил. Феноменологическая стехиометрия

изменяется вместе со способом и степенью сопряжения.

Для каждой из систем уравнений (10) – (12), (14) – (15), (16) - (17), необходимо провести нормирование потоков на входной поток при нулевой выходной силе. При введенных обозначениях сил, потоков и феноменологических коэффициентов, каждую из указанных систем можно представить в виде:

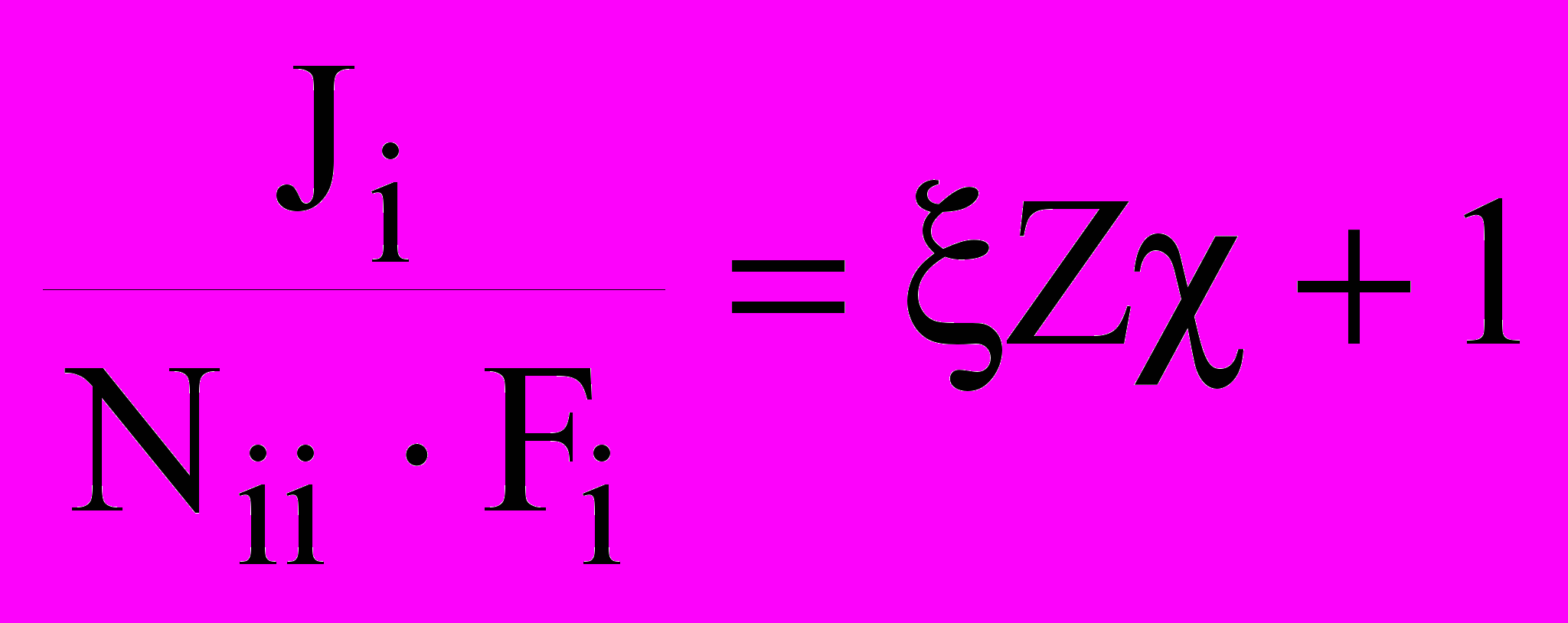, (18)

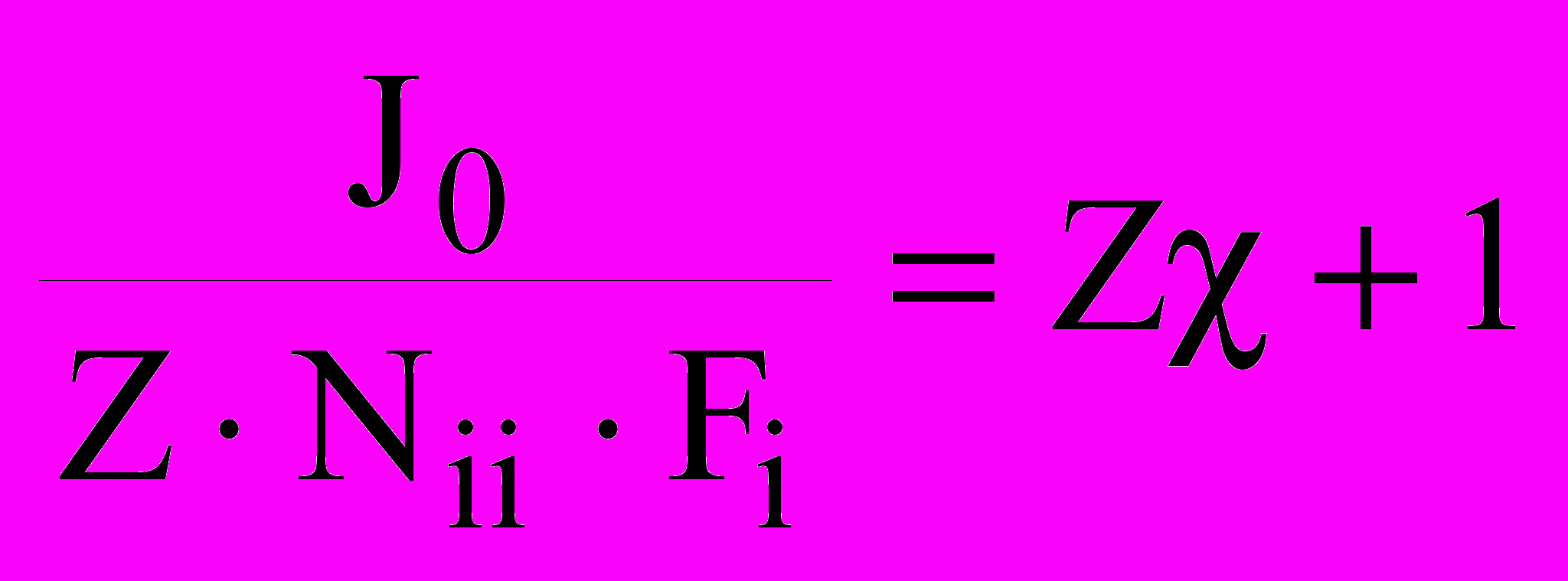. (19)

Далее определяем нормированное отношение выходного потока к входному 5:

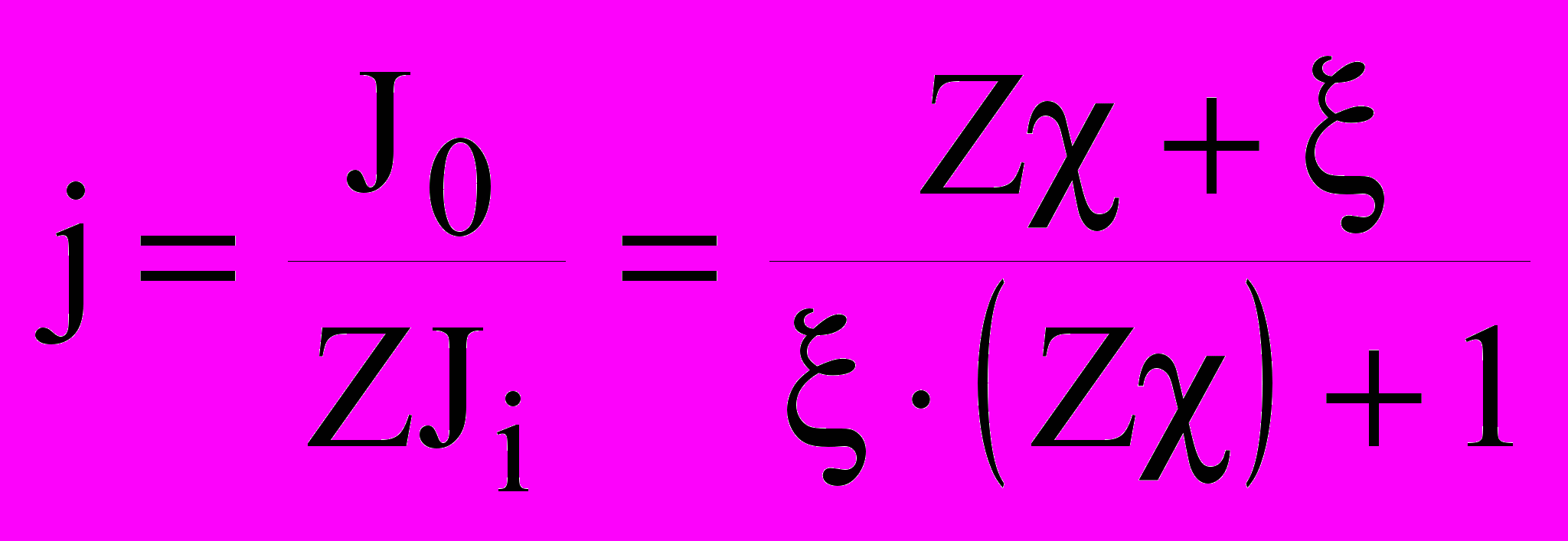. (20)

Как видно из выражения (20), при =1 выходной поток отличается от входного всегда в постоянное число раз, равное Z, т.е. оба потока жестко сопряжены. При =0 выходной поток вызывается своей собственной силой F_о, течет самопроизвольно и направлен в сторону уменьшения F_о. Это тот случай, когда выходной поток вообще не сопряжен с входным потоком. Например, выравнивание температур ротора и материала, либо снижение скорости и остановка ротора при отключении ЭТМП от сети.

Таблица 1 -

Соотношение потоков и сил для систем феноменологических уравнений ДМ и ТМ

№ п/п	Вид преобразования	Модуль ЕТМП	Соотношение потоков	Соотношение сил
1.	Эл.энергия мех.энергия	ДМ
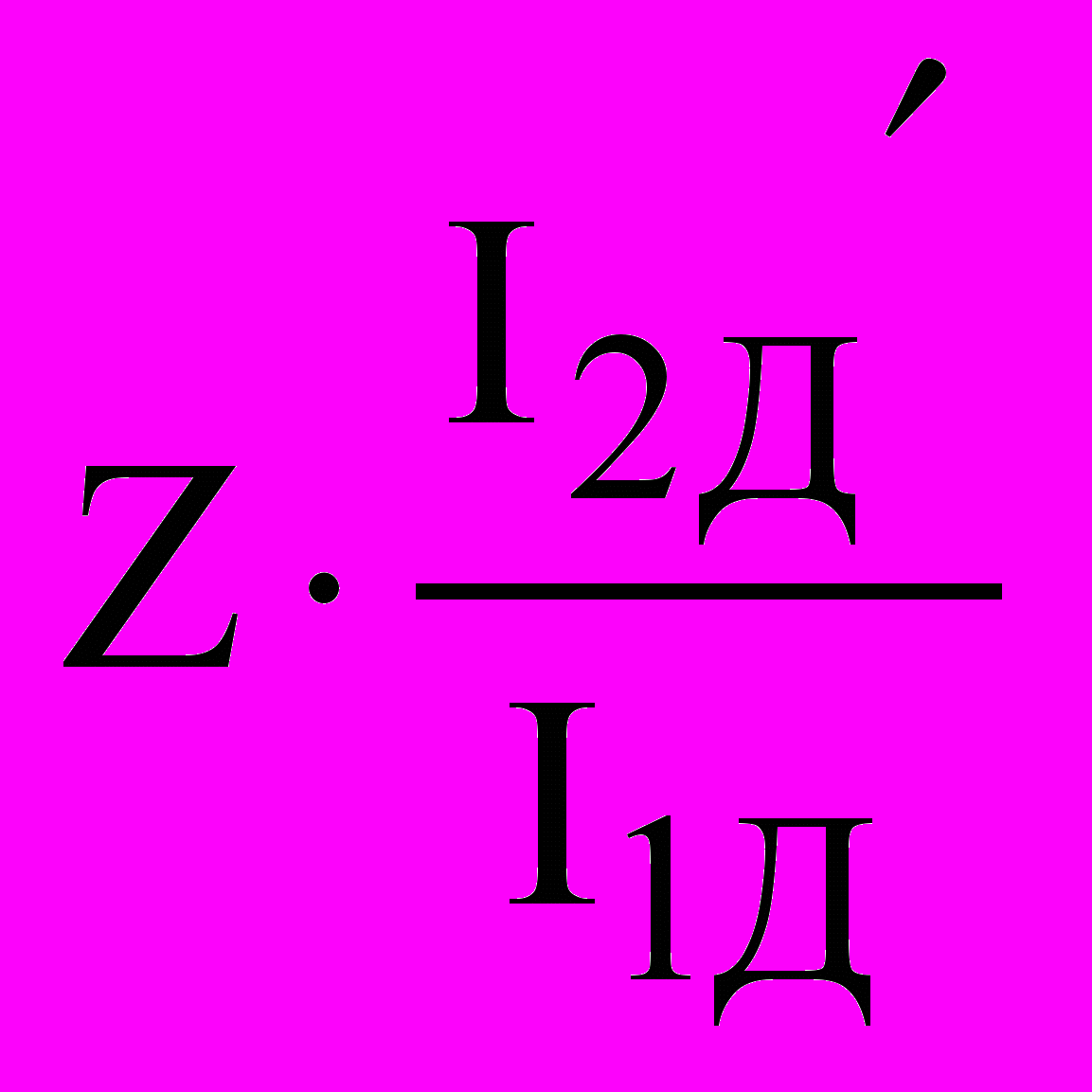
2.	Эл.энергия тепловая энергия	ДМ
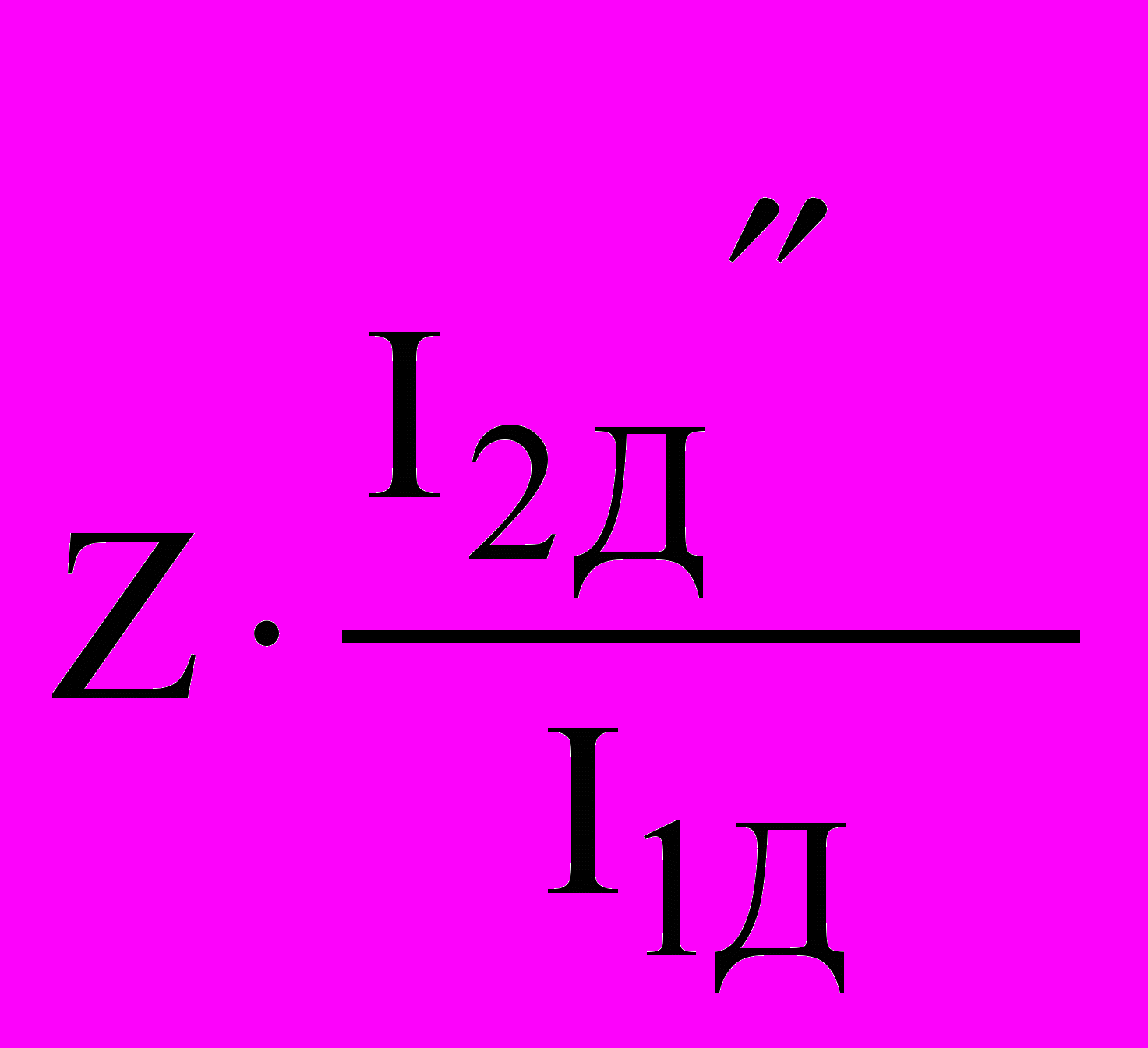
3.	Эл.энергия тепловая энергия	ТМ
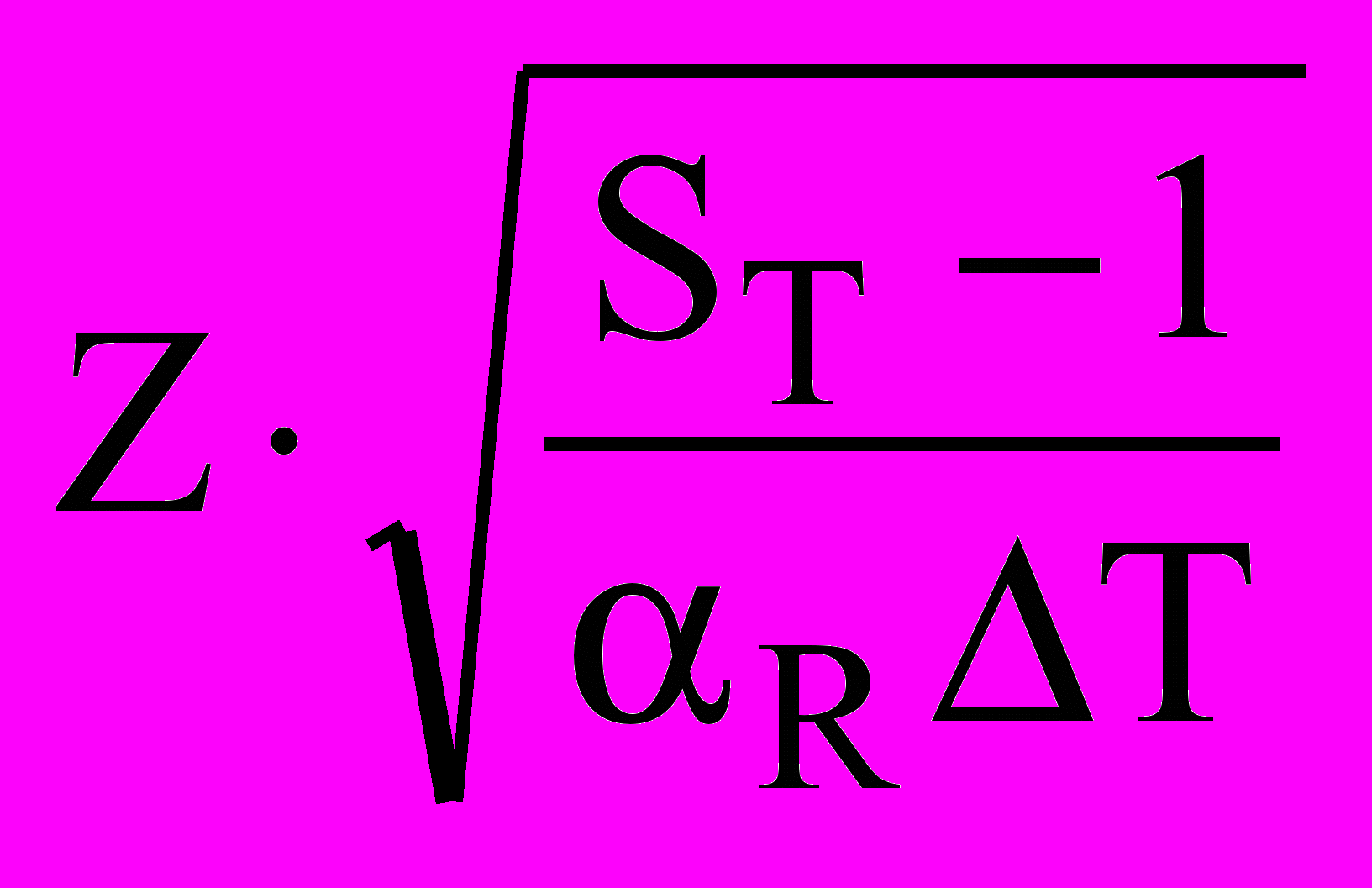
4.	Эл.энергия тепловая энергия	ТМ

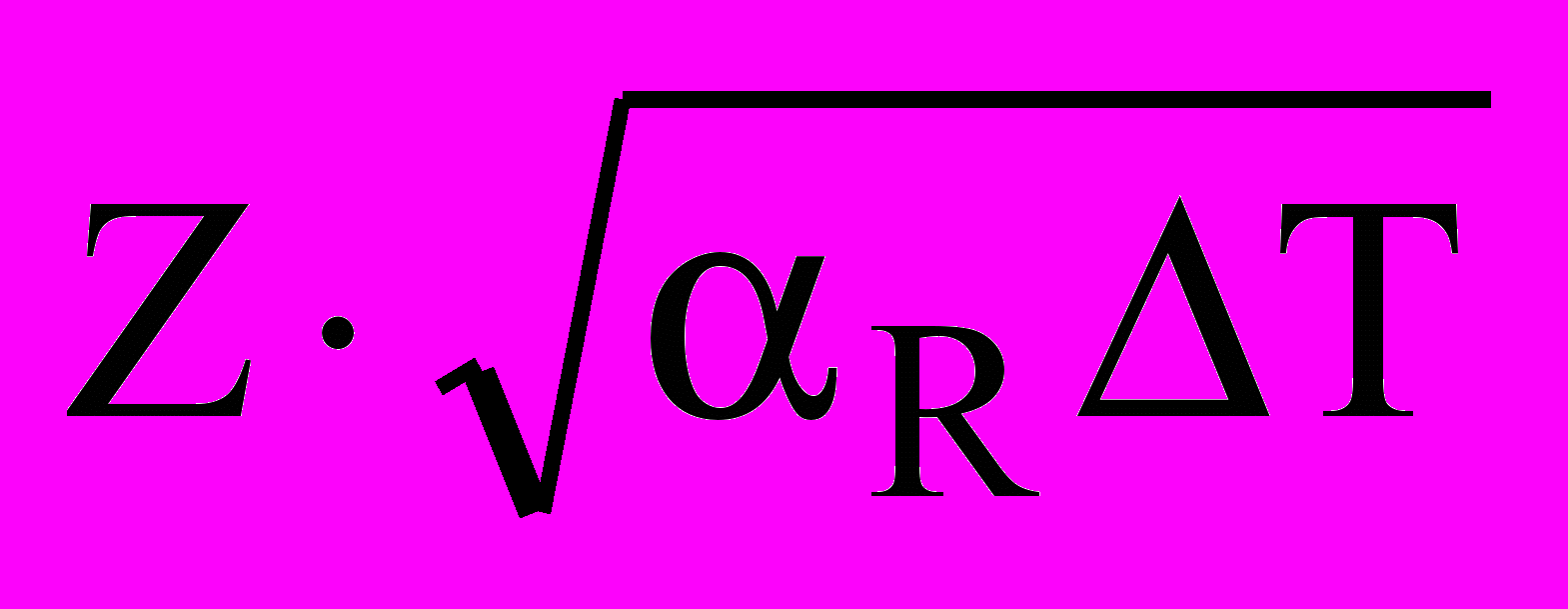
При значениях , заключенных между –1 и 0, выходной поток поддерживается входным потоком, но отношение двух потоков изменяется вместе с изменением отношения сил (

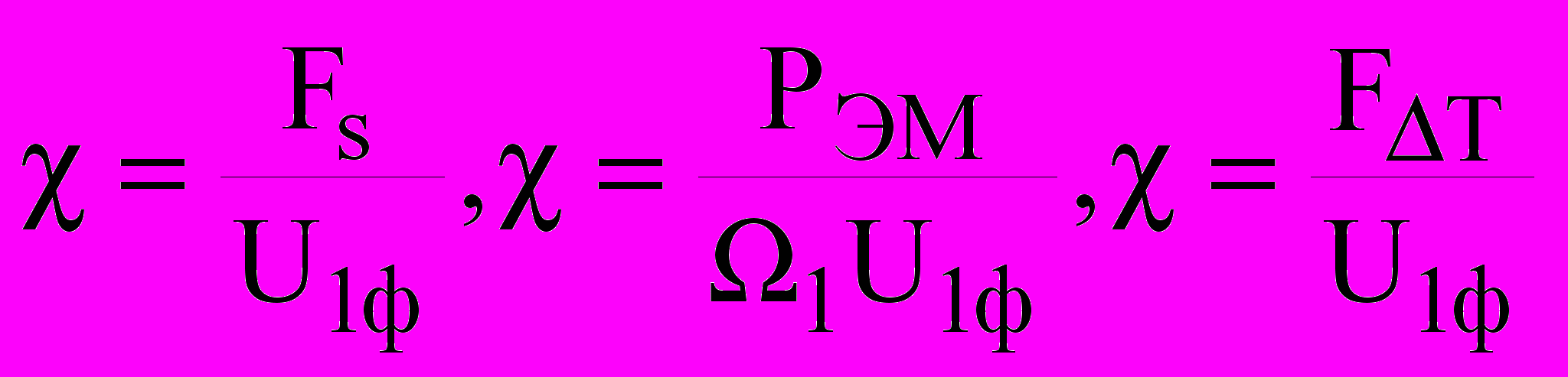). При этом входной и выходной процессы только частично сопряжены.

При высоких значениях отношения сил, и даже при значениях , близких к –1, отношение потоков может быть достаточно низким. В табл. 1 представлены нормированные соотношения потоков и сил для систем феноменологических уравнений ДМ и ТМ.

В преобразовании «1» при понижении фазного напряжения U_1ф и увеличении скольжения s_д соотношении сил возрастает. При этом растет и соотношение потоков. В режиме, когда s_д=1, значительное понижение первичного напряжения ДМ приводит к низкому значению напряженности магнитного поля и величины магнитного потока и, следовательно, к снижению магнитной проницаемости ферромагнитных участков ДМ. Как следствие, возрастает намагничивающая составляющая первичного тока I₁_ и наблюдается снижение соотношения потоков выходного и входного процессов. В преобразованиях «2» и «3» при устремлении разности температур T между ротором ЕТМП и материалом (охлаждающая среда) к нулю, что соответствует либо «холодному» состоянию системы «ЭТМП – материал», либо выравниванию температур в «горячем» состоянии, соотношение сил растет, а соотношение потоков снижается. Увеличение T сопровождается увеличением соотношения потоков, поскольку наряду с одновременным снижением первичных и вторичных токов происходит ухудшение теплообмена между статором и ротором модулей. Последнее обстоятельство и вызывает опережающее снижение первичного тока.

Преобразование «4» характеризуется тем, что рост разности температуры T ведет к увеличению соотношения сил, которое в реальных конструкциях ЭТМП может достигать значений, близких к 1 уже при T=160⁰С. Как ведет себя в этом случае соотношение потоков? Если входной поток механической энергии М поступает на «вал» (ротор) ТМ со стороны ДМ и, в общем случае, не зависит от разности температур T, то выходной поток Р_ЭМ.Т/_1Т при увеличении T снижается. В целом при Мconst наблюдается уменьшение соотношения потоков при значениях Z ≈ 1.

Выводы.

Разработана энергетическая и физическая модель ЭТМП, отражающая три вида одновременно происходящих процесса преобразования энергии.
Впервые получены системы феноменологических уравнений преобразования свободной энергии в ЭТМП, которые являются базовыми для оптимизационных расчетов, формирования систем управления, а также для создания энергосберегающих технологий переработки сыпучих и легкоплавких веществ.

ЛИТЕРАТУРА

Патент України № 39226, 7НО5В 6/10. Заглибний електронагрівач // Заблодський М.М. та інш. – Бюл. № 5, част. 1. – 2001.
Патент України № 50242, 7F26B17/18. Шнековий сушильний апарат // Заблодський М.М., Плюгін В.Є. та інш. – Бюл. № 1. – 2005.
Патент України № 49409, 7Е21В37/00. Пристрій для видалення парафіну зі стінок нафтогазових свердловин // Заблодський М.М., Плюгін В.Є. та інш. – Бюл. № 10. – 2004.
Щур І.З. Моделювання електроприводів постійного струму методами лінійної термодинаміки нерівноважних процесів // Віст. НТУ “ХПІ”. Темат. зб. наук. праць “Проблеми автоматизованого електроприводу. Теорія і практика”. – Харків: НТУ “ХПІ”, 2002, № 12. – Т2. С 413 – 416.
Вестерхоф Х., ван Дам К. Термодинамика и регуляция превращений свободной энергии в биосистемах: Пер. с англ. М: Мир, 1992. – 686 с.
Теория и методы расчета асинхронных турбогенераторов. Под. ред. И.М. Постникова. К.: Наукова думка, 1977. – 176с.

Стаття надійшла 26.04.2006 р.

Рекомендовано до друку

д.т.н., проф. Родькіним Д.Й.

Вісник КДПУ. Випуск 3/2006 (38). Частина 2