Нформаційні системи І моделювання

Вид материала

Документы

Содержание Цель работы. Материалы и результаты исследований. Таблица 1 - Параметры линеаризованной модели магнитного подвеса

Подобный материал:

• Нформаційні системи І моделювання, 61.42kb.
• Нформаційні системи І моделювання, 135.57kb.
• Нформаційні системи І моделювання, 107.78kb.
• Нформаційні системи І моделювання, 93.99kb.
• Нформаційні системи І моделювання, 60.18kb.
• Іhформаційhі процеси в суспільстві. Іhформаційhі системи. Штучний інтелект. Експертні, 155.22kb.
• Конспект лекцій з дисципліни "Інформаційні системи та технології у фінансових установах", 1112.81kb.
• На державний iспит з циклу професійної підготовки та спеціальних курсів, 134.32kb.
• Иємства та сформувати комплекс захисних реакцій, спрямований на забезпечення стійкого, 175.84kb.
• 1 опис засобів моделювання складних динамічних систем, 175.64kb.

УДК 62-83-52

РАСЧЕТ КОЭФФИЦИЕНТОВ КЛАССИЧЕСКИХ РЕГУЛЯТОРОВ
МЕТОДОМ ГЕНЕТИЧЕСКИХ АЛГОРИТМОВ В СРЕДЕ MATLAB

Моисеев А.Н.

Национальный технический университет «Харьковский политехнический институт»

Цепковский Ю.А.

Магдебургский университет имени Отто фон Герине, Германия

Введение. Данная статья посвящена вопросам построения систем автоматического регулирования (САР) с использованием классических, ПИД и модальных регуляторов. Расчет коэффициентов этих регуляторов осуществляется по классическим формулам исходя из требуемых критериев качества переходных процессов.

Цель работы. В работе рассматривается метод синтеза ПИД-регулятора для системы ТП – Д, а также ПИД-регулятора и регулятора состояния на примере модели магнитного подвеса с применением генетического алгоритма (ГА). Приводится сравнение с аналогичными регуляторами, полученными классическими методами проектирования.

Материалы и результаты исследований. Передаточная функция ПИД-регулятора представлена формулой (1):

.

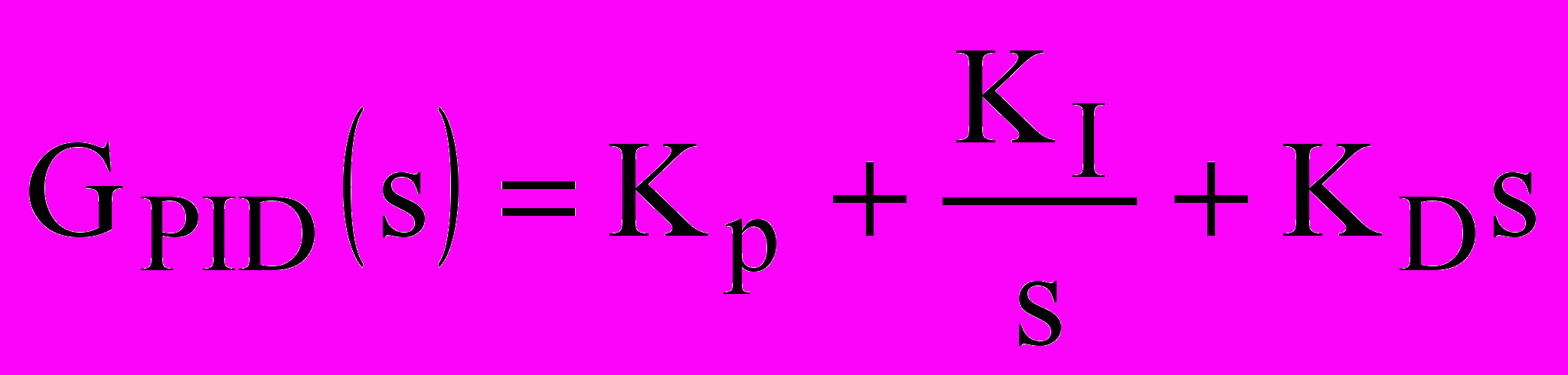(1)

Видно, что необходимо определить три коэффициента регулятора: 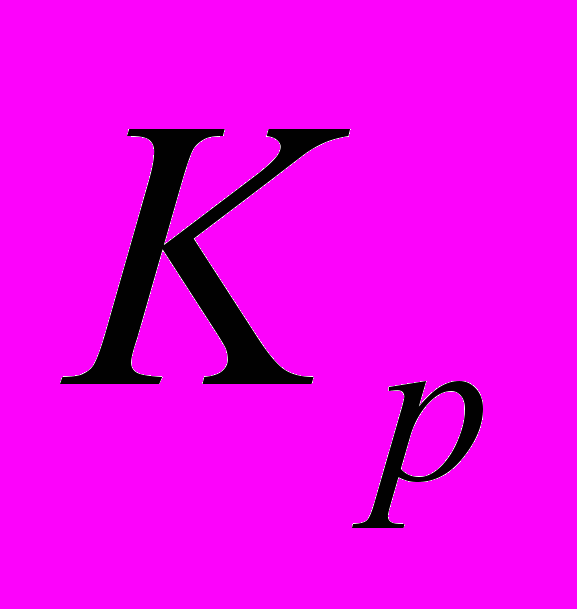, , 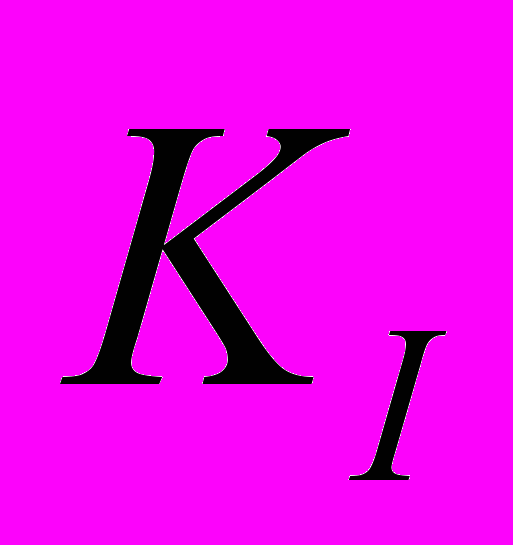, 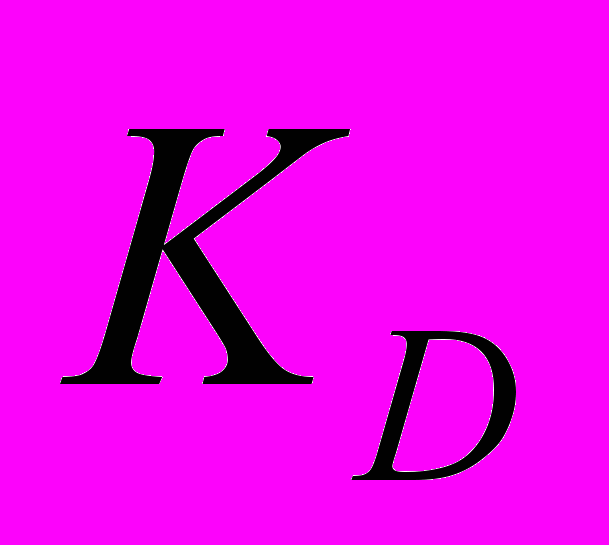которые можно рассчитать, воспользовавшись любым классическим подходом синтеза ПИД-регулятора с использованием диаграмм Боде или методом корневого годографа, но при этом необходимо, чтобы система была устойчивой и имела запас по фазе и амплитуде. Следовательно, необходимо построение корневого годографа, ЛАЧХ, ФЧХ, что соответственно занимает некоторое время, и при изменении параметров системы необходимо производить построение ЛАЧХ и ФЧХ заново [1]. Таких же результатов можно достичь при помощи ГА, для которого не нужно определять запасы устойчивости и строить диаграммы. Для нахождения коэффициентов методом ГА можно использовать как устойчивый, так и неустойчивый объект управления. Коэффициенты регулятора подбираются самим ГА таким образом, что система станет устойчивой. Если система изначально устойчива, то проблем при использовании ГА не возникает, он всегда подберёт коэффициенты такими, чтобы переходной процесс (ПП) удовлетворял требуемым показателям качества регулирования [2, 3].

При синтезе коэффициентов регулятора для устойчивого объекта метод ГА определит коэффициенты, при которых система приобретет требуемую динамику. Рассмотрим пример получения коэффициентов ПИД-регулятора с использованием метода генетических алгоритмов в среде MATLAB для устойчивого объекта системы тиристорный преобразователь – двигатель (ТПД). Структурная схема системы приведена на рис. 1.




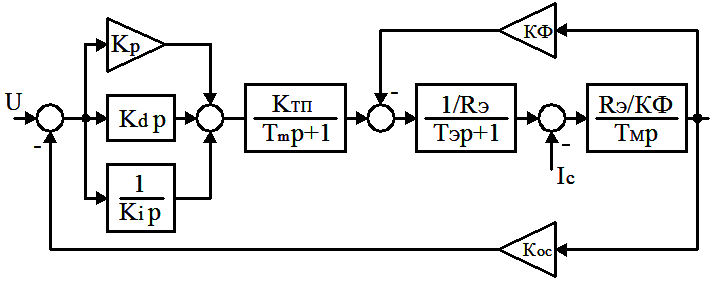
Рисунок 1 - Структурная схема системы ТПД
с ПИД-регулятором


Переходные процессы в системе ТПД и системы с ПИД-регулятором приведены на рис. 2.



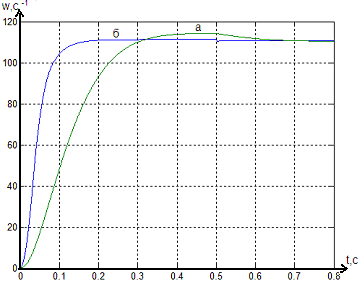
Рисунок 2 - Переходные процессы:
а) в разомкнутой системе ТПД;
б) в системе с ПИД-регулятором


При моделировании, в момент времени 0.55 с, прикладывалась нагрузка, система с ПИД-регуля-тором отработала возмущение.

Анализируя полученные результаты можно сделать вывод, что ГА довольно быстро и точно определил коэффициенты ПИД-регулятора.

Метод ГА можно с таким же успехом использовать при синтезе коэффициентов классических регуляторов для неустойчивых нелинейных объектов. Рассмотрим пример получения коэффициентов ПИД-регулятора и регулятора состояния на примере модели магнитного подвеса [4].

Объект представляет собой нелинейную, неустойчивую систему третьего порядка. Математическая модель системы представлена дифференциальными уравнениями:

,

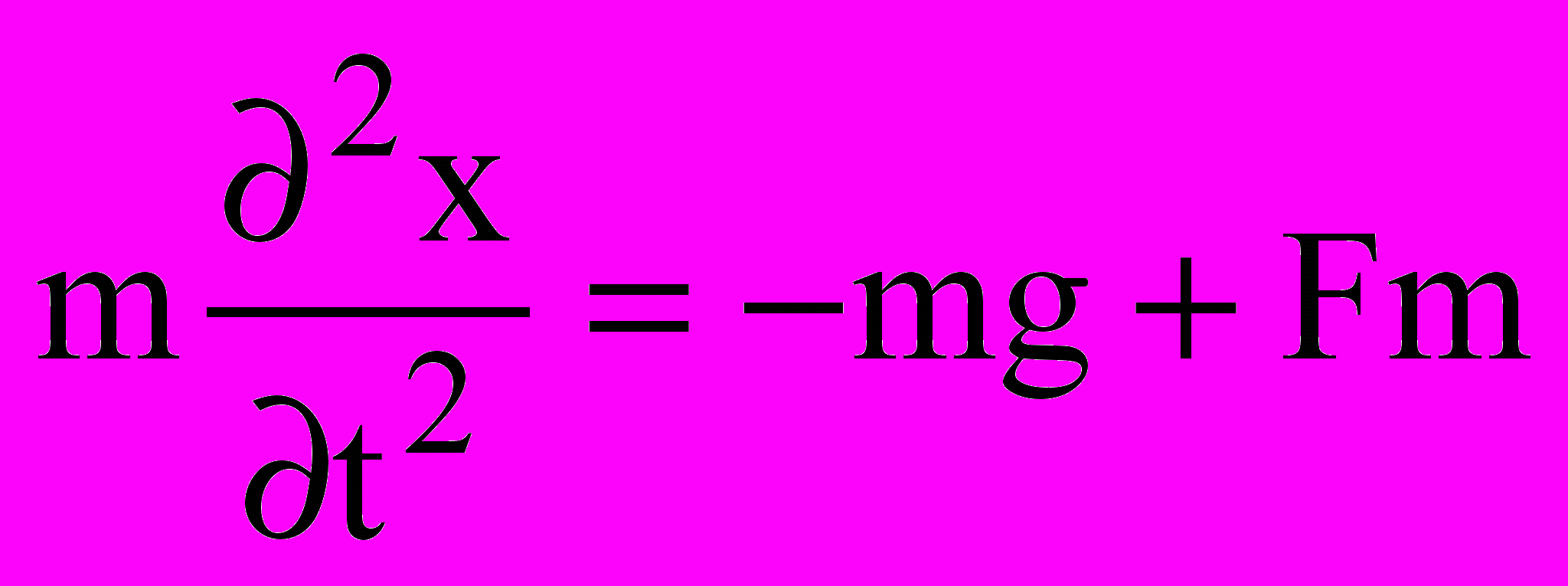(2)

где m – масса подвижной части подшипника, кг;

g – сила тяжести м/с²; Fm – магнитная сила, Н;

x – перемещение подвижной части (ротора) магнитного подвеса.

Зависимость магнитной силы от тока и положения описывается уравнением:

.

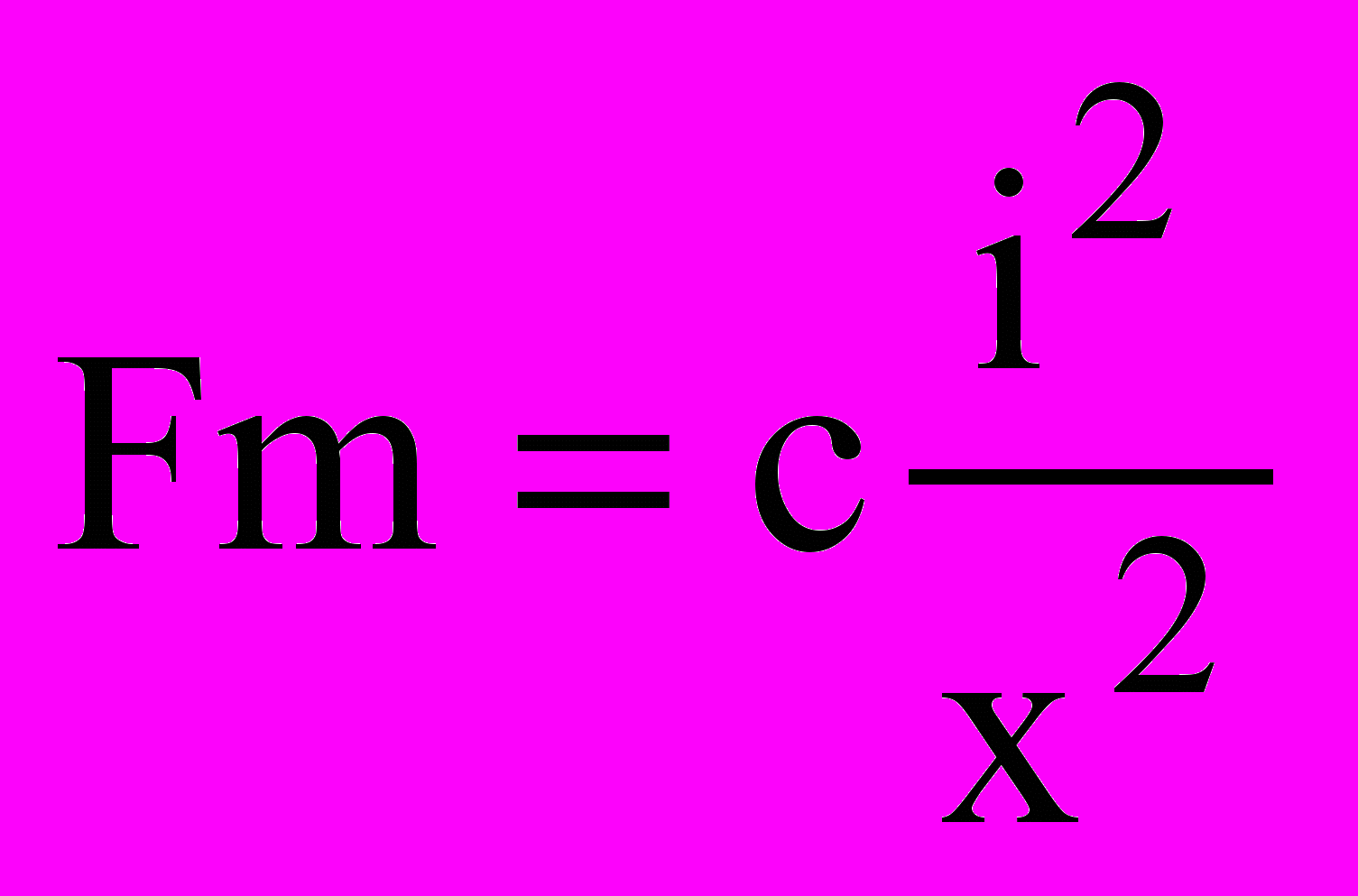(3)

Константа в уравнении (3) определяет положение рабочей точки на кривой намагничивания и зависит от конкретных параметров электрической катушки и материала проводника магнитопровода. Рабочая точка также определяется из уравнения равновесия (4), когда сила тяжести компенсируется магнитной силой:

.

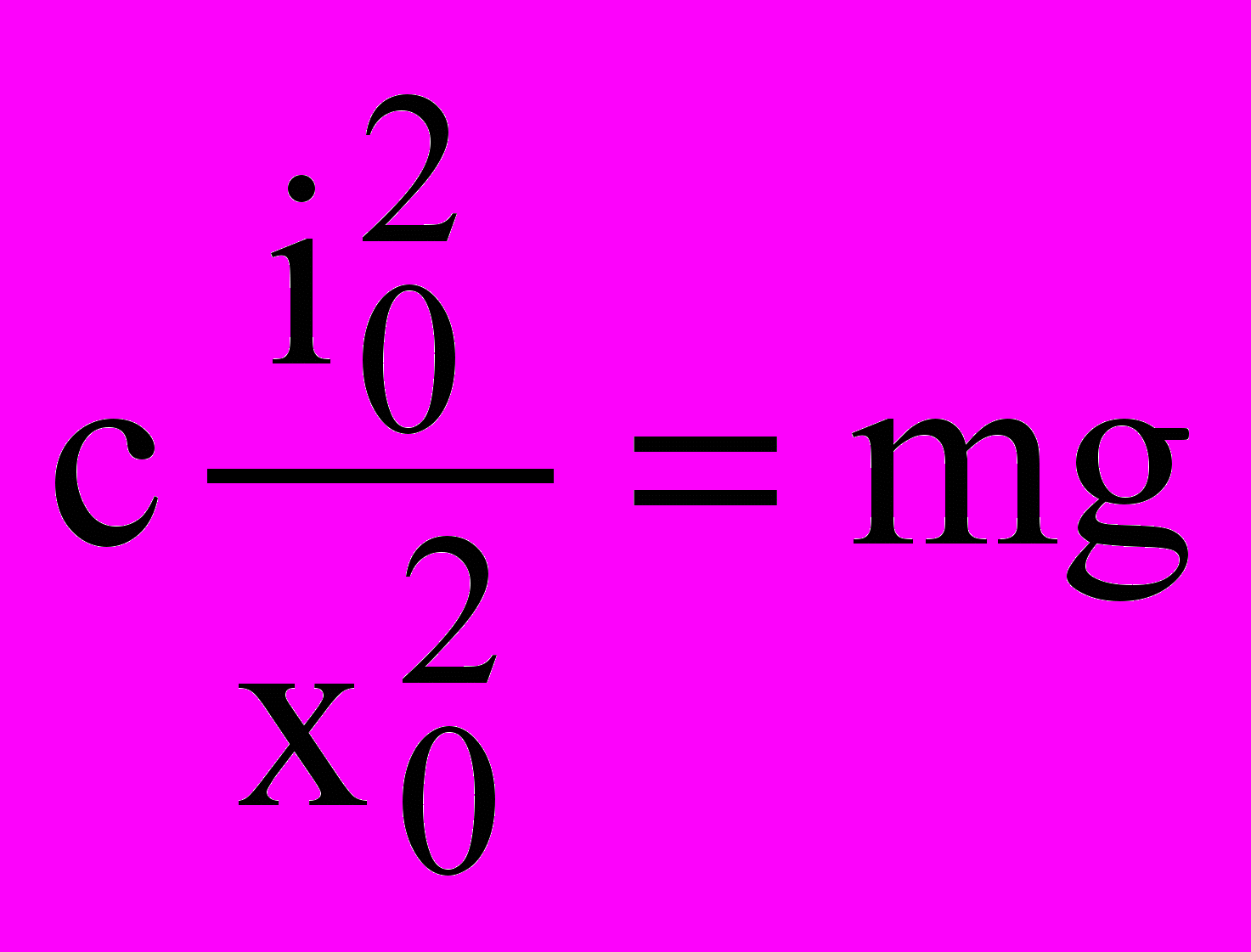(4)

Уравнение электрической части магнита представлено дифференциальным уравнением:

,

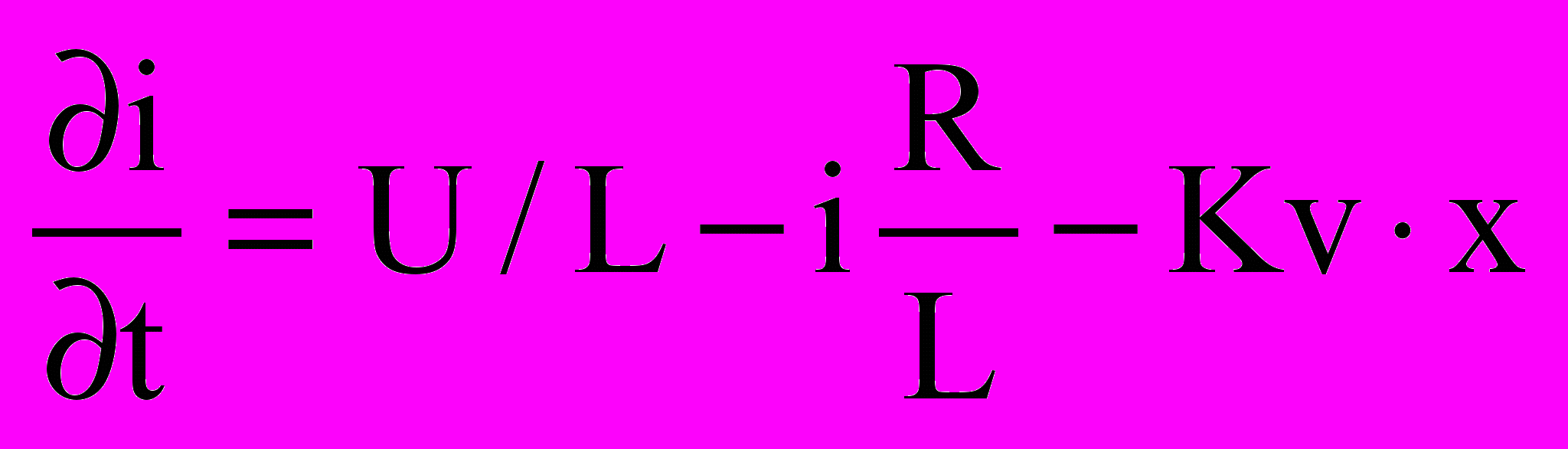(5)

где I – ток, А; U – управляющее напряжение, В;

L – индуктивность, Гн; R – сопротивление обмотки возбуждения, Ом; Kv – коэффициент линеаризации зависимости магнитной силы от скорости изменения положения ротора;

x – положение ротора, м.

Схематически магнитный подвес изображен на рис. 3.



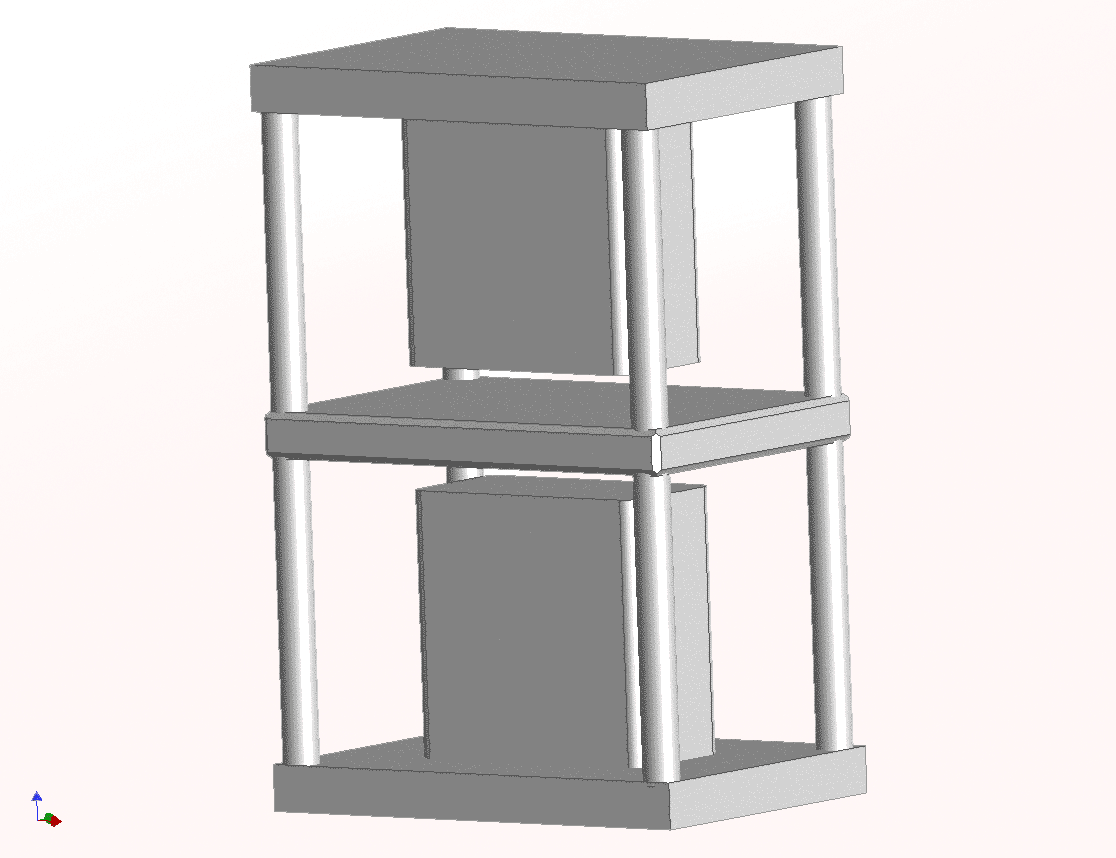
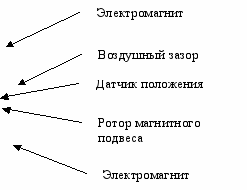
Рисунок 3 - Схема магнитного подвеса


Ротор магнитного подвеса представляет собой остроконечный металлический стержень, свободно подвешенный в воздушном зазоре магнита. Когда ток питания электромагнита равен нулю, ротор находится в крайнем нижнем положении. В случае, если ток электромагнита обеспечивает возникновение магнитной силы, ротор поднимается вверх, до тех пор, пока не упирается в верхний полюс магнита. Практически, задача управления сводится к удержанию ротора электромагнитного подвеса в заданном положении, между крайними точками. Для обеспечения движения только с одной степенью свободы ротор помещен в отрезок трубы, ограничивающей движение по другим степеням свободы. В этом же месте расположен датчик движения ротора.

Модель была рассчитана для реальной экспериментальной установки с параметрами, представленными в таблице 1.

Таблица 1 -

Параметры линеаризованной модели
магнитного подвеса

Kv=63.333	Kw=4000	xo=0.001
Tv=0.0015	g=9.81	io=0.293
m=0.844	KKs=(2*g*m)/xo	KKi=(2*g*m)/io

Для расчета системы управления все уравнения были нормализованы, таким образом единичному входному воздействию отвечает единичный выходной сигнал, соответствующий реальному номинальному значению координаты положения ротора в зазоре магнитного подвеса.

Структурная схема представленных ранее дифференциальных уравнений изображена на рис. 4.



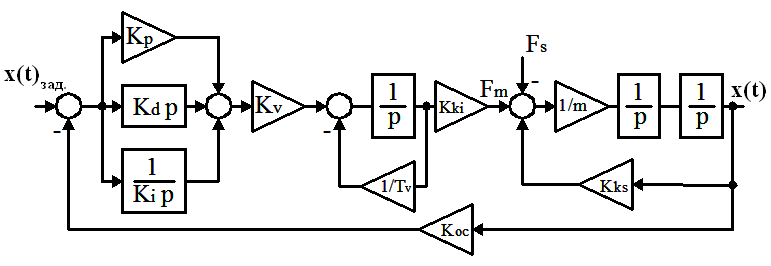
Рисунок 4 - Структурная схема магнитного
подвеса с ПИД-регулятором


Классическая теория расчета применима только при условии, что система линеаризована в рабочей точке, т.е. не учитывает нелинейностей характеристики трения и кривой намагничивания [5, 6]. Нелинейности заменятся коэффициентами KKs, KKi.

В представленном примере оптимизация производилась по минимизации среднеквадратичной ошибки по:

,

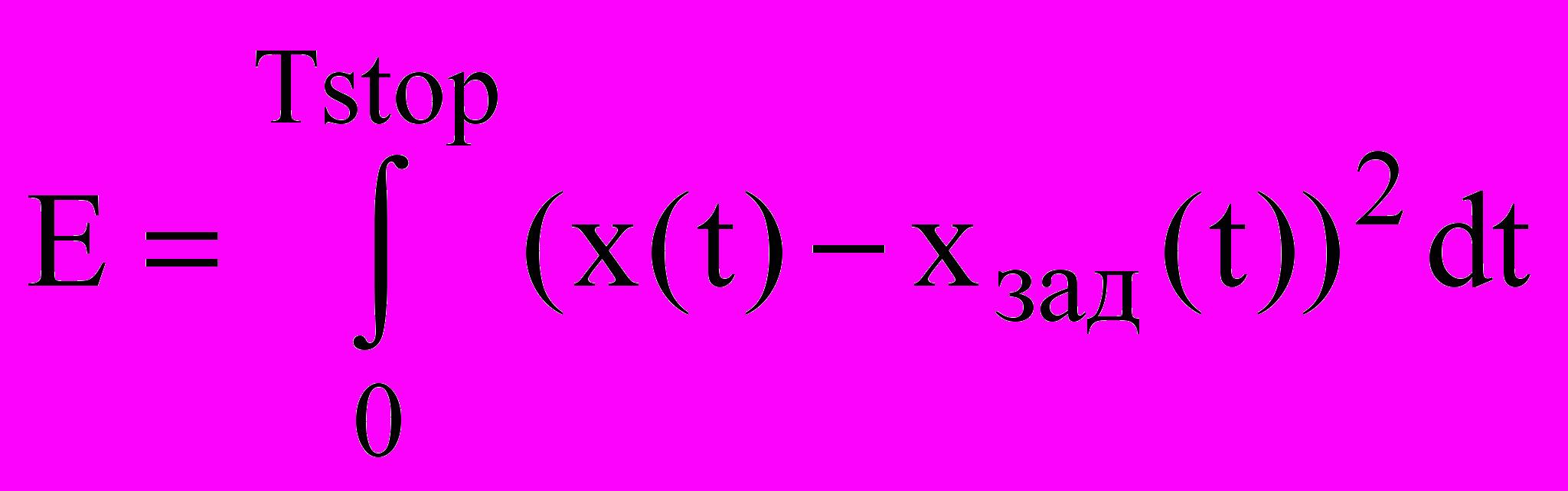(6)

где: 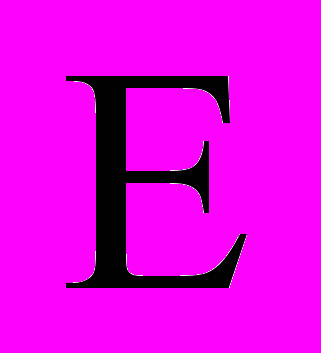 критерий качества; 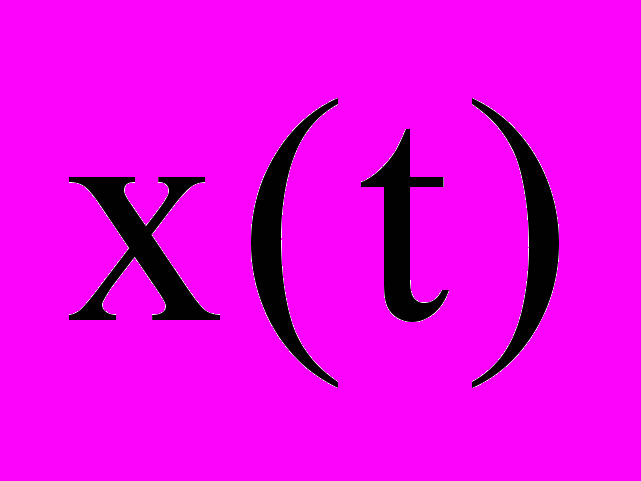 выходной, контролируемый процесс, положение магнитного подвеса; 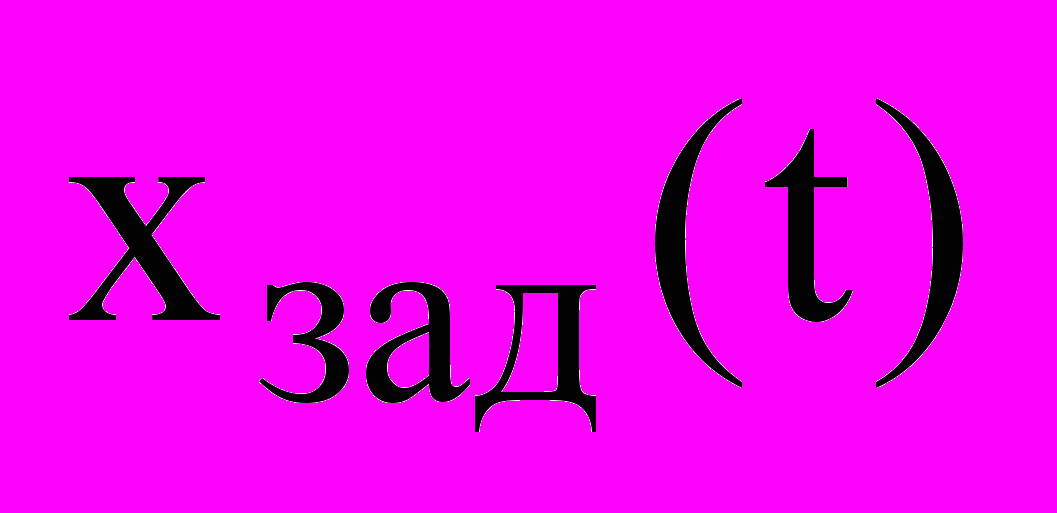 входной, управляющий процесс.

При расчете переходного процесса неустойчивой системы генетический алгоритм может выдавать сообщение, что произошло деление на ноль и расчет модели будет остановлен, это связано с тем, что система неустойчива, выходная координата достигла очень больших значений. Чтобы все-таки получить коэффициенты, в модели, которую использует ГА, необходимо вести ограничение той координаты, по которой произошел останов просчета переходного процесса [2]. Т.е. необходимо, чтобы при достижении этой координатой определенного уровня происходил останов и ГА генерировал следующую особь и производил для нее расчет. Если же в ходе проверки полученных коэффициентов переходной процесс все равно будет расходящимся, то необходимо изменить время расчета, шаг интегрирования модели или изменить настройки в самом ГА, такие как: Population, Mutation, Crosover, Migration [2]. Изменение этих параметров приводит к расширенному поиску, например при изменении параметров мутации и миграции происходит генерирование особей, далеко отстоящих от лучшей особи на данной эпохе, объем популяции обеспечивает хорошее прощупывание зоны поиска, но при больших значениях ведет к замедлению расчета.

Если производить оптимизацию только по ограничению выходного сигнала, по формуле (6), то получим П оптимальный по быстродействию с перерегулированием, рис. 5.




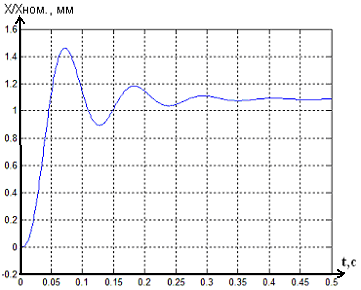
Рисунок 5 - Переходной процесс в системе
магнитного подвеса с ПИД-регулятором


Если же при оптимизации ограничивать еще и входной сигнал, как в формуле (7), то в этом случае мы получим апериодический ПП, рис. 6:

,

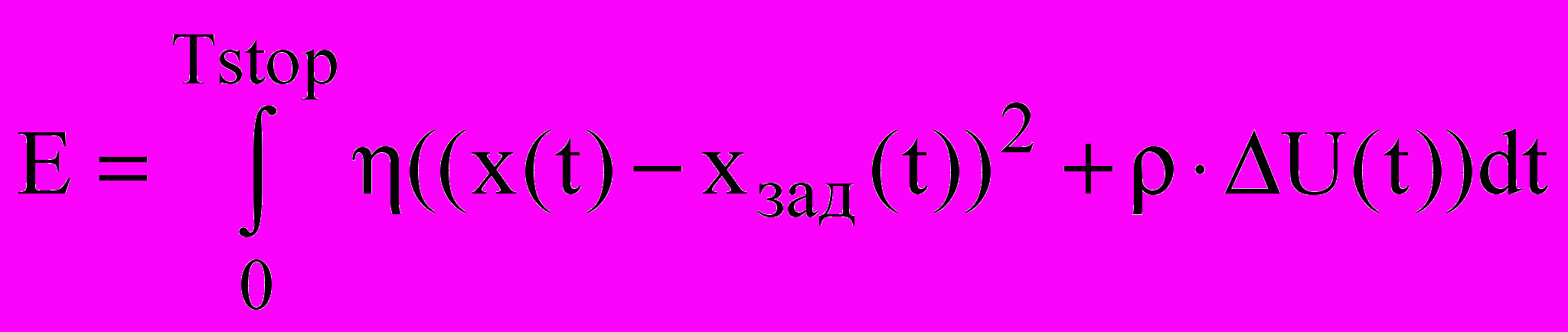(7)

где: 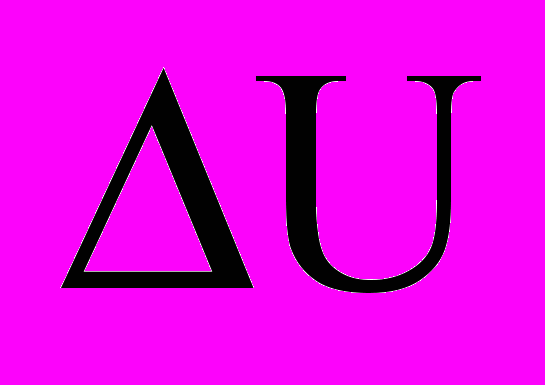 мгновенное изменение управляющего напряжения; 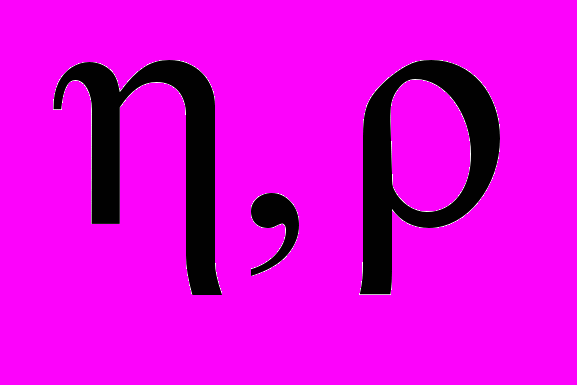 коэффициент пропорциональности (коэффициент влияния).

Для получения коэффициентов регулятора состояния необходимо описать объект, получить характеристический полином системы, выбрать стандартное распределение, приравнять полином системы и стандартное распределение и только после этого вычисляются коэффициенты, причем если в систему вводится дополнительный интегратор, то приходится заново получать характеристическое уравнение системы, задаваться распределением другого порядка [6].




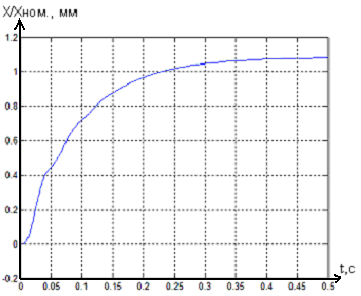
Рисунок 6 - Переходной процесс в системе
магнитного подвеса с ПИД-регулятором с
ограничением по управляющему сигналу


Нельзя не отметить сходство полученных результатов средствами ГА по формуле (7) с аналогичным по структуре линейно-квадратичным регулятором (LQR). Последний получают путем решения уравнения Риккати, однако результат практически одинаков. В данном случае, коэффициенты 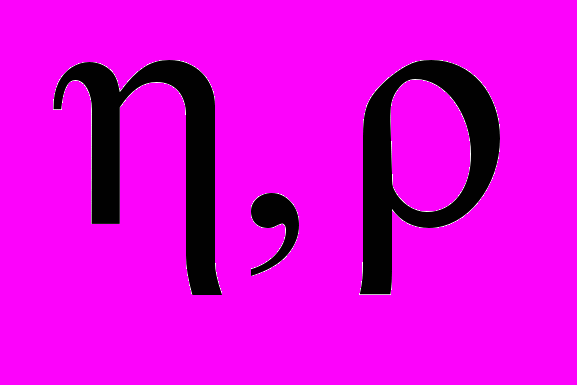играют роль матриц пропорциональности, используемых в расчете LQR регуляторов. Теория расчета таких регуляторов подробно описана в [6].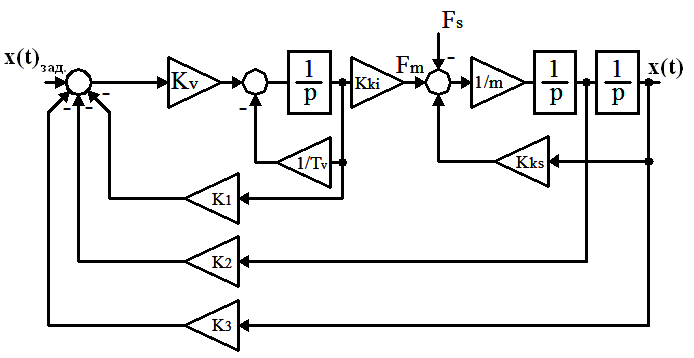



Рисунок 7 - Структурная схема магнитного
подвеса с регулятором состояния


При использовании ГА, строим модель, задаем критерий оптимизации и получаем результат. Вводим в систему дополнительный интегратор, добавляем его в модель, запускаем ГА и получаем коэффициенты.

ПП в системе с использованием регулятора состояния представлены на рис. 8. и рис. 9.

При использовании ГА можно учесть нелинейности при моделировании и просчитать коэффициенты, при которых система будет устойчива и обеспечит требуемые показатели качества регулирования, так как генетический алгоритм будет подбирать коэффициенты, просчитывая модель с нелинейностями и оптимизировать их под заданный критерий качества. Если в модели для просчета коэффициентов заменить 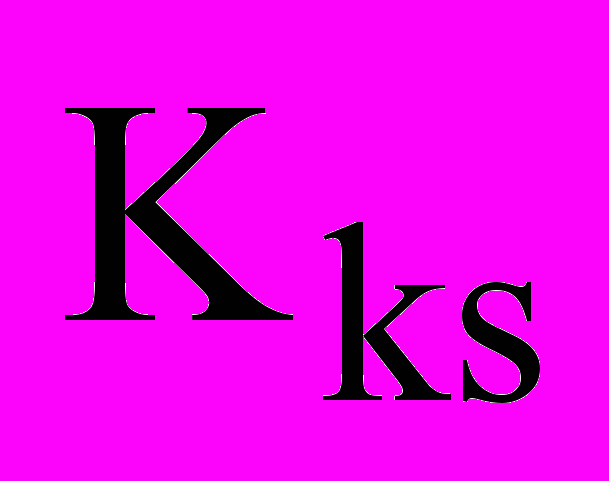и 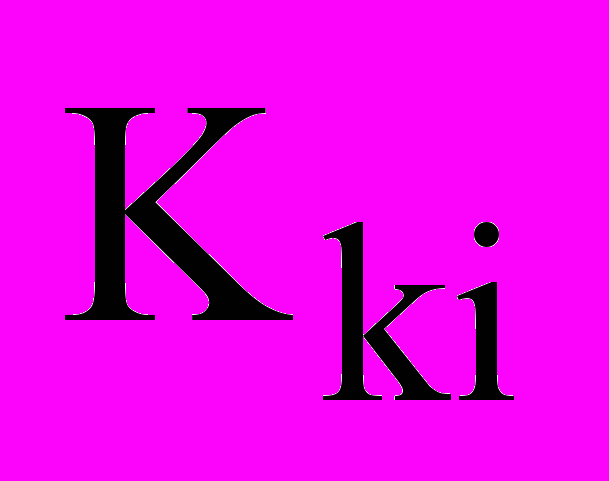на соответствующие выражения нелинейностей (8), то получим модель более близкую к реальному объекту, рис. 10, и соответственно ГА вычислит коэффициенты для такой модели.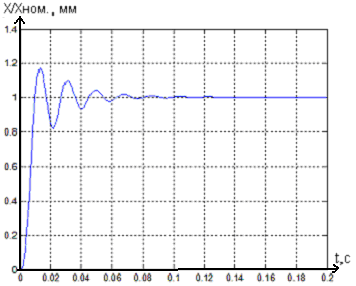



Рисунок 8 - Переходной процесс в системе
магнитного подвеса с регулятором состояния




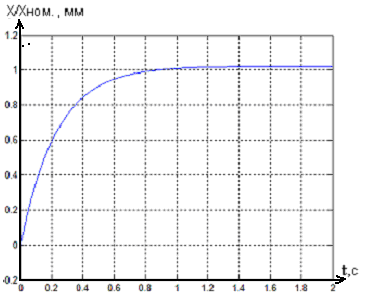
Рисунок 9 - Переходной процесс в системе
магнитного подвеса с регулятором состояния
при ограничении управляющего сигнала


ПП в системе с ограничением по выходной координате представлен на рис 11. На рис. 12, представлен ПП в системе с ограничением по управляющему воздействию и по выходной координате.

, .

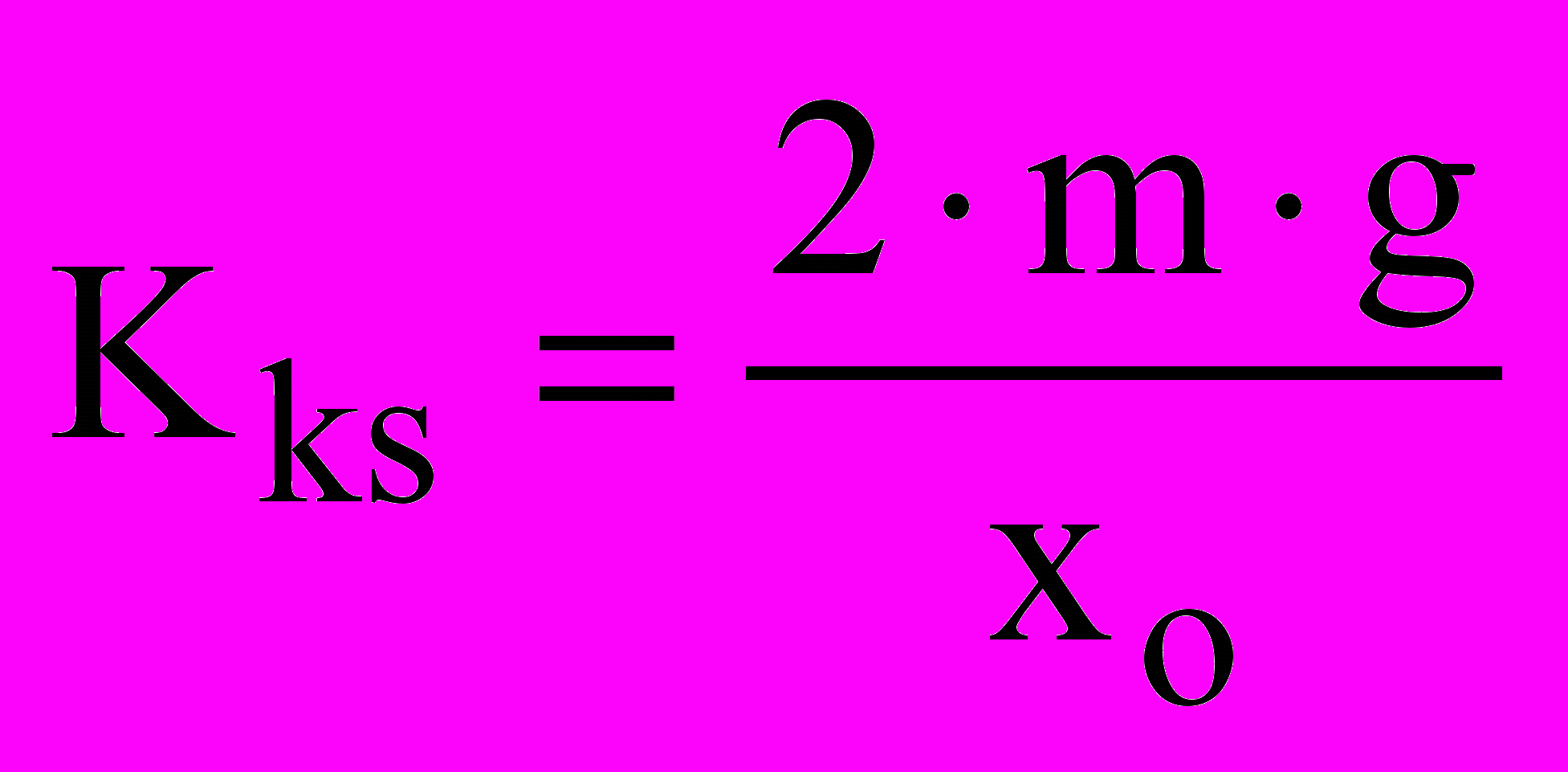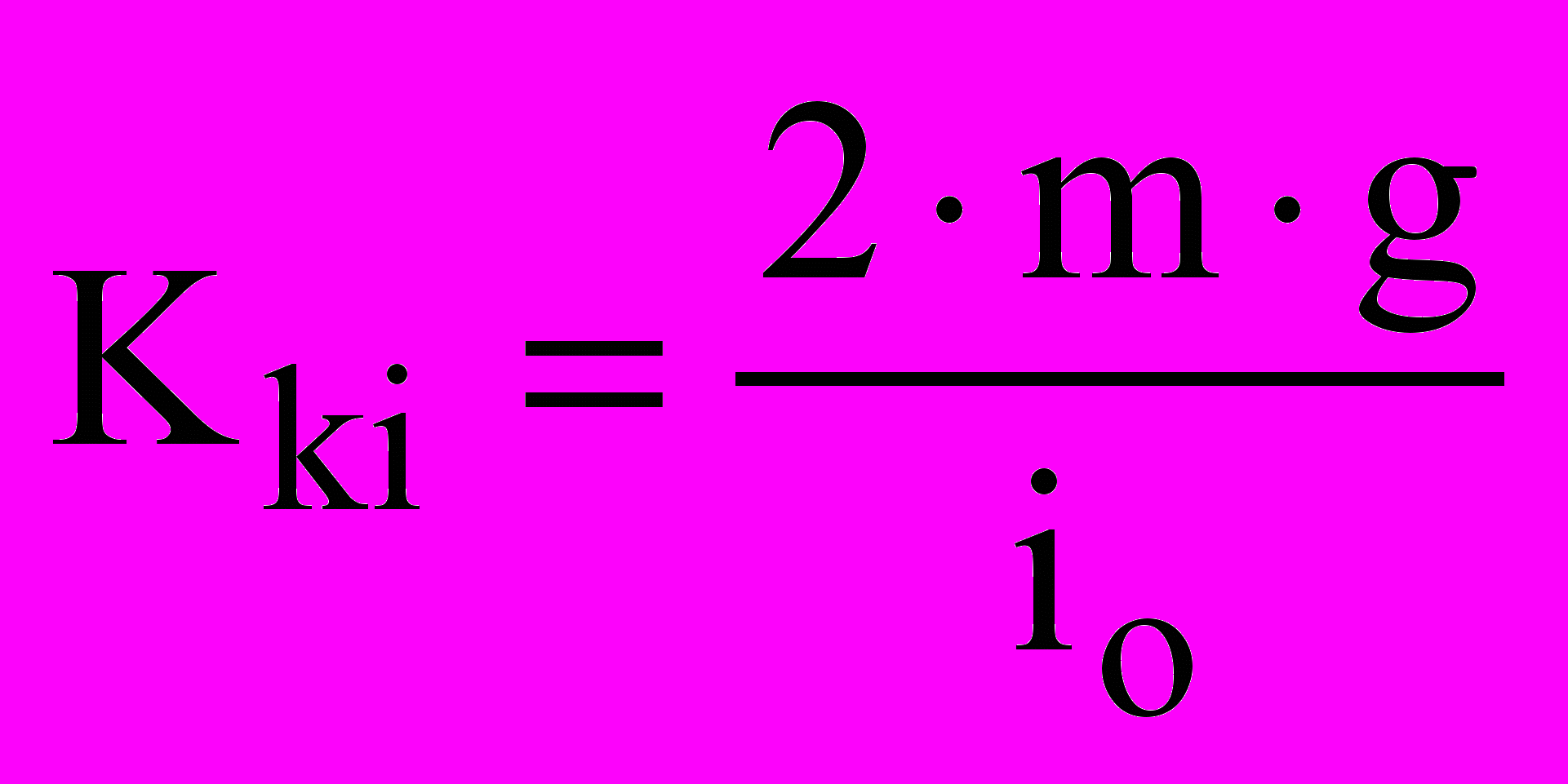(8)

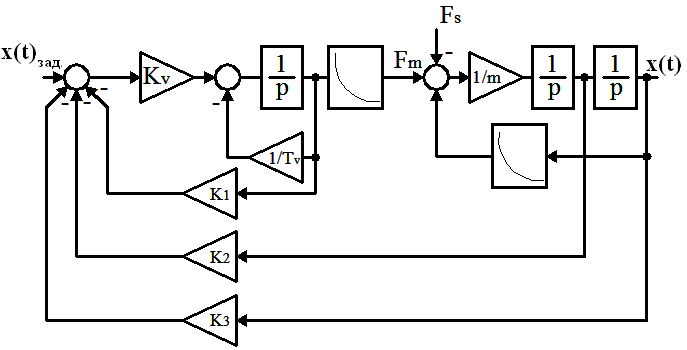
Рисунок 10 - Структурная схема магнитного подвеса
с регулятором состояния с учетом нелинейностей



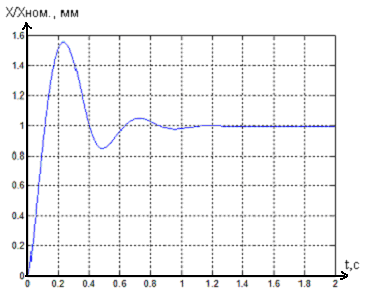
Рисунок 11 - Переходной процесс в системе
магнитного подвеса с регулятором состояния с
учётом нелинейностей при ограничении
выходной координаты


Из всего выше сказанного следуют достоинства применения ГА для получения коэффициентов регулятора. При использовании toolbox «Genetic Algorithm and direct search» Matlab можно рассчитать коэффициенты регуляторов, затратив при этом минимум времени. Для моделирования можно использовать сложную модель с учётом нелинейностей и шумов.

Система может быть изначально неустойчивой. Для определения коэффициентов методом ГА необходимо создать модель и задать критерий оптимизации.

При классическом подходе к синтезу коэффициентов ПИД-регулятора коэффициенты определяются для рабочей точки при допущении, что датчики не вносят в систему шумы, не учитывается влияние нелинейностей. При каждом изменении параметров системы необходимо строить корневой годограф или ЛАЧХ и ФЧХ.




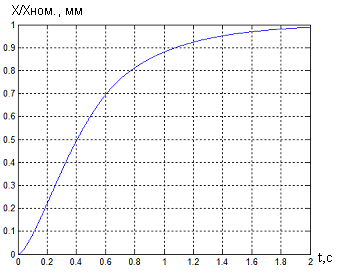
Рисунок 12 - Переходной процесс в системе
магнитного подвеса с регулятором состояния с
учётом нелинейностей при ограничении
управляющего сигнала и выходной координаты


Выводы. Анализируя полученные результаты моделирования, можно сделать вывод, что данный подход получения коэффициентов классических регуляторов даёт хорошие результаты как для устойчивых, так и не устойчивых объектов.

Главное достоинство метода ГА в том, что его применение не требует от разработчика приводить описание объекта управления или контроллера к определенному виду, например, к описанию в матрицах состояния, что необходимо для нахождения коэффициентов регулятора состояния. Единственное требование, которое необходимо соблюдать – это вычисление критерия качества при любых настройках регулятора.

Очевидно, что в случае применения ГА модель объекта может быть существенно нелинейной, может иметь шумы и ограничения, может иметь любой порядок и параметрические возмущения. Все это делает невозможным расчет классических регуляторов без внесения существенных упрощений и допущений. Что на практике совершенно не гарантирует применимость полученных результатов.

Преимущества метода особенно заметны в условиях ограниченного времени на проектирование системы управления.


ЛИТЕРАТУРА

1. Дорф Р., Бишоп Р. Современные системы управления.–.М.: Лаборатория Базовых Знаний, 2002. – 832 с.: ил.
   
2. The Genetic Algorithm and Direct Search Toolbox User Guide. MATLAB 7.04.
   
3. Методы робастного, нейро-нечеткого и адаптивного управления / Под ред. Н.Д. Егупова. - М.: Изд-во МГТУ им. Баумана, 2002. – 744 c.
   
4. Цепковский Ю.А., Палис Ф. Синтез скользящего нейро-фаззи регулятора для управления магнитным подвесом / Вестник НТУ «ХПИ» № 45,
   Харьков 2005, с. 493-497.
   
5. Shinskey G.F. Process Control Systems. 4th ed. New York: McGraw-Hill, 1996.
   
6. Goodwin Graham C., Graebe Stefan F., Saldago Mario E. Control System Design. - Prience Hall, 2001.
   

Стаття надійшла 15.04. 2006 р.

Рекомендовано до друку

д.т.н., проф. Родькіним Д.Й.