Нформаційні системи І моделювання
| Вид материала | Документы |
- Нформаційні системи І моделювання, 61.42kb.
- Нформаційні системи І моделювання, 135.57kb.
- Нформаційні системи І моделювання, 93.99kb.
- Нформаційні системи І моделювання, 60.18kb.
- Нформаційні системи І моделювання, 103.77kb.
- Іhформаційhі процеси в суспільстві. Іhформаційhі системи. Штучний інтелект. Експертні, 155.22kb.
- Конспект лекцій з дисципліни "Інформаційні системи та технології у фінансових установах", 1112.81kb.
- На державний iспит з циклу професійної підготовки та спеціальних курсів, 134.32kb.
- Иємства та сформувати комплекс захисних реакцій, спрямований на забезпечення стійкого, 175.84kb.
- 1 опис засобів моделювання складних динамічних систем, 175.64kb.
ІНФОРМАЦІЙНІ СИСТЕМИ І МОДЕЛЮВАННЯ
УДК 531.7.08
ДО ПИТАННЯ РОЗВ’ЯЗКУ ПРОБЛЕМИ СИСТЕМАТИЗАЦІЇ МАТЕМАТИЧНИХ МОДЕЛЕЙ І МЕТОДІВ ПЕРЕТВОРЕННЯ МОМЕНТУ ІНЕРЦІЇ.
ОГЛЯД ТА ПЕРСПЕКТИВА
Ведміцький Ю. Г., Кухарчук В. В.
Вінницький національний технічний університет
Вступ. Визначення моменту інерції тіл обертання з осьовою симетрією відносно центральної осі обертання є задачею на сьогодні і важливою, і поширеною в багатьох галузях науки та техніки [1].
На сьогодні існують два напрями визначення моменту інерції: розрахунковий [2] та експериментальний.
Оскільки геометрія об’єктів вимірювання та розподіл мас в них зазвичай бувають доволі складними, розрахунковий підхід при визначенні моменту інерції є малоефективним та неточним.
У зв’язку з цим, особливого значення набули експериментальні методи.
Питанням експериментального визначення моменту інерції присвячено багато публікацій, розроблено чимало методів та пристроїв [3 - 7]. Вони є різними за суттю, мають свої переваги, мають і недоліки.
Наразі, за умов такої різноманітності постає сукупний для існуючих методів недолік – відсутність чітко окресленої за єдиними критеріями систематизації, що суттєво гальмує можливе удосконалення методів, їх модифікацію та подальшу розробку нових методів перетворення моменту інерції.
Причину автори вбачають у відсутності єдиного підходу у формуванні математичних моделей перетворювачів моменту інерції.
Мета роботи – розгляд та застосування загальної методики математичного моделювання перетворювачів моменту інерції; огляд, систематизація та класифікація існуючих методів перетворення; створення необхідних сприятливих передумов для розробки нових перспективних методів перетворення моменту інерції.
Матеріал і результати дослідження базуються на матеріалах доповіді “Рівняння Лагранжа як основа теорії перетворювачів” [1], де була розроблена загальна методика математичного моделювання перетворювачів моменту інерції, і являють собою її логічне продовження.
Математична модель перетворювача моменту інерції 1-го порядку. На рис. 1 наведена модель механічної частини перетворювача моменту інерції 1-го порядку, яка являє собою механічну дисипативну систему з одним накопичувачем механічної (кінетичної) енергії.
Відповідно до [1] для даної системи рівняння Лагранжа другого роду має вид:
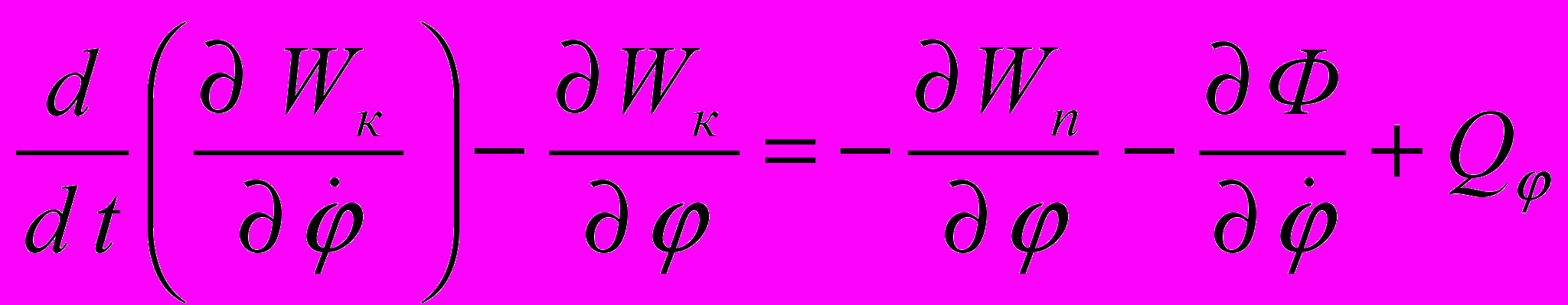, (1)а рівняння руху відносно кутової швидкості обертання –
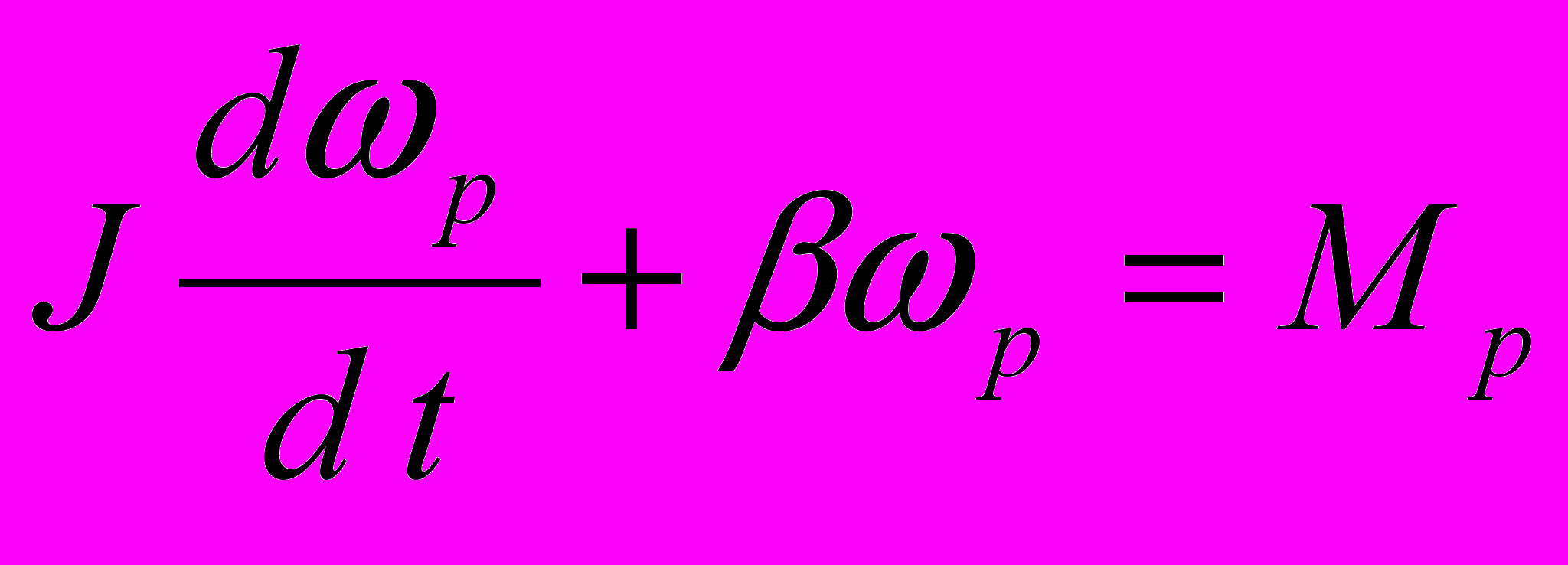. (2)
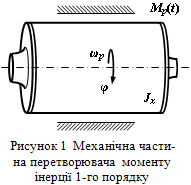
Рисунок 1 - Механічна частина перетворювача
моменту інерції 1-го порядку
Загальний розв’язок цього диференціального рівняння, як відомо,
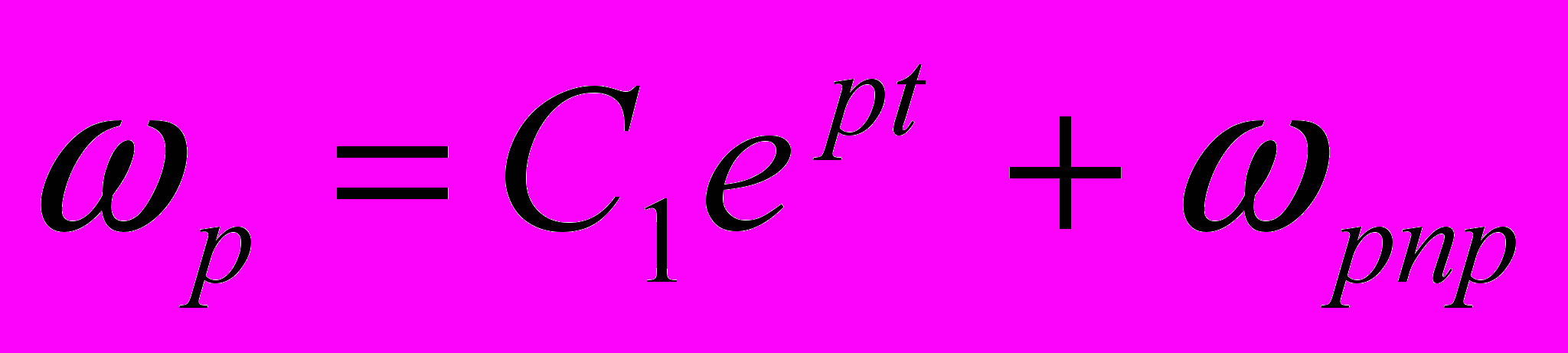, (3)де
- деяка стала інтегрування, що визначається за незалежною початковою умовою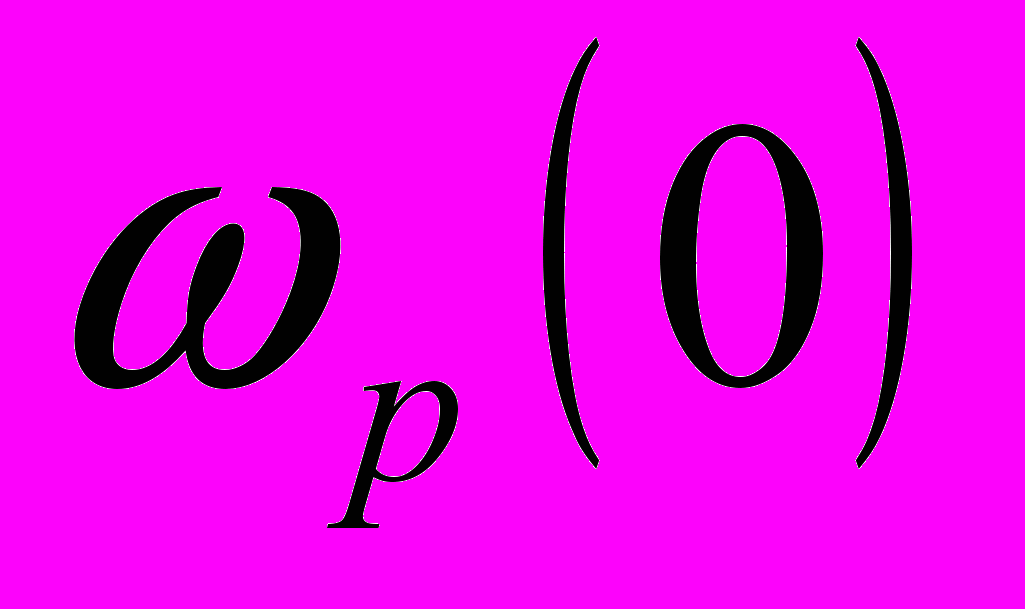 
; 
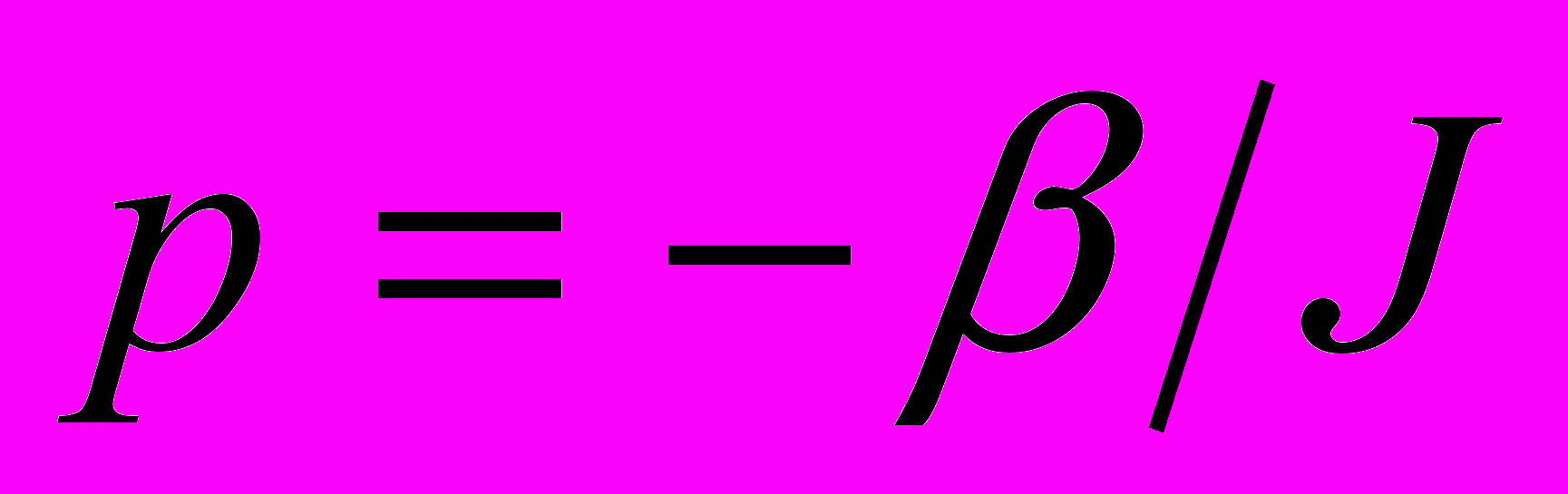- корінь характеристичного рівняння 
; 
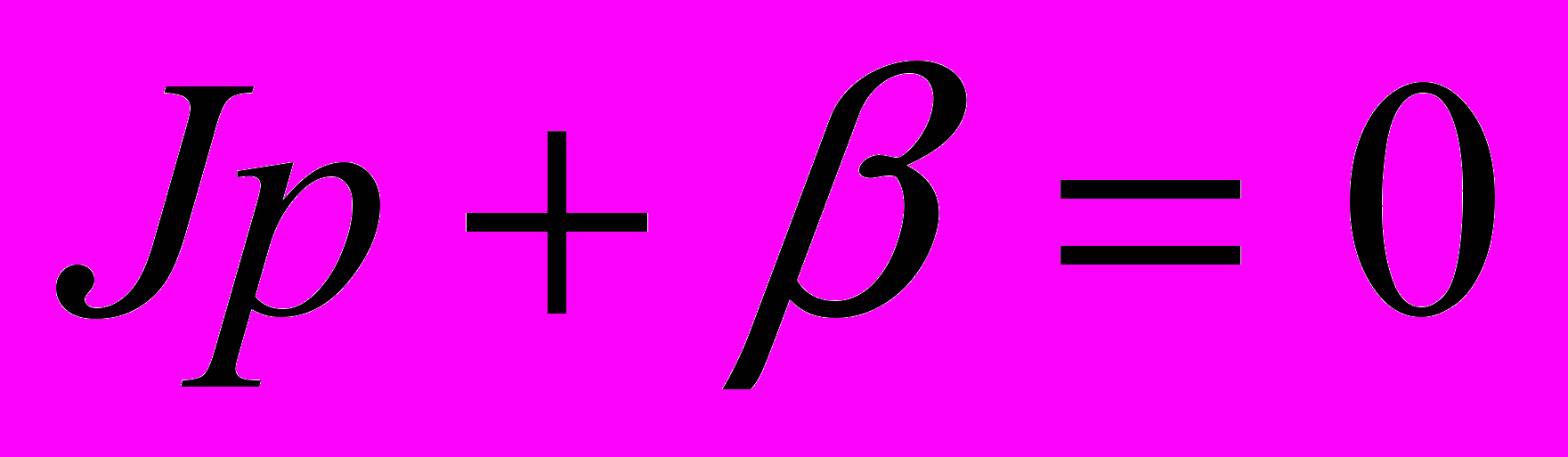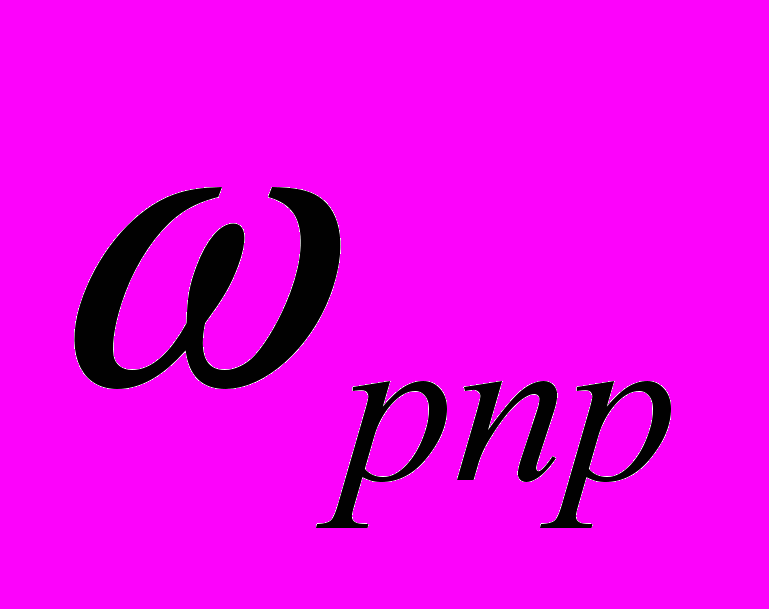- окремий розв’язок неоднорідного диференціального рівняння, що є кутовою швидкістю обертання твердого тіла в усталеному режимі роботи.Існуючі методи перетворення моменту інерції перетворювачів 1-го порядку. Необхідно зауважити, серед основних існуючих методів перетворення моменту інерції до методів даного класу відноситься лише метод самогальмування [6].
Метод самогальмування.
Суть методу полягає в тому, що в режимі самогальмування, тобто:
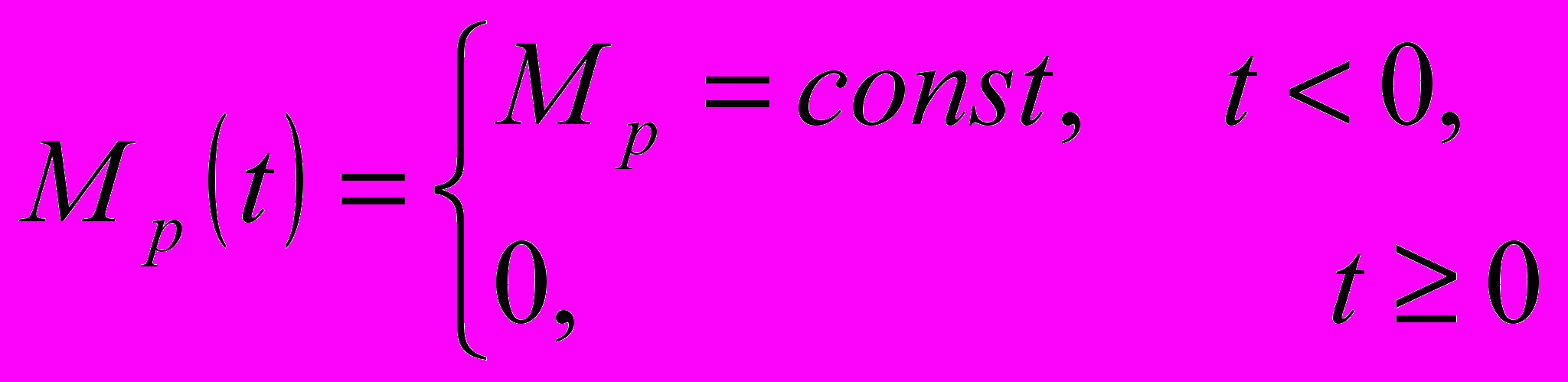(4)вимірюють спочатку кутове прискорення ротора електродвигуна
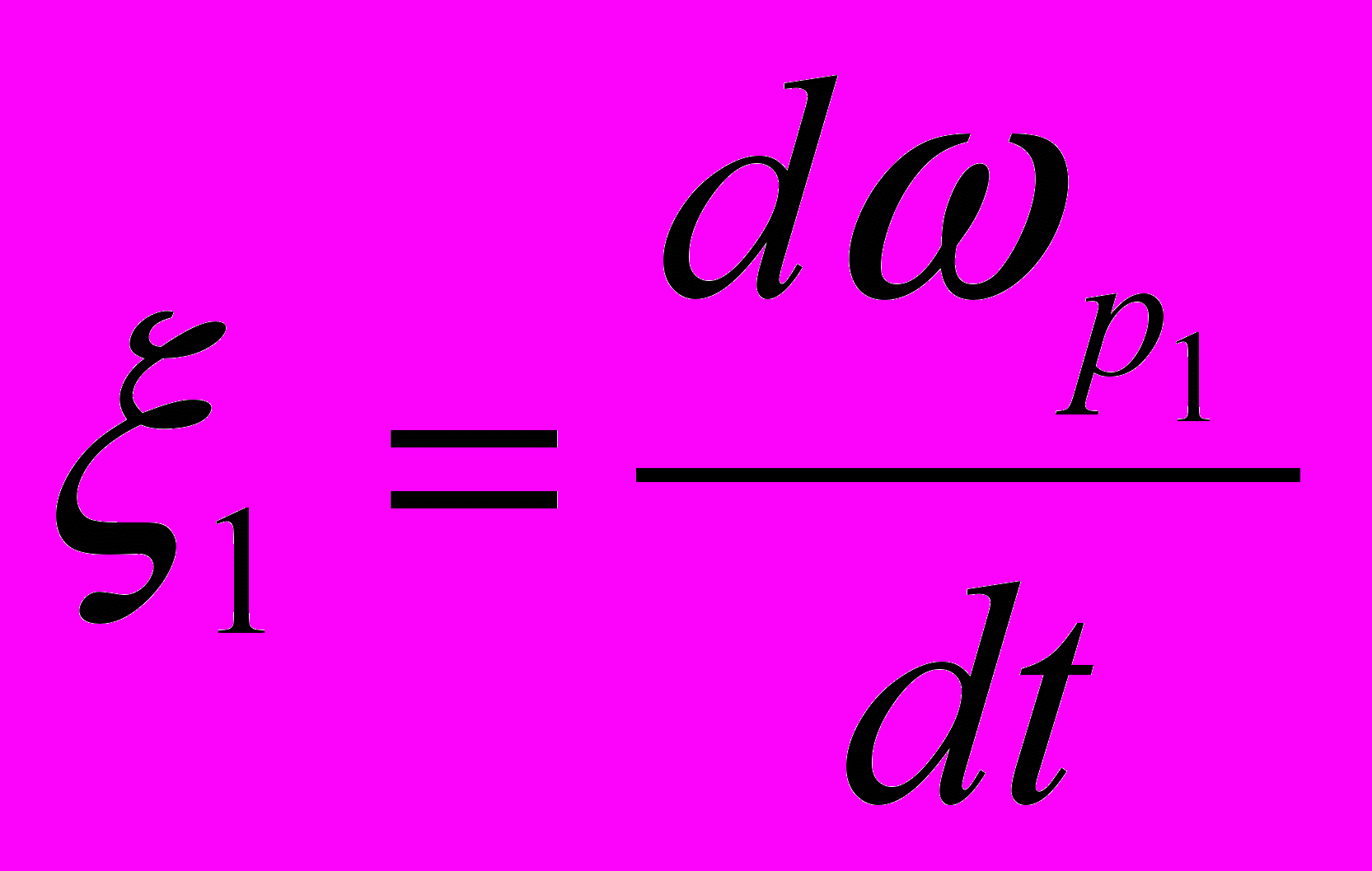спочатку з деяким зразковим моментом інерції, а потім без нього 
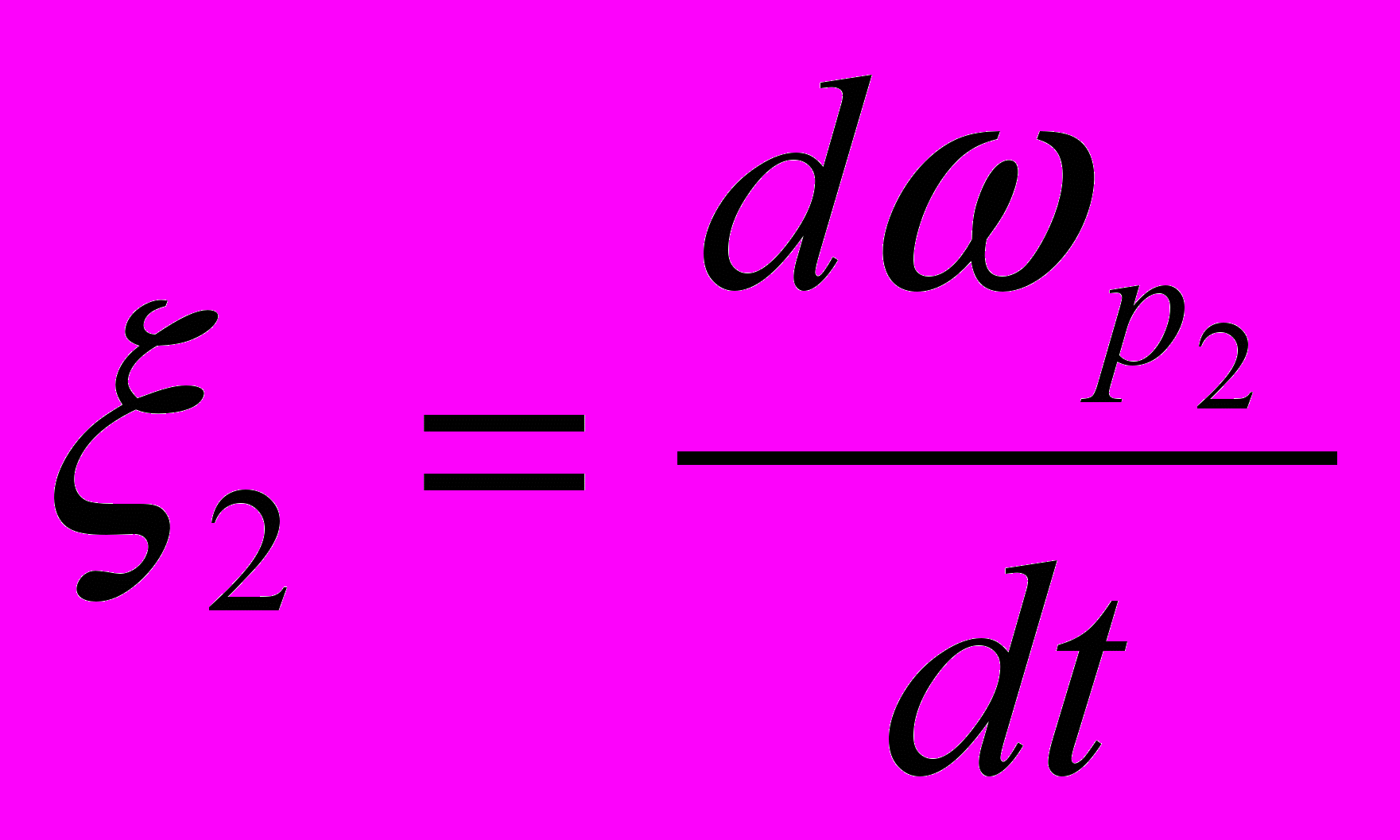.Рівняння руху для цієї вимірювальної процедури має вигляд:
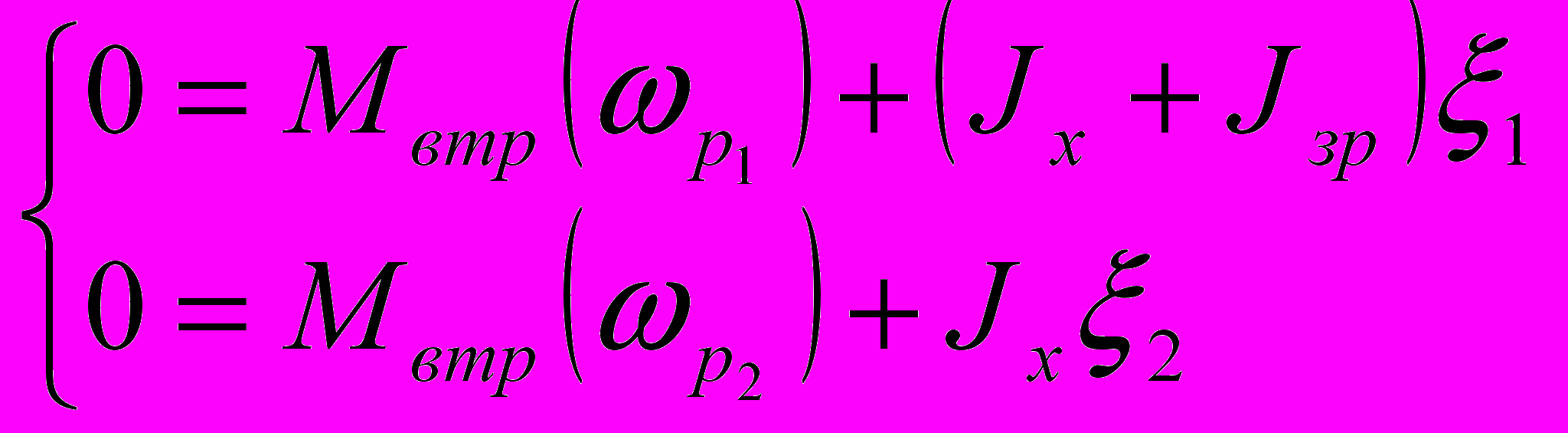,де
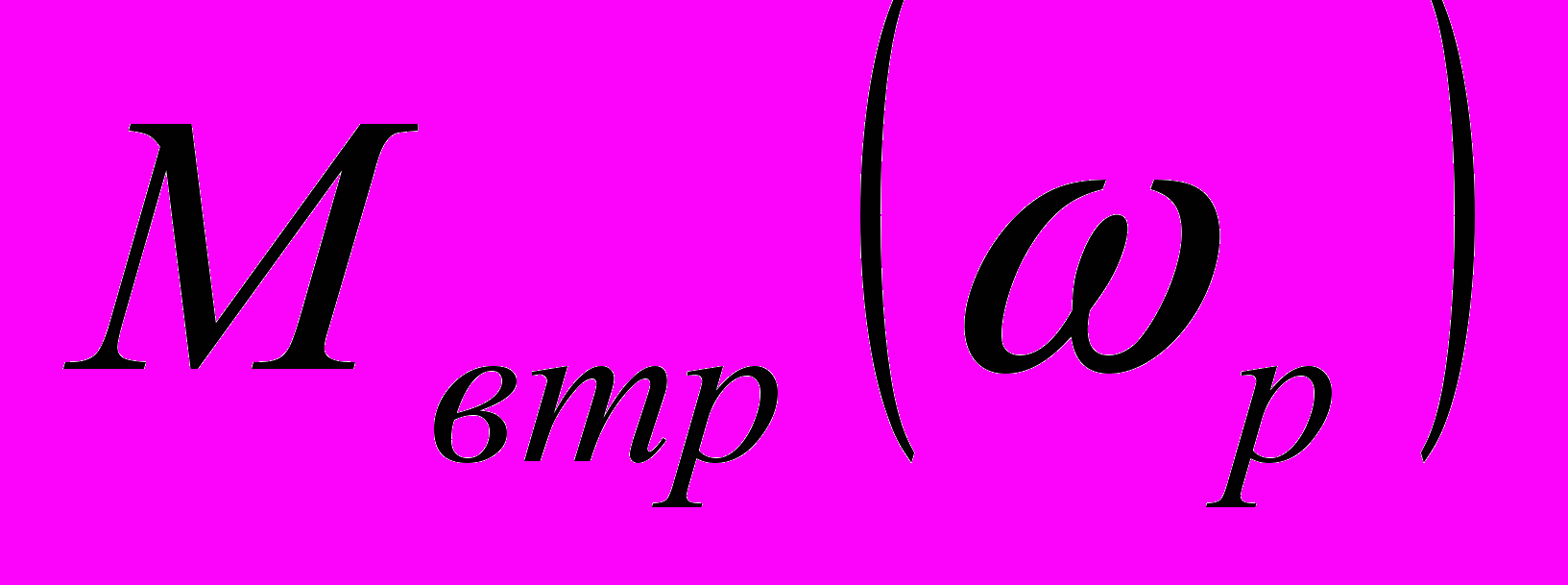- момент механічних втрат електродвигуна та перетворювача; 
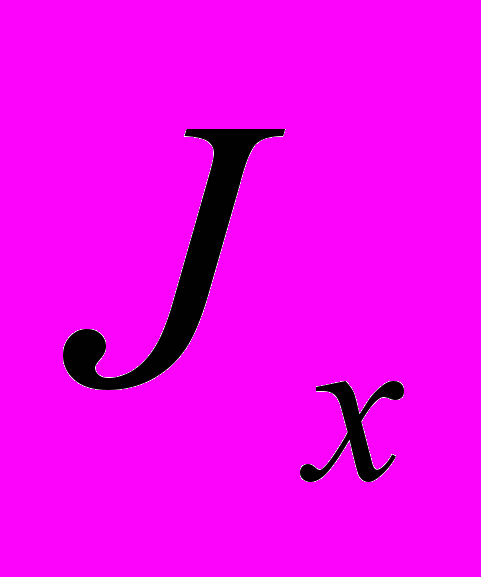- вимірюваний момент інерції; 
- зразковий момент інерції тіла.З цих рівнянь випливає, що:
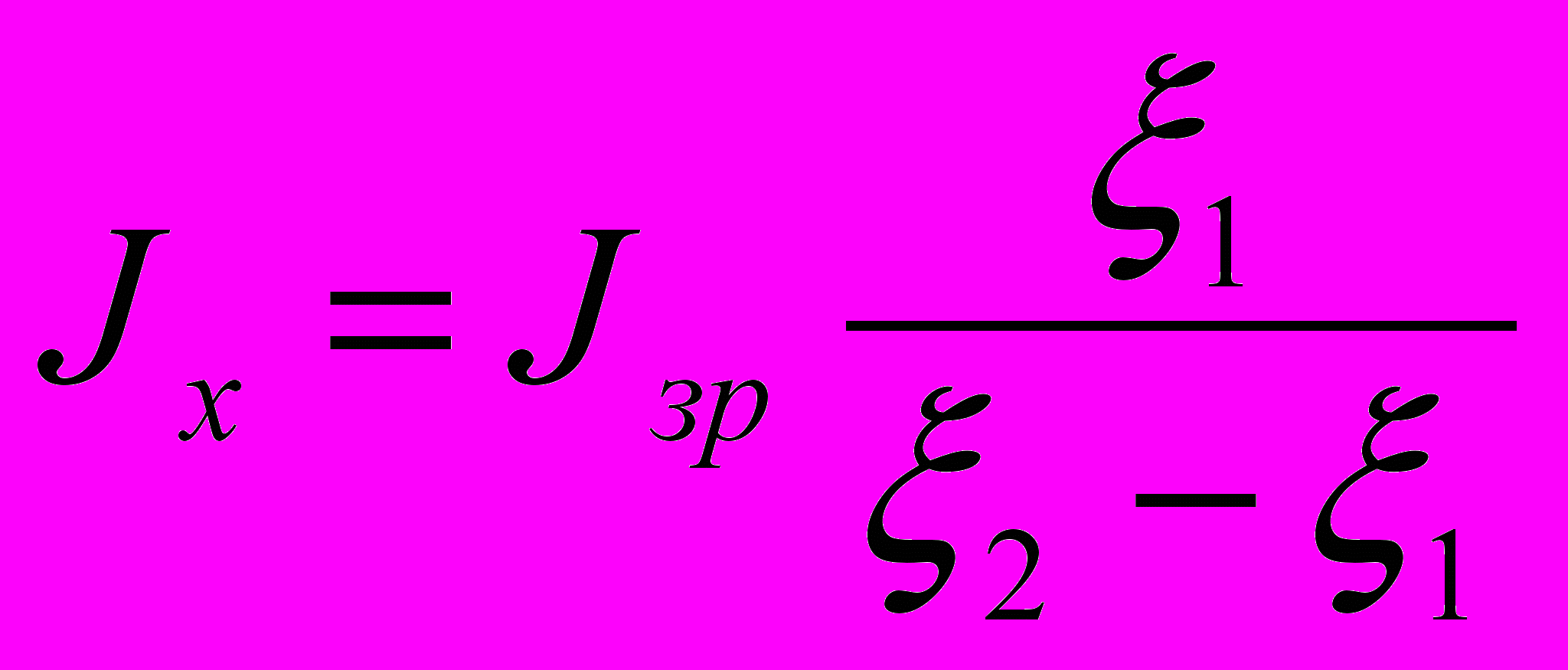.Отже, визначення інформативного параметру
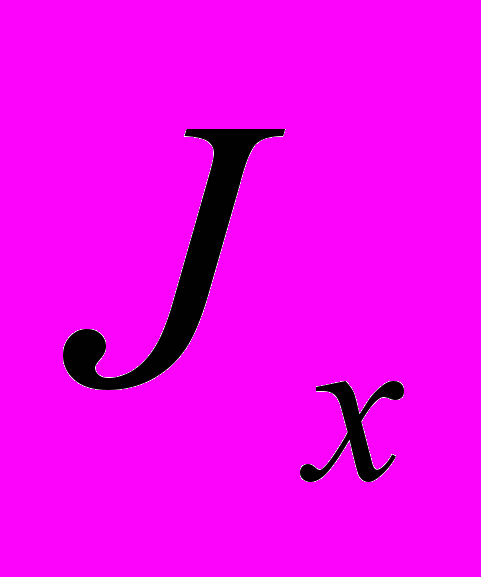зводиться до вимірювання кутової швидкості 
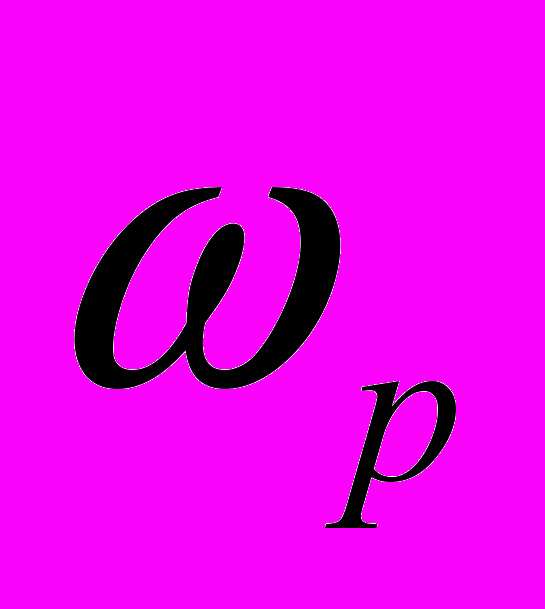, її цифрового диференціювання та опосередкованого визначення 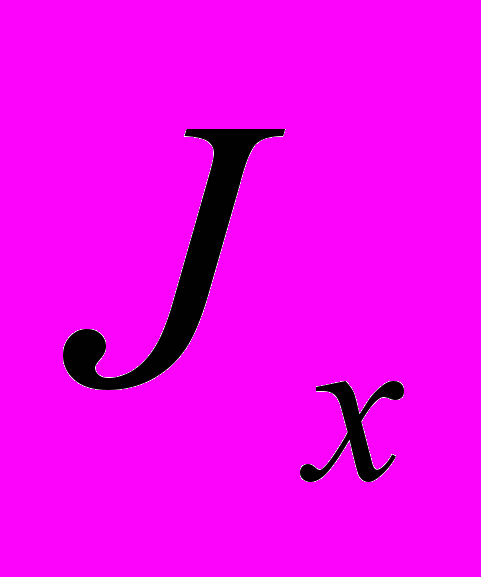.Недоліками цього методу є невисока швидкодія та низька точність.
Відповідно до [4] час вимірювання щонайменше складається з
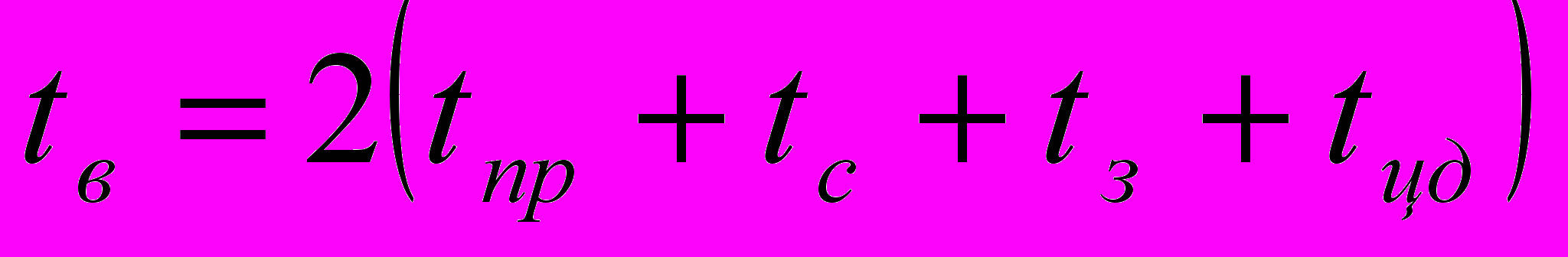,де
- тривалість перехідного процесу об’єкта контролю;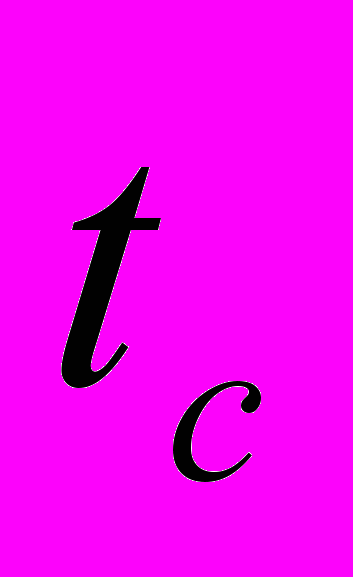 
- час самогальмування електричної машини; 
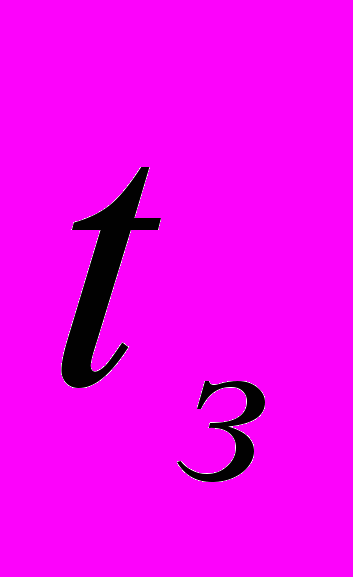- час на виконання операцій згладжування результатів вимірювання кутової швидкості; 
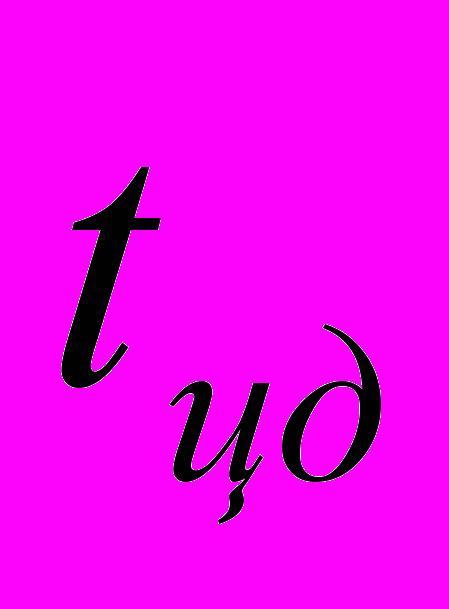- час на виконання операції цифрового диференціювання.Тому тривалість процедури вимірювання моменту інерції за даним методом складає ~ 5 хв., що не зовсім задовольняє вимогам замовника.
Невисока точність зумовлена двома чинниками.
Перший – це невисока точність реалізації операції цифрового диференціювання.
Другий, що більш суттєво, - це існуюча залежність моменту механічних втрат від кутової швидкості. Звідси випливає, що:
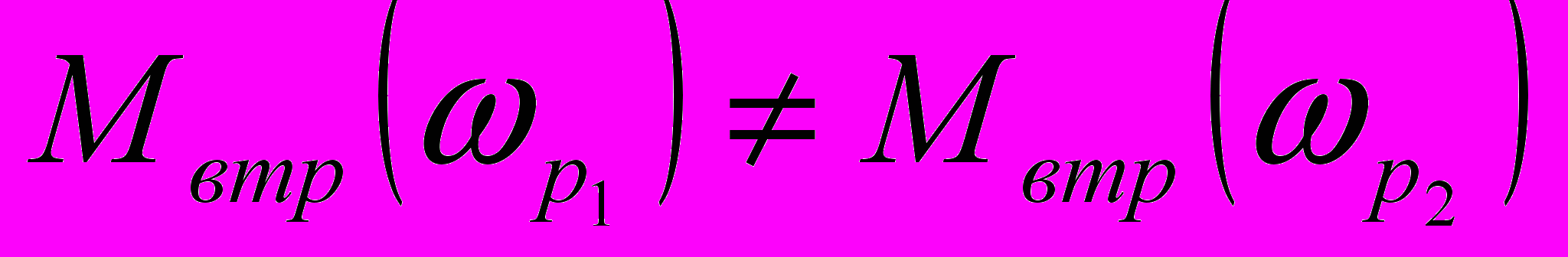при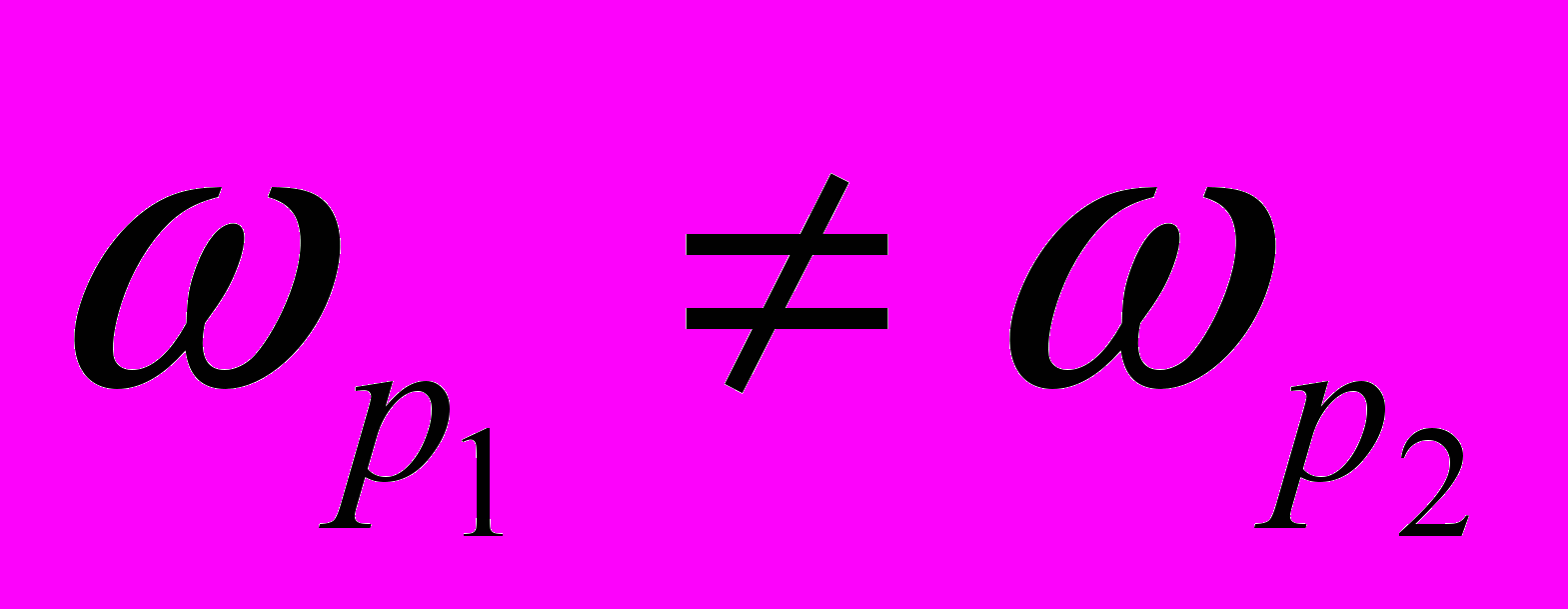 
.Ця відмінність буде тим більшою, чим більшою буде відмінність сталої часу перехідного процесу в першому досліді від сталої часу в другому досліді і чим раніше буде проводитись процедура вимірювання після початку перехідного процесу.
Можливі методи перетворення моменту інерції перетворювачів 1-го порядку. Як бачимо, наведений існуючий метод має ряд суттєвих недоліків. Проте математична модель перетворювача, що базується на диференціальному рівнянні 1-го порядку (2) та його розв'язки (3) передбачають існування як інших нових методів цього класу, позбавлених означених недоліків, так і модифікацію даного методу.
Наприклад, в режимі самогальмування можна спочатку провести вимірювання часу
повної зупинки ротора зі зразковим моментом інерції, а потім без нього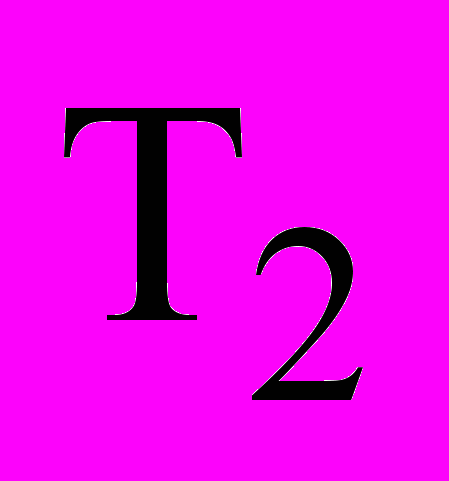 
.Оскільки обертальний момент змінюється за законом (4), то початковою умовою має бути:
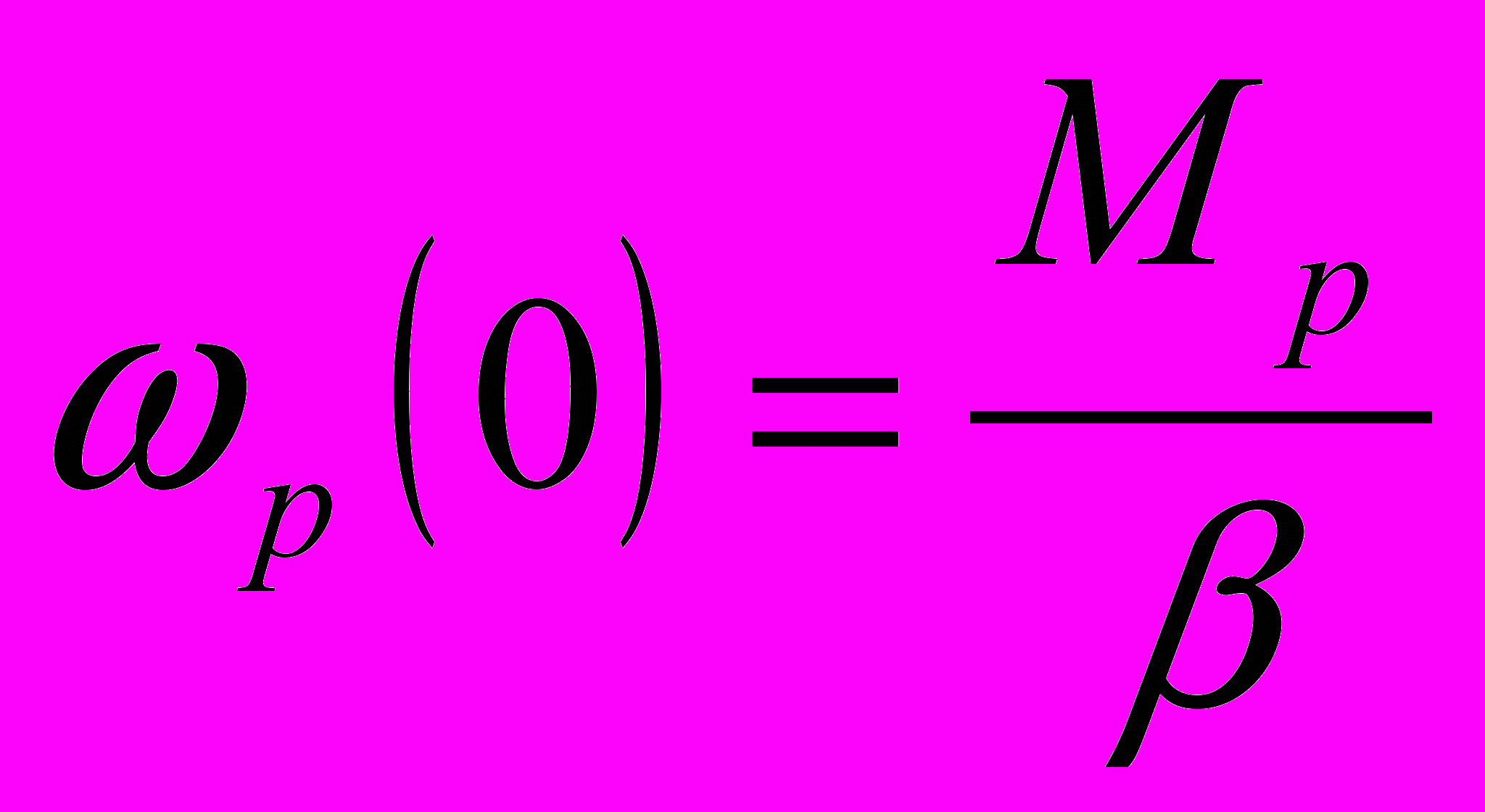,а примусовою складовою
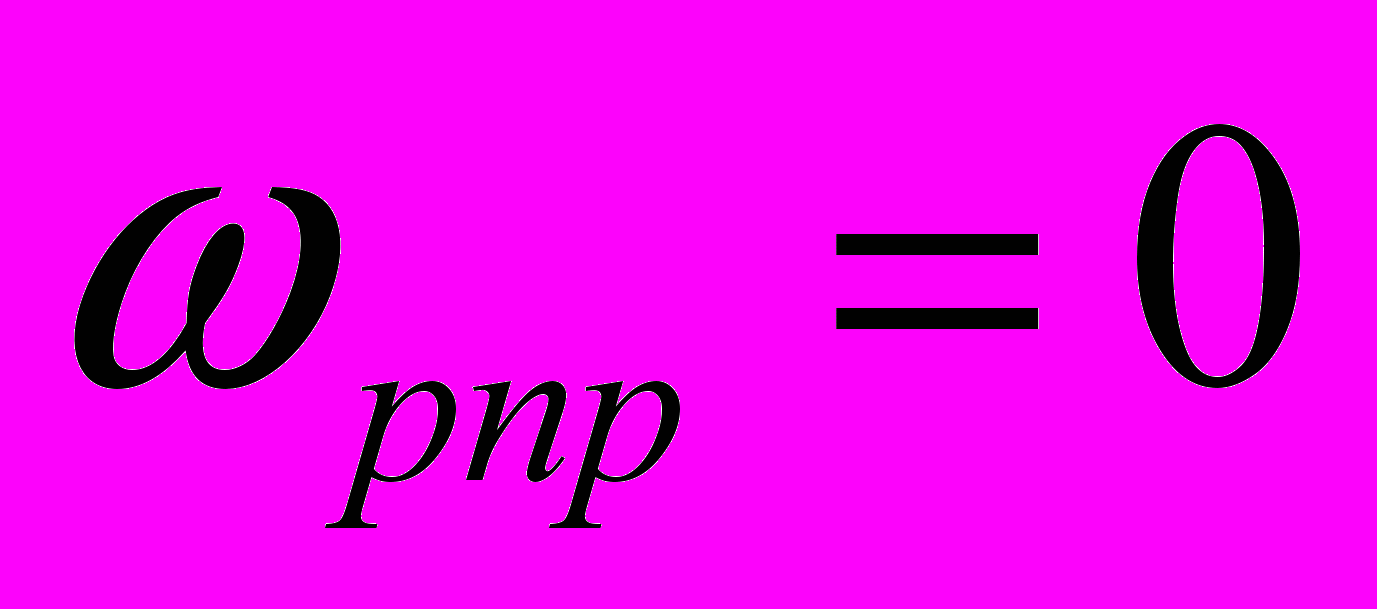. Тоді відповідно до (3) кутова швидкість тіла обертання має змінюватися за законом (рис. 2)
.
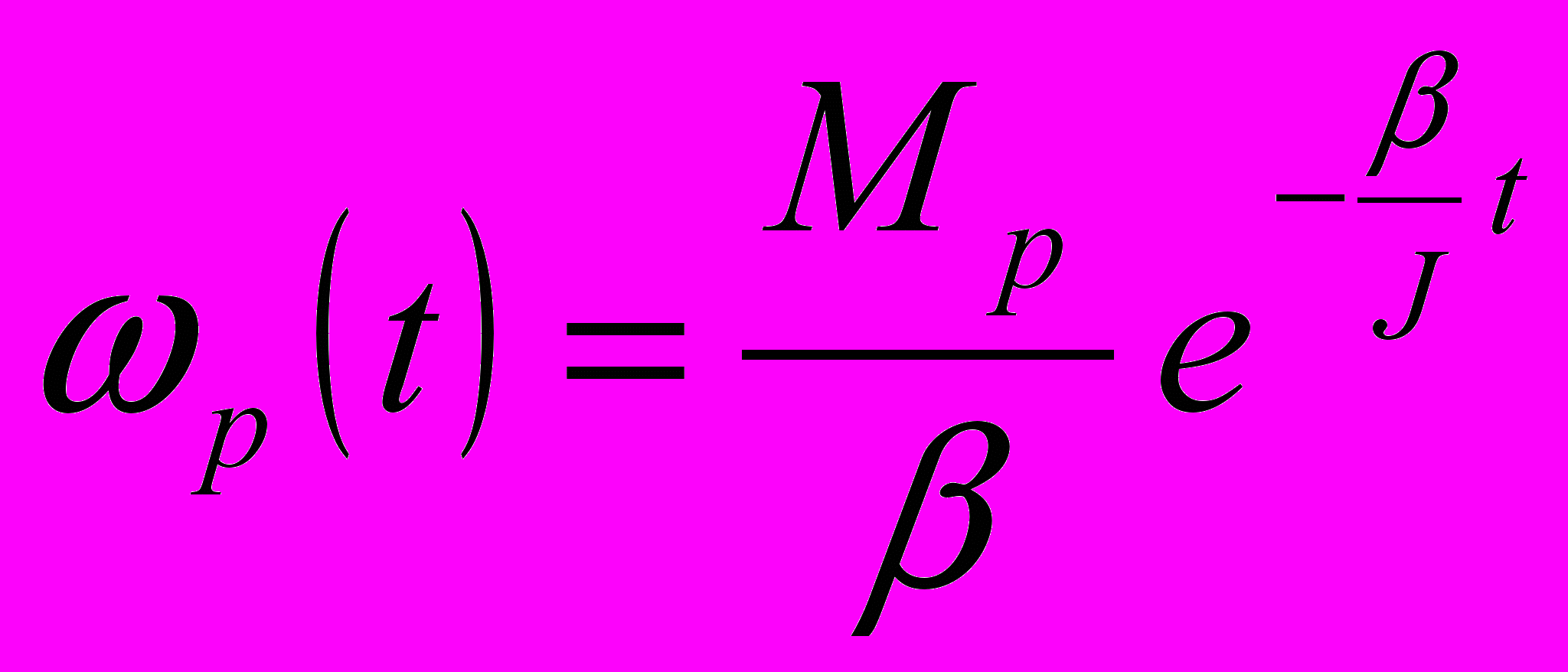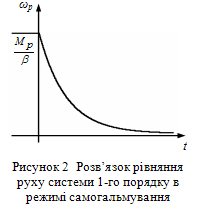
Рисунок 2 - Розв’язок рывняння руху системи 1-го порядку в режимі самогальмування
Оскільки повна зупинка ротора зі зразковим моментом інерції та без нього відбувається за однакової кутової швидкості
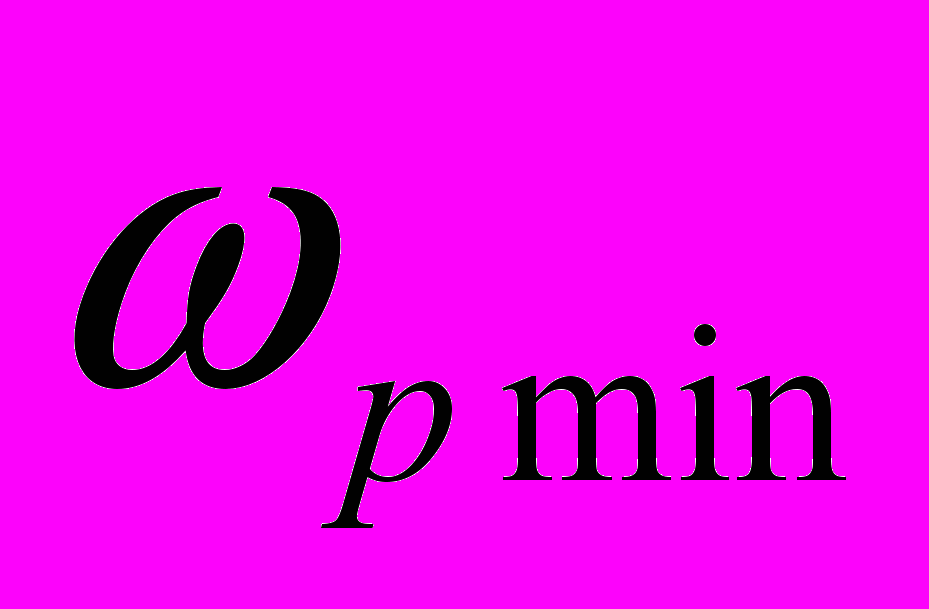, то: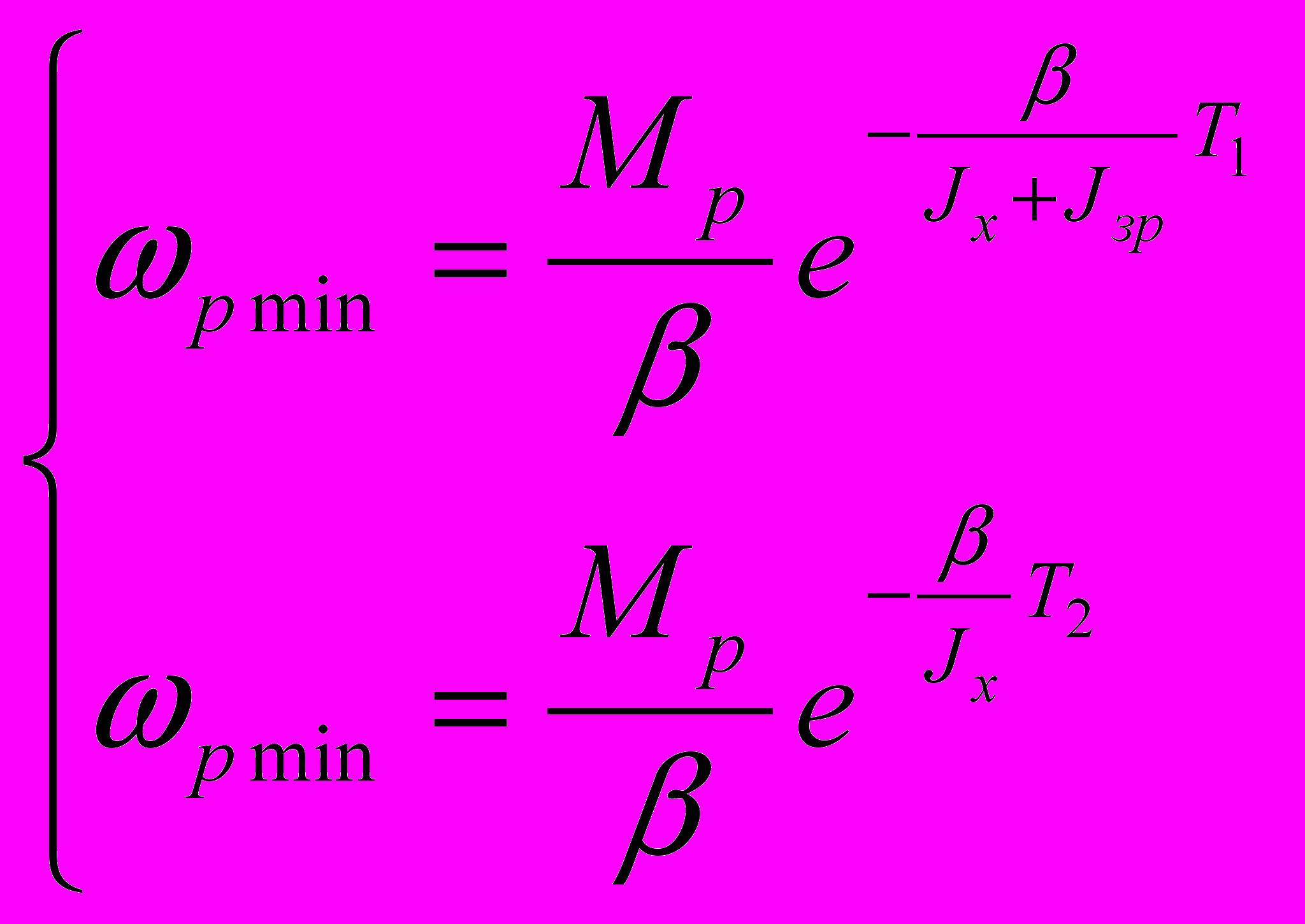
,звідки випливає, що:
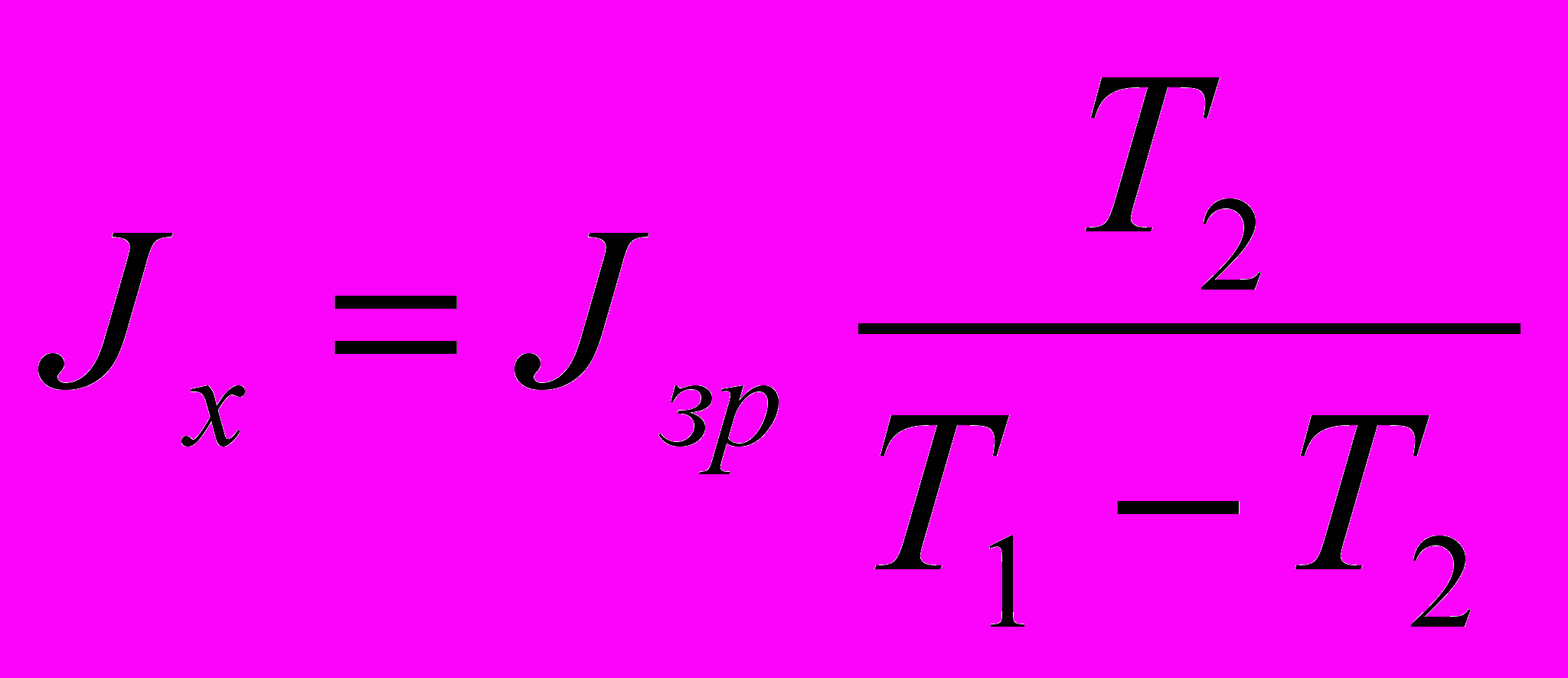.Як бачимо, такий підхід хоча і має певні вади, дозволяє позбутися тих недоліків, які мають місце в існуючому методі самогальмування.
Математична модель перетворювача моменту інерції 2-го порядку. Відповідно до [1], рівнянням руху таких систем (механічна частина деяких з них показана на рис. 3) буде:
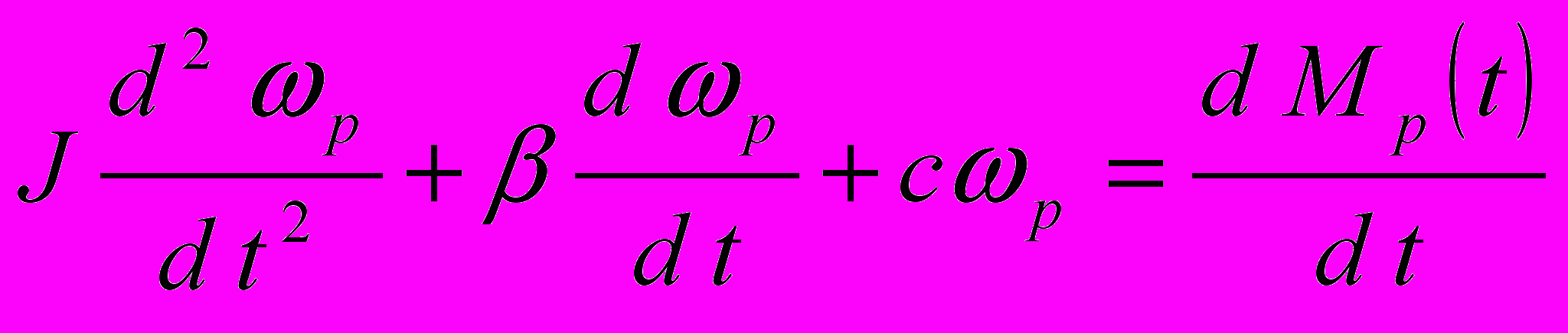, (5)яке отримано на підставі рівняння (1).
В залежності від співвідношення між моментом інерції
та коефіцієнтами розсіювання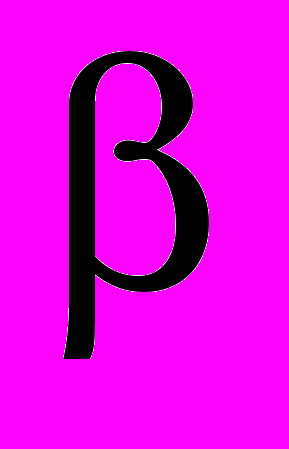 
і жорсткості 
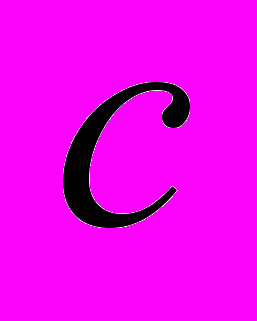можливі, як відомо, три режими роботи перетворювача: - аперіодичний (
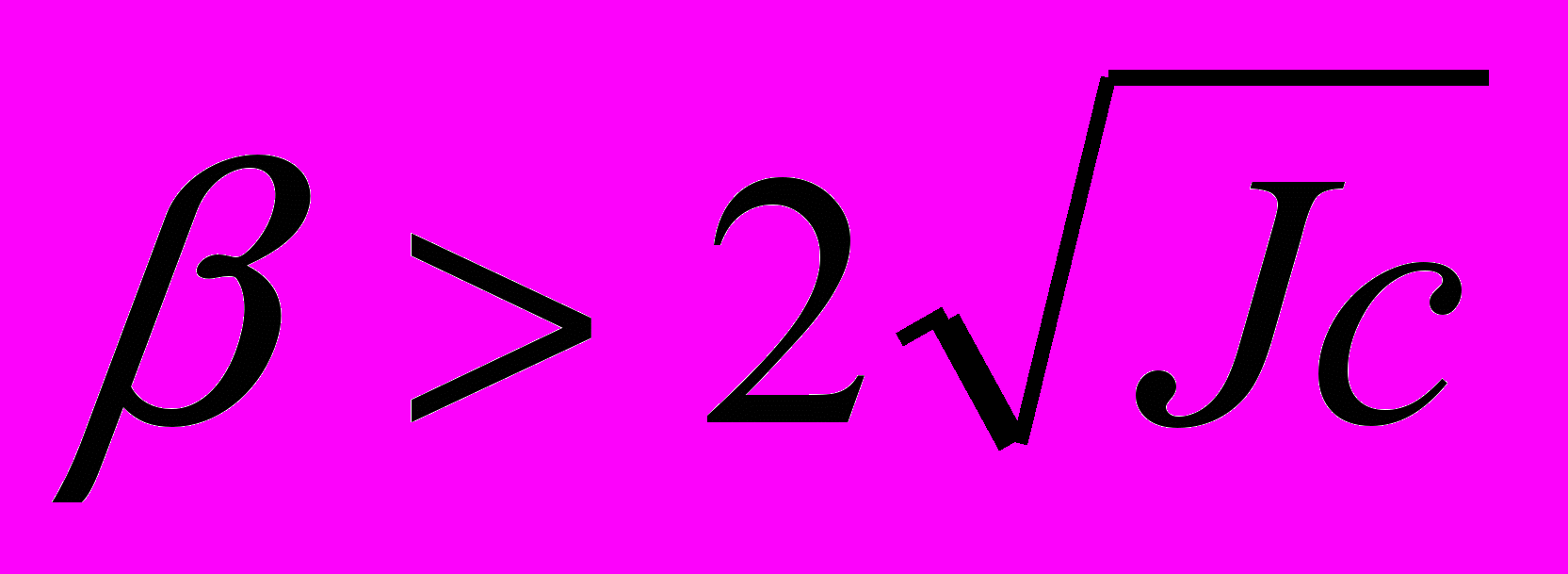) з розв’язком
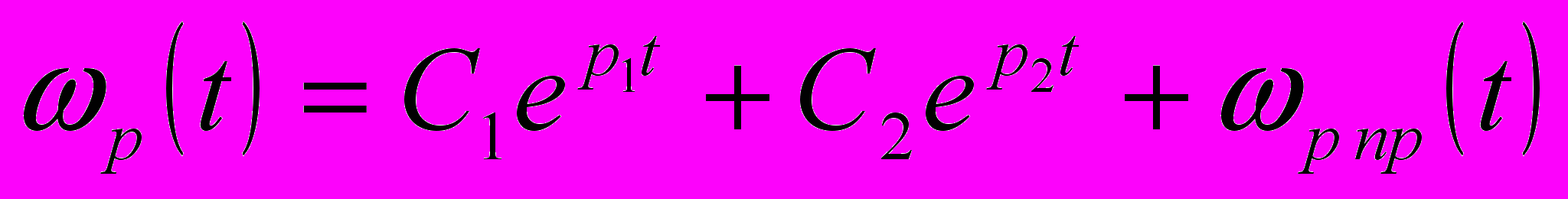, (6)де
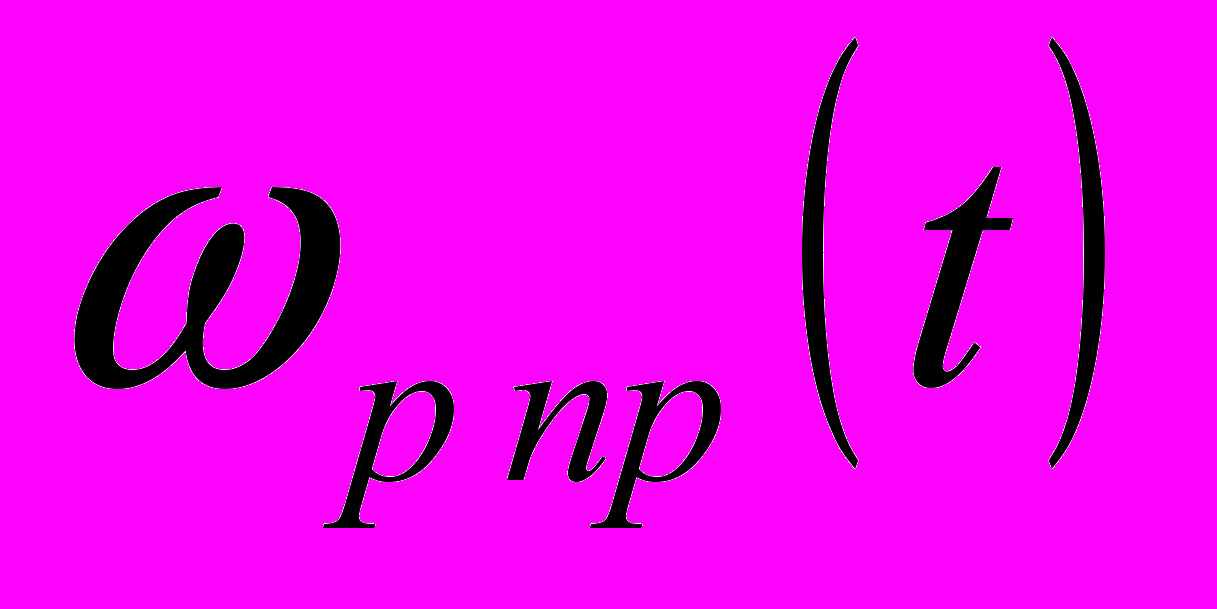- примусова складова кутової швидкості; 
, 
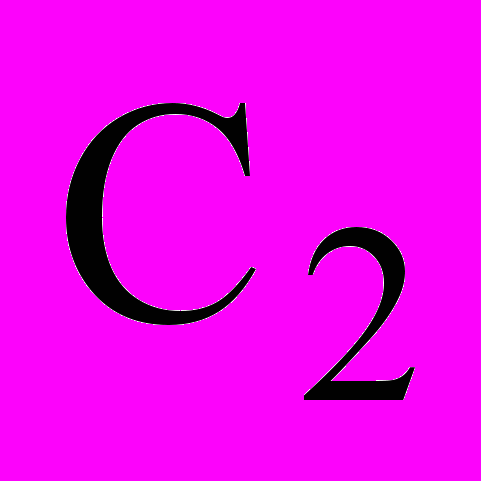- сталі інтегрування, що враховують незалежні початкові умови, а 
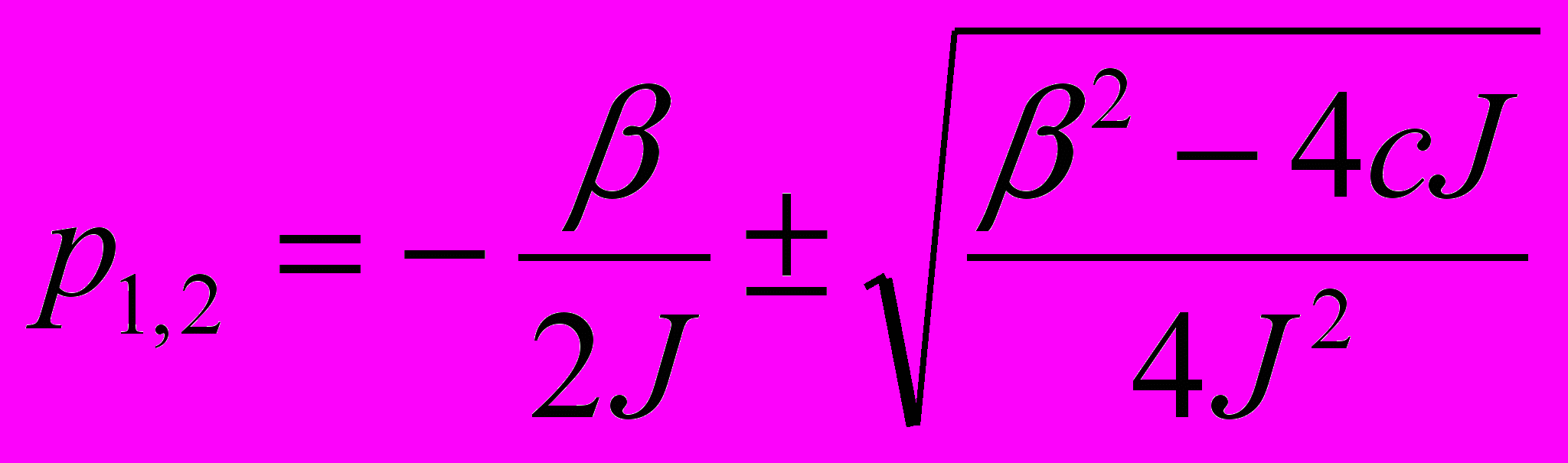- корені характеристичного рівняння; - коливальний (
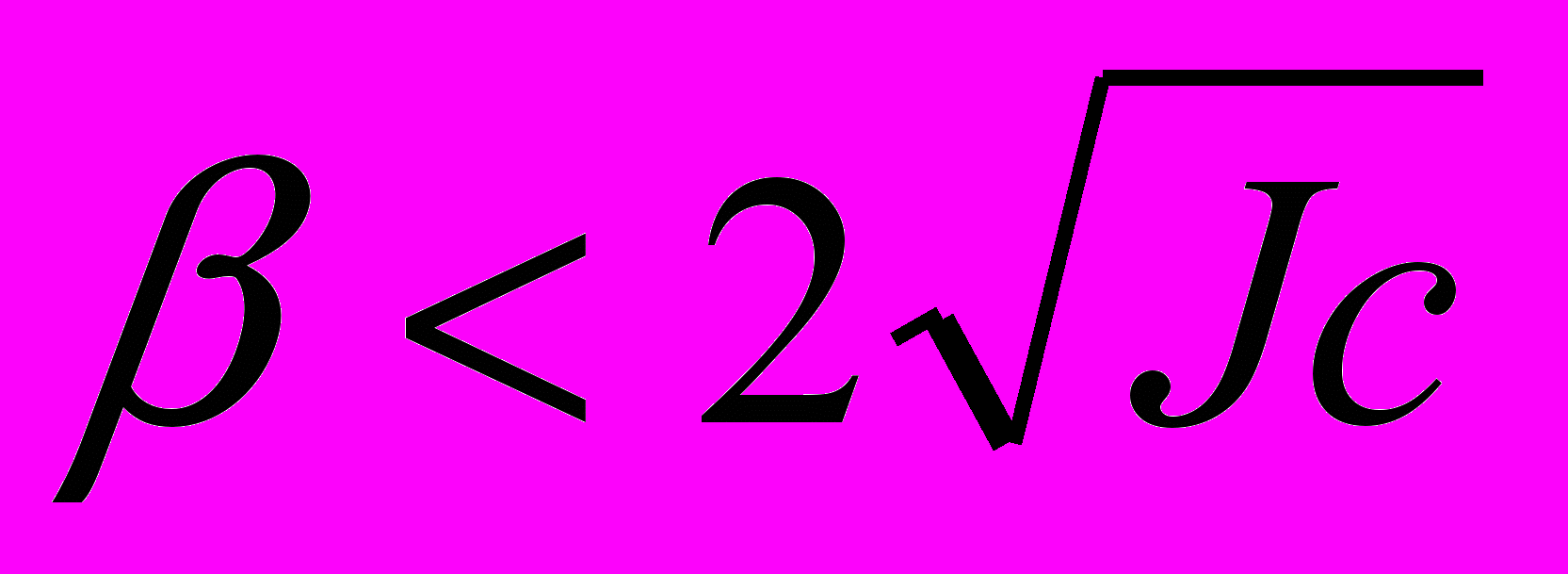) з розв’язком
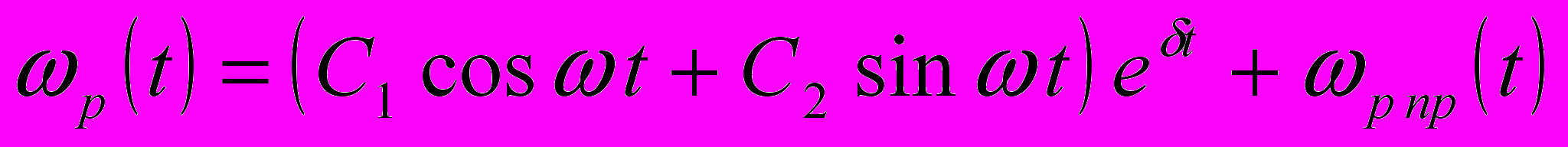, (7)де
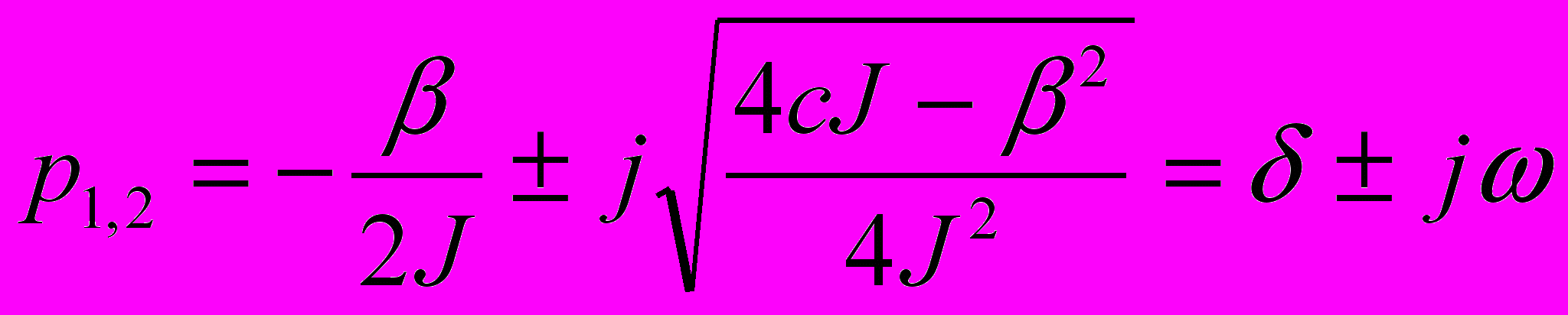; - критичний (
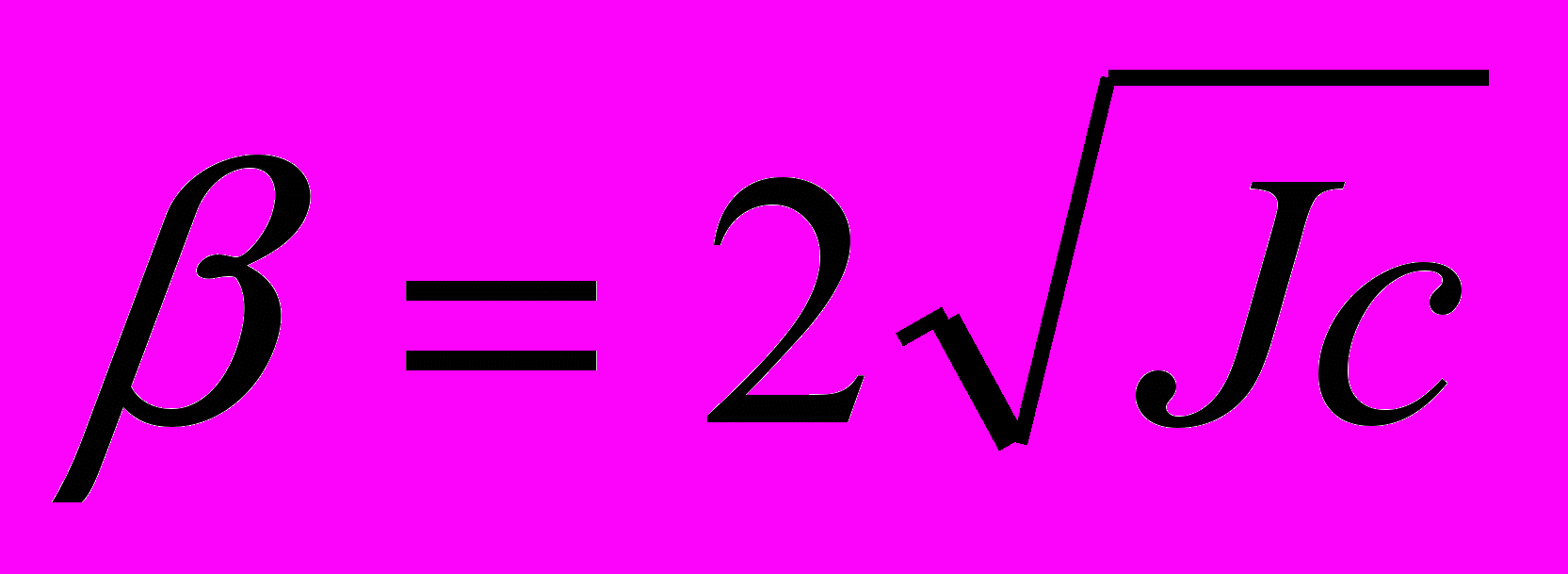) з розв’язком
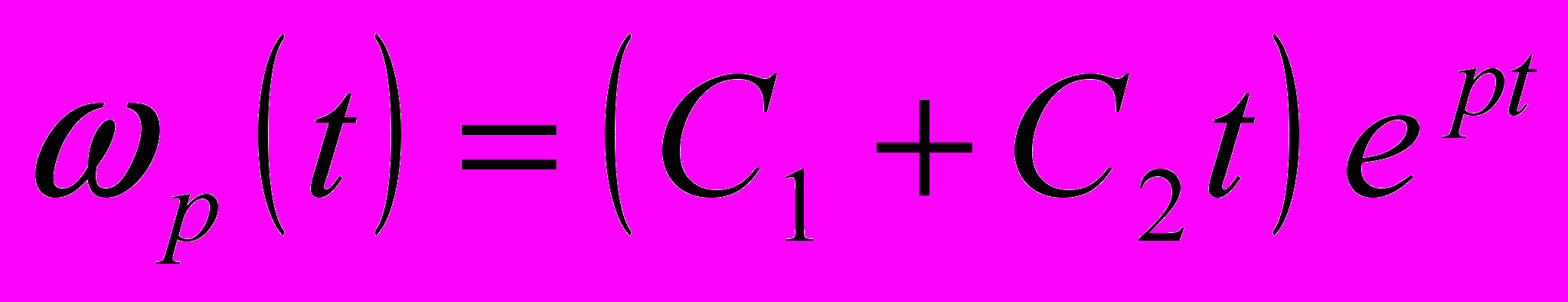, (8)де
. 
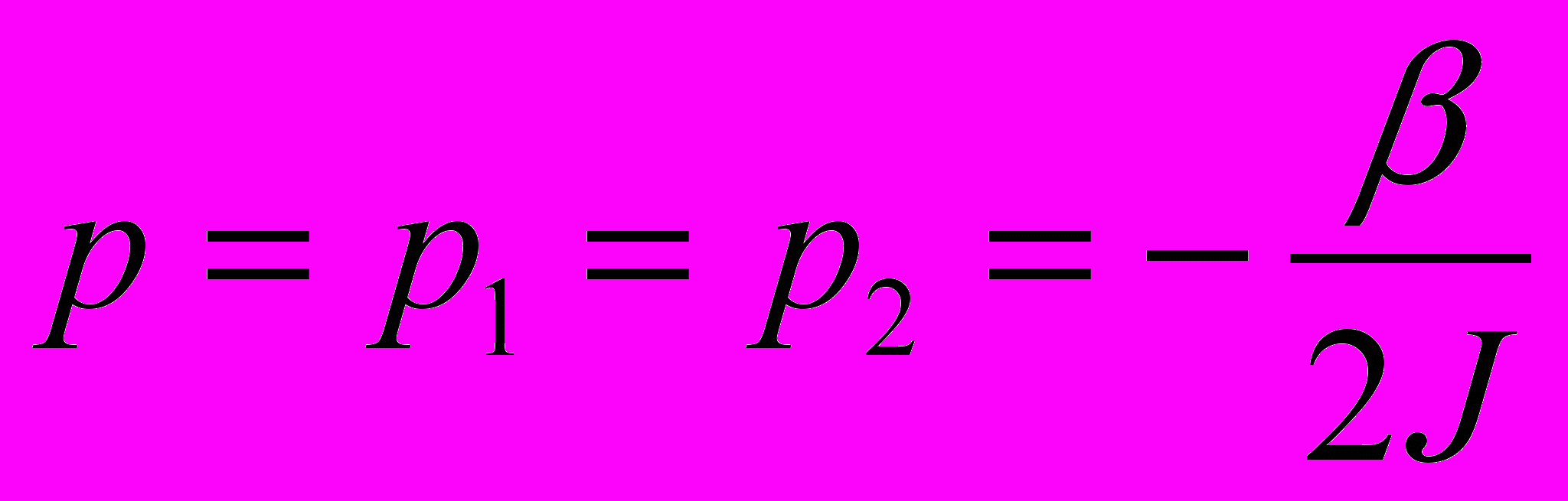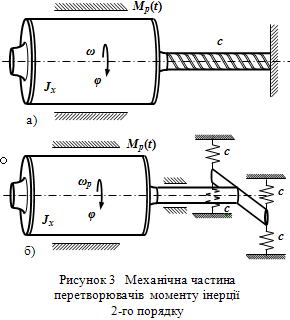
Рисунок 3 - Механічна частина перетворювачів моменту інерції 2-го порядку
Існуючі методи перетворення моменту інерції перетворювачів 2-го порядку. Серед основних існуючих методів перетворення моменту інерції до даної групи, тобто таких, які базуються на рівняннях руху механічних систем, що мають 2-й порядок, необхідно віднести три методи: метод крутильних коливань [3, 7], прямий метод вимірювання [4], метод допоміжного маятника [3].
Всі три методи використовують коливальний режим роботи. Слід зауважити, що останній метод дещо відрізняється від двох перших, оскільки в ньому обертальний рух відбувається навколо точки, а не осі, а ротор є накопичувачем і кінетичної енергії, і потенціальної. Проте диференціальне рівняння руху має другий порядок і даний метод слід віднести до названої групи методів.
Метод допоміжного маятника.
Суть методу полягає в тому, що ротор, який встановлено на призмі, здійснює коливання як фізичний маятник. За періодом коливань маятника
можна визначити момент інерції [3]: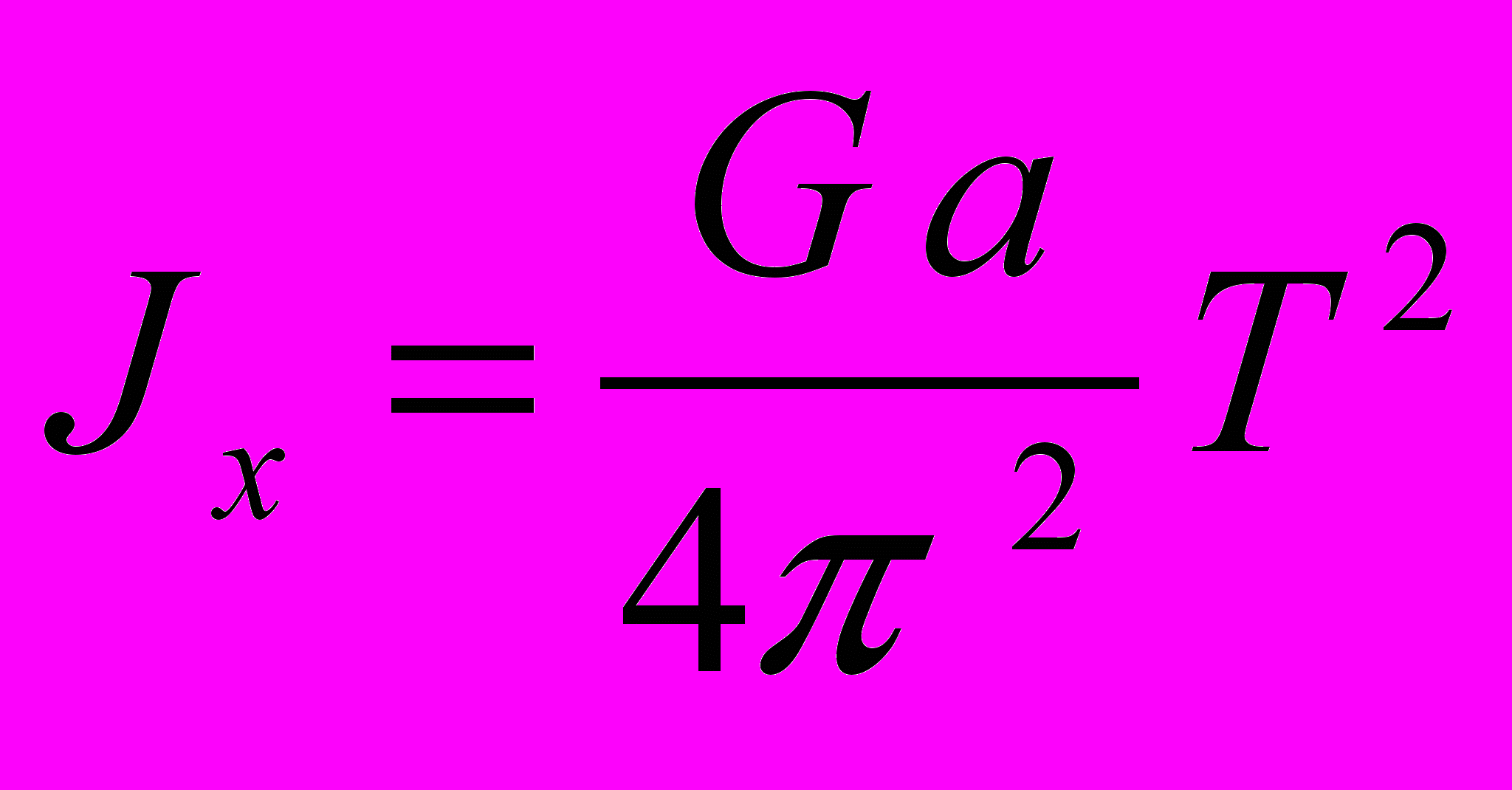
,де
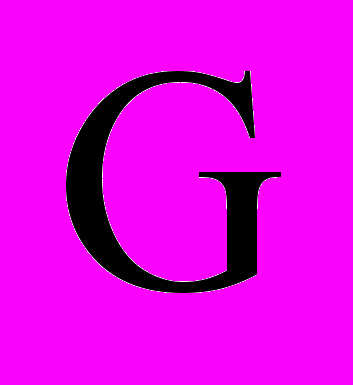- вага ротора; 
- до центра тяжіння від осі обертання.Основним і суттєвим недоліком цього методу є необхідність розбирання системи.
Крім того, результат отримано на основі лінеаризації нелінійного диференціального рівняння руху фізичного маятника і може бути застосовано за умови малих амплітуд коливань. Чим більше кут відхилення
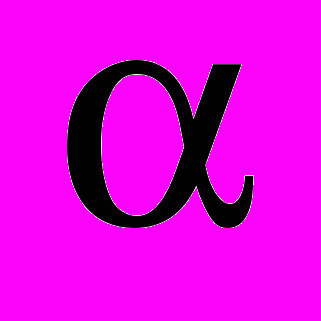буде відрізнятися від 
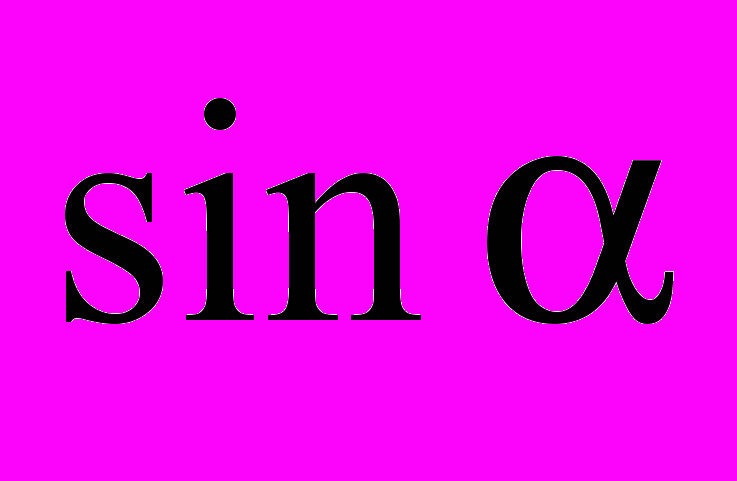, тим менш точним буде результат вимірювання за цим методом.Метод крутильних коливань.
Суть методу полягає в тому, що ротор двигуна підвішують у вертикальному положенні на стальному дроті і приводять його в крутильний коливальний рух. При цьому визначається період малих крутильних коливань, який потім порівнюють з періодом коливань зразкового тіла, що має зазделегіть відомий момент інерції.
Момент інерції ротора при цьому визначають наступним чином [7]:
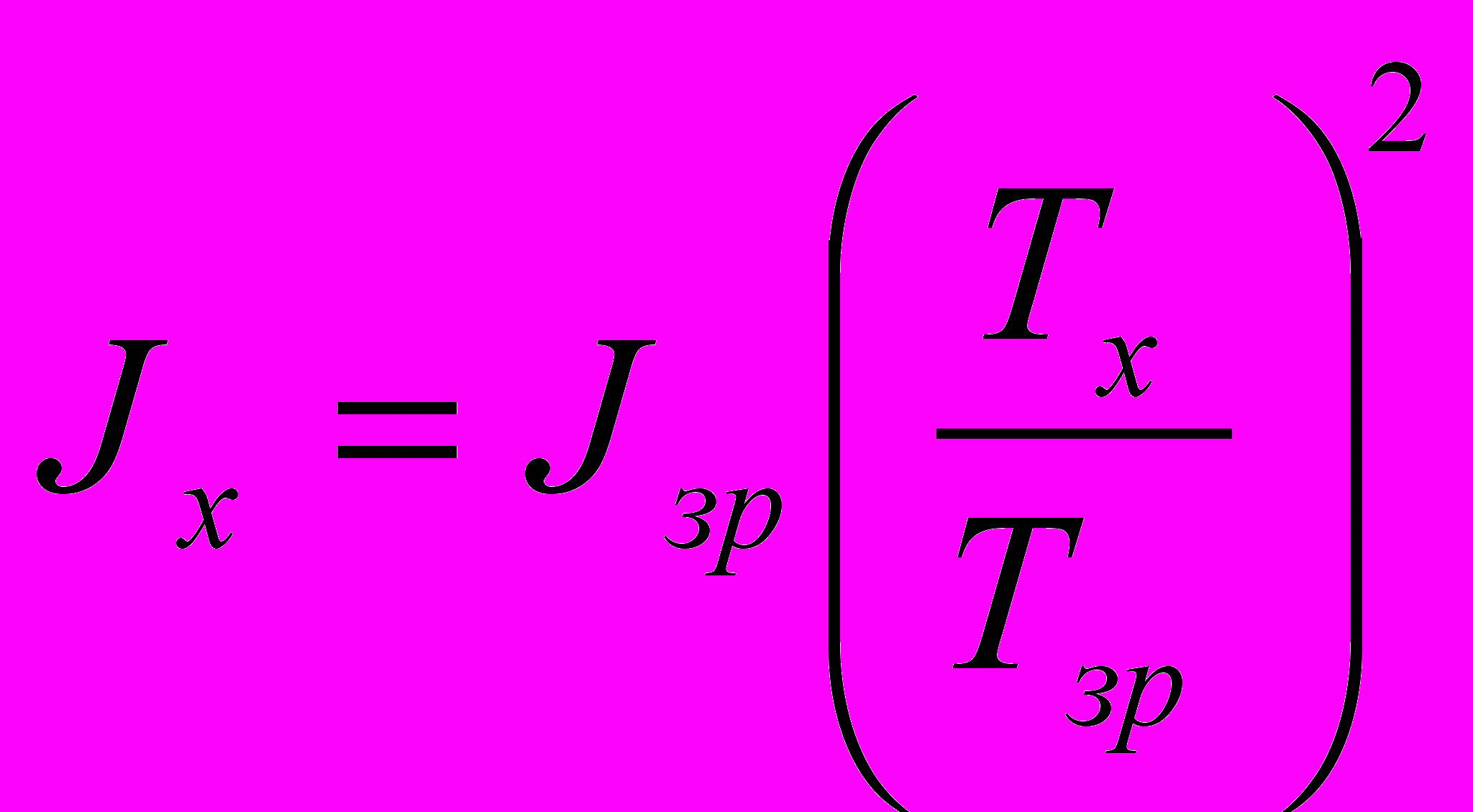, (9)де
- момент інерції зразкового тіла; 
- період коливань зразкового тіла;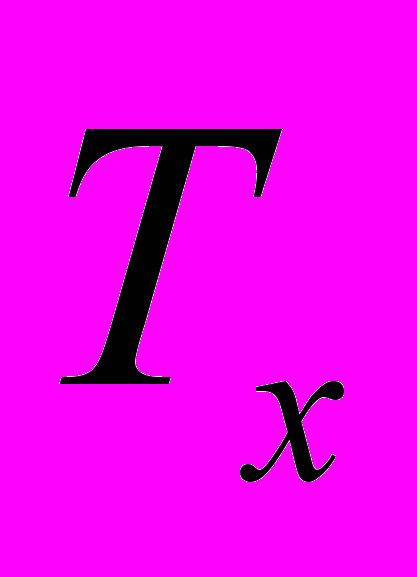 
- період коливань ротора, момент інерції якого визначають.Основним і суттєвим недоліком розглянутого методу вимірювання моменту інерції є необхідність розбирання машини, що підвищує собівартість даної операції і принципово не дозволяє автоматизувати процес визначення інформативного параметра.
Крім того, як це випливає з формули (7) для коливального режиму роботи, співвідношення (9) не є точним, оскільки не враховує механічних втрат енергії в системі. І якщо для даного методу, враховуючи мале значення коефіцієнта розсіювання енергії
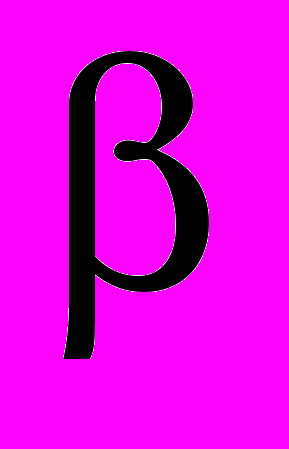, яким можна в межах допустимої похибки знехтувати, це не суттєво, то для різних модифікацій методу крутильних коливань, які дозволяють не розбирати електричну машину, наприклад [7], ця обставина значно зменшує точність вимірювання моменту інерції і накладає на цей процес суттєві обмеження.Прямий метод (метод пружного гальмування).
В цьому методі пропонується вимірювати момент інерції асинхронної машини, коли її ротор загальмовано, обмотки статора заживлені симетричною напругою номінальної частоти, а до ротора випробовуваного двигуна закріплено вимірювальний важіль, що взаємодіє із сенсором зусилля [4].
Суть методу полягає в формуванні на обмотці її статора прямокутного імпульсу номінальної напруги, тривалість якого перевищує час перехідного процесу перетворювача, та в гальмуванні валу ротора через вимірювальний важіль сенсором зусилля.
При заживлених обмотках статора після завершення в перетворювачі перехідного процесу, вимірюють момент
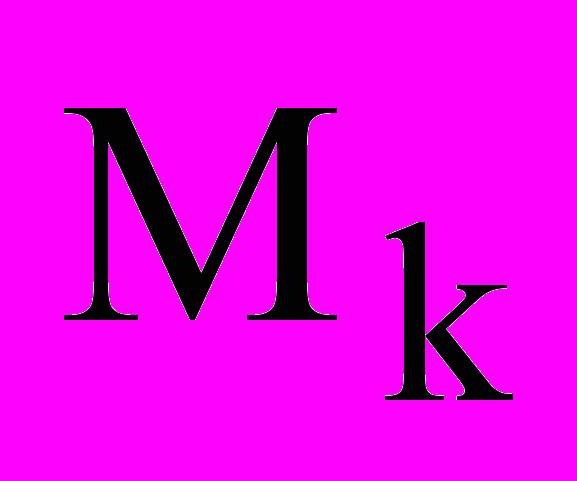, а після знеживлення обмоток вимірюють час 
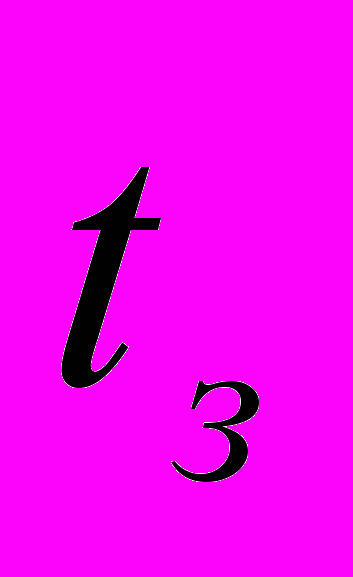заспокоєння вільних коливань ротора. Тоді значення моменту інерції 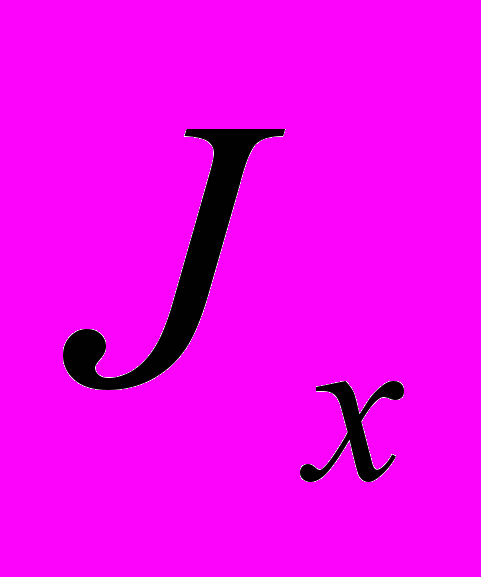знаходять за формулою:
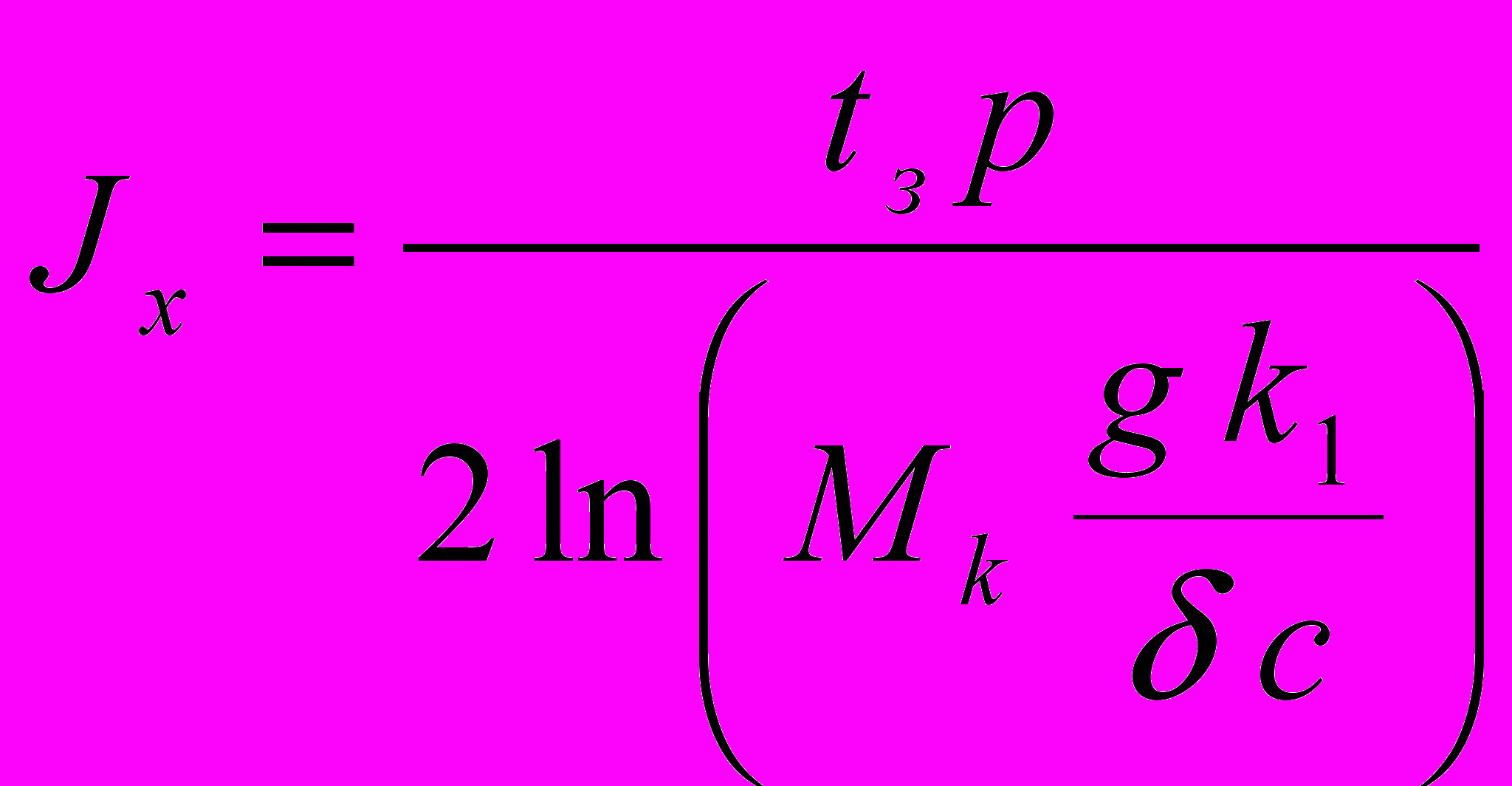,де
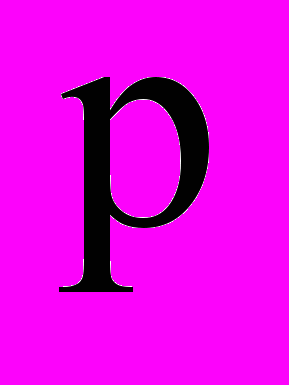- коефіцієнт заспокоєння; 
- постійна тяжіння;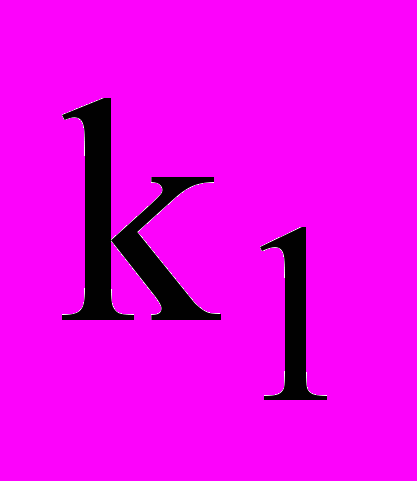 
- функція перетворення сенсора зусилля; 
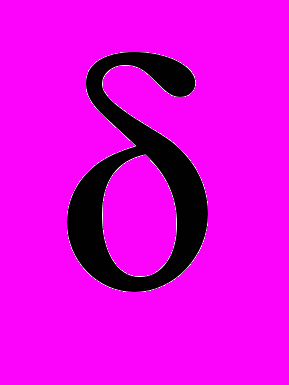- нормована величина, що характеризує момент закінчення вільних коливань ротора.Даний метод реалізує методологію неруйнівного контролю і має значно вищу швидкодію (
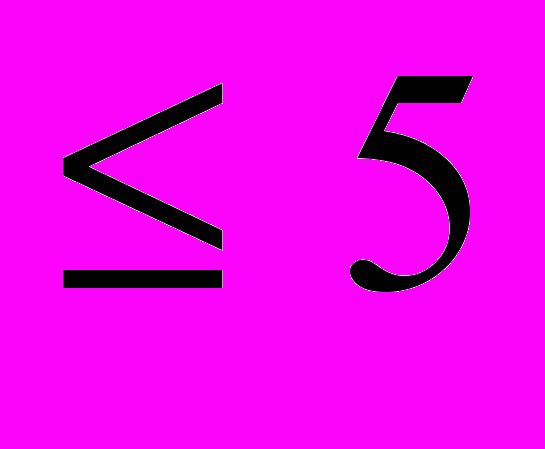сек) та меншу похибку вимірювання (
) в порівнянні з вищенаведеними методами.До недоліків даного способу визначення моменту інерції слід віднести необхідність застосування до електродвигуна під час проведення вимірювання “короткого замикання”, який є аварійним режимом роботи цього електротехнічного пристрою.
Можливі методи перетворення моменту інерції перетворювачів 2-го порядку. Аналіз рівняння (5) механічної системи та його розв’язків (6-8) показує, що принципово існують і інші можливості експериментального визначення моменту інерції, математичні моделі яких будуть базуватися на диференціальному рівнянні стану 2-го порядку.
Наприклад, якщо в режимі коливального самогальмування (рис. 5) визначити логарифмічний декремент
загасання коливання механічної системи перетворювача, то на підставі (5, 7) момент інерції ротора можна розрахувати за формулою: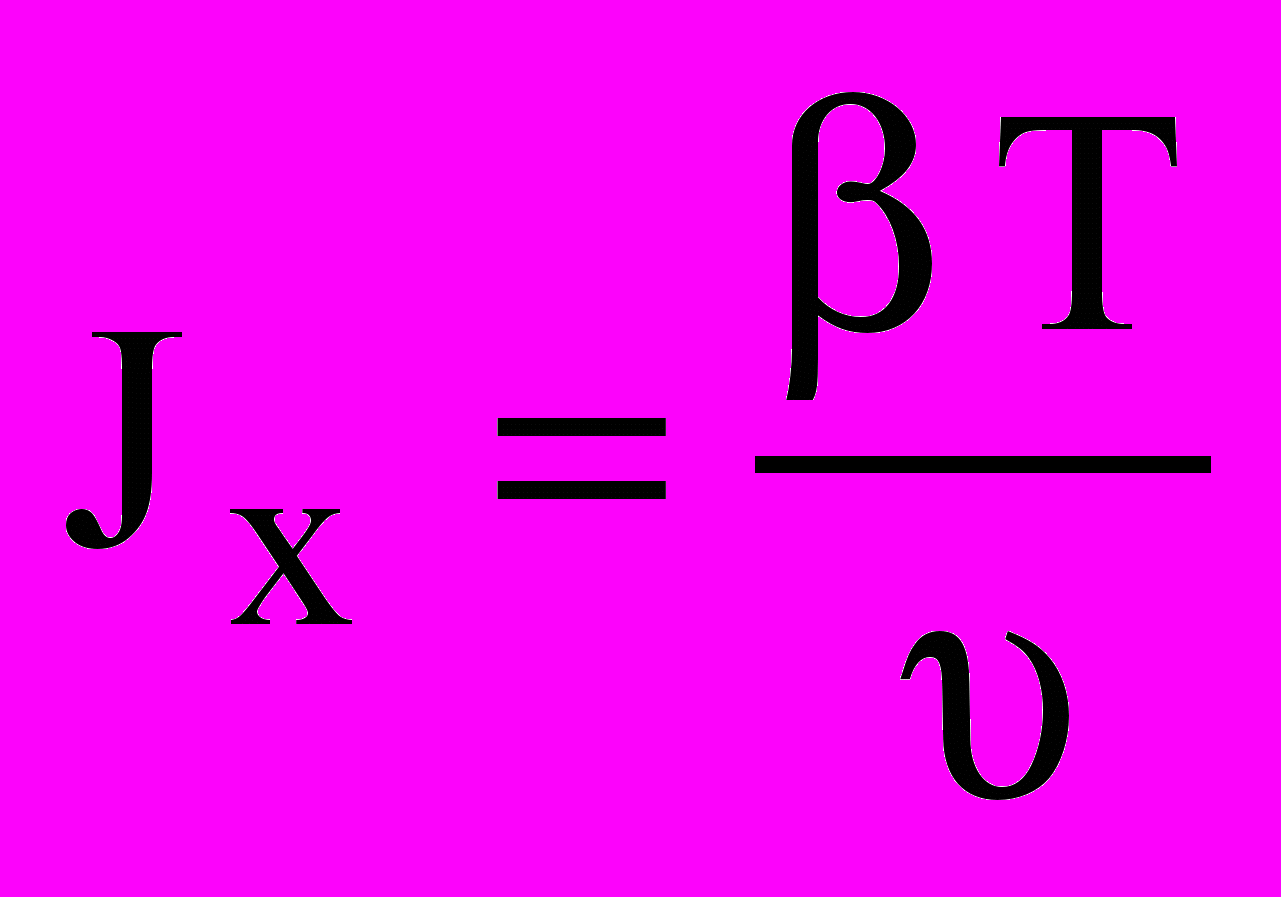
.
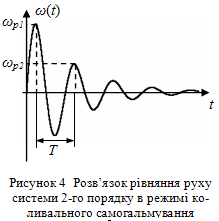
Рисунок 4 - Розв’язок рівнянння руху системи 2-го порядку в режимі коливального самогальмування
Вимірювання ж часу для підвищення точності визначення моменту інерції доцільно здійснювати не в точках максимумів або мінімумів кутової швидкості, а в точках зміни напряму обертання, в яких кутова швидкість дорівнює нулю.
Математична модель перетворювача моменту інерції 3-го порядку. Відповідно до [5] для даної механічної системи (рис. 5) система рівнянь Лагранжа другого роду має вид:
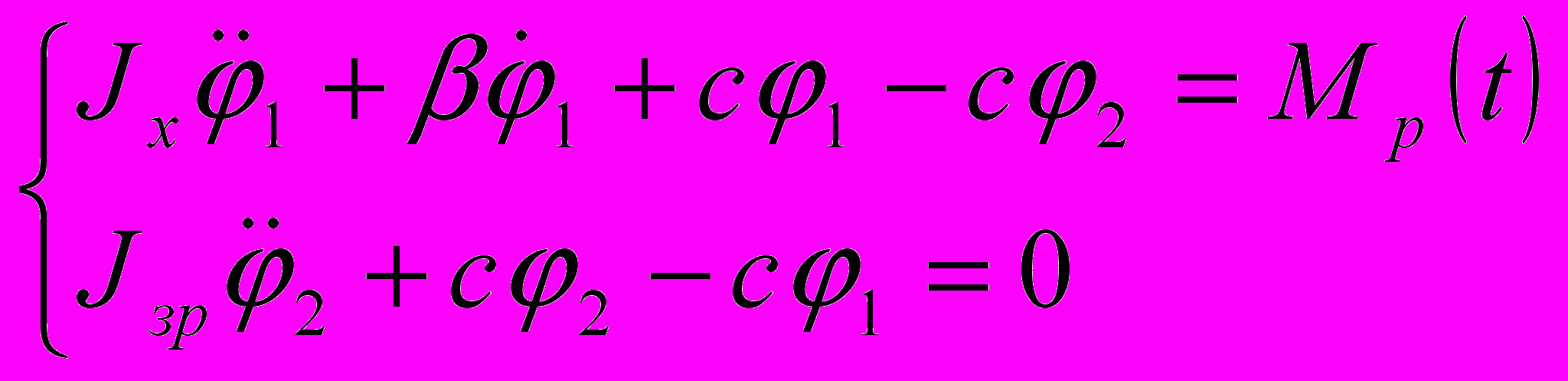,а рівняння руху відносно кутової швидкості обертання –
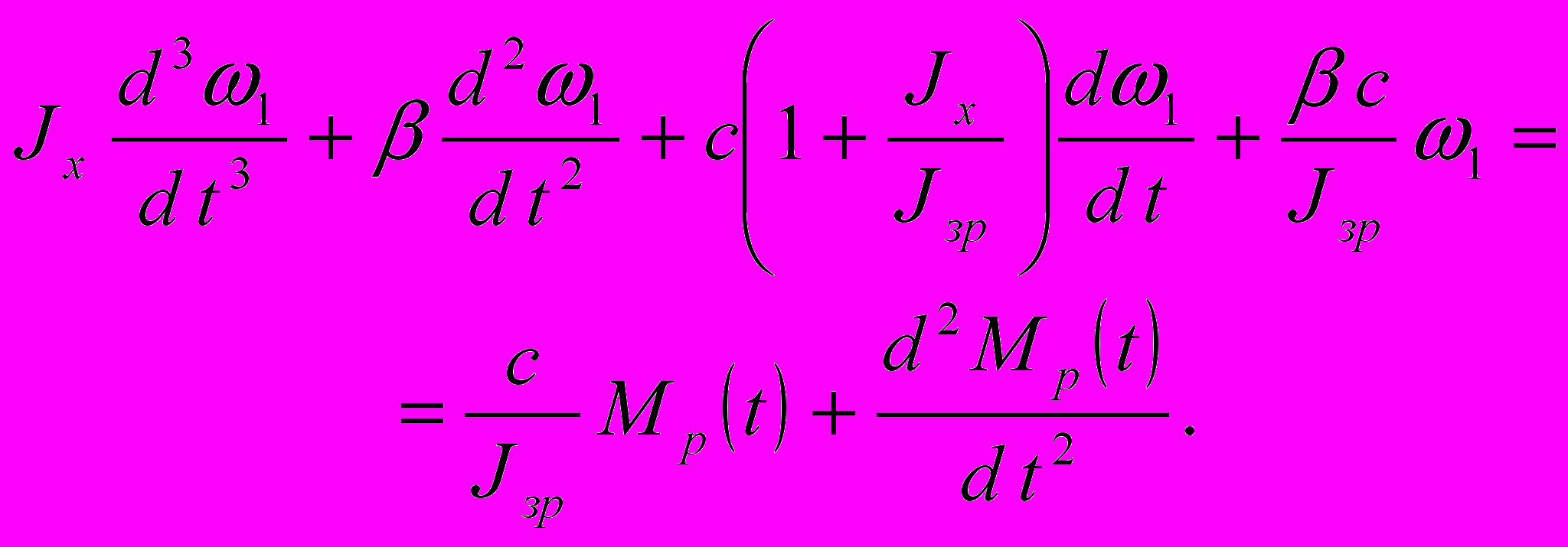
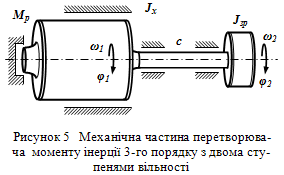
Рисунок 5 - Механічна частина перетворювача моменту інерції 3-го порядку з двома ступенями вільності
Існуючі та можливі методи перетворення моменту інерції перетворювачів 3-го і більш високих порядків. Що ж стосується перетворювачів моменту інерції 3-го і більш високих порядків, то ні методів, ні самих пристроїв на даний час не існує.
Висновки. В роботі розглянута та застосована загальна методика математичного моделювання перетворювачів моменту інерції. Наведені їх математичні моделі. Здійснені огляд, систематизація і класифікація існуючих та можливих методів перетворення. Створені необхідні сприятливі умови для розробки нових перспективних методів перетворення моментів інерції тіл обертання.
ЛІТЕРАТУРА
- Ведміцький Ю.Г., Кухарчук В.В. Рівняння Лагранжа як основа теорії перетворювачів моменту інерції // Вісник КДПУ. – вип. 3/2005 (32). – С.89-91.
- Фаворин М. В. Моменты инерции тел: Справочник. – М.: Машиностроение, 1977. – 511 с.
- Гернет М. М., Ратобыльский В. Ф. Определение моментов инерции. – М.: Машиностроение, 1985. – 248 с.
- Кухарчук В. В. Спосіб вимірювання моменту інерції ротора електричних машин //Ученые записки Симферопольского государственного университета. – 1998 – Спец. Выпуск. - С. 214-219.
- Кухарчук В.В., Ведміцький Ю.Г. Математична і електричні моделі перетворювача моменту інерції тіл обертання з двома ступенями вільності. // VІІІ МКУСС-2005, 2005. - Вінниця. - С. 69.
- Поджаренко В.О., Кучерук В.Ю. Новий спосіб вимірювання моменту інерції електричних машин // Автоматизація технологічних процесів та промислова екологія. -1997.- вип. №1. - С. 23-27.
- Потапов Л. А., Юферов Ф. М. Измерение вращающих моментов и скоростей вращения микроэлектродвигателей. - М.: Энергия, 1976. – 121 с.
Стаття надійшла 15.04.2006 р.
Рекомендована до друку
д.т.н., проф. Родькіним Д.Й.
Вісник КДПУ. Випуск 3/2006 (39). Частина 1.