Классические законы г. Менделя 42

Вид материала

Закон

Содержание Глава VIII СТАТИСТИЧЕСКИЕ МЕТОДЫ ПСИХОГЕНЕТИКИ 1. Генетика количественных признаков и ее значение для психогенетики Модель одного гена Генотипическое значение. Аддитивное генотипическое значение. Доминантные отклонения. Таблица 8.1 Определение среднего значения генотипа в популяции

Подобный материал:

• Лекции тема 7, 852.45kb.
• Законы делимости (дискретности) в мире животных и растений. Законы наследственности, 276.87kb.
• Н. брумберг, В. Попов, 78.9kb.
• Решение задач по генетике с использованием законов Г. Менделя, 419.2kb.
• Лекция 18. Генетика. Первый и второй законы Г. Менделя, 108.91kb.
• Темы уирс: Этапы развития медицинской генетики. Наследственно обусловленные патологические, 69.44kb.
• Применение flash – анимаций на уроках биологии, 68.93kb.
• Направление: Искусство и гуманитарные науки, 1316.91kb.
• Основные причины и условия жестокого поведения Введение, 1346.89kb.
• Лекция Классические маркеры I типа, 237.04kb.

Глава VIII СТАТИСТИЧЕСКИЕ МЕТОДЫ ПСИХОГЕНЕТИКИ

Образно говоря, статистика является «правой рукой» психогене­тики. Как уже отмечалось, психогенетика изучает вопросы наследова­ния поведенческих признаков и психологических функций в популя­циях, и по определению эта наука озабочена не отдельными индиви­дуальностями, а их разнообразием, т.е. популяционной изменчивостью (вариативностью, дисперсией) изучаемого признака. Иными слова­ми, психогенетику интересуют вопросы, касающиеся характеристик распределений (среднего, дисперсии и других моментов распределе­ния) индивидуальных значений по изучаемому признаку в популя­ции, а также вопросы о том, влиянием каких факторов — генетичес­ких или средовых — можно объяснить наблюдаемую изменчивость. Статистики, описывающие параметры популяции (выборки), приво­дятся в любом руководстве по статистике, поэтому здесь мы их ка­саться не будем, а перейдем сразу к статистическим решениям соб­ственно психогенетических задач.

Как уже говорилось, психологические признаки принадлежат к классу количественных признаков, законы наследования которых су­щественно отличаются от менделевских. Особая здесь и статистика. Последовательно рассмотрим связанные с этим вопросы.

Конец страницы №183

Начало страницы №184

1. ГЕНЕТИКА КОЛИЧЕСТВЕННЫХ ПРИЗНАКОВ И ЕЕ ЗНАЧЕНИЕ ДЛЯ ПСИХОГЕНЕТИКИ

Генетика количественных признаков предоставляет психогенети­ке общую теорию, на базе которой строится методологический аппа­рат изучения природы индивидуальных психологических различий.

В самом общем виде генетика количественных признаков — при­менительно к психологическим задачам — исходит из того, что люди отличаются друг от друга по ряду сложных психологических призна­ков, и предлагает модель, в рамках которой межиндивидуальные раз­личия по этим признакам могут быть описаны в терминах фенотипи-ческой дисперсии признака в популяции, а сама фенотипическая дис­персия может быть разложена на составляющие ее генетические и средовые компоненты.

МОДЕЛЬ ОДНОГО ГЕНА

Количественные генетические модели позволяют описать измеря­емые эффекты различных генотипов, возможных в отдельно взятом локусе, и суммировать эффекты всех локусов, контролирующих тот или иной поведенческий признак. Причем количество локусов, конт­ролирующих данный признак, обычно неизвестно, и чаще всего уче­ные делают допущение о том, что генетический контроль большин­ства поведенческих признаков осуществляется большим количеством генов, вклад которых в дисперсию изучаемого признака примерно одинаков. Одним из характерных признаков количественных генети­ческих моделей является то, что они предполагают существование нормально распределенных фенотипических значений признаков, контролируемых множеством генов, эффекты которых, в свою оче­редь, опосредованы средовыми влияниями. Многолетние психологи­ческие исследования показали, что распределение большинства по­веденческих признаков действительно соответствует нормальной кри­вой. Поэтому допущение о нормальности распределения признака, контролируемого большим количеством генов и значимых средовых влияний (т.е. являющегося мультифакторным), — психологически адек­ватная и статистически удобная модель для психогенетики. Важно за­метить, что ожидаемая от полигенной системы нормальность распре­деления, будучи статистически удобной и эмпирически оправданной, не зависит от количества генов, контролирующих эту систему. Как статистические характеристики, так и теоретические положения, ле­жащие в основе моделей количественной генетики, одинаково пра­вомерны для моделей, содержащих 1, 2, 25 или более генов. Именно поэтому мы начнем изложение основных признаков количественной генетики с рассмотрения модели одного гена и только потом перейдем к модели множественных генов (так называемой полигенной модели).

Конец страницы №184

Начало страницы №185



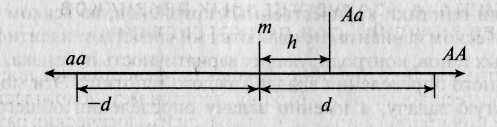
Рис. 8.1. Соотношение трех генотипов, возможных для двуаллельной сис­темы.

Параметры dnh представляют собой разницы эффектов генов А-а. Аа может нахо­диться на любой из сторон от т, что, соответственно, будет влиять на знак h. В примере, показанном на рисунке, значение h положительно [253, 342].

Генотипическое значение. Генотипическим значением называется некоторое количественное значение, приписываемое определенному генотипу. Так, в рамках простейшей двуаллельной системы (А и а) существуют два параметра, определяющие измеряемые эффекты трех возможных генотипов (АА, Аа и аа). Этими параметрами являются параметр d, представляющий собой удвоенную разницу между гомо­зиготами АА и аа, и параметр И, определяющий измеряемый эффект гетерозиготы Аа таким образом, что он не является точным усреднен­ным эффектом двух гомозигот. Средняя точка между двумя гомозиго­тами, точка т, отражает среднее эффектов двух гомозиготных геноти­пов. Параметры d и И называются эффектами генотипов. Графически соотношение трех генотипов показано на рис. 8.1. Если в локусе отсут­ствует доминантность, то h будет равняться нулю, а значение геноти­па Аа будет соответствовать значению в точке т. При полной доми­нантности значение Аа будет равняться значению АА. Если же доми­нантность А частична, то Аа будет находиться ближе к точке АА (или аа, в зависимости от направления доминантности) и значение h бу­дет положительным.

Приведем пример. Предположим, что известны гены, которые влияют на вес человека. Предположим также, что нормальный вес женщин среднего ро­ста составляет 48-70 кг, т.е. разница между максимальным и минимальным значениями по весу равна 22 кг. Теперь предположим, что гены, контролирую­щие вариативность веса человека, расположены на каждой из 22 аутосомных хромосом (по одному на каждой), причем все гены вызывают примерно одина­ковые эффекты. Тогда в рамках нашей гипотетической системы гомозиготы по каждому из изучаемых генов вкладывают примерно ± Уг кг (от средней точки), в зависимости от того, являются они гомозиготами по аллелям, обозначаемым заглавной буквой (АА, ВВ, СС и т.д. — обладание этими генотипами повышает рост), или гомозиготами по аллелям, обозначаемым строчными буквами (aa, bb, ее и т.д. — обладание этими генотипами понижает рост). Рассмотренный при­мер, однако, невероятен по крайней мере по двум причинам: во-первых, генов, контролирующих вариативность веса человека, мы не знаем и, во-вторых, в ре­альной ситуации вклады генотипов, скорее всего, будут меньше или больше, чем ^х/г кг, затрудняя подсчет генотипического значения.

Конец страницы №185

Начало страницы №186

Модели генетики количественных признаков, во всяком случае в их классическом варианте, не являются ни средством идентификации конкретных генов, контролирующих вариативность признака, ни сред­ством точного определения вклада каждого генотипа. Эти модели ре­шают другую задачу, а именно задачу определения общего вклада генотипа в вариативность изучаемого признака в популяции.

Аддитивное генотипическое значение. «Аддитивное генотипическое значение» представляет собой фундаментальное понятие количествен­ной генетики, поскольку оно отражает, насколько генотип «истинно наследуется». Аддитивный (суммарный) эффект генов представляет собой не что иное, как сумму эффектов отдельных аллелей. Более точно, аддитивное генотипическое значение есть генотипическое зна­чение, обусловленное действием отдельных аллелей данного локуса. Генная доза генотипа подсчитывается на основе того, сколько алле­лей определенного типа (например, аллелей А) присутствует в дан­ном генотипе. Если наличие определенного аллеля в генотипе увели­чивается на 1 (как это происходит, например, в случае перехода от генотипа аа к генотипу Ad), то аддитивное значение увеличивается на некоторую определенную величину. На рис. 8.2 дана графическая иллюстрация аддитивного генотипического значения при отсутствии доминантности. Эффект генотипа аа = — d, поэтому эффект аллеля (гена) а = Vi{— d); эффект генотипа AA — d, поэтому эффект аллеля А = Vi(d); соответственно, эффект генотипа Аа = Vi(d) + ^lh{— d) — 0. Заметим, что аддитивные генные значения зависят от частоты встречаемости аллелей в популяции. При отсутствии доминирования аддитивный эффект полностью определяет генотипическое значение. Доминантность, однако, вносит самые разные отклонения от ожида­емых значений, — об этом пойдет речь ниже.

Теперь допустим, что каждый аллель генотипа имеет некоторый средний эффект. В этом смысле аддитивное генотипическое значение

представляет собой сумму сред­них эффектов каждого аллеля для всех аллелей, входящих в гено­тип. Каждый аллель характеризу­ется определенным аддитивным эффектом, соответственно, при унаследовании определенного ал­леля от родителя ребенок насле­дует и аддитивный эффект этого аллеля, т.е. вклад аллеля в гено­тип ребенка будет таким же, ка-

Рис. 8.2. При отсутствии доминант- ким был ег0 (ge) вклад в ге_
ности (п = 0) аддитивное генотипи- нотип родителя. И неважно,
ческое значение определяется генной сколько (много или мало) ajme.
дозои- лей присутствует в данном локу-

Конец страницы №186

Начало страницы №187



Рис. 8.3. Графическое изображение доминантных отклонений.

Наличие доминантности вносит разного рода изменения в аддитивное генотипи­ческое значение.

Обозначения: • — аддитивные генотипические значения при условии полной до­минантности; * — наблюдаемые аддитивные значения, определяемые на основе генных доз; D — доминантные отклонения, которые представляют собой разницу между ожидаемыми аддитивными значениями, соответствующими ситуации пол­ной доминантности, и значениями, наблюдаемыми для определенных генных доз.

се или сколько локусов вовлечено в контроль вариативности по тому или другому признаку. Иными словами, аддитивное генотипическое значение представляет собой не что иное, как сумму вкладов каждого аллеля в генотип.

Доминантные отклонения. Доминантные отклонения есть мера того, насколько генотип отличается от своего ожидаемого аддитивного зна­чения.

Доминантные отклонения (рис. 8.3) — это разница между ожида­емыми и наблюдаемыми значениями генотипов. Феномен доминант­ности допускает, что два аллеля одного локуса могут взаимодейство­вать друг с другом и тем самым менять генотипическое значение, которое наблюдалось бы в том случае, если бы они были независимы друг от друга и делали независимые вклады в генотипическое значе­ние. Так, в результате взаимодействия аллелей Аа наблюдаемое гено­типическое значение меньше того, которое ожидалось бы при усло­вии полной доминантности. Напротив, значения ААи аа выше ожи­даемых при допущении, что аллель А полностью доминантен по отношению к аллелю а.

Доминантность обязана своим возникновением уникальному со­четанию аллелей в данном локусе. Очевидно, что генотип потомка, наследующего только один аллель от каждого из родителей, в подав­ляющем большинстве случаев не может воспроизвести уникальность генотипа одного из них. Поэтому потомки будут отличаться от своих родителей в той мере, в какой аллели данного локуса не суммируются линейным образом при определении генотипического значения.

Конец страницы №187

Начало страницы №188

Рассмотрев типы генетических влияний, определим, как частоты встречаемости аллелей, определяющие эти типы, задают среднее зна­чение генотипа в популяции. Допустим, что в популяции аллели А и а встречаются с частотами р и д, соответственно. Тогда первая колонка в табл. 8.1 показывает три возможных генотипа, вторая — частоты их встре­чаемости в популяции (при допущении, что особи в этой популяции образуют родительские пары случайным образом) и третья — значение генотипа. Популяционное среднее получается путем умножения значений генотипа на частоту встречаемости тех аллелей, которые этот генотип составляют, и последующего суммирования значений все трех генотипов.

Таблица 8.1 Определение среднего значения генотипа в популяции

Генотип	Частота	Значение	Частота х значение
АА Аа Аа	Р2 2pq q2	+d h -d	рЧ 2pqh -q4
2 =d(p2-q2) +2hpq