Профессиональная направленность обучения математике студентов химико-технологических специальностей технических вузов (на примере раздела «Дифференциальные уравнения») 13.

Вид материала

Автореферат

Содержание Научный руководитель Гусев Валерий Александрович Общая характеристика исследования Теоретико-методологическую основу Методами исследования Научная новизна Теоретическая значимость Практическая значимость На защиту выносится следующие положения Достоверность результатов Апробация и внедрение основных положений и результатов исследования. Основное содержание работы Пропедевтика основных изучаемых понятий Теоретический курс включает следующие направления Практический курс включает решение следующих типов задач Используются следующие методы На основе деятельностного подхода используются следующие виды организации учебной деятельности Q при изменении температуры T Задача на химическую реакцию первого порядка (уравнение с разделяющимися переменными). Задача на химическую реакцию второго порядка (уравнение с разделяющимися переменными). ... Полное содержание

Подобный материал:

• Программа-минимум кандидатского экзамена по специальности 01. 01. 02 «Дифференциальные, 37.38kb.
• Учебное пособие для модульно-рейтинговой технологии обучения Бийск, 2035.37kb.
• Дифференциальные уравнения (вопросы к экзамену), 26.43kb.
• Календарный план чтения лекций, 27.51kb.
• Методическая направленность обучения элементарной математике студентов математических, 292.15kb.
• Обыкновенные дифференциальные уравнения, 17.54kb.
• Вопросы к экзамену по курсу «Дифференциальные уравнения», 22.85kb.
• Планы семинарских занятий по дисциплине «Экономическая теория» для студентов технических, 527.66kb.
• Уравнения математической физики направление подготовки, 18.02kb.
• Методики преподавания иностранных языков является организация обучения иностранному, 148.71kb.

На правах рукописи


ЛЬВОВА Валерия Дмитриевна

Профессиональная направленность обучения математике студентов химико-технологических специальностей технических вузов (на примере раздела «Дифференциальные уравнения»)


13.00.02 – теория и методика обучения и воспитания

(математика, уровень профессионального образования)


АВТОРЕФЕРАТ

диссертации на соискание ученой степени

кандидата педагогических наук


Астрахань 2009

Работа выполнена на кафедре математического анализа Астраханского государственного университета


Научный руководитель: доктор педагогических наук,

профессор

Аммосова Надежда Васильевна.


Официальные оппоненты: доктор педагогических наук,

профессор

Гусев Валерий Александрович


кандидат физико-математических наук,

доцент

Коваленко Борис Борисович


Ведущая организация: Российский университет дружбы народов


Защита диссертации состоится 15 декабря 2009 года в 13.00 часов на заседании диссертационного совета ДМ 212.009.05 при Астраханском государственном университете по адресу: 414056, г. Астрахань, пл. Шаумяна, д.1, ауд.101


С диссертацией можно ознакомиться в научной библиотеке Астраханского государственного университета.


Текст автореферата размещен на официальном сайте Астраханского государственного университета http: www.aspu.ru 13 ноября 2009 года.


Автореферат разослан____ ноября 2009 года.


Ученый секретарь

диссертационного совета Кенжалиева С.З.

Общая характеристика исследования


Актуальность исследования. В Федеральном Законе от 30 марта 2002 года «Основы политики Российской Федерации в области развития науки и технологий на период до 2010 года и дальнейшую перспективу» отмечена необходимость повышения престижа и привлекательности научно-технической деятельности. Меняются приоритеты в профессиональном образовании. Одними из наиболее перспективных вновь становятся инженерные профессии. Намеченные приоритеты в науке и технологиях обусловливают необходимость в высококвалифицированных инженерных кадрах, в том числе и химико-технологических специальностей.

На современном этапе в образовании усиливается роль фундаментальных наук, ставится акцент на их прикладное использование. Математика – язык инженерных исследований, основа инженерного образования, в работе инженера призвана решать профессиональные задачи. Этим объясняется необходимость тесной связи преподавания математики с потребностями профессии.

Профилирующие дисциплины на разных специальностях технических вузов применяют различный математический аппарат, используют разные математические методы, в том числе численные и приближенные, но, практика показывает, что разница в изложении курса фундаментальной математики обусловлена чаще всего лишь требованиями Государственного образовательного стандарта. Изучение опыта математической подготовки студентов химико-технологических специальностей говорит о том, что студенты 1-го и 2-го курсов плохо осведомлены о роли математики в будущей профессии, слабо мотивированы на изучение предмета, а преподаватели специальных дисциплин в дальнейшем часто отмечают отсутствие необходимой математической базы. Это говорит о том, что нет преемственности между курсом фундаментальной математики и профилирующими дисциплинами, а в преподавании математики недостаточно соблюдается профессиональная направленность.

Проблема профессиональной направленности давно интересует исследователей и достаточно широко представлена в работах Н.А. Аитова, Н.В. Аммосовой, П.Р. Атутова, Ю.К. Бабанского, В.А. Гусева, А.Я. Кудрявцева, Г.Л. Луканкина, М.И. Махмутова, В.М. Монахова, А.Г. Мордковича, Р.А. Низамова, Э.Д. Новожилова, Г.И. Саранцева, М.Ф. Фахтулина, М.И. Шабунина, Л.В. Шкериной.

Реализацию профессиональной направленности при обучении студентов- гуманитариев описывали Т.А. Гаваза, Н.А. Дергунова, Р.М. Зайкин, А.А. Соловьева. Проблеме профессиональной направленности математической подготовки в средних специальных учебных заведениях посвящены диссертационные работы Т.М. Алиевой, Ю.В. Булычевой, Н.Н. Грушевой, Л.М. Наумовой, Н.Н. Лемешко.

Совершенствованию математической подготовки в техническом вузе уделяли большое внимание А.Н. Колмогоров, Б.В. Гнеденко, Л.Д. Кудрявцев,
Е.Н. Мирославлев, А.Д. Мышкис, С.М. Никольский, В.Е.Шукшунов, А.Р. Янпольский, С.А. Яновская и др. Свое видение решения проблемы профессиональной направленности преподавания математики в техническом вузе для разных специальностей описывали в диссертационных исследованиях М.С. Аммосова, И.В. Бабичева, О.В. Бочкарева, Е.А. Василевская, З.Г. Дибирова, И.Г. Михайлова, С.В. Плотникова, Н.А. Тарасова, С.И. Федорова.

Ф.К. Мацур разработаны направления математической подготовки студентов-химиков классических университетов на основе межпредметных задач, И.Г. Михайловой исследована степень применения тем курса математики, используемых в подготовке инженера, в том числе и инженера-химика, в условиях профессиональной направленности межпредметных связей. Однако ни одним из этих авторов не затрагивается проблема профессиональной направленности методики обучения математике студентов химико-технологических специальностей технических вузов. Некоторые задачи с химическим и химико-технологическим содержанием представлены в учебниках и пособиях И.И. Баврина, А.А. Гусака, В.В. Шершакова.

В то же время недостаточно разработан комплексный подход решения проблемы профессиональной направленности преподавания математики для химико-технологических специальностей. Существует необходимость определения профессионально значимых для химико-технологических специальностей разделов математики, выявления роли профессиональной направленности при обучении математике на этих специальностях, описания системы мер, необходимых для ее реализации, разработки методики профессионально направленного обучения математике на химико-технологических специальностях технических вузов.

В этой связи выявлены основные противоречия:

• между потребностями химической промышленности в высококвалифицированных инженерных химико-технологических кадрах, обладающих достаточной математической компетентностью для решения профессиональных задач в современных условиях, и реально осуществляемой математической подготовкой в технических вузах;
  
• между фактическими математическими знаниями студентов и требованиями общетехнических и специальных дисциплин;
  
• между требованиями усиления фундаментализации технического образования и необходимостью реализации профессиональной направленности на химико-технологических специальностях;
  
• между широтой направлений изучения профессиональной направленности, представленной в современной педагогической и научно-методической литературе, и отсутствием соответствующих разработок для химико-технологических специальностей.
  

Обнаруженные противоречия обусловливают актуальность нашего исследования.

Проблема исследования состоит в разработке научно-обоснованного комплексного подхода к реализации профессиональной направленности обучения математике на химико-технологических специальностях втузов.

Объектом исследования является процесс обучения математике студентов химико-технологических специальностей технических вузов.

Предмет исследования – методика преподавания математики с целью реализации профессиональной направленности на химико-технологических специальностях технических вузов.

Цель нашего исследования – теоретическое обоснование и разработка методики профессионально направленного обучения на химико-технологических специальностях технических вузов.

Гипотеза исследования: если вести преподавание математики на химико-технологических специальностях технического вуза («Химическая технология природных энергоносителей и углеродных материалов», «Химическая технология неорганических веществ и материалов», «Химическая технология и биотехнология», «Химическая технология органических веществ и топлива» и т. п.) по разработанной методике реализации профессиональной направленности, включающей:

• преподавание теоретического курса математики с акцентом на профессионально значимый материал: ознакомление студентов с аспектами применения математики в будущей профессии, использование профессиональных примеров, установление соответствия между математическими знаниями и их интерпретацией на химико-технологических специальностях в общетехнических (физика, теоретическая механика, сопротивление материалов, электротехника) и в специальных дисциплинах (математическое моделирование основных процессов химических производств, техническая термодинамика и теплотехника, общая химическая технология и др.);
  
• использование внутрипредметной и межпредметной пропедевтики;
  
• применение совокупностей специально разработанных и подобранных задач: профессионально ориентированных (о концентрации раствора, о разложении вещества, на химические реакции, об очищении газа, об ионизации газа, о теплообмене и др.); пропедевтических; тестовых на закрепление базовых знаний; задач, решаемых численными, приближенными, качественными методами, применимыми в химической технологии, творческих заданий по составлению концептуальных карт, блок-схем, таблиц и планов решения, направленных на закрепление теоретических знаний;
  
• организацию самостоятельной работы студентов химико-технологических специальностей с использованием профессионально направленных дидактических материалов, электронных пособий, включающих теоретический, практический, тестовый и контрольный материал, методических рекомендаций для решения профессионально-прикладных задач, −
  

то это способствует повышению качества математических знаний студентов химико-технологических специальностей и формирует умения применять их в процессе дальнейшего обучения и в будущей профессиональной деятельности.

В соответствии с целью и гипотезой исследования были поставлены следующие задачи:

1. Провести анализ психолого-педагогической литературы по проблеме профессиональной направленности обучения математике в вузах, в частности обучения химиков-технологов.

2. Выявить особенности содержания и методов осуществления математической подготовки студентов химико-технологических специальностей технических вузов и определить, как используются математические знания общетехническими и специальными дисциплинами на химико-технологической специальности, установить соответствие между математическими и профессиональными понятиями.

3. Теоретически обосновать и разработать методику реализации профессиональной направленности для химико-технологических специальностей втуза.

4. Разработать совокупности задач: профессионально-прикладных, формирующих умение математически моделировать процесс или явление; пропедевтических задач; тестовых задач на отработку базовых математических знаний, являющихся математическим аппаратом специальности; творческих заданий на закрепление теоретических знаний; методические рекомендации по решению задач.

5. Разработать профессионально ориентированные дидактические материалы и комплексное электронное пособие для самостоятельной работы студентов химико-технологических специальностей (раздел «Дифференциальные уравнения»).

6. Проверить результативность предложенной методики в ходе экспериментальной работы.

Теоретико-методологическую основу исследования составляют психологическая и общедидактическая теория деятельностного подхода в обучении, труды по общей педагогике и дидактике, философским и методологическим основам математики, работы, посвященные общему математическому образованию, а также проблемам преподавания математики в технических вузах, исследования профессиональной направленности обучения математике в высших учебных заведениях, работы, отражающие использование математических методов в химической технологии.

Методами исследования являются:

• изучение и анализ историко-педагогической, психологической, педагогической, научно-методической и математической литературы по проблеме исследования,
  
• анализ Государственного образовательного стандарта по химико-технологическим специальностям,
  
• анализ учебной и учебно-методической литературы по математике и специальным и общетехническим дисциплинам,
  
• обобщение опыта преподавания в технических вузах,
  
• наблюдение за студентами, беседы с преподавателями,
  
• анкетирование преподавателей и студентов, педагогический эксперимент и обработка его результатов методами математической статистики.
  

Диссертационное исследование проводилось с 2002 по 2009 годы.

Научная новизна исследования заключается в следующем:

1) разработана процедура анализа изучаемого в высшей школе курса математики для выбранной специальности (на примере химико-технологической), вскрыта взаимосвязь таких разделов математики на химико-технологических факультетах технических вузов, как «Дифференцирование и интегрирование», «Дифференциальные уравнения», «Дифференциальные уравнения в частных производных», «Ряды Фурье», «Векторная алгебра», «Линейная алгебра», «Теория вероятностей и математическая статистика» со специальными дисциплинами химико-технологического цикла – «Физическая химия», «Общая химическая технология», «Системы управления химико-технологическими процессами», спецкурсами «Математическое моделирование основных процессов химических производств», «Процессы и аппараты химической технологии»:

− выделены темы математического курса, наиболее значимые при обучении химиков-технологов (производная, дифференциал, оптимизация процессов, неопределенный и определенный интегралы, кратные интегралы, несобственные интегралы, дифференциальные уравнения обыкновенные и в частных производных) и определены основные области использования в химической технологии математических моделей разного типа (задачи гидродинамики, моделирование теплообменных процессов, процессов ректификации, абсорбции, кристаллизации, сушки химических продуктов, моделирование в химической кинетике);

− установлено соответствие между математическими понятиями и их интерпретацией в специальных дисциплинах (производная – скорость химического процесса, интегральная функция распределения – функция распределения времени пребывания в проточных реакторах, дифференциальное уравнение – математическая модель химико-технологических процессов, например гидродинамическая модель потоков частиц в реальных аппаратах и др.);

− выявлена востребованность аппарата дифференциальных уравнений для решения задач химико-технологического содержания при обучении студентов химико-технологических специальностей;

2) раскрыто содержание и разработаны принципы и методика профессионально направленного обучения математике студентов химико-технологических специальностей, основанная на деятельностном подходе:

а) выделен для более глубокого изучения материал изучаемого курса из разделов «Дифференцирование и интегрирование», «Дифференциальные уравнения», «Дифференциальные уравнения в частных производных», «Ряды Фурье», являющийся математическим аппаратом специальности;

б) предложена методика

• осуществления пропедевтики наиболее важных понятий (интеграл – собственный и несобственный, неопределенный и определенный, дифференциальное уравнение, решение дифференциального уравнения, дифференциальное уравнение с разделяющимися переменными, общего и частного решения дифференциальных уравнений);
  
• использования качественных, численных и приближенных методов решения задач химической технологии;
  
• применения метода математического моделирования к профессионально-прикладным задачам (о концентрации раствора; об охлаждении тела; о переходе вещества в раствор; задачи на химические реакции первого и второго порядков; ионизация газа; очищение газа; теплообмен через трубу);
  
• реализации самостоятельной работы студентов с использованием разработанного электронного обучающего пособия, содержащего теоретический, практический, тестовый и контрольный материалы; профессионально ориентированных индивидуальных заданий; организации активной учебной деятельности с элементами проблемного, поискового и перспективно-опережающего обучения;
  

в) разработаны методические требования к совокупностям задач по каждому из перечисленных методических путей;

3. разработаны:
   

а) совокупности задач для химико-технологических специальностей, формирующие умение математически моделировать процесс или явление; пропедевтических задач, необходимых для общетехнических дисциплин; тестовых задач, направленных на отработку базовых математических знаний, являющихся математическим аппаратом специальности; творческих заданий, направленных на закрепление теоретических знаний; математические модели предлагаемых задач химико-технологического содержания;

б) методические рекомендации по преподаванию теоретической и практической частей курса «Дифференциальные уравнения», основанные на применении элементов проблемного, поискового и перспективно-опережающего обучения (использование концептуальных карт, блок-схем, таблиц, планов решения, докладов и др.);

в) комплексное электронное пособие по обыкновенным дифференциальным уравнениям для самостоятельной работы студентов химико-технологических специальностей и профессионально-направленные дидактические материалы.

Теоретическая значимость проведенного исследования состоит в разработке процедуры анализа изучаемого в высшей школе курса математики, выявлении разделов и тем математики, наиболее часто применяемых в общетехнических и специальных дисциплинах на химико-технологических специальностях, определении наиболее применимых в химической технологии математических моделей, установлении соответствия между математическими понятиями и их интерпретацией в химических технологиях, в выявлении востребованности дифференциальных уравнений в профессиональной подготовке студентов химиков-технологов, определении методических путей, позволяющих реализовать профессионально направленное изучение математики на химико-технологических специальностях в техническом вузе, разработке требований к совокупностям задач по каждому из перечисленных методических путей.

Практическая значимость исследования заключается в разработке профессионально-направленной методики преподавания на химико-технологических специальностях, создании методических рекомендаций по изложению теоретического и практического курса (на примере раздела «Дифференциальные уравнения»), в профессионально направленных дидактических материалах и электронном обучающем пособии, содержащем теоретический, практический, тестовый и контрольный материалы, предназначенном для самостоятельной работы студентов, в совокупностях задач: формирующих умение математически моделировать процесс или явление; пропедевтических, необходимых для общетехнических дисциплин; тестовых, направленных на отработку базовых математических знаний, являющихся математическим аппаратом специальности; творческих заданий, направленных на закрепление теоретических знаний.

На защиту выносится следующие положения:

1. С целью эффективной профессиональной подготовки студентов химико-технологических специальностей в процессе обучения математике необходимо: знакомить студентов с аспектами применения профессионально значимых разделов математики в будущей профессии; приводить примеры интерпретации математических понятий в общетехнических и специальных дисциплинах, химико-технологических процессов, описываемых посредством математических моделей; усилить профессиональную направленность изучения разделов математики, выделенных как наиболее важных для будущих химиков-технологов.

2. Разработанный комплексный подход к методике преподавания на химико-технологических специальностях (пропедевтика, адекватные будущей профессии методы решения задач, использование совокупностей профессионально ориентированных задач для реализации разных дидактических целей, организация самостоятельной работы) способствует осуществлению профессиональной направленности обучения и повышению качества математических знаний студентов химико-технологических специальностей.

3. Методика профессионально направленного обучения дифференциальным уравнениям на химико-технологической специальности, включающая:

• пропедевтику дифференциальных уравнений на первом курсе, основанную на необходимости их использования в общетехнических предметах во втором семестре;
  
• использование не только аналитических, но и качественных, численных, приближенных способов решения дифференциальных уравнений, наиболее часто применяющихся в химической технологии;
  
• методические рекомендации по преподаванию теоретической и практической частей курса «Дифференциальные уравнения», включающие использование метода математического моделирования – основного математического метода решения химико-технологических задач, элементы проблемного, поискового и перспективно-опережающего обучения;
  
• совокупности профессионально ориентированных задач, дидактические материалы для самостоятельной работы, электронное обучающее пособие по разделу «Дифференциальные уравнения».
  

Достоверность результатов исследования и обоснованность сформулированных на их основе выводов обеспечивается: методологической обоснованностью теоретических положений с опорой на теоретические труды в области психологии, педагогики, методики преподавания математики, анализ вузовской практики, данные экспериментальной проверки предлагаемой методики, положительной оценкой преподавателями вузов разработанных учебных материалов и методики их использования.

Апробация и внедрение основных положений и результатов исследования. Эксперимент проводился на химико-технологической специальности Астраханского государственного технического университета («Химическая технология природных энергоносителей и углеродных материалов»), теоретические положения и результаты диссертационного исследования докладывались:

• на методических семинарах АГТУ и АГПУ с 2002–2009 годы;
  
• научно-практических региональных конференциях: на итоговой научной конференции АГПУ, Астрахань, 2002; II региональной научно-практической конференции «Реализация принципа непрерывности в системе учебных дисциплин в образовательных учреждениях», Астрахань 2009;
  
• Всероссийской научно-практической конференции «Педагогическое мастерство в современных условиях», Волгоград, 2009;
  
• международных научно-практических и научно-методических конференциях: VIII Международной конференции «Образование. Экология. Экономика. Информатика», Астрахань, 2003; XII Международной конференции «Математика в высшем образовании», Чебоксары, 2004; IX Всероссийской конференции «Наука. Экология. Образование», Краснодар 2004; V Международной междисциплинарной конференции «Современные проблемы науки и образования», Алушта (Украина), 2004; XII Международной конференции «Математика. Компьютер. Образование», Пущино, 2005; VI Международной конференции «Современные проблемы науки и образования», Алушта (Украина), 2005;
  II Международной конференции «Математика. Образование. Культура», Тольятти, 2005; II региональной научно-практической конференции «Реализация принципа непрерывности в системе учебных дисциплин в образовательных учреждениях», Астрахань, 2009; Всероссийской научно-практической конференции «Педагогическое мастерство в современных условиях», Волгоград, 2009.
  

Материалы и результаты исследования одобрены и внедрены в практику работы кафедры математики Астраханского государственного технического университета.

Результаты исследования отражены в 16 публикациях, в том числе в двух научных изданиях, рекомендованных ВАК РФ.

Структура диссертации обусловлена логикой и последовательностью поставленных задач и состоит из введения, двух глав, заключения, библиографии (193 наименования) и 4 приложений. Диссертация имеет объем 185 страниц основного текста, содержит 33 рисунка, 4 диаграммы, 6 таблиц.

ОСНОВНОЕ СОДЕРЖАНИЕ РАБОТЫ

Во Введении обоснована актуальность темы исследования, определены цель, объект, предмет, гипотеза и задачи исследования. Раскрыты научная новизна, теоретическая и практическая значимость, положения, выносимые на защиту. Приведены сведения об апробации диссертационного исследования.

Первая глава диссертации «Общая характеристика математической подготовки студентов химико-технологических специальностей технических вузов и пути ее совершенствования» посвящена исследованию проблемы профессиональной направленности преподавания математики, анализу математического образования на химико-технологических специальностях технических вузов, разработке путей реализации профессиональной направленности на химико-технологических специальностях технических вузов.

Анализ историко-педагогической, психолого-педагогической и научно-методической литературы по проблеме исследования показывает, что вопрос о профессиональной направленности обучения математике является основополагающим в математическом образовании инженера. Исследования реализации профессиональной направленности ведутся в содержательном, методическом и психологическом направлениях.

Понятие «профессиональная направленность» в современной научно-методической литературе трактуется неоднозначно. Опираясь на необходимость обоснования дальнейшей методики преподавания, берем за основу точку зрения Р.А. Низамова, М.И. Махмутова, Е.А. Василевской, Г. И. Худяковой и др., рассматривающих профессиональную направленность преподавания математики как дидактический принцип. Под профессиональной направленностью обучения математике студентов химико-технологических специальностей технических вузов понимаем основополагающий дидактический принцип, заключающийся в целенаправленной корректировке программы и содержания образования с учетом анализа применения математических знаний в химической технологии, использовании определенным образом подобранных педагогических приемов и методов, имеющих целью усилить профессиональную направленность личности и сформировать математическую готовность будущего химика-технолога к профессиональной деятельности.

Выделяем принципы, являющиеся условиями реализации профессиональной направленности на химико-технологических специальностях втуза: научность содержания образования, методологическая направленность обучения, усиление фундаментализации математического образования, осуществление межпредметных связей, согласование методической системы обучения с психологическими особенностями студентов, активность обучения (характеризует степень участия студентов в учебной деятельности), самостоятельность как характер участия обучаемых в учении.

Выявляются потребности в математических знаниях для успешного освоения общетехнических и специальных дисциплин на химико-технологических специальностях, вскрывается проблема необходимости некоторой коррекции программы по математике, так как, в частности, знание простейших дифференциальных уравнений с разделяющимися переменными необходимо в физике и теоретической механике уже во втором семестре.

В результате проведенного анализа использования математических знаний в общетехнических и специальных дисциплинах: физике, физической химии, теоретической механике, сопротивлении материалов, электротехнике, общей химической технологии, системах управления химико-технологическими процессами, технической термодинамике и теплотехнике, спецкурсе «Математическое моделирование основных процессов химических производств», процессах и аппаратах химической технологии − выделили разделы математики, наиболее часто используемые в химической технологии (рис. 1), а также наиболее профессионально значимые темы математики из соответствующих разделов. Установили соответствия между основными применяемыми математическими понятиями (алгебраическое уравнение, векторы, градиент, производная, дифференциальное уравнение, неопределенный, определенный, несобственный, кратный интегралы, системы дифференциальных уравнений, интегральная и дифференциальная функции распределения и др.) и их интерпретацией в химической технологии.

Выяснили, что дифференциальные уравнения (обыкновенные и в частных производных) – математический аппарат химико-технологических специальностей, средство для решения профессиональных задач, соответственно, один из наиболее часто применяемых разделов математики в решении задач химической технологии. Заметим, что элементы линейной и векторной алгебр, теории вероятностей и математической статистики также используются в математической подготовке студентов химиков-технологов, и что общие направления методики изучения этих разделов описаны Н.А. Дергуновой (для студентов-социологов) и Н.Н. Грушевой (для курсантов речных училищ), поэтому разработанный нами комплексный подход проиллюстрируем, в основном, на примере раздела «Дифференциальные уравнения».

Рассмотрев применение дифференциальных уравнений в выше перечисленных дисциплинах, делаем вывод, что чаще используются в химической технологии дифференциальные уравнения первого порядка с разделяющимися переменными, линейные дифференциальные уравнения первого и высших порядков, системы дифференциальных уравнений первого порядка с разделяющимися переменными и линейных. Решают дифференциальные уравнения и их системы в химической технологии в основном численными и приближенными методами.



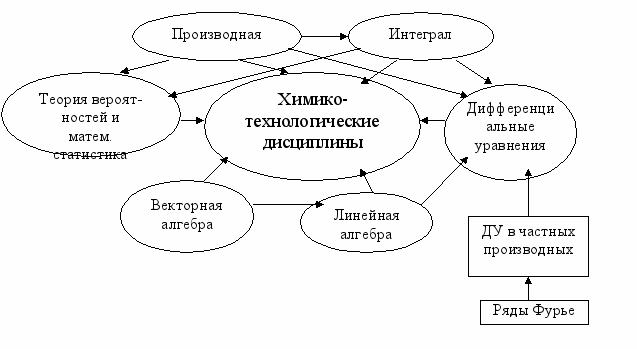
Рис. 1


С опорой на деятельностный подход в обучении описана необходимость применения активных методов и форм обучения − перспективно-опережающего, проблемного обучения, использования метода математического моделирования в теоретическом курсе и при решении задач, использования концептуальных карт, блок-схем, электронных пособий и материалов, усовершенствования самостоятельной работы студентов.

В преподавании курса необходимо учитывать уровень готовности к обучению студентов младших курсов, особенности мышления студентов технических вузов, не допускать перегрузки студентов.

Далее предложены и описаны пути реализации профессиональной направленности обучения математике студентов химико-технологических специальностей технических вузов.

Пропедевтика основных изучаемых понятий. Требование пропедевтики в нашем случае обосновано не только внутрипредметными потребностями, но и необходимостью более раннего изучения некоторых понятий с учетом требований общетехнических дисциплин. Например, учитывая необходимость в знаниях простейших дифференциальных уравнений с разделяющимися переменными в физике и теоретической механике уже во втором семестре, вводим простейшие уравнения с разделяющимися переменными на базе школьных знаний первообразной в разделе «Производная» в конце первого семестра (межпредметная потребность). В разделе «Определенный интеграл» решаются задачи на составление простейших интегральных уравнений, приводящихся к дифференциальным (внутрипредметная и межпредметная потребность). Таким образом, используемую в курсе математики пропедевтику условно определяем в зависимости от целей ее применения как внутрипредметную и межпредметную.

Теоретический курс включает следующие направления: выделение и фундаментальное изучение материала, являющегося математическим аппаратом в данной специальности; подбор и введение в теоретический материал примеров практических ситуаций, связанных с профессиональной деятельностью, профессионально-прикладных задач, ознакомление студентов с аспектами применения математики в будущей профессии, использование аналитических, качественных, численных и приближенных методов решений.

Практический курс включает решение следующих типов задач:

1) пропедевтических, способствующих лучшему восприятию дальнейшего материала, являющихся элементом перспективно-опережающего обучения;

2) творческих заданий, направленных на закрепление теоретических знаний (составление концептуальных карт, блок-схем, планов решения, таблиц);

3) на отработку необходимых базовых навыков решения различных типов задач, с акцентом на освоение математического аппарата специальности;

4) текстовых профессионально-прикладных, основная цель которых – научить составлять математическую модель реальной ситуации, анализировать ее и полученный результат, т. е. применять математические знания в своей специальности, а также повысить мотивацию обучения;

5) на использование приближенных, численных и качественных методов, наиболее часто употребляемых в специальных дисциплинах.

Разработаны методические требования к каждому типу задач.

Используются следующие методы:

• математические: метод математического моделирования, координатный метод, метод линейной и векторной алгебры и т. д.;
  
• методы обучения: проблемный, поисковый, перспективно-опережающий.
  

На основе деятельностного подхода используются следующие виды организации учебной деятельности:

1) использование таких форм обучения, как индивидуально-дифференцированный отчет, консультация-тренинг, лекционно-семинарское занятие с элементами опережающего обучения, индивидуально-групповое практическое занятие;

2) творческая работа по составлению концептуальных карт, блок-схем и таблиц, отражающих основные моменты изучаемого, их дальнейшее использование;

3) совершенствование самостоятельной работы студентов, включающей выделение материала, изучаемого самостоятельно, с учетом потребностей специальности, индивидуальный подход в ходе самостоятельной работы и на этапе контроля (использование индивидуальных заданий), самостоятельное изучение теоретического материала (работа над конспектами, докладами на заданную тему, использование электронного обучающего пособия в самостоятельной работе).

Во второй главе «Методика обучения дифференциальным уравнениям студентов химико-технологических специальностей с целью реализации профессиональной направленности» описана методика изложения теоретического материала, методика решения совокупности задач, используемых на практических занятиях, реализация самостоятельной работы студентов.

Учитывая потребности общетехнических дисциплин, дифференциальные уравнения первого порядка с разделяющимися переменными вводим впервые в конце первого семестра обучения в разделе «Дифференциальное исчисление», после изучения основных понятий и приемов дифференцирования, перед приложениями (основными теоремами дифференциального исчисления и исследованием функций), выбирая примеры и прикладные задачи, преимущественно физические с простейшим интегрированием, основанные на школьных знаниях первообразной.

На первой лекции по теме «Производная» помимо геометрического смысла производной (тангенс угла наклона касательной) перечисляем наиболее часто применимые механические, физические и другие прикладные значения производной: скорость движения тела 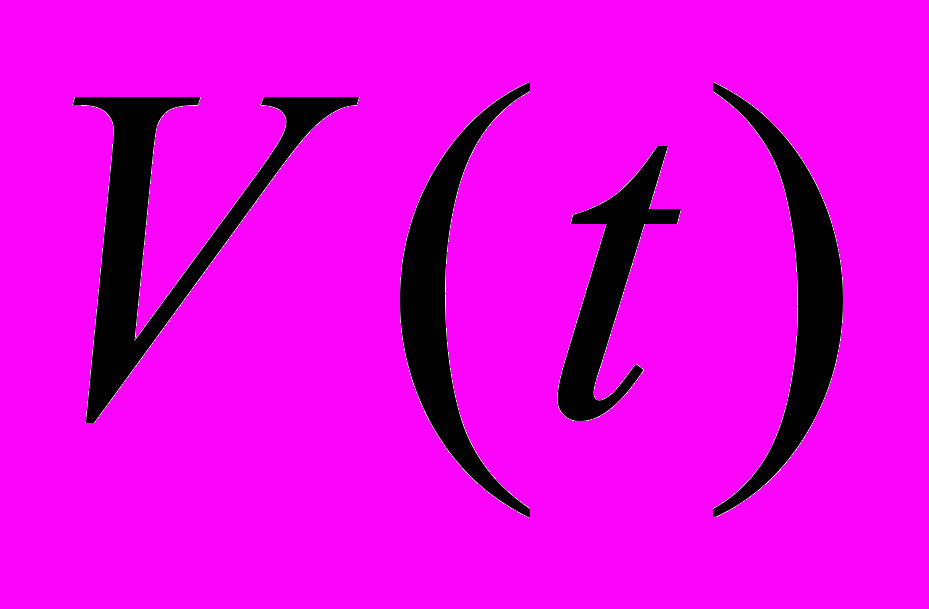в момент времени 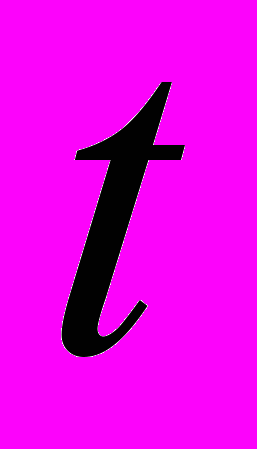− 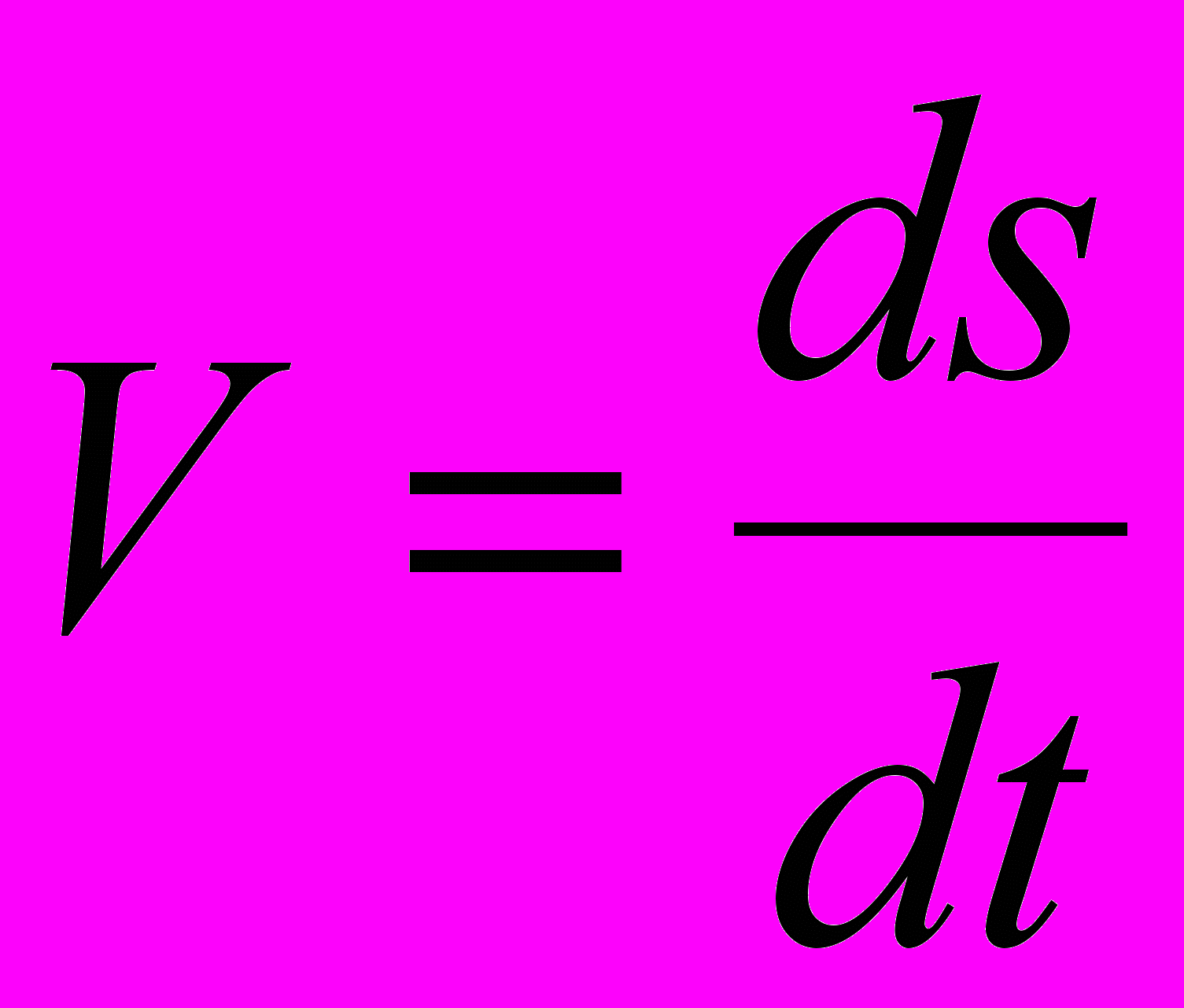; ускорение 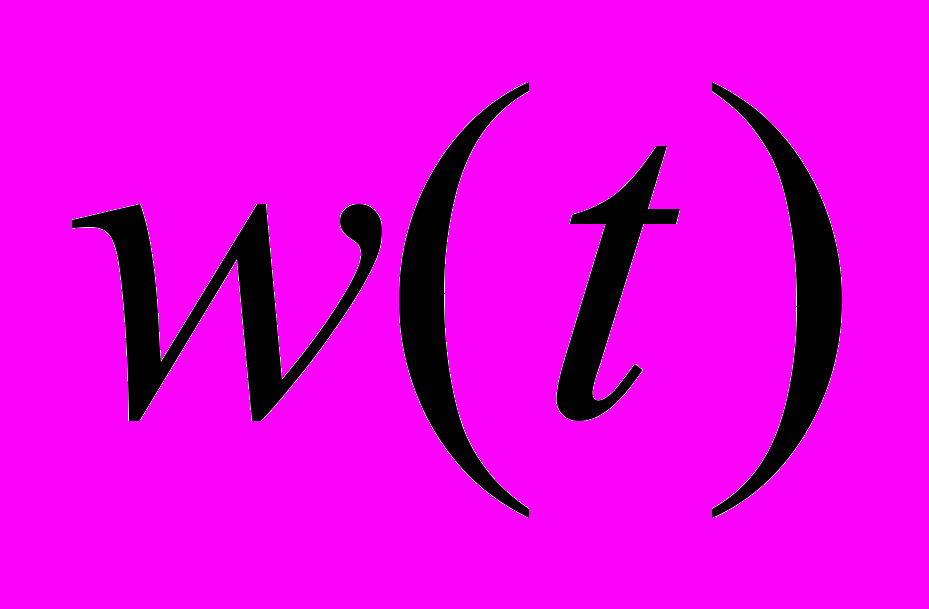в момент 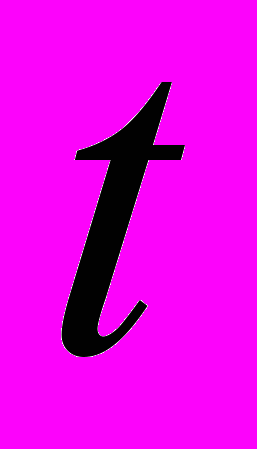, т. е. 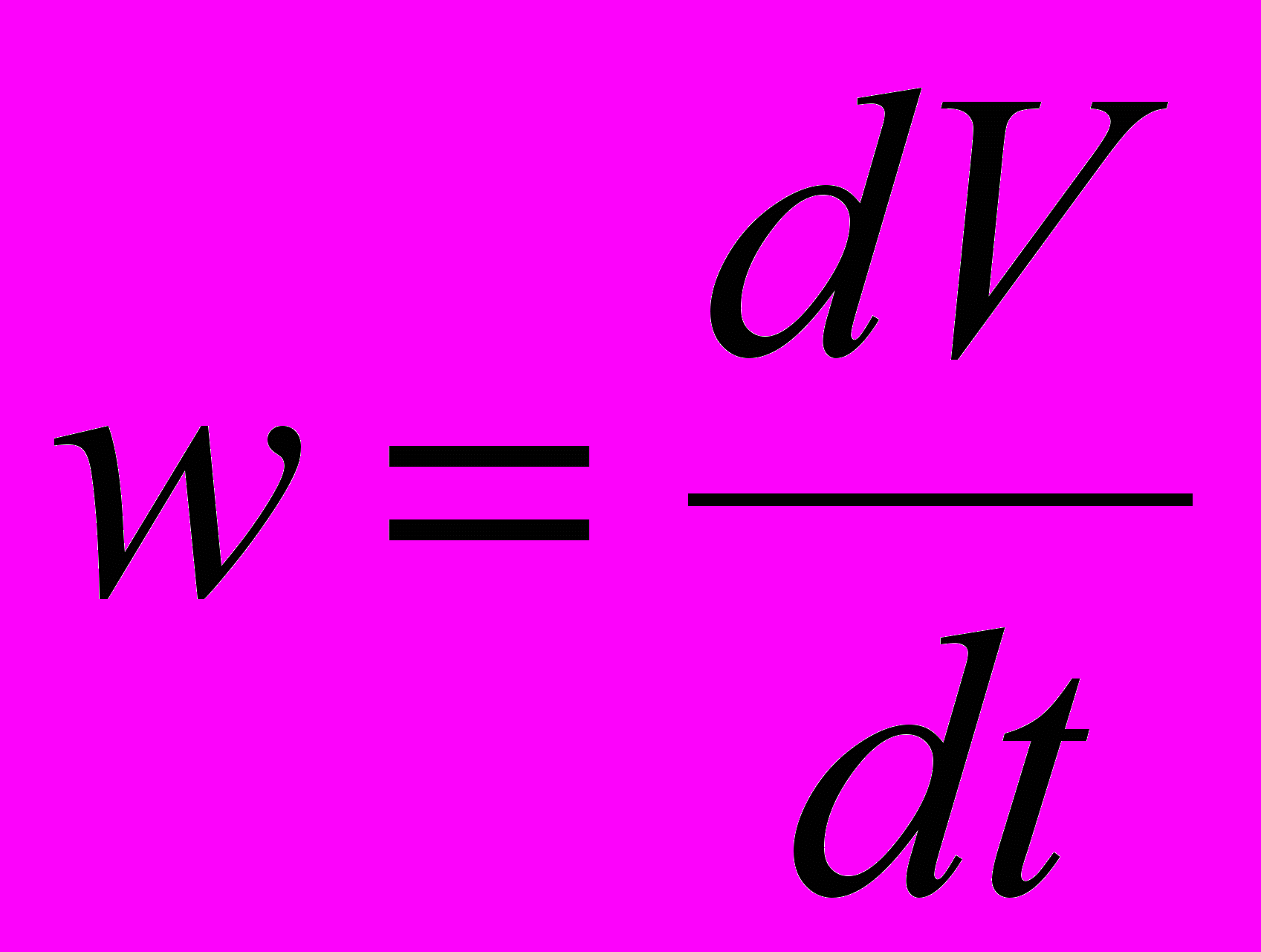; скорость охлаждения тела за единицу времени 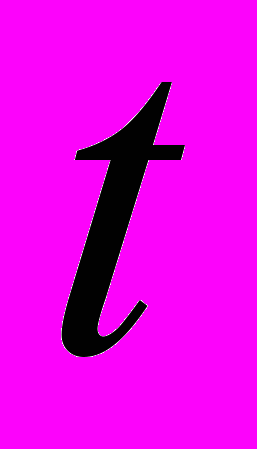: 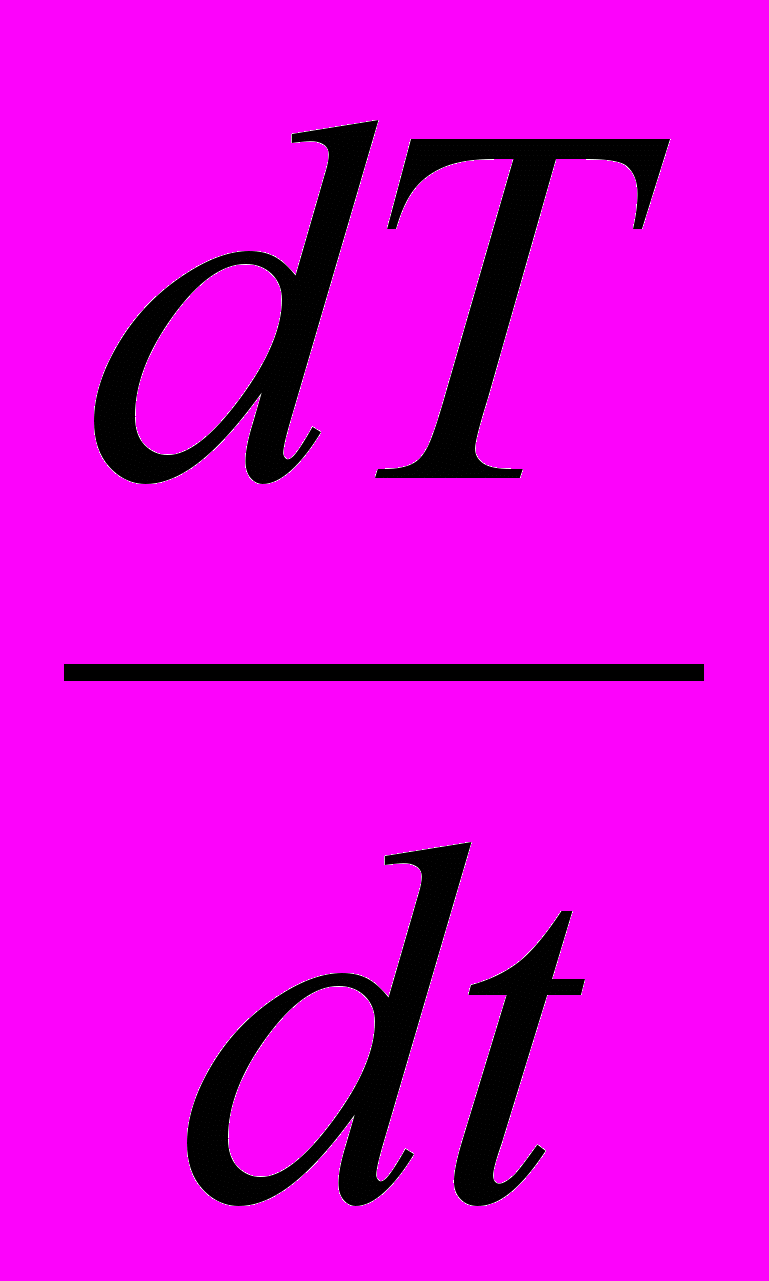; теплоемкость тела − скорость изменения количества теплоты Q при изменении температуры T: 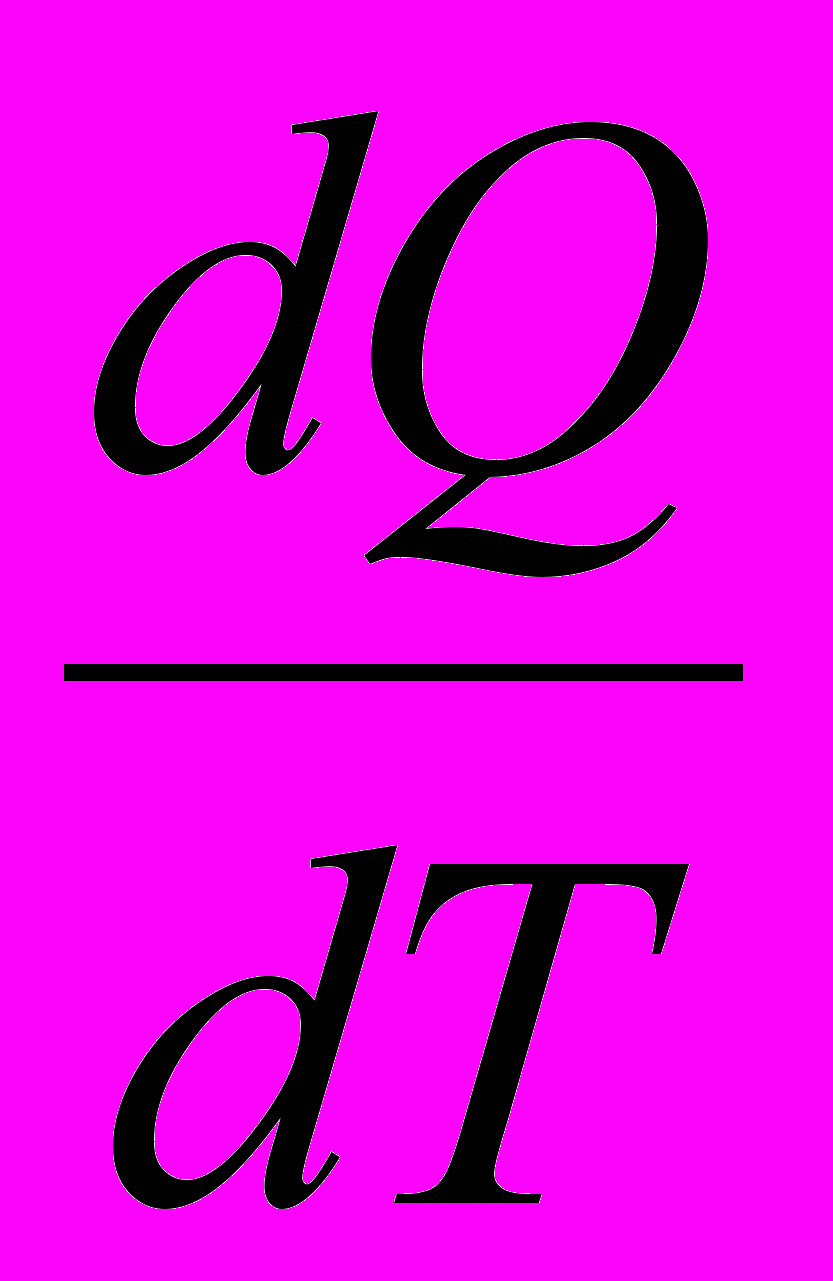; сила 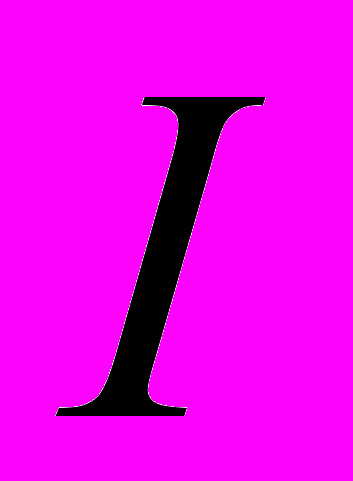электрического тока как производная количества электричества q, протекшего через проводник за время t, т. е. 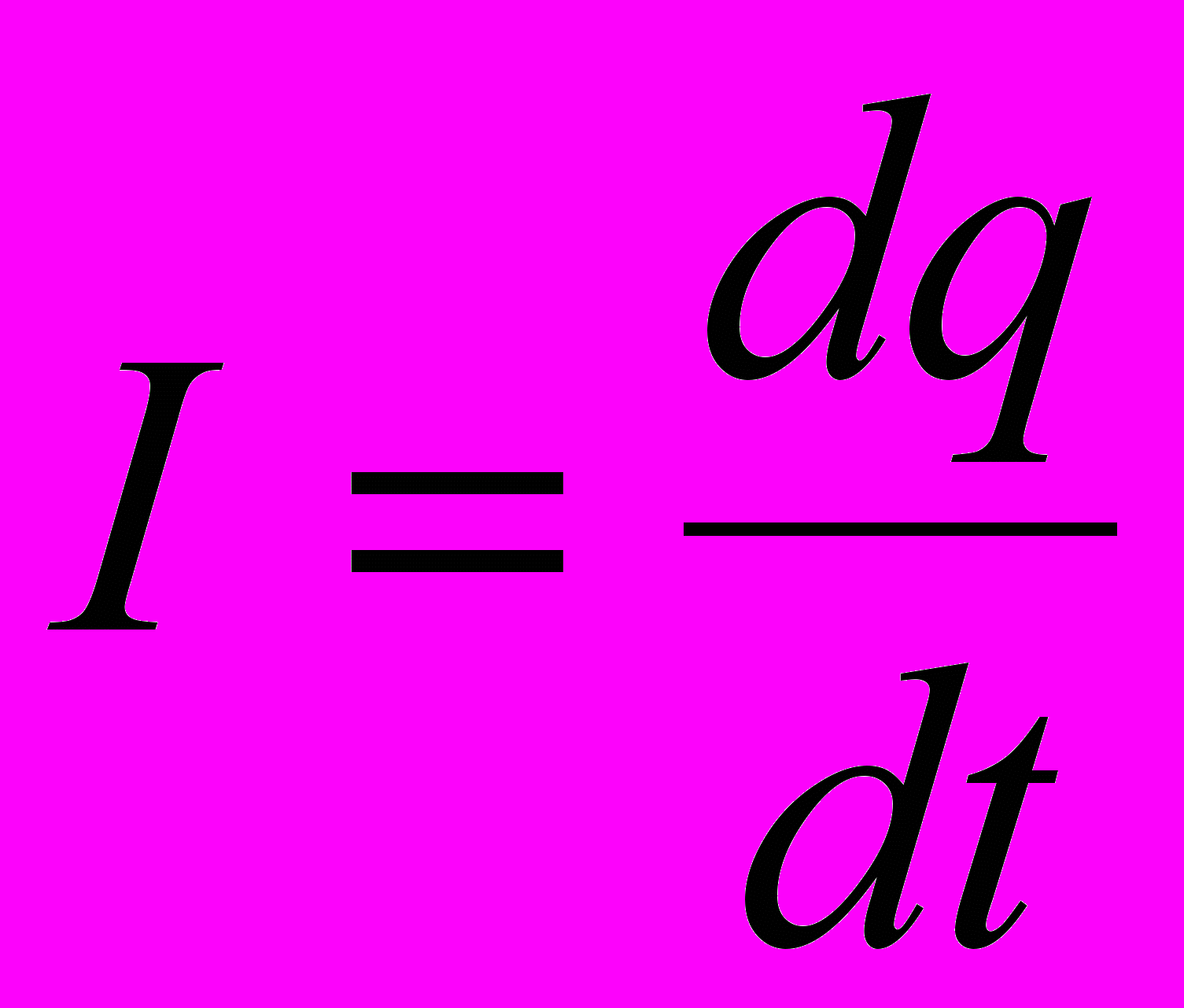; скорость различных процессов, например химической реакции 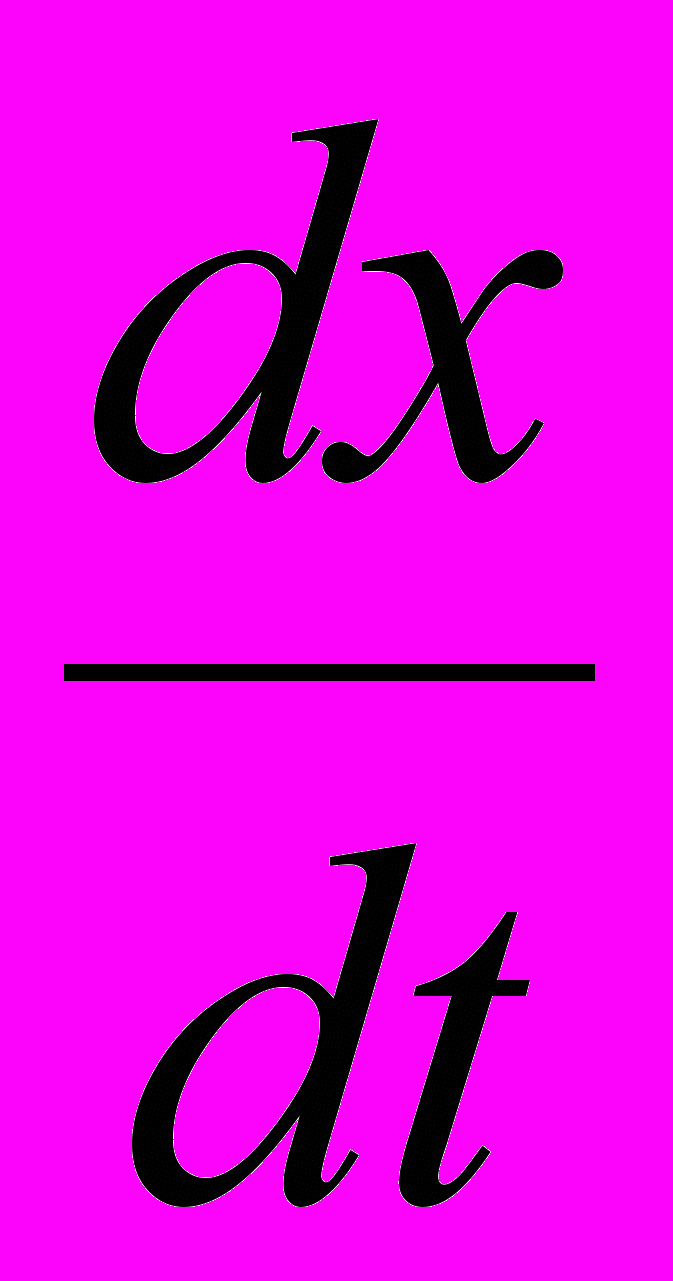, где х − количество молей на литр, прореагировавших за время 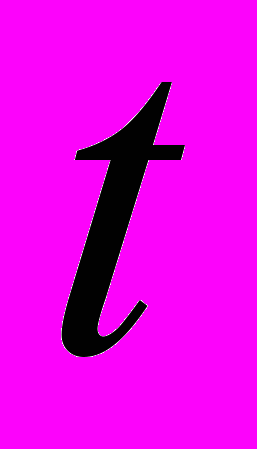от начала реакции. С дифференциальными уравнениями студенты знакомятся на следующей лекции, в процессе решения профессионально-прикладной задачи на определение количества теплоты, требуемого для нагревания тела. Впервые вводятся понятия дифференциального уравнения, уравнения первого порядка с разделяющимися переменными, общего и частного решения дифференциальных уравнений. На практических занятиях решаются простейшие дифференциальные уравнения и задачи на их составление, в большей степени физические.

Далее в работе описывается методика пропедевтики решения задач, приводящих к дифференциальным уравнениям при изучении приложений определенного интеграла. Так, например, при изучении нахождения площадей криволинейных трапеций на лекции предлагается решить задачу, приводящую к интегральному уравнению вида: 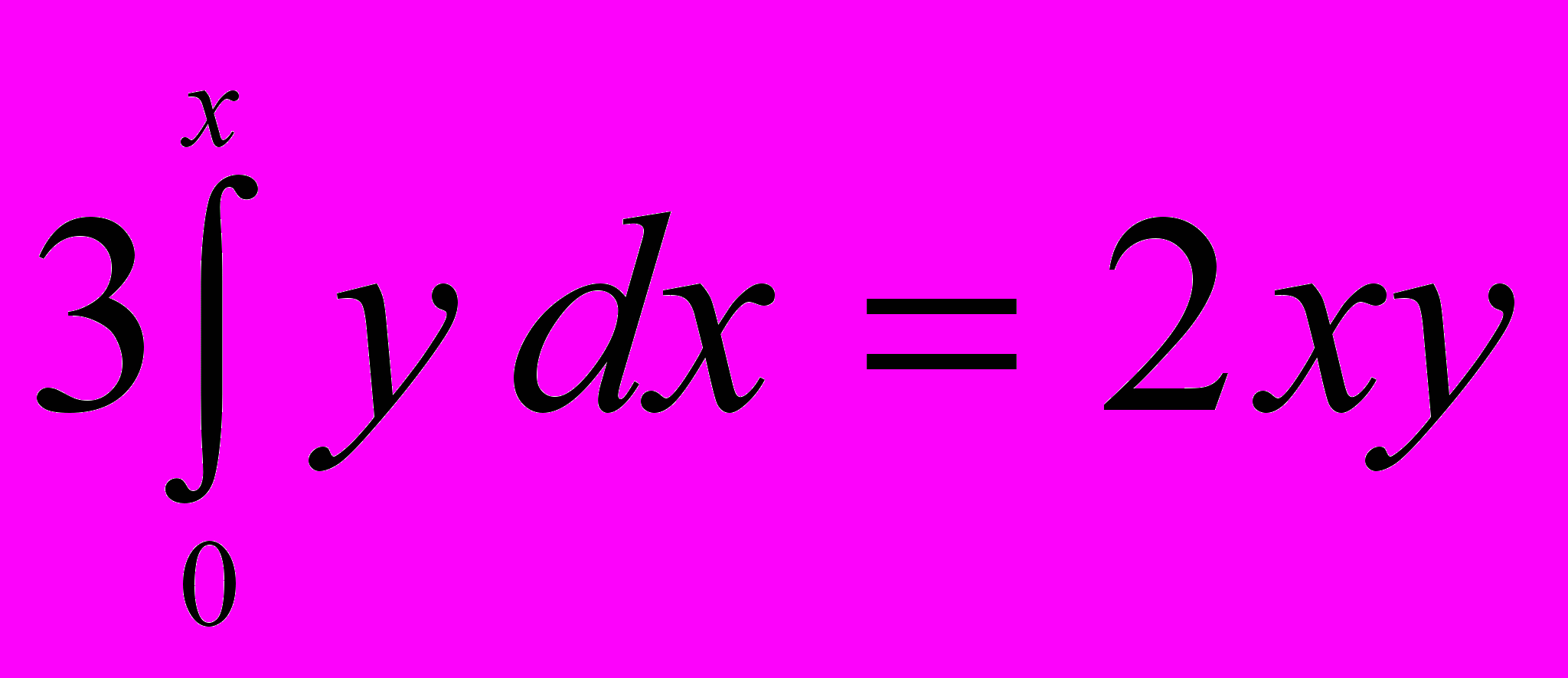, которое в свою очередь сводится к дифференциальному. Задачи такого типа решаются в лекционном курсе и на практических занятиях, причем в процессе решения соблюдаются этапы математического моделирования: составление математической модели, решение полученного уравнения, анализ результата.

В процессе изложения лекционного курса «Дифференциальные уравнения» в начале третьего семестра студенты получают необходимую информацию об использовании дифференциальных уравнений в качестве математических моделей задач химической технологии, об этапах математического моделирования химических процессов, приводятся примеры дифференциальных уравнений из химической технологии, например уравнение массоотдачи для процесса кристаллизации:





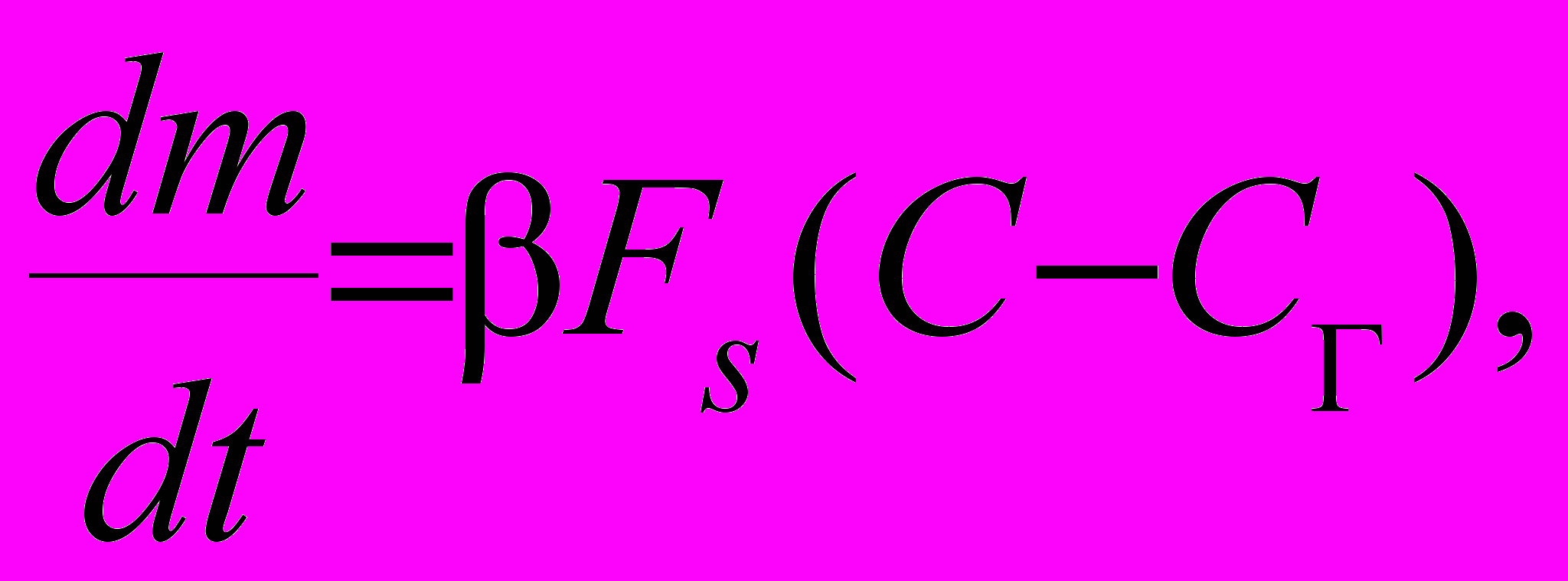
где β − коэффициент массоотдачи, m – масса кристалла, F_S − поверхность кристалла, С_Г и С – концентрации кристаллизующегося вещества. В лекционный курс включены профессионально-прикладные задачи химико-технологической направленности, решаемые с большой степенью активности студентов, с применением элементов проблемного обучения. Одним из элементов перспективно-опережающего обучения является использование концептуальной карты № 1, выданной студентам перед изучением раздела «Дифференциальные уравнения». Она представляет собой схему связей основных понятий раздела. Студенты обращаются к ней в процессе всего изучения раздела.

С целью наилучшего усвоения материала, имеющего большое значение для химико-технологической специальности, используются творческие задания по разработке концептуальных карт и блок-схем, способствующие более быстрому запоминанию и усвоению соответствующих методов решения. Описано их применение в лекционном и практическом курсах.

Приводится методика изложения на лекциях качественных, приближенных и численных методов решения дифференциальных уравнений, а также систем дифференциальных уравнений, широко использующихся в химической технологии.

В параграфе, посвященном преподаванию практического курса, выделены совокупности задач, способствующие реализации профессиональной направленности. В качестве упражнений на закрепление теоретических знаний материала, являющегося математическим аппаратом химико-технологической специальности, используются устные задания на выбор нужного или лишнего. Например, выбрать нужную подстановку для решения того или иного уравнения, выбрать нужную формулу для выражения той или иной величины в профессионально-прикладной задаче, найти требуемый тип дифференциальных уравнений, либо просто определить типы предложенных дифференциальных уравнений, выбрать лишнее уравнение.

Профессионально-прикладные задачи для химико-технологических специальностей, решаемые методом математического моделирования, по тематике и виду математической модели можно разделить на следующие типы:

1. Задачи на химические реакции первого и второго, о растворении или разложении вещества.

2. Задачи о концентрации раствора, ионизации газа и т. д.

3. Задачи, решаемые путем выделения элементарного слоя (об очищении газа, теплообмен через трубу, на определение работы и т. д.).

4. Механические задачи, где производная − скорость или ускорение движения тела.

5. Физические, использующие разного рода физические законы.

6. Геометрические, где производная – тангенс угла наклона касательной.

На первом практическом занятии студенты вспоминают, что решение таких задач состоит из трех этапов (об этом говорилось на лекции): 1) перевод условий задачи на язык математики, составление математической модели,
т. е. соответствующего дифференциального уравнения; 2) решение полученного уравнения; 3) анализ результата. Этап составления математической модели обычно приводит к уравнению в производных или к уравнению в дифференциалах.

Используются задачи, приводимые ко всем изучаемым типам дифференциальных уравнений. Приведем примеры используемых авторских профессионально-прикладных задач.

Задача на химическую реакцию первого порядка (уравнение с разделяющимися переменными). Органическое вещество пентан изомеризуется в изопентан со скоростью, пропорциональной количеству не преобразованного пентана. Масса не преобразованного пентана через 1 час от начала реакции 31,4 г, через 3 часа – 9,7 г. Найти: а) исходную массу пентана; б) через какое время (час) от начала процесса останется 1 % исходной массы пентана?

Задача на химическую реакцию второго порядка (уравнение с разделяющимися переменными). В реакторе проводится реакция окисления меркаптана в потоке жидкости в дисульфид перекисью водорода: 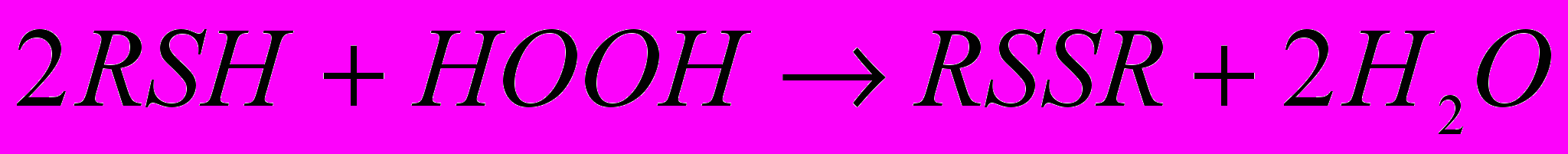. Концентрации первоначальных веществ в потоке соответственно а и b. Через 20 минут концентрация меркаптана уменьшилась на 15 %, за какое время она уменьшится на 25 %?

Весь материал практических занятий разбивается на два блока: дифференциальные уравнения первого порядка и дифференциальные уравнения высших порядков и системы дифференциальных уравнений.

Самостоятельная работа включает выполнение индивидуальных домашних заданий (двух, по одному для каждого блока), состоящих из совокупности задач по изучаемым блокам раздела и перечня тем раздела, предлагаемых студентам для самостоятельного изучения, а также творческих заданий. На первом практическом занятии каждого блока студенты получают индивидуальные расчетные задания (16 задач разной трудности, среди них и профессионально-прикладные задачи). Они направлены на отработку материала, изученного на занятии. Отчет о проделанной работе происходит индивидуально на консультации перед каждой контрольной точкой.

Общий балл за контрольную точку суммируется из балла за отчет и балла за контрольную работу. Контрольная работа, проводимая после каждого блока, дифференцируемая. Студент выбирает карточку А («на 3») или В («на 4−5»). За правильно выполненную работу по карточке А студент получает минимальный зачетный балл; если работа по карточке В выполнена с большим количеством ошибок (и ее нельзя оценить отметкой «4»), то студенту предлагается выполнить работу по карточке А.

Темы раздела «Дифференциальные уравнения», рекомендуемые для самостоятельного изучения на химико-технологических специальностях втуза.

1. Самостоятельное исследование по теме: «Применение дифференциальных уравнений в химической технологии» с дальнейшим конкурсом на выбор лучшей работы, рекомендующийся к доработке для участия в студенческой научно-практической конференции.

2. Решение дифференциального уравнения методом изоклин: решение примеров.

3. Метод Рунге-Кутта численного решения дифференциальных уравнений.

4. Линейные однородные системы дифференциальных уравнений (когда корни характеристического уравнения – действительные, кратные).

Приводятся тексты специально разработанных индивидуальных заданий по каждому блоку изучаемого материала.

Специально разработанное электронное обучающее пособие по разделу «Дифференциальные уравнения» включает: теоретический материал по всему курсу, примеры решения задач, авторские тесты на отработку теоретических знаний и практических навыков решения уравнений разных типов и профессионально-прикладных задач, варианты контрольных работ, предназначенные для подготовки студентов к аудиторным контрольным мероприятиям. Перечислим типы заданий в электронных тестах. Выбрать правильное утверждение (для решения прикладной задачи); нужную подстановку; вид частного решения y* для линейного однородного дифференциального уравнения со специальной правой частью; математическую модель или правильный ответ в профессионально-прикладной задаче; метод решения дифференциального уравнения высшего порядка, линейного неоднородного дифференциального уравнения высшего порядка; решить уравнение и выбрать правильный ответ (рис. 2).





Рис. 2

После решения каждого теста студент получает оценку по 100-балльной шкале. В качестве основного инструмента для реализации электронного методического пособия была выбрана среда разработки Borland C++Builder –мощная система визуального объектно-ориентированного программирования. Теоретический материал написан в виде html – страниц (Hyper Text Markup Language) на языке гипертекстовой разметки документов html с использованием текстового редактора Notepad++.

Экспериментальное исследование включало в себя констатирующий (2003−2004), поисковый (2004−2005) и обучающий (2006−2008) эксперименты.

Об эффективности разработанного методического обеспечения мы судили по двум критериям: качество математической подготовки студентов и умение применять математические знания при решении профессиональных задач.

Чтобы выявить уровень понимания значимости математических знаний и роли дифференциальных уравнений студентам в конце первого курса была предложена анкета. Для определения уровня готовности к изучению дифференциальных уравнений и профессионально-прикладных задач в начале третьего семестра студентам была предложена проверочная работа, содержащая примеры по нахождению неопределенных интегралов и текстовые задачи на приложения определенного интеграла.

В ходе констатирующего этапа эксперимента мы пришли к выводу, что при традиционном изложении курса математики студенты мало знают о применимости математики в будущей профессии и при изучении специальных дисциплин; не выделяют дифференциальные уравнения как важный раздел для использования в химической технологии; наиболее значимым мотивом обучения является желание хорошо сдать экзамен, а не изучить предмет для его использования в своей профессии; из текстовых задач студенты лучше решают геометрические, хуже − физические и профессионально-прикладные.

Участниками обучающего этапа эксперимента на протяжении трех лет являлись студенты второго курса специальности «Химическая технология природных энергоносителей и углеродных материалов».

Выбирались две группы: контрольная и экспериментальная. Были проведены проверочные работы в обеих группах студентов. Одна – до эксперимента, вторая – после. Обе содержали по три стандартные математические задачи и по три профессионально-прикладные.

В соответствии с выбранными критериями диагностировались умения решать общематематические и профессиональные задачи. Количественное выражение диагностируемого показателя вычислялось по формуле: 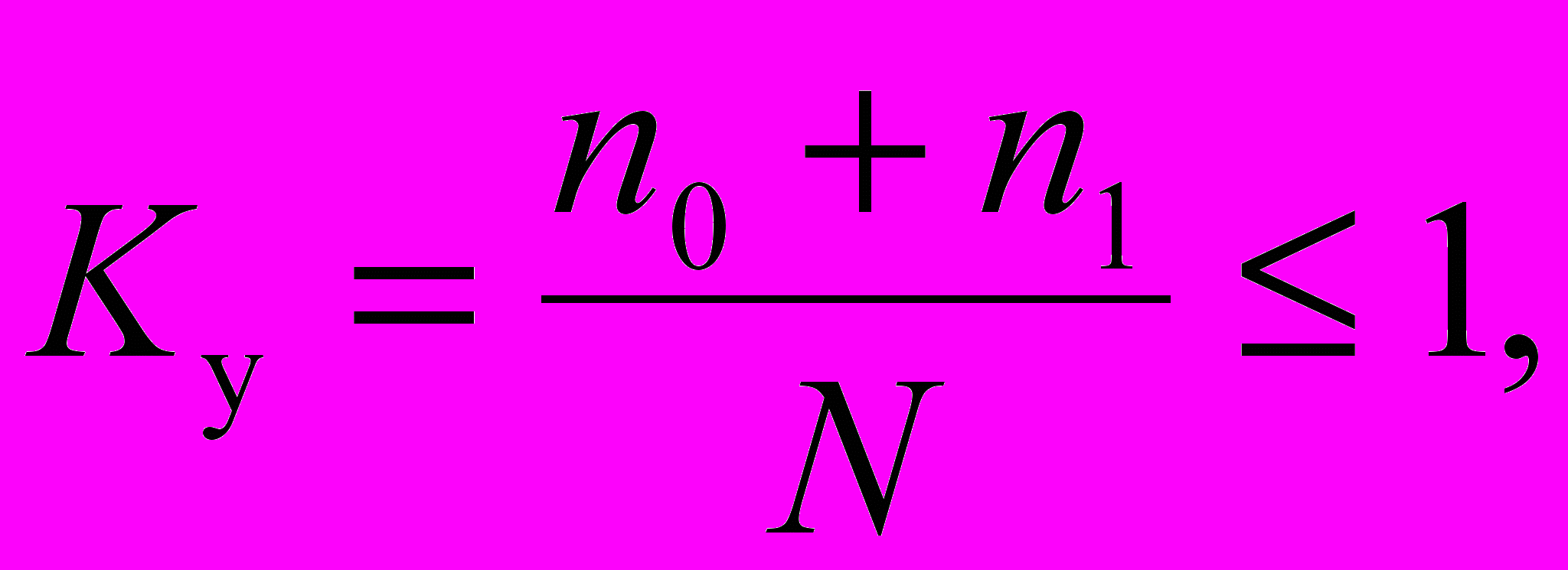где K_у – коэффициент уровня сформированности умения решать задания профессионально-прикладного содержания, 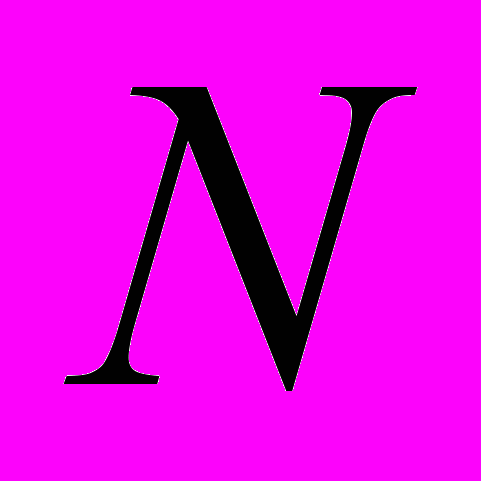– число студентов в группе, 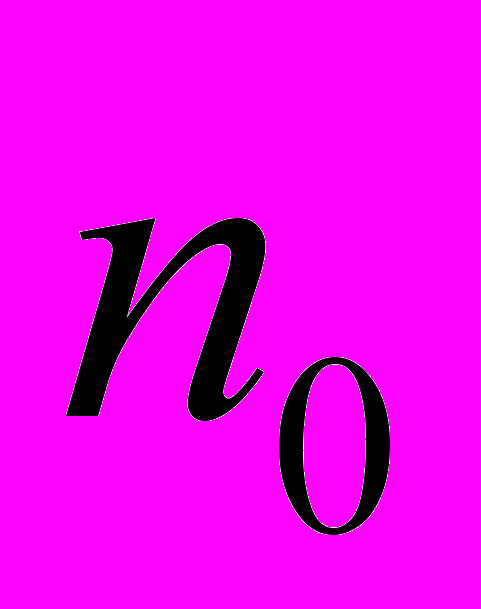– число студентов, правильно и полно решивших задачи, 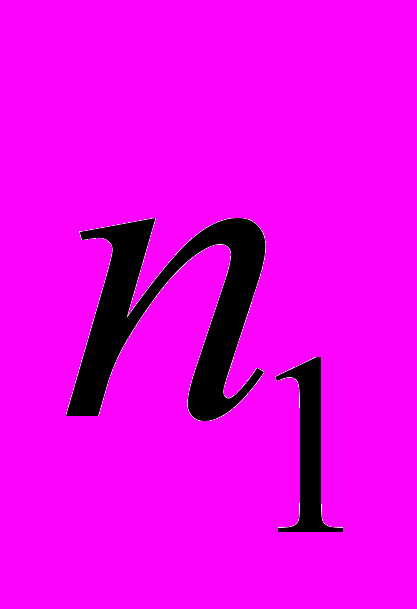– число студентов, которые правильно построили математическую модель задачи, но недостаточно точно решили ее или решили на 50−80 %.

Для статистической обработки результатов эксперимента мы провели сравнение качества математической подготовки в экспериментальной и контрольной группах с помощью критерия Пирсона хи-квадрат (χ²).×. χ² = 7,81.

Поскольку 7, 81> 5,99, верно неравенство χ² (итог. пров. раб.) > χ² (крит.). На основании результатов проведенного исследования можно утверждать, что проверяемая гипотеза подтвердилась и разработанная методика профессионально направленного обучения в большей мере, чем традиционная, способствует повышению качества математической подготовки студентов химико-технологической специальности и формированию умений будущих специалистов применять математические знания в своей профессиональной деятельности (р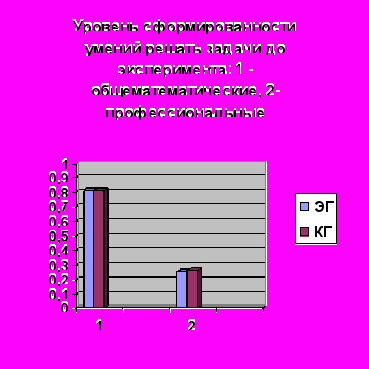ис. 3).


Рис.3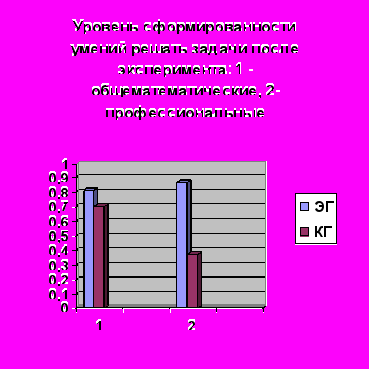


В Заключении были сформулированы следующие выводы.

1. Реализация профессионально направленного обучения является одним из перспективных направлений совершенствования математической подготовки студентов химико-технологических специальностей технического вуза.

2. При обучении химиков-технологов необходимо знакомить студентов с аспектами применения профессионально значимых разделов математики («Дифференцирование», «Интегрирование», «Дифференциальные уравнения», «Дифференциальные уравнения в частных производных», «Теория вероятностей и математическая статистика», «Линейная и векторная алгебра») в будущей профессии, приводить примеры интерпретации математических понятий в общетехнических и специальных дисциплинах, математических моделей химико-технологических процессов, формировать понятие о дифференциальных уравнениях как о математическом аппарате специальности.

3. Разработанный комплексный подход к методике преподавания на химико-технологических специальностях, включающий внутрипредметную и межпредметную пропедевтику, адекватные будущей профессии методы решения задач, использование совокупностей профессионально ориентированных задач, самостоятельную работу с использованием профессионально ориентированных дидактических материалов и комплексного электронного пособия, организацию учебной деятельности с элементами проблемного, поискового и перспективно-опережающего обучения, способствует реализации профессиональной направленности и улучшает уровень математической подготовки будущего специалиста.

4. Предложенная методика преподавания теоретического материала раздела «Дифференциальные уравнения», основанная на деятельностном подходе, включает пропедевтику дифференциальных уравнений в разделах «Производная» и «Определенный интеграл», использование качественных, численных и приближенных методов решения дифференциальных уравнений, применимых в химической технологии, профессионально-прикладных задач и примеров ситуаций химической технологии, разрешаемых математическими методами, концептуальных карт как элемента перспективно-опережающего обучения.

5. Применение активных форм обучения: лекционно-семинарских занятий, индивидуально-дифференцированных отчетов, консультаций-тренингов, индивидуально-групповых практических занятий и поискового, проблемного, перспективно-опережающих методов обучения − позволяет активизировать мыслительную деятельность студентов.

6. Разработанные совокупности задач для химико-технологических специальностей, включающие пропедевтические задачи, межпредметные и внутрипредметные; профессионально ориентированные задачи, решаемые путем построения математических моделей; творческие задания по составлению концептуальных карт, блок-схем, таблиц и планов решений, тестовые задачи на отработку базовых знаний, необходимых для математического образования химиков-технологов, позволяют закрепить теоретические знания и выработать необходимые навыки и умения использования математики в будущей профессии.

7. Самостоятельная работа, включающая использование специально составленных профессионально направленных дидактических материалов и созданного электронного обучающего пособия, содержащего теоретический, практический, тестовый и контрольный материал, активизирует деятельность студентов по сознательному приобретению знаний, способствует индивидуализации и личностной ориентации учебного процесса, позволяет формировать математическую, профессиональную и информационную компетентность будущих специалистов.

8. Проведенная экспериментальная работа подтверждает гипотезу исследования.

Статьи в изданиях, рекомендованных ВАК РФ

1. Львова, В.Д. Обучение математике студентов химико-технологической специальности [Текст] / В.Д. Львова // Известия Южного федерального университета. Сер.: Педагогические науки. − Ростов-на-Дону. – 2009. – № 6. − С. 167−175.
   
2. Львова, В.Д., Аммосова, Н.В. Организация самостоятельной работы студентов химико-технологических вузов при изучении математики [Текст] / В.Д. Львова, Н.В. Аммосова, // Вестник Московского университета МВД. – 2009. − № 6. – С. 22−25. (Авторский вклад 50 %).
   

Другие публикации

3. Львова, В.Д. Методика изложения во втузе метода моделирования реальных процессов и явлений с помощью аппарата дифференциальных уравнений [Текст] / В.Д. Львова // Итоговая научная конференция АГПУ : тез. докл. − Астрахань : Изд-во АГПУ, 1999. – С. 11.
   
4. Львова, В.Д. Историко-педагогический анализ преподавания математики в техническом вузе [Текст] / В.Д. Львова // Итоговая научная конференция АГПУ : тез. докл. − Астрахань : Изд-во АГПУ, 2002. – С. 50.
   
5. Львова, В.Д. Профессиональная направленность как основополагающий и системообразующий принцип обучения математике в техническом вузе [Текст] / В.Д. Львова // Педагогическое мастерство в современных условиях : матер. Всерос. науч.-практ. конф. –– Волгоград-М. : ООО «Глобус», 2009, – С. 298−295.
   
6. Львова, В.Д. Прикладная направленность при обучении дифференциальным уравнениям студентов химико-технологической специальности втуза [Текст] / В.Д. Львова // Реализация принципа непрерывности в системе учебных дисциплин в образовательных учреждениях : сб. тр. II региональной науч.-практ. конф. − Астрахань : ОГОУ ДПО «АИПКП», 2009. – С. 53−60.
   
7. Львова, В.Д. Основные принципы обучения высшей математике во втузах [Текст] / В.Д. Львова // Тез. VIII Междунар. конф. «Образование. Экология. Экономика. Информатика». − Астрахань, 2003. – С. 189.
   
8. Львова, В.Д. О принципах преподавания математики в техническом вузе [Текст] / В.Д. Львова // Сб. науч. тр. VIII Междунар. конф. «Образование. Экология. Экономика. Информатика». − Астрахань, 2003. С. 65−68.
   
9. Львова, В.Д. Методика обеспечения профессионально-прикладной направленности изучения дифференциальных уравнений в техническом вузе [Текст] / В.Д. Львова // Тез. докл. XII Междунар. конф. «Математика в высшем образовании». – Чебоксары, 2004. – С. 60.
   
10. Львова, В.Д. Решение задач на составление дифференциальных уравнений для химико-технологических специальностей [Текст] : метод. реком. / В.Д. Львова, Н.А. Мамаева. − Астрахань : Изд-во АГТУ, 2005. – С. 37.
    
11. Львова, В.Д. Сочетание фундаментальности и прикладной направленности курса высшей математики во втузе [Текст] / В.Д. Львова // Сб. матер. IX Всерос. конф. «Наука. Экология. Образование». – Краснодар, 2004. – С. 118−119.
    
12. Львова, В.Д. Сочетание логической и психологической основ преподавания математики в техническом вузе [Текст] / В.Д. Львова // Сб. матер. V Междунар. междисцип. науч.-практ. конф. «Современные проблемы науки и образования», Алушта 2004 г. – Харьков, 2004. – С. 103.
    
13. Львова, В.Д. Реализация прикладной направленности в преподавании дифференциальных уравнений для химико-технологической специальности втуза [Текст] / В.Д. Львова // Тез. XII Междунар. конф. «Математика. Компьютер. Образование», Пущино 2005 г. – Москва-Ижевск, 2005. – С. 316.
    
14. Львова, В.Д. О повышении эффективности обучения математике в техническом вузе [Текст] / В.Д. Львова // Сб. матер. VI Междунар. конф. «Современные проблемы науки и образования», Алушта 2005 г. – Харьков, 2005. – С. 151.
    
15. Львова, В.Д. Подбор задач при обучении дифференциальным уравнениям на химико-технологической специальности втуза [Текст] /
    В.Д. Львова // Сб. тр. II Междунар. науч. конф. «Математика. Образование, культура», 1−3 ноября 2005 г – Тольятти, 2005, – С. 175−177.
    
16. Львова, В.Д. Сочетание фундаментальности и профессионально-прикладной направленности в преподавании математики в техническом вузе [Текст] / В.Д. Львова // Наука Кубани. − 2005 − № 2 – С. 69−71.