Самостоятельная работа студентов 45 часов. Распределение часов по семестрам

Вид материала

Самостоятельная работа

Содержание 2.Требования стандарта по дисциплине 3.Принципы и цели Контролирующие материалы и учебно-методическое обеспечение 1.Составить двойственную задачу и найти решение обеих З.Л.П. 4. Решить графически З.Л.П. 5. Определить план капиталовложений, максимизирующий общую прибыль 1.Составить двойственную задачу и найти решение обеих З.Л.П. 4. Решить графически З.Л.П. 5. Определить план капиталовложений, максимизирующий общую прибыль Перечень зачетных вопросов 1. Основная литература 2. Дополнительная литература

Подобный материал:

• Курс 4 Семестр 7 Учебный план набора 2009 года Распределение учебного времени Лекции, 1025.06kb.
• Курс: управление недвижимостью (46 часов, 7 семестр) Количество учебных часов Лекции, 14.94kb.
• Основы научно-методической деятельности, 176.24kb.
• Рабочая программа Специальность Государственное муниципальное управление Статус дисциплины, 211.12kb.
• Выписка из рабочей программы и методические указания к выполнению лабораторных работ, 344.11kb.
• Программа дисциплины Нейропсихология Направление подготовки специалистов, 29.9kb.
• Стилистика рекламного текста, 218.29kb.
• 1. Криминология: цели и задачи дисциплины, 498.49kb.
• Рекомендации для самостоятельной внеаудиторной работы студентов по дисциплине «Сестринское, 182.37kb.
• Рекомендации для самостоятельной внеаудиторной работы студентов по дисциплине «Сестринское, 232.55kb.

ЕН.В 02 – Математическое моделирование

Автор: Муксунов А.И., ст. преподаватель каф. ТМОИ ИМИ ЯГУ

1.ВЫПИСКА ИЗ УЧЕБНОГО ПЛАНА

Объем работы студента (в часах) в 9 семестре из учебного плана по специальности 030500.06 – ПРОФЕССИОНАЛЬНОЕ ОБУЧЕНИЕ (информатика, вычислительная техника и компьютерные технологии) составляет:


всего - 90 часов.

в том числе

аудиторные занятия: 45 часа

из них

лекции - 28 часов

практические 17 часов

самостоятельная работа студентов 45 часов.


Распределение часов по семестрам

Семестр	Всего часов	СРС	Аудитор ных	Лекции	Практика	Форма Контроля
9	90	45	45	28	17	Зачет
Итого:	90	45	45	28	17	-

Недельная нагрузка по семестрам

Виды занятий	СЕМЕСТРЫ
	9
1. Аудиторные занятия в том числе: лекционные практические 2. Самостоятельная работа	4 2,5 1,5 4

2.ТРЕБОВАНИЯ СТАНДАРТА ПО ДИСЦИПЛИНЕ

Выпускник высшего профессионального учебного заведения должен уметь решать задачи, соответствующие его квалификации, указанной в государственном образовательном стандарте. Педагог профессионального обучения должен:

знать и уметь использовать:

• математические модели простейших систем и процессов в естествознании и обучении;
  
• вероятностные модели для конкретных процессов, методы их анализа в рамках построенной модели;
  
• профессионально ориентированные математические методы анализа, синтеза, оптимизации и моделирования различных систем;
  

уметь:

• применять методы математического анализа для решения исследовательских задач;
  
• применять основы теории вероятностей и математической статистики;
  
• применять математическое моделирование, методы и средства системного моделирования;
  
• применять прикладные программные продукты в научных исследованиях, экспериментах, при обработке результатов экспериментов;
  

3.ПРИНЦИПЫ И ЦЕЛИ

3.1. Принципы построения программы

3.1.1. курс имеет как практическую, так и теоретическую направленность;

3.1.2. особое внимание уделено моделированию экономических процессов и явлений.

3.2. Цели.

Общие цели:

3.2.1. повышение общей математической культуры студента;

3.2.2. формирование у студента прочных знаний по изучаемым разделам дисциплины;

3.2.3. ознакомление студента с математическими моделями простейших систем и процессов;

3.2.4. воспитание у студента умений применять математические методы и модели для решения исследовательских задач;

3.2.5. привитие студенту навыков самостоятельной работы над изучением литературы по математике и ее приложениям;

Цели курса:

3.2.6. ознакомить с основами математического моделирования экономических систем;

3.2.7. дать общие принципы построения математических моделей;

3.2.8. научить использовать на практике методы математического моделирования в управлении различными системами;

3.2.9. научить составлять некоторые классические математические модели, применительно приближенным к реальным ситуациям;

3.2.10. научить находить решения классических задач математического моделирования;

3.2.11. научить применять основы теории вероятностей и математической статистики, строить статистические (вероятностные) модели, произвести анализ экономических явлений по статистическим моделям, сделать прогноз.

. КОНТРОЛИРУЮЩИЕ МАТЕРИАЛЫ И УЧЕБНО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ

6.1. Фонд материалов, контролирующих деятельность студента содержит:


Вариант 1.


1.Составить двойственную задачу и найти решение обеих З.Л.П.:

F=x₁+12x₂+18x₃ →max


16x₁+ 10x₂+ 10x₃ ≤ 22

4x₁+ x₂+20x₃ ≤ 12

x₁, x₂, x₃, x₄, x₅ 0


2. Найти решение транспортной задачи. Первоначальный план определить методом Фогеля.

Поставщики	Потребители				ЗАПАСЫ
	В1	В2	В3	В4
А1	9	6	5	6	133
А2	1	6	9	5	200
А3	4	3	3	5	127
ПОТРЕБНОСТИ	106	110	135	109

3. Найти решение матричной игры:

-2	3	2	4
5	1	4	2

4. Решить графически З.Л.П.


F=3x₁+4x₂ →max

5x₁+ 5x₂ ≤ 45

6x₁+ 4x₂ ≤ 60

7x₁+ 7x₂ ≤ 14

x₁, x₂, x₃, x₄ 0


5. Определить план капиталовложений, максимизирующий общую прибыль:

КАПИТАЛ	I	II	III	IV
0 10 20 30 40 50	0 11 15 20 30 40	0 12 18 21 28 39	0 13 17 22 26 37	0 15 15 23 30 40

Вариант 2.


1.Составить двойственную задачу и найти решение обеих З.Л.П.:

F=20x₁+7x₂+13x₃ →max




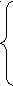
2x₁+ 4x₂+ 8x₃ ≤ 40

6x₁+ 2x₂+4x₃ ≤ 38

x₁, x₂, x₃, x₄, x₅ 0


2. Найти решение транспортной задачи. Первоначальный план определить методом Фогеля.

Поставщики	Потребители				ЗАПАСЫ
	В1	В2	В3	В4
А1	5	3	2	7	154
А2	5	6	9	4	250
А3	2	3	4	5	146
ПОТРЕБНОСТИ	125	135	135	155

3. Найти решение матричной игры:

4	-3	2	-2
2	1	4	3

4. Решить графически З.Л.П.


F=3x₁+4x₂ →max

5x₁+ 5x₂ ≤ 45

6x₁+ 4x₂ ≤ 60

7x₁+ 7x₂ ≤ 14

x₁, x₂, x₃, x₄ 0


5. Определить план капиталовложений, максимизирующий общую прибыль:

КАПИТАЛ	I	II	III	IV
0 10 20 30 40 50	0 13 17 23 30 39	0 12 18 24 29 38	0 13 17 22 28 37	0 14 15 23 30 40

Перечень зачетных вопросов

1. Линейные балансовые модели в экономике.
   
2. Понятие о межотраслевом балансе.
   
3. Модель Леонтьева.
   
4. Теория трудовой стоимости Маркса в модели Леонтьева.
   
5. Модель Неймана.
   
6. Линейная модель торговли.
   
7. Постановка задачи целочисленного программирования.
   
8. Методы отсечения. Метод Гомори.
   
9. Метод ветвей и границ.
   
10. Общая постановка задачи динамического программирования.
    
11. Рекуррентное соотношение Беллмана.
    
12. Задача о распределении средств между предприятиями.
    
13. Общая схема применения метода ДП. Задача об оптимальном распределении ресурсов между отраслями на n лет.
    
14. Задача о замене оборудования
    
15. Задачи параметрического программирования.
    
16. Задачи дробно-линейного программирования.
    
17. Построение сетевого графика. Временные характеристики сетевого графика.
    
18. Классификация экономико - математических моделей. Этапы экономико-математического моделирования
    
19. Основные понятия экономической динамики.
    
20. Многофакторные модели экономического роста.
    
21. Производственные функции. Основные понятия. Макромодели.
    
22. Неоклассические производственные функции.
    
23. Понятие магистрали. Теоремы о магистрали для простейших динамических моделей.
    
24. Отношение предпочтения и функции полезности.
    
25. Неоклассическая теория спроса. Функции спроса и предложения. Оптимум Парето.
    

1. ЛИТЕРАТУРА
   

1. Основная литература

1. Экономико – математические методы и прикладные модели: Учебник. / Под редакцией проф. Федосеева В.В.– М.: ЮНИТИ, 2000.
   
2. Исследование операций в экономике: Учебн.пособие для вузов/ Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман; Под ред.проф. Н.Ш. Кремера. – М.: Банки и биржи, ЮНИТИ, 1997.
   
3. Бахтин А.Е. Математическое моделирование в экономике: Учебное пособие. – Новосибирск: НГЭАУ, 1995.
   
4. Трояновский В.М. Математическое моделирование в менеджменте: Учебное пособие. – М.: Изд. «Русская деловая литература», 1999.
   

2. Дополнительная литература

1. Ларичев О.И. Теория и методы принятия решений. – М.: «Логос», 2000.
   
2. Никитина Н.Ш. Математическая статистика для экономистов.- М.- Новосибирск: ИНФРА – М - НГТУ, 2001.
   
3. Бабешко Л.О. Коллокационные модели прогнозирования в финансовой сфере. – М.: «Экзамен», 2001.
   
4. Мулен Э. Теория игр с примерами из математической экономики. – М.: Мир, 1985.
   
5. Дубров А.М., Лагоша Б.А., Хрусталев Е.Ю. Моделирование рисковых ситуаций в экономике и бизнесе. – М.: «Финансы и статистика», 1999.
   
6. Коршунова Н.И., Плясунов В.С. Математика в экономике: - М.: Издательство «Вита - Пресс», 1996.
   
7. Малыхин В.И. математика в экономике: Учебное пособие. – М.: ИНФРА – М, 2001.
   
8. Солодовников А.С., Бабайцев В.А., Браилов А.В., Шандра И.Г. Математика в экономике: Учебник: В 2-х ч. – М.: Финансы и статистика, 1999.
   
9. Куликов Ю.Г., Шеховцова Н.Ф., Зикеева Л.П. Экономико-математические методы и модели. – М.: НПО «МОДЭК», 2000.
   
10. Общий курс высшей математики для экономистов: Учебник. / Под редакцией проф. Ермакова В.И.– М.: ИНФРА-М, 1999.
    
11. Сборник задач по высшей математике для экономистов: Учебное пособие. Под редакцией проф. Ермакова В.И.– М.: ИНФРА-М, 2001.
    
12. Высшая математика для экономистов: Учебн. Пособие для вузов/ Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман; Под ред. Проф. Н.Ш. Кремера. – М.: Банки и биржи, ЮНИТИ, 1997.
    
13. Замков О.О., Черемных Ю.Н., Толстопятенко А.В. Математические методы в экономике: Учебник. – М.: МГУ им. М.В. Ломоносова, Издательство «Дело и сервис», 1999.