Учебное пособие для выполнения курсовой работы утверждено

Вид материала

Содержание

Подобный материал:

1 2 3 4 5 6

Московский авиационный институт
(государственный технический университет)
–––––––––––––––
Аэрокосмический факультет
––––––––––––––––
кафедра «системный анализ и управление»

В.Е. Усачов

Методы оптимизации
организационно-технических систем

Учебное пособие для выполнения курсовой работы

УТВЕРЖДЕНО

на заседании кафедры 604,

«Системный анализ и управление»,

протокол №13, 20.12.2007

Москва, 2007г.

содержание

содержание 3

Введение 4

Введение 4

1. Содержание и требования к выполнению курсовой работы 5

1.1. Содержание курсовой работы 5

1.2. Общие требования к проведению и оформлению курсовой работы 7

2. Методическое Обеспечение курсовой работы 11

1.3. Методика аналитического решения задачи условной оптимизации с ограничениями типа неравенств 11

1. Формирование функции Лагранжа. 11

2. Применение необходимых условий (НУ) в форме Куна и Таккера для определения условных стационарных точек для задачи (1.1, 1.2). 11

3. Исключение всех стационарных точек, не удовлетворяющих пассивным ограничениям. 12

4. Исключение стационарных точек, не удовлетворяющих условиям неотрицательности множителей Лагранжа. 13

5. Проверка оставшихся стационарных точек на достаточные условия локального минимума функции. 13

6. Определение условного глобального минимума. 14

1.4. Методические рекомендации по численному решению задачи условной оптимизации с ограничениями типа неравенств 16

2. Варианты Заданий к курсовой работе 22

2.1. Задания по аналитической части курсовой работы 22

2.2. Задания по методам численной оптимизации для выполнения второй части курсовой работы 28

3. рекомендации по формированию заключения и Приложений к курсовой работе 33

Введение

Учебное пособие предназначено для студентов, выполняющих курсовую работу по дисциплине: «Методы оптимизации организационно-технических систем», читаемой в рамках специальности 0722: «Моделирование и исследование операций в организационно – технических системах».

Целями курсовой работы являются:

овладение аналитическими и численными методами математического программирования в приложении к задачам условной оптимизации параметров организационно-технических систем по целевым функциям, заданным различными способами;

приобретение навыков применения широкого спектра современных методов математического программирования, включая детерминированные методы нулевого, первого и второго порядков, а также методы поиска экстремумов целевых функций, учитывающие элементы случайности;

развитие способностей к проведению аналитических исследований на примере сравнительного анализа свойств сходимости различных численных методов условной оптимизации целевых функций;

умение ставить задачу, конкретизировать методику ее решения, формировать и разрабатывать программное обеспечение, а также формулировать выводы по результатам проделанной работы;

накопление опыта объектно-ориентированного программирования.

В пособии описано содержание выполнения курсовой работы, сформулированы требования к ней, представлены варианты заданий, приведены теоретические сведения, необходимые для выполнения работы.

1.Содержание и требования к выполнению курсовой работы

1.1.Содержание курсовой работы

Курсовая работа состоит из двух логически связанных частей, соответствующих содержанию лекций, читаемых по дисциплине «Методы оптимизации организационно-технических систем».

Первая часть работы посвящена аналитическим методам решения задач условной оптимизации целевых функций с ограничениями типа неравенств, накладываемых на векторный аргумент, то есть:

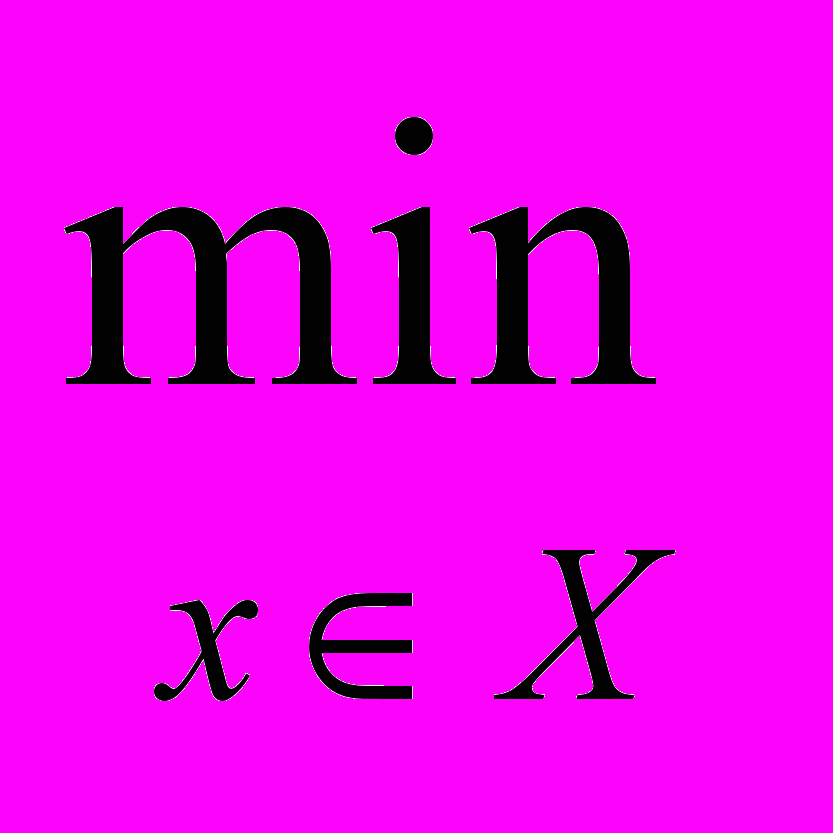f (x)

(1.1)

Где х – вектор аргументов (параметров), имеющий в общем случае размерность [n1], f(x) – скалярная унимодальная дифференцируемая функция, Х – множество допустимых значений аргументов х, заданное совокупностью ограничений типа неравенств:

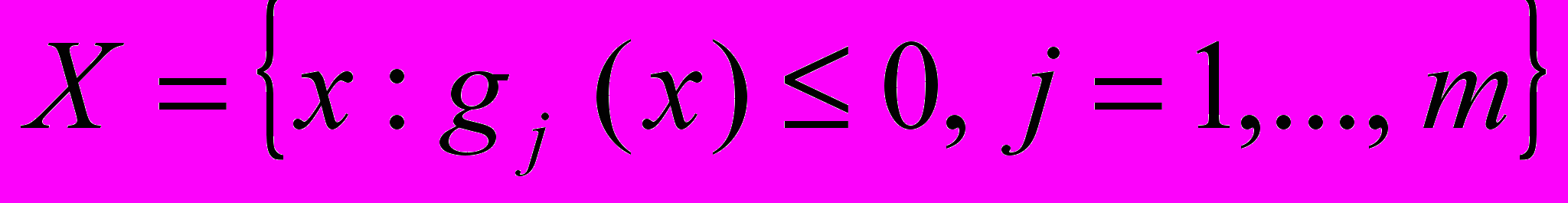(1.2)

Где g_j(x) - дифференцируемая функция векторного аргумента, j - число ограничивающих функций.

Задача (1.1) считается поставленной корректно, если ограничения g_j(x)≤0, j=1,…,m совместимы и образуют непустое множество Х , на котором существует целевая функция f(x) .

Аналитическое решение задачи условной оптимизации следует найти с помощью необходимых условий оптимальности – теоремы Куна и Таккера. Существо этой теоремы и построенный на ее основе алгоритм решения поставленной задачи излагаются в разделе 2.1.

В результате аналитического решения задачи типа должен быть получен набор локальных условных минимумов, из которых путем сравнения выбирается решение. Кроме того, полученное решение необходимо сопроводить графической иллюстрацией т.е. построить линии уровня целевой функции, ограничения и найденных точек глобального и локальных минимумов. Для графических построений рекомендуется использовать доступные математические пакеты, например MatCAD, MatLab и др.

Во второй части работы та же самая задача должна быть решена с помощью численных методов безусловной оптимизации. Для этого задачу условной оптимизации следует свести к безусловной с помощью метода штрафных функций.

Перечень методов безусловной оптимизации определяется индивидуально для каждого задания. В данной работе рассматриваются численные методы безусловной оптимизации, приведенные в классификации (см. раздел 2.2).

В процессе решения поставленной задачи с помощью задаваемых численных методов должны быть решены следующие подзадачи:

Разработка алгоритмов (блок-схем) и подпрограмм численных методов безусловной оптимизации, определенных индивидуальным заданием;
Разработка основной программы, в которой задаются все исходные данные, связанные с конкретной задачей условной оптимизации и фиксируются параметры соответствующих численных методов безусловной оптимизации;
Разработка подпрограммы, реализующей метод «штрафных функций», из которой происходит непосредственный вызов подпрограммы конкретного численного метода безусловной оптимизации;
Отладка и тестирование сформированной программы численного решения конкретной задачи условной оптимизации одним из заданных численных методов безусловной оптимизации (эта задача повторяется для каждого заданного метода отдельно);
Решение задачи условной оптимизации одним из заданных численных методов безусловной оптимизации (эта задача повторяется для каждого заданного метода отдельно);
Исследование влияния варьируемых параметров методов безусловной оптимизации (задаваемых в основной программе) на скорость сходимости к искомому решению, фиксируемому с заданной точностью;
Проведение сравнительного анализа заданных методов безусловной оптимизации по скоростям сходимости к искомому решению;
Написание выводов по проделанной работе.