Учебное пособие для выполнения курсовой работы утверждено
| Вид материала | Учебное пособие |
- Учебное пособие для выполнения курсовой работы в 7-м семестре Утверждено, 19.62kb.
- Методическое пособие для выполнения курсовой работы по внутренним незаразным болезням, 539.05kb.
- Учебное пособие для выполнения курсовой работы Челябинск, 218.99kb.
- Учебное пособие к выполнению курсовой работы Владивосток, 1907.89kb.
- Учебно-методическое пособие содержит следующие структурные разделы: введение, цели, 335.07kb.
- Методические рекомендации по организации и защите курсовой работы по дисциплине для, 794.15kb.
- Учебное пособие к написанию курсовой и дипломной работы на факультете pr и рекламы, 1417.71kb.
- Учебное пособие к написанию курсовой и дипломной работы на факультете pr и рекламы, 1417.56kb.
- Учебное пособие Челябинск Издательство юургу 1999, 543.67kb.
- Учебное пособие Москва, 2007 удк 50 Утверждено Ученым советом мгупи, 1951kb.
1.4.Методические рекомендации по численному решению задачи условной оптимизации с ограничениями типа неравенств
Численное решение задачи условной оптимизации с ограничениями типа неравенств должно осуществляться посредством нескольких методов с цель последующего сравнительного анализа соответствующих реализаций решения. Сравнение должно осуществляться как с точки зрения эвристических оценок показателей сходимости методов, так и с точки зрения затрат машинного времени на реализацию численного решения конкретной задачи с заданной точностью.
Выбор и фиксация вариантов численных методов безусловной оптимизации осуществляется исходя из их классификации (см. рис. 2.2).
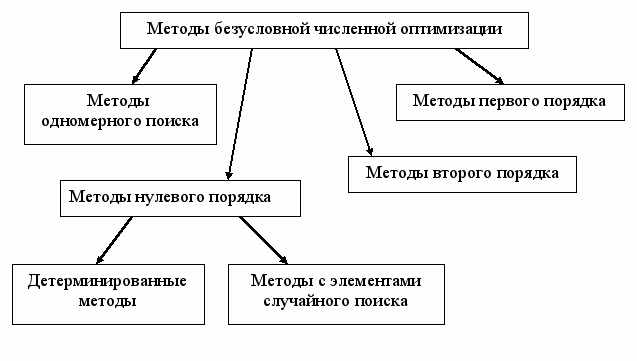 | |
| Рис | 2.2 |
Каждый вариант задания должен включать не менее двух методов безусловной оптимизации. При этом они должны представлять различные классы методов и их суммарные трудоемкости в смысле программирования и отладки должны быть близкими.
В отчете по КР должны быть представлены промежуточные результаты, связанные с программированием и тестированием заданных вариантов численных методов оптимизации, а именно: алгоритмы этих методов, оформленные в виде соответствующих блок-схем, и результаты тестирования, показывающие работоспособность методов (распечатки программ и результатов счета для безусловной минимизации рекомендуется поместить в Приложении к КР).
Для численного поиска условного минимума целевой функции (1.1) при условиях (1.2) предлагается применить метод «Штрафных функций» [1, 2], позволяющий свести задачу условной минимизации к последовательности итеративно решаемых задач безусловной минимизации. Суть этого метода заключается в следующем.
На основе целевой функции формируется функция вида:
| Φ(x, α) = f(x) + αТ s((g(x)) | (2.10) |
Где s(g(x)) – сложная функция вектора х, называемая функцией «штрафа» (или «штрафной» функцией), α – вектор коэффициентов «штрафа», размера [m1].
Функция s(g(x)) должна иметь следующие свойства.
| s((g(x)) = 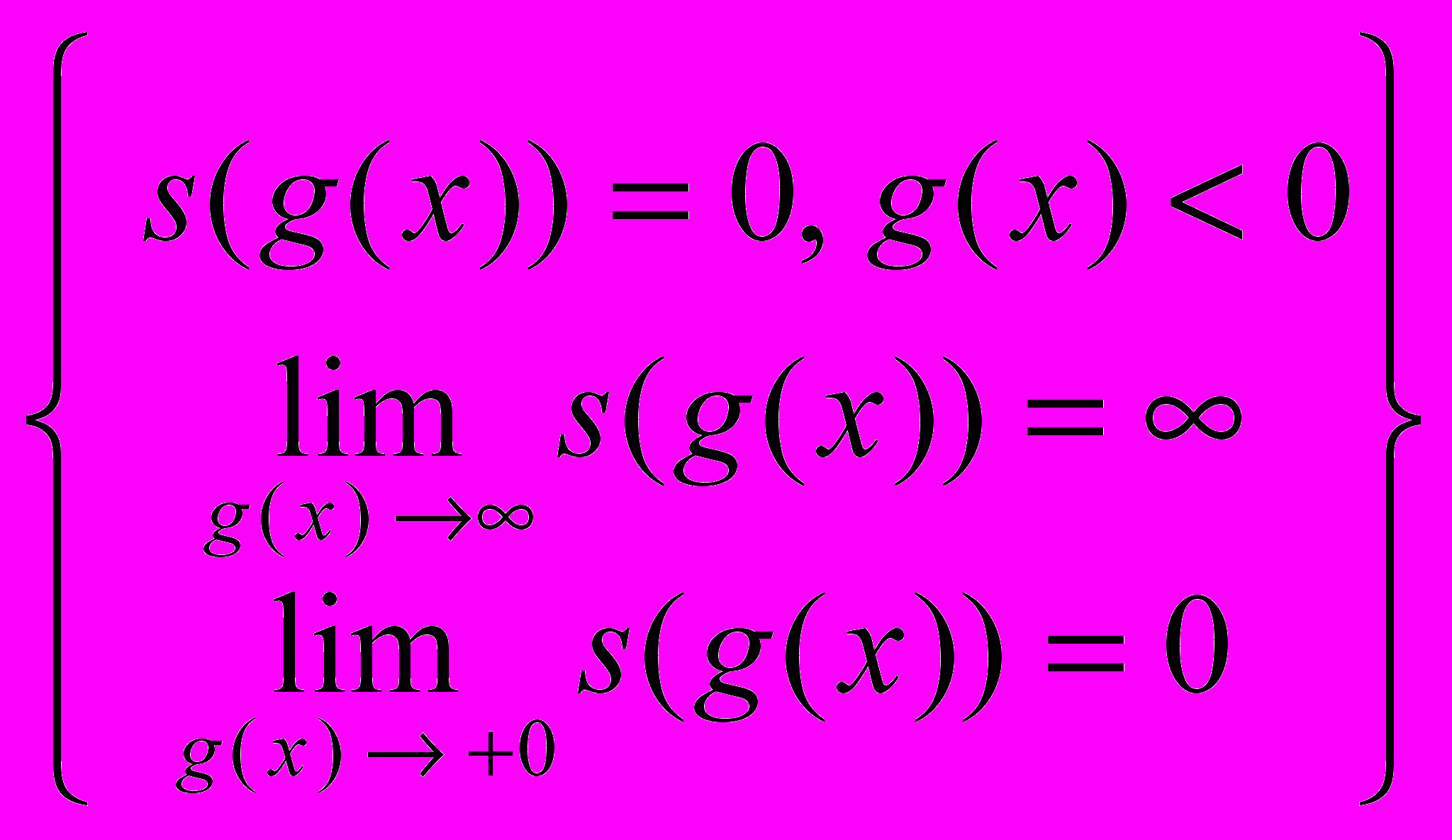 | (2.11) |
То есть, если ограничения типа неравенств не нарушаются (g(x) < 0) , то функция «штрафа» не должна никак себя проявлять в функции (2.10), и если это ограничение нарушено, то с ростом этого нарушения должен расти «штраф» за него, вплоть до бесконечности. При этом в точках g(x) = 0 функция «штрафа» должна быть непрерывной справа.
Обоснованием для применения метода штрафных функций является принятие следующей принципиально важной гипотезы:
Предполагается, что последовательность аргументов решений задач безусловной оптимизации {x*i безусл}, i = 1, 2,….., а именно:
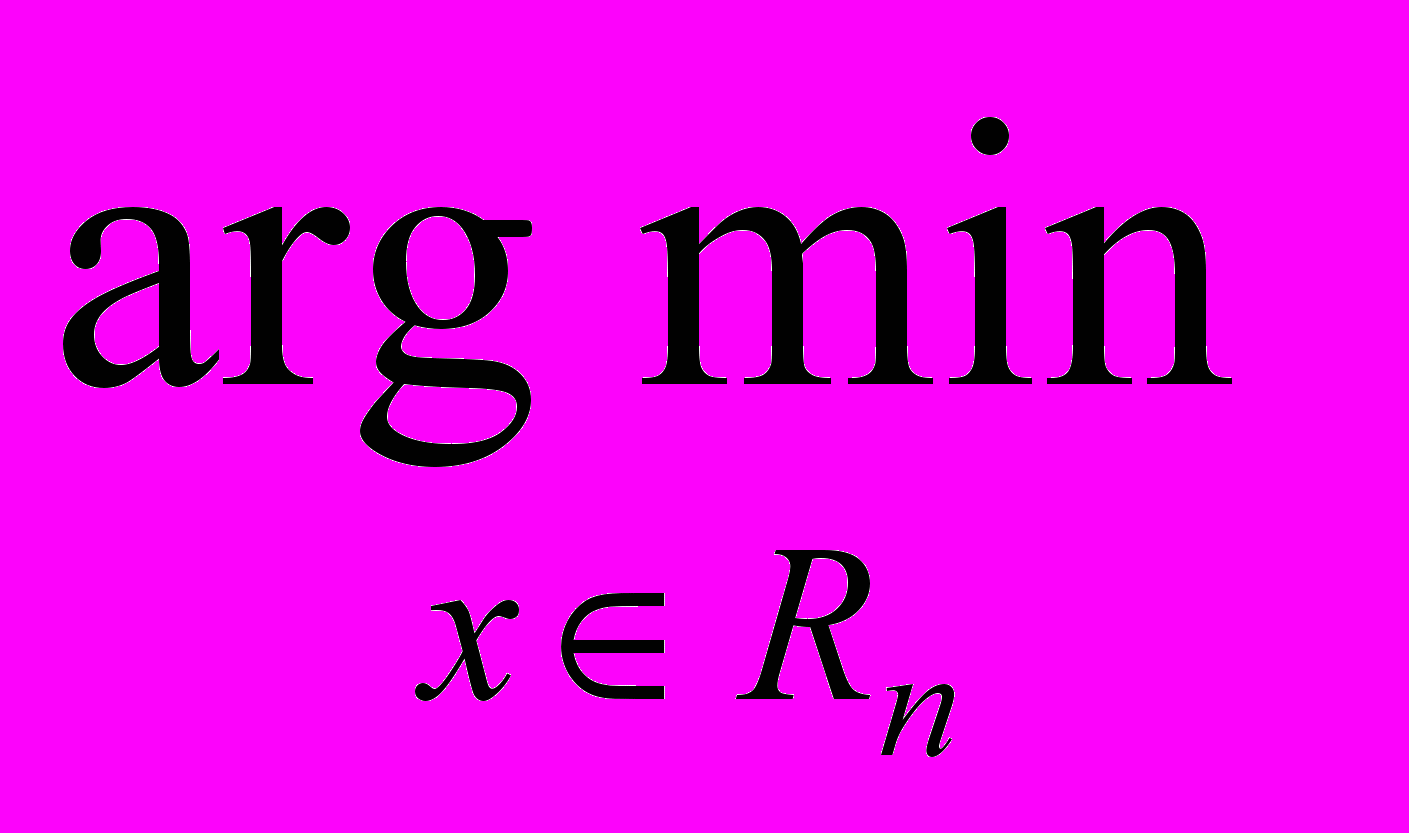 Φ(x, αi ) = Φ(x, αi ) = 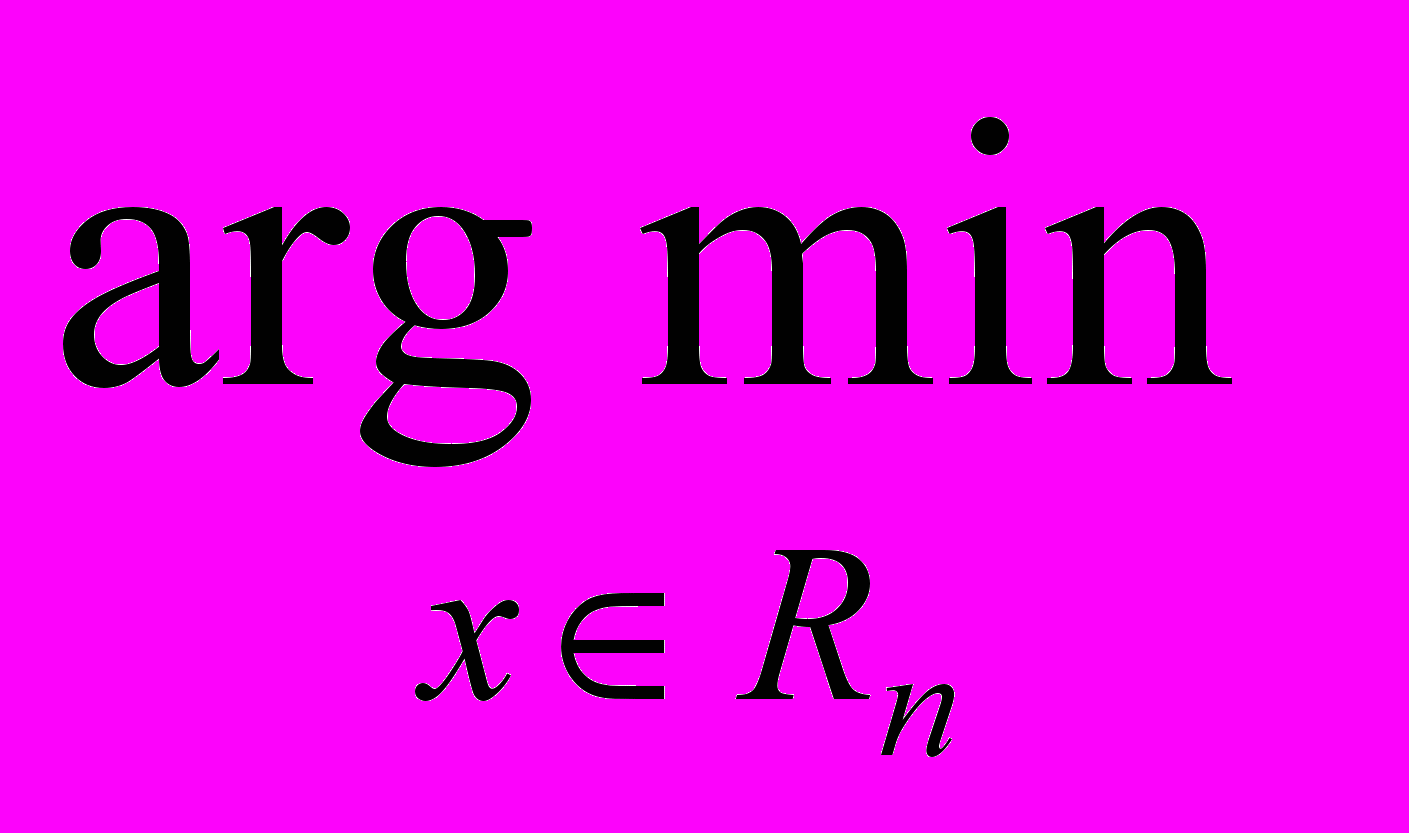 [ f(x) + αi s((g(x))] = x*i безусл [ f(x) + αi s((g(x))] = x*i безусл | (2.12) |
стремится к решению задачи условной оптимизации (1.1, 1.2) при неограниченном росте последовательности коэффициентов «штрафа» {ai} , то есть:
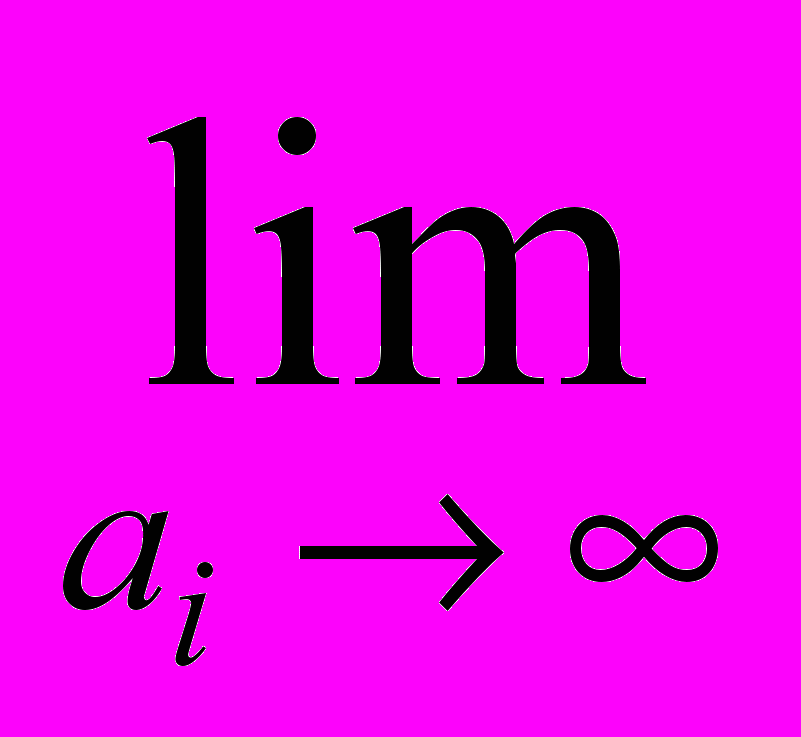 x*i безусл (αi ) = x* усл x*i безусл (αi ) = x* усл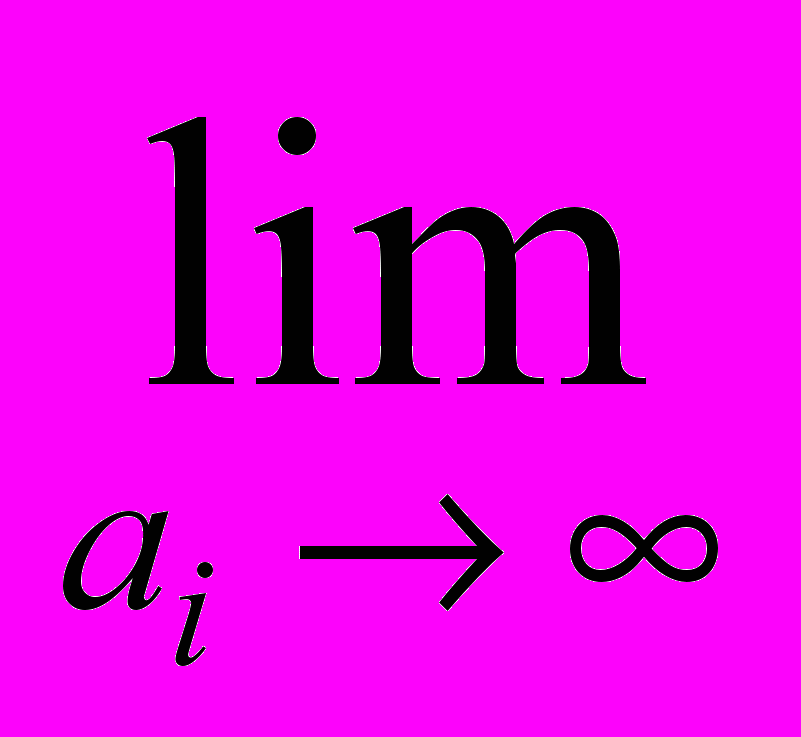 Φ(x*i безусл (αi ), αi ) = f(x* усл) Φ(x*i безусл (αi ), αi ) = f(x* усл) | (2.13) |
Где x*i безусл – вектор безусловного минимума функции Φ(x, αi) , зависящий от конкретного значения коэффициента «штрафа» αi, x*усл - вектор координат условного минимума, соответствующего поставленной задачи.
Таким образом, согласно приведенной гипотезе алгоритм приближенного численного решения задачи (1.1, 1.2) должен включать следующие операции.
- Ввод в программу: конкретных целевой функции - f(x) и ограничений - g(x) < 0 .
- Определение и ввод в программу конкретной функции «штрафа» - s(g(x)) .
- Фиксация исходных значений коэффициентов «штрафа» - α0 и сопутствующих параметров (например, параметра итеративного роста коэффициентов «штрафа» и параметра допустимого числа итераций).
- Определение метода безусловной оптимизации.
- Фиксация параметров выбранного метода.
- Задание начального приближения вектора аргументов x(0) .
- Организацию с помощью программных средств «охватывающего» цикла перебора коэффициентов «штрафа» - αi , i = 1, 2, …. (с нарастанием до определенного значения).
- Организацию с помощью программных средств и в соответствии с выбранным методом безусловной оптимизации «внутреннего» цикла поиска минимума функции Φ(x, αi) для текущего значения αi и определение промежуточного значения x*i безусл (αi ). В случае применения в рамках заданного численного метода конкретной процедуры одномерной оптимизации, необходимо «внутри» этого цикла организовать еще один цикл - минимизации функции в заданном направлении.
- Проверка условий окончания процедуры поиска условного минимума целевой функции и в случае их выполнения – прекращение процедуры, в противном случае – назначение новых значений αi и x(0i) и переход к пункту 6 алгоритма (рекомендуется в качестве новых значений x(0i) выбирать последние значения этого вектора на предыдущей итерации «внутреннего» цикла, то есть - x(p)i-1 ).
Этот алгоритм может быть представлен в виде укрупненной блок-схемы (см. рис. 2.3).
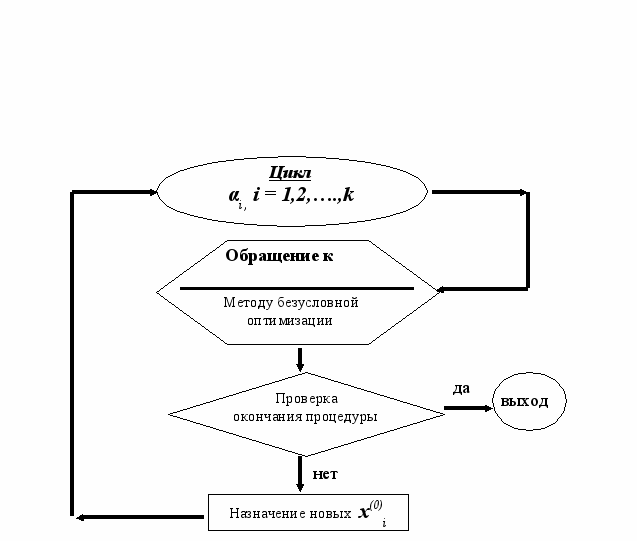  вход  Задание исходных данных (параметров, коэффициентов и др.) 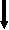 | |
| Рис | 2.3 |
В качестве функции «штрафа» предлагается использовать следующую составную функцию.
| s((g(x)) = 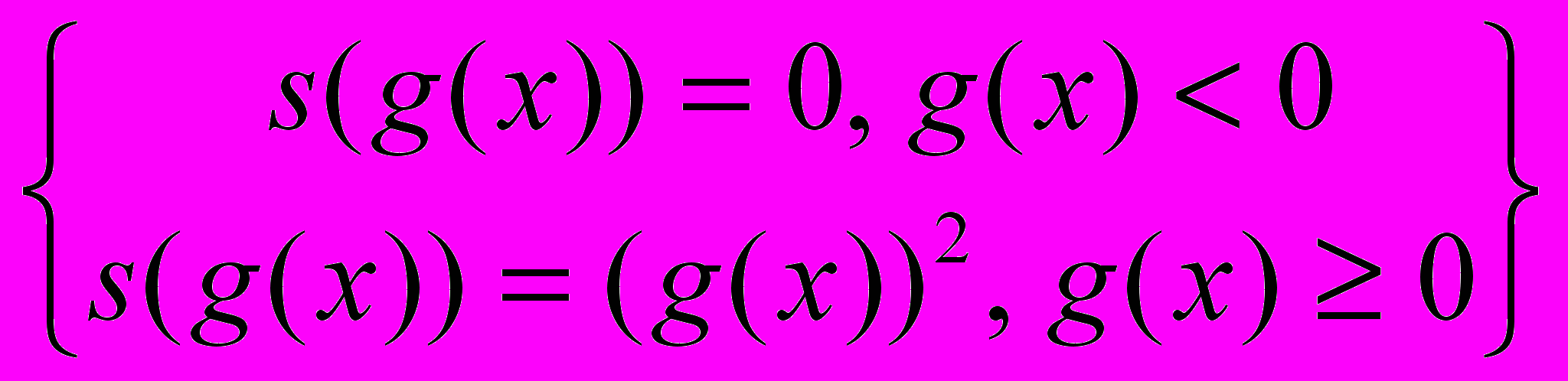 | (2.14) |
Где gj(x) одна из m функций ограничений.
В общем случае для каждой функции gj(x) должна быть определена своя функции «штрафа» - sj((gj(x)) типа (2.14). В результате функция Φ(x, α) приобретет более конкретный вид:
| Φ(x, αi) = f(x) +  αij sj((gj(x)) αij sj((gj(x)) | (2.15) |
Коэффициенты «штрафа» αij могут быть различны для каждого ограничения gj(x), однако, имея в виду абстрактность рассматриваемой задачи, они могут определяться одинаковой последовательностью значений {ai}, i = 1,2,…. Тогда (2.14) с учетом этого и (2.15) будет иметь вид:
| Φ(x, αi) = f(x) + 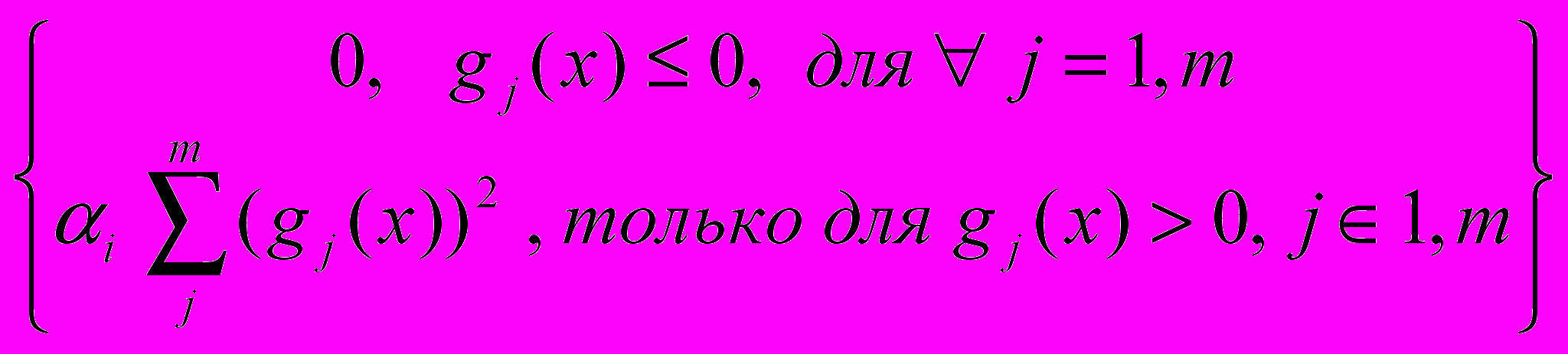 | (2.16) |
Таким образом, в случае правильного подбора параметров используемых методов и рационального выбора последовательности коэффициентов «штрафа» {ai}, i = 1,2,…., значение которых увеличиваются с ростом номера последовательности i , каждое новое решение задачи на безусловный минимум функции Φ(x, αi), должно приближаться к решению задачи условной минимизации (1.1, 1.2).
