Geum.ru

Крутецкий В. А. Психология математических способностей школьников

Вид материалаДокументы

Содержание


Приложение № 1.
Серия II.
Серия III.
Инструкционные карточки по решению задач
Фрагмент урока № 1.
Фрагмент урока № 2.
Подобный материал:
1   2

ПРИЛОЖЕНИЕ № 1.

Серия I.

1) Задачи с несформулированным вопросом:
  • Масса ящика с апельсинами 28 кг, а масса ящика с яблоками 27 кг. В школьную столовую привезли два ящика апельсинов и один ящик с яблоками.
  • В одной вазе 15 цветов, а в другой на 6 цветов больше.
  • Рыбаки вытащили сеть с 30 рыбами. Среди них было 17 лещей, а остальные – окуни.

2) Задачи с неполным составом условия:
  • В коробке на 4 карандаша больше, чем в пенале. На сколько в пенале карандашей меньше, чем в коробке?

- На какой вопрос ты можешь ответить, а на какой нет? Почему?

- Подумай! Как дополнить условие задачи, чтобы ответить на оба вопроса?

3) Задачи с избыточным составом условия:
  • Задача. У кормушки было 6 серых и 5 белых голубей. Один белый голубь улетел. Сколько белых голубей стало у кормушки?

Анализ текста показывает, что одно из данных лишнее - 6 серых голубей. Для ответа на вопрос оно не нужно. После ответа на вопрос задачи учитель предлагает внести в текст задачи такие изменения, чтобы это данное понадобилось, что приводит к составной задаче. У кормушки было 6 серых и 5 белых голубей. Один голубь улетел. Сколько голубей осталось у кормушки?

Эти изменения повлекут необходимомсть выполнить два действия
(6 + 5) - 1 или (6 - 1) + 5 или (5 - 1) + 6

4) Работа по классификации задач.

Разбейте эти задачи по две так, чтобы из них можно было составить одну:

1. На уроках труда ученики сшили 7 зайчиков и 5 мишек. Сколько всего игрушек сшили ученики?

2. Первая бригада собрала 10 тонн огурцов, а вторая в два раза больше. Сколько всего тонн огурцов собрали рабочие?

3. У Светы было 18 конфет, она съела 6 конфет. Сколько конфет у неё осталось?

4. Ученики сшили 12 игрушек. 8 игрушек они отдали в группы садика. Сколько игрушек осталось у учеников?

5. Рабочие собрали 45 тонн огурцов и погрузили их на 9 машин поровну. Сколько тонн увезла каждая машина?

6. У Светы было 9 конфет. Она раздала их трём подругам поровну. Сколько конфет получила каждая подруга?

5) Составление задач.

а) Составление задач по выражению на определённую тему:

10 ∙ 3 + 5 ∙ 2

- Составьте задачу о покупке школьных принадлежностей.

б) С помощью опорных слов:

(17 + 15) – 14 - Вырастили, продали, осталось.

3 ∙ 5 + 2 ∙ 4 – Яблоки, бананы, всего.

в) Составление задач по решению:

7 – 5 = 2 (б.) 3 ∙ 5 = 15 (л) 4 ∙ 9 = 36 (ящ.)

Серия II.

1) Решение задач одного типа (простые задачи на кратное сравнение):

На первой полке 27 книг, на второй 9 книг. Во сколько раз на первой полке больше книг, чем на второй?

В одном оркестре 12 скрипок и 2 арфы. Во сколько раз меньше в оркестре арф, чем скрипок?

2) Решение задач разного типа (простые задачи на кратное сравнение, на увеличение, уменьшение числа в несколько раз):

Морская звезда живёт 5 лет, а паук в 4 раза больше. Сколько лет живёт паук? Морская звезда живёт 5 лет, а паук 20 лет. Во сколько раз больше живёт па-ук, чем морская звезда?

Длина краба-паука 20 см , а краба-скрипача в 4 раза меньше. Чему равна длина краба-скрип

3) Решение задач с постепенной трансфармацией из конкретного в абстрактный план: Тетрадь стоит 6 рублей, а карандаш 3 рубля. Сколько стоят 5 тетрадей и 8 карандашей?

Тетрадь стоит а рублей, а карандаш 3 рубля. Сколько стоят 5 тетрадей и 8 карандашей?

Тетрадь стоит а рублей, а карандаш в рублей. Сколько стоят 5 тетрадей и 8 карандашей?

Тетрадь стоит а рублей, а карандаш в рублей. Сколько стоят х тетрадей и 8 карандашей?

Тетрадь стоит а рублей, а карандаш в рублей. Сколько стоят х тетрадей и у карандашей?

4) Составление уравнения по условию задачи:

После того как Шарик послал в районную газету 125 фотографий коровы Мурки, у него осталось ещё 13 её фотографий. Сколько всего фотографий коровы Мурки было у Шарика? Дядя Фёдор отправил маме и папе 150 посланий. Третью часть этих посланий составляли письма. Сколько писем отправил дядя Фёдор маме и папе? Почтальон Печкин получил к празднику 160 посылок. 3 из них он уже открыл. Сколько посылок предстоит открыть почтальону Печкину? 5) Решение задач с неопределёнными данными.

Составьте решение этой задачи (можно выражением, можно по действиям)

Картофеля – кг Решение: ( + ) ∙

Моркови - кг

Лука - ? кг, в раз больше, чем

Для развития гибкости мышления предлагаются упражнения:

Серия III.

1) Задачи, имеющие несколько способов решения:

На спинах трёх стоящих рядом слонов могут танцевать 60 дрессированных мышей. Сколько слонов нужно поставить рядом, чтобы на их спинах могли танцевать 30 дрессированных мышей?

В походе Дениса назначили летописцем. Он заполнил 3 зелёные тетради по 25 листов в каждой и 3 такие же синие тетради. Сколько всего страниц заполнил Денис заметками и рисунками?

2) Решение и составление задач, обратных данной:

Реши задачу. Рыболовы поймали несколько окуней. Из 9 они сварили уху, и у них осталось ещё 7 окуней. Сколько всего окуней поймали рыболовы?

Составь и реши задачи, обратные данной.

3) Решение задач обратным ходом:

Том Сойер проиграл Джо Гарперу 30 стеклянных шариков, в следующей

игре он увеличил число своих шариков в 2 раза, затем снова проиграл 60 шариков, после чего снова увеличил число оставшихся шариков в 2 раза. Когда он после всех игр подарил Геку Финну 90 шариков, у него осталось 70 шариков.

Сколько шариков было вначале?



4) Решение задач с альтернативным условием.

Это задачи, в ходе решения которых необходимо рассматривать несколько возможных вариантов условия, а ответ находится после того, как все воз-можные варианты будут исследованы.

1 уровень

Катя вырезала 16 белых снежинок и 18 голубых. 6 снежинок одного цвета она отдала Пете. Сколько белых и сколько голубых снежинок осталось у Кати?

2 уровень

Катя вырезала 16 белых снежинок и 18 голубых. 6 снежинок она отдала Пете. Сколько белых и сколько голубых снежинок осталось у Кати?


ПРИЛОЖЕНИЕ 2.

ИНСТРУКЦИОННЫЕ КАРТОЧКИ ПО РЕШЕНИЮ ЗАДАЧ:


Реши задачу:

В парке 100 деревьев. Из них 28 лип, 34 клёна, а остальные – дубы. Сколько дубов в парке?

Найду объекты: Дам им характеристики:

Определю требование задачи.

Выбери краткую запись:

а) I – 28 л. б) Л. – 28 д. в) Липы - 28 д.

II – 34 д. ? д. Кл. – 34 д. Клёны – 34 д. 100 д.

III – 100 д. Д. - ? д. Дубы - ? д.

Выбери верное решение:

а) 1)28 + 34 = 62 (д.) – лип и клёнов. б) 1)100 - 28=72 (д.) - клёнов и лип.

2) 100 - 62 = 38 (д.) – дубов. 2) 72 - 28= 44 (д.) - дубов.

в) 1)100 - 28=72(д.) - клёнов и дубов. г) 1)100 – 34 = 66(д.) – дубов и лип.

2) 72 – 34 = 38 (д.) – дубов. 2) 66 – 28 = 38 (д.) – дубов.



Реши задачу:

Из посёлка и города выехали одновременно навстречу друг другу велосипедист и мотоциклист. Велосипедист ехал со скоростью 16 км/ч, а мотоциклист со скоростью 48 км/ч. Велосипедист проехал до встречи 96 км. Какое расстояние до встречи проехал мотоциклист?

Найду время, которое был в пути велосипедист?

Найду расстояние, которое проехал мотоциклист?

Проверь ответ:

а) 288км/ч б) 8 км в) 288км г) среди ответов нет правильного

Исправь допущенные ошибки:

а) ошибок нет б) ошибки исправил(а) в) я не уверен в правильности решения



ПРИЛОЖЕНИЕ 3.

Листы заданий по темам.

Лист 1.

Составные задачи, при решении которых используется смысл действий сложения и вычитания.

1 уровень. Реши задачу:

К школе привезли 48 берёз и 36 осин. В первый день школьники посадили 32 берёзы. Сколько деревьев осталось посадить школьникам?

2 уровень. Дополни условие задачи согласно схеме и реши её.

3 уровень. Поясни выражение и запиши ответ:

(48 - 32) – (36 – 30)

1 уровень. Реши задачу:

Для детского сада закупили 7 ковров красного цвета и 11 ковров коричневого цвета. Сколько мотков шерсти пошло на ковры, если красной шерсти израсходовали на 20 мотков меньше, чем коричневой?

2 уровень. Выбери схему к данной задаче и ответь на поставленный вопрос.

3 уровень. Реши задачу:

Сколько овец надо постричь, если с одной овцы получают 2 кг шерсти, а масса мотка 200 грамм.

Лист 2.

Составные задачи, при решении которых используется смысл действий сложения и вычитания, умножения и деления.

1 уровень. Реши задачу:

Огородник собрал 2 ящика помидоров по 9 кг в каждом и 8 таких же ящиков огурцов. Сколько килограммов овощей собрал огородник?

2 уровень. Реши задачу:

Все овощи огородник засолил в бочках по 18 кг в каждой. Сколько бочек с

овощами получилось?

3 уровень. Реши задачу:

За первые 3 месяца семья съела овощи из 3 бочек. Какие овощи это могут быть, если в бочке овощи одного вида?

1 уровень. Реши задачу:

Для уроков труда купили 20 пачек цветной бумаги по 12 рублей за каждую и столько же пачек картона по 18 рублей за пачку. Сколько стоила вся покупка?

2 уровень. Реши задачу другим способом.

3 уровень. Ответь на вопрос: Что стоило больше - цветная бумага или картон и на сколько?


ПРИЛОЖЕНИЕ 4.

ФРАГМЕНТ УРОКА № 1.

Урок № 2. 2 класс. Сложение и вычитание чисел (Повторение и закрепление знаний)

Цели:

1. Закреплять умение делать письменные и устные вычисления в соот-ветствии с изученными во 2-м классе алгоритмами сложения и вычитания двузначных чисел, а также осуществлять проверку вычислений на основе знаний о сложении и вычитании как взаимно обратных действиях.

2. Закреплять умение решать простые и составные задачи на сложение и вычитание, изученные во втором классе.

3. Учить решать задачи с помощью построения цепочки умозаключений, выраженных во внешней речи.

Ход урока.

I. Организационный момент. Урок математики мы проведём в форме игры- путешествия. Мы отправимся в поход вместе с Дядей Фёдором, котом Матроскиным и псом Шариком.

II.Актуализация знаний.

Индивидуальная работа.

- Реши примеры, выполнив запись в столбик (к доске вызываются 4 ученика):

_80 _51 48 73

36 29 42 19

Самостоятельная работа.

Остальные учащиеся выполняют задание:

Кот Матроскин задумал несколько двузначных чисел. Запишите их.

4 д. 3 ед., 7 д. 5 ед., 9 д. 9 ед., 3 д. 8 ед.

Взаимопроверка.

Фронтальная работа.

а) – Что можно сделать с этими числами? ( попарно сравнить, назвать их в порядке возрастания (убывания), найти закономерность в полученном ряде чисел. Выбрать любое число, назвать его разрядные слагаемые и составить 4 возможных равенства на сложение и вычитание.)

12, 24, 18, 15, 21.

б) – Что можно сделать с этими высказываниями? (Придумайте к ним вопросы и решите полученные задачи.)
  • Коту Матроскину почтальон Печкин принёс 18 писем, а псу Шарику на 25 больше.
  • Шарик сделал 27 фотоснимков в лесу, а в поле 15.
  • В начале лета Дядя Фёдор сделал 10 рисунков. К концу лета их количество увеличилось в 5 раз.

в) – Подберите выражение к задаче.

Кот Матроскин привёз на рынок 90 литров сметаны. Утром он продал 15 литров сметаны. Сколько литров сметаны он продал днём, если к вечеру у него осталось 5 литров?

90 – 15 – 5; 90 – ( 15 - 5); 90 – ( 15 + 5)

г) Что можно сделать с этими геометрическими фигурами? ( Дать название каждой фигуре, разбить их на группы, найти периметр плоских фигур)







III. Решение логической задачи.

Основная цель работы – учить строить цепочки умозаключений, выраженных во внешней речи.

Во время разбора акцентируем внимание на том, что решение задач, аналогичных этой, начинается с того, что более определено (то, что больше всего известно). В данной задаче начинаем с определения того, что налито в миску.

Для того, чтобы ученики смогли построить развёрнутое высказыва-ние строим граф, который заполняется поэтапно по мере решения задачи.

а) Миска Кувшин Банка б) Миска Кувшин Банка в) Миска Кувшин Банка Сметана Молоко Простокваша Сметана Молоко Простокваша Сметана Молоко Простокваша

Эту же работу выполняем с помощью таблицы истинности-ложности. Составляем таблицу возможностей, расставив знак + или – в соответствии с условием.
Молоко
Сметана
Просто-кваша

Кувшин
+
-
-

Банка






-

Миска
-
-
+



Теперь учащиеся могут сами построить цепочку умозаключений: «В миске не сметана и не молоко, значит, в миске простокваша. Теперь можно узнать, что налито в кувшин. Если в миске простокваша, то в кувшине не может быть ни простокваши, ни сметаны, значит, там молоко. В миске простокваша, в кувшине молоко, значит, в банке сметана.

ФРАГМЕНТ УРОКА № 2.

Урок № 67. 2 класс. Тема: « Умножение с нулём и единицей». На этапе введения нового знания используется групповая форма работы (состав группы - 2 человека)

III. Введение нового знания. Далеко – далеко за морями и горами была страна Цифирия. Жили в ней трудолюбивые числа. Королева Арифметика пригласила жителей страны к себе на службу. Она предлагает выполнить задания:

1. Соедините прмеры на сложение с примерами на умножение:

6 х 1 1 + 1 + 1 + 1 + 1 + 1

1 х 5 6

1 х 8 1 + 1 + 1 + 1 + 1 + 1

1 + 1 + 1 + 1 + 1 + 1 + 1 + 1

2. Решите задачи. №1. а) У 5 котят по одной ленточке. Сколько всего ленточек? б) У 9 слонов по 1 хоботу. Сколько всего хоботов? в)У 12 школьников по 1 учебнику математики. Сколько всего учебников?

1 ряд (дети с низким и средним уровнем математических способностей) №1 а) 1 вариант решает задачу сложением, 2 – умножением.

2 ряд (дети со средним и высоким уровнем математических способнос-тей)(№1 б) 1 вариант решает задачу сложением, 2 – умножением.

3 ряд (дети с низким и средним уровнем математических способностей) №1 в) 1 вариант решает задачу сложением, 2 – умножением. Задание: сформулировать правило умножения 1 на любое число.

6 человек решают эти же задачи на доске. Работа проверяется. Формули-руется правило умножения 1 на любое число. Задание для всех учащихся:

Придумайте несколько похожих задач и решите их.


ПРИЛОЖЕНИЕ 5.

Игра «Следопыты»

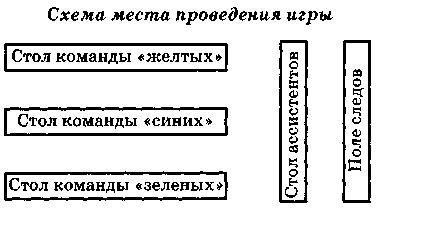В игре участвуют все учащиеся 3 «Б» класса, разделённые на три команды. В каждой команде выбирается «следопыт»- капитан. Он следит за порядком и дисциплиной в команде, участвует в игре, предоставляет выполненные зада­ния ассистенту, обращается к нему за консультацией, отправляется на поиск следующего «следа», которые находятся на игровом поле. Ассистентом может быть старшеклассник, родитель или учитель. Ассистент даёт консультации, следит за правильностью выпол­нения командой поставленных задач, при правильном решении дает разрешение на поиск следующего «сле­да»- задания. Каждая команда выбирает свой цвет из числа предложенных (синий, желтый, зеленый) и располагается за столом с флажком этого цвета. Сле­ды разных цветов, но с одинаковыми заданиями хао­тично расположены на игровом поле, невидимом для команды.

Первый «след» с заданием выдается одновременно всем следопытам. Начинается решение первой задачи. Когда команда получает ответ, следопыт обращается к ассистенту для сверки ответа. Ассистент, оценив правильность ответа, дает разрешение на поиск сле­дующего «следа» или просит еще раз решить данную задачу. В случае верного ответа следопыт подходит к игровому полю, где располагаются «следы», и ищет «след» с нужным номером. Номер «следа» соответс­твует ответу, полученному в предыдущем задании. Следопыт имеет право взять «след» только цвета сво­ей команды. Последним заданием является поиск «послания» юным любителям математики. Чья команда первой найдёт это послание, та и является победителем игры. В конце игры все послания зачитываются. «След» вырезается из цветной бумаги цвета коман­ды. На одной стороне «следа» написано задание. На обороте — номер «следа», то есть результат, получив­шийся при выполнении предыдущей задачи, необхо­димо изготовить всего 15 «следов», плюс 2-5 ложных (с произвольными номерами). Послания также в раз­ноцветных конвертах.

Задания, записанные на «следах»

Первый «след» (без номера). Выполните действия с числами, записанными в римской нумерации: (V ∙ V + V) : (VV : V – V)

Второй «след», № 6 (ответ первого следа). Колесо имеет 10 спиц. Сколько промежутков между спицами?

Третий «след», № 9. Решите ребус. Найдите сум­му цифр в ответе, это число и будет номером следую­щего «следа»:



Четвертый «след», №19. Решите задачу. Возраст дедушки выражается наименьшим трёхзначным числом, которое записывается различными цифрами. Сколько лет дедушке?

Пятый «след», № 102. Красная Шапочка несла бабушке пироги: 7 - с капустой, 6-с яблоками, 3-с мясом. По дороге она съела 2 пирога. Что могло при этом получиться?

а) Бабушке не досталось пирогов с мясом.

б) Пирогов с яблоками стало меньше, чем с мя­сом.

в) Пирогов всех видов стало поровну.

г) Пирогов с капустой стало больше, чем осталь­ных вместе.

д) Пирогов с капустой стало столько же, чем осталь­ных вместе.

Шестой «след», д). Решите задачу. Ребята пилят бревно на части определенной дли­ны. Отпиливание одного такого куска занимает одну минуту. За сколько минут они распилят бревно дли­ной 5 м на пять частей?

Седьмой «след», № 4. Задача. В автобусе ехали 25 человек. На первой останов­ке вышли 7 человек, зашли 4 человека. На следующей остановке вышли 12 человек, зашли 5 человек. На сле­дующей остановке вышли 8 человек, зашли 6 человек. На следующей остановке вышли 2 человека, зашли 16 человек. На следующей остановке вышли 5 чело­век. Сколько было остановок?

Восьмой «след», № 5. Пассажир автобуса ехал в село. По дороге он встретил пять грузовиков и три легковые машины. Сколько всего машин ехало в село?

Девятый «след», № 1. Рост Буратино 1 метр, а длина его носа раньше была 9 сантиметров. Каждый раз, когда Буратино врал, длина его носа удваивалась. Как только длина его стала больше его роста, Буратино перестал врать. Сколько раз он соврал?

Десятый «след», № 3. У охотника в корзине лежат зайцы и гуси. Всего насчитали десять голов и 28 ног. Сколько зайцев подстрелил охотник?

Одиннадцатый «след», № 4. Яблоко и груша весят 300 граммов. Определите вес яблока, если:



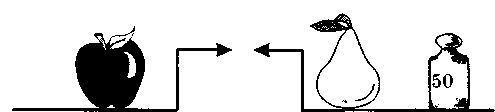
Двенадцатый «след», № 175.

В царстве Кощея томится Василиса Прекрасная. Надо её освободить. В подземелье три темницы: в одной из них заперта Василиса, в другой расположился Змей Горыныч, а третья темница – пустая. На дверях есть надписи, но все они ложные. На двери первой темницы написано:

«Здесь Василиса», на двери второй: «Темница 3 – не пустая», на двери третьей: «Здесь змей». В какой же темнице находится Василиса?

Тринадцатый «след», во второй темнице.

На майках спортсменов написаны их порядковые номера. Каких номеров больше – чётных или нечётных.

Четырнадцатый «след», нечётных (13). Линейка попугая длиннее линейки слонёнка, но короче линейки удава, а линейка мартышки короче линейки слонёнка. У кого самая длинная линейка?

Пятнадцатый «след», у удава. Спешите в кабинет № 1, там вы найдете послание в конверте цвета вашей команды.



ПРИЛОЖЕНИЕ 6.

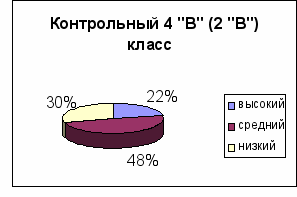
Диаграмма 1


Количественные результаты после проверки работ на констатирующем этапе эксперимента:



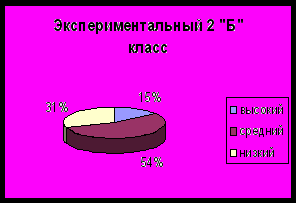
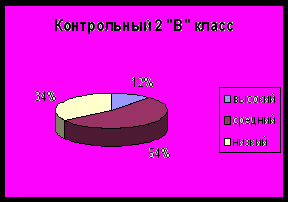
Диаграмма 2


Количественные результаты после проверки работ на контрольном этапе эксперимента: