Рабочая программа по учебному предмету «Алгебра» для 7 класса (базовый уровень)

Вид материала

Рабочая программа

Содержание Рабочая программа Основные развивающие и воспитательные цели Требования к уровню подготовки семиклассников Содержание тем учебного курса 2. Функции (18 ч) Цель – познакомить учащихся с основными функциональными понятиями и с графиками функций y=kx+b, y=kx. Знать 3. Степень с натуральным показателем (21 ч) 4. Многочлены (23 ч) 5. Формулы сокращённого умножения (23 ч) 6. Системы линейных уравнений (21 ч) 7. Повторение. Решение задач (4 ч) Требования к уровнюподготовки выпускников Алгебра уметь Календарно-тематическое планирование Выражения, тождества, уравнения (26 ч) Степень с натуральным показателем (21 ч) Формулы сокращенного умножения (23) Системы линейных уравнений (21 ч)

Подобный материал:

• Рабочая программа по учебному предмету «Музыка» для 5 класса (базовый уровень), 174.7kb.
• Рабочая программа по учебному предмету «Природоведение» для 5 класса (базовый уровень), 270.17kb.
• Рабочая программа по учебному предмету «Литературное чтение» для 1 класса (базовый, 264.5kb.
• Рабочая программа по учебному предмету «Мировая художественная культура» для 8 класса, 173.6kb.
• Рабочая программа по учебному предмету «Биология. Общие закономерности» для 9 класса, 858.64kb.
• Рабочая программа по учебному предмету «Биология. Многообразие живых организмов» для, 570.45kb.
• Приказ №86 от «29.» 08. 2011 г. Рабочая программа педагога зубковой Ирины Александровны,, 449.16kb.
• Рабочая программа педагога шашаевой татьяны георгиевны, II квалификационная категория, 400.13kb.
• Кунаревой Арины Вячеславовны по учебному курсу «Алгебра и начала анализа» 10-11 класс, 408.51kb.
• Рабочая программа по немецкому языку для 10 класса филологического профиля Пояснительная, 775kb.

Администрация г.Котовска Тамбовской области

Муниципальное общеобразовательное учреждение

«Основная общеобразовательная школа №1»

г. Котовска Тамбовской области


«Утверждаю»

Директор: ____________С.Л. Попова

Приказ № 135 от 31.09.2010г.

Рассмотрена и рекомендована Методическим советом МОУ «ООШ №1» Протокол №1 от 27.08.2009г.

Рассмотрена и рекомендована Управляющим Советом МОУ «ООШ №1» Протокол №2 от 28.08.2009г.

Рабочая программа

по учебному предмету «Алгебра»

для 7 класса

(базовый уровень)

на 2009 – 2013 годы


РАБОЧАЯ ПРОГРАММА

ДЛЯ ОСНОВНОГО ОБЩЕГО ОБРАЗОВАНИЯ

(Базовый уровень)

Пояснительная записка

Рабочая программа по алгебре составлена на основе примерной программы, опубликованной на сайте Министерства образования, на основе федерального компонента государственного стандарта основного общего образования на базовом уровне, утвержденного приказом Министерства образования от 5 марта 2004 года № 1089.

Данная рабочая программа ориентирована на учащихся 7классов, соответствует учебнику « Алгебра» для 7 класса общеобразовательных учреждений / Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова / Просвещение, 2005-2010г.

Данная программа рассчитана на 136 учебных часа, по 4 часа в неделю. При этом в ней предусмотрен резерв свободного учебного времени в объеме 4 учебных часов для реализации авторских подходов, использования разнообразных форм организации учебного процесса, внедрения современных методов обучения и педагогических технологий. Данной программой предусмотрено проведение 10 контрольных и 19 самостоятельных работ.

В ходе освоения содержания курса учащиеся получают возможность:

• развить представления о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;
  
• овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
  
• изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
  
• развить пространственные представления и изобразительные умения, освоить основные факты и методы планиметрии, познакомиться с простейшими пространственными телами и их свойствами;
  
• получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
  
• развить логическое мышление и речь – умениия логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
  
• сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
  

   Изучение алгебры на ступени основного общего образования направлено на достижение следующих целей:

• овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
  
• интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;
  
• формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
  
• воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.
  

Система уроков условна, но все же выделяются следующие виды: урок-лекция, урок-практикум, комбинированный урок, урок решения задач, урок-тест, урок-самостоятельная работа, урок-контрольная работа.

Основные развивающие и воспитательные цели

 Развитие:

•       Ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
  
•       Математической речи;
  
•       Сенсорной сферы; двигательной моторики;
  
•       Внимания; памяти;
  
•       Навыков само и взаимопроверки.
  

Формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов.

 Воспитание:

•       Культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса;
  
•       Волевых качеств;
  
•       Коммуникабельности;
  
•       Ответственности.
  

Общеучебные умения, навыки и способы деятельности.

В ходе преподавания математики в основной школе, работы над формированием у учащихся перечисленных в программе знаний и умений, следует обращать внимание на то, чтобы они овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:

планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;

решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;

исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;

ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;

проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;

поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.


Требования к уровню подготовки семиклассников

В результате изучения алгебры в 7 классе ученик должен уметь:

• составлять буквенные выражения и формулы по условиям задач, осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
  
• выполнять основные действия со степенями с натуральным показателем, с многочленами; выполнять тождественные преобразования целых выражений; выполнять разложение многочленов на множители;
  
• решать линейные уравнения и уравнения, сводящиеся к ним, системы двух линейных уравнений,
  
• решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
  
• изображать числа точками на координатной прямой
  
• определять координаты точки плоскости, строить точки с заданными координатами;
  
• находить значение функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
  
• описывать свойства изученных функций (y = kx + b, y = kx, y = x², y = x³) и строить их графики.
  

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• выполнения расчётов по формулам, составления формул, выражающих зависимость между реальными величинами; нахождения нужной формулы в справочных материалах
  
• моделирования практических ситуаций и исследование построенных моделей с использованием аппарата алгебры; описания зависимости между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;
  
• интерпретации графиков реальных зависимостей между величинами.
  

Содержание тем учебного курса

Количество часов 136 ч.

Алгебра 7 класс

1. Выражения, тождества, уравнения (26 ч.)

Числовые выражения и выражения с переменными. Простейшие преобразования выражений. Уравнение с одним неизвестным и его корень, линейное уравнение. Решение задач методом уравнений.

 Цель – систематизировать и обобщить сведения о преобразовании выражений и решении уравнений с одним неизвестным, полученные учащимися в курсе математики 5,6 классов.

Знать какие числа являются целыми, дробными, рациональными, положительными, отрицательными и др.; свойства действий над числами; знать и понимать термины «числовое выражение», «выражение с переменными», «значение выражения», тождество, «тождественные преобразования».

Уметь осуществлять в буквенных выражениях числовые подстановки и выполнять соответствующие вычисления; сравнивать значения буквенных выражений при заданных значениях входящих в них переменных; применять свойства действий над числами при нахождении значений числовых выражений.

2. Функции (18 ч)

Функция, область определения функции, Способы задания функции. График функции. Функция y=kx+b и её график. Функция y=kx и её график.

Цель – познакомить учащихся с основными функциональными понятиями и с графиками функций y=kx+b, y=kx.

Знать определения функции, области определения функции, области значений, что такое аргумент, какая переменная называется зависимой, какая независимой; понимать, что функция – это математическая модель, позволяющая описывать и изучать разнообразные зависимости между реальными величинами, что конкретные типы функций (прямая и обратная пропорциональности, линейная) описывают большое разнообразие реальных зависимостей.

Уметь правильно употреблять функциональную терминологию (значение функции, аргумент, график функции, область определение, область значений), понимать ее в тексте, в речи учителя, в формулировке задач; находить значения функций, заданных формулой, таблицей, графиком; решать обратную задачу; строить графики линейной функции, прямой и обратной пропорциональности; интерпретировать в несложных случаях графики реальных зависимостей между величинами, отвечая на поставленные вопросы

3. Степень с натуральным показателем (21 ч)

Степень с натуральным показателем и её свойства. Одночлен. Функции y=x², y=x³, и их графики.

Цель – выработать умение выполнять действия над степенями с натуральными показателями.

Знать определение степени, одночлена, многочлена; свойства степени с натуральным показателем, свойства функций у=х², у=х³.

Уметь находить значения функций, заданных формулой, таблицей, графиком; решать обратную задачу; строить графики функций у=х², у=х³; выполнять действия со степенями с натуральным показателем; преобразовывать выражения, содержащие степени с натуральным показателем; приводить одночлен к стандартному виду.

4. Многочлены (23 ч)

Многочлен. Сложение, вычитание и умножение многочленов. Разложение многочлена на множители.

Цель – выработать умение выполнять сложение, вычитание, умножение многочленов и разложение многочленов на множители.

Знать определение многочлена, понимать формулировку заданий: «упростить выражение», «разложить на множители».

Уметь приводить многочлен к стандартному виду, выполнять действия с одночленом и многочленом; выполнять разложение многочлена вынесением общего множителя за скобки; умножать многочлен на многочлен, раскладывать многочлен на множители способом группировки, доказывать тождества.

5. Формулы сокращённого умножения (23 ч)

Формулы 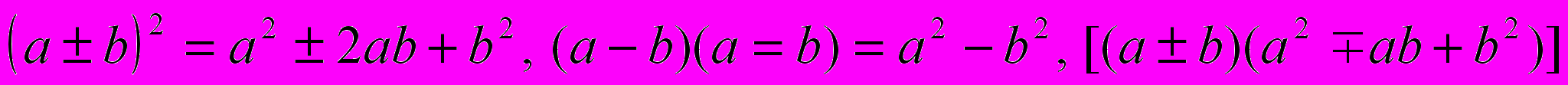. Применение формул сокращённого умножения к разложению на множители.

Цель – выработать умение применять в несложных случаях формулы сокращённого умножения для преобразования целых выражений в многочлены и для разложения многочленов на множители.

Знать формулы сокращенного умножения: квадратов суммы и разности двух выражений; различные способы разложения многочленов на множители.

Уметь читать формулы сокращенного умножения, выполнять преобразование выражений применением формул сокращенного умножения: квадрата суммы и разности двух выражение, умножения разности двух выражений на их сумму; выполнять разложение разности квадратов двух выражений на множители; применять различные способы разложения многочленов на множители; преобразовывать целые выражения; применять преобразование целых выражений при решении задач.

6. Системы линейных уравнений (21 ч)

Система уравнений с двумя переменными. Решение систем двух линейных уравнений с двумя переменными. Решение задач методом составления систем уравнений..

Цель – познакомить учащихся со способами решения систем линейных уравнений с двумя переменными, выработать умение решать системы уравнений и прменять их при решении текстовых задач.

Знать, что такое линейное уравнение с двумя переменными, система уравнений, знать различные способы решения систем уравнений с двумя переменными: способ подстановки, способ сложения; понимать, что уравнение – это математический аппарат решения разнообразных задач из математики, смежных областей знаний, практики.

Уметь правильно употреблять термины: «уравнение с двумя переменными», «система»; понимать их в тексте, в речи учителя, понимать формулировку задачи «решить систему уравнений с двумя переменными»; строить некоторые графики уравнения с двумя переменными; решать системы уравнений с двумя переменными различными способами.

7. Повторение. Решение задач (4 ч)

Закрепление знаний, умений и навыков, полученных на уроках по данным темам (курс алгебры 7 класса).


Учебно-тематический план

Название раздела	Количество часов	Форма контроля
Выражения, тождества, уравнения	26	к/р№1, к/р№2, с/р№1, с/р№2, с/р№3
Функции	18	к/р№3, с/р№4. с/р5
Степень с натуральным показателем	21	к/р№4, с/р№6, с/р№7
Многочлены	23	к/р№5, к/р№6, с/р№8, с/р№9, с/р№10, с/р№11, с/р№12
Формулы сокращенного умножения	23	к/р№7, к/р№8, с/р№13, с/р№14, с/р№15, с/р№16
Системы линейных уравнений	21	к/р№9, с/р№17, с/р№18, с/р№19
Повторение. Решение задач	4	к/р№10

ТРЕБОВАНИЯ К УРОВНЮ
ПОДГОТОВКИ ВЫПУСКНИКОВ

В результате изучения математики ученик должен

знать/понимать¹

• существо понятия математического доказательства; примеры доказательств;
  
• существо понятия алгоритма; примеры алгоритмов;
  
• как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
  
• как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
  
• как потребности практики привели математическую науку к необходимости расширения понятия числа;
  
• вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
  
• каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;
  
• смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;
  

Алгебра

уметь

• составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
  
• выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
  
• применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
  
• решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы;
  
• решать линейные и квадратные неравенства с одной переменной и их системы;
  
• решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
  
• изображать числа точками на координатной прямой;
  
• определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;
  
• распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов;
  
• находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
  
• определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
  
• описывать свойства изученных функций, строить их графики;
  

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;
  
• моделирования практических ситуаций и исследовании построенных моделей с использованием аппарата алгебры;
  
• описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;
  
• интерпретации графиков реальных зависимостей между величинами;
  

Литература и материально-технические средства обучения


1.Алгебра, учебник для 7 класса общеобразовательных учреждений /Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова – М.: Просвещение, 2009 г.


2. Уроки алгебры в 7 классе /В.И.Жохов, Л.Б.Крайнева. Пособие для учителей/ М.: Просвещение, 2009 г.


3.Дидактические материалы по алгебре для 7 класса/ Ю.Н.Макарычев, Н.Г.Миндюк, Л.М.Короткова/ М.: Просвещение, 2007 г.


4.Разноуровневые дидактические материалы по алгебре, 7 класс/ Н.Г.Миндюк, М.Б.Миндюк/ М.: Генжер, 2007 г.


5.Тесты по алгебре, 7 класс, П.И.Алтынов, М. «Экзамен», 2008 г.


6.Контрольные и проверочные работы по алгебре в 7 классе / Л.И.Звавич, Л.Я.Шляпочник, Б.В.Козулин/ Москва «Дрофа», 2005 г.


Календарно-тематическое планирование

учебного материала по алгебре в 7 классе при 4 уроках в неделю по учебнику авт. Ю.Н.Макарычева, Н.Г.Миндюка, К.И.Нешкова, С.Б.Суворовой

№п	Содержание учебного материала	Кол-во часов	Сроки изучения
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45	Выражения, тождества, уравнения (26 ч) Числовые выражения Выражения с переменными Сравнение значений выражений Свойства действий над числами Тождества. Тождественные преобразования выражений Контрольная работа №1 Уравнение и его корни Линейное уравнение с одной переменной Решение задач с помощью уравнений Контрольная работа №2 Среднее арифметическое, размах, мода Медиана как статистическая характеристика Функции (18 ч) Понятие функции Вычисление значений функции по формуле График функции Прямая пропорциональность и ее график Линейная функция и ее график Задание функции несколькими формулами Контрольная работа №3 Степень с натуральным показателем (21 ч) Определение степени с натуральным показателем Умножение и деление степеней Возведение в степень произведения и степени Одночлен и его стандартный вид Умножение одночленов. Возведение одночлена в степень Функции у= О простых и составных числах Контрольная работа№4 Многочлены (23 ч) Многочлен и его стандартный вид Сложение и вычитание многочленов Умножение одночлена на многочлен Вынесение общего множителя за скобки Контрольная работа№5 Умножение многочлена на многочлен Разложение на множители способом группировки Деление с остатком Контрольная работа № 6 Формулы сокращенного умножения (23) Возведение в квадрат и в куб суммы и разности двух выражений Разложение на множители с помощью формул квадрата суммы и квадрата разности Умножение разности двух выражений на их сумму Разложение разности квадратов на множители Разложение на множители суммы и разности кубов Контрольная работа № 7 Преобразование целого выражения в многочлен Применение различных способов для разложения на множители Возведение двучлена в степень Контрольная работа № 8 Системы линейных уравнений (21 ч) Линейное уравнение с двумя переменными График линейного уравнения с двумя переменными Системы линейных уравнений с двумя переменными Способ подстановки Способ сложения Решение задач с помощью уравнений Линейные неравенства с двумя переменными и их системы Контрольная работа № 9 Повторение Контрольная работа № 10	2 2 1 2 4 1 2 3 4 1 2 2 2 2 3 3 3 4 1 2 3 4 3 3 2 3 1 2 2 4 4 1 3 3 3 1 3 3 2 2 3 1 2 4 2 1 3 3 2 3 2 4 2 1 4 1	1.09-27.09 28.09-24.10 25.10-5.12 6.12-29.01 30.01-14.03 15.03-16.05 17.05-30.05