Программа дисциплины по кафедре "Экономическая кибернетика" математическая экономика
| Вид материала | Программа дисциплины |
- Программа дисциплины по кафедре «Экономическая кибернетика» специальностей «Математические, 195.68kb.
- Программа дисциплины по кафедре «Экономическая кибернетика» основы управленческого, 356.46kb.
- Программа дисциплины по кафедре «Экономическая кибернетика» организация и планирование, 238.78kb.
- Программа дисциплины по кафедре «Экономическая кибернетика» для специальности «Математические, 205.71kb.
- Программа дисциплины по кафедре "Экономическая кибернетика" экономика фирмы, 571.84kb.
- Программа дисциплины по кафедре Экономическая кибернетика экономическая информатика, 271.22kb.
- Программа дисциплины по кафедре Экономическая кибернетика логистика, 167.77kb.
- Программа дисциплины по кафедре «Экономическая кибернетика» разработка пакета прикадных, 252.14kb.
- Программа дисциплины по кафедре "Экономическая кибернетика" Статистика, 411kb.
- Программа дисциплины по кафедре "Экономическая кибернетика" Статистика, 459.37kb.
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение высшего профессионального образования
Тихоокеанский государственный университет
-
Утверждаю
Проректор по учебной работе
______________ С.В. Шалобанов
“_____” ________________200_ г.
Программа дисциплины
по кафедре "Экономическая кибернетика"
МАТЕМАТИЧЕСКАЯ ЭКОНОМИКА
Утверждена научно-методическим советом университета для направлений подготовки (специальностей) в области экономики и управления
Специальность: 080801.65 «Прикладная информатика в экономике»
Хабаровск 2008 г.
Программа разработана в соответствии с требованиями государственного образовательного стандарта, предъявляемыми к минимуму содержания дисциплины и в соответствии с примерной программой дисциплины, утвержденной департаментом образовательных программ и стандартов профессионального образования с учетом особенностей региона и условий организации учебного процесса Тихоокеанского государственного технического университета.
Программу составил (и)
-
Мардашёва Е. В.
Преподаватель, кафедра «Экономическая кибернетика»
Ф.И.О. автора (ов)
Ученая степень, звание, кафедра
Программа рассмотрена и утверждена на заседании кафедры
протокол № ______ от «____»__________________ 2008 г.
Зав. кафедрой_________«___»_________ 200__г
Пазюк К. Т. Т.
Подпись дата
Ф.И.О.
Программа рассмотрена и утверждена на заседании УМК и рекомендована к изданию
протокол № ______ от «____»_____________ 200__г
Председатель УМК _______«__» ______ 200__г
Корнилов А. М. Т
Подпись дата
Ф.И.О.
Директор института _______«__»______ 200__г
Зубарев А.Е. о
(декан факультета) Подпись дата
Ф.И.О.
Директор института _______«__»______ 200__г
о
(декан факультета) Подпись дата
Ф.И.О.
- ЦЕЛИ И ЗАДАЧА ДИСЦИПЛИНЫ
Целью курса «Математическая экономика» является освоение студентами современных математических методов анализа, научного прогнозирования поведения экономических объектов, а также получение представлений об особенностях экономико-математического моделирования распределительных процессов в экономике и широко используемых процедурах поиска решений в экономических системах.
Задача курса «Математическая экономика» состоит в том, чтобы научить студентов, обучающихся по специальности “Прикладная информатика в экономике” проводить исследование экономико-математических моделей на основе применения аппарата математических методов, прогнозировать развитие экономической системы или процесса. Знания в области математической экономики будут полезны при прогнозировании и выполнении многовариантных аналитических расчетов в области экономической и управленческой деятельности. Объектами профессиональной деятельности экономиста–информатика являются: органы государственного, регионального и муниципального управления, финансовые, экономические и аналитические подразделения предприятий и учреждений всех организационно-правовых форм, включая отделы развития и маркетинга частных фирм и ассоциаций, банков и страховых компаний, инвестиционных и пенсионных фондов, требующие профессиональных знаний в области экономики, математики, статистики и компьютерных технологий.
Основное внимание в содержании данного курса уделено вопросам математического моделирования экономических процессов, протекающих в реальных экономических объектах на микро- и макроуровнях.
Освоение данного курса будет способствовать развитию у студентов умения и навыков анализа поведения экономических объектов, глубокому пониманию особенностей их функционирования в условиях рыночной экономики, освоению методов выбора наиболее эффективных решений, развитию у студентов аналитического мышления.
Программа курса рассчитана на 68 часов аудиторных занятий в виде лекций, лабораторных и практических занятий.
В качестве контрольных мероприятий предусмотрено выполнение по основным темам курса контрольных заданий с последующей сдачей в конце учебного года экзамена и написания курсовой работы.
2 ТРЕБОВАНИЯ К НАЧАЛЬНОМУ УРОВНЮ ЗНАНИЙ СТУДЕНТОВ
Для усвоения дисциплины студенты должны владеть знаниями основных разделов математики, теории вероятностей, математической статистики и экономической теории, преподаваемых в соответствии с учебным планом специальности.
3 ТРЕБОВАНИЯ К УРОВНЮ ОСВОЕНИЯ СОДЕРЖАНИЯ ДИСЦИПЛИНЫ
В результате изучения материалов курса «Математическая экономика» студенты должны
- понимать основные различия между классами моделей и зависимостей, применяемых в экономике;
- обладать теоретическими знаниями об основных способах моделирования экономических объектов и процессов;
- ориентироваться в различных методах нахождения решений возникающих задач;
- приобрести навыки формулирования и решения наиболее простых моделей;
знать:
- основные принципы и этапы построения экономико-математических моделей экономических процессов;
- виды экономико-математических моделей и возможные сферы их применения;
- уметь:
- строить модели экономических систем и объектов;
- решать экономические задачи с использованием математического аппарата, в том числе с помощью компьютерных прикладных программ;
- анализировать и прогнозировать экономические процессы, опираясь на результаты, полученные путем математического моделирования;
- владеть:
- терминологией дисциплины;
- навыками построения и анализа экономико-математических моделей;
- навыками работы с прикладными программами и уметь применить их к решению задач моделирования.
4 ОБЪЕМ ДИСЦИПЛИНЫ И ВИДЫ УЧЕБНОЙ РАБОТЫ
Таблица 1 – Объем дисциплины и виды учебной работы
| Наименование | По учебным планам (УП) | |
| с максимальной трудоёмкостью | с минимальной трудоёмкостью | |
| Общая трудоёмкость дисциплины по ГОС по УП | 136 | |
| Изучается в семестрах | 6 | |
| Вид итогового контроля по семестрам зачёт экзамен курсовой проект (КП) курсовая работа (КР) расчётно-графическая работа (РГР) реферат (РФ) домашние задания (ДЗ) | 6 6 | |
| Аудиторные занятия по семестрам Всего лекции (Л) лабораторные занятия (ЛР) практические занятия (ПЗ) | 6 68 34 17 17 | |
| Самостоятельная работа Общий объем часов (С2) В т.ч. на подготовку к лекциям на подготовку к лабораторным занятиям на подготовку к практическим занятиям на выполнение КР на выполнение РГР на написание РФ на выполнение ДЗ | 6 68 34 - 17 17 - - | |
5 СОДЕРЖАНИЕ ДИСЦИПЛИНЫ
5.1 Разделы дисциплины и виды занятий и работ
Таблица 2 – Разделы дисциплины и виды занятий и работ
| № | Раздел дисциплины | Л | ПЗ | ЛР | С2 |
| 1 | Введение в дисциплину. Основы моделирования экономических процессов. | 2 | | | 4 |
| 2 | Модели оптимального планирования в экономических организациях. Методы оптимизации. | 8 | 6 | 6 | 16 |
| 3 | Математическая модель межотраслевого баланса. Линейные балансовые модели. Модель равновесных цен. | 8 | 3 | 4 | 16 |
| 4 | Моделирование макроэкономических процессов и систем. | 8 | 4 | 4 | 16 |
| 5 | Моделирование микроэкономических процессов и систем. | 8 | 4 | 3 | 16 |
- Содержание разделов дисциплин
5.2.1 Введение в дисциплину. Основы моделирования экономических процессов.
Система. Модель. Основные типы соотношений, формирующие математическую модель. Аналитические выражения физических законов или общепринятых правил учета хозяйственной деятельности, эмпирические соотношения, соотношения нормативного характера, соотношения, выражаемые бинарным отношением предпочтения на области допустимых значений. Полная, упрощенная и имитационная математическая модель. Экономическая система как объект управления. Основные методы изучения экономики и её подсистем.
5.2.2 Модели оптимального планирования в экономических организациях. Методы оптимизации.
Линейное программирование. Целевая функция. Ограничения. Свойства моделей ЛП экономических систем. Выбор оптимального хозяйственного решения. Анализ чувствительности решения. Статус ресурсов. Пределы изменения ресурсов. Ценность ресурсов. Изменения коэффициентов целевой функции.
Решение задач линейного программирования: графический метод, симплекс-метод. Применение компьютерных программ нахождения оптимальных решений.
Приложения моделей линейного программирования для экономических систем. Планирование ассортимента. Составление смесей, сплавов, соединений. Модели оптимального раскроя материалов. Транспортные модели, задача о назначениях, модели производства с запасами.
5.2.3 Математическая модель межотраслевого баланса. Линейные балансовые модели. Модель равновесных цен.
Балансовые модели в экономике. Статическая модель линейной многоотраслевой экономики Леонтьева, её свойства продуктивности и прибыльности. Матрица Леонтьева (структурная), балансовые уравнения, свойства технологических коэффициентов. Матрица прямых и полных материальных затрат. Коэффициенты косвенных затрат.
Агрегирование нормативных показателей. Коэффициенты прямых и полных затрат труда и капиталовложений. Линейная модель обмена (модель международной торговли). Динамическая модель планирования. Линейная модель производства.
Векторы валового выпуска, цен и норм добавленной стоимости, прогноз изменения цен и инфляции по изменению норм добавленной стоимости.
5.2.4 Моделирование макроэкономических процессов и систем.
Производственные функции
Понятие производственной функции. Производственная функция как основа моделирования экономических объектов на макроуровнях. Некоторые наиболее общие свойства производственных функций. Двухфакторная производственная функция. Неоклассическая производственная функция. Мультипликативная производственная функция. Производственная функция Кобба-Дугласа. Производственная функция в темповой записи. Понятие эластичности функции. Экономическая интерпретация параметров мультипликативной производственной функции. Средние и предельные (маржинальные) значения производственной функции.
Изокванты, изоклинали и их свойства. Связь между изоквантами и изоклиналями. Эластичность и норма замещения производственных факторов. Оценка с помощью производственной функции масштаба и эффективности производства.
Основные типы производственных функций, использующиеся в экономико-математических исследованиях. Методы построения производственных функций.
Модели макроэкономической динамики
Динамическая односекторная модель экономического роста Солоу. Стационарный и переходный режимы. Типы переходных процессов. Оптимальная норма накопления. «Золотое правило» накопления. Динамическая односекторная модель оптимального экономического роста при переменной норме накопления. Стационарный режим управления. Оптимальные траектории фондовооруженности и удельного потребления. Учет запаздывания при вводе фондов. Принцип максимума Понтрягина. Односекторная модель оптимального экономического роста. Модель смены технологического уклада в экономике. Переходный период и стационарный режим нового способа производства. Оптимальная норма накопления. Траектории фондовооруженности, производительности труда и удельного потребления.
Классическая модель рыночной экономики и модель Кейнса
Классическая модель рыночной экономики. Модели рынков рабочей силы, денег и товаров. Их взаимосвязь и условия равновесного состояния. Равновесие в классической модели рыночной экономики при отсутствии переполнения рынков товаров и рабочей силы. Механизм поддержания равновесия.
Модель Кейнса. Модели рынков рабочей силы, денег и товаров и их взаимосвязь. Равновесие в модели рыночной экономики Кейнса при линейных зависимостях. Механизм поддержания общего равновесия.
Математические модели финансового рынка
Содержание финансового рынка. Финансовые операции. Финансовый риск. Оптимизация портфеля ценных бумаг. Модификация портфеля ценных бумаг. Равновесие на рынке ценных бумаг.
5.2.5 Моделирование микроэкономических процессов и систем.
Модели поведения потребителя
Предпочтения потребителя. Функция полезности. Поверхность безразличия. Предельные полезности и предельные нормы замещения товаров. Бюджетное множество. Функция спроса на товары в зависимости от доходов и цен. Уравнение Слуцкого. Различные типы товаров.
Модели фирмы и монополии
Производственное множество. Поверхность производственных возможностей. Производственная функция фирмы. Закон убывающей предельной эффективности и предельной нормы замены ресурсов. Функция издержек. Выбор объемов производства на основе влияния налоговой ставки на деятельность фирм. Поведение фирм на конкурентных рынках. Алгоритм Курно, стратегия Стакельберга.
Моделирование формирования цен на товары и факторы производства в условиях действия монополий, а также потерь потребителя от монополий.
Модели распределения богатства в обществе
Общественные блага и математическая теория общественного выбора. Групповая функция полезности. Кривая Лоренца. Модели перераспределения доходов.
Модели государственного регулирования экономики
Роль государства в экономике. Регулирование потребления и накопления малосекторных моделях экономики. Математические модели структурных сдвигов. Модели распределения налогового бремени. Математические критерии эффективности государственного регулирования экономики.
6 ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
Таблица 3 – Практические занятия
| № | № раздела дисциплины | Наименование тем |
| 1 | 2 | Линейное программирование: графический метод, симплекс-метод. |
| 2 | 2 | Двойственные задачи линейного программирования. Методы решения. Анализ чувствительности оптимального решения. |
| 3 | 2 | Практическое применение методов линейного программирования при решение экономических задач. Транспортные задачи линейного программирования. |
| 4 | 3 | Прогнозирование экономики на основе МОБ. |
| 5 | 4 | Построение производственных функций, на примере функции Кобба-Дугласа. Изучение свойств производственных функций. Оценка с помощью ПФ масштаба и эффективности производства. |
| 6 | 4 | Решение задач по модели Солоу. |
| 7 | 5 | Модель поведения потребителя. Уравнение Слуцкого. |
| 8 | 5 | Поведение фирм на конкурентных рынках. Равновесие Курно. Равновесие и неравновесие Стакельберга. |
Краткие характеристики практических занятий
Линейное программирование: графический метод, симплекс-метод.
Задание. Рассмотреть модели и методы решения ЗЛП.
Исполнение. Решение задач по теме «Линейное программирование: графический метод, симплекс-метод».
Оценка. Формирует необходимые представления о применимости того или иного методы к заданному классу задач.
Время выполнения заданий: 2 часа.
Двойственные задачи линейного программирования. Методы решения. Анализ чувствительности оптимального решения.
Задание. Рассмотреть модели и методы решения ЗЛП.
Исполнение: Решение ДЗЛП. Проведение анализа чувствительности решения на изменение параметров задачи.
Оценка. Формирует необходимые представления о возможностях использования математических методов и моделей для оценки и анализа оптимального решения задачи.
Время выполнения заданий: 2 часа.
Практическое применение методов линейного программирования при решение экономических задач. Транспортные задачи линейного программирования.
Задание. Рассмотреть модели и методы решения ЗЛП.
Исполнение: Решение транспортных задач линейного программирования.
Оценка. Формирует необходимые представления о применимости того или иного метода к заданному классу задач.
Время выполнения заданий: 2 часа.
Прогнозирование экономики на основе МОБ.
Задание. Расчет прогнозных показателей МОБ по отраслям экономики.
Исполнение. Решение задач по теме «Математическая модель межотраслевого баланса. Линейные балансовые модели. Модель равновесных цен».
Оценка. Формирует необходимые представления о возможностях прогнозирования экономики на основе балансовых моделей.
Время выполнения заданий: 3 часа.
Построение производственных функций, на примере функции Кобба-Дугласа. Изучение свойств производственных функций. Оценка с помощью ПФ масштаба и эффективности производства.
Задание. Рассмотреть подходы и методы построения ПФ, изучить их свойства. Рассмотреть методы оценки масштаба и эффективности производства.
Исполнение: Решение задач. Интерпретация результатов решения.
Оценка. Формирует необходимые представления о возможностях и методах анализа и оценки экономических процессов с помощью производственных функций.
Время выполнения заданий: 2 часа.
Анализ экономики на основе модели Солоу.
Задание. Рассмотреть ряд методов применяемых для изучения тенденций и факторов роста экономики.
Исполнение: Решение задач. Интерпретация результатов решения.
Оценка. Формирует необходимые представления о применении динамических малосекторных моделей экономического роста к анализу и прогнозированию в экономике.
Время выполнения заданий: 2 часа.
Модель поведения потребителя. Уравнение Слуцкого.
Задание. Рассмотреть модель поведения потребителя и проанализировать, как изменится спрос потребителя, определяемый моделью, если изменится цена одного из товаров.
Исполнение: Решение задач. Интерпретация результатов решения.
Оценка. Формирует необходимые представления о применении математических моделей микроэкономики к анализу потребительских предпочтений в экономике.
Время выполнения заданий: 2 часа.
Поведение фирм на конкурентных рынках. Равновесие Курно. Равновесие и неравновесие Стакельберга.
Задание. Рассмотреть модели поведения производителей на рынке совершенной конкуренции, когда участников рынка много, и цены на рынке напрямую зависят от стратегий, применяемых его участниками..
Исполнение: Решение задач. Интерпретация результатов решения.
Оценка. Формирует необходимые представления о применении математических моделей микроэкономики к анализу поведения фирм в экономике.
Время выполнения заданий: 2 часа.
6 ЛАБОРАТОРНЫЙ ПРАКТИКУМ
Таблица 4 – Лабораторный практикум
| № | № раздела дисциплины | Наименование тем |
| 1 | 2 | Анализ оптимальных решений с использованием двойственных оценок в ЗЛП. |
| 2 | 2 | Определение оптимального плана транспортных задач, имеющих некоторые усложнения в их постановке, и их анализ. |
| 3 | 3 | Межотраслевые балансовые модели в анализе экономических показателей. |
| 4 | 4 | Прогнозирование показателей экономики на основе двухфакторной мультипликативной производственной функции Кобба-Дугласа |
| 5 | 5 | Анализ равновесия в экономике на основе модели Солоу. |
Краткие характеристики лабораторных работ
Анализ оптимальных решений с использованием двойственных оценок в ЗЛП.
Задание. Провести анализ оптимального решения ЗЛП с использованием двойственных оценок, полученных при решении ДЗЛП.
Исполнение: Выполнение индивидуального задания с использованием Excel. Интерпретация результатов решения.
Оценка. Практическая реализация теоретических методов математического программирования.
Время выполнения заданий: 3 часа.
Определение оптимального плана транспортных задач, имеющих некоторые усложнения в их постановке, и их анализ.
Задание. Рассмотреть виды ТЗ, имеющие некоторые усложнения в своей постановке и проанализировать результаты решения.
Исполнение: Выполнение индивидуального задания с использованием Excel. Интерпретация результатов решения.
Оценка. Практическая реализация теоретических методов математического программирования.
Время выполнения заданий: 3 часа.
Межотраслевые балансовые модели в анализе экономических показателей.
Задание. Рассмотреть пятисекторную экономическую систему. Рассчитать прогнозные показатели на основе модели МОБ. Проследить эффект распространения, вызванный увеличеснием спроса на конечную продукцию одной из отраслей. Определить равновесные цены.
Исполнение: Выполнение индивидуального задания с использованием Excel. Интерпретация результатов решения.
Оценка. Практическая реализация теоретических методов математического программирования.
Время выполнения заданий: 4 часа.
Прогнозирование показателей экономики на основе двухфакторной мультипликативной производственной функции Кобба-Дугласа
Задание. На основе данных об экономическом развитии некоторой страны за определенный период построить математическую модель (в форме ПФ Кобба-Дугласа) и рассчитать прогнозные значения ВНП. Оценить тонность полученной модели. Рассчитать показатели эластичности. Построить изокванту и изоклинали.
Исполнение: Выполнение индивидуального задания с использованием Excel. Интерпретация результатов решения.
Оценка. Практическая реализация теоретических методов математического программирования.
Время выполнения заданий: 4 часа.
Анализ равновесия в экономике на основе модели Солоу.
Задание. Провести анализ удельных показателей по модели Солоу и рассмотреть экономическую систему в стационарном виде.
Исполнение: Выполнение индивидуального задания с использованием Excel. Интерпретация результатов решения.
Оценка. Практическая реализация теоретических методов математического программирования.
Время выполнения заданий: 3 часа.
7 ТЕМАТИКА КУРСОВОЙ РАБОТЫ
Изучение дисциплины заканчивается написанием и защитой курсовой работы. Целью курсовой работы является обретение навыков построения экономико-математических моделей и использование их для анализа и решения поставленных задач.
Объектом исследования курсовой работы является применение методов оптимизации и исследование операций в экономике, для разрешения экономических проблем.
Курсовая работа включает в себя три части. В первой части студентом раскрывается один из теоретических вопросов по дисциплине, оставленных на самостоятельное изучение. Вторая и третья части являются практическим применением теоретических знаний в решении определенных задач.
7 КОНТРОЛЬ ЗНАНИЙ СТУДЕНТА
7.1. Входной контроль
Входной контроль осуществляется в форме контрольного задания по разделам дисциплины базового курса «Экономическая теория», «Математический анализ», «Теория вероятностей и математическая статистика».
7.2. Тематика текущего контроля
Текущий контроль знаний осуществляется в процессе выполнения практических заданий путём индивидуального и группового опроса, собеседования и тестового контроля. Результаты текущего контроля знаний учитываются при промежуточной аттестации.
7.3. Выходной контроль
Выходной контроль осуществляется в форме экзамена по дисциплине.
Примерный набор тестов на экзамен:
Вариант 1
- Условия продуктивности матрицы коэффициентов прямых материальных затрат.
- Какой экономический смысл имеют коэффициенты А, 1, 2 мультипликативной производственной функции F(K,L) =
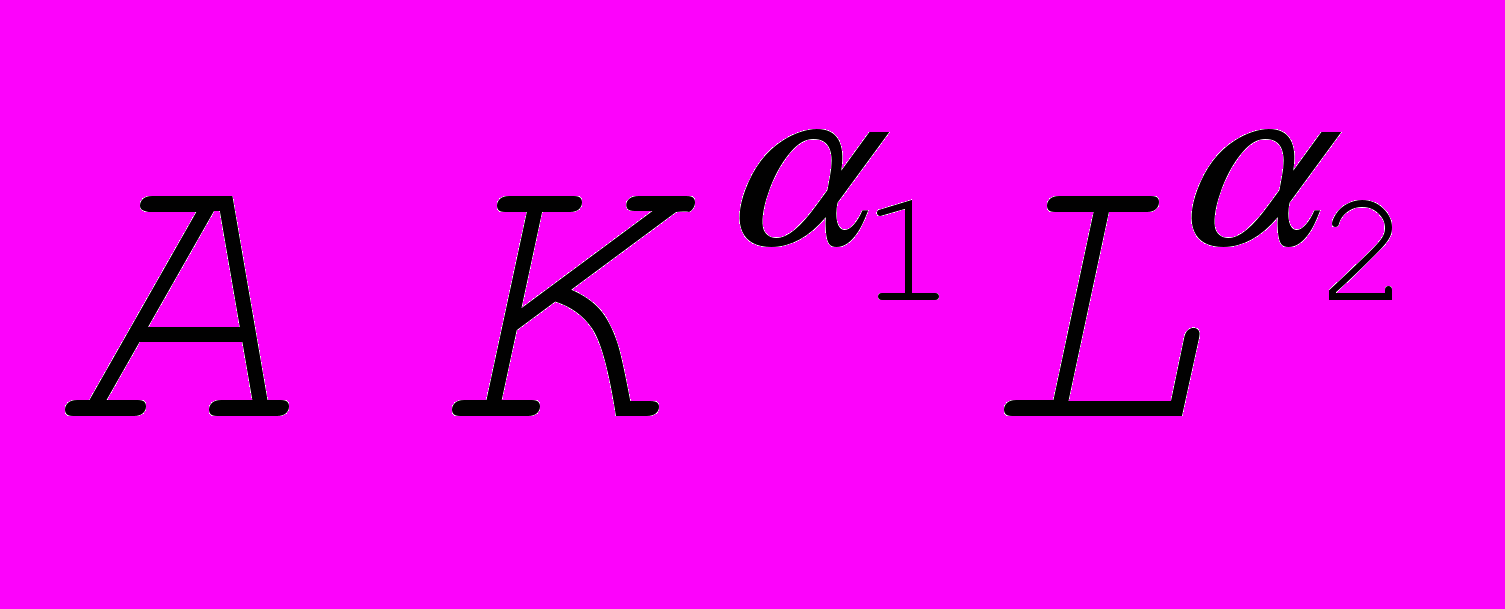 ?
?
- Первый квадрант МОБ отражает:
- отраслевую материальную структуру национального дохода;
- национальных доход как стоимость условно чистой продукции;
- межотраслевые потоки продукции.
- отраслевую материальную структуру национального дохода;
- Мультипликативная производственная функция и её свойства.
- Что показывает коэффициент эластичности:
- на сколько изменится факторный признак при изменении результативного признака на один процент;
- на сколько процентов изменится результативный признак при изменении факторного признака на один процент;
- долю изменения результативного признака под действием факторного признака.
- Используя теорию двойственности и графический метод, найти решение следующей ЗЛП
.
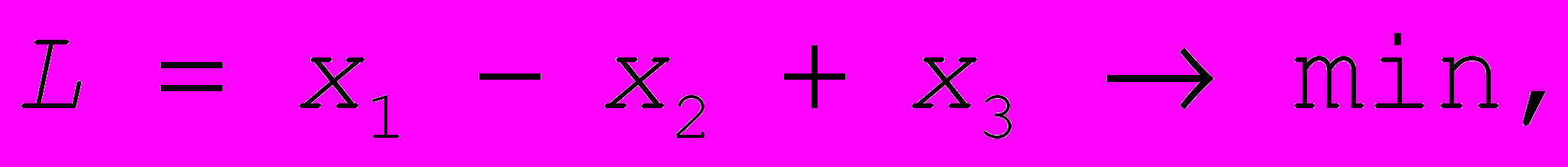
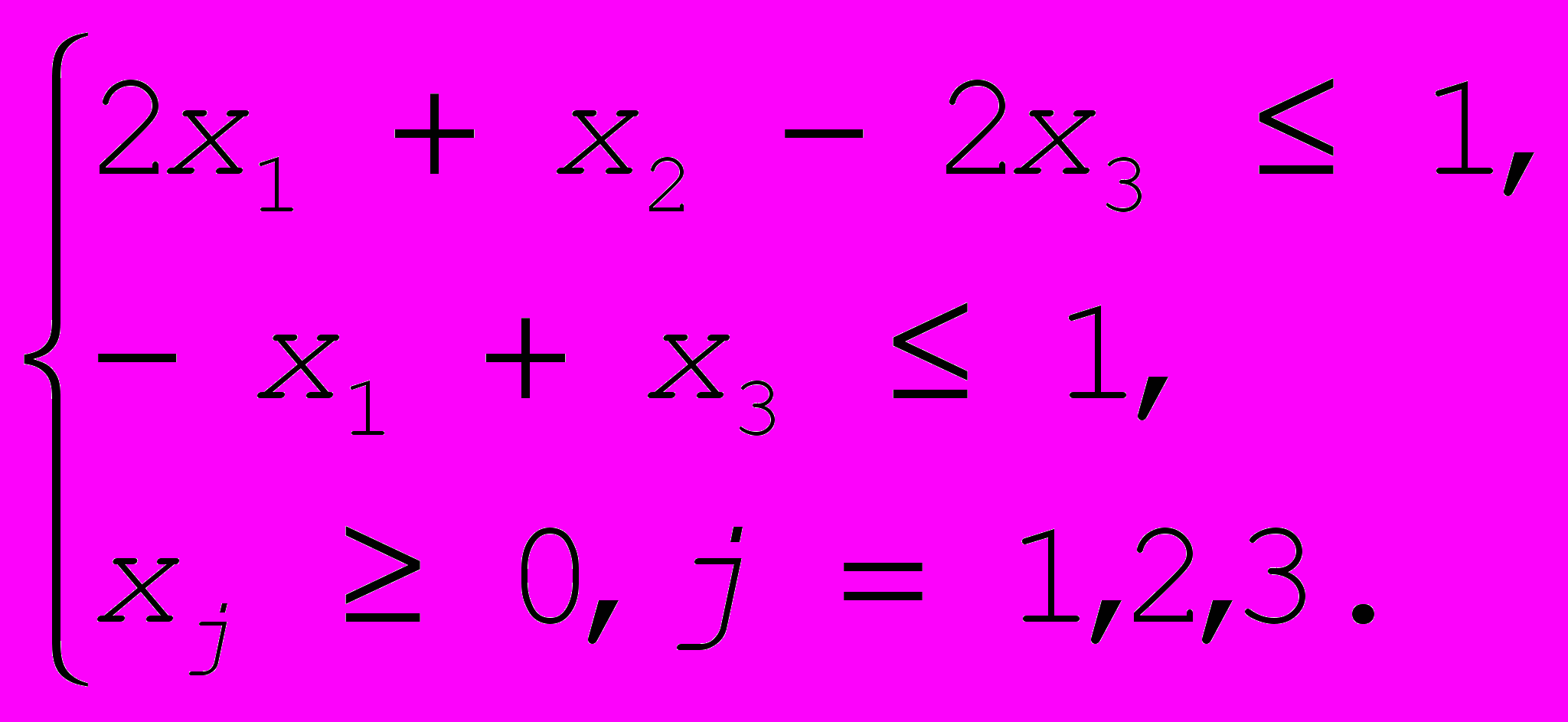
- Предельная производительность (предельный продукт) i – го ресурса рассчитывается по формуле:
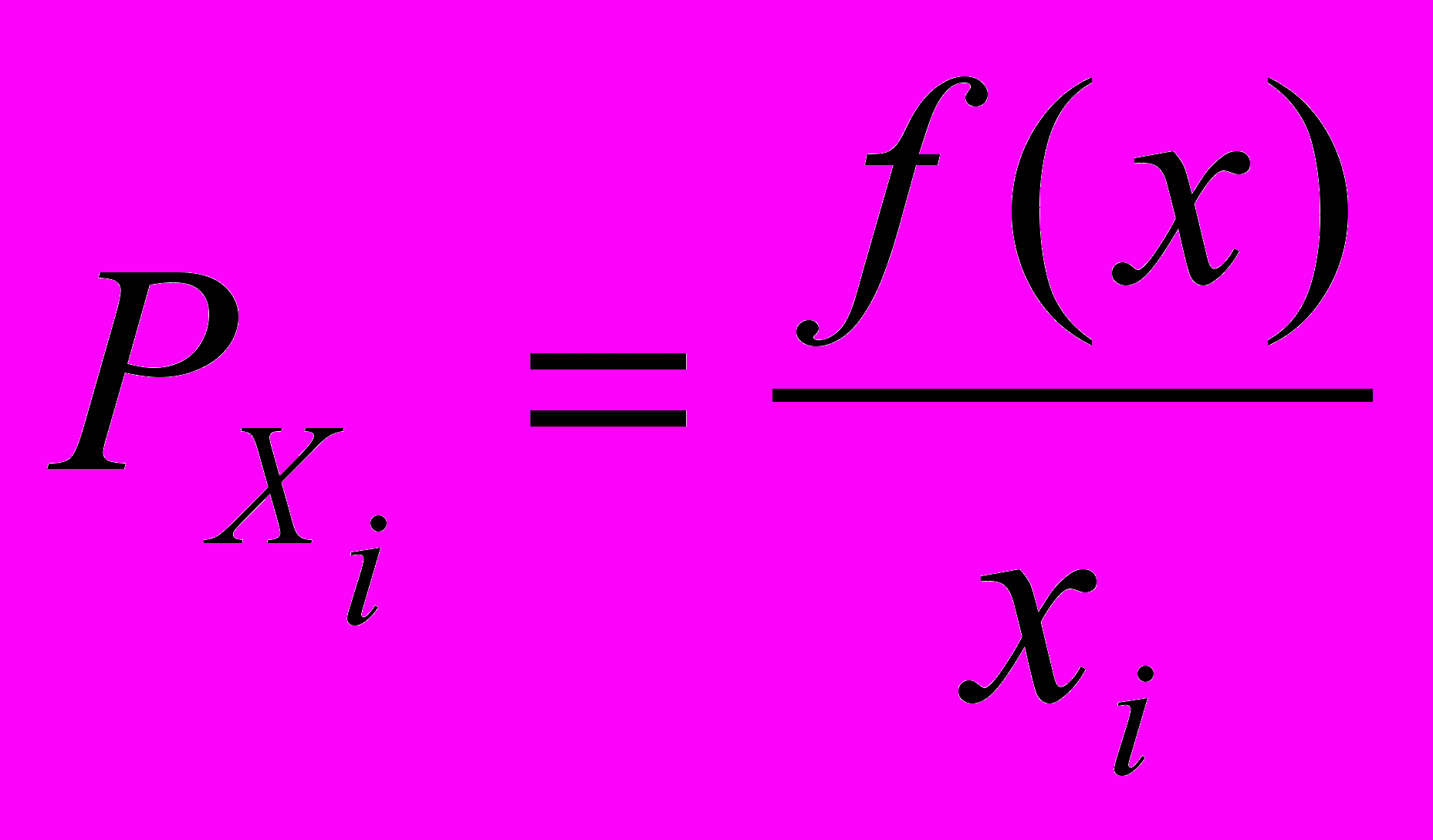 ; б)
; б) 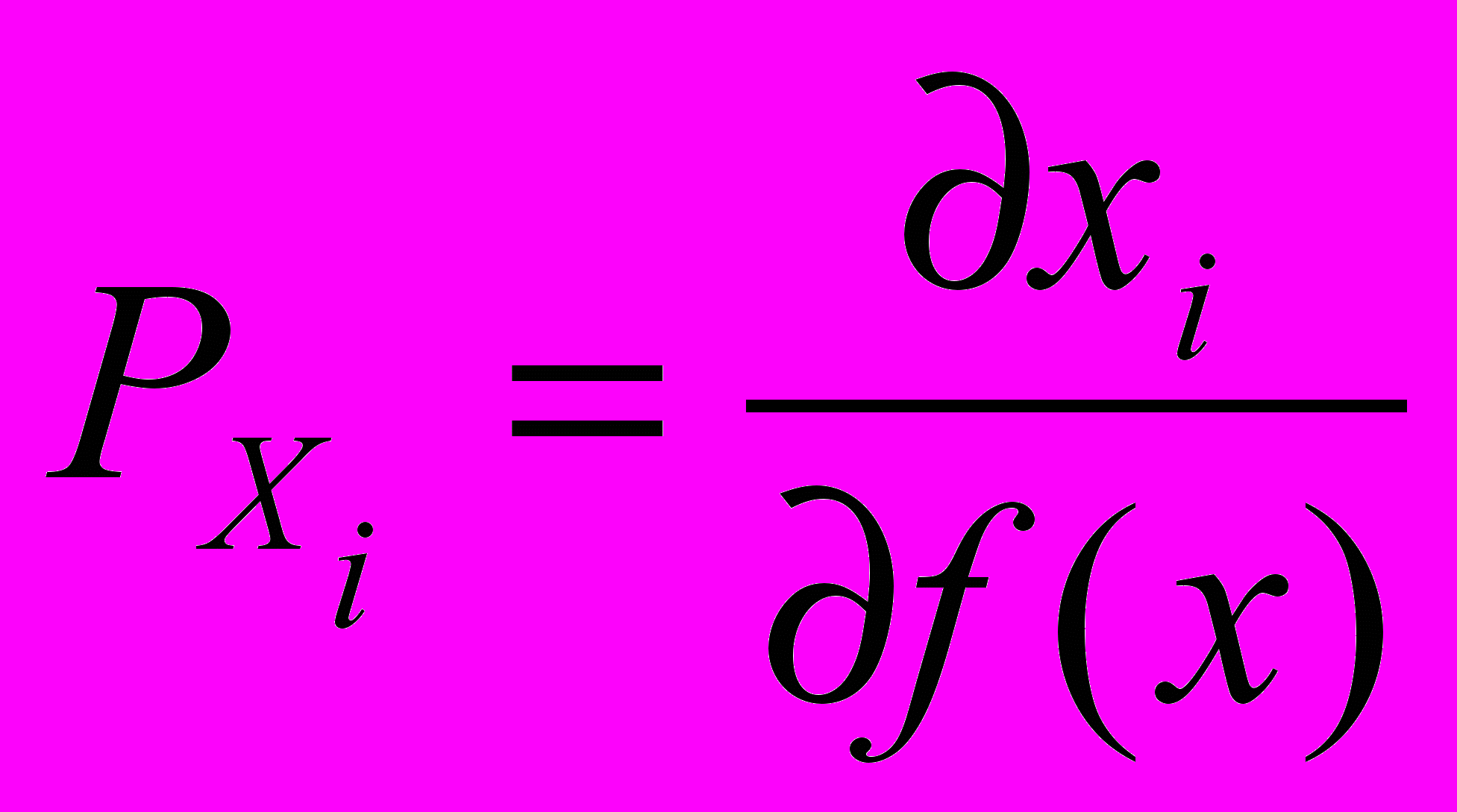 ; в)
; в) 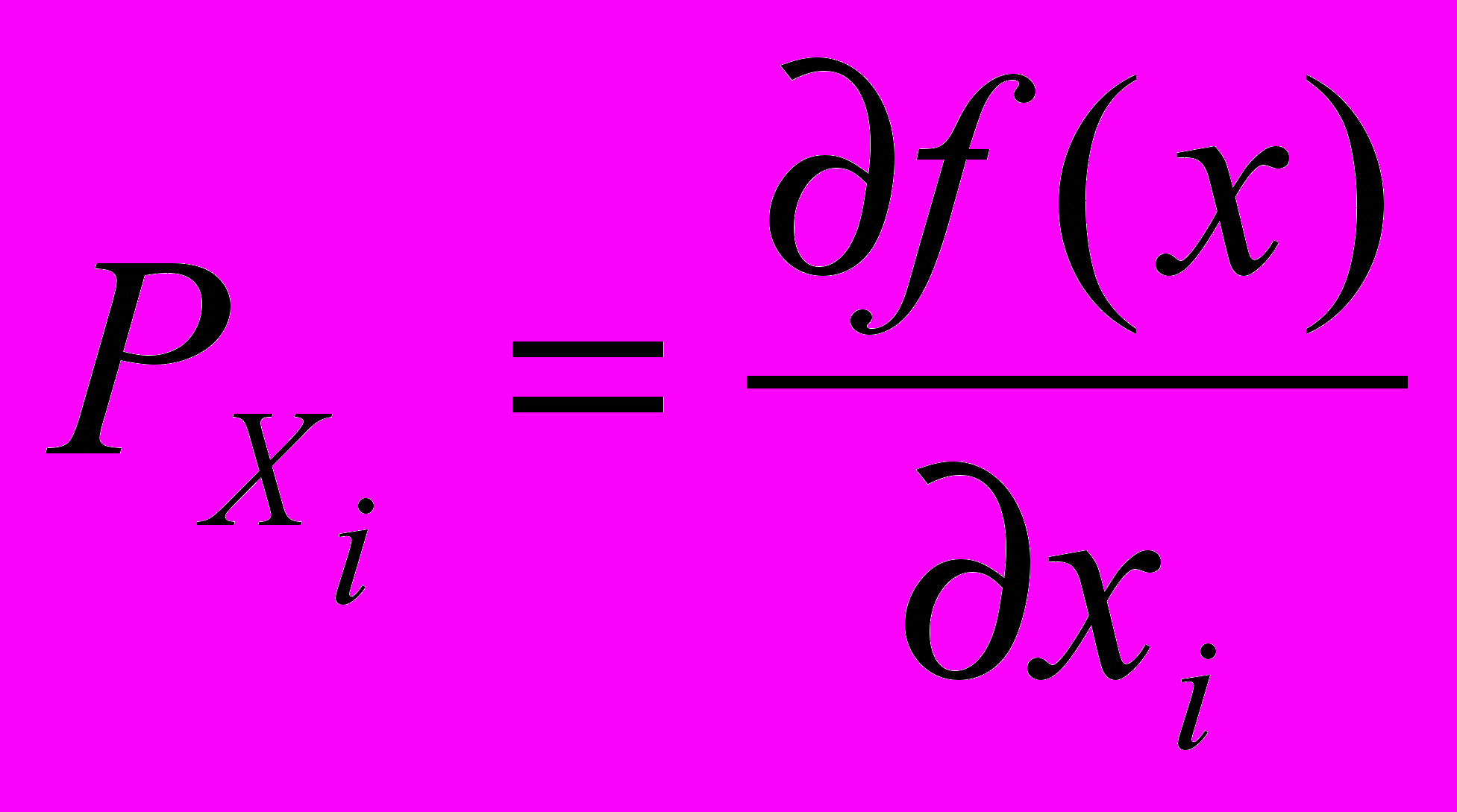
- Рассчитать коэффициенты полных материальных затрат
А =

- Коэффициенты прямых материальных затрат рассчитываются:
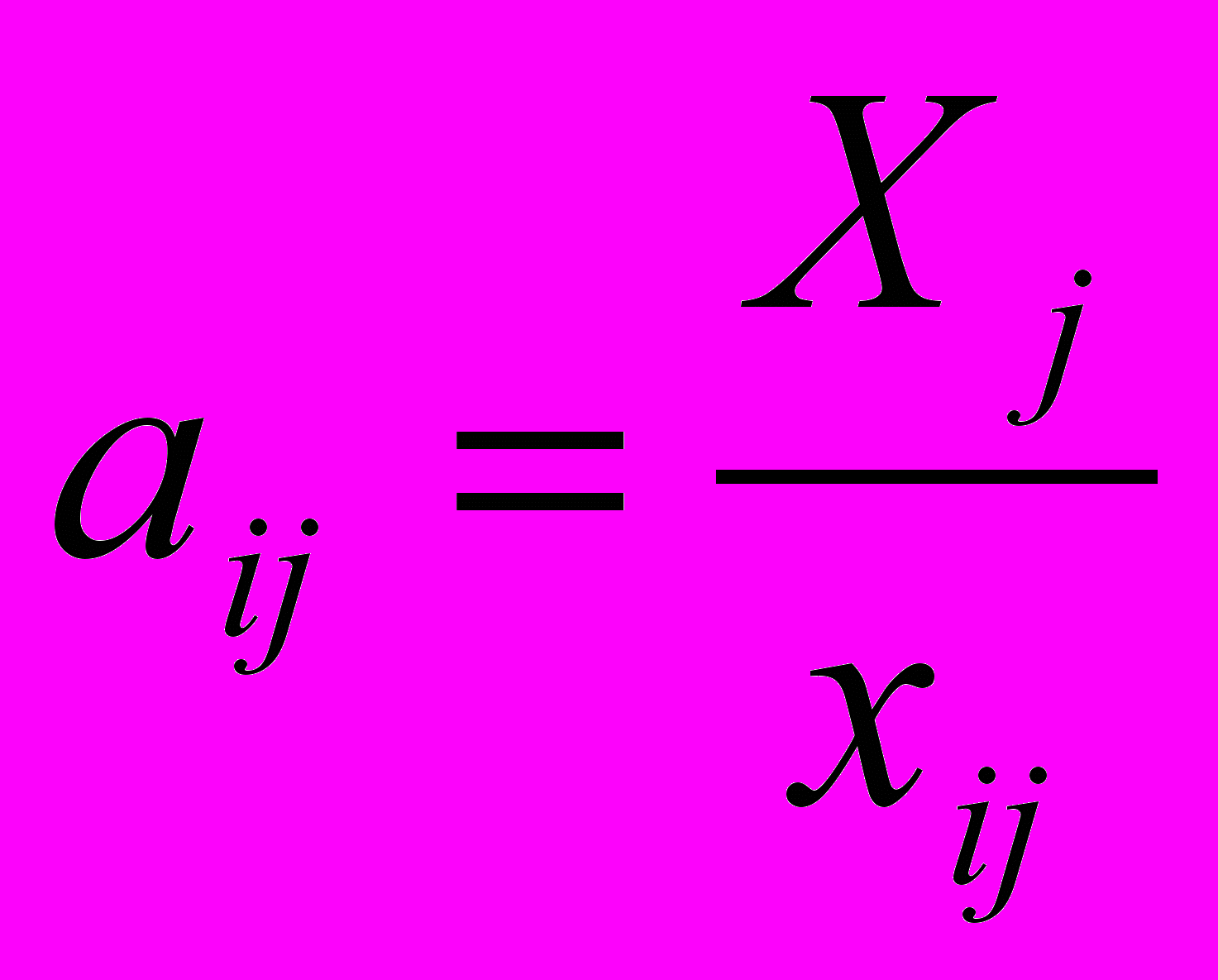 ; б)
; б) 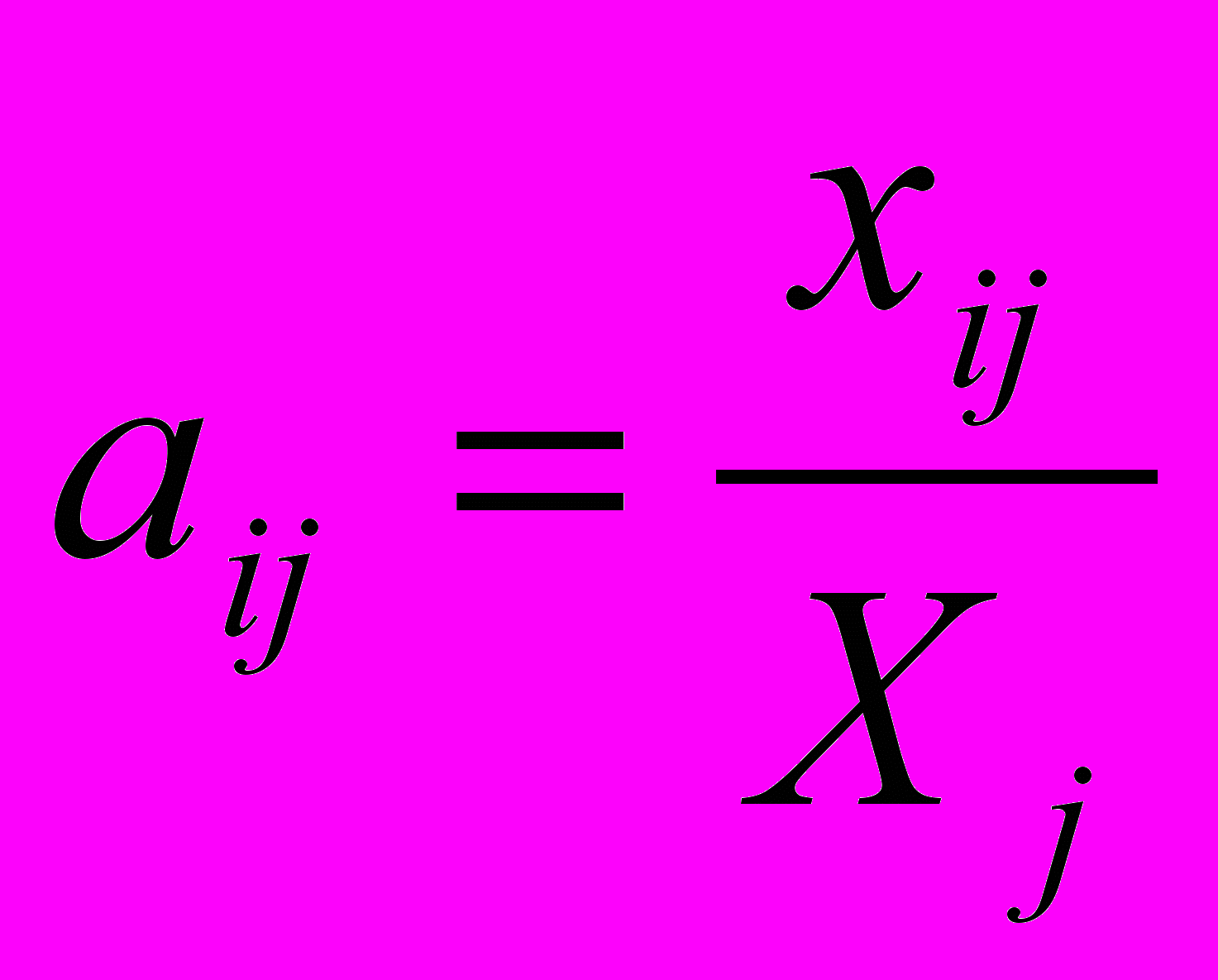 ; в)
; в) 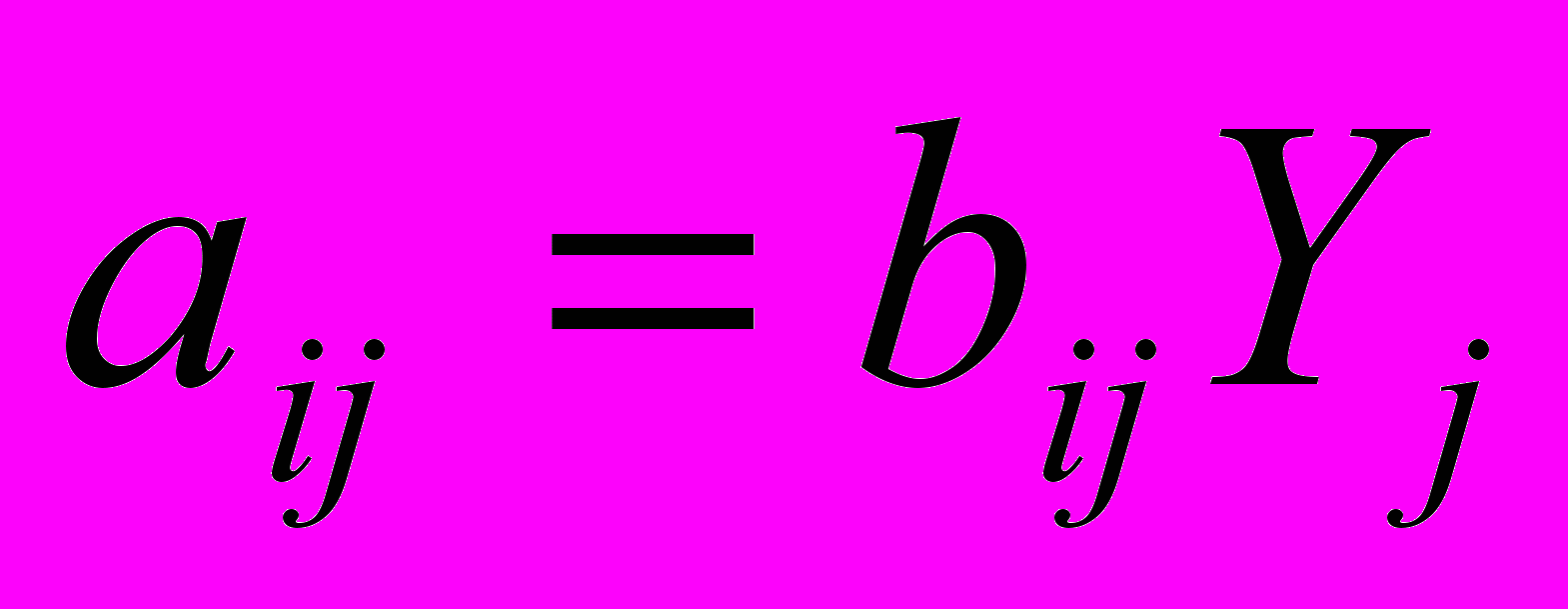
- Дана производственная функция Кобба-Дугласа: Y = 1,038 K0,655 L0.345. Какова норма замены труда фондами?
Вариант 2
- Какой смысл имеют коэффициенты технологической матрицы А модели Леонтьева?
- Что такое изоклинали? В чем их экономический смысл?
- Экономико – математическая модель Леонтьева в матричной форме имеет вид:
- Х = ВХ + Y; б) Х = (Е-А)-1Y; в) Х = АХ + Y.
- Сформулируйте "золотое правило" накопления в модели экономики Солоу.
- Межотраслевой баланс отражает:
- производство и распределение валового национального продукта по отраслям;
- межотраслевое распределение национальной валюты;
- использование материальных и трудовых ресурсов.
- Средняя производительность (средний продукт) i – го ресурса рассчитывается по формуле:
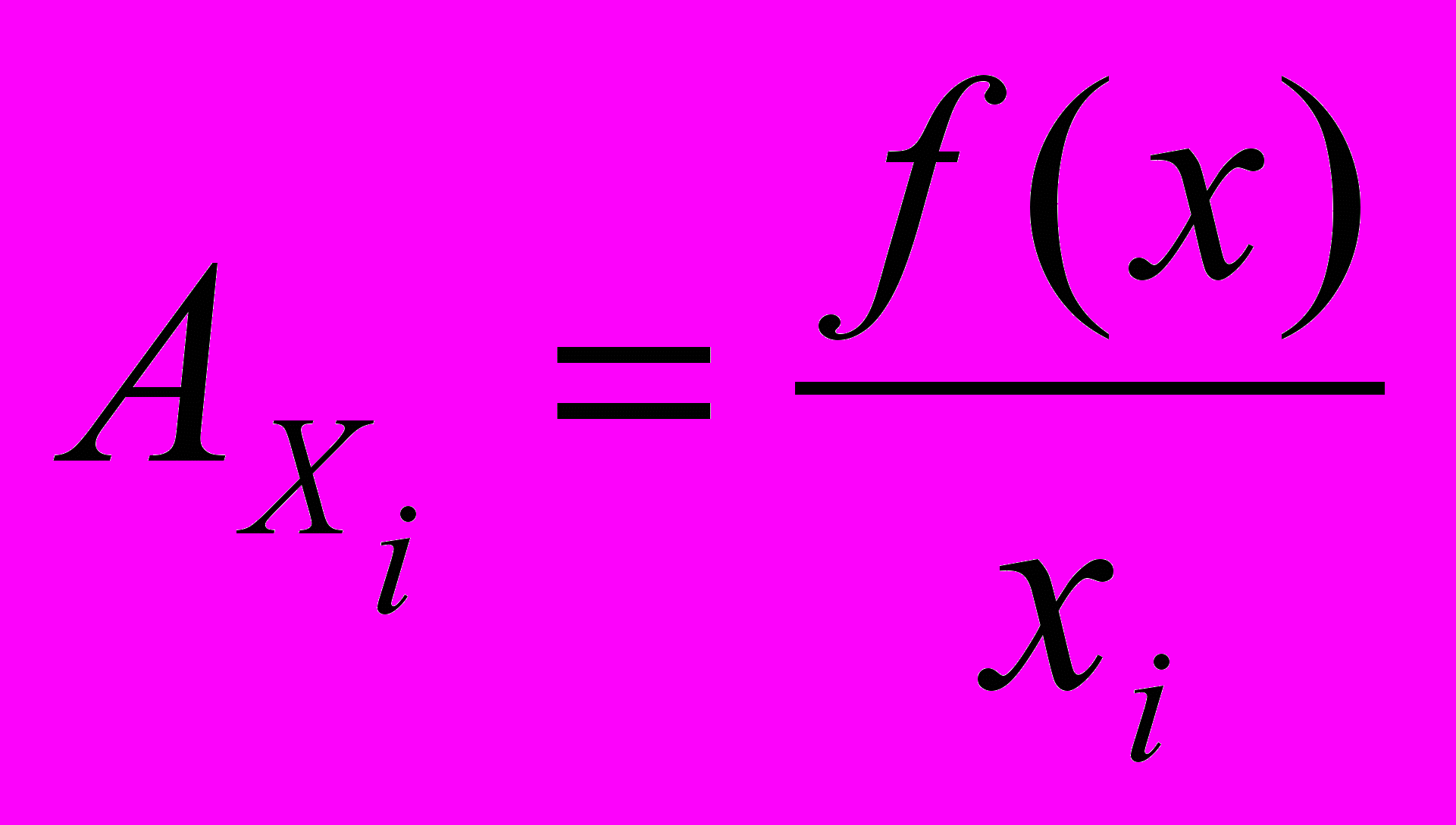 ; б)
; б) 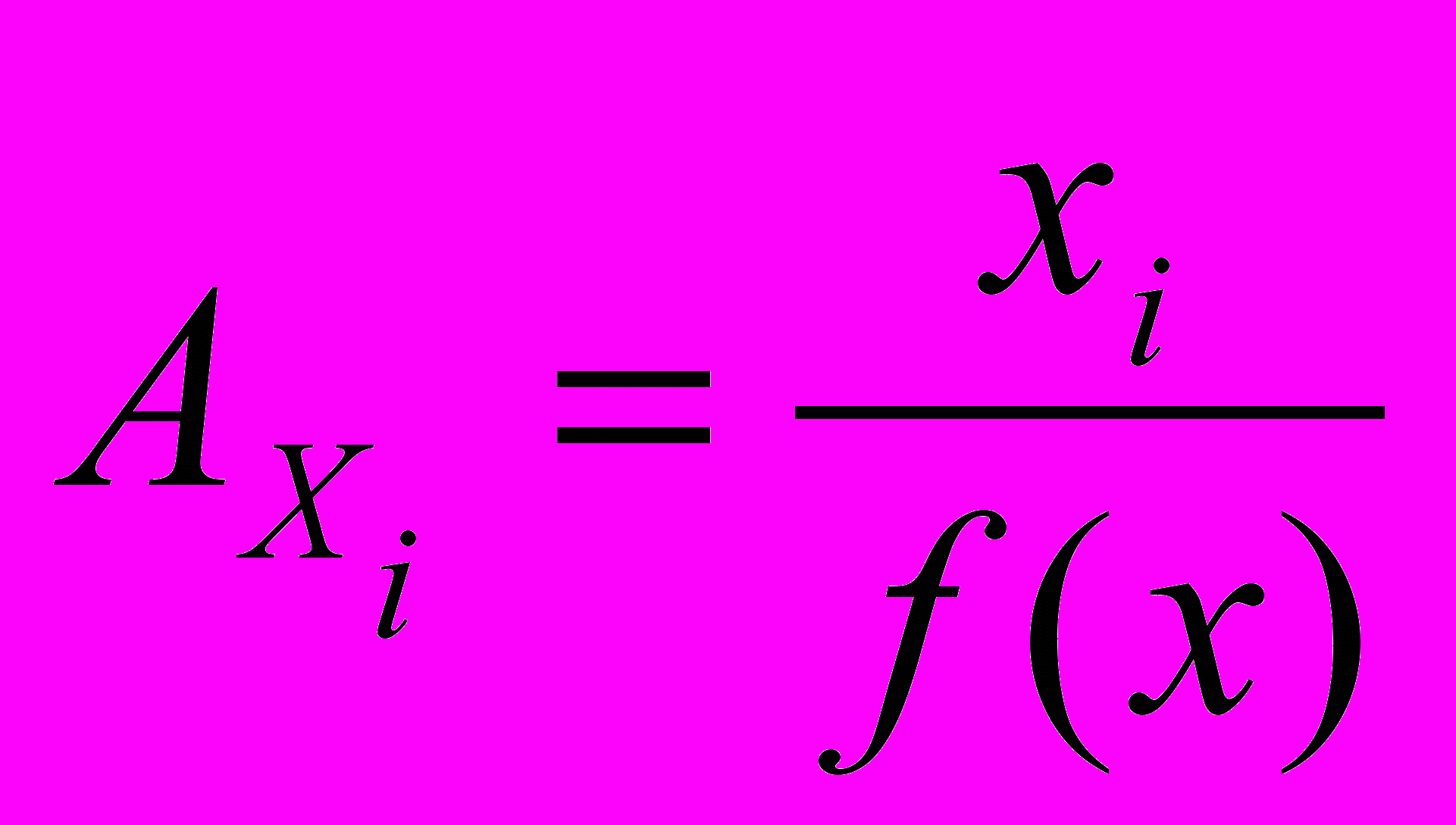 ; в)
; в) 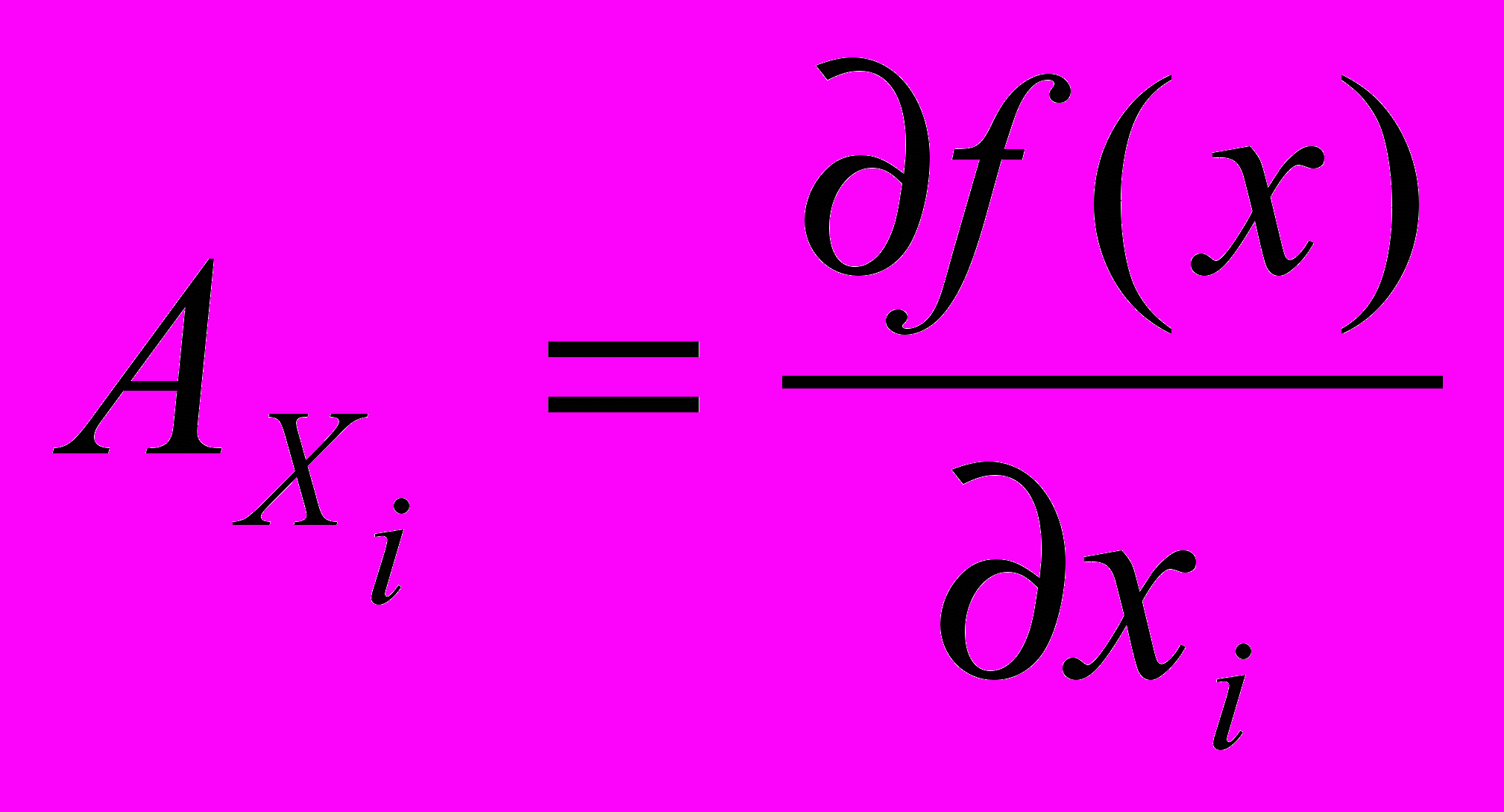
- Первый квадрант МОБ отражает:
- отраслевую материальную структуру национального дохода;
- межотраслевые потоки валовой продукции;
- конечное распределение и использование национального дохода.
- Проверить продуктивность матрицы коэффициентов прямых материальных затрат
А =
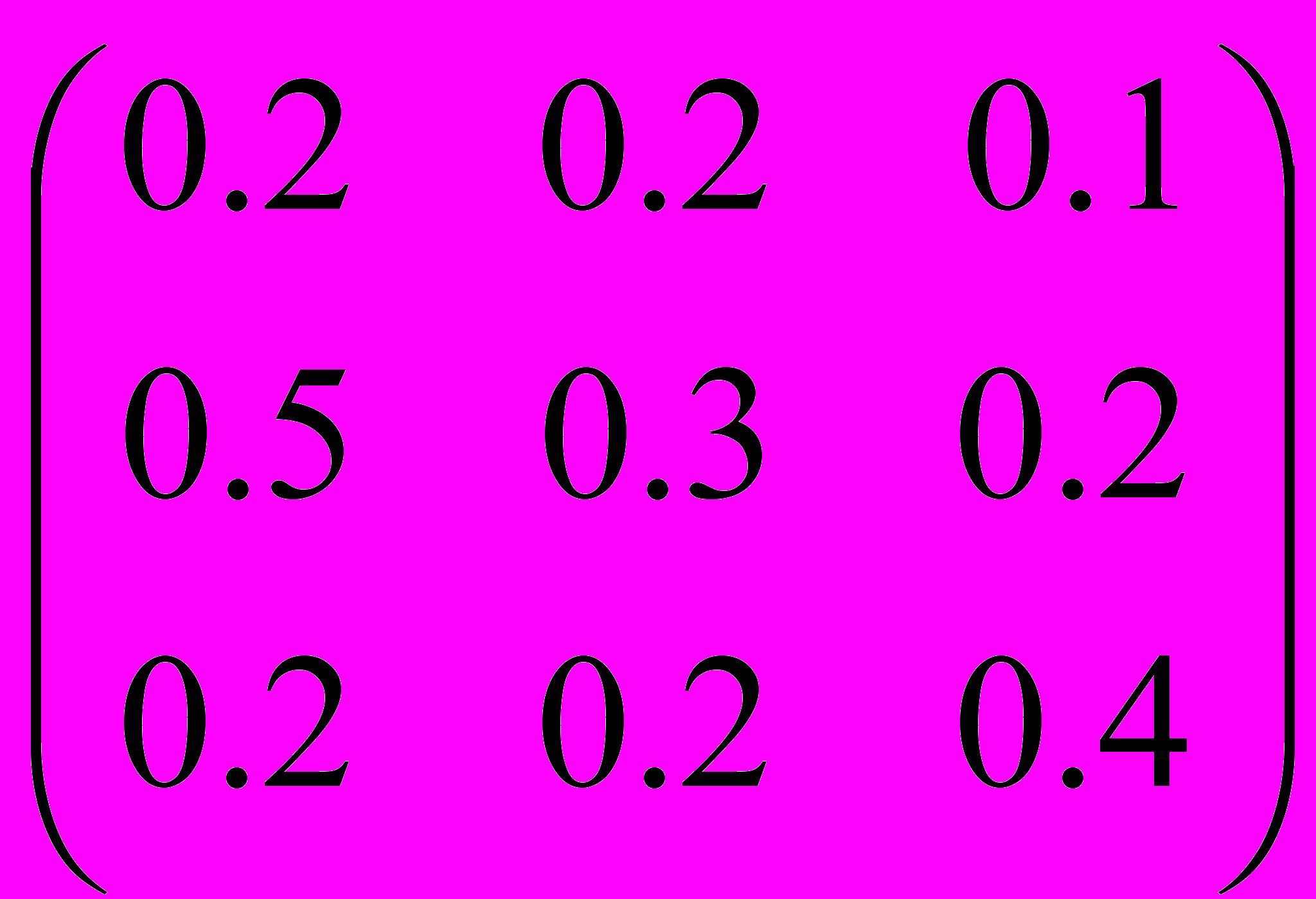
- На основании данных, приведенных в нижеследующей таблице восстановить схемы межотраслевого материального баланса.
| Отрасль | Прямые межотраслевые потоки | Конечная продукция | ||
| 1 | 2 | 3 | ||
| 1 | 50 | 60 | 80 | 60 |
| 2 | 25 | 90 | 40 | 25 |
| 3 | 25 | 60 | 40 | 35 |
- Для трех видов продукции А, В и С модели зависимости удельных постоянных расходов от объема выпускаемой продукции выглядят следующим образом:
yA = 600, yВ = 80 + 0,7х, yС = 40х0,5
Определить коэффициенты эластичности по каждому виду продукции.
8 УЧЕБНО – МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ
8.1 Основная литература
1. Ашманов С. А. Введение в математическую экономику. -М.: Наука, 1984.
2. Громенко В. М. Математические методы исследования экономики. Учебно-
практическое пособие, 2000.
- Иванилов Ю. П. Математические модели оптимизации в экономике. - М.: Наука, 1979.
- Котов И. В. Математическое моделирование макроэкономических процессов. -Л.: ЛГУ, 1980.
- Колемаев В. А. Математические модели макроэкономики. - М.: ГАУ, 1994.
- Интриллигатор М. Математические методы оптимизации и экономическая тео
рия. - М.: Прогресс, 1975.
- Лебедев В. В. Математические модели децентрализованной экономики. - М.:
ГАУ, 1992.
- Колемаев В. А. Малыхин В. И. Математическая экономика в примерах и задачах.-М.:ГАУ, 1995.
- Экланд И. Элементы математической экономики. - М.: Мир, 1988.
- Самуэльсон П. Экономика. - М.: Прогресс, 1992.
- Аллен Р. Математическая экономика.» М.: Изд-во иностр. лит. 1963.
- Маленво Э. Лекции по микроэкономическому анализу. - М.: Наука, 1986.
- Экономико-математические методы и прикладные модели: Учебное пособие.для Вузов /В.В. Федосеев и др./-М.: ЮНИТИ, 2002.
При разработке контрольных заданий использовались материалы, изложенные в пособиях:
1. Колемаев В. А. и др. Математическая экономика в примерах и задачах. - М.: ГАУ, 1995.
2. Громенко В.М. Математические методы исследования экономики. Учебно-практическое пособие, 2000.
8.2 Дополнительная литература
1. Данилов Н.И., Иноземцева Л.П. Основы математической экономики. АН РФ. Новосибирск. 2003.
2. Математическая экономика на персональном компьютере. // Под ред. М.Кубонива. М..: Финансы и статистика, 1991
3. Иванов Ю.П. Математические модели в экономике- М., Наука, 1979.
4. Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике. – М.: МГУ, 2001
9 МАТЕРИАЛЬНО – ТЕХНИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ
Для освоения данной дисциплины необходим определенный объем информации. Это информация об основных финансово – экономических показателях предприятий, стран, методах и моделях исследования экономики. При чтении курса используются классические аудиторные методы и самостоятельные расчеты студентов с использованием ЭВМ (ППП MS Excel).
10 МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ОРГАНИЗАЦИИ ИЗУЧЕНИЯ ДИСЦИПЛИНЫ
На основании программы разрабатываются рабочие учебные программы дисциплины с учетом фактического количества часов, отведенных на ее изучение. Исходя из этого, в рабочей программе отдельные разделы программы могут быть либо усилены, либо сокращены, либо опущены. Практические занятия курса должны быть нацелены на изучение и анализ методов математической экономики.
Знания и навыки, полученные при изучении данного курса, широко применяются студентами в дальнейшем изучении дисциплин по специальности.
Программа составлена в соответствии с государственными образовательными стандартами высшего профессионального образования.
11 СЛОВАРЬ ТЕРМИНОВ
Автономная модель – часть системы моделей, которую можно анализировать независимо от других частей. Этот подход применим всюду, где отдельные хозяйственные звенья обладают самостоятельностью в своих действиях. Однако в экономике все связано, поэтому автономность частичных моделей всегда относительна.
Авторегрессивная модель – статистическое описание связи значений одного и того же показателя в разные моменты времени.
Агрегирование – объединение, укрупнение показателей по какому-либо признаку. С математической точки зрения агрегирование рассматривается как преобразование модели в модель с меньшим числом переменных и ограничений (агрегированную модель), дающую приближенное (по сравнению с исходным) описание изучаемого процесса или объекта.
Адаптация – приспособление системы к реальным условиям. Различают адаптацию пассивную – реагирование системы на изменение среды и активную – воздействие системы на среду.
Адекватность модели – соответствие модели моделируемому объекту или процессу.
Аналитическая модель – формула, представляющая математические зависимости в экономике.
Балансовая модель – 1. Система уравнений (балансовых уравнений), которые удовлетворяют требованию соответствия двух элементов: наличие ресурса и его использования. 2. При описании экономической системы в целом – система уравнений, каждое из которых выражает требование баланса между производимым отдельными экономическими объектами количеством продукции и совокупной потребность в этой продукции.
Бюджетное множество – множество наборов товаров (x1, x2, . . ., xn), доступных индивиду при его доходе Q ценах (p1, p2, . . ., pn).
Валовой выпуск – стоимость продуктов и услуг, являющихся результатом деятельности хозяйственных объектов страны в течение данного периода (года). Включает выпуск продуктов, рыночных и нерыночных услуг. При вычитании из валового выпуска промежуточного потребления получается валовой внутренний продукт – как конечный результат производственной деятельности.
Вальраса система уравнений – одна из первых экономико-математических моделей. В ней сформулирован процесс автоматического стремления рыночной
экономики к стабильному равновесию в форме линейных уравнений, переменными в которых выступают количества товаров и ресурсов, а также цены на каждый из них, балансирующие спрос и предложение. Основное равенство (закон Вальраса) утверждает, что общая величина спроса должна быть при соответствующей системе цен равна общей величине предложения.
Вектор “затрат – выпуска” – вектор, содержащий компоненты двух видов: выпускаемые продукты (обычно положительные) и продукты, затрачиваемые в производстве (отрицательные).
Взаимозаменяемость ресурсов – возможность альтернативного использования разных ресурсов: а) для сохранения или достижения заданного уровня производства, б) для достижения оптимума.
Выпуклость, вогнутость – 1. Выпуклая область (выпуклое множество) – часть плоскости, обладающая тем свойством, что отрезок, соединяющий две ее любые точки, целиком содержится в ней. Это понятие переносится с двумерного пространства на многомерное. 2. Выпуклая функция – свойство кривой y=f(x), заключающееся в том что каждая дуга кривой лежит не выше, а если функция вогнутая не ниже своей хорды.
Гессе матрица – матрица вторых частных производных функций нескольких переменных. Характеристика матрицы Гессе (ее положительная или отрицательная определенность и полуопределенность) служит условием для определения вида стационарной точки: является ли она, соответственно, минимумом, максимумом или седловой точкой в задаче оптимизации функции.
Госсена законы – 1. Предельная полезность любого товара уменьшается по мере увеличения его потребления. 2. Индивиду невыгодно потреблять одно благо вместо другого и вообще как-то изменять структуру потребления, поскольку всякое такое изменение только ухудшает его благосостояние.
Градиент – вектор, направленный в сторону наискорейшего возрастания функции и равный по величине ее производной в этом направлении.
Динамические модели экономики – модели , описывающие экономику в развитии (в отличие от статических, характеризующих ее состояние в определенный момент).
Изокванта – геометрическое место точек, в которых различные сочетания факторов производства дают одно и то же количество выпускаемой продукции.
Изоклиналь – линия наибольшего роста производственной функции. Изоклинали ортогональны изоквантам.
Кейнсианская теория экономики – модели, описывающие экономику в развитии.
Кобба – Дугласа функция – производственная функция, примененная американскими исследователями Ч. Коббом и П. Дугласом при анализе развития экономики США в 20-30 гг. нашего века. Имеет следующую форму
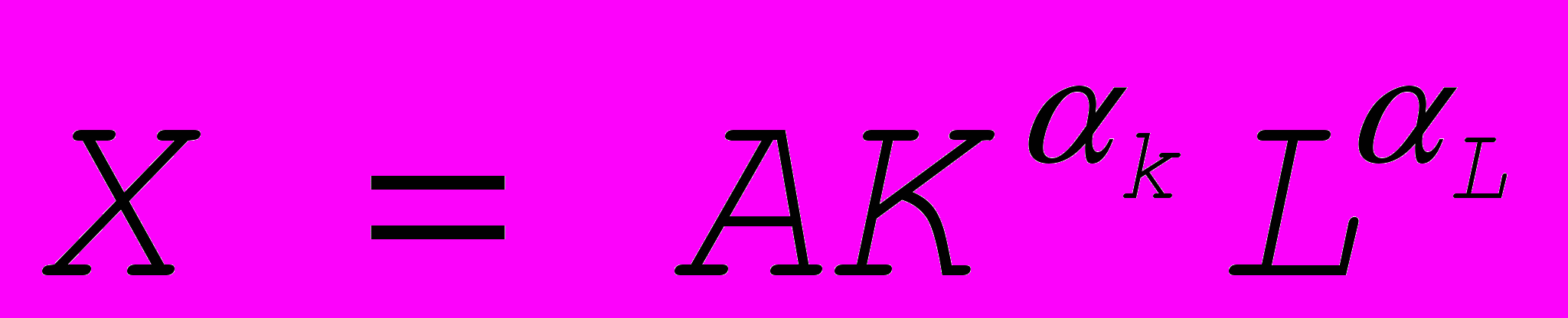 , где X – национальный доход, A – коэффициент размерности, K , L – соответственно бъемы приложения капитала и труда,
, где X – национальный доход, A – коэффициент размерности, K , L – соответственно бъемы приложения капитала и труда, 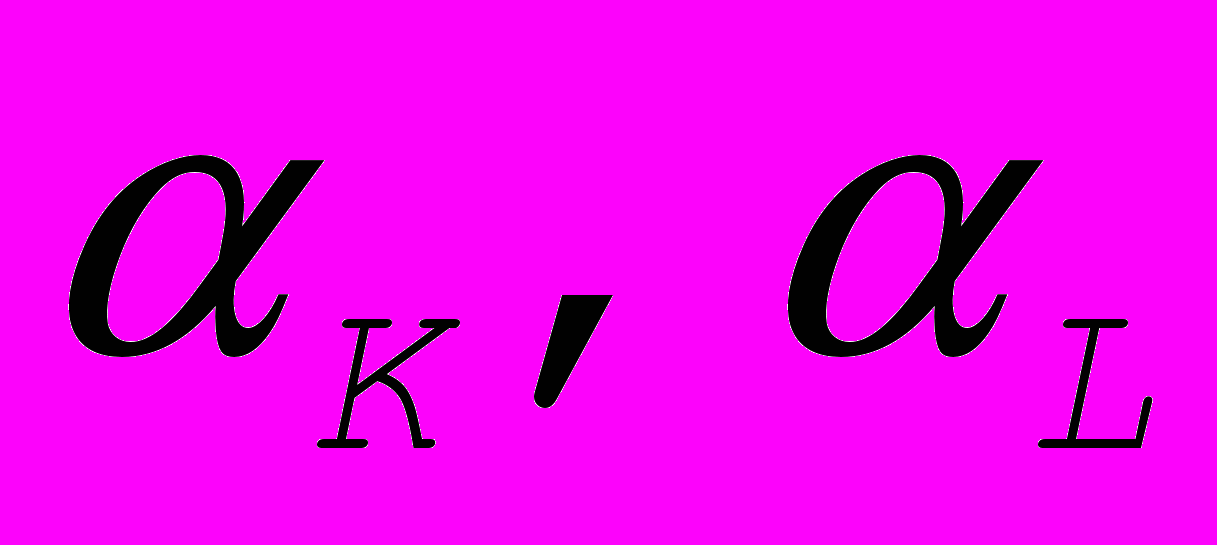 - константы, коэффициенты эластичности по капиталу и по труду.
- константы, коэффициенты эластичности по капиталу и по труду. Коэффициенты прямых затрат – (технологические коэффициенты) в межотраслевом балансы – средние величины непосредственных затрат продукции одной отрасли (в качестве средств производства) на выпуск единицы продукции другой отрасли. Они могут быть выражены в натуральной форме и в ценностной.
Коэффициенты эластичности производства – показатели производственной функции, характеризующие относительное изменение результатов на единицу относительного изменения затрат i-го ресурса.
Кривая безразличия – геометрическое место точек пространства товаров, характеризующихся состоянием безразличия с точки зрения потребителя или производителя.
Линия уровня – линией уровня на поверхности Y= F(K,L) называется множество тех точек поверхности, для которых F(K,L)=const.
Магистраль – основное понятие математической теории равномерного пропорционального роста экономики, основы которой были заложены американским математиком Дж. Фон Нейманом. Это траектория (путь) развития, при которой теоретически, за длительное время, достигается максимальная скорость роста экономики.
Макроэкономическая модель – экономико-математическая модель, отражающая функционирование народного хозяйства как единого целого. Макромодели оперируют, как правило, стоимостными показателями – национальный доход, валовые капиталовложения и другие. Важным приложением является прогнозирование народнохозяйственных процессов. Для этого используются макроэкономические производственные функции.
Микроэкономическая модель – экономико-математическая модель, отражающая функционирование и структуру отдельного элемента экономической системы, взаимодействие его с другими элементами системы в процессе ее функционирования. Сюда относятся, например, модель фирмы, модель спроса и потребления, модель ценообразования, модель рынка товаров и т. д.
Многосекторная модель – модель народного хозяйства, представляющая его как совокупность крупных секторов. Ими могут быть, например, производство средств производства и производство предметов потребления, и тогда перед нами двух секторная модель. Могут быть выделены такие секторы, как государственный, кооперативный, частный. Если в качестве секторов принимаются отрасли производство, то такая модель называется многоотраслевой.
Модель – математическое и логическое описание объекта.
Неймана модель – (модель расширяющейся экономики) – В этой модели производство всех продуктов растет в одном темпе, цены не зависят от времени, прирост производства финансируется путем инвестирования прибыли.
Оптимальность по Парето – итальянский экономист В. Парето в начале ХХ в. сформулировал один из самых распространенных критериев оптимальности: “Следует считать, что любое изменение, которое никому не причиняет убытков и которое приносит некоторым людям пользу (по их собственной оценке), является улучшением.
Паутинообразная модель – одна из простейших динамических моделей для демонстрации процесса формирования цен в условиях конкурентного рынка.
Первичные ресурсы – элементы производства, поступающие в экономическую систему извне, в отличие от ресурсов, порожденных самой системой, и продуктов – результатов производства, выходящих за ее пределы.
Показатель – выраженная числом характеристика какого-либо свойства экономического объекта, процесса или решения.
Предельная норма замены – SK труда фондами называется отношение модулей дифференциалов основных фондов и труда
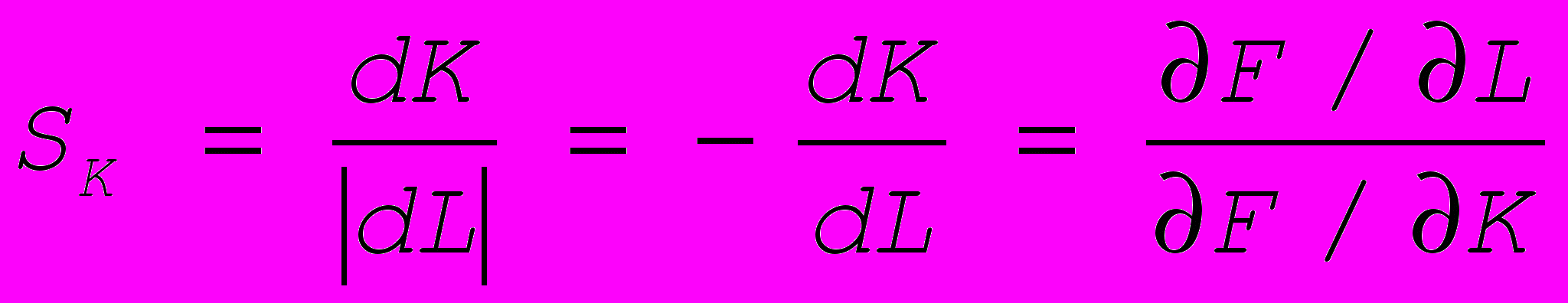 ; SL фондов трудом
; SL фондов трудом 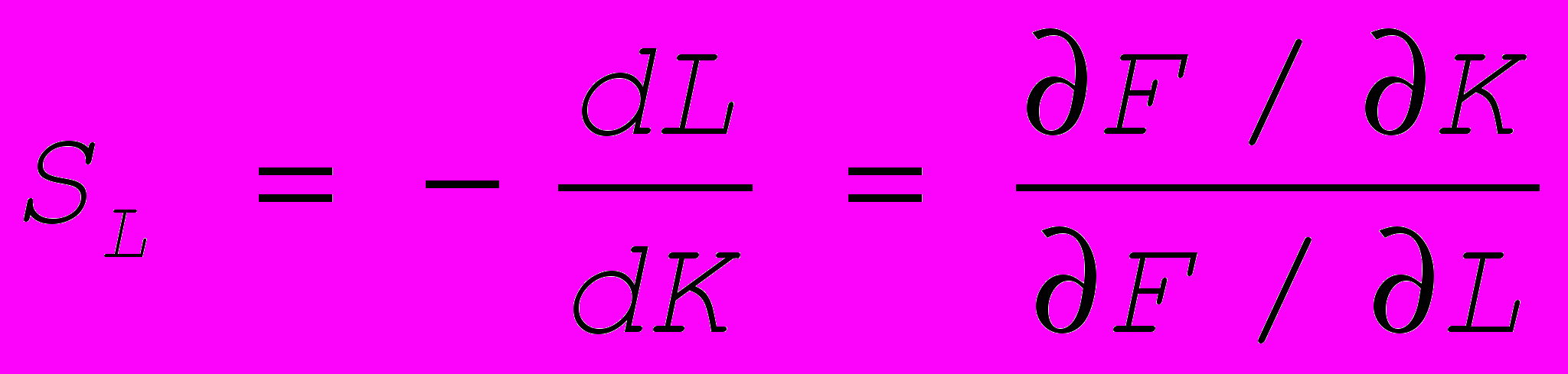 . Для мультипликативной функции
. Для мультипликативной функции 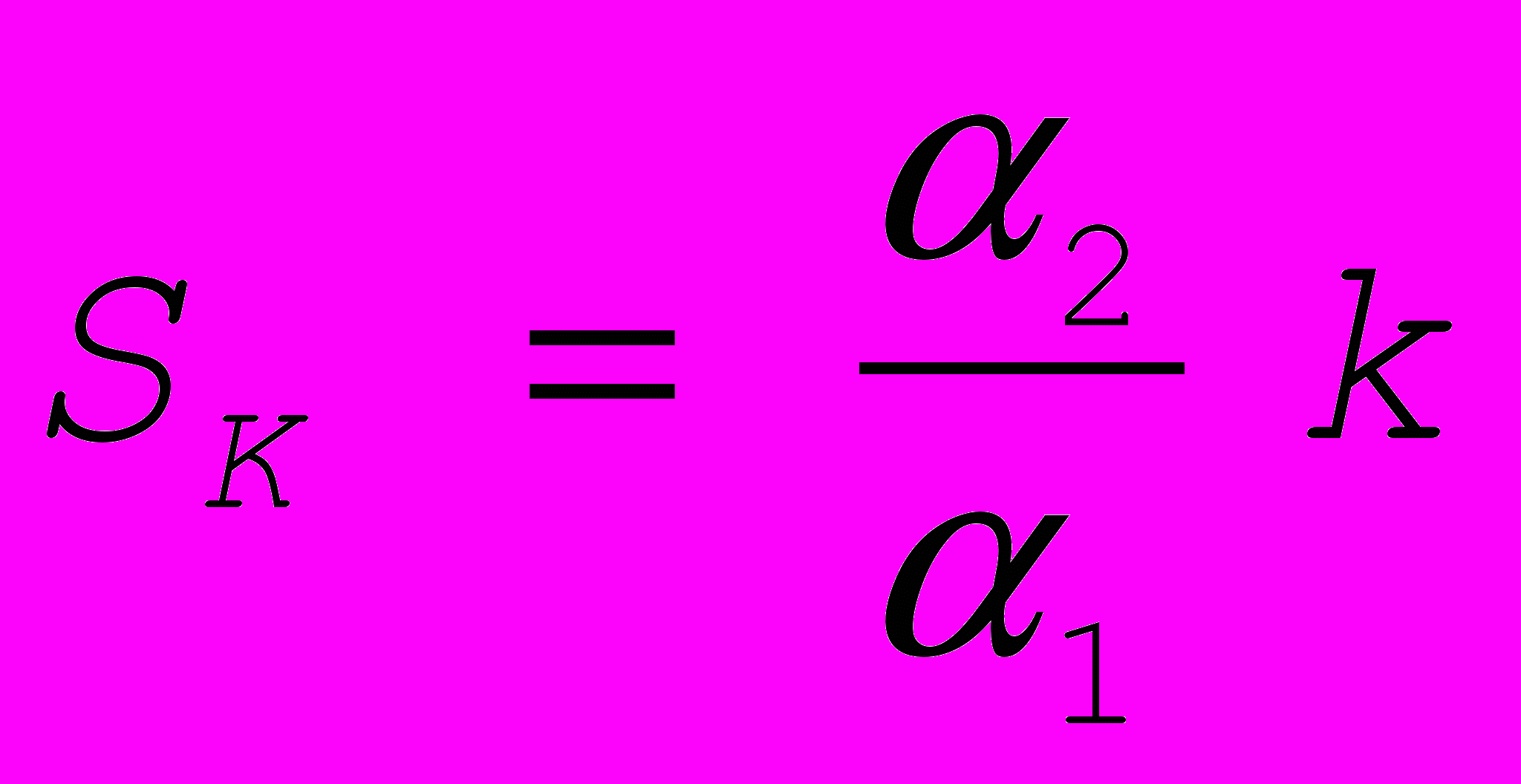 : недостаток труда можно компенсировать его лучшей фондовооруженностью.
: недостаток труда можно компенсировать его лучшей фондовооруженностью.Предельная полезность – дополнительная полезность, получаемая от потребления дополнительной единицы какого-либо блага (частная производная функции полезности по этому благу).
Приведенные затраты – 1. Расчетная категория, отражающая величину текущих и единовременных (капитальных) затрат на производство продукции. 2. Затраты в базовый момент времени, равноценные по своему народнохозяйственному значению оцениваемым затратам, произведенным (или возможным) в другие моменты времени. Такое приведение по времени производится с помощью коэффициента дисконтирования.
Производительность труда – продуктивность деятельности людей, измеряемая количеством продукции, произведенной работником в сфере материального производства за единицу рабочего времени.
Производственная функция – функция характеризующая зависимость между количеством применяемых ресурсов и объемом выпускаемой продукции.
Пространство товаров – множество всех возможных наборов благ (товаров), потенциально доступных потребителям.
Равновесие (экономической системы) – 1) состояние, которое характеризуется равенством спроса и предложения всех ресурсов; 2) состояние, когда ни один из многих взаимосвязанных участников системы не заинтересован в изменении этого состояния, так как при этом он не может ничего выиграть, но может проиграть.
Рынок – общественный механизм распределения благ посредством добровольного обмена. Обмен может осуществляться непосредственно, в форме бартера, и посредством промежуточного обмена благ на особый товар – деньги. Во втором случае обмен принимает форму купли-продажи, а его участники приобретают статус продавцов и покупателей. Продавцы обменивают товары на деньги, покупатели – деньги на товар.
Солоу модель роста – одна из односекторных моделей экономического роста. Экономическая система рассматривается как единое целое без структурных подразделений, производит единый продукт, который может как потребляться, так и инвестироваться. Эта модель достаточно адекватно отражает важнейшие макроэкономические аспекты процесса воспроизводства.
Слуцкого уравнения – уравнения, характеризующие количественные зависимости между изменением цен на отдельные товары и доходов потребителей, с одной стороны, и структурой покупательного спроса – с другой.
Теория фирмы – теория поведения фирмы в различных условиях (принципы и мотивы принятия решений о ценах, о выпуске продукции, инвестициях и т.д.).
Теория экономического роста – экономико-математическая дисциплина, в центре которой исследование макроэкономических моделей, характеризующих основные взаимосвязи общих показателей развития народного хозяйства, таких, как национальный доход, конечный продукт, норма накопления, объем капиталовложений и др.
Фондоемкость – показатель, определяемый объемом производственных фондов, приходящихся на единицу продукции. На макроэкономическом уровне измеряется фондоемкость совокупного общественного продукта (или конечного общественного продукта, или национального дохода). На микроэкономическом уровне – фондоемкость производства в целом и фондоемкость производства отдельных видов продукции.
Фондоотдача – величина , обратная фондоемкости производства, объем продукции в расчете на единицу используемых производственных фондов.
Функция полезности – функция на множестве потребительских наборов товаров u(x1, x2, . . ., xn), значение которой на потребительском наборе (x1, x2, . . ., xn) равно потребительской оценке индивидуума для этого набора.
Функция потребления – функция, отражающая зависимость объема потребления от дохода или иного показателя.
Функция спроса – зависимость объема спроса от определяющих его факторов.
Экзогенные величины – переменные внешние по отношению к моделируемой системе. При использовании моделей в экономических расчетах все величины, характеризующие моделируемые объекты, подразделяются на экзогенные, или входные и эндогенные, или выходные.
