Курсовой проект №1 Моделирование наблюдающего устройства Математическая модель объекта описывается уравнениями состояния

Вид материала

Курсовой проект

Содержание Целью курсового проекта

Подобный материал:

• Курсовой проект по учебной дисциплине «Микропроцессорные средства» на тему «Система, 521.9kb.
• 1 Описание объекта диагностирования, 674.93kb.
• Гагарин В. Г., Козлов В. В. Математическая модель и инженерный метод расчета влажностного, 113.96kb.
• Лекция №3 Применение эксперимента для построения математических моделей статики объектов, 134.24kb.
• Курсовой проект по дисциплине «технология научного исследования» на тему «методы программно-целевого, 122.89kb.
• Л. М. Чирок Математическая модель электрохимического датчика, 44.36kb.
• Лекция 1 Тема: Введение в экономико-математическое моделирование, 121.17kb.
• Антипов А. Н., Корытный, 787.52kb.
• Игра как математическая модель конфликтной ситуации. Антагонистические игры, 56.39kb.
• Программа государственного квалификационного экзамена по дисциплине «Математическая, 43.58kb.

Задание на курсовой проект № 1


Моделирование наблюдающего устройства


Математическая модель объекта описывается уравнениями состояния:



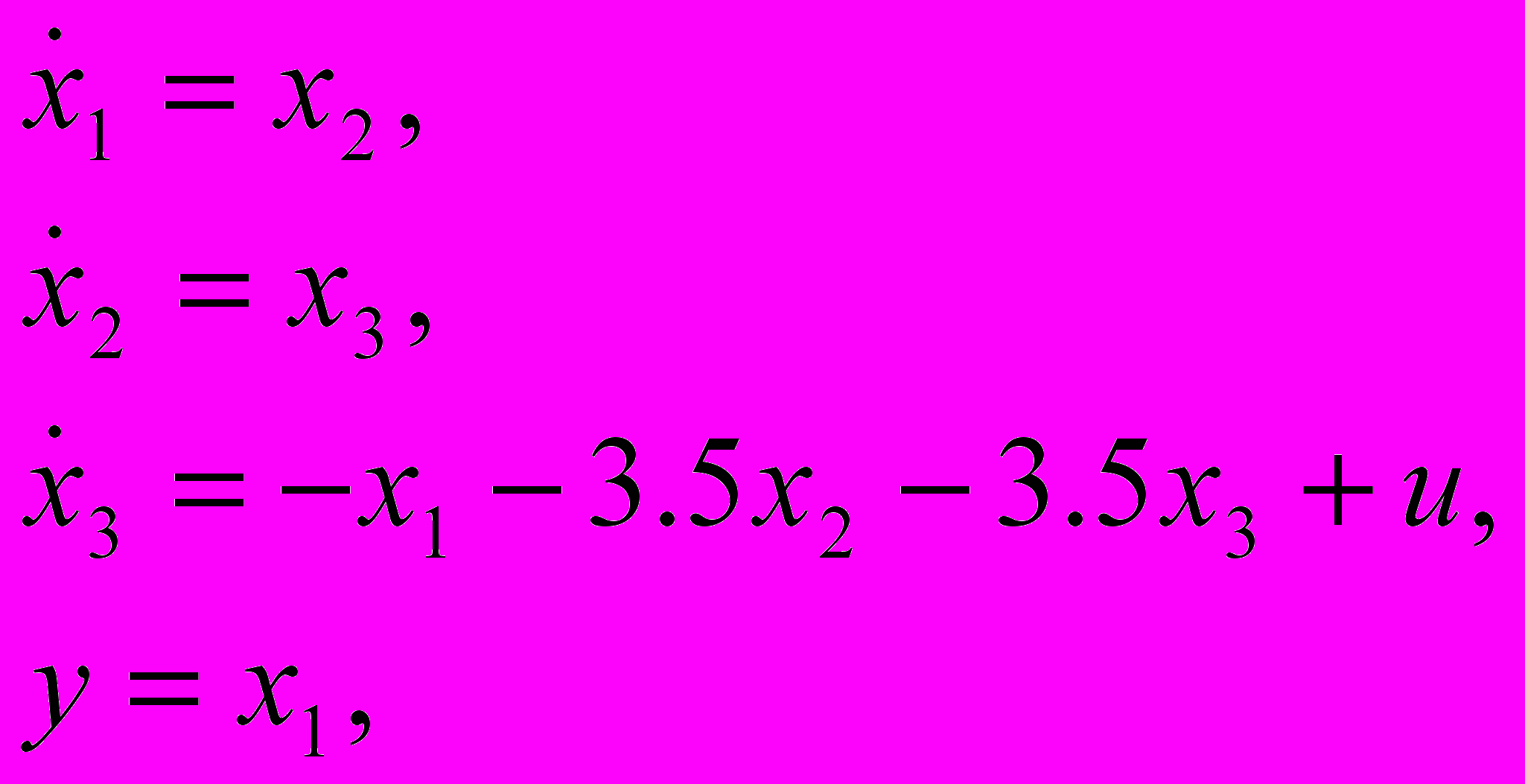
где х- вектор состояния, у – выход, u - управление.

Уравнение наблюдающего устройства, с помощью которого по значениям выходного и входного сигналов восстанавливаются переменные состояния:



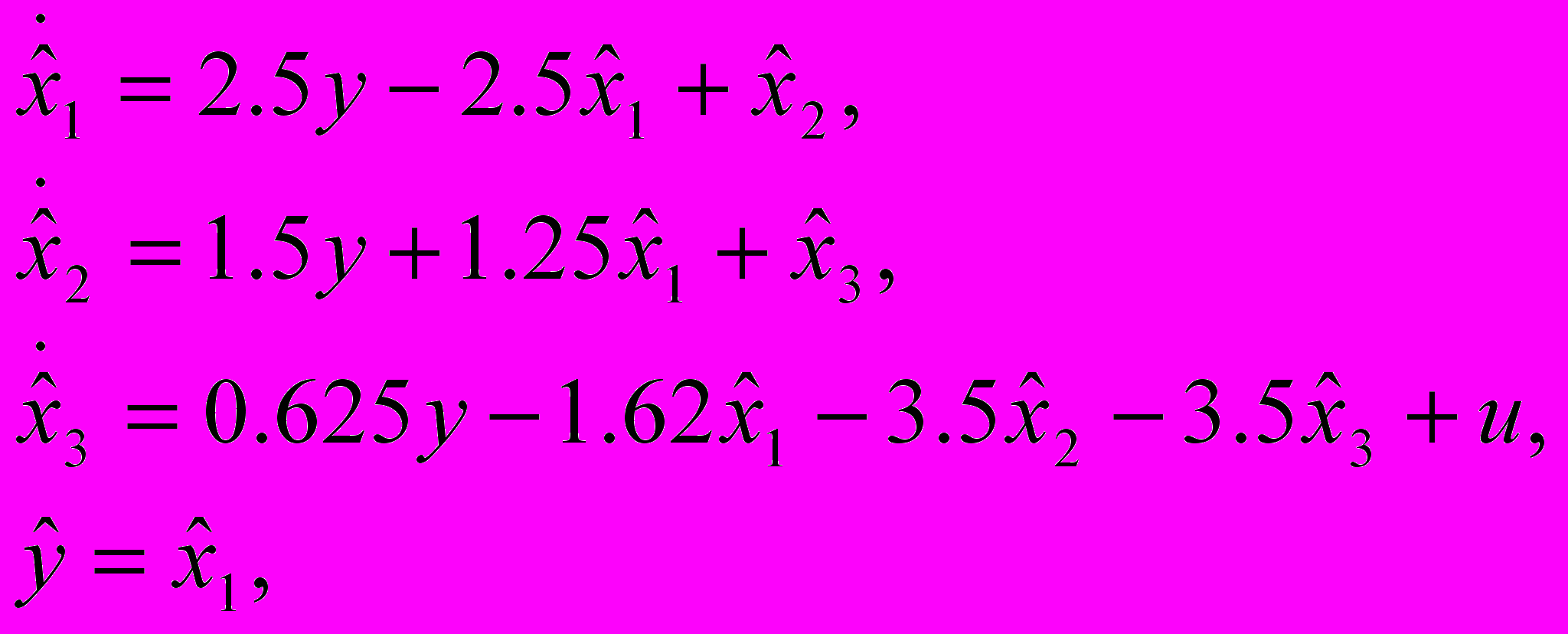
где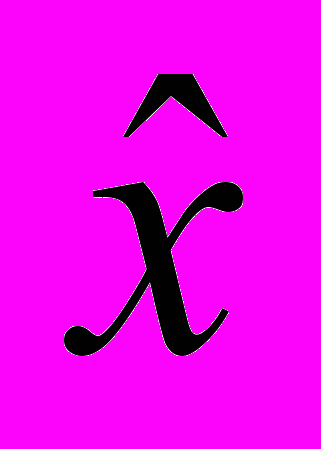- вектор состояния наблюдающего устройства.


Разрабатываемая программа моделирования должна обеспечивать:

• ввод, редактирование и сохранение в файле начальных условий объекта x(t₀), начальных условий наблюдающего устройства 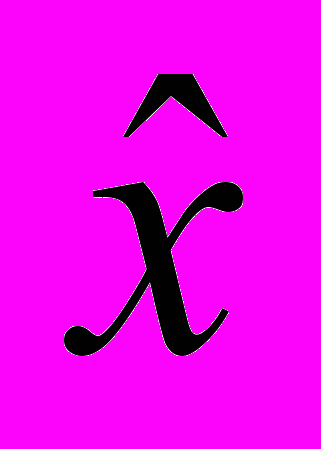(t₀), и значение входного воздействия u = const;
  
• ввод, редактирование и сохранение в файле параметров моделирования: шага моделирования , времени моделирования t_к;
  
• вывод результатов моделирования в виде таблицы и в виде графика. Должны выводится следующие переменные y, , .
  

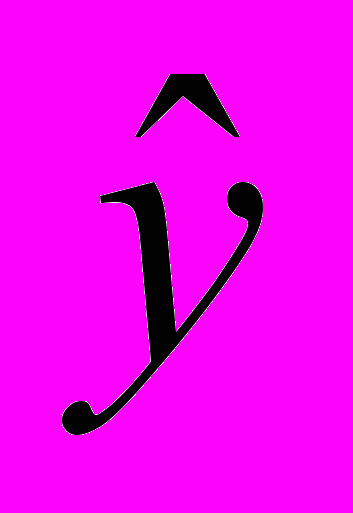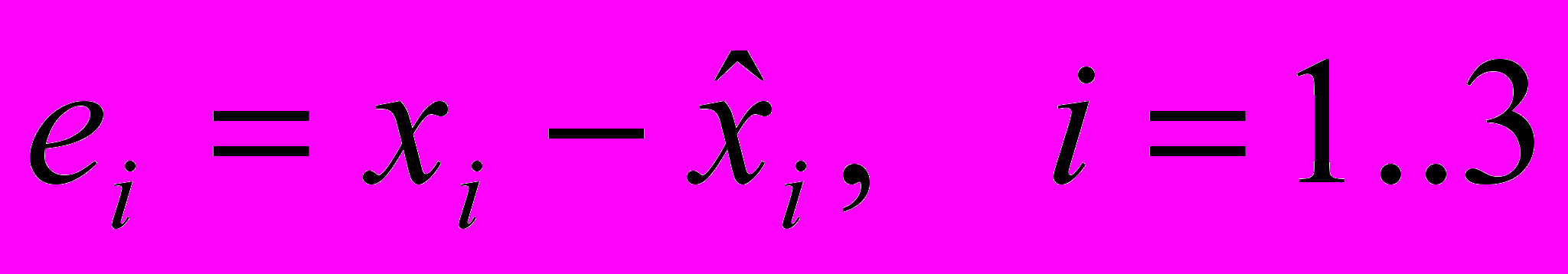Моделирование произвести:

1. при u = 0 и начальных условиях ;
   

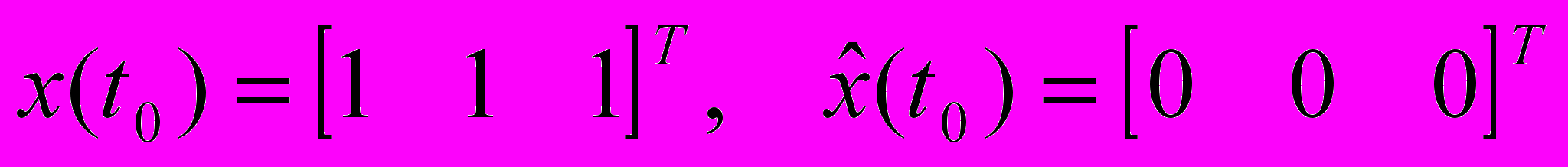2) при u = 1 и начальных условиях .

Задание на курсовой проект № 2


Моделирование процесса изменения уровня в цилиндрическом резервуаре


Математическая модель цилиндрического резервуара (рис.1) имеет вид:



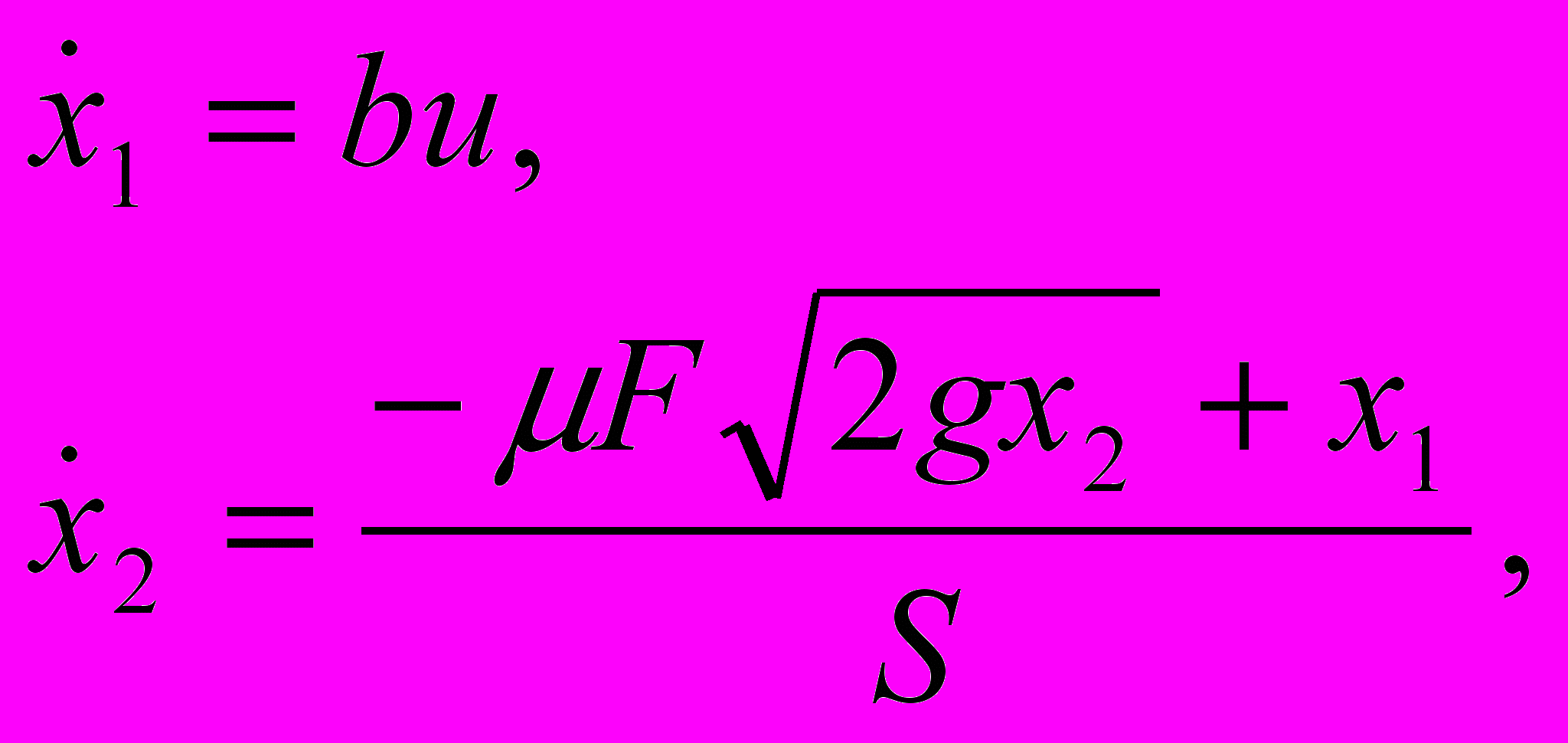
г
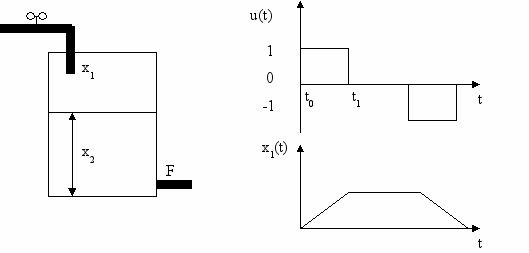
де x₁ – расход жидкости, втекающей в резервуар (м³/с), х₂ – уровень жидкости в резервуаре (м), F – площадь проходного сечения сливной трубы (м²), 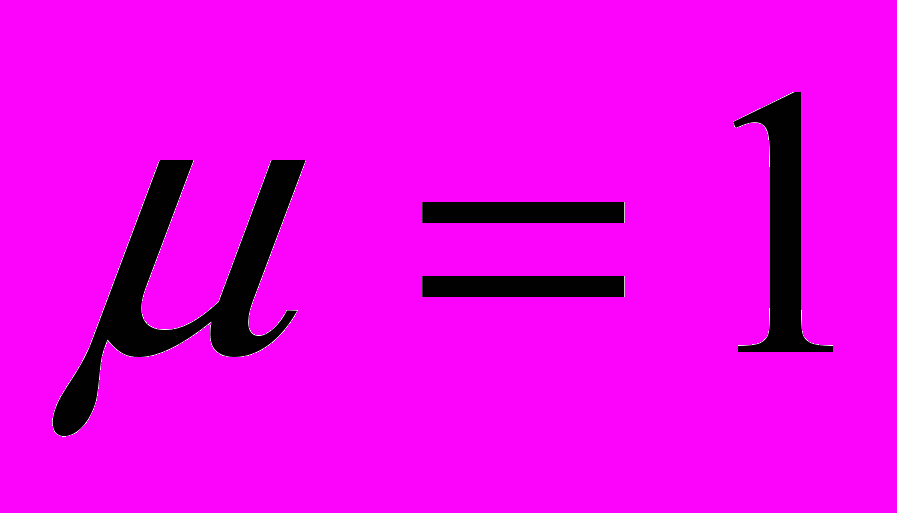- коэффициент гидравлического сопротивления, g – ускорение свободного падения (м/с²), S – площадь поверхности жидкости (м²).

Рис.1

Рис. 2

Входное воздействие u =  const задает скорость открытия вентиля на входном трубопроводе, поэтому для изменения расхода x₁ входное воздействие необходимо задавать в виде прямоугольного импульса (рис.2).


Разрабатываемая программа моделирования должна обеспечивать:

• ввод, редактирование и сохранение в файле параметров математической модели: b, F, , S.
  
• ввод, редактирование и сохранение в файле начальных условий объекта x(t₀), и значение входного воздействия u = const, промежутка времени [t₀,t₁], на котором действует входное воздействие;
  
• ввод, редактирование и сохранение в файле параметров моделирования: шага моделирования , времени моделирования t_к;
  
• вывод результатов моделирования в виде таблицы и в виде графика. Должны выводится следующие переменные u, x₁, x₂.
  

Задание на курсовой проект № 3


Моделирование процесса изменения уровня в сферическом резервуаре


Математическая модель сферического резервуара (рис.1) имеет вид:



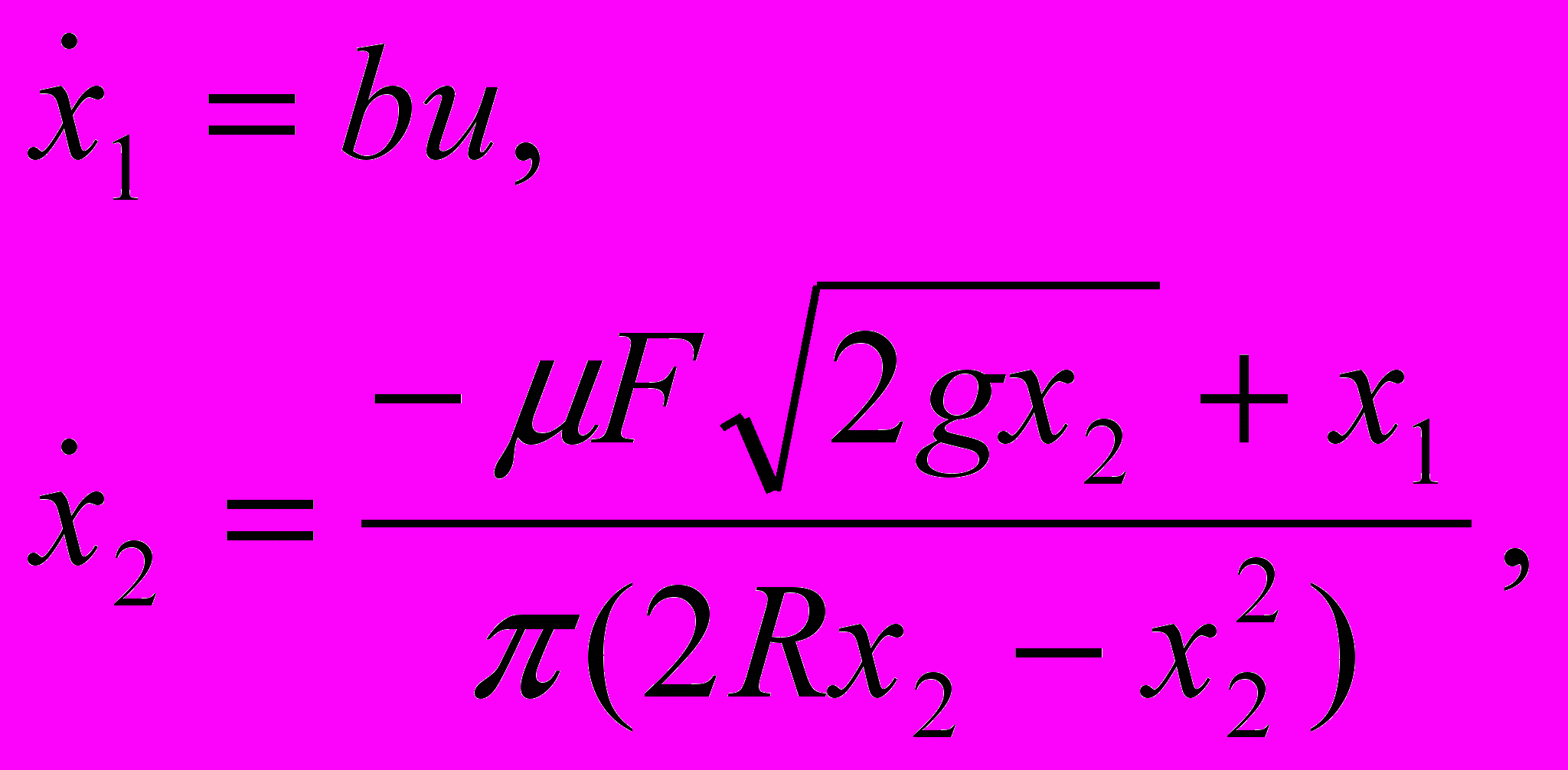
г
де x₁ – расход жидкости, втекающей в резервуар (м³/с), х₂ – уровень жидкости в резервуаре (м), F – площадь проходного сечения сливной трубы (м²), 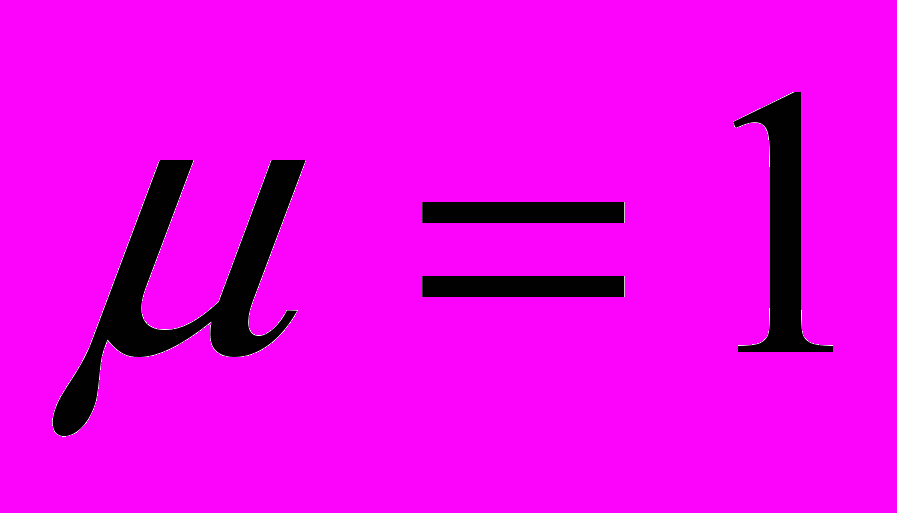- коэффициент гидравлического сопротивления, g – ускорение свободного падения (м/с²), R – радиус резервуара (м).

Рис.1

Рис. 2

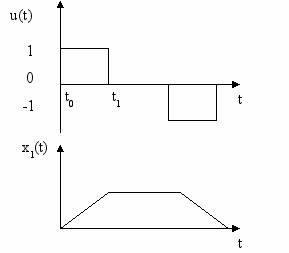
В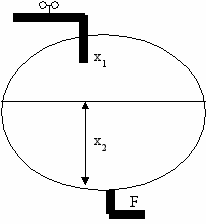ходное воздействие u =  const задает скорость открытия вентиля на входном трубопроводе, поэтому для изменения расхода x₁ входное воздействие необходимо задавать в виде прямоугольного импульса (рис.2).


Разрабатываемая программа моделирования должна обеспечивать:

• ввод, редактирование и сохранение в файле параметров математической модели: b, F, , S.
  
• ввод, редактирование и сохранение в файле начальных условий объекта x(t₀), и значение входного воздействия u = const, промежутка времени [t₀,t₁], на котором действует входное воздействие;
  
• ввод, редактирование и сохранение в файле параметров моделирования: шага моделирования , времени моделирования t_к;
  
• вывод результатов моделирования в виде таблицы и в виде графика. Должны выводится следующие переменные u, x₁, x₂.
  

Задание на курсовой проект № 4


Теплообменник для разогрева протекающей жидкости


Математическая модель теплообменника (рис.1) имеет вид:



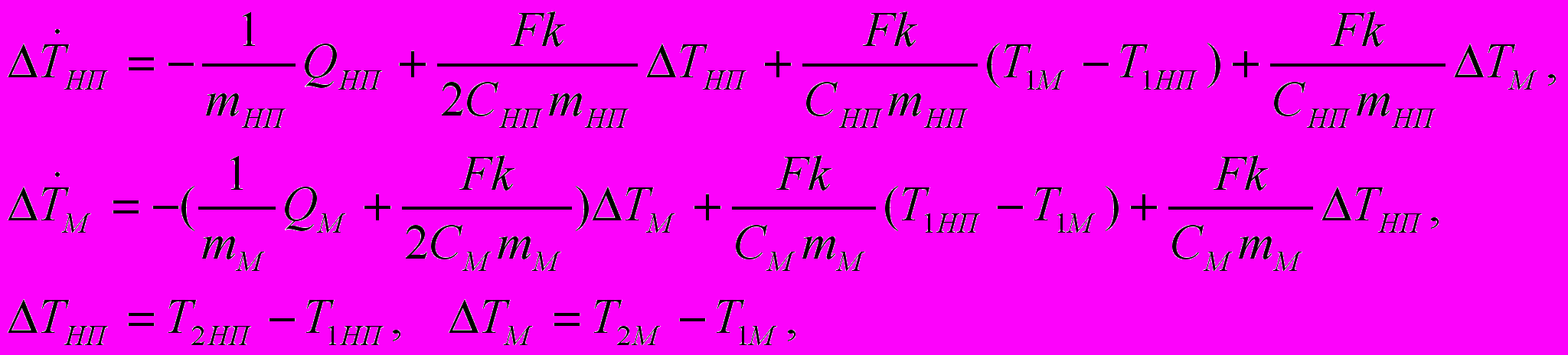
где:

T_1НП – температура нефтепродукта на входе в теплообменник;

T_2НП – температура нефтепродукта на выходе из теплообменника;

T_НП – разность температур нефтепродукта на выходе и входе;

T_1М – температура масла на входе в теплообменник;

T_1М – температура масла на выходе из теплообменника;

T_М – разность температур масла на выходе и входе;

Q _НП – массовый расход нефтепродукта;

Q _M – массовый расход масла;

m _НП – масса нефтепродукта, находящегося в теплообменнике;

m _M – масса масла, находящегося в теплообменнике;

F
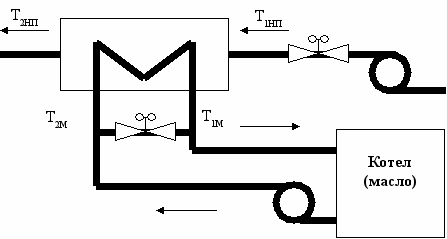
– площадь, на которой происходит теплообмен;

k – коэффициент теплопередачи от масла к нефтепродукту.

Рис. 1.

Входным воздействием для системы является расход масла Q_М (кг/с), расход нефтепродукта Q_НП (кг/с) является возмущающим воздействием на систему.


Разрабатываемая программа моделирования должна обеспечивать:

• ввод, редактирование и сохранение в файле параметров теплообменника: массы масла и нефтепродукта в теплообменнике, теплоемкости масла и нефтепродукта, площадь теплообмена, коэффициента теплопередачи.
  
• ввод, редактирование и сохранение в файле начальных условий объекта: T_НП, T_М;
  
• ввод, редактирование и сохранение в файле параметров моделирования: шага моделирования , времени моделирования t_к;
  
• вывод результатов моделирования в виде таблицы и в виде графика. Должны выводится следующие переменные T_НП, T_М.
  

Задание на курсовой проект № 5


Нагревательная установка


Математическая модель нагревательной установки (рис.1) имеет вид:



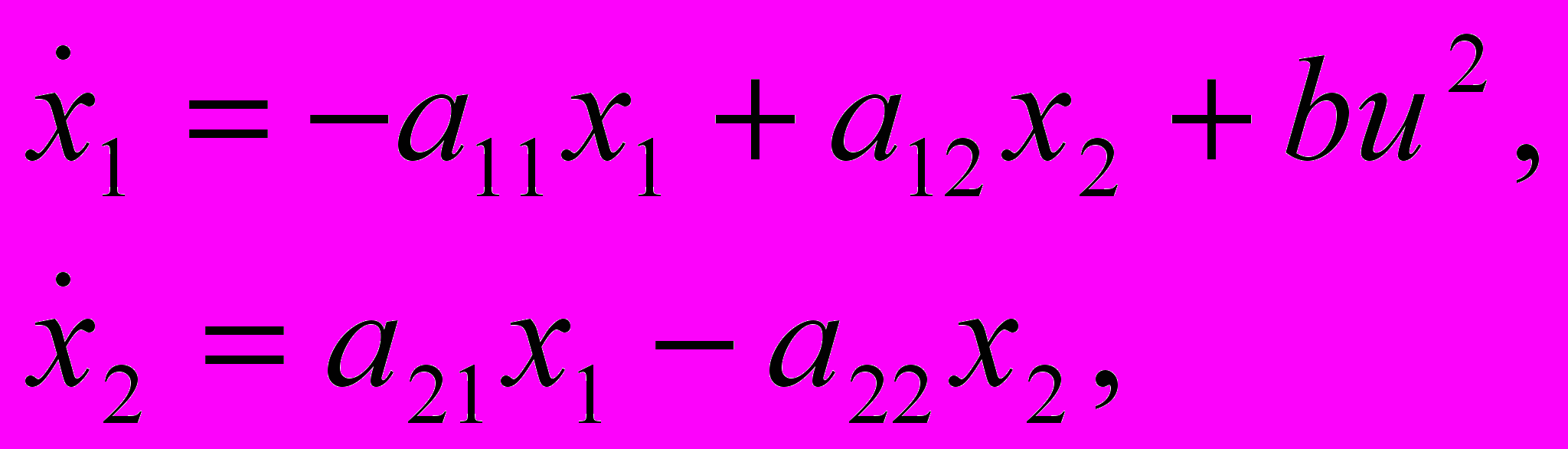
где: х₁ – температура водяной рубашки, х₂ – температура жидкости в нагревательной установке, u = const – напряжение на нагревательном элементе.

Р
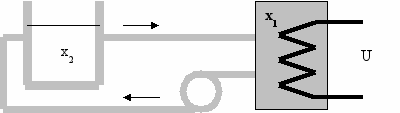
ис. 1.

Входным воздействием для системы является напряжение на нагревательном элементе (В).


Разрабатываемая программа моделирования должна обеспечивать:

• ввод, редактирование и сохранение в файле параметров нагревательной установки а_ij.
  
• ввод, редактирование и сохранение в файле начальных условий объекта: x₁(t₀), x₂(t₀);
  
• ввод, редактирование и сохранение в файле параметров моделирования: шага моделирования , времени моделирования t_к;
  
• вывод результатов моделирования в виде таблицы и в виде графика. Должны выводится следующие переменные x₁, x₂.
  

Тестовое моделирование провести при следующих значении параметров: а₁₁ = 0.1, а₁₂ = 0.2, а₂₁ = 0.08, а₂₂ = 0.18, b = 30.


Задание на курсовой проект № 6


"Разработка программных средств моделирования

магнитного подвеса"


Целью курсового проекта является разработка программных средств моделирования системы управления высотой подвеса тела в магнитном поле (рис.1).




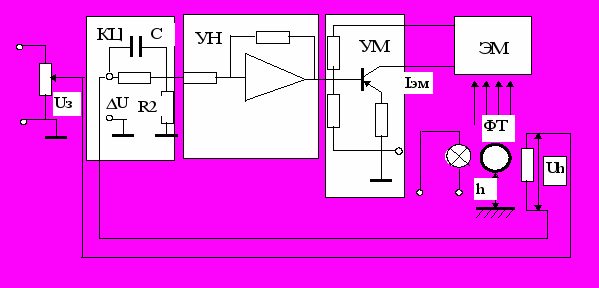
Рис.1.


Ферромагнитное тело (ФТ) подвешивается в пространстве в поле электромагнита (ЭМ) с регулируемым током Iэм. Высота подвеса h измеряется при помощи фотооптической системы, состоящей из лампочки-осветителя (О) и фотоэлемента (ФЭ), вырабатывающего ЭДС Uh, пропорциональную высоте подвеса h. ЭДС Uh сравнивается с задающим напряжением Uз, величина которого определяет высоту подвеса h . Разность напряжений Uз - Uh = U составляет ошибку регулирования, которая усиливается по величине и мощности усилителями напряжения (УН) и мощности (УМ), и определяет ток, а следовательно, и силу притяжения ФТ электромагнитом.

При движении ФТ вниз ЭДС Uh уменьшается, т.к. ФТ больше перекрывает световой поток освещающий ФЭ. При этом напряжение ошибки регулирования, ток ЭМ и сила притяжения тела ЭМ увеличиваются, что обеспечивает стабилизацию высоты подвеса тела. Корректирующая RC- цепь (КЦ) служит для обеспечения устойчивости системы управления.

Математическая модель данной системы выводится на основе 2-го закона Ньютона и уравнений теории электрических цепей.

На основании 2-го закона Ньютона можно записать

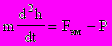( 1 )

где m - масса тела; Fэм - сила, создаваемая ЭМ; P = mg - вес тела.

Сила, создаваемая ЭМ, пропорциональна току ЭМ, т.е.

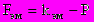( 2 )

где k_эм - коэффициент пропорциональности.


Ток ЭМ связан с напряжением ошибки дифференциальным уравнением

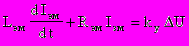( 3 )

где Lэм - индуктивность обмотки; Rэм - активное сопротивление; Ку - коэффициент усиления усилителей УН и УМ.

Последнее уравнение определяет ошибку регулирования

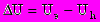( 4 )

где Uh = Kфэ h; Кфэ - коэффициент передачи датчика высоты подвеса. Уравнения (1 - 4) представляют собой упрощенную математическую модель системы управления. При включении корректирующей цепи КЦ до бавляется еще одно уравнение

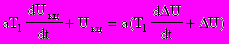( 5 )

где T₁ = R₁ C; a = R₂ / (R₁ + R₁).

Если при моделировании используется КЦ, то в уравнение (3) вместо U следует записать Uкц.

Численные значения коэффициентов математической модели:

m = 100г = 0,1кг Lэм = 5 Гн Кэм = 10 н/А, Rэм = 100 ом

Ку = 10 Т1 = 1с а = 0,05 Кфэ = 1 в/м

Исходные данные для моделирования:

• параметры математический модели;
  
• начальные условия;
  
• значение входного воздействия;
  
• det - шаг численного решения диф. уравнений;
  
• fintim - промежуток времени моделирования;
  
• outdel - шаг по времени для табличного вывода результатов моделирования.
  

Все исходные данные должны сохраняться в файле с

расширением dat.

Задание на курсовой проект № 7


Моделирование уравнений теплопроводности


Целью курсового проекта является разработка программных средств моделирующих изменение температуры в тонком металлическом стержне, вытянутом вдоль оси x (рис.1).



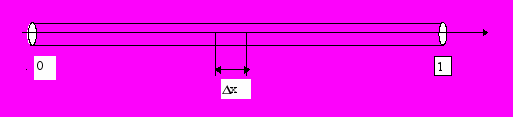
Рис.1.

Стержень является полностью теплоизолированным. Поток тепла распространяется только в направлении оси x. Уравнения теплопроводности имеют вид

( 1 )

где U - температура; U_t- производная по времени; U_xx- вторая производная по пространственной координате x; C = k/(s ) = 1 - постоянный коэффициент, численное значение которого зависит от коэффициента теплопроводности k, удельной теплоемкости материала s, плотности материала .


При решении дифференциальных уравнений в частных производных используются начальные условия, задающие распределение температуры по стержню в нулевой момент времени

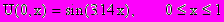( 2 )

и граничные условия, задающие температуру на концах стержня для всех значений времени

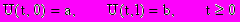. ( 3 )

Для моделирования изменения температуры в стержне можно использовать конечно разностную аппроксимацию

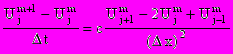( 4 )

уравнений теплопроводности (1).

Исходными данными для моделирования являются:

• начальные условия ( 2 );
  
• граничные условия ( 3 );
  
• параметры моделирования, к которым относятся шаг сетки по времени t , шаг сетки по пространственной координате x , промежуток времени моделирования fintim, шаги вывода результатов моделирования по времени t и по пространственной переменной x .
  

Результаты моделирования должны представляться в виде таблицы:

t	x0	x1	…	xn+1
ti, i = 0..k

Задание на курсовой проект № 8

Моделирование линейных динамических систем


Целью курсового проекта является разработка программных средств моделирования линейных динамических систем:

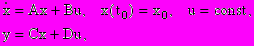( 1 )

где xRⁿ - вектор систояния; uR^m - вектор управления; yR^m - вектор выхода; AR^nxn, BR^nxm , CR^lxn , DR^lxm - матрицы постоянных коэффициентов; x0 - начальные условия.


Исходные данные для моделирования:

• n, m, l - размеры векторов;
  
• A, B, C, D - матрицы системы управления;
  
• x₀ - начальные условия;
  
• u - значение входного воздействия;
  
• t - шаг численного решения диф. уравнений (1);
  
• t_к - промежуток времени моделирования;
  
• outdel - шаг по времени для табличного вывода результатов моделирования.