Лекция 1 Тема: Введение в экономико-математическое моделирование
| Вид материала | Лекция |
СодержаниеПостроение экономической модели. Целевая функция Условие неотрицательности |
- Учебно-методический комплекс экономико-математическое моделирование для специальности:, 818.67kb.
- Программа дисциплины имитационное моделирование в экономике для направления 080100., 228.47kb.
- «Экономико-математическое моделирование экономических процессов», 531.62kb.
- Задков д. А. Распи сание учебных занятий студентов III курса горного факультета с 19., 34.25kb.
- Рабочая программа научного кружка экономико-математическое моделирование, 30.9kb.
- Университет, 228.94kb.
- Рабочая программа По дисциплине «Экономико-математическое моделирование производственных, 373.58kb.
- Программа вступительных экзаменов по специальности 08. 00. 13 «Математические и инструментальные, 40.42kb.
- «Экономико-математическое моделирование», 12.86kb.
- Лекция Моделирование физических процессов, 111.71kb.
Лекция 1
Тема: Введение в экономико-математическое моделирование.
Три формы записи задач линейного программирования.
Вопросы лекции:
- Основные понятия моделирования.
- Основные типы моделей.
- Формулировка задачи линейного программирования.
- Общая форма записи задач ЛП.
- Стандартная форма записи задач ЛП.
- Основная (каноническая) форма записи задач ЛП.
- Переход от одной формы записи к другой.
Основным понятием курса является понятие математической модели. В настоящее время в литературе насчитывается несколько десятков определений понятия "модель", отличающихся друг от друга. В общем случае слово модель – это отражение реального объекта. Такое отражение объекта может быть представлено схемой, эскизом, фотографией, моделью описательного характера в виде графиков и таблиц и т.д.
Модель – условный образ объекта, построенный для упрощения его исследования. Экономико-математическая модель – это математическое описание исследуемого экономического процесса или объекта. Эта модель выражает закономерности экономического процесса в абстрактном виде с помощью математических соотношений. Предполагается, что изучение модели дает новые знания об объекте, либо позволяет определить наилучшие решения в той или иной ситуации.
Процесс построения экономико-математической модели называют экономико-математическим моделированием. Естественно, моделирование и построение математической модели экономического объекта позволяют свести экономический анализ производственных процессов к математическому анализу и принятию эффективных решений.
^ Построение экономической модели.
- Формулируется предмет и цели исследования.
- В рассматриваемой экономической системе выделяются структурные или функциональные элементы, соответствующие данной цели, выявляются наиболее важные качественные характеристики. Этих элементов.
- Словесно, качественно описываются взаимосвязи между элементами модели.
- Вводятся символические обозначения для учитываемых характеристик экономического объекта и формализуются, насколько возможно, взаимосвязи между ними. Тем самым, формулируется математическая модель.
- Проводятся расчеты по математической модели и анализ полученного решения.
Существуют следующие типы моделей:
- Модели линейного программирования.
- Модели нелинейного программирования.
- Модели динамического программирования.
- Модели целочисленного программирования.
- Стохастические модели (задачи, имеющие случайные элементы).
- Модели теории игр.
- Модели теории массового обслуживания.
- Модели управления запасами.
- Модели сетевого планирования и управления.
Общая и основная задача линейного программирования
Рассмотренный пример позволяет сформулировать общую задачу линейного программирования.
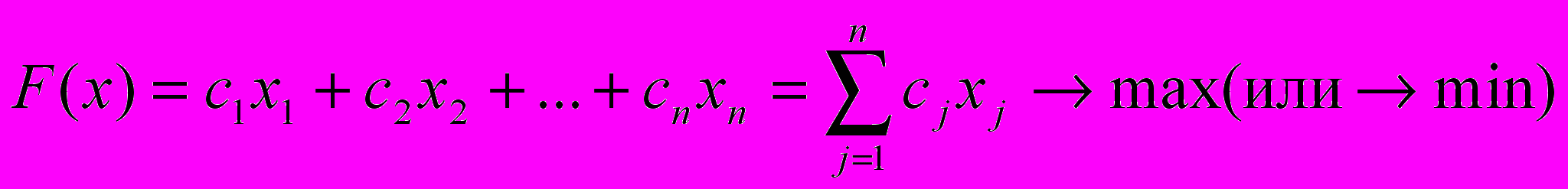 (1)
(1)Система ограничений:
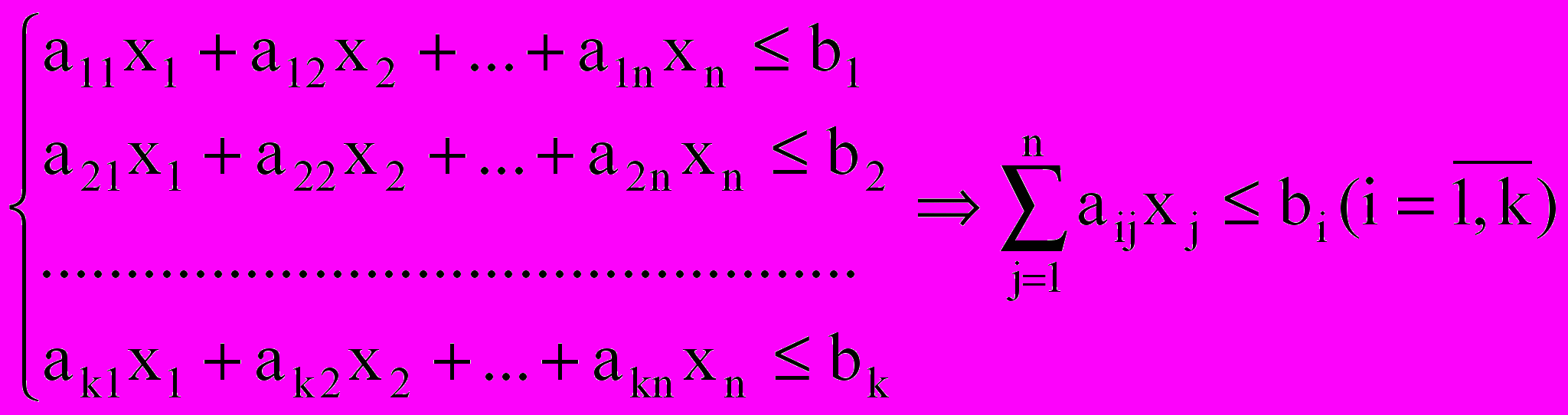 (2)
(2)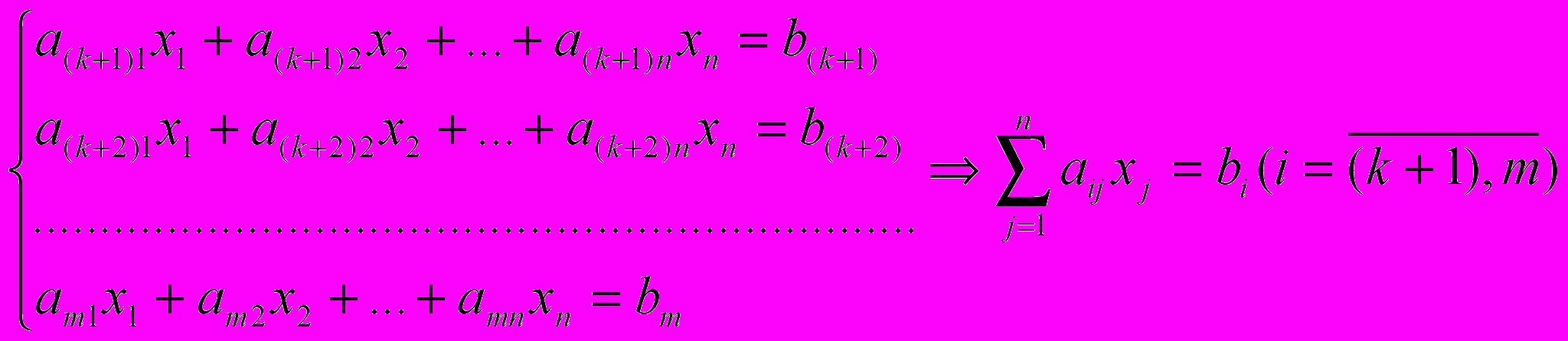 (3)
(3)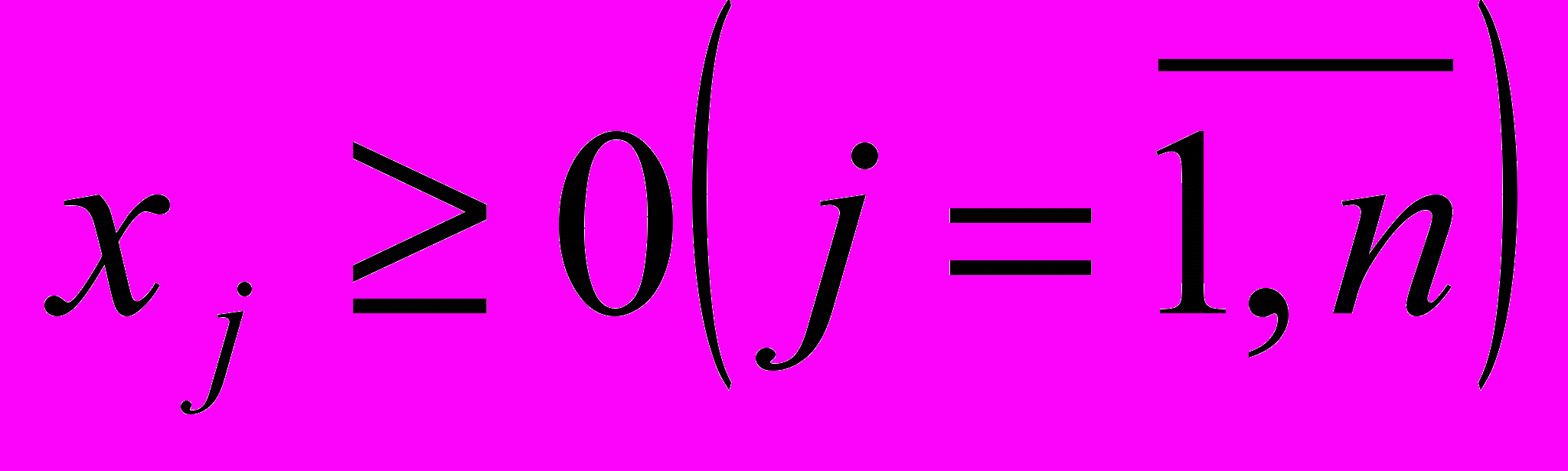 (4)
(4)Определение 1 Общей задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции (1) при условиях (2)-(4), где
 ,
, 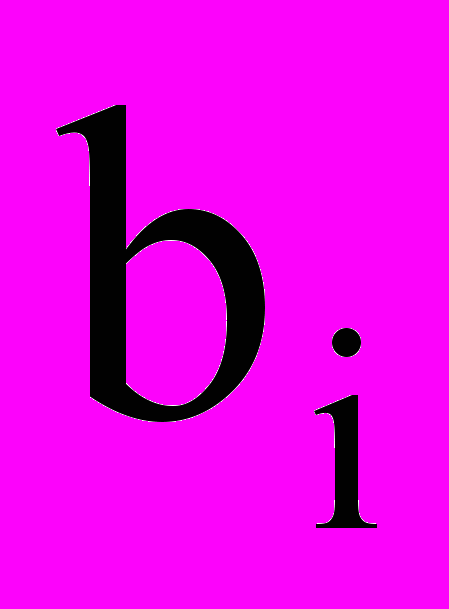 и
и  - есть постоянные величины.
- есть постоянные величины.Определение 2 Функция (1) называется целевой функцией задачи (1)-(4), а условия (2), (3), (4) – ограничением данной задачи.
Определение 3 Стандартной задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции (1) при выполнении условий (2) и (4).
Определение 4 Канонической (основной) задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции (1) при выполнении условий (3) и (4).
Определение 5 Совокупность чисел
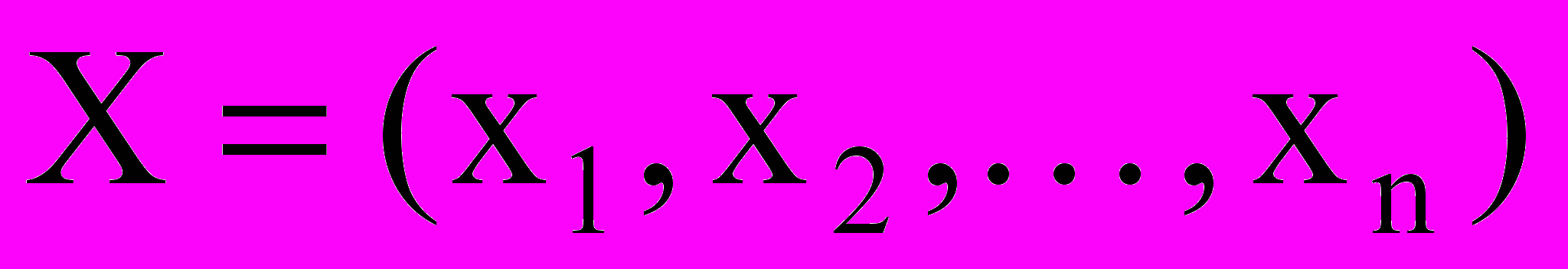 , удовлетворяющие условиям ограничения задачи (2) и (4), называется допустимым решением или планом (или же базисным решением).
, удовлетворяющие условиям ограничения задачи (2) и (4), называется допустимым решением или планом (или же базисным решением).Определение 6 План
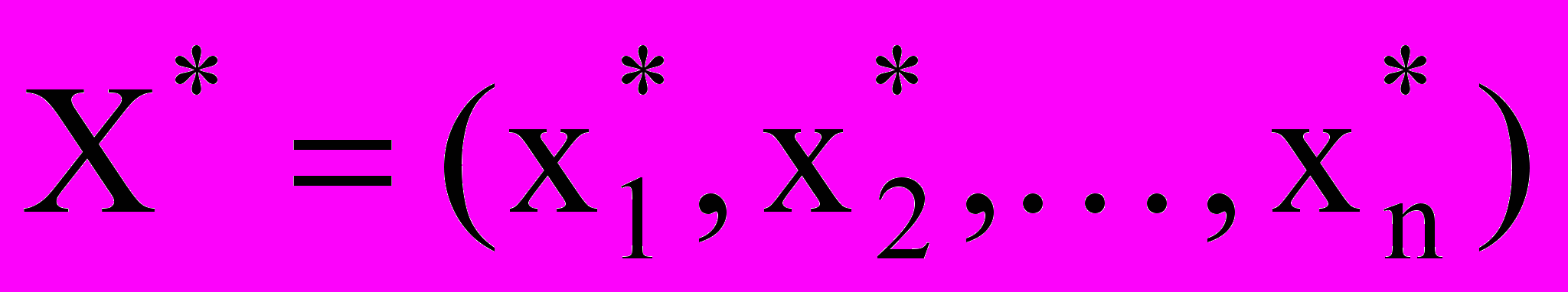 , при котором целевая функция задачи (1) принимает максимальное (минимальное) значение, называется оптимальным планом.
, при котором целевая функция задачи (1) принимает максимальное (минимальное) значение, называется оптимальным планом.Теорема 1: Всякому решению
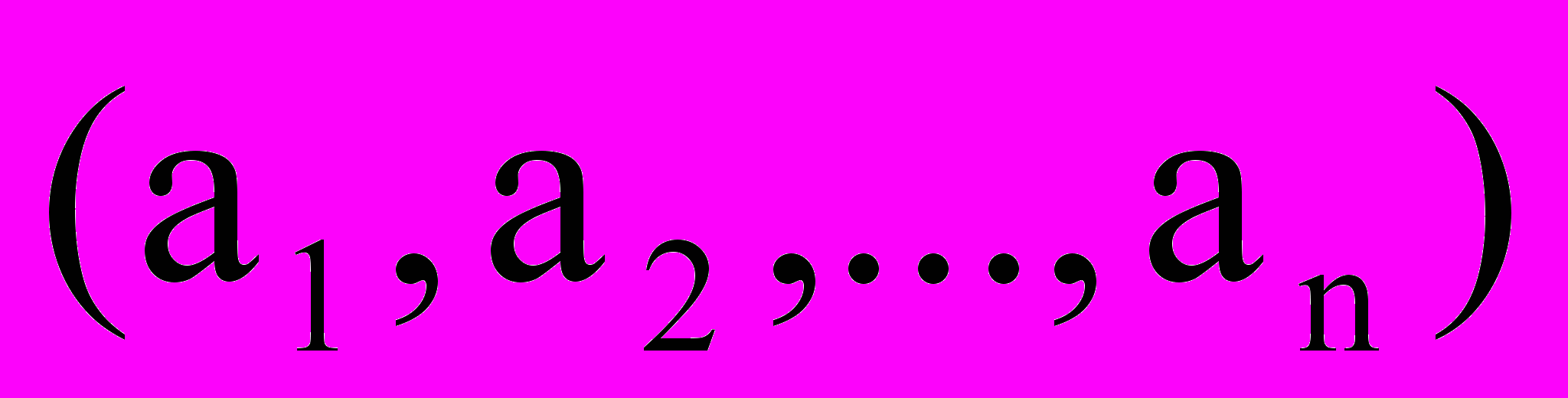 неравенства
неравенства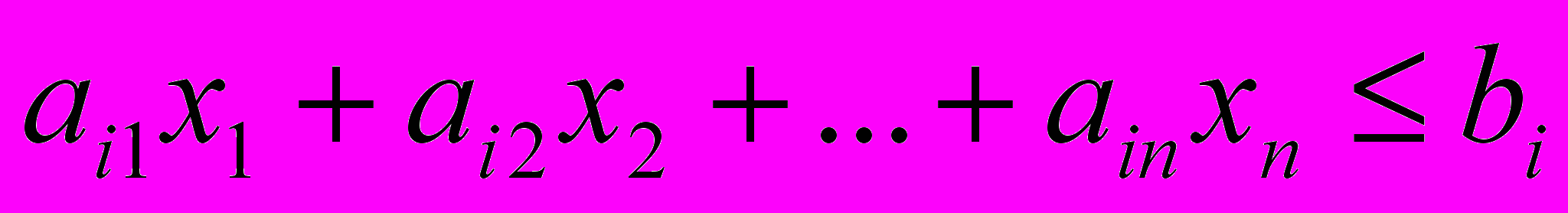 (5)
(5)соответствует определенное решение
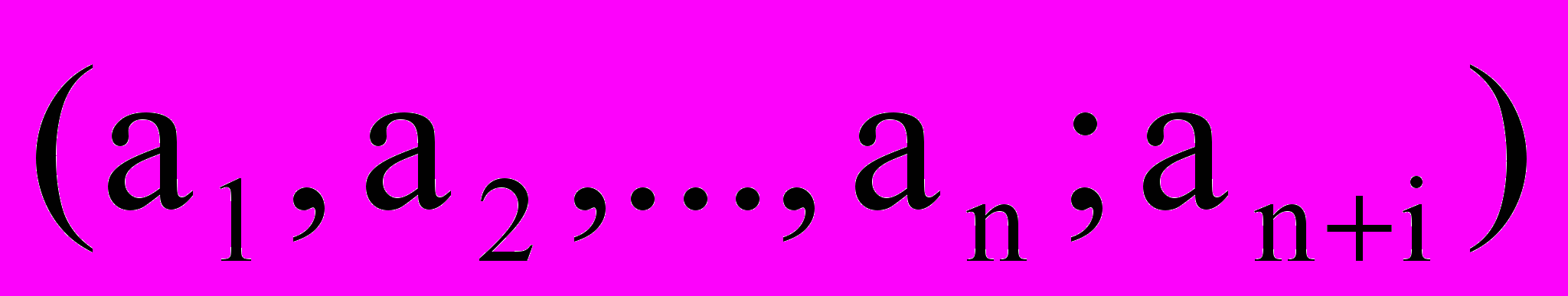 уравнения
уравнения (6)
(6)в котором
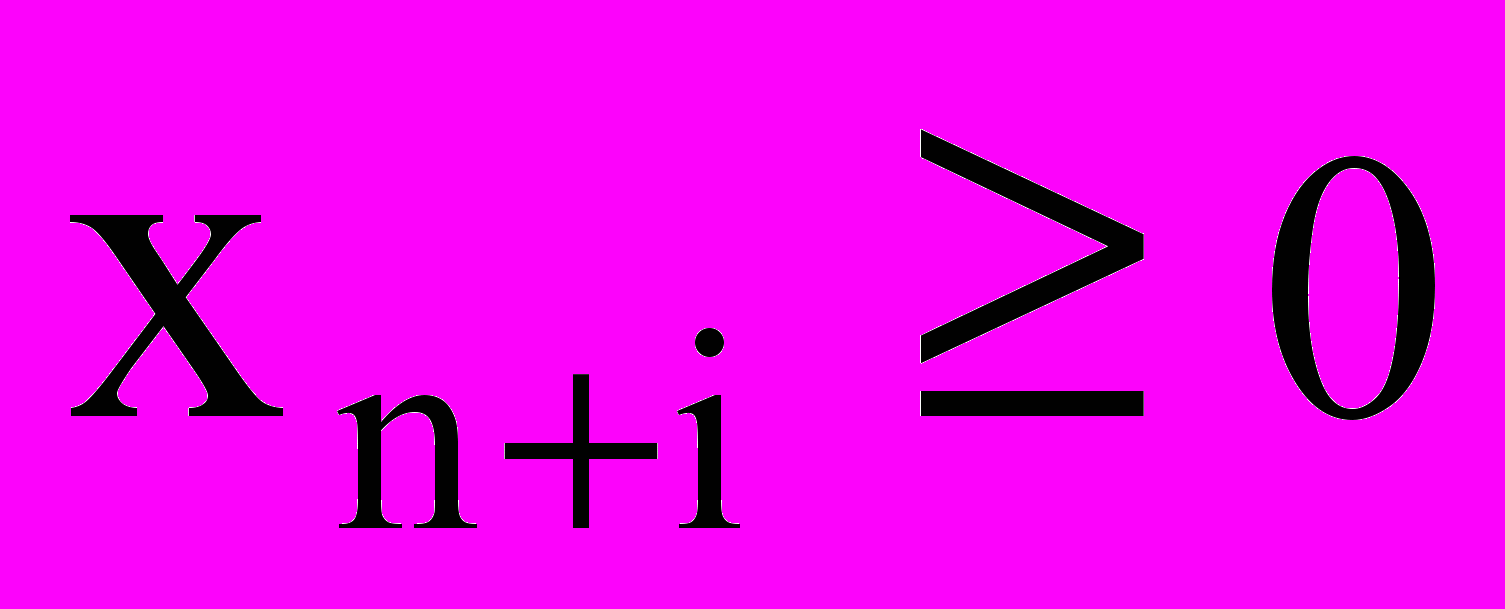 (7)
(7)и, наоборот, каждому решению
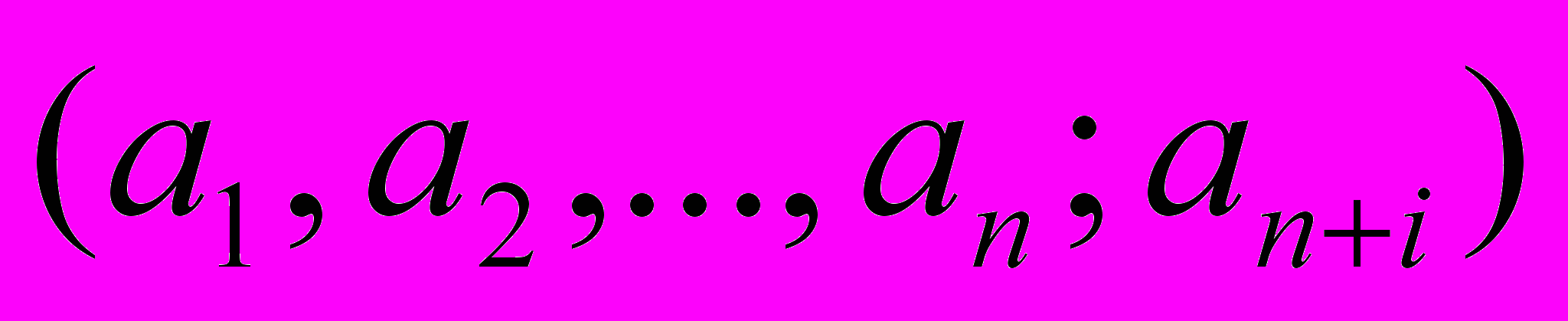 уравнения (6) и неравенства (7) соответствует определенное решение
уравнения (6) и неравенства (7) соответствует определенное решение 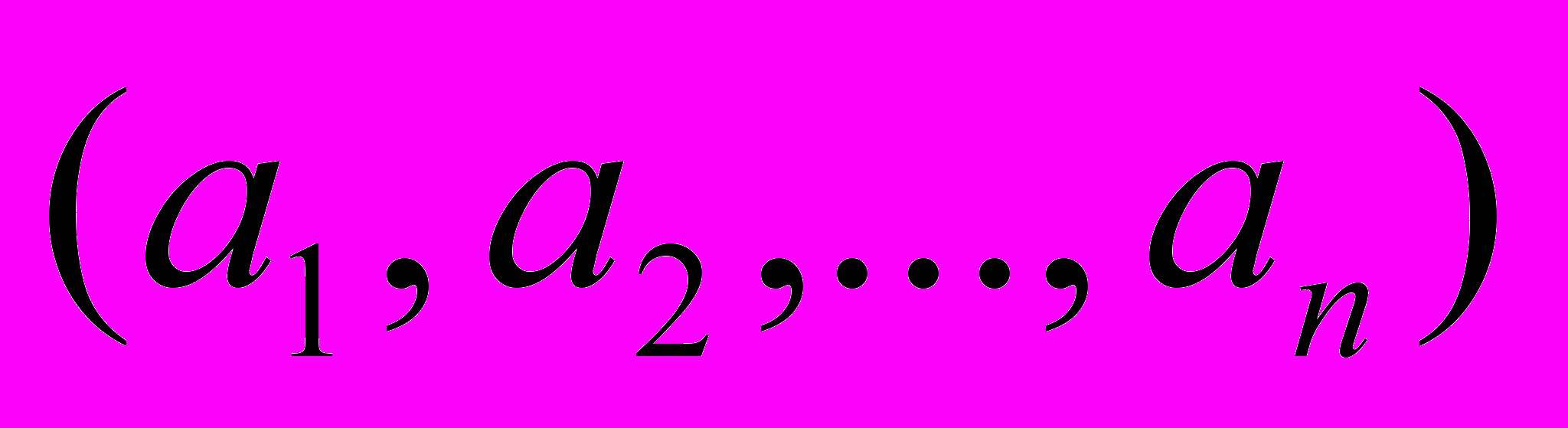 неравенства (5).
неравенства (5).Различия между тремя формами записи задач линейного программирования (ЗЛП) представим в таблице:
| Общая форма ЗЛП | Стандартная форма ЗЛП | Основная (каноническая) форма ЗЛП |
| ^ Целевая функция | ||
| Max, Min | Max, Min | Max |
| Система ограничений | ||
| , , , ≤, ≥ | , , ≤, ≥ | = |
| ^ Условие неотрицательности | ||
| Некоторые переменные могут быть неотрицательны | Все переменные неотрицательны | Все переменные неотрицательны |
Три формы записи ЗЛП эквивалентны в том смысле, что задачу записанную в одной из форм можно перевести в другую. Для этого нужно уметь:
- Переходить от задачи на Max к задаче на Min. Для этого необходимо Целевую функцию умножить на (-1).
Например:

- Переходить от ограничений-неравенств к ограничениям-уравнениям. При этом необходимо включить в ограничения-неравенства дополнительные переменные, которые считаем неотрицательными. Причем, если ограничение имеет знак ≤ переменная включается со знаком «+», а если ≥ - со знаком «—».
Например:
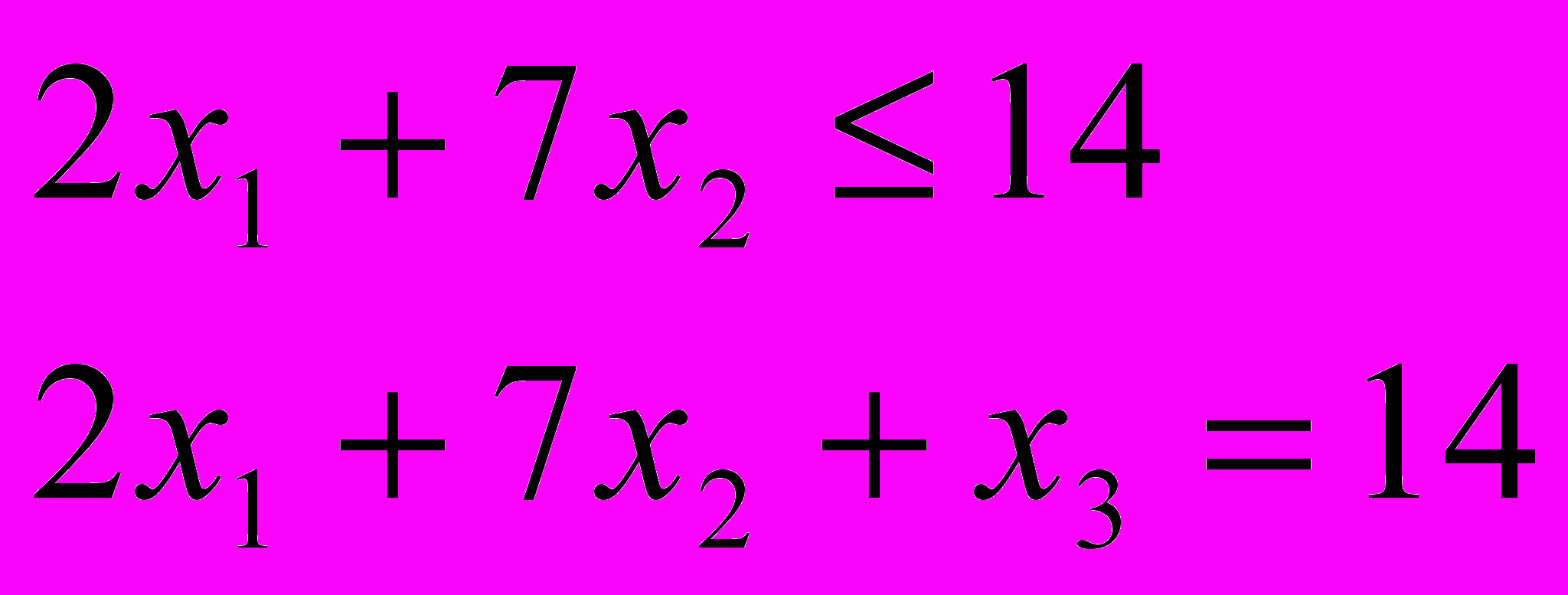
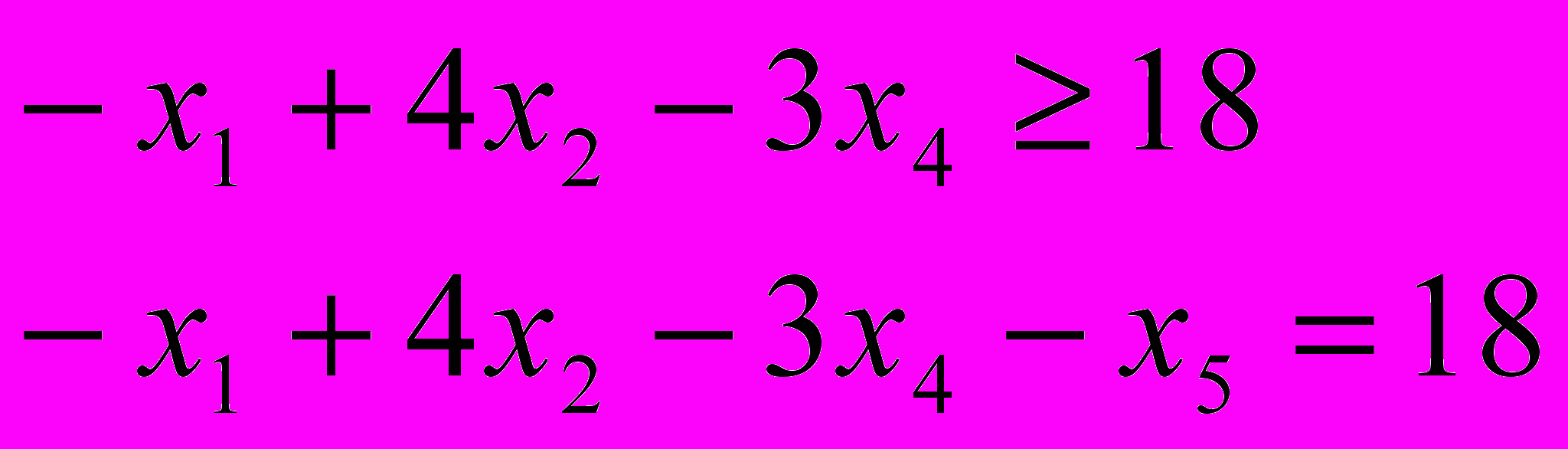
- Переходить к задаче, где все переменные неотрицательны. Пусть на переменную xi не накладывается условие неотрицательности, тогда ее заменяют двумя новыми – неотрицательными уi и yi+1. Причем xi=уi - yi+1.
Например:
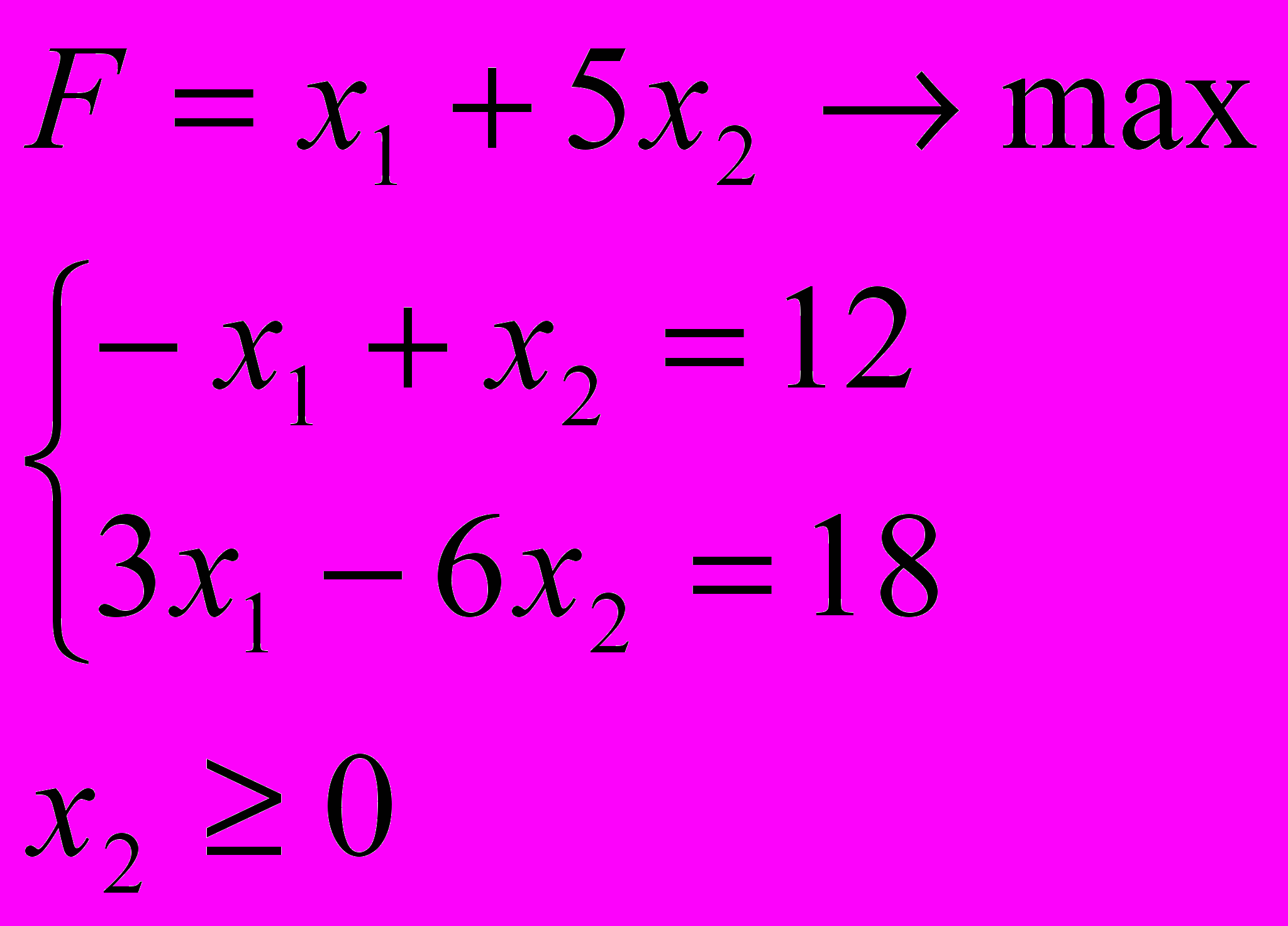
Решение:
x1=y1 - y2
x2=y3

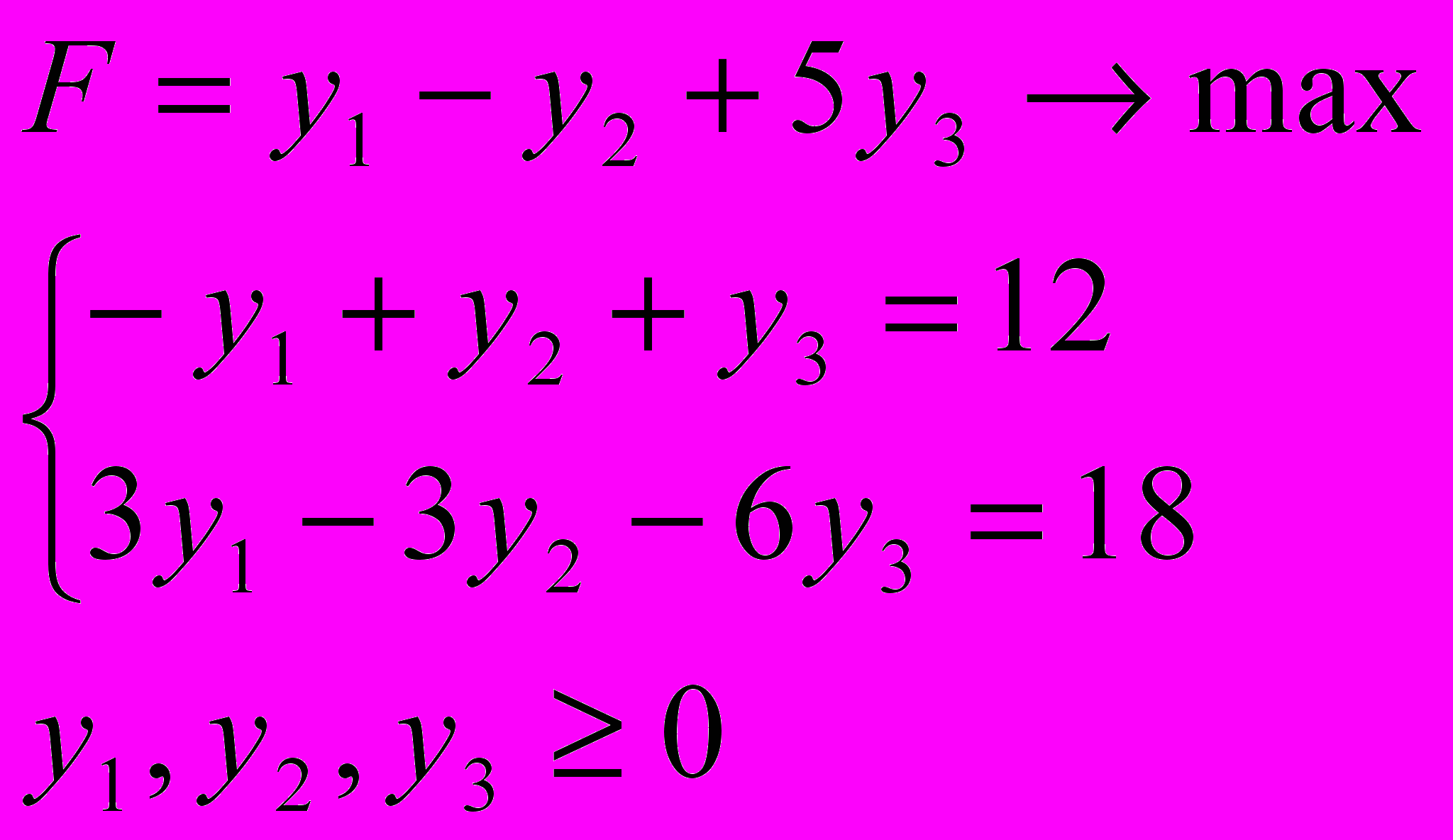
1..Задача о банке.
Пусть собственные средства банка в сумме с депозитами составляют 100 млн. долларов. Часть этих средств, но не менее 35 миллионов, должна быть размещена в кредитах. Кредиты являются неликвидными активами банка, так как в случае непредвиденной потребности в наличности обратить кредиты в деньги без существенных потерь невозможно. Другое дело ценные бумаги (особенно государственные) - их можно в любой момент продать, получив некоторую прибыль или, во всяком случае, без большого убытка. Поэтому существует правило, согласно которому коммерческие банки должны покупать в определенной пропорции ликвидные активы - ценные бумаги, чтобы компенсировать неликвидность кредитов. В нашем примере ликвидное ограничение таково: ценные бумаги должны составлять не менее 30% средств, размещенных в кредитах и ценных бумагах.
2. Задача о диете.
В описательной форме задача ставится так: из имеющихся в нашем распоряжении видов пищи требуется составить такую диету, которая, с одной стороны, удовлетворяла бы минимальные потребности организма в питательных веществах (белках, жирах, углеводах, минеральных солях, витаминах), с другой - требовала бы наименьших затрат.
Рассмотрим простую математическую модель этой задачи.
Пусть имеется два вида продуктов: П1 и П2, содержащих питательные вещества А, В, С. Известно, сколько питательного вещества того или иного вида содержится в 1 кг продуктов П1 и П2: эти сведения указаны в таблице
| | A | B | C |
| в 1 кг П1 | a1 | b1 | c1 |
| в 1 кг П2 | a2 | b2 | c2 |
Кроме этих данных, нам известны: а, b, с - ежесуточные потребности организма в А, В, С (соответственно) и s1, s2 - стоимости 1 кг продуктов П1и П2 (соответственно). Требуется рассчитать количество х1 продукта П1 и количество х2 продукта П2 так, чтобы обеспечить необходимое количество питательных веществ при минимальных затратах на продукты.
Так как s1- стоимость одного кг продукта П1, то x1 s1 - стоимость х1 кг продукта П1;
аналогично х2s2 - стоимость х2 кг продукта П2, следовательно общая стоимость продуктов, которую надо минимизировать будет f (
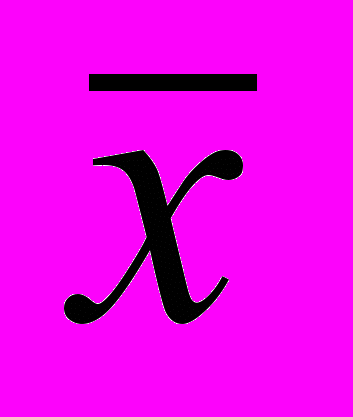 )= sl • х1 + s2 • х2.
)= sl • х1 + s2 • х2.3. Задача об использовании ресурсов.
Предприятие имеет в своем распоряжении определенное количество ресурсов разного рода: рабочую силу, деньги, сырье, оборудование, производственные ресурсы, площади и т.п. Допустим, например, ресурсы трех видов R1, R2, R3 имеются в количестве соответственно b1, b2, b3 условных единиц. Предприятие выпускает два вида товаров T1, T2, причем известно, сколько единиц каждого ресурса требуется для производства одной единицы каждого товара. Пусть аij - число единиц ресурса Ri(i =1, 2, 3), необходимое для производства единицы товара Tj(j= 1, 2).
Известно, что доход, получаемый предприятием от единицы каждого товаров, соответственно равен с1, с2. Требуется при данных ресурсах выпустить такую комбинацию товаров, при которой доход предприятия оказался бы максимальным. Обозначим через х1, х2 соответственно количества товаров Т1,Т2. Очевидно, доход предприятия f = с1x1 +с2х2.
4. Транспортная задача.
Уголь, добываемый в нескольких месторождениях, отправляется ряду потребителей: заводам, электростанциям и т.п. Известно, сколько угля добывается в каждом месторождений, скажем, за месяц, и сколько его требуется на тот же срок любому из потребителей. Известны расстояния между месторождениями и потребителями, а также условия сообщения между ними; учитывая эти данные, можно подсчитать во что обходится перевозка каждой тонны угля из любого месторождения в любой пункт потребления. Требуется при этих условиях спланировать перевозки угля таким образом, чтобы затраты на них были минимальными.
Примем для простоты, что имеются лишь два месторождения М,,М2 и три потребителя П1, П 2, П 3. Количество угля в М1 и в М2 равно соответственно a1 и а2; запросы потребителей П1, П2, П3 пусть будут соответственно b1, b2, b3. Будем считать, что суммарные запасы равны суммарным потребностям: a1 +а2 = b1 +b2 + b3 (такое предположение вполне естественно). Наконец, заданы числа сij (i =1, 2, j= 1,2,3) - стоимости перевозки тонны угля из Mi в Пj. Задача состоит в нахождении шести чисел х11, x12, x13, x21, x22, x23, где xij - количество угля, предназначенное к отправке из Мi в П j.
Для удобства обозрения составим такую таблицу:
| | П1 | П2 | П3 | Всего отправлено |
| М1 | x11 | x12 | x13 | a1 |
| М2 | x21 | x22 | x23 | a2 |
| Всего | b1 | b2 | b3 | |
5. Задача об использовании мощностей оборудования.
Предположим, что предприятию задан план по времени и номенклатуре: требуется за время Т выпустить N1 единиц продукции П1 и N2 единиц продукции П2. Каждый из видов продукции может производиться двумя машинами А и В с различными мощностями. Пусть машина А выпускает a1 единиц продукции П1 в час и а2 единиц продукции П2 в час. Пусть машина В выпускает b1 единиц продукции П1 в час и b2 единиц продукции П2 в час. Так же задана цена единицы рабочего времени машин А и В. Цена единицы рабочего времени машины А при изготовлении продукции П1 равна А1, а при изготовлении продукции П2 равна А2. Цена единицы рабочего времени машины В при изготовлении продукции П1 равна В1, a при изготовлении продукции П2 равна В2.
Эти данные можно записать в таблицы:
Таблица 1. (Мощности оборудования)
| | П1 | П2 |
| А | a1 | а2 |
| В | b1 | b2 |
Таблица 2. (Стоимости единицы рабочего времени)
| | П1 | П2 |
| А | A1 | А2 |
| В | В1 | В2 |
Требуется составить оптимальный (наиболее рациональный) план использования машин, а именно найти, сколько времени каждая из машин должна быть занята изготовлением каждого из видов продукции П1 и П2 с тем, чтобы стоимость использованного рабочего времени была минимальной, и в то же время был бы выполнен заданный план как по времени, так и по номенклатуре.
6. Задача об использовании оборудования (задача на минимакс).
Производству задан план по номенклатуре: нужно изготовить три вида продукции П1, П2, П3 соответственно в количествах N1, N2, N3 двумя машинами А1, А2 - различной производительности. Время на изготовление одной единицы продукции на каждой машине указано в таблице.
| | Виды продукции | ||
| П1 | П2 | П3 | |
| A1 | a11 | a12 | a13 |
| A2 | a21 | a22 | a23 |
Составить оптимальный план использования оборудования, т.е. такой план, чтобы нужная номенклатура продукции была изготовлена в минимальное время. Иными словами, найти количество каждого вида продукции, изготовляемой на каждой машине при наименьшей затрате времени.
