Тест к зачету по дисциплине «Математические методы в экономике» Специальность 80116 «Многомерные статистические методы»
| Вид материала | Документы |
- Программа производственной практики специальность: 080116. 65 Математические методы, 63.49kb.
- Рабочая программа учебной дисциплины «Аналитический маркетинг» (специальность «Математические, 151.09kb.
- Рабочей программы учебной дисциплины математические методы и модели в экономике уровень, 37.32kb.
- Примерная программа дисциплины "Математические методы финансового анализа", 464.29kb.
- Рабочая программа по дисциплине «Математические методы финансового анализа» специальности:, 139.06kb.
- Магистерской программы «Математические методы в экономике» реализуемой на кафедре №31, 26.25kb.
- Рабочая программа учебной дисциплины «Теория вероятностей» Специальность «Математические, 91.14kb.
- Рабочая программа учебной дисциплины «Математический анализ» Специальность «Математические, 187.35kb.
- Учебно-методический комплекс (для студентов Института «Математические методы в экономике, 238.16kb.
- Методические указания по проведению преддипломной практики, подготовке и защите дипломной, 399.7kb.
Тест к зачету по дисциплине «Математические методы в экономике»
Специальность 80116 «Многомерные статистические методы»,
IV курс, 8-й семестр
Разработчики: проф. Иванов Е.Е., доц. Шустов Д.А., учебно-методическая лаборатория кафедры ЭК и ЭММ
Преподаватель: проф. Иванов Е.Е.
1 МНОГОМЕРНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА ЭТО:
ВЕКТОР
МАТРИЦА
СКАЛЯР
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
2 ИМЕЕТСЯ k-МЕРНАЯ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ F(X). В КАКОМ СЛУЧАЕ F(X)=0?
ЕСЛИ ХОТЯ БЫ ОДНА КОМПОНЕНТА X РАВНА МИНУС БЕСКОНЕЧНОСТИ
ЕСЛИ ХОТЯ БЫ ОДНА КОМПОНЕНТА X РАВНА БЕСКОНЕЧНОСТИ
ЕСЛИ ВСЕ КОМПОНЕНТЫ X РАВНЫ БЕСКОНЕЧНОСТИ
ЕСЛИ ВСЕ КОМПОНЕНТЫ X РАВНЫ БЕСКОНЕЧНОСТИ
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
3 ИМЕЕТСЯ k-МЕРНАЯ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ F(X). В КАКОМ СЛУЧАЕ F(X)=1?
ЕСЛИ ВСЕ КОМПОНЕНТЫ X РАВНЫ БЕСКОНЕЧНОСТИ
ЕСЛИ ХОТЯ БЫ ОДНА КОМПОНЕНТА X РАВНА МИНУС БЕСКОНЕЧНОСТИ
ЕСЛИ ХОТЯ БЫ ОДНА КОМПОНЕНТА X РАВНА БЕСКОНЕЧНОСТИ
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
4 ИМЕЕТСЯ ФУНКЦИЯ ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ f(x1,x3/x2,x4,x5). ЭТО ОПИСАНИЕ КАКОГО РАСПРЕДЕЛЕНИЯ?
УСЛОВНОГО РАСПРЕДЕЛЕНИЯ x1,x3
УСЛОВНОГО РАСПРЕДЕЛЕНИЯ x2,x4,x5
РАСПРЕДЕЛЕНИЯ x1,x2,x3,x4,x5
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
5 В КАКОМ СЛУЧАЕ ДЛЯ k-МЕРНОГО СЛУЧАЙНОГО ВЕКТОРА X СПРАВЕДЛИВО РАВЕНСТВО F(x1,x2,...,xk)=F(x1)*F(x2)*...*F(xk) ?
ПРИ НЕЗАВИСИМОСТИ ВСЕХ КОМПОНЕНТ ВЕКТОРА X
В ЛЮБОМ
ПРИ НОРМАЛЬНОМ ЗАКОНЕ РАСПРЕДЕЛЕНИЯ ВСЕХ КОМПОНЕНТ ВЕКТОРА X
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
6 КАКОЙ ЯВЛЯЕТСЯ КОВАРИАЦИОННАЯ МАТРИЦА МНОГОМЕРНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ?
КВАДРАТНОЙ
ПРЯМОУГОЛЬНОЙ
ТРЕУГОЛЬНЫЙ
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
7 КАКОЙ ЯВЛЯЕТСЯ КОВАРИАЦИОННАЯ МАТРИЦА МНОГОМЕРНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ?
СИММЕТРИЧЕСКОЙ
КОСОСИММЕТРИЧЕСКОЙ
ВСЕГДА ОРТОГОНАЛЬНОЙ
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
8 КОВАРИАЦИОННАЯ МАТРИЦА МНОГОМЕРНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ НЕОТРИЦАТЕЛЬНО ОПРЕДЕЛЕНА?
ДА
НЕТ
ДА, ЕСЛИ X ПОДЧИНЯЕТСЯ МНОГОМЕРНОМУ НОРМАЛЬНОМУ ЗАКОНУ РАСПРЕДЕЛЕНИЯ
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
9 ЧЕМУ СООТВЕТСТВУЕТ M(x3/x1,x2,x4)?
РЕГРЕССИИ x3 НА КОМПОНЕНТЫ x1,x2,x4
РЕГРЕССИИ КОМПОНЕНТ x1,x2,x4 НА x3
МАТЕМАТИЧЕСКОМУ ОЖИДАНИЮ ВЕКТОРА X
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
10 В КАКОМ СЛУЧАЕ КВАДРАТ КОЭФФИЦИЕНТА МНОЖЕСТВЕННОЙ КОРРЕЛЯЦИИ СОВПАДАЕТ С КОРРЕЛЯЦИОННЫМ ОТНОШЕНИЕМ?
ПРИ ЛИНЕЙНОЙ ЗАВИСИМОСТИ КОМПОНЕНТЫ xi ВЕКТОРА X ОТ ОСТАЛЬНЫХ ЕГО КОМПОНЕНТ
ПРИ НОРМАЛЬНОМ ЗАКОНЕ РАСПРЕДЕЛЕНИЯ ВСЕХ КОМПОНЕНТ ВЕКТОРА X
В ЛЮБОМ
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
11 КАКОЙ МЕТОД ПРИМЕНЯЕТСЯ ПРИ ОЦЕНИВАНИИ ПАРАМЕТРОВ МНОГОМЕРНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ?
МЕТОД ВЫБОРОЧНОГО АНАЛИЗА
МЕТОД "ПРОБ И ОШИБОК"
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
12 ОЦЕНКА МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ СЛУЧАЙНОГО ВЕКТОРА ЯВЛЯЕТСЯ СЛУЧАЙНЫМ ВЕКТОРОМ?
ДА
НЕТ
ЭТО ЗАВИСИТ ОТ ВИДА РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОГО ВЕКТОРА
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
13 ОЦЕНКА КОВАРИАЦИОННОЙ МАТРИЦЫ СОДЕРЖИТ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ?
ДА
НЕТ, СОДЕРЖИМОЕ МАТРИЦЫ - КОНСТАНТЫ
В ЗАВИСИМОСТИ ОТ ЗАКОНА РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОГО ВЕКТОРА X
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
14 ЧТО ПРЕДСТАВЛЯЕТ СОБОЙ ДОВЕРИТЕЛЬНАЯ ОБЛАСТЬ ДЛЯ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ k-МЕРНОГО НОРМАЛЬНО РАСПРЕДЕЛЕННОГО ВЕКТОРА?
k-МЕРНЫЙ ЭЛЛИПСОИД
k-МЕРНЫЙ ВЕКТОР
k-МЕРНЫЙ ПАРАЛЛЕЛЕПИПЕД
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
15 ПРОВЕРЯЕТСЯ ГИПОТЕЗА О РАВЕНСТВЕ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ MX СЛУЧАЙНОГО, НОРМАЛЬНО РАСПРЕДЕЛЕННОГО ВЕКТОРА X ЗНАЧЕНИЮ A.КАКИМ УСЛОВИЯМ ДОЛЖНА УДОВЛЕТВОРЯТЬ КОВАРИАЦИОННАЯ МАТРИЦА ВЕКТОРА X?
ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ ДОЛЖЕН БЫТЬ ОТЛИЧЕН ОТ НУЛЯ
ЛЮБЫМ
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ ДОЛЖЕН БЫТЬ БОЛЬШЕ НУЛЯ
ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ ДОЛЖЕН БЫТЬ МЕНЬШЕ НУЛЯ
16 ПРОВЕРЯЕТСЯ ГИПОТЕЗА О РАВЕНСТВЕ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ MX СЛУЧАЙНОГО, НОРМАЛЬНО РАСПРЕДЕЛЕННОГО ВЕКТОРА X ЗНАЧЕНИЮ A. КАКАЯ СТАТИСТИКА ИСПОЛЬЗУЕТСЯ ПРИ ПРОВЕРКЕ ГИПОТЕЗЫ?
ХОТЕЛЛИНГА
ФИШЕРА
t-СТАТИСТИКА
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
17 ПРОВЕРЯЕТСЯ ГИПОТЕЗА О РАВЕНСТВЕ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ MX СЛУЧАЙНОГО, НОРМАЛЬНО РАСПРЕДЕЛЕННОГО ВЕКТОРА X ЗНАЧЕНИЮ A. ПУСТЬ РАЗМЕРНОСТЬ ВЕКТОРА k, ОБЪЕМ ВЫБОРКИ n. ПРИ КАКОМ СООТНОШЕНИИ k И n ВОЗМОЖНА ПРОВЕРКА ГИПОТЕЗЫ?
n>k
n=k
n
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
18 ПРОВЕРЯЕТСЯ ГИПОТЕЗА О РАВЕНСТВЕ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ MX СЛУЧАЙНОГО, НОРМАЛЬНО РАСПРЕДЕЛЕННОГО ВЕКТОРА X ЗНАЧЕНИЮ A. ДАННЫЕ ПРОТИВОРЕЧАТ ГИПОТЕЗЕ ПРИ УРОВНЕ ЗНАЧИМОСТИ 0,05. БУДУТ ЛИ ОНИ ПРОТИВОРЕЧИТЬ ГИПОТЕЗЕ ПРИ УРОВНЕ ЗНАЧИМОСТИ 0,02, ЕСЛИ p-Value РАВНО 0,015?
ДА
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
НЕТ
ДА, ЕСЛИ ВЕКТОР НОРМАЛЬНО РАСПРЕДЕЛЕН
19 КАКОЙ ЯВЛЯЕТСЯ КОРРЕЛЯЦИОННАЯ МАТРИЦА R?
СИММЕТРИЧНОЙ И НЕОТРИЦАТЕЛЬНО ОПРЕДЕЛЕННОЙ
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
СИММЕТРИЧНОЙ И ОТРИЦАТЕЛЬНО ОПРЕДЕЛЕННОЙ
СИММЕТРИЧНОЙ И ПОЛОЖИТЕЛЬНО ОПРЕДЕЛЕННОЙ
СИММЕТРИЧНОЙ И НЕПОЛЖИТЕЛЬНО ОПРЕДЕЛЕННОЙ
20 КОЭФФИЦИЕНТЫ КОРРЕЛЯЦИИ КАКОГО ПОРЯДКА СОДЕРЖАТСЯ В КОРРЕЛЯЦИОННОЙ МАТРИЦЕ R?
НУЛЕВОГО
ПЕРВОГО
ВТОРОГО
ПРИ НОРМАЛЬНОМ ЗАКОНЕ РАСПРЕДЕЛЕНИЯ - ПЕРВОГО
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
21 КАКОЙ ПОРЯДОК ИМЕЕТ ЧАСТНЫЙ КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ r12/456?
ТРЕТИЙ
ПЕРВЫЙ
ВТОРОЙ
НУЛЕВОЙ
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
22 КАК СООТНОСЯТСЯ КОЭФФИЦИЕНТЫ ДЕТЕРМИНАЦИИ 1/2 И 1/234
1/2 НЕ БОЛЕЕ 1/234
1/2 БОЛЬШЕ 1/234
1/2 МЕНЬШЕ 1/234
1/2 НЕ МЕНЕЕ 1/234
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
23 ЧЕМУ РАВНО ЗНАЧЕНИЕ КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ НЕЗАВИСИМЫХ СЛУЧАЙНЫХ ВЕЛИЧИН?
0
1
НУЛЮ, ЕСЛИ РАСПРЕДЕЛЕНИЕ СЛУЧАЙНЫХ ВЕЛИЧИН ПОДЧИНЕНО НОРМАЛЬНОМУ ЗАКОНУ
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
24 КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ ДВУХ НОРМАЛЬНО РАСПРЕДЕЛЕННЫХ СЛУЧАЙНЫХ ВЕЛИЧИН РАВЕН НУЛЮ. МОЖНО УТВЕРЖДАТЬ, ЧТО СЛУЧАЙНЫЕ ВЕЛИЧИНЫ НЕЗАВИСИМЫ?
ДА, СЛУЧАЙНЫЕ ВЕЛИЧИНЫ НЕЗАВИСИМЫ
НЕТ, СЛУЧАЙНЫЕ ВЕЛИЧИНЫ НЕЛЬЗЯ СЧИТАТЬ НЕЗАВИСИМЫМИ
НЕ ХВАТАЕТ ДАННЫХ ДЛЯ ОТВЕТА
25 УРОВЕНЬ ЗНАЧИМОСТИ, НАЗНАЧЕННЫЙ ИССЛЕДОВАТЕЛЕМ РАВЕН 0,05. КОРРЕЛЯЦИОННАЯ МАТРИЦА, ВЫЧИСЛЕННАЯ СРЕДСТВАМИ ППП STATGRAPHICS ИМЕЕТ ВИД (НАЖМИТЕ КНОПКУ ПРОСМОТРА). МОЖНО СЧИТАТЬ, ЧТО ИМЕЕТ МЕСТО КОРРЕЛИРОВАННОСТЬ СЛУЧАЙНЫХ ВЕЛИЧИН VAR1 И VAR2?

ДА
НЕТ
ДА, ЕСЛИ VAR1 И VAR2 РАСПРЕДЕЛЕНЫ ПО НОРМАЛЬНОМУ ЗАКОНУ
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
26 УРОВЕНЬ ЗНАЧИМОСТИ, НАЗНАЧЕННЫЙ ИССЛЕДОВАТЕЛЕМ РАВЕН 0,05. КОРРЕЛЯЦИОННАЯ МАТРИЦА, ВЫЧИСЛЕННАЯ СРЕДСТВАМИ ППП STATGRAPHICS ИМЕЕТ ВИД (НАЖМИТЕ КНОПКУ ПРОСМОТРА). КАКОВА ТЕНДЕНЦИЯ ВЗАИМНОГО ИЗМЕНЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН VAR1 И VAR2?

ПРИ УВЕЛИЧЕНИИ VAR1 НАБЛЮДАЕТСЯ ТЕНДЕНЦИЯ УВЕЛИЧЕНИЯ VAR2
ПРИ УВЕЛИЧЕНИИ VAR1 НАБЛЮДАЕТСЯ ТЕНДЕНЦИЯ УМЕНЬШЕНИЯ VAR2
ОТСУТСТВУЕТ КОРРЕЛЯЦИЯ СЛУЧАЙНЫХ ВЕЛИЧИН VAR1 И VAR2
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
27 УРОВЕНЬ ЗНАЧИМОСТИ, НАЗНАЧЕННЫЙ ИССЛЕДОВАТЕЛЕМ РАВЕН 0,05. КОРРЕЛЯЦИОННАЯ МАТРИЦА, ВЫЧИСЛЕННАЯ СРЕДСТВАМИ ППП STATGRAPHICS ИМЕЕТ ВИД (НАЖМИТЕ КНОПКУ ПРОСМОТРА). КАКОВА ТЕНДЕНЦИЯ ВЗАИМНОГО ИЗМЕНЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН VAR1 И VAR2?

ОТСУТСТВУЕТ КОРРЕЛЯЦИЯ СЛУЧАЙНЫХ ВЕЛИЧИН VAR1 И VAR2
ПРИ УВЕЛИЧЕНИИ VAR1 НАБЛЮДАЕТСЯ ТЕНДЕНЦИЯ УМЕНЬШЕНИЯ VAR2
ПРИ УВЕЛИЧЕНИИ VAR1 НАБЛЮДАЕТСЯ ТЕНДЕНЦИЯ УВЕЛИЧЕНИЯ VAR2
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
28 УРОВЕНЬ ЗНАЧИМОСТИ, НАЗНАЧЕННЫЙ ИССЛЕДОВАТЕЛЕМ РАВЕН 0,05. КОРРЕЛЯЦИОННАЯ МАТРИЦА, ВЫЧИСЛЕННАЯ СРЕДСТВАМИ ППП STATGRAPHICS ИМЕЕТ ВИД (НАЖМИТЕ КНОПКУ ПРОСМОТРА). КАКОВА ТЕНДЕНЦИЯ ВЗАИМНОГО ИЗМЕНЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН VAR1 И VAR2?

ПРИ УВЕЛИЧЕНИИ VAR1 НАБЛЮДАЕТСЯ ТЕНДЕНЦИЯ УМЕНЬШЕНИЯ VAR2
ОТСУТСТВУЕТ КОРРЕЛЯЦИЯ СЛУЧАЙНЫХ ВЕЛИЧИН VAR1 И VAR2
ПРИ УВЕЛИЧЕНИИ VAR1 НАБЛЮДАЕТСЯ ТЕНДЕНЦИЯ УВЕЛИЧЕНИЯ VAR2
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
29 УРОВЕНЬ ЗНАЧИМОСТИ, НАЗНАЧЕННЫЙ ИССЛЕДОВАТЕЛЕМ РАВЕН 0,05. КОРРЕЛЯЦИОННАЯ МАТРИЦА, ВЫЧИСЛЕННАЯ СРЕДСТВАМИ ППП STATGRAPHICS ИМЕЕТ ВИД (НАЖМИТЕ КНОПКУ ПРОСМОТРА). МОЖНО ЛИ УТВЕРЖДАТЬ О НАЛИЧИИ ИЛИ ОТСУТСТВИИ ЗАВИСИМОСТИ МЕЖДУ VAR1 И VAR2?

НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
ДА СУЩЕСТВУЕТ ЗАВИСИМОСТЬ МЕЖДУ VAR1 И VAR2
ЗАВИСИМОСТЬ МЕЖДУ VAR1 И VAR2 ОТСУТСТВУЕТ
30 ДОПУСТИМЫ ЛИ В КОРРЕЛЯЦИОННОМ АНАЛИЗЕ ОШИБКИ В ИЗМЕРЕНИЯХ ИССЛЕДУЕМЫХ СЛУЧАЙНЫХ ВЕЛИЧИН?
ДА
ДА, ЕСЛИ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ РАСПРЕДЕЛЕНЫ НОРМАЛЬНО
НЕТ
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
31 ЧТО ЯВЛЯЕТСЯ ЦЕЛЬЮ КЛАСТЕРНОГО АНАЛИЗА?
ОБРАЗОВАНИЕ ГРУПП СХОЖИХ МЕЖДУ СОБОЙ ОБЪЕКТОВ
УПОРЯДОЧЕНИЕ ОБЪЕКТОВ
ОПРЕДЕЛЕНИЕ ПРИНАДЛЕЖНОСТИ ОБЪЕКТА К КАКОЙ-ЛИБО СУЩЕСТВУЮЩЕЙ ГРУППЕ
ОЦЕНИВАНИЕ ПАРАМЕТРОВ ОБЪЕКТОВ
ИЗМЕНЕНИЕ СВОЙСТВ ОБЪЕКТОВ
32 КАКАЯ МЕРА РАССТОЯНИЯ МЕЖДУ ОБЪЕКТАМИ В КЛАСТЕРНОМ АНАЛИЗЕ ЯВЛЯЕТСЯ ГЕОМЕТРИЧЕСКИМ РАССТОЯНИЕМ МЕЖДУ ТОЧКАМИ В МНОГОМЕРНОМ ПРОСТРАНСТВЕ?
ЕВКЛИДОВО РАССТОЯНИЕ
КВАДРАТ ЕВКЛИДОВА РАССТОЯНИЯ
ВЗВЕШЕННОЕ ЕВКЛИДОВО РАССТОЯНИЕ
МАНХЭТТЕНСКОЕ РАССТОЯНИЕ
РАССТОЯНИЕ МАХАЛАНОБИСА
33 КАКАЯ МЕРА РАССТОЯНИЯ МЕЖДУ ОБЪЕКТАМИ В КЛАСТЕРНОМ АНАЛИЗЕ ОПРЕДЕЛЯЕТСЯ СУММОЙ МОДУЛЕЙ РАЗНОСТЕЙ МЕЖДУ ТОЧКАМИ В МНОГОМЕРНОМ ПРОСТРАНСТВЕ?
МАНХЭТТЕНСКОЕ РАССТОЯНИЕ
ЕВКЛИДОВО РАССТОЯНИЕ
КВАДРАТ ЕВКЛИДОВА РАССТОЯНИЯ
ВЗВЕШЕННОЕ ЕВКЛИДОВО РАССТОЯНИЕ
РАССТОЯНИЕ МАХАЛАНОБИСА
34 КАКАЯ МЕРА РАССТОЯНИЯ МЕЖДУ ОБЪЕКТАМИ В КЛАСТЕРНОМ АНАЛИЗЕ ОПРЕДЕЛЯЕТСЯ С ИСПОЛЬЗОВАНИЕМ ОБРАТНОЙ КОВАРИАЦИОННОЙ МАТРИЦЫ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ?
РАССТОЯНИЕ МАХАЛАНОБИСА
МАНХЭТТЕНСКОЕ РАССТОЯНИЕ
ЕВКЛИДОВО РАССТОЯНИЕ
КВАДРАТ ЕВКЛИДОВА РАССТОЯНИЯ
ВЗВЕШЕННОЕ ЕВКЛИДОВО РАССТОЯНИЕ
35 В КЛАСТЕРНОМ АНАЛИЗЕ РЕКОМЕНДУЮТ НОРМИРОВАНИЕ ЗНАЧЕНИЙ ПРИЗНАКОВ. ДЛЯ ЧЕГО?
ДЛЯ ИСКЛЮЧЕНИЯ ЗАВИСИМОСТИ ОЦЕНКИ СХОДСТВА МЕЖДУ ОБЪЕКТАМИ ОТ АБСОЛЮТНЫХ ЗНАЧЕНИЙ И ВАРИАЦИИ ПРИЗНАКОВ
ДЛЯ УЛУЧШЕНИЯ УСЛОВИЙ СХОДИМОСТИ ПРИ КЛАССИФИКАЦИИ
ДЛЯ ОБЪЕДИНЕНИЯ В ОДНУ ГРУППУ КАК МОЖНО БОЛЬШЕГО ЧИСЛА ОБЪЕКТОВ
ДЛЯ ОБЕСПЕЧЕНИЯ НАИБОЛЬШЕГО РАЗЛИЧИЯ МЕЖДУ ОБЪЕКТАМИ
ДЛЯ УПРОЩЕНИЯ ВЫЧИСЛИТЕЛЬНЫХ ПРОЦЕДУР КЛАССИФИКАЦИИ
36 В КАКИХ МЕТОДАХ КЛАСТЕРНОГО АНАЛИЗА ПРОЦЕДУРА КЛАСТЕРИЗАЦИИ ЗАКАНЧИВАЕТСЯ ОБРАЗОВАНИЕМ ОДНОГО КЛАСТЕРА?
В ИЕРАРХИЧЕСКИХ АГЛОМЕРАТИВНЫХ
В ИЕРАРХИЧЕСКИХ ДИВИЗИМНЫХ
В ИЕРАРХИЧЕСКИХ ПАРАМЕТРИЧЕСКИХ
В ИЕРАРХИЧЕСКИХ ОБЪЕКТНО-ОРИЕНТИРОВАННЫХ
37 В КАКИХ МЕТОДАХ КЛАСТЕРНОГО АНАЛИЗА ПРОЦЕДУРА КЛАСТЕРИЗАЦИИ ЗАКАНЧИВАЕТСЯ ОБРАЗОВАНИЕМ КЛАСТЕРОВ СОДЕРЖАЩИХ ТОЛЬКО ПО ОДНОМУ ОБЪЕКТУ?
В ИЕРАРХИЧЕСКИХ ДИВИЗИМНЫХ
В ИЕРАРХИЧЕСКИХ АГЛОМЕРАТИВНЫХ
В ИЕРАРХИЧЕСКИХ ПАРАМЕТРИЧЕСКИХ
В ИЕРАРХИЧЕСКИХ ОБЪЕКТНО-ОРИЕНТИРОВАННЫХ
38 КАКОЙ ИЗ АЛГОРИТМОВ ИСПОЛЬЗУЕТСЯ ДЛЯ ВКЛЮЧЕНИЯ НОВОГО ОБЪЕКТА В КЛАСТЕР?
МЕТОД УОРДА
МЕТОД БЛИЖАЙШЕГО СОСЕДА
МЕТОД ДАЛЬНЕГО СОСЕДА
МЕТОД МЕДИАННОЙ СВЯЗИ
39 КАКОЙ ИЗ АЛГОРИТМОВ ИСПОЛЬЗУЕТСЯ ДЛЯ ОБЪЕДИНЕНИЯ КЛАСТЕРОВ?
МЕТОД МЕДИАННОЙ СВЯЗИ
МЕТОД УОРДА
МЕТОД ПОЛНЫХ СВЯЗЕЙ
МЕТОД ОДИНОЧНОЙ СВЯЗИ
40 ПРИ КЛАСТЕРНОМ АНАЛИЗЕ БЫЛИ ПРОНОРМИРОВАНЫ ЗНАЧЕНИЯ ПРИЗНАКОВ. УКАЖИТЕ ЗНАЧЕНИЯ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ И ДИСПЕРСИИ ЭТИХ ПРИЗНАКОВ
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ РАВНО 0, ДИСПЕРСИЯ РАВНА 1
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ РАВНО 1, ДИСПЕРСИЯ РАВНА 0
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ РАВНО 1, ДИСПЕРСИЯ РАВНА 1
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ РАВНО 0, ДИСПЕРСИЯ РАВНА 0
41 КАКОЙ ЯВЛЯЕТСЯ МАТРИЦА РАССТОЯНИЙ ПРИ ПРИМЕНЕНИИ АГЛОМЕРАТИВНОГО МЕТОДА КЛАССИФИКАЦИИ?
СИММЕТРИЧНОЙ
ДИАГОНАЛЬНОЙ
ПРЯМОУГОЛЬНОЙ
ТРЕУГОЛЬНОЙ
ЕДИНИЧНОЙ
42 ОТ ЧЕГО ЗАВИСИТ РЕЗУЛЬТАТ КЛАССИФИКАЦИИ?
ТОЛЬКО ОТ МЕТОДА КЛАССИФИКАЦИИ, ПРИМЕНЯЕМОЙ МЕТРИКИ И НОРМАЛИЗАЦИИ
ТОЛЬКО ОТ ПРИМЕНЯЕМОЙ МЕТРИКИ И НОРМАЛИЗАЦИИ
ТОЛЬКО ОТ МЕТОДА КЛАССИФИКАЦИИ И НОРМАЛИЗАЦИИ
ТОЛЬКО ОТ МЕТОДА КЛАССИФИКАЦИИ И ПРИМЕНЯЕМОЙ МЕТРИКИ
43 К ГРУППЕ КАКИХ МЕТОДОВ КЛАСТЕРИЗАЦИИ ОТНОСИТСЯ МЕТОД k-СРЕДНИХ?
К ИТЕРАТИВНЫМ
К ИЕРАРХИЧЕСКИМ АГЛОМЕРАТИВНЫМ
К ИЕРАРХИЧЕСКИМ ДИВИЗИМНЫМ
К МЕТОДУ ПОИСКА СГУЩЕНИЙ
44 МЕТОДОМ k-СРЕДНИХ НЕОБХОДИМО МНОЖЕСТВО ОБЪЕКТОВ РАЗДЕЛИТЬ НА ТРИ ГРУППЫ. сКОЛЬКО КЛАСТЕРОВ БУДЕТ ОБРАЗОВАНО ПО ЗАВЕРШЕНИИ КЛАСТЕРИЗАЦИИ?
3
1
2
4
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
45 ПРИ ИСПОЛЬЗОВАНИИ В КЛАСТЕРНОМ АНАЛИЗЕ МЕТОДА СГУЩЕНИЙ НЕОБХОДИМО УКАЗЫВАТЬ НАЧАЛЬНОЕ КОЛИЧЕСТВО КЛАСТЕРОВ?
НЕТ
ДА
ДА, НАЧАЛЬНОЕ КОЛИЧЕСТВО КЛАСТЕРОВ ВСЕГДА ДОЛЖНО БЫТЬ РАВНО ДВУМ
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
46 ЧЕМ ЯВЛЯЕТСЯ МЕРА КАЧЕСТВА КЛАССИФИКАЦИИ ОБЪЕКТОВ?
ФУНКЦИОНАЛОМ
ФУНКЦИЕЙ
ПЕРЕМЕННОЙ
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
47 ЗНАЧЕНИЕ МЕРЫ КАЧЕСТВА КЛАССИФИКАЦИИ
ВСЕГДА НЕОТРИЦАТЕЛЬНО
ВСЕГДА ПОЛОЖИТЕЛЬНО
ВСЕГДА НЕПОЛОЖИТЕЛЬНО
ВСЕГДА ОТРИЦАТЕЛЬНО
48 ЧЕМУ РАВНО ЗНАЧЕНИЕ МЕРЫ КАЧЕСТВА КЛАССИФИКАЦИИ ПО СУММАРНОЙ ОЦЕНКЕ ДИСПЕРСИИ?

8
4
16
20
49 ЧЕМУ РАВНО ЗНАЧЕНИЕ МЕРЫ КАЧЕСТВА КЛАССИФИКАЦИИ ПО СУММЕ ВНУТРИКЛАССОВЫХ РАССТОЯНИЙМЕЖДУ ОБЪЕКТАМИ?

16
8
4
20
50 ЧЕМУ РАВНО ЗНАЧЕНИЕ МЕРЫ КАЧЕСТВА КЛАССИФИКАЦИИ ПО СУММЕ КВАДРАТОВ РАССТОЯНИЙ ДО ЦЕНТРОВ КЛАССОВ?

8
4
16
20
51 ДИСКРИМИНАНТНЫЙ АНАЛИЗ ПРЕДПОЛАГАЕТ ПРЕДВАРИТЕЛЬНОЕ РАЗБИЕНИЕ НА КЛАССЫ?
ДА
НЕТ
ДА, НО ТОЛЬКО ПРИ БОЛЬШОМ КОЛИЧЕСТВЕ НАБЛЮДЕНИЙ
В ЗАВИСИМОСТИ ОТ ЗАКОНА РАСПРЕДЕЛЕНИЯ ПЕРЕМЕННЫХ
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
52 В КАКОМ СООТНОШЕНИИ ДОЛЖНЫ БЫТЬ ЧИСЛО ПАР ДИСКРИМИНАНТНЫХ ПЕРЕМЕННЫХ p И КОЛИЧЕСТВО НАБЛЮДЕНИЙ n?
p
p>n
p=n
В ЛЮБОМ СООТНОШЕНИИ
53 КАКОМУ ЗАКОНУ РАСПРЕДЕЛЕНИЯ ДОЛЖНЫ ПОДЧИНЯТЬСЯ ДИСКРИМИНАНТНЫЕ ПЕРЕМЕННЫЕ?
НОРМАЛЬНОМУ
ПИРСОНА
РАВНОМЕРНОМУ
ЛЮБОМУ
54 ИМЕЕТСЯ НОВЫЙ ОБЪЕКТ (НАБЛЮДЕНИЕ). С ПОМОЩЬЮ ЧЕГО ОПРЕДЕЛЯЕТСЯ ПРИНАДЛЕЖНОСТЬ ОБЪЕКТА К ТОМУ ИЛИ ИНОМУ КЛАССУ?
ФУНКЦИИ КЛАССИФИКАЦИИ
КАНОНИЧЕСКОЙ ДИСКРИМИНАНТНОЙ ПЕРЕМЕННОЙ
ДИСКРИМИНАНТНОЙ ФУНКЦИИ
КОНСТАНТЫ ДИСКРИМИНАЦИИ
55 КАКОМУ ЗАКОНУ РАСПРЕДЕЛЕНИЯ В ДИСКРИМИНАНТНОМ АНАЛИЗЕ ДОЛЖНЫ ПОДЧИНЯТЬСЯ ПОДВЕКТОРЫ (КЛАССЫ) СЛУЧАЙНОГО ВЕКТОРА X?
НОРМАЛЬНОМУ
ПИРСОНА
РАВНОМЕРНОМУ
ЛЮБОМУ
56 В КАКОМ СЛУЧАЕ В ДИСКРИМИНАНТНОМ АНАЛИЗЕ ПО АБСОЛЮТНОМУ ЗНАЧЕНИЮ ОЦЕНКИ КОЭФФИЦИЕНТА МОЖНО СУДИТЬ О ВКЛАДЕ СООТВЕТСТВУЮЩЕЙ ДИСКРИМИНАНТНОЙ ПЕРЕМЕННОЙ ВЗНАЧЕНИЕ ДИСКРИМИНАНТНОЙ ФУНКЦИИ?
КОГДА КОЭФФИЦИЕНТЫ СТАНДАРТИЗОВАНЫ
КОГДА ЧИСЛО КОЭФФИЦИЕНТОВ НЕ БОЛЕЕ ДВУХ
В ЛЮБОМ
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
57 СКОЛЬКО ФУНКЦИЙ КЛАССИФИКАЦИИ В ДИСКРИМИНАНТНОМ АНАЛИЗЕ НЕОБХОДИМО ПОСТРОИТЬ ПРИ НАЛИЧИИ ТРЕХ КЛАССОВ?
3
2
1
4
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
58 СКОЛЬКО В ДИСКРИМИНАНТНОМ АНАЛИЗЕ НЕОБХОДИМО ПОСТРОИТЬ ДИСКРИМИНАНТНЫХ ФУНКЦИЙ ПРИ НАЛИЧИИ ТРЕХ КЛАССОВ?
2
1
3
4
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
59 ПРИ ПОСТРОЕНИИ РЕГРЕССИОННОЙ МОДЕЛИ ДОЛЖНЫ ВЫПОЛНЯТЬСЯ ОПРЕДЕЛЕННЫЕ ПРЕДПОСЫЛКИ. ДОПУСТИМО ИЗМЕНЕНИЕ ДИСПЕРСИИ ВОЗМУЩЕНИЙ ПРИ ИЗМЕНЕНИИ ЗНАЧЕНИЙ ВХОДНЫХ ПЕРЕМЕННЫХ?
НЕТ
ДА
НЕТ, НО ТОЛЬКО ПРИ ПОСТРОЕНИИ ЛИНЕЙНОЙ РЕГРЕССИИ
ДА, ЕСЛИ ВХОДНЫЕ ПЕРЕМЕННЫЕ НЕ КОРРЕЛИРУЮТ ДРУГ С ДРУГОМ
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
60 ПРИ ПОСТРОЕНИИ РЕГРЕССИОННОЙ МОДЕЛИ ДОЛЖНЫ ВЫПОЛНЯТЬСЯ ОПРЕДЕЛЕННЫЕ ПРЕДПОСЫЛКИ. ДОПУСТИМА КОРРЕЛИРОВАННОСТЬ ВОЗМУЩЕНИЙ ПРИ ИЗМЕНЕНИИ ЗНАЧЕНИЙ ВХОДНЫХ ПЕРЕМЕННЫХ?
НЕТ
ДА
НЕТ, НО ТОЛЬКО ПРИ ПОСТРОЕНИИ ЛИНЕЙНОЙ РЕГРЕССИИ
ДА, ЕСЛИ ВХОДНЫЕ ПЕРЕМЕННЫЕ НЕ КОРРЕЛИРУЮТ ДРУГ С ДРУГОМ
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
61 УРАВНЕНИЕ ОДНОМЕРНОЙ (ПРОСТОЙ) РЕГРЕСИИ ЭТО:
ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ МЕЖДУ МАТЕМАТИЧЕСКИМ ОЖИДАНИЕМ СЛУЧАЙНОЙ ВЕЛИЧИНЫ И НЕСЛУЧАЙНОЙ ВЕЛИЧИНОЙ
ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ МЕЖДУ ДВУМЯ СЛУЧАЙНЫМИ ВЕЛИЧИНАМИ
ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ МЕЖДУ СЛУЧАЙНОЙ И НЕСЛУЧАЙНЫМИ ВЕЛИЧИНАМИ
ЛЮБАЯ ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ ДВУХ НЕСЛУЧАЙНЫХ ВЕЛИЧИН
ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ МЕЖДУ ДВУМЯ НОРМАЛЬНО РАСПРЕДЕЛЕННЫМИ СЛУЧАЙНЫМИ ВЕЛИЧИНАМИ
62 УРОВЕНЬ ЗНАЧИМОСТИ РАВЕН 0,02. ПРИ ПОСТРОЕНИИ РЕГРЕССИОННОЙ МОДЕЛИ ВИДА: Y = A + B*X. РЕЗУЛЬТАТЫ ОЦЕНИВАНИЯ ПРЕДСТАВЛЕНЫ В ТАБЛИЦЕ (ЩЕЛКНИТЕ КНОПКУ ПРОСМОТРА). УКАЖИТЕ КАКОГО ВИДА МОДЕЛЬ ВЫ БУДЕТЕ ИССЛЕДОВАТЬ В ДАЛЬНЕЙШЕМ
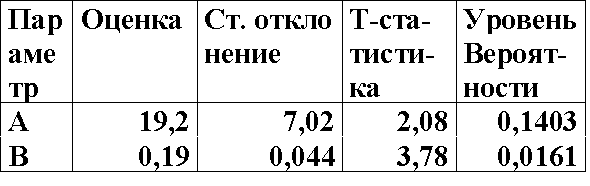
Y=B*X
Y=A+B*X
Y=A
ТАКОГО ВИДА МОДЕЛЬ ОТСУТСТВУЕТ
63 ПОСТРОЕНА РЕГРЕССИОННАЯ МОДЕЛЬ ВИДА: Y = 2,5 + 1,5*X ЧЕМУ РАВНО ЗНАЧЕНИЕ ТОЧЕЧНОГО ПРОГНОЗА ПРИ X=3
7
4,5
3,5
8,5
6
64 ОПРЕДЕЛЕНА РЕГРЕССИОННАЯ МОДЕЛЬ ВИДА: Y = 1,2*X2 + 10,6*X - 16,4 В СОВМЕСТНЫХ НАБЛЮДЕНИЯХ ПЕРЕМЕННЫХ X И Y ПЕРЕМЕННАЯ X ИЗМЕНЯЛАСЬ В ПРЕДЕЛАХ ОТ 5 ДО 10. МОЖНО ЛИ ИСПОЛЬЗОВАТЬ МОДЕЛЬ ДЛЯ ПРОГНОЗИРОВАНИЯ ПРИ ЗНАЧЕНИИ НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ X = 11?
НЕТ
ДА
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
65 ПРИ ПОСТРОЕНИИ РЕГРЕССИОННОЙ МОДЕЛИ ВЫЧИСЛЯЮТСЯ ОЦЕНКИ КОЭФФИЦИЕНТОВ МОДЕЛИ. НУЖНО ЛИ ПРОВЕРЯТЬ ГИПОТЕЗЫ О РАВЕНСТВЕ НУЛЮ ИСТИННЫХ ЗНАЧЕНИЙ КОЭФФИЦИЕНТОВ?
ДА
НЕТ
НЕТ, ЕСЛИ ВОЗМУЩЕНИЯ РАСПРЕДЕЛЕНЫ ПО НОРМАЛЬНОМУ ЗАКОНУ
ДА, ЕСЛИ ВОЗМУЩЕНИЯ РАСПРЕДЕЛЕНЫ ПО ЗАКОНУ ОТЛИЧНОМУ ОТ НОРМАЛЬНОГО
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
66 ПРИ ПОСТРОЕНИИ РЕГРЕССИОННОЙ МОДЕЛИ НЕЗАВИСИМЫЕ ПЕРЕМЕННЫЕ НЕ КОРРЕЛИРУЮТ ДРУГ С ДРУГОМ. НУЖНО ЛИ ПРИ УДАЛЕНИИ НЕЗНАЧИМЫХ СОСТАВЛЯЮЩИХ ИЗ МОДЕЛИ ВНОВЬ ПЕРЕСЧИТЫВАТЬ ОЦЕНКИ КОЭФФИЦИЕНТОВ?
НЕТ
ДА
ДА, ЕСЛИ ВОЗМУЩЕНИЯ РАСПРЕДЕЛЕНЫ ПО ЗАКОНУ ОТЛИЧНОМУ ОТ НОРМАЛЬНОГО
НЕТ, ЕСЛИ ВОЗМУЩЕНИЯ РАСПРЕДЕЛЕНЫ ПО НОРМАЛЬНОМУ ЗАКОНУ
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
67 ПОСТРОЕНА РЕГРЕССИОННАЯ МОДЕЛЬ. ДОВЕРИТЕЛЬНАЯ ВЕРОЯТНОСТЬ ПРОГНОЗА РАВНА 0,95. ЧЕМУ РАВНА ВЕРОЯТНОСТЬ ТОГО, ЧТО ТОЧЕЧНЫЙ ПРОГНОЗ ПОЛУЧЕННЫЙ ПО МОДЕЛИ СОВПАДАЕТ С СОВПАДЕТ С ИСТИННЫМ ЗНАЧЕНИЕМ ВЫХОДНОЙ, ЗАВИСИМОЙ ПЕРЕМЕННОЙ?.
0
0,95
0,05
1
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
68 ЧТО ВЛИЯЕТ НА ШИРИНУ ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА ИНТЕРВАЛЬНОЙ ОЦЕНКИ ПРОГНОЗА ПО РЕГРЕССИОННОЙ МОДЕЛИ:
КОЛИЧЕСТВО НАБЛЮДЕНИЙ И ДИСПЕРСИЯ ВОЗМУЩЕНИЙ
КОЛИЧЕСТВО НАБЛЮДЕНИЙ
ДИСПЕРСИЯ ВОЗМУЩЕНИЙ
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
69 НА РИСУНКЕ (ЩЕЛКНИТЕ КНОПКУ ПРОСМОТРА) ПРИВЕДЕН ГРАФИК ЛИНИИ РЕГРЕССИИ. НАНЕСЕНЫ ЛИНИИ 95% ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА ПРОГНОЗА. УКАЖИТЕ ИНТЕРВАЛЬНУЮ ОЦЕНКУ ПРОГНОЗА ПРИ X=5.
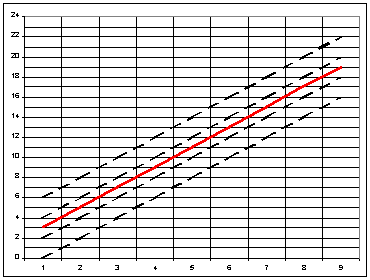
(9,15)
(11,13)
(9,13)
(11,15)
70 НА РИСУНКЕ (ЩЕЛКНИТЕ КНОПКУ ПРОСМОТРА) ПРИВЕДЕН ГРАФИК ЛИНИИ РЕГРЕССИИ. НАНЕСЕНЫ ЛИНИИ 95% ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА ПРОГНОЗА. УКАЖИТЕ ТОЧЕЧНУЮ ОЦЕНКУ ПРОГНОЗА ПРИ X=2.

6
5
7
8
71 НА РИСУНКЕ (ЩЕЛКНИТЕ КНОПКУ ПРОСМОТРА) ПРЕДСТАВЛЕНА ТАБЛИЦА РЕЗУЛЬТАТОВ ОЦЕНИВАНИЯ КОЭФФИЦИЕНТОВ МОДЕЛИ ВИДА: Y=B0+B1*X1+B2*X2+B3*X3. УРОВЕНЬ ЗНАЧИСМОСТИ РАВЕН 0,05. УКАЖИТЕ КАКОЙ ВИД МОДЕЛИ НЕОБХОДИМО РАССМОТРЕТЬ НА СЛЕДУЮЩЕМ ЭТАПЕ ИССЛЕДОВАНИЯ

Y=B1*X1+B3*X3
Y=B0+B2*X2
Y=B0+B3*X3
Y=B1*X1+B2*X2+B3*X3
72 НА РИСУНКЕ (ЩЕЛКНИТЕ КНОПКУ ПРОСМОТРА) ПРЕДСТАВЛЕНА ТАБЛИЦА РЕЗУЛЬТАТОВ ОЦЕНИВАНИЯ КОЭФФИЦИЕНТОВ МОДЕЛИ ВИДА: Y=B0+B1*X1+B2*X2+B3*X3. УРОВЕНЬ ЗНАЧИСМОСТИ РАВЕН 0,05. УКАЖИТЕ КАКОЙ ВИД МОДЕЛИ НЕОБХОДИМО РАССМОТРЕТЬ НА СЛЕДУЮЩЕМ ЭТАПЕ ИССЛЕДОВАНИЯ?

Y=B0+B3*X3
Y=B1*X1+B2*X2
Y=B0+B2*X2
Y=B0+B1*X1+B3*X3
73 ОЦЕНКИ КОЭФФИЦИЕНТОВ РЕГРЕССИОННОЙ МОДЕЛИ, ПОЛУЧЕННОЙ МЕТОДОМ ГРЕБНЕВОЙ РЕГРЕССИИ ЯВЛЯЮТСЯ СМЕЩЕННЫМИ?
ДА
НЕТ
ДА, ЕСЛИ ВОЗМУЩЕНИЯ РАСПРЕДЕЛЕНЫ ПО НОРМАЛЬНОМУ ЗАКОНУ
НЕТ, ЕСЛИ ВОЗМУЩЕНИЯ РАСПРЕДЕЛЕНЫ ПО НОРМАЛЬНОМУ ЗАКОНУ
ДА, ЕСЛИ ВХОДНЫЕ ФАКТОРЫ ИЗМЕНЯЛИСЬ НЕЗАВИСИМО
74 ЧЕМУ ДОЛЖЕН БЫТЬ РАВЕН ПАРАМЕТР ГРЕБНЕВОЙ РЕГРЕССИИ, ЧТОБЫ ОЦЕНКИ КОЭФФИЦИЕНТОВ ГРЕБНЕВОЙ РЕГРЕССИИ СОВПАДАЛИ С ОЦЕНКАМИ ОБЫЧНОЙ РЕГРЕССИИ (ОЦЕНКАМИ МНК). ЕСЛИ К - ПАРАМЕТР ГРЕБНЕВОЙ РЕГРЕСИИ, ТО ОН ДОЛЖЕН БЫТЬ РАВЕН:
0
ПАРАМЕТР К ВЫБИРАЕТСЯ ПО ГРАФИКУ ОЦЕНОК КОЭФФИЦИЕНТОВ ГРЕБНЕВОЙ РЕГРЕССИИ
1
2
ПАРАМЕТР К ДОЛЖЕН ЛЕЖАТЬ В ПРЕДЕЛАХ ОТ 0,2 ДО 0,4
75 ЧЕМУ ДОЛЖЕН БЫТЬ РАВЕН ПАРАМЕТР ГРЕБНЕВОЙ РЕГРЕССИИ, ЧТОБЫ ОЦЕНКИ КОЭФФИЦИЕНТОВ ГРЕБНЕВОЙ РЕГРЕССИИ ОБЛАДАЛИ МИНИМАЛЬНЫМ СКО. ЕСЛИ К - ПАРАМЕТР ГРЕБНЕВОЙ РЕГРЕСИИ, ТО ОН ДОЛЖЕН БЫТЬ РАВЕН:
ПАРАМЕТР К ВЫБИРАЕТСЯ ПО ГРАФИКУ ОЦЕНОК КОЭФФИЦИЕНТОВ ГРЕБНЕВОЙ РЕГРЕССИИ
0
1
2
ПАРАМЕТР К ДОЛЖЕН ЛЕЖАТЬ В ПРЕДЕЛАХ ОТ 0,2 ДО 0,4
76 МЕТОД ГЛАВНЫХ КОМПОНЕНТ ПРЕДНАЗНАЧЕН
ДЛЯ УМЕНЬШЕНИЯ РАЗМЕРНОСТИ МОДЕЛИ
ДЛЯ ФИКСИРОВАНИЯ РАЗМЕРНОСТИ МОДЕЛИ
ДЛЯ УВЕЛИЧЕНИЯ РАЗМЕРНОСТИ МОДЕЛИ
ДЛЯ ОПРЕДЕЛЕНИЯ ЗНАЧИМЫХ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
77 КАКОМУ ЗАКОНУ РАСПРЕДЕЛЕНИЯ ДОЛЖНЫ ПОДЧИНЯТЬСЯ МНОГОМЕРНЫЕ ВЕКТОРЫ В МЕТОДЕ ГЛАВНЫХ КОМПОНЕНТ?
НОРМАЛЬНОМУ
РАВНОМЕРНОМУ
ПИРСОНА
ЛЮБОМУ
78 В МЕТОДЕ ГЛАВНЫХ КОМПОНЕНТ ПЕРВАЯ ГЛАВНАЯ КОМПОНЕНТА СООТВЕТСТВУЕТ НАПРАВЛЕНИЮ, ВДОЛЬ КОТОРОГО ДИСПЕРСИЯ ВЕКТОРОВ ИСХОДНОГО НАБОРА
МАКСИМАЛЬНА
ПОСТОЯННА
МИНИМАЛЬНА
ЛЮБАЯ
79 ЧТО ЯВЛЯЕТСЯ ОЦЕНКАМИ ДИСПЕРСИЙ ГЛАВНЫХ КОМПОНЕНТ ПРИ ОТСУТСТВИИ СТАНДАРТИЗАЦИИ ДАННЫХ (МАТРИЦЫ X)?
КВАДРАТЫ СОБСТВЕННЫХ ЧИСЕЛ МАТРИЦЫ ОЦЕНОК КОВАРИАЦИЙ МНОГОМЕРНЫХ ВЕКТОРОВ
СОБСТВЕННЫЕ ЧИСЕЛА МАТРИЦЫ ОЦЕНОК КОВАРИАЦИЙ МНОГОМЕРНЫХ ВЕКТОРОВ
КОРНИ КВАДРАТНЫЕ СОБСТВЕННЫХ ЧИСЕЛ МАТРИЦЫ ОЦЕНОК КОВАРИАЦИЙ МНОГОМЕРНЫХ ВЕКТОРОВ
ЗАВИСИТ ОТ ВИДА РАСПРЕДЕЛЕНИЯ МНОГОМЕРНЫХ ВЕКТОРОВ
80 МАТРИЦА НАБЛЮДЕНИЙ МНОГОМЕРНЫХ ВЕКТОРОВ ИМЕЕТ РАЗМЕРНОСТЬ 10*5. КАКОВА РАЗМЕРНОСТЬ ОЦЕНКИ КОРРЕЛЯЦИОННОЙ МАТРИЦЫ R?
5*5
10*5
5*10
10*10
81 МАТРИЦА НАБЛЮДЕНИЙ МНОГОМЕРНЫХ ВЕКТОРОВ ИМЕЕТ РАЗМЕРНОСТЬ 10*5. СКОЛЬКО СОБСТВЕННЫХ ЧИСЕЛ И СОБСТВЕННЫХ ВЕКТОРОВ ИМЕЕТ ОЦЕНКА КОРРЕЛЯЦИОННОЙ МАТРИЦЫ R?
5 СОБСТВЕННЫХ ЧИСЕЛ И 5 СОБСТВЕННЫХ ВЕКТОРОВ
5 СОБСТВЕННЫХ ЧИСЕЛ И 10 СОБСТВЕННЫХ ВЕКТОРОВ
10 СОБСТВЕННЫХ ЧИСЕЛ И 5 СОБСТВЕННЫХ ВЕКТОРОВ
10 СОБСТВЕННЫХ ЧИСЕЛ И 10 СОБСТВЕННЫХ ВЕКТОРОВ
82 МАТРИЦА НАБЛЮДЕНИЙ МНОГОМЕРНЫХ ВЕКТОРОВ ИМЕЕТ РАЗМЕРНОСТЬ 10*5. ЧЕМУ РАВНА СУММА СОБСТВЕННЫХ ЧИСЕЛ ОЦЕНКИ КОРРЕЛЯЦИОННОЙ МАТРИЦЫ R?
5
1
10
СУММЕ ОЦЕНОК ДИСПЕРСИЙ ГЛАВНЫХ КОМПОНЕНТ
83 В КАКОМ СЛУЧАЕ СУЩЕСТВУЕТ КОРРЕЛЯЦИЯ ГЛАВНЫХ КОМПОНЕНТ
КОРРЕЛЯЦИЯ ОТСУТСТВУЕТ В ЛЮБОМ СЛУЧАЕ
ПРИ НОРМАЛЬНОМ ЗАКОНЕ РАСПРЕДЕЛЕНИЯ МНОГОМЕРНЫХ ВЕКТОРОВ
ПРИ КОРРЕЛИРОВАННОСТИ МНОГОМЕРНЫХ ВЕКТОРОВ
ПРИ РАЗМЕРНОСТИ ВЕКТОРОВ БОЛЕЕ 5
84 КАКАЯ ГИПОТЕЗА ПРОВЕРЯЕТСЯ МЕТОДОМ ОДНОФАКТОРНОГО ДИСПЕРСИОННОГО АНАЛИЗА?
О РАВЕНСТВЕ МАТЕМАТИЧЕСКИХ ОЖИДАНИЙ НЕСКОЛЬКИХ ГЕНЕРАЛЬНЫХ СОВОКУПНОСТЕЙ
О РАВЕНСТВЕ ДИСПЕРСИЙ НЕСКОЛЬКИХ ГЕНЕРАЛЬНЫХ СОВОКУПНОСТЕЙ
О РАВЕНСТВЕ ДИСПЕРСИИ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ ЗАДАННОЙ ВЕЛИЧИНЕ
О РАВЕНСТВЕ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ ЗАДАННОЙ ВЕЛИЧИНЕ
85 ПРИ ОДНОФАКТОРНОМ ДИСПЕРСИОННОМ АНАЛИЗЕ ДОЛЖНЫ ВЫПОЛНЯТЬСЯ ОПРЕДЕЛЕННЫЕ ПРЕДПОСЫЛКИ. ДОПУСТИМО ИЗМЕНЕНИЕ ДИСПЕРСИИ ВОЗМУЩЕНИЙ ПРИ ИЗМЕНЕНИИ УРОВНЯ ВХОДНОГО ФАКТОРА?
НЕТ
ДА
ДА, ЕСЛИ ВОЗМУЩЕНИЯ РАСПРЕДЕЛЕНЫ ПО НОРМАЛЬНОМУ ЗАКОНУ
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
86 КАКАЯ ИЗ ОЦЕНОК ДИСПЕРСИЙ В ОДНОФАКТРОНОМ ДИСПЕРСИОННОМ АНАЛИЗЕ ХАРАКТЕРИЗУЕТ ИЗМЕНЧИВОСТЬ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ НАБЛЮДАЕМОГО ПАРАМЕТРА ОТ УРОВНЕЙ ФАКТОРА?
ОЦЕНКА ДИСПЕРСИИ УРОВНЕЙ
ОЦЕНКА ОБЩЕЙ ДИСПЕРСИИ
ОЦЕНКА ДИСПЕРСИИ ОШИБКИ
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
87 ДЛЯ ПРОВЕРКИ СТАТИСТИЧЕСКОЙ ГИПОТЕЗЫ О РАВЕНСТВЕ ЦЕН НА ПРОДУКЦИЮ ТРЕХ ФИРМ БЫЛ ИСПОЛЬЗОВАН ОДНОФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ. НА РИСУНКЕ (ЩЕЛКНИТЕ КНОПКУ ПРОСМОТРА) ПРЕДСТАВЛЕНА ТАБЛИЦА РЕЗУЛЬТАТОВ УРОВЕНЬ ЗНАЧИМОСТИ РАВЕН 0,05. МОЖНО УТВЕРЖДАТЬ, ЧТО ДАННЫЕ НЕПРОТИВОРЕЧАТ ГИПОТЕЗЕ?
ДА, ДАННЫЕ НЕПРОТИВОРЕЧАТ ГИПОТЕЗЕ
НЕТ, ДАННЫЕ ПРОТИВОРЕЧАТ ГИПОТЕЗЕ
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
88 КАКАЯ ГИПОТЕЗА ПРОВЕРЯЕТСЯ МЕТОДОМ ДВУХФАКТОРНОГО ДИСПЕРСИОННОГО АНАЛИЗА?
О РАВЕНСТВЕ МАТЕМАТИЧЕСКИХ ОЖИДАНИЙ НЕСКОЛЬКИХ ГЕНЕРАЛЬНЫХ СОВОКУПНОСТЕЙ ПРИ РАЗЛИЧНЫХ УРОВНЯХ ФАКТОРОВ
О РАВЕНСТВЕ ДИСПЕРСИЙ НЕСКОЛЬКИХ ГЕНЕРАЛЬНЫХ СОВОКУПНОСТЕЙ ПРИ РАЗЛИЧНЫХ УРОВНЯХ ФАКТОРОВ
О РАВЕНСТВЕ ДИСПЕРСИЙ НЕСКОЛЬКИХ ГЕНЕРАЛЬНЫХ СОВОКУПНОСТЕЙ ЗАДАННОЙ ВЕЛИЧИНЕ ПРИ РАЗЛИЧНЫХ УРОВНЯХ ФАКТОРОВ
О РАВЕНСТВЕ МАТЕМАТИЧЕСКИХ ОЖИДАНИЙ НЕСКОЛЬКИХ ГЕНЕРАЛЬНЫХ СОВОКУПНОСТЕЙ ЗАДАННОЙ ВЕЛИЧИНЕ ПРИ РАЗЛИЧНЫХ УРОВНЯХ ФАКТОРОВ
89 ПРИ ДВУХФАКТОРНОМ ДИСПЕРСИОННОМ АНАЛИЗЕ ДОЛЖНЫ ВЫПОЛНЯТЬСЯ ОПРЕДЕЛЕННЫЕ ПРЕДПОСЫЛКИ. ДОПУСТИМО ИЗМЕНЕНИЕ ДИСПЕРСИИ ВОЗМУЩЕНИЙ ПРИ ИЗМЕНЕНИИ УРОВНЕЙ ВХОДНЫХ ФАКТОРОВ?
НЕТ
ДА
ДА, ЕСЛИ ВОЗМУЩЕНИЯ РАСПРЕДЕЛЕНЫ ПО НОРМАЛЬНОМУ ЗАКОНУ
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
90 ЧИСЛО УРОВНЕЙ ПЕРВОГО ФАКТОРА РАВНО 5, ВТОРОГО РАВНО 6. ЧЕМУ РАВНО ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ ОЦЕНКИ ДИСПЕРСИИ УРОВНЕЙ ПЕРВОГО ФАКТОРА?
4
2
3
5
91 ЧИСЛО УРОВНЕЙ ПЕРВОГО ФАКТОРА РАВНО 5, ВТОРОГО РАВНО 6. ЧЕМУ РАВНО ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ ОЦЕНКИ ДИСПЕРСИИ УРОВНЕЙ ВТОРОГО ФАКТОРА?
5
2
3
4
92 МЕТОД ГЛАВНЫХ КОМПОНЕНТ ПРЕДПОЛАГАЕТ НЕЗАВИСИМОСТЬ ЭТИХ КОМПОНЕНТ?
ДА
НЕТ
ДА, ЕСЛИ КОЛИЧЕСТВО КОМПОНЕНТ НЕ БОЛЕЕ 3
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
93 КАКАЯ МАТРИЦА В ФАКТОРНОМ АНАЛИЗЕ ИСПОЛЬЗУЕТСЯ ДЛЯ ОПРЕДЕЛЕНИЯ МАТРИЦЫ ЗНАЧЕНИЙ ФАКТОРОВ?
КОРРЕЛЯЦИОННАЯ МАТРИЦА ИСХОДНЫХ НАБЛЮДЕНИЙ
ЕДИНИЧНАЯ МАТРИЦА
ОБРАТНАЯ МАТРИЦА ИСХОДНЫХ НАБЛЮДЕНИЙ
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
94 В ФАКТОРНОМ АНАЛИЗЕ МАТРИЦА ФАКТОРНЫХ НАГРУЗОК ДИАГОНАЛЬНА?
НЕТ
ДА
ДА, ЕСЛИ ФАКТОРОВ НЕ БОЛЕЕ 3-х
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
95 В ФАКТОРНОМ АНАЛИЗЕ МАТРИЦА ФАКТОРНЫХ НАГРУЗОК СИММЕТРИЧНА?
ДА
НЕТ
ДА, ЕСЛИ КОЛИЧЕСТВО ФАКТОРОВ НЕ БОЛЕЕ 3-х
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
96 В ФАКТОРНОМ АНАЛИЗЕ ДОПУСТИМА КОРРЕЛЯЦИЯ ФАКТОРОВ?
ДА
НЕТ
ДА, ЕСЛИ КОЛИЧЕСТВО ФАКТОРОВ НЕ БОЛЕЕ 3-х
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
97 ФАКТОРНЫЙ АНАЛИЗ УЧИТЫВАЕТ ОШИБКУ МОДЕЛИРОВАНИЯ ДЛЯ КАЖДОЙ ИЗ НАБЛЮДАЕМЫХ ПЕРЕМЕННЫХ?
ДА
НЕТ
В ЗАВИСИМОСТИ ОТ ЗАКОНА РАСПРЕДЕЛЕНИЯ НАБЛЮДАЕМЫХ ПЕРЕМЕННЫХ
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
98 В ФАКТОРНОМ АНАЛИЗЕ НАБЛЮДАЕМЫЕ ПЕРЕМЕННЫЕ ЯВЛЯЮТСЯ
ЛИНЕЙНЫМИ КОМБИНАЦИЯМИ ОБЩИХ И СПЕЦИФИЧЕСКИХ ФАКТОРОВ
ЛИНЕЙНЫМИ КОМБИНАЦИЯМИ ОБЩИХ ФАКТОРОВ
ЛИНЕЙНЫМИ КОМБИНАЦИЯМИ СПЕЦИФИЧЕСКИХ ФАКТОРОВ
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
99 В КАКОМ СЛУЧАЕ МЕТОД ГЛАВНЫХ КОМПОНЕНТ МОЖНО РАССМАТРИВАТЬ КАК ЧАСТНЫЙ СЛУЧАЙ ФАКТОРНОГГО АНАЛИЗА?
КОГДА ВСЕ СПЕЦИФИЧЕСКИЕ ФАКТОРЫ РАВНЫ НУЛЮ И ОБЩИЕ ФАКТОРЫ ОРТОГОНАЛЬНЫ
КОГДА ВСЕ СПЕЦИФИЧЕСКИЕ ФАКТОРЫ РАВНЫ НУЛЮ
КОГДА ОБЩИЕ ФАКТОРЫ ОРТОГОНАЛЬНЫ
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
100 В ФАКТОРНОМ АНАЛИЗЕ ГЕНЕРАЛЬНЫМ ФАКТОРОМ НАЗЫВАЕТСЯ ФАКТОР, У КОТОРОГО ВСЕ НАГРУЗКИ ЗНАЧИМЫ?
ДА
НЕТ
ЕСЛИ ЗНАЧИМА ХОТЯ БЫ ОДНА НАГРУЗКА
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
101 МЕТОД КАНОНИЧЕСКИХ КОРРЕЛЯЦИЙ ПРЕДНАЗНАЧЕН ДЛЯ:
ОПРЕДЕЛЕНИЯ МАКСИМАЛЬНЫХ КОРРЕЛЯЦИОННЫХ СВЯЗЕЙ МЕЖДУ ДВУМЯ ГРУППАМИ СЛУЧАЙНЫХ ВЕЛИЧИН
ОПРЕДЕЛЕНИЯ МАКСИМАЛЬНЫХ КОРРЕЛЯЦИОННЫХ СВЯЗЕЙ МЕЖДУ ЛЮБЫМ КОЛИЧЕСТВОМ ГРУПП СЛУЧАЙНЫХ ВЕЛИЧИН
ОПРЕДЕЛЕНИЯ МАКСИМАЛЬНЫХ КОРРЕЛЯЦИОННЫХ СВЯЗЕЙ ВНУТРИ ВЫДЕЛЕННОЙ ГРУППЫ СЛУЧАЙНЫХ ВЕЛИЧИН
ОПРЕДЕЛЕНИЯ МАКСИМАЛЬНОЙ КОРРЕЛЯЦИИ ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИН
102 ИСХОДНЫЙ ВЕКТОР НАБЛЮДАЕМЫХ ЗНАЧЕНИЙ X РАЗМЕРНОСТИ 9*1 РАЗБИТ НА ДВА ПОДВЕКТОРА С РАЗМЕРНОСТЯМИ 4*1 И 5*1. СКОЛЬКО ПАР КАНОНИЧЕСКИХ ПЕРЕМЕННЫХ СУЩЕСТВУЕТ В ЭТОМ СЛУЧАЕ?
4
1
2
3
5
103 КАНОНИЧЕСКИЕ ПЕРЕМЕННЫЕ КОРРЕЛИРУЮТ ДРУГ С ДРУГОМ?
НЕТ
ДА
ТАКИХ ПЕРЕМЕННЫХ НЕТ
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
104 В МЕТОДЕ КАНОНИЧЕСКИХ КОРРЕЛЯЦИЙ ДОПУСТИМА КОРРЕЛИРОВАННОСТЬ КОМПОНЕНТ ПОДВЕКТОРОВ?
НЕТ
ДА
ДА, ЕСЛИ ПОДВЕКТОРЫ ОДИНАКОВОЙ РАЗМЕРНОСТИ
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
105 СОБСТВЕННЫЕ ЗНАЧЕНИЯ МАТРИЦЫ КАНОНИЧЕСКИХ КОРРЕЛЯЦИЙ ЯВЛЯЮТСЯ
КВАДРАТАМИ КОЭФФИЦИЕНТОВ КАНОНИЧЕСКИХ КОРРЕЛЯЦИЙ
КОЭФФИЦИЕНТАМИ КАНОНИЧЕСКИХ КОРРЕЛЯЦИЙ
МОДУЛЯМИ КОЭФФИЦИЕНТОВ КАНОНИЧЕСКИХ КОРРЕЛЯЦИЙ
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
106 КАНОНИЧЕСКИЕ КОРРЕЛЯЦИИ
УПОРЯДОЧЕНЫ ПО УБЫВАНИЮ
УПОРЯДОЧЕНЫ ПО ВОЗРАСТАНИЮ
НЕУПОРЯДОЧЕНЫ
ВСЕГДА РАВНЫ НУЛИ
107 ЗНАЧИМОСТЬ КОЭФФИЦИЕНТОВ КАНОНИЧЕСКОЙ КОРРЕЛЯЦИИ ПРОВЕРЯЕТСЯ С ПОМОЩЬЮ СТАТИСТИКИ
ПИРСОНА
ФИШЕРА
СТЬЮДЕНТА
ХОТЕЛЛИНГА
108 ЗНАЧЕНИЯ КОЭФФИЦИЕНТОВ КАНОНИЧЕСКИХ КОРРЕЛЯЦИЙ
ВСЕГДА БОЛЬШЕ ИЛИ РАВНЫ НУЛЮ
ВСЕГДА БОЛЬШЕ НУЛЯ
ВСЕГДА МЕНЬШЕ НУЛЯ
ВСЕГДА МЕНЬШЕ ИЛИ РАВНЫ НУЛЮ
109 В КАКОМ СЛУЧАЕ ПРИ ПРОВЕРКЕ ЗНАЧИМОСТИ КОЭФФИЦИЕНТА КАНОНИЧЕСКОЙ КОРРЕЛЯЦИИ ЕГО СЛЕДУЕТ СЧИТАТЬ РАВНЫМ НУЛЮ?
ПРИ p-Value БОЛЬШЕМ УРОВНЯ ЗНАЧИМОСТИ
ПРИ p-Value МЕНЬШЕ УРОВНЯ ЗНАЧИМОСТИ
ПРИ p-Value РАВНОМ УРОВНЮ ЗНАЧИМОСТИ
ПРИ ЛЮБОМ ЗНАЧЕНИИ p-Value
110 ЧИСЛА СТЕПЕНЙ СВОБОДЫ (ЧСС) ОЦЕНОК КОЭФФИЦИЕНТОВ КАНОНИЧЕСКИХ КОРРЕЛЯЦИЙ
УМЕНЬШАЮТСЯ С УВЕЛИЧЕНИЕМ НОМЕРА ОЦЕНКИ КОЭФФИЦИЕНТА КАНОНИЧЕСКОЙ КОРРЕЛЯЦИИ
УВЕЛИЧИВАЮТСЯ С УВЕЛИЧЕНИЕМ НОМЕРА ОЦЕНКИ КОЭФФИЦИЕНТА КАНОНИЧЕСКОЙ КОРРЕЛЯЦИИ
РАВНЫ
НЕОБХОДИМЫ ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
