Кирилина Лидия Ивановна 2008 Содержание Введение 3 История математики на урок

Вид материала

Урок

Содержание История математики на уроках геометрии. История математики на первых уроках тригонометрии. 1.3. История появления и развития тригонометрии. 1.4 Геометрия в древних практических задачах. I. Организация класса. Из истории теоремы Пифагора Пифагоровы штаны III. Разминка. IV.Доказательство теоремы V.Закрепление материала VI. Решение старинных задач

Подобный материал:

• Лидия Ивановна Логачёва урок литературного чтения в 4классе по системе Л. В. Занкова., 59.43kb.
• Ямщикова Лариса Ивановна Оренбург, 2008 Содержание Введение глава I. Теоретическое, 871.1kb.
• Лидия Ивановна Норина, Заслуженный учитель рф, учитель гимназии №10 г. Новосибирска., 79.44kb.
• Содержание: Введение, 2332.37kb.
• Колодинская Людмила Ивановна 2011 Содержание Введение Интерактивные методы обучения, 239.59kb.
• Воробьева Анна Ивановна Содержание Введение. Игра как средство организации работы, 752.63kb.
• Чугунова Лидия Ивановна 2010-2011 уч год Тема урок, 140.18kb.
• Гусельникова Лидия Ивановна, учитель 1 категории Петуховской средней общеобразовательной, 909.18kb.
• Вашакидзе Нателла Семеновна Зав кафедрой математики: Доманский Андрей Владимирович, 503.36kb.
• Моисеева Лидия Алексеевна 2009 г. Содержание выписка из Государственного образовательного, 341.53kb.

МОУ « Основная общеобразовательная школа с. Арбузовка Ивантеевского района Саратовской области» НОМИНАЦИЯ: МЕТОДИКА ПРЕПОДАВАНИЯ ТЕМА: Кирилина Лидия Ивановна 2008

Содержание

Введение 3

1. История математики на уроках геометрии.

1.1 Исторические сведения, применяемые на уроках геометрии. 4

1.2 История математики на первых уроках тригонометрии. 7

1.3. История появления и развития тригонометрии. 11

1.4 Геометрия в древних практических задачах. 13

Заключение. 16

Приложение 1. 17

Список литературы. 26


ВСТУПЛЕНИЕ.


Математика как учебный предмет имеет большие возможности для раскрытия роли научных методов в познании окружающего нас мира. Одной из таких возможностей является введение в курс математики средней школы элементов историзма.

Эмоциональный рассказ учителя или короткие заранее подготовленные сообщения учащихся на уроках, доклады на кружковых, факультативных занятиях, на математических вечерах помогают учителю проводить работу по воспитанию материалистического мировоззрения в комплексе.

При изучении любой учебной темы учителя волнует мотивация обучения, а точнее, мотивация учебной деятельности учащихся. Мотивация начинается тогда, когда учитель пытается объяснить, как возникло то или иное математическое понятие, как открыли математический факт, какие задачи практики привели к их появлению, какой путь прошло человечество, прежде чем формулировка изучаемого понятия стала современной. Говоря проще, учителю надо ответить на стандартный детский вопрос: « Кто впервые придумал рассматривать изучаемое математическое понятие и зачем?»

Для того чтобы понимание учащимися опытного происхождения математических понятий переросло в мировоззрение, необходимо останавливаться на этих вопросах неоднократно, систематически. Для кратких исторических сведений достаточно 2-5 минут урока. Затрата времени окупается повышением интереса к данной теме. Исторический материал может быть использован на любом этапе урока (но не на каждом уроке). Иногда эти сведения полезно дать перед объяснением нового, а в других случаях использовать их для обобщения какого- нибудь раздела. Это зависит от педагогической интуиции учителя.

В своей работе я сделаю попытку ответить на вопрос о том, какие историко-

математические сведения может использовать учитель, чтобы сделать более интересными свои уроки, посвященные изучению геометрии.

3

1. История математики на уроках геометрии.
   

1.1 Исторические сведения, применяемые на уроках геометрии.

Совершая экскурсы в историю математики, рассказывая об основных понятиях науки, учитель должен ставить вопрос перед учащимися: «Что явилось в реальном мире прообразом этих понятий?» Необходимо научить школьников видеть прообразы математических понятий, доводить до их сознания слова Ф.Энгельса о том, что понятия числа и фигуры взяты не откуда- нибудь, а только из действительного мира» Широкие возможности для этого представляются учителю на уроках геометрии.

Хочу привести фрагменты исторических материалов, которые можно использовать на уроках в соответствии с действующей программой. Приведенный материал не является исчерпывающим. В нем отобраны только те вопросы, которые более доступны ученикам 7 -11 классов.

Первый урок геометрии начинается с беседы учителя о возникновении геометрии.

Учитель может рассказать своим ученикам, что в становлении геометрии как науки внесли большой вклад ученые Древней Греции: Фалес, Пифагор, Евдокс, Евклид, Архимед. Особенно большая роль в истории развития геометрии принадлежит Евклиду, который в 3 веке до н. э. обобщил и собрал воедино геометрические сведения своих современников, дополнил их собственными исследованиями и дал их систематическое изложение в 13 томах своих «Начал».

При изучении темы « Симметрия фигур» учитель может сообщить, что слово «симметрия» – греческого происхождения и буквально означает «соразмерность». Опыт применения симметрии в строительстве и искусстве привел к созданию учения о симметрии. О ней писал в своем трактате «Об архитектуре» римский инженер Витрувий ( 1 век), ее изучали и применяли

архитекторы и художники эпохи Возрождения. В геометрию элементы учения о симметрии ввел французский математик А.М.Лежандр ( 1752 – 1833).

4

Тема « Окружность». Большая часть употребляемых ныне в школе терминов сложились в Древней Греции. Например, «диаметр» от греческого перечник, «хорда» - от греческого chorde –струна, тетива. Еще вавилоняне и древние индийцы считали самым важным элементом окружности радиус. Слово это латинское и означает «луч». В древности не было этого термина, говорили так: «прямая из центра». Термин «радиус» впервые встречается в «Геометрии» (1569 г..) у французского ученого П.Рамуса, а затем у Ф.Виета.

Фалес из Милета – один из семи мудрецов древности. Считается родоначальником греческой философии и науки. С его именем связывается появление первых доказательств некоторых теорем геометрии. В том числе теоремы о конгруэнтности вертикальных углов, теоремы о делении круга пополам его диаметром. Об этом может рассказать учитель при изучении знаменитой теоремы Фалеса в 8 классе.

При изучении темы «Векторы» детям интересно будет узнать, что начала исчисления направленных отрезков, были впервые изложены уроженцем Норвегии Каспаром Весселем (1745 – 1818). Термин «вектор» ввел английский математик Уильям Гамильтон (1809 – 1877). Независимо от него к понятию вектора пришел и немецкий ученый Герман Грассман (1809 – 1877). Слово «вектор» происходит от латинского vector-переноситель. Учение о векторах позволило дать удовлетворительное объяснение действий с отрицательными числами. Например, (-1) *(+1)=-1,(-1)*(-1)=+1 трактуется как поворот вектора (-1; 0) соответственно на 0⁰ и на 180⁰ вокруг точки 0 (0;0).

Изучение темы «Теорема Пифагора» позволяет учителю расширить знания исторических сведений из геометрии. В древнем Вавилоне умели решать задачи, требующие применения «теоремы Пифагора» по меньшей мере, за

1000 лет до Пифагора. Пифагору (580 – 500 гг.до н.э.) приписывают доказательство важнейших теорем. В том числе:

1) сумма внутренних углов треугольника равна двум прямым;

2) площадь квадрата, построенного на гипотенузе, равна сумме площадей

5

квадратов, построенных на катетах (теорема Пифагора). Одно из старейших

наглядных доказательств теоремы Пифагора содержится у индийского математика Бхаскары (род. в 1114 г.). Известно более 150 доказательств этой теоремы.


6

2. История математики на первых уроках тригонометрии.
   

Впервые тригонометрические соотношения вводятся в курсе геометрии следующим образом. Рассматривается прямоугольный треугольник АВС (угол С – прямой), и на уровне определений утверждается:

sin a =АС/АВ, cos a = ВС/АВ, tg а = АС/ВС, ctg а = ВС/АС.. (*)

Учащимся легче запоминаются эти определения, если учитель пользуется опорными сигналами:

sin a = противоположный катет/гипотенуза

cos a = прилежащий катет/ гипотенуза

tg a = противолежащий катет / прилежащий катет

ctg a = прилежащий катет / противолежащий катет.

Представленные определения и использованная для них символика являются необычными и сложными для учащихся, поэтому понимание учебного материала во многом зависит от иллюстрации глубинной сущности понятий, а для этого полезно обратиться к истории математики.

В первую очередь нас будут интересовать вопросы: «Откуда появилась необходимость рассматривать представленные выше соотношения сторон прямоугольного треугольника?» и «Как появилась символика, используемая в определениях(*)?»

Ключ к отгадке надо искать в практической деятельности людей. Причем речь идет о временах настолько далеких (может второе тысячелетие до н.э., а может и ранее), что никакими письменными свидетельствами, позволяющими дать однозначный ответ мы не располагаем. Поэтому позволим себе высказать некоторые догадки.

В древние времена строительство сооружений велось примерно, таким образом и такими средствами, как сегодня строят небольшие дома и подсобные помещения. При этом строители используют нехитрые инструменты: веревку, отвес, колышки и прочее. Между прочим, в Древнем Египте существовали люди специальной профессии, которых называли

7

гарпедонапты, что значит, натягивали веревки. С них начиналось строительство. А зачем нужны веревки строителям? Чтобы ровно в линию выкладывать кирпичи и камни.

Предложим учащимся вслушаться в слова «линия» и «лен». Действительно, откроем этимологический словарь: Линия. Через посредство немецкого языка заимствовано в начале 18 века из латыни. Лат.linea – «нитка» - производное от linum – «лен».

Еще веревка нужна для того, чтобы получить прямой угол, например в целях строительства привычного нам четырехугольного дома. Ведь такой дом построить легче всего. А строительство домов иных форм и сейчас является трудной архитектурной задачей.

Учащиеся уже знают, что одним из важнейших изобретений человечества было изобретение колеса. А почему? Да потому, что в природе колеса нет. Колесо - это именно человеческое изобретение. Теперь другой вопрос: а есть ли в природе прямой угол? Примеры привести можно (ветка, растущая перпендикулярно стволу дерева; само дерево , растущее перпендикулярно к земле и т. п.), но вряд ли перечисленное годится для того, чтобы создать шаблон прямого угла.

Издавна строители научились получать прямой угол с помощью веревки. В Древнем Египте заметили, что если на веревке завязать узелки на равном расстоянии друг от друга, и натянуть веревку так, чтобы, говоря современным языком, получился треугольник со сторонами 3, 4, 5, то угол, лежащий против наибольшей стороны, окажется прямым. С тех пор треугольник со сторонами 3, 4, 5 называют египетским.

Историю с натягиванием веревки продолжают еще несколько древних терминов: катет – значит «отвес», гипотенуза – «натянутая», другой катет прямоугольного треугольника не назывался катетом (т.е. отвесом), о нем говорили как об основании.

По натянутой веревке (другими словами, по гипотенузе) можно проводить стачивание боковой грани строящейся пирамиды.

8

Теперь мы подошли к главному вопросу: «Как объяснить строителям, по какому углу стачивать грань пирамиды?» ( В Древнем Египте пирамиду выкладывали из грубых крупных камней, и надо было их отшлифовать или иным образом подкорректировать.) Один из способов: задать отношение высоты пирамиды к апофеме, или, если говорить о плоскости, задать отношение катета – отвеса к гипотенузе. Вот и получается прообраз косинуса угла стачивания. А когда задавались другие отношения – отношение катета – основания к катету – отвесу или отношение катета – основания к гипотенузе – это были прообразы понятий тангенса и синуса угла.

Теперь мы понимаем: рассматривать отношение длин сторон прямоугольного треугольника очень удобно, так как для всех подобных прямоугольных треугольников эти отношения сохраняются ( все правильно, как потом узнают учащиеся, у подобных треугольников углы равны, а, значит, равны и тригонометрические функции углов.

Судя по всему, на идею подобных фигур люди обратили внимание достаточно давно. Одинаковые по форме, но различные по величине фигуры встречаются в вавилонских и египетских памятниках. В сохранившееся

погребальной камере отца фараона Рамеса II имеется стена, покрытая сетью квадратиков, с помощью которой на стену перенесены в увеличенном виде рисунки меньших размеров (своего рода «палетка»).

До этого момента рассматривалась самая глубинная предыстория зарождения тригонометрических знаний, но именно она отразилась в самом слове тригонометрия, которое буквально означает измерение треугольников.

Действительно, термин тригонометрия состоит из двух греческих слов: тригоном, что означает «треугольник» и метрейн, что означает «измерять». Кроме того, данный первичный исторический рассказ помогает объединить в сознании учащихся такие темы, как знакомство с прямоугольным треугольником, теорема Пифагора, тригонометрические соотношения в прямоугольном треугольнике. И главное, у учащихся возникает желание посмотреть на эти темы как с исторической, та и с современной точки зрения,

9

т. е. повышается интерес к изучению геометрии.

Теперь учитель может перейти к моменту, когда он обратится непосредственно к истории тригонометрии, которые можно изложить в курсе планиметрии.


10

1.3. История появления и развития тригонометрии.

Тригонометрия, как и всякая наука, вырастала из потребностей человеческой практики, но эти потребности не ограничивались, как мы уже упоминали выше, только лишь потребностями строительства или нахождения расстояний до недоступных объектов. Задачи мореплавания, требовавшие по звёздам определять правильный курс корабля, задачи определения по звёздам пути при движении караванов в пустыне, задачи земледелия, требовавшие введения точного календаря, и многие другие обусловили развитие астрономии, а с ней и тригонометрии. Причём сферическая тригонометрия развивалась наряду с плоской.

По сути, тригонометрия появилась в древности как один из разделов астрономии. Дело в том, что преобладающей гипотезой о строении

Вселенной была геоцентрическая, согласно которой Земля есть шар, расположенный в центре небесной сферы, которая равномерно вращается вокруг своей оси. Светила считаются расположенными на этой сфере. При изучении их движения большое значение приобретают задачи о расположении точек и фигур на сфере. Работы, в которых подобные задачи решаются, получили название сферики. Плоская тригонометрия при таких условиях отнюдь не играла лишь второстепенную роль по сравнению со сферической тригонометрией. У неё была своя область приложений: помимо решения задач на определение расстояний до недоступных объектов, она являлась частью практической астрономии – фигуры на сфере проектировались на плоскость горизонта, меридиана и т.д., и таким образом многие задачи сводились к плоским случаям.

Отдельные вопросы из тригонометрии уже успешно решали древнегреческие астрономы, однако они рассматривали хорды, а не синусы, косинусы и другие, как говорили в древности, линии. Если говорить точнее, то греческие астрономы рассматривали, по сути, только синус, вместо которого использовали хорду, равную удвоенной линии синуса половинной дуги.

11

Начало учению о тригонометрических величинах было положено в Индии, начиная с IV – VI вв. Индийские учёные впервые в науке стали употреблять линию синуса как половину хорды, и составили первые тригонометрические таблицы синусов (полухорд). Им были известны также основное тригонометрическое тождество, формулы приведения, формулы синуса половинного угла.

В IX – X вв. центр математических исследований, значит и центр развития тригонометрического знания, переместился в Среднюю Азию, где трудами арабских математиков тригонометрия впервые выделилась из астрономии

как самостоятельная наука. В частности, учёные стран ислама ввели новые тригонометрические величины: тангенс и котангенс. В трактате «Плоские четырёхугольники» учёного – энциклопедиста и государственного деятеля XIII в. Насирэддина Туси плоская и сферическая тригонометрия выступают как самостоятельные предметы. Для сравнения, в Европе тригонометрия достигла этого уровня, стала успешно развиваться и трактоваться как самостоятельная наука лишь в XV в., и начало этому было положено трудами немецкого астронома и математика, профессора Региомонтана.


12

1.4 Геометрия в древних практических задачах.

Использование египетского треугольника древними строителями.

В строительстве очень важно знать площадь участка, отведённого на застройку. Для измерения площади древние египтяне использовали особый треугольник, у которого были фиксированные длины сторон. Занимались измерениями особые специалисты, которые назывались «натягивателями каната» (гарпедонаптай). Они брали длинную верёвку, делили её на 12 равных частей узелками или какими – то другими метками, а концы верёвки связывали. На направлении север – юг они устанавливали два кола на расстоянии четырёх частей, отмеченных на верёвке. Затем при помощи третьего кола натягивали связанную верёвку так, чтобы образовался треугольник, у которого одна сторона имела три части, другая – четыре, а третья пять частей. Получался прямоугольный треугольник, площадь которого могла быть принята за эталон, если ремесленники пользовались верёвкой всегда одной и той же строго определённой длины. При этом одна сторона, имеющая три части, указывала восточно-западное направление.

Вряд ли египетские строители осознавали, что их метод нуждается в каком – либо обосновании. Но мы теперь знаем, что он основан на доказанной гораздо позже теореме, служащей обратной теореме Пифагора. А эта теорема «открыта» Пифагором через много веков после того, как ею научился пользоваться обыкновенный древнеегипетский мастеровой.

Определение недоступных расстояний.

История геометрии хранит немало приёмов решения задач на нахождение расстояний. Определение расстояний до кораблей, находящихся в море, - одна из таких задач. Предполагают, что оба способа её решения принадлежат древнегреческому учёному, путешественнику и купцу Фалесу Милетскому (VI в. до н.э.).

Первый из них основан на одном из признаков равенства треугольников. Второй способ, в дальнейшем получивший название метода триангуляции, нашёл применение в астрономии. С его помощью измерялись расстояния до

13

небесных тел.

Древнекитайский приём измерения высоты недоступного предмета.

Огромный вклад в развитие прикладной геометрии внёс крупнейший китайский математик III в. Лю Хуэй. Ему принадлежит трактат «Математика морского острова», в котором приведены решения различных задач на определение расстояний до предметов, расположенных на отдалённом острове, и вычисление недоступных высот. Задачи Лю Хуэя довольно сложны. Решение своих задач он обычно давал в виде правил. Ввиду практической ценности эти задачи получили широкое распространение не только в Китае, но и за его пределами. Приведём задачу из трактата Лю Хуэя.

Наблюдают морской остров.




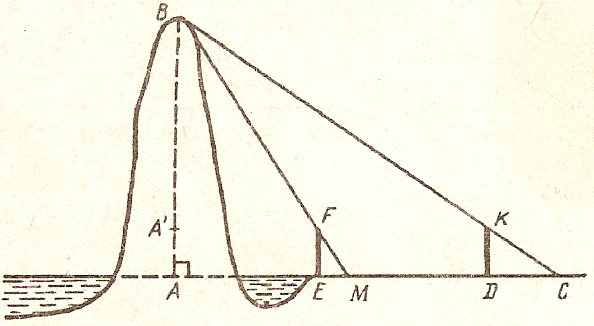
Для этого установили пару шестов одинаковой высоты в 3 чжана (1 чжан = 5/3 бу) на расстоянии 1000 бу. Основания обоих шестов находятся на одной прямой с островом. Если отойти по прямой от первого шеста на 123 бу, то глаз человека, лежащего на земле, будет наблюдать верхний конец шеста совпадающим с вершиной острова. Такая же картина получится, если отойти от второго шеста на 127 бу. Спрашивается, какова высота острова и его расстояние от первого шеста. Решение: « Взяв высоту шеста, умножь её на расстояние между шестами, это делимое.

Разность между отступлениями будет делителем, раздели на неё. К тому, что получится, прибавь высоту шеста, получится высота острова. Чтобы найти расстояние от предыдущего шеста до острова, надо (отступление) от

14

предыдущего шеста умножить на расстояние между шестами, это делимое. Разность между отходами будет делителем, раздели на неё, получишь расстояние, на которое остров удалён от шеста».

Измерение площади прямоугольного участка.


3
Наши предки для определения площадей прямоугольных участков использовали так называемый метод наложения. Суть его состоит в следующем.


эталон



4




1



Измеряемая площадь




2






«Линейная мера площади» рис. 1 рис. 2


К измеряемому прямоугольнику прикладывается эталон площади (рис. 1). В прямоугольнике, образованном стороной эталона и стороной измеряемого

13

участка, проводится диагональ до пересечения с продолжением второй стороны эталона. Получаются три новых прямоугольника. Два из них, через которые прошла диагональ, подобны, а третий равновелик эталону (рис. 2). Сторона равновеликого прямоугольника и служит так называемой линейной мерой площади. Так, измерение площади сводилось к подсчёту числа линейных мер в стороне измеряемого прямолинейного участка. Преимущество данного метода в удобстве его использования при нарезании участков земли, когда за эталон можно брать квадрат любой величины.


15


Заключение.

В данной работе рассмотрен особый вид деятельности учащихся – изучение исторического материала на уроках геометрии. Систематическое использование в школьном курсе математики элементов истории науки способствует развитию у учащихся интереса к предмету, более глубокому и прочному усвоению математики, формированию у школьников диалектико-материалистического мировоззрения. Показывая коллективный и интернациональный характер математического творчества, учитель внесет ощутимый вклад в дело воспитания учащихся в духе интернациолизма. В то же время рассказ о великих ученых народов нашей страны вызовет у ребят чувство гордости за нашу Родину.

Основным в использовании исторического материала является обучение математике. Данный этап урока активизирует учащихся, делает восприятие более активным, эмоциональным, творческим. Применение исторического материала дает эффект в классе, повышает эмоциональность урока, снимает утомление, развивает внимание, речь, мировоззрение, умственную деятельность, положительно влияет на повышение качества знаний, умений и навыков учащихся. Словом историзм на уроках заслуживает право дополнить традиционные формы обучения и воспитания школьников, вовлекает их в исследовательскую деятельность.


16

Приложение 1.

Урок по теме



Цели:

1.Изучить теорему Пифагора.

2. Формировать научное мировоззрение.

3. Развивать логическое мышление.

4. Воспитывать интерес к геометрии.


Ход урока.

I. Организация класса.

II. Исторический экскурс.

Рассказ о Пифагоре.

Говоря о Пифагоре, следует сразу отметить, что о его жизни известно немного. Мы знаем, что в VI в. до н.э. в Древней Греции жил ученый по имени Пифагор родом из Самоса. В молодости он много путешествовал по странам Востока, побывал в Египте и Вавилоне, где изучал разные науки, в том числе математику. Вернувшись на родину, Пифагор основал философскую школу закрытого типа — так называемый пифагорейский союз. Каждый вступающий в него отрекался от имущества и давал клятву хранить в тайне учение основателя.

Пифагорейцы занимались математикой, философией, естественными науками. Ими были сделаны важные открытия в арифметике и геометрии. В школе существовало правило, по которому авторство всех работ приписывалось Пифагору. Так что достоверно неизвестно, какие открытия принадлежат самому ученому.

Из истории теоремы Пифагора

Богатую историю имеет теорема, носящая имя Пифагора. Во времена самого

17

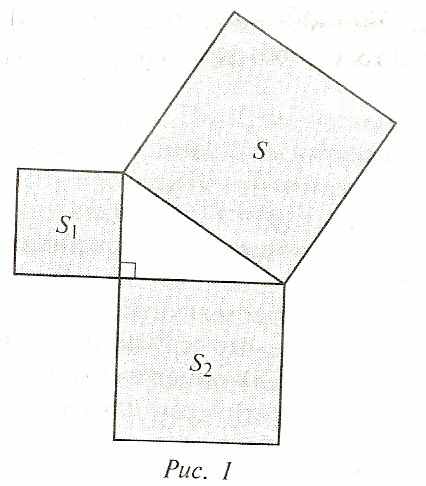
ученого ее формулировали так: «Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах. Или в виде задачи: «Доказать, что квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на катетах: S = S₁ + S₂» (рис. 1).

Согласно легенде, в честь своего открытия Пифагор принес в жертву сто быков (хотя согласно другой легенде он был вегетарианцем).



Известный немецкий писатель-романист А. Шамиссо писал:

Пребудет вечной истина, как скоро

Все познает слабый человек!

И ныне теорема Пифагора

Верна, как и в его далекий век.

Обильно было жертвоприношенье

Богам от Пифагора. Сто быков

Он отдал на закланье и сожженье

За свет луча, пришедший с облаков.

Поэтому всегда с тех самых пор,

Чуть истина рождается на свет,

Быки ревут, ее почуя, вслед.

Они не в силах свету помешать,

А могут лишь, закрыв глаза, дрожать

От страха, что вселил в них Пифагор.

18

Долгое время считалось, что до Пифагора эта теорема не была известна. В настоящее время установлено, что она встречается в вавилонских текстах, написанных за 1200 лет до Пифагора! Вероятно, тогда теорема еще не была доказана, а соотношение между гипотенузой и катетами было получено опытным путем. Была она известна и древним китайцам, и индусам. Таким образом, Пифагор не открыл замечательное свойство прямоугольного треугольника, но, вероятно, первым обобщил и доказал его, перенеся тем самым из области практики в область науки. К сожалению, сведения о доказательстве до нас не дошли.

Сегодня известно более ста различных доказательств теоремы Пифагора. Возможно, автором одного из них является сам ученый или его ученик. Отметим, что соотношение между катетами и гипотенузой, вероятно, сначала было установлено для равнобедренного прямоугольного треугольника.

По рис. 2 видим, что квадрат, построенный на его гипотенузе, разбивается диагоналями на четыре равных треугольника, а квадраты, построенные на катетах, содержат по два таких же треугольника. Замечаем, что площадь большого квадрата равна сумме площадей малых квадратов.



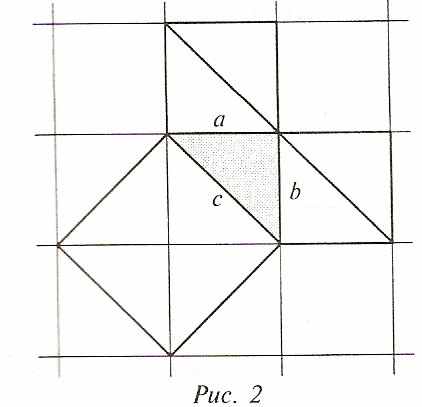
Учащиеся средних веков считали доказательство теоремы Пифагора очень трудным и прозвали его «ослиным мостом» или «бегством убогих», так как слабые ученики бежали от геометрии, а те, кто заучивал теоремы наизусть, без понимания, были не в состоянии осилить теорему Пифагора: она служила для них чем – то вроде непреодолимого моста. Из – за иллюстрирующих

теорему чертежей учащиеся называли её также «ветреной мельницей»,

19

рисовали забавные карикатуры (рис. 3) и придумывали шутливые стишки вроде такого:


Пифагоровы штаны

Во все стороны равны.



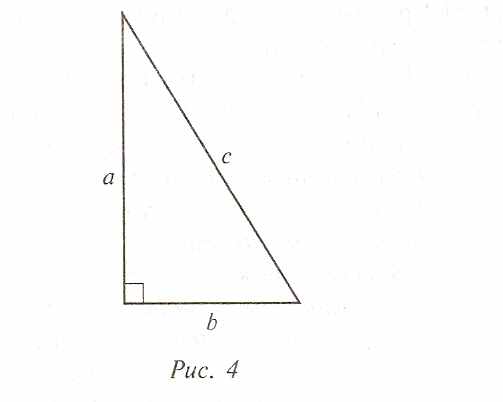
Теорема Пифагора занимает в геометрии особое место. На её основе можно вывести или доказать большинство теорем. А ещё она замечательна тем, что сама по себе вовсе не очевидна. Сколько ни смотри на прямоугольный треугольник, никак не увидишь, что его стороны a, b и c связывает простое соотношение: c² = а² + b² (рис. 4)

20

III. Разминка.

(Перед доказательством теоремы Пифагора рекомендуется провести устную разминку, предложив ученикам несколько заданий по готовым чертежам. В процессе их решения фактически воспроизводятся некоторые фрагменты будущего доказательства.)

1.Определите вид треугольника, изображенного на рис.5. Как называются стороны такого треугольника? Укажите названия каждой стороны данного треугольника.

2. По данным рис. 6 найти угол β.



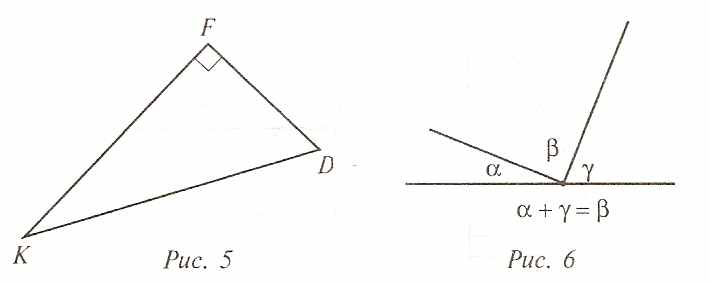
3. По данным рис. 7 определите вид четырехугольника КМNР.



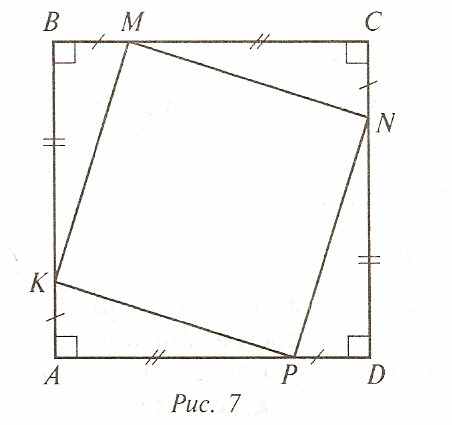
Замечание. В последней задаче учащиеся должны доказать, что четырехугольник КМNР — квадрат. Ее необходимо обсудить подробно, так как такая же конфигурация используется при доказательстве теоремы Пифагора.

IV.Доказательство теоремы

После разминки формулируем теорему и доказываем ее (по учебнику).

21

Затем можно познакомить детей с забавным стихотворением И. Дырченко, которое помогает запомнить формулировку теоремы Пифагора.

Если дан нам треугольник,

И притом с прямым углом,

То квадрат гипотенузы

Мы всегда легко найдем:

Катеты в квадрат возводим,

Сумму степеней находим —

И таким простым путем

К результату мы придем.

V.Закрепление материала

На следующем этапе предлагаем учащимся несколько задач по готовым чертежам, демонстрируя их с помощью кодоскопа.

1. Вычислите, если возможно:

а) сторону АС треугольника АВС (рис. 8);

б) сторону МN треугольника КМN (рис. 9);

в) диагональ ВD квадрата ВСВF (рис. 19);

г) сторону КР треугольника КРR? (рис. 11).



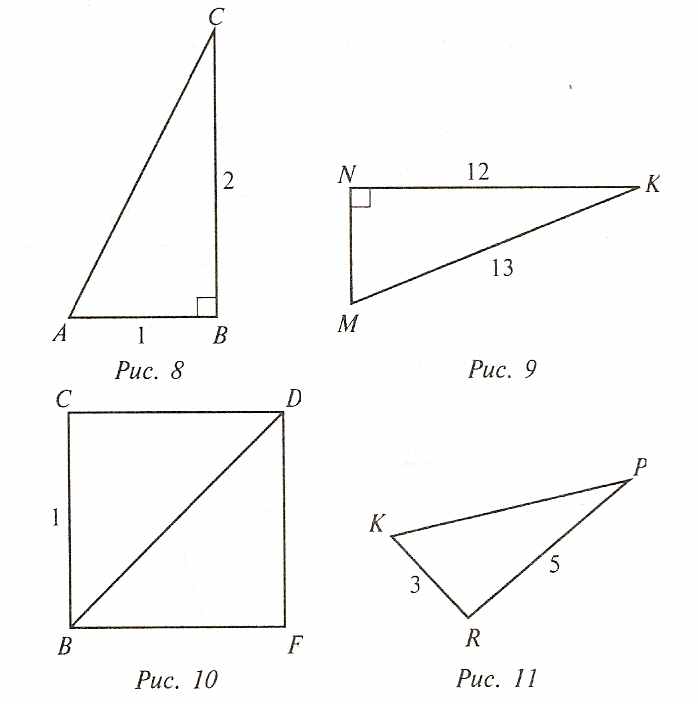
Ответы: а) √ 5; б) 5; в) 5; г) сторону треугольника вычислить нельзя.

22

Замечание. Следует обратить внимание учеников на то, что в задаче 1, г не хватает данных для решения. Неясно, какой вид имеет треугольник КРR? В такой ситуации теорема Пифагора, конечно, неприменима.

2. Найдите сторону СD параллелограмма АВСD (рис. 12).

Ответ: 4 √2

3. Вычислите высоту СF трапеции АВСD? (рис. 13).




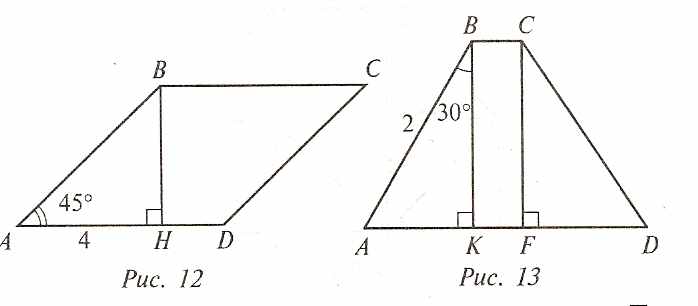
Ответ: √3

VI. Решение старинных задач

На заключительном этапе урока рассматриваем несколько старинных задач на применение теоремы Пифагора.

Задача 1 (из «Арифметики» Л.Ф.Магницкого).

Случися некоему человеку к стене лествицу прибрати, стены же тоя высота есть 117 стоп. И обрете лествицу долготою 125 стоп. И ведати хощет, колико стоп сея лестницы нижний конец от стены отстояти имать.

Решение. Треугольник АВС — прямоугольный (рис. 14). Пусть ВС = х стоп, тогда по теореме Пифагора АС² + СВ² = АВ²,

117² + х² = 125²;

Х² = 125² – 117²,

Х² = (125 - 117)(125 + 117),

Х² = 8 ·242,

х = 44.


23



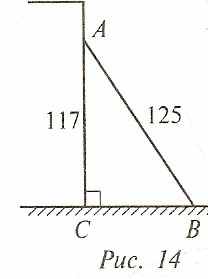
О т в е т: 44 стопы.


Задача 2 (индийского математика ХII в. Бхаскары).

На берегу реки рос тополь одинокий.

Вдруг ветра порыв его ствол надломал.

Бедный тополь упал. И угол прямой

С теченьем реки его ствол составлял.

Запомни теперь, что в том месте река

В четыре лишь фута была широка.

Верхушка склонилась у края реки,

Осталось три фута всего от ствола.

Прошу тебя, скоро теперь мне скажи:

У тополя как велика высота?

Решение. Пусть АВ — высота тополя, тогда АВ=АС+СD (рис. 15). Найдем СD. Треугольник АСD — прямоугольный. По теореме Пифагора

СD² = АС² + АD², СD² = 3² + 4², откуда СD = 5 футов.

Значит, АВ = З + 5 = 8 футов.



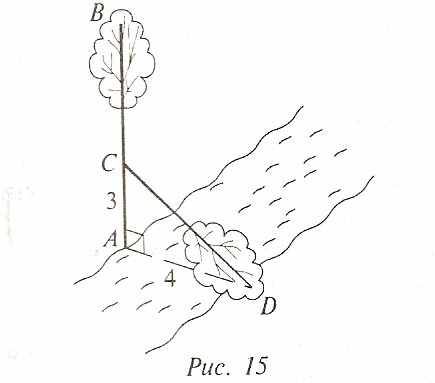
24

Ответ: 8 футов.

Задача З (из древнеиндийского трактата).

Над озером тихим,

С полфута размером, высился лотоса цвет.

Он рос одиноко. И ветер порывом

Отнес его в сторону.

Нет, боле цветка над водой.

Нашел же рыбак его ранней весной

В двух футах от места, где рос.

Итак, предложу я вопрос:

Как озера вода здесь глубока?

Решение. Треугольник АВС — прямоугольный, АВ = АС + ½ (рис. 16). Тогда по теореме ПифагораАВ² =АС²+СВ², (АС + ½ )² =АС² + 2²,

АС=З ¾ фута.



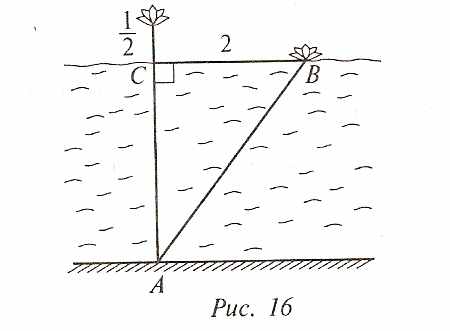
Ответ: З ¾ фута.

VII. Рефлексия.

Что нового узнали на уроке?


25


Список литературы.

1. Г.И. Глейзер, История математики в школе. 7 – 8 кл. – М.: Просвещение, 1982

2. П.А.Карасев, Задачи по геометрии – М., Просвещение, 1965

3. Л.М.Лоповок, Математика на досуге – М., Просвещение, 1981

4. А.С.Чесноков, Внеклассная работа по геометрии – М., Просвещение, 1974

5. Математика в школе, № 3, 1980

6. Математика в школе, № 6, 2001

7. Математика в школе, № 5, 1978

9. Математика школьника, № 1, 2006