Рабочая программа дисциплины «математика» Рекомендуется для направления подготовки 080200 Менеджмент
| Вид материала | Рабочая программа |
- Рабочая программа дисциплины «финансовая математика» Рекомендуется для направления, 178.05kb.
- Рабочая программа дисциплины «Сравнительный менеджмент» Рекомендуется для направления, 193.76kb.
- Рабочая программа дисциплины «логистика международного товародвижения» Рекомендуется, 250.46kb.
- Рабочая программа дисциплины «правоведение» Рекомендуется для направления подготовки, 182.08kb.
- Рабочая программа дисциплины «правоведение» Рекомендуется для направления подготовки, 173.32kb.
- Рабочая программа дисциплины «финансы» Рекомендуется для направления подготовки 080200, 218.7kb.
- Рабочая программа дисциплины «erp-системы» Рекомендуется для направления подготовки, 145.93kb.
- Рабочая программа дисциплины «функциональная логистика» Рекомендуется для направления, 621.26kb.
- Рабочая программа дисциплины управление инновационными проектами рекомендуется для, 169.69kb.
- Рабочая программа дисциплины «международный контракт» Рекомендуется для направления, 116.77kb.
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ЭКОНОМИКИ И ФИНАНСОВ
РАБОЧАЯ ПРОГРАММА ДИСЦИПЛИНЫ
«МАТЕМАТИКА»
Рекомендуется для направления подготовки
080200 Менеджмент
Квалификация выпускника - бакалавр
Санкт-Петербург
2011 год
1. Цели и задачи дисциплины: накопление необходимого запаса сведений по математике (основные определения, теоремы, правила), а также освоение математического аппарата, помогающего моделировать, анализировать и решать экономические задачи, помощь в усвоении математических методов, дающих возможность изучать и прогнозировать процессы и явления из области будущей деятельности студентов; развитие логического и алгоритмического мышления, способствование формированию умений и навыков самостоятельного анализа исследования экономических проблем, развитию стремления к научному поиску путей совершенствования своей работы.
2. Место дисциплины в структуре ООП: дисциплина «Математика» относится к циклу Б.2 Математический и естественнонаучный цикл, Базовая часть. Входные знания, умения и компетенции студентов должны соответствовать курсу математики общеобразовательной школы. Дисциплина «Математика» является предшествующей для следующих дисциплин: «Статистика», «Методы принятия управленческих решений», «Теория вероятностей и математическая статистика», «Математические методы и модели в принятии решений», «Финансовая математика», «Экономико-математические методы в управлении качеством продукции», «Теория менеджмента», «Маркетинг», «Управление изменениями», «Логистика».
3. Требования к результатам освоения дисциплины:
Процесс изучения дисциплины направлен на формирование следующих компетенций:
владеть методами количественного анализа и моделирования, теоретического и экспериментального исследования (ОК-15); пониманием роли и значения информации и информационных технологий в развитии современного общества и экономических знаний (ОК-16); владеть основными методами, способами и средствами получения, хранения, переработки информации, навыками работы с компьютером как средством управления информацией (ОК-17); способностью работать с информацией в глобальных компьютерных сетях и корпоративных информационных системах (ОК-18).
В результате изучения дисциплины студент должен:
Знать: основные понятия и инструменты алгебры и геометрии, математического анализа, теории вероятностей, математической и социально-экономической статистики; основные математические модели принятия решений.
Уметь: решать типовые математические задачи, используемые при принятии управленческих решений; использовать математический язык и математическую символику при построении организационно-управленческих моделей; обрабатывать эмпирические и экспериментальные данные; применять информационные технологии для решения управленческих задач.
Владеть: математическими, статистическими и количественными методами решения типовых организационно-управленческих задач.
4. Объем дисциплины и виды учебной работы
Общая трудоемкость дисциплины составляет 8 зачетных единиц.
| Вид учебной работы | Всего часов | Семестры | |
| 1 | 2 | ||
| Аудиторные занятия (всего) | 126 | 54 | 72 |
| В том числе: | - | - | - |
| Лекции | 62 | 22 | 40 |
| Практические занятия (ПЗ) | 64 | 32 | 32 |
| Самостоятельная работа (всего) | 162 | 54 | 36 |
| В том числе: | - | - | - |
| Тест 1 | 20 | 20 | |
| Тест 2 | 20 | 20 | |
| Контрольная работа 1 | 14 | 14 | |
| Тест 3 | 15 | | 15 |
| Тест 4 | 15 | | 15 |
| Контрольная работа 2 | 6 | | 6 |
| Экзамен | 72 | 36 | 36 |
| Общая трудоемкость час зач. ед. | 288 | 144 | 144 |
| 8 | 3+1 | 3+1 | |
5. Содержание дисциплины
5.1. Содержание разделов дисциплины
1. Линейная алгебра и аналитическая геометрия
Геометрические векторы. Векторы и действия с ними. Координатные орты. Разложение вектора по координатным осям, координаты вектора. Длина вектора. Угол между векторами. Скалярное произведение и его свойства.
Метод координат. Прямоугольные (декартовы) координаты на плоскости и в пространстве. Расстояние между двумя точками. Деление отрезка в данном отношении. Преобразование координат на плоскости. Полярные координаты.
Прямая на плоскости. Уравнение линии на плоскости. Уравнение прямой с угловым коэффициентом. Общее уравнение прямой и его исследование. Уравнение прямой, проходящей через заданную точку в заданном направлении. Уравнение пучка прямых. Уравнение прямой, проходящей через 2 заданные точки. Угол между 2-мя прямыми. Условие параллельности и перпендикулярности 2-х прямых. Прямая и плоскость в пространстве. Поверхности и линии в пространстве. Общее уравнение плоскости и его исследование. Канонические уравнения прямой в пространстве. Взаимное расположение плоскостей и прямых в пространстве.
Кривые и поверхности 2-го порядка. Окружность. Эллипс, гипербола, парабола. Канонические уравнения и свойства. Экономические примеры (линия спроса и предложения, точка равновесия, равновесная цена и равновесный объем).Простейшие поверхности второго порядка (сфера, параболоид вращения).
Алгебра матриц. Матрицы и их классификации. Действия над матрицами. Экономические примеры.
Определители. Определители 2-го и 3-го порядка. Понятие об определителях n-го порядка. Свойства определителей. Способы вычисления определителей n-го порядка.
Обратная матрица. Теорема существования и единственности обратной матрицы. Способы вычисления обратной матрицы.
Ранг матрицы. Элементарные преобразования и их применение для нахождения ранга.
Системы линейных уравнений. Основные понятия, связанные с системы линейных уравнений,. Матричная и векторная формы записи системы линейных уравнений. Теорема Крамера. Понятие о базисном миноре. Теорема Кронекера-Капелли. Исследование системы линейных уравнений. Метод Гаусса. Однородные системы. Экономические примеры. Геометрическая интерпретация систем линейных уравнений и неравенств.
Векторные пространства. Пространство Rn; n-мерные векторы и действия над ними. n-мерное векторное пространство. Линейная зависимость и линейная независимость системы векторов, критерии линейной зависимости и независимости системы векторов. Базис пространства Rn , разложение вектора по базису. Собственные числа и собственные векторы квадратной матрицы и их свойства. Модель международной торговли. Линейная балансовая модель.
2. Математический анализ
Введение в математический анализ. Множества: основные операции, свойства, геометрическое истолкование. Формулы Моргана. Множество действительных чисел и числовая прямая. Числовые промежутки. Декартово произведение множеств. Понятие отображения.
Числовые последовательности. Определение и свойства числовых последовательностей. Пределы числовой последовательности. Свойства сходящихся числовых последовательностей. Существование предела у ограниченной монотонной последовательности.
Понятие функции. Основные элементарные функции и их графики. Предел функции в точке и на бесконечности. Замечательные пределы. Экономические примеры (непрерывное начисление процента). Понятие непрерывной функции. Непрерывность элементарных функций. Вычисление пределов с использованием свойства непрерывности. Бесконечно малые функции и их свойства. Сравнение бесконечно малых функций. Эквивалентные бесконечно малые функции и их применение при вычислении пределов. Бесконечно большие функции. Связь между бесконечно большими функциями и бесконечно малыми. Свойства функций, непрерывных на отрезке (существование наибольшего и наименьшего значений, существование промежуточных значений).
Дифференциальное исчисление функций одной переменной. Производная функции в точке, ее геометрический, механический и экономический смысл. Производная суммы, произведения и частного. Производная сложной функции. Производная обратной функции. Производные элементарных функций. Производные высших порядков. Дифференцируемость функции. Дифференциал и его геометрический смысл. Приложения дифференциала к приближенным вычислениям. Экономические понятия, связанные с понятием производной. Логарифмическая производная и эластичность функции. Теоремы Ферма, Ролля, Лагранжа, Коши. Правило Лопиталя.
Исследование функций одной переменной. Условия возрастания и убывания функции. Точки экстремума. Необходимое условие экстремума дифференцируемой функции. Достаточные условия экстремума. Отыскание наибольшего и наименьшего значений функции, дифференцируемой на отрезке. Направление выпуклости графика функции. Точки перегиба. Асимптоты кривых. Общая схема исследования и построения графика функции. Примеры функций, встречающихся в экономике. Многочлен Тейлора для функции одной переменной. Формулы Тейлора и Маклорена (без доказательства). Примеры разложений элементарных функций. Применение разложений для приближенных вычислений, оценка точности приближенных формул.
Интегрирование функций одной переменной. Первообразная функция и неопределенный интеграл. Определения и простейшие свойства. Таблица основных неопределенных интегралов. Правила интегрирования. Основные методы интегрирования (метод замены переменной и интегрирования по частям). Определенный интеграл как предел интегральных сумм. Основные свойства определенного интеграла, теорема о среднем. Определенный интеграл с переменным верхним пределом. Формула Ньютона-Лейбница. Вычисление определенного интеграла методами замены переменной и интегрирования по частям. Приложение определенного интеграла к вычислению площадей плоских фигур. Несобственные интегралы. Экономические понятия, связанные с определенным интегралом. Использование определенных интегралов в экономических задачах.
Функции нескольких переменных. Открытые и замкнутые области на плоскости и в пространстве. Функция двух переменных, область определения, график. Функция n –переменных. Предел функции. Непрерывность функции, свойства непрерывных функций. Функции нескольких переменных в экономике.
Дифференцирование функций нескольких переменных. Частные производные. Эластичность функций нескольких переменных. Частные производные сложной функции. Дифференцируемость функции нескольких переменных. Дифференциал и его геометрический смысл. Производная функции по направлению Градиент и его свойства. Частные производные высших порядков. Экономические понятия, связанные с понятием частной производной. Однородные функции. Экономические примеры.
Экстремумы функции нескольких переменных. Локальный экстремум функции нескольких переменных. Необходимое условие экстремума. Достаточное условие экстремума для функций двух переменных. Условный экстремум. Метод подстановки и метод неопределенных множителей Лагранжа. Экономические примеры.
Задача оптимизации функций. Нахождение наименьшего и наибольшего значения функции нескольких переменных в замкнутой области. Метод наименьших квадратов. Экономические приложения.
Кратные интегралы. Двойные и повторные интегралы. Вычисление двойных интегралов в прямоугольных и полярных координатах.
Числовые и степенные ряды. Числовой ряд и его сумма. Необходимое условие сходимости. Свойства сходящихся рядов. Признаки сходимости рядов с положительными членами. Ряды с произвольными членами. Абсолютная и условная сходимости. Знакочередующиеся ряды. Признак Лейбница. Степенные ряды. Область и радиус сходимости степенного ряда. Примеры разложений элементарных функций в степенные ряды.
5.2 Разделы дисциплины и междисциплинарные связи с обеспечиваемыми (последующими) дисциплинами
| № п/п | Наименование обеспе-чиваемых (последую-щих) дисциплин | № № разделов данной дисциплины, необходимых для изучения обеспечиваемых (последующих) дисциплин | |
| 1 | 2 | ||
| 1 | Статистика | * | * |
| 2 | Методы принятия управленческих решений | * | * |
| 3 | Теория вероятностей и математическая статистика | * | * |
| 4 | Математические методы и модели в принятии решений | * | * |
| 5 | Финансовая математика | * | * |
| 6 | Экономико-математические методы в управлении качеством продукции | * | * |
| 7 | Теория менеджмента | * | * |
| 8 | Маркетинг | * | * |
| 90 | Управление изменениями | | * |
| 10 | Логистика | * | * |
5.3. Разделы дисциплин и виды занятий
| № п/п | Наименование раздела дисциплины | Лекц. | Практ. зан. | СРС | Все-го час. |
| 1. | Линейная алгебра и аналитическая геометрия | 22 | 32 | 54 | 108 |
| 2. | Математический анализ | 40 | 32 | 36 | 108 |
6. Лабораторный практикум не предусмотрен.
7. Практические занятия (семинары)
| № п/п | № раздела дисциплины | Тематика практических занятий (семинаров) | Трудо-емкость (час.) |
| 1 | 1 | Векторная алгебра. | 2 |
| 2 | 1 | Метод координат. Прямая линия на плоскости. | 2 |
| 3 | 1 | Прямая линия на плоскости. | 2 |
| 4 | 1 | Прямая и плоскость в пространстве. | 2 |
| 5 | 1 | Прямая и плоскость в пространстве. | 2 |
| 6 | 1 | Полярные координаты. Кривые второго порядка. | 2 |
| 7 | 1 | Кривые второго порядка. | 2 |
| 8 | 1 | Действия над матрицами. | 2 |
| 9 | 1 | Вычисление определителей. | 2 |
| 10 | 1 | Вычисление обратной матрицы и решение матричных уравнений | 2 |
| 11 | 1 | Системы линейных уравнений. Теорема Крамера. | 2 |
| 12 | 1 | Вычисление ранга матрицы. Исследование системы линейных уравнений. | 2 |
| 13 | 1 | Решение неопределенных и однородных систем линейных уравнений. | 2 |
| 14 | 1 | Действия с n-мерными векторами. Линейная зависимость и линейная независимость векторов. | 2 |
| 15 | 1 | Разложение вектора по базису. | 2 |
| 16 | 1 | Контрольная работа №1. | 2 |
| 17 | 2 | Операции над множествами. Диаграммы Эйлера-Венна. Предел числовой последовательности. | 2 |
| 18 | 2 | Непрерывные функции. Вычисление пределов. | 2 |
| 19 | 2 | Производная и дифференциал функции. | 2 |
| 20 | 2 | Исследование функции и построение графика. | 2 |
| 21 | 2 | Исследование функции и построение графика. | 2 |
| 22 | 2 | Оптимизация функций. Формула Тейлора. | 2 |
| 23 | 2 | Частные производные. Полный дифференциал. | 2 |
| 24 | 2 | Градиент и производная по направлению. | 2 |
| 25 | 2 | Локальные экстремумы функции двух переменных. | 2 |
| 26 | 2 | Условный экстремум. Оптимизация функций. | 2 |
| 27 | 2 | Неопределенный интеграл. | 2 |
| 28 | 2 | Определенный интеграл. Несобственные интегралы. | 2 |
| 29 | 2 | Двойные интегралы. | 2 |
| 30 | 2 | Сходимость и расходимость числового ряда | 2 |
| 31 | 2 | Исследование степенных рядов | 2 |
| 32. | 2 | Контрольная работа №2. | 2 |
8. Примерная тематика курсовых работ – курсовые работы не предусмотрены.
9. Учебно-методическое и информационное обеспечение дисциплины:
а) основная литература
- Письменный Д.Т. Конспект лекций по высшей математике: полный курс. - М.: Айрис-пресс, 2006. - 608
- Шипачев В.С. Курс высшей математики: Учебник. – М.: ТК Велби, Изд-во Проспект, 2004.
- Шипачев В.С. Задачник по высшей математике: Учебное пособие для ВУЗов. – М.: Высшая школа, 2001.
- Минорский В.П. Сборник задач по высшей математике: Учебное пособие для ВТУЗов. – М.: Физматлит, 2006. – 336 с.
б) дополнительная литература
- Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики: Учебник. – М.: Гос.Изд.физ-мат.литература,1983.
- Математика в экономике: учебно-методическое пособие. Под ред. Н.Ш Кремера. – М.: Финстатинформ, 1999.
- Математический анализ для экономистов (под редакцией Гриба А.А. и Тарасюка А.Ф.) – М.: ФИЛИН, 2000.
- Солодовников А.С., Бабайцев В.А., Бранков А.В. Математика в экономика. – М.: Финансы и статистика, 1998.
- Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. – М.: Наука, 1984.
- Бугров Я.С. , Никольский С.М. Дифференциальное и интегральное исчисление. – М.: Наука, 1980.
- Бугров Я.С. Никольский С.М. Высшая математика: Задачник. – М.: Наука, 1982.
- Кузнецов Л.А. Сборник задач по высшей математике (типовые расчеты). – М.: Высшая школа, 1983.
в) программное обеспечение не предусмотрено
г) базы данных, информационно-справочные и поисковые системы:
10. Материально-техническое обеспечение дисциплины:
Документ-сканер, принтеры, компьютеры и пакеты программ обработки результатов тестирования.
11. Методические рекомендации по организации изучения дисциплины:
В течение первого семестра изучается раздел линейная алгебра и аналитическая геометрия. Во втором семестре изучается раздел математический анализ. Оба семестра заканчивается экзаменом. В процессе обучения студенты в каждом семестре сдают два теста и пишут контрольную работу. Максимальное число баллов за каждый тест равно 38, за контрольную работу – 24. Тест или контрольная работа считаются сданными, если за них получено не менее, соответственно, 20 и 15 баллов. Максимальное и минимальное число баллов, которое можно получить за работу в семестре, равно, соответственно, 100 и 55. Максимальное число баллов, которое можно получить на экзамене, также равно 100. Итоговая оценка (в баллах) вычисляется по формуле
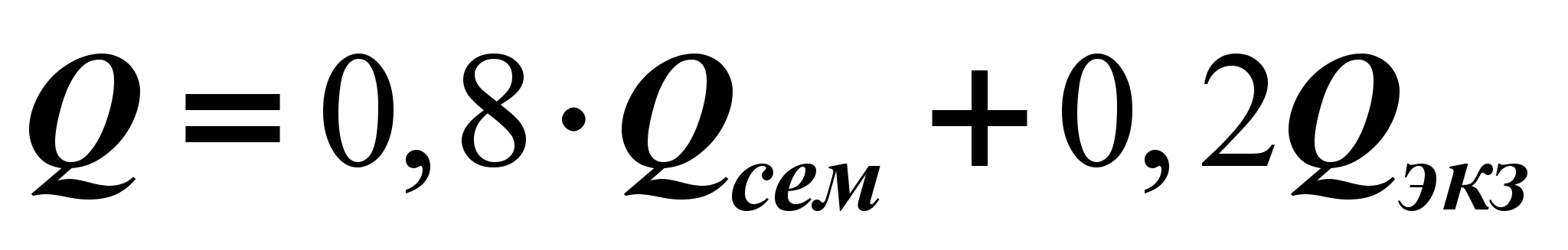 , где
, где 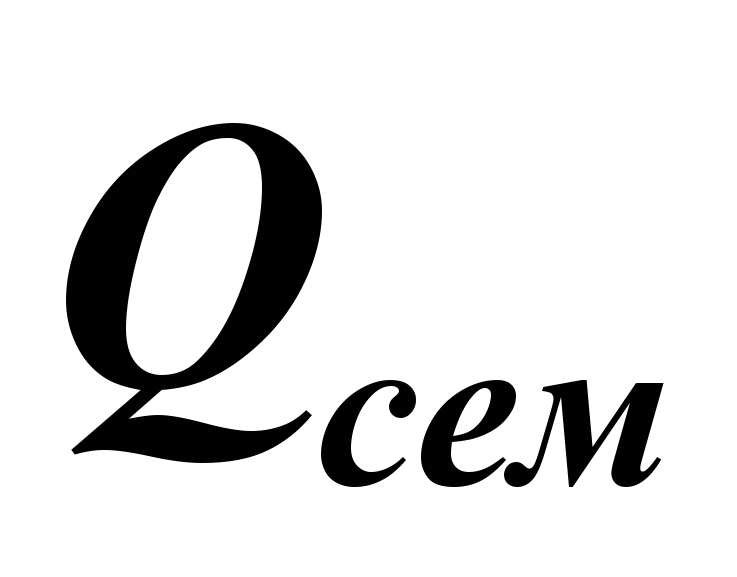 – баллы, полученные за работу в семестре, а
– баллы, полученные за работу в семестре, а 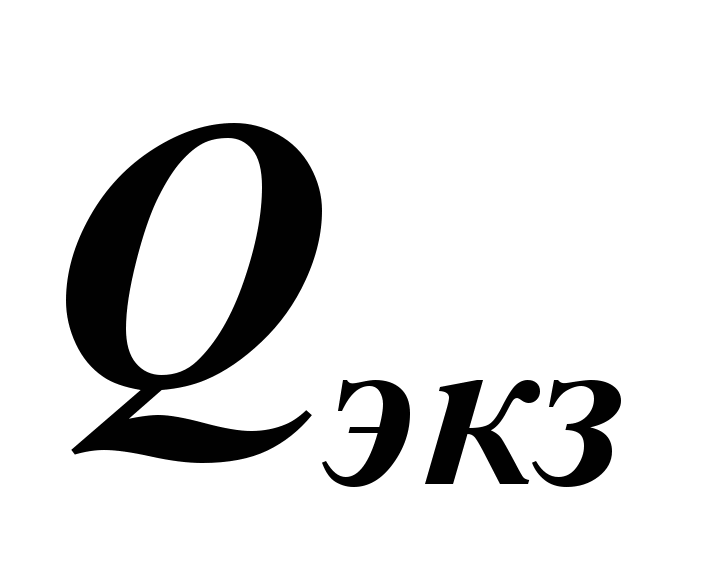 – за экзамен. Набранное итоговое количество баллов переводится в оценку согласно следующей таблице:
– за экзамен. Набранное итоговое количество баллов переводится в оценку согласно следующей таблице:| Итоговое количество баллов | оценка |
| до 55  | неудовлетворительно |
| от 55 до 70 | удовлетворительно |
| от 70 до 85 | хорошо |
| от 85 | отлично |
Примеры заданий теста №1.
Требуется ответить да или нет на предлагаемые вопросы.
Прямая задана уравнением
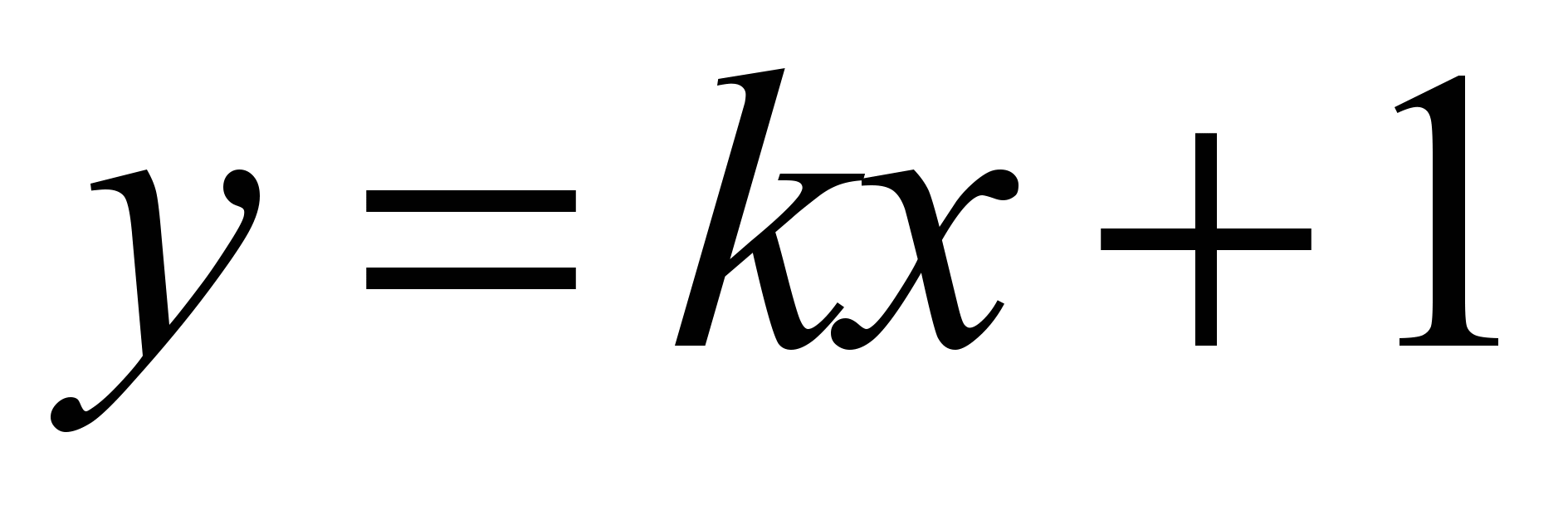 . Верно утверждение:
. Верно утверждение:Существует значение
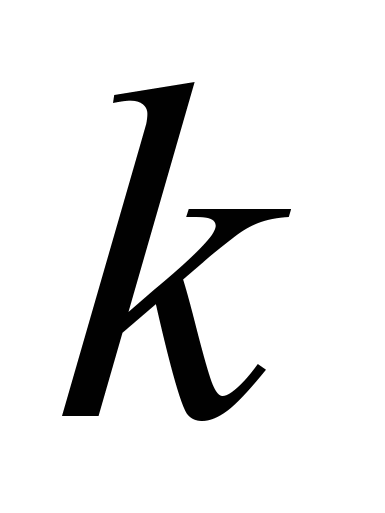 , при котором прямая проходит через точку
, при котором прямая проходит через точку 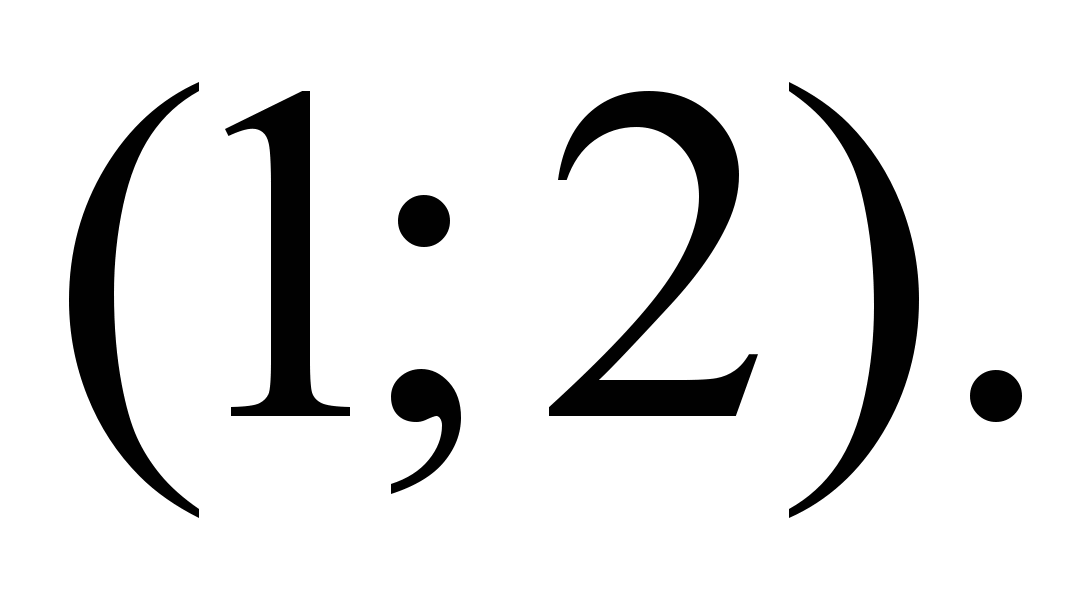
Абсцисса точки пересечения прямой с осью
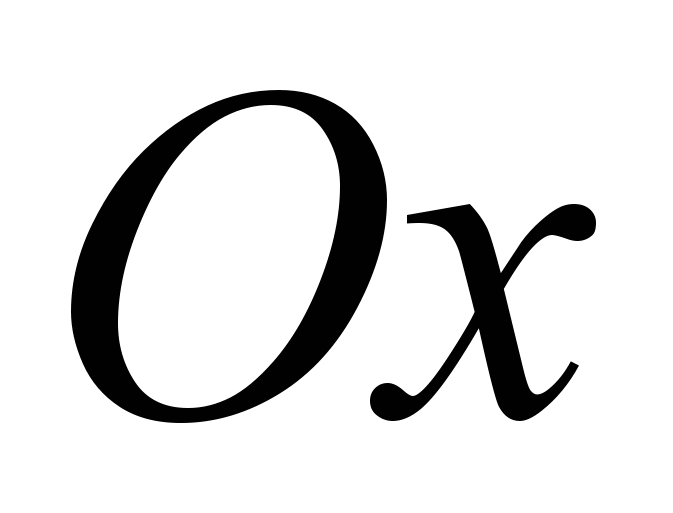 положительна только при отрицательных значениях
положительна только при отрицательных значениях 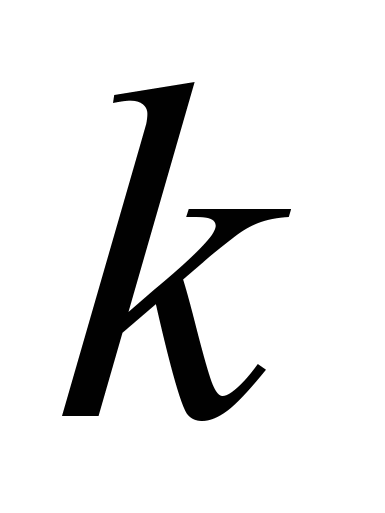 .
.При
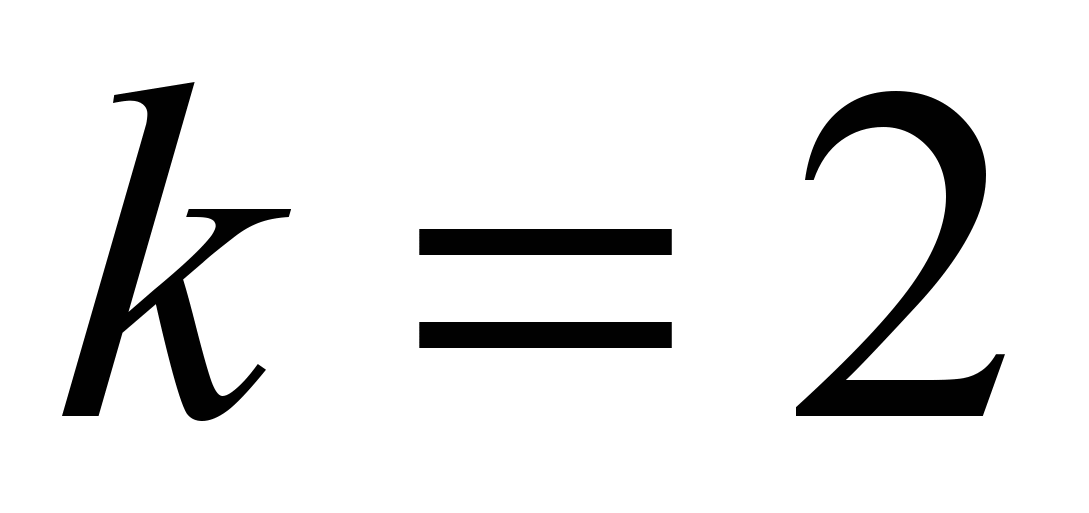 данная прямая перпендикулярна прямой
данная прямая перпендикулярна прямой  .
.Если
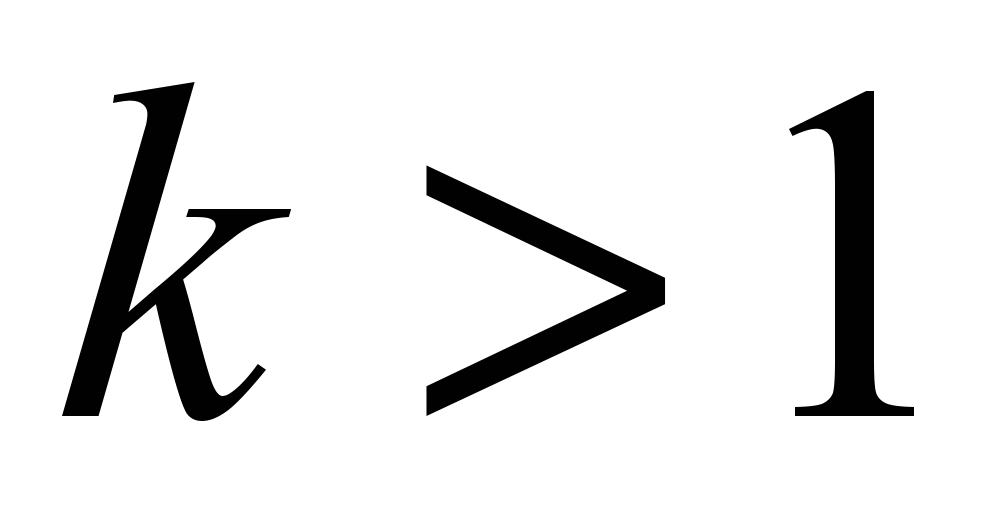 , то прямая пересекает ось абсцисс в точке с координатой больше, чем
, то прямая пересекает ось абсцисс в точке с координатой больше, чем 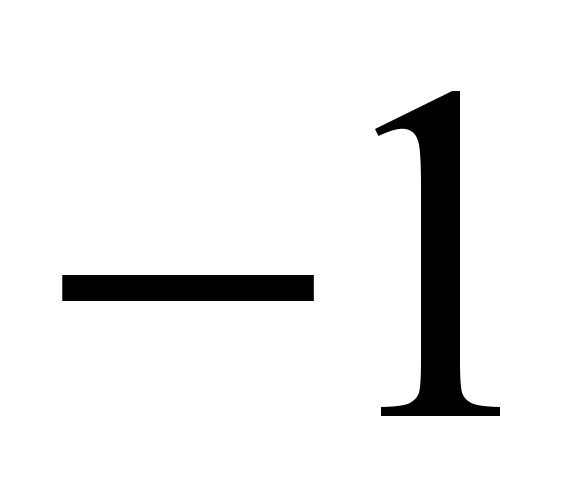 .
.Существует значение
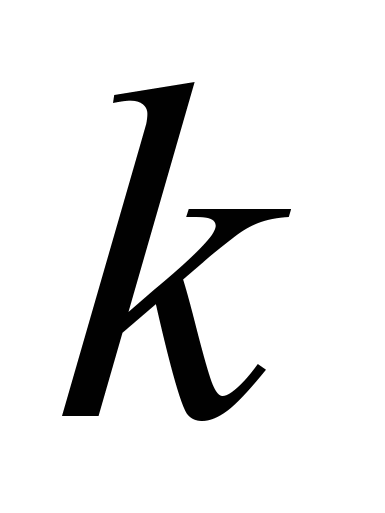 , при котором прямая проходит через точки
, при котором прямая проходит через точки  и
и 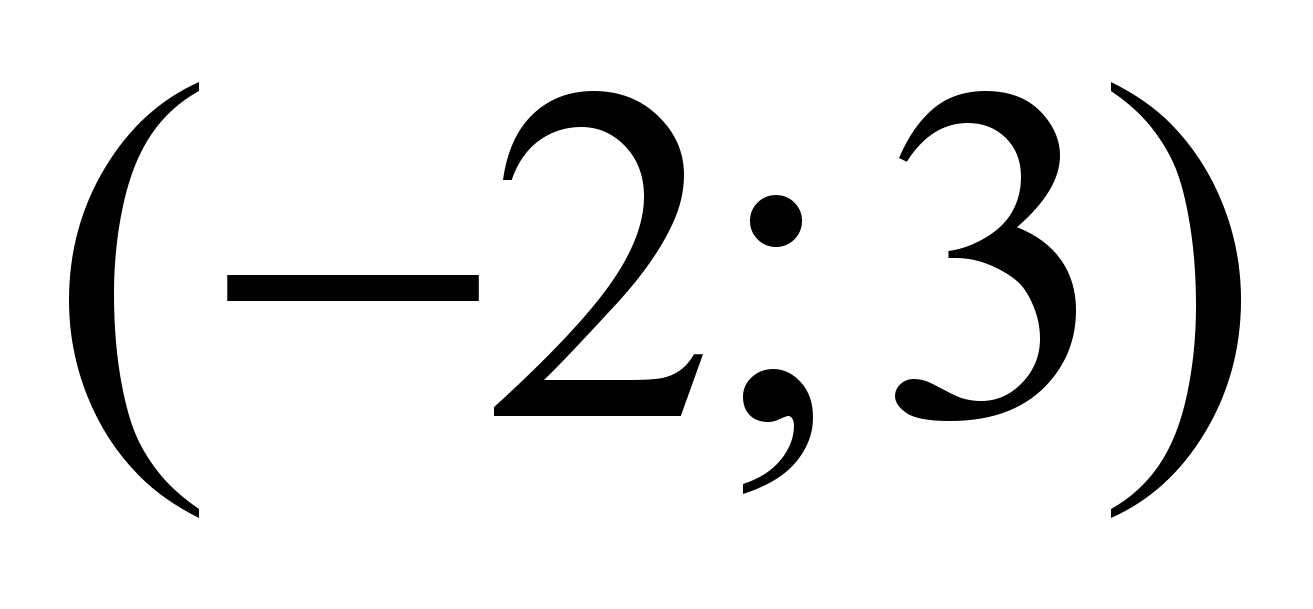 .
.Требуется выбрать правильные ответы.
На координатной плоскости имеется отрезок, соединяющий две точки с абсциссами разных знаков. Тогда этот отрезок…
А. обязательно пересекает ось ординат
Б. обязательно пересекает ось абсцисс
В. обязательно пересекает каждую из осей координат
Г. не пересекает ни одну из осей координат
Требуется вычислить значение.
Найдите радиус окружности, касающейся оси
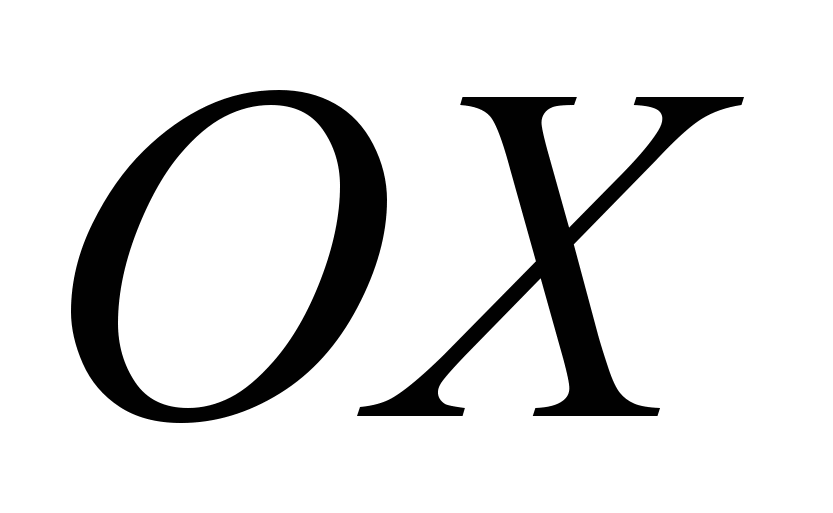 в точке
в точке 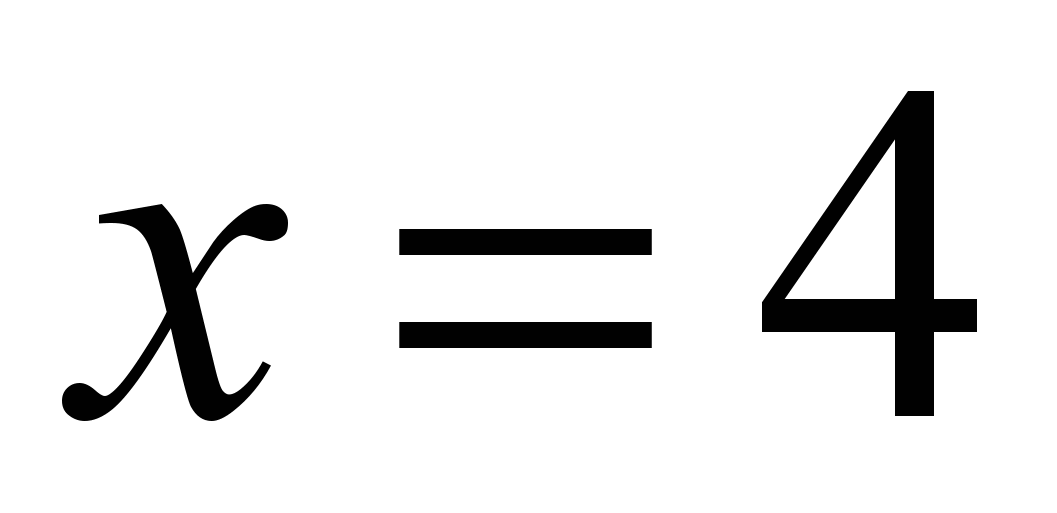 , если центр окружности лежит на прямой
, если центр окружности лежит на прямой  .
.Примеры заданий теста №2.
Требуется ответить да или нет на предлагаемые вопросы.
Дана система
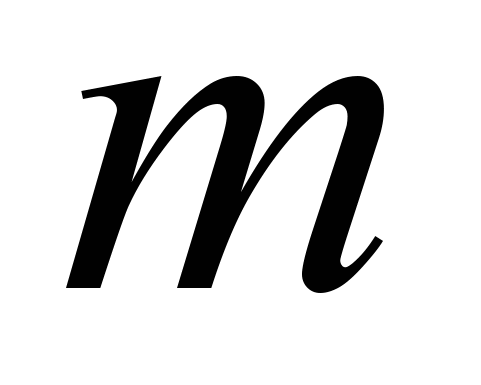 линейных уравнений с
линейных уравнений с 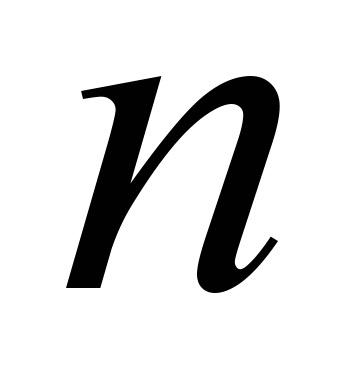 неизвестными. Пусть ранг матрицы этой системы равен
неизвестными. Пусть ранг матрицы этой системы равен 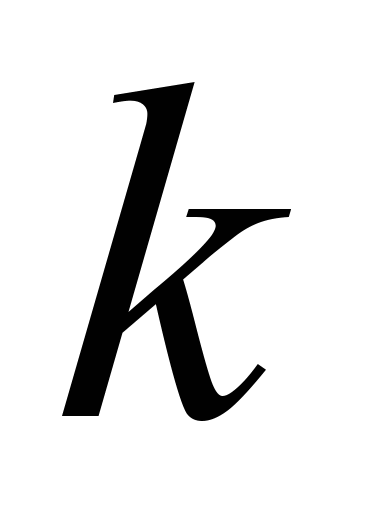 , а ранг расширенной матрицы системы равен
, а ранг расширенной матрицы системы равен 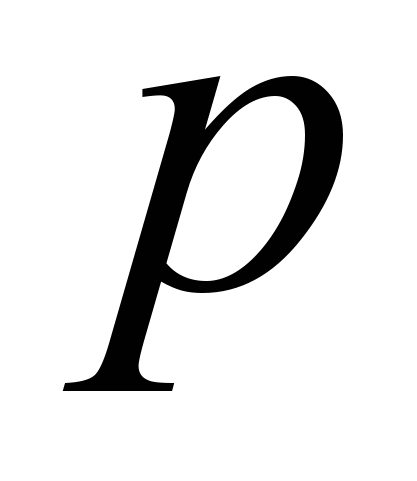 . Правильными утверждениями являются…
. Правильными утверждениями являются…если система имеет хотя бы одно решение, то

если
 и
и 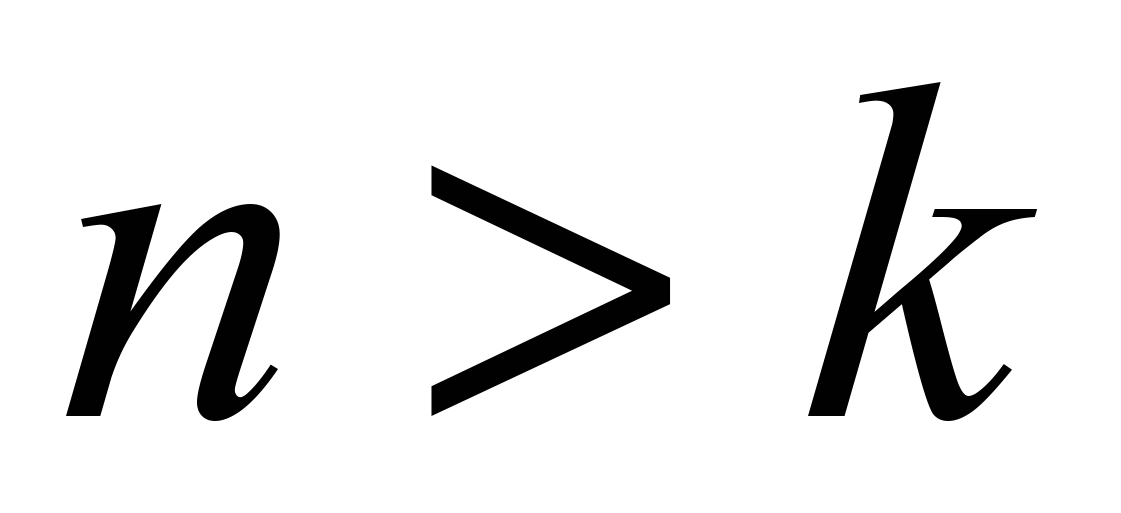 , то система имеет бесконечное множество решений
, то система имеет бесконечное множество решенийесли
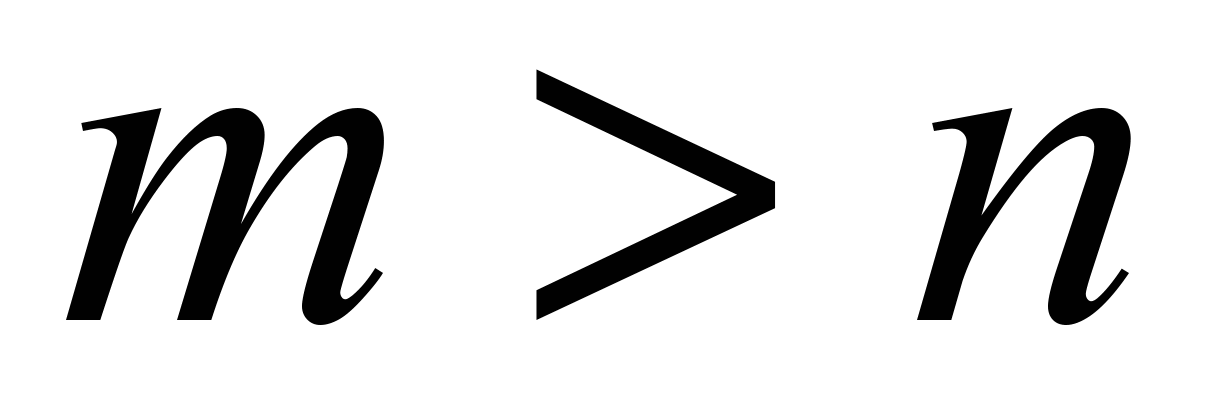 , то система не имеет решений
, то система не имеет решенийесли
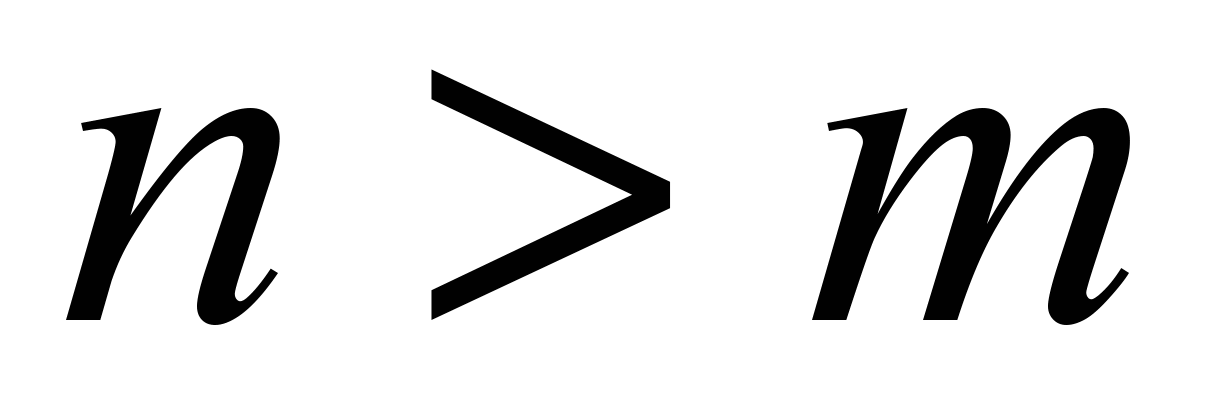 , то система имеет хотя бы одно решение
, то система имеет хотя бы одно решениеТребуется выбрать правильные ответы.
Некоторый элемент определителя равен 2, его алгебраическое дополнение равно 5. Если этот элемент определителя увеличить на 3, то новый определитель будет больше исходного…
А. на 15 Б. на 3 В. на 6 Г. в 15 раз
Требуется вычислить значение.
Даны матрица
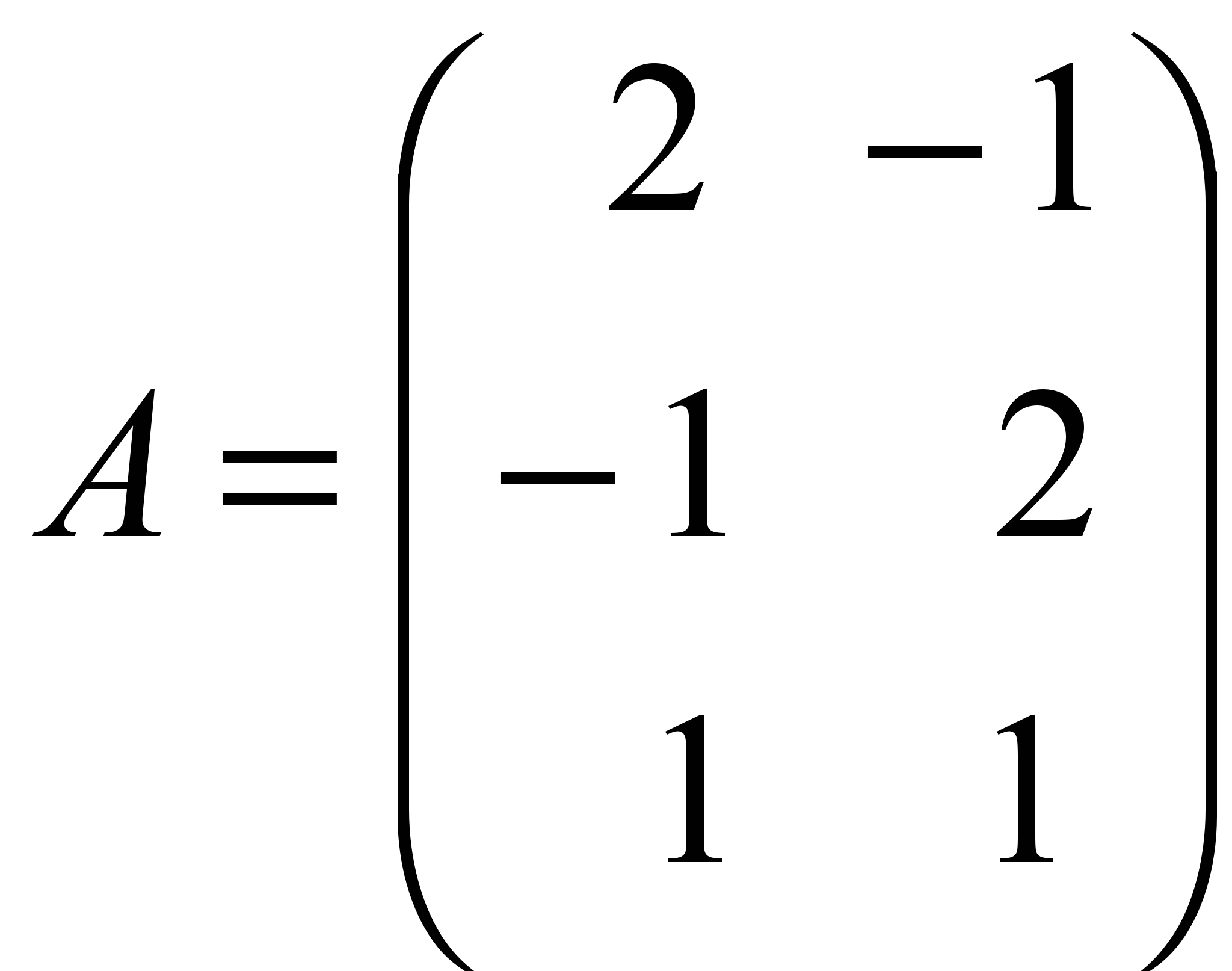 и два вектора
и два вектора  и
и 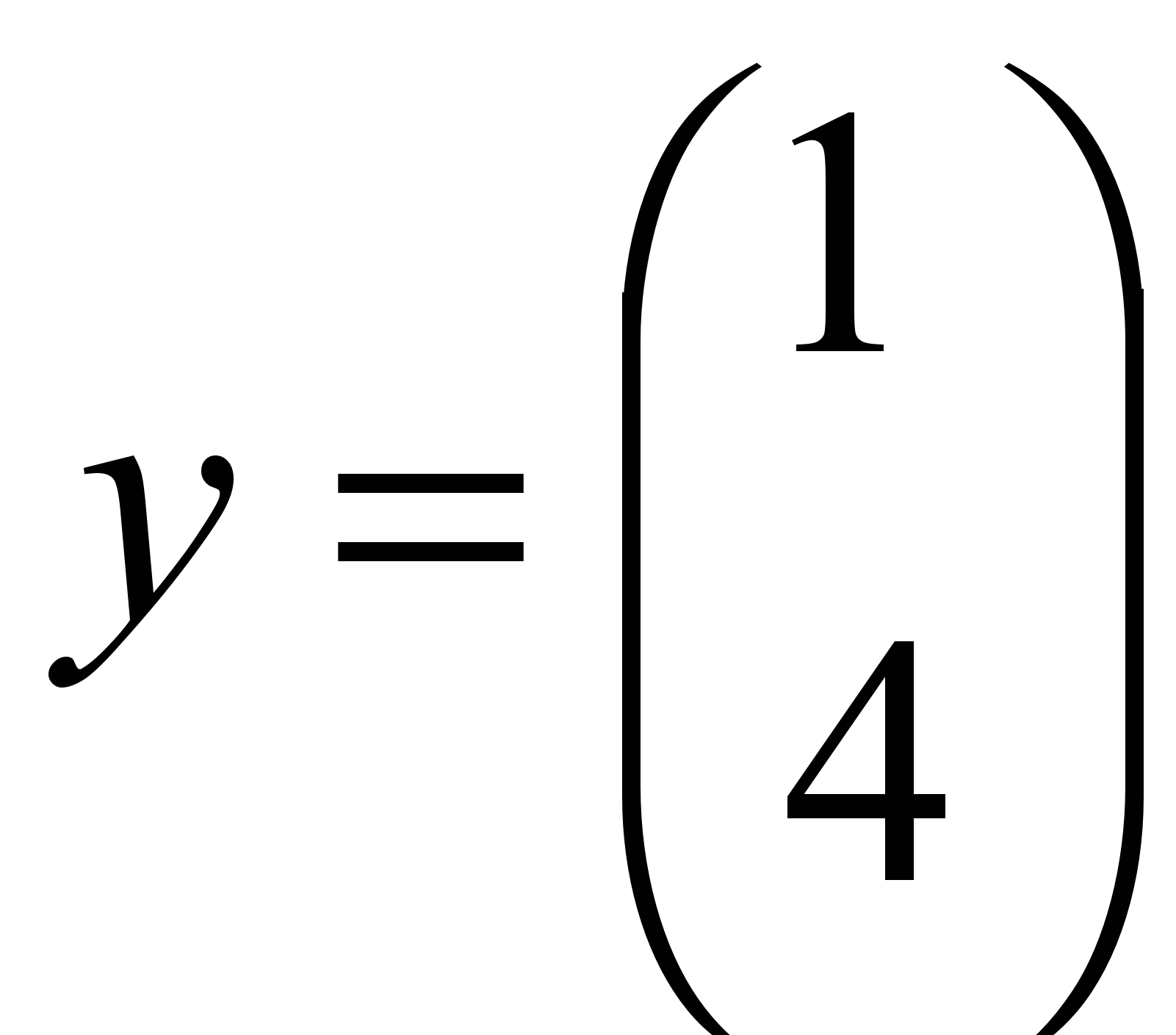 . Найти значение параметра
. Найти значение параметра  , при котором векторы
, при котором векторы 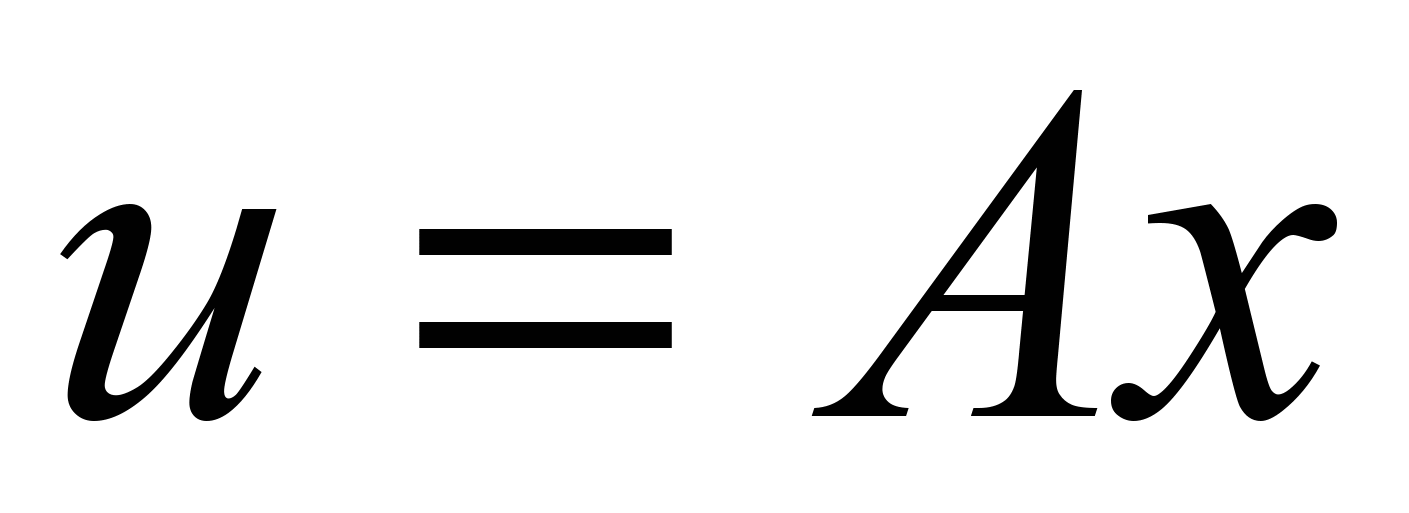 и
и  перпендикулярны.
перпендикулярны.Примеры задач и вопросов теста №3.
Требуется ответить да или нет на предлагаемые вопросы.
Дан график производной
 некоторой функции
некоторой функции 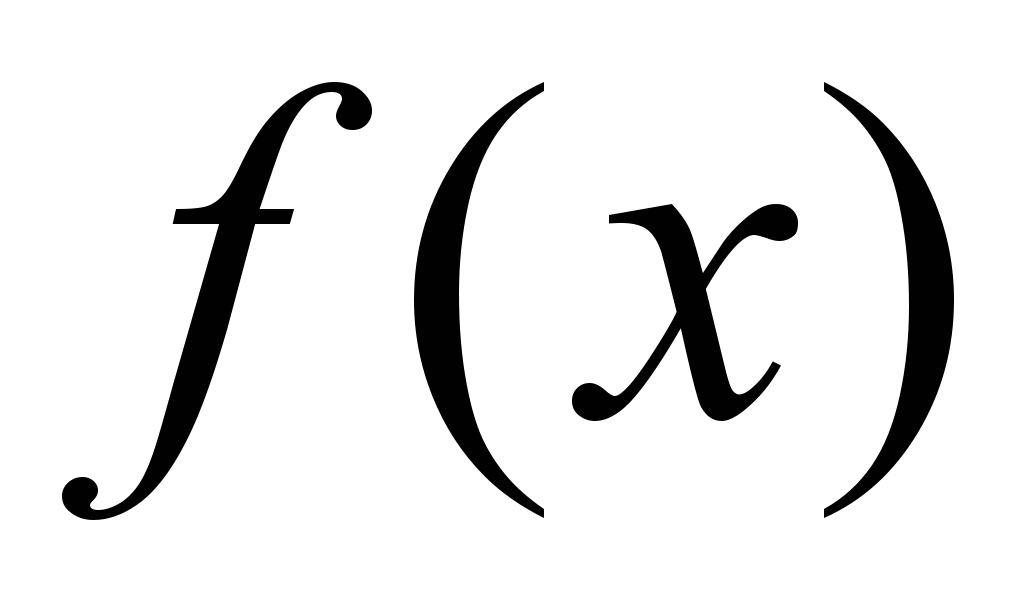 :
: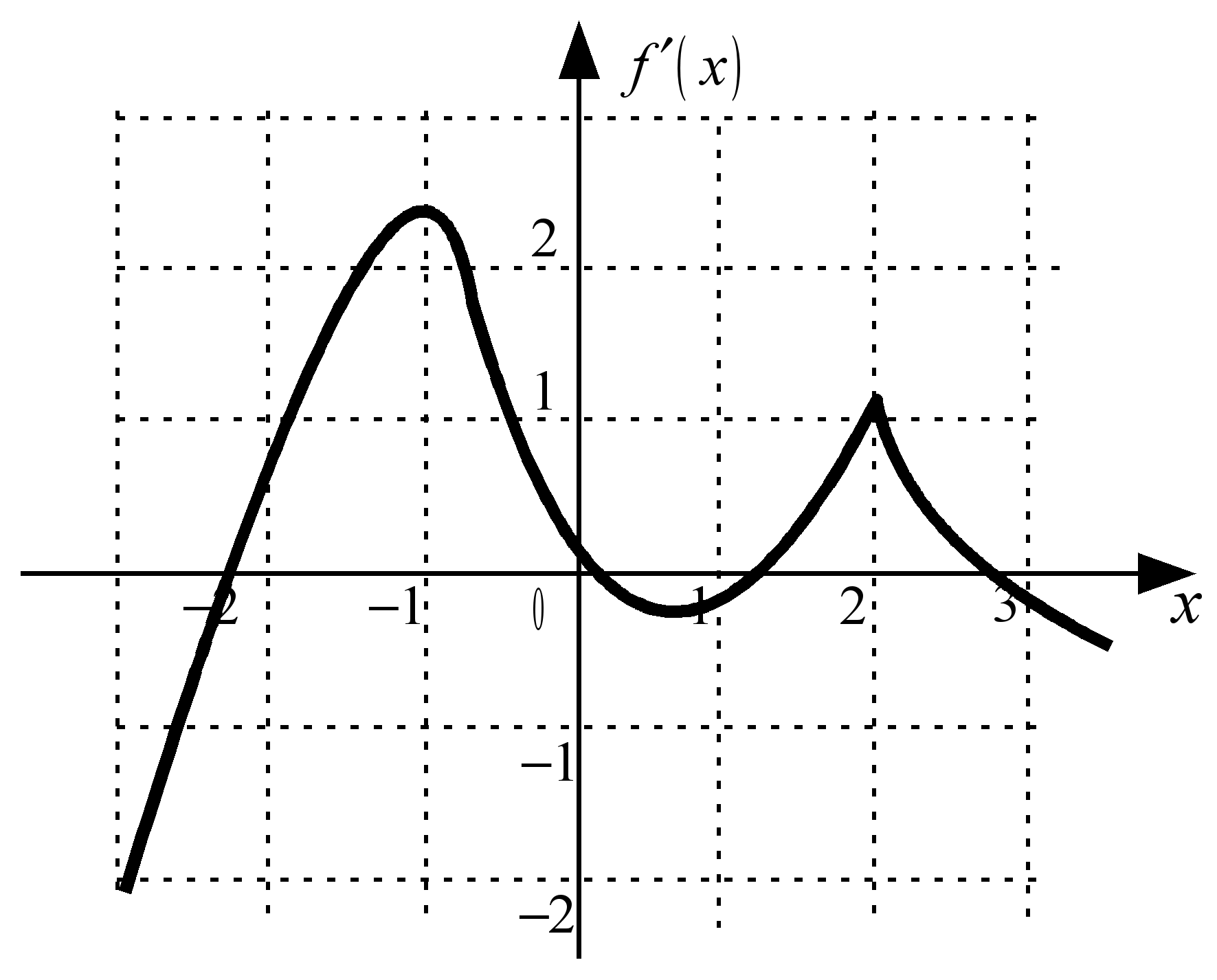
Справедливо утверждение:
на промежутке
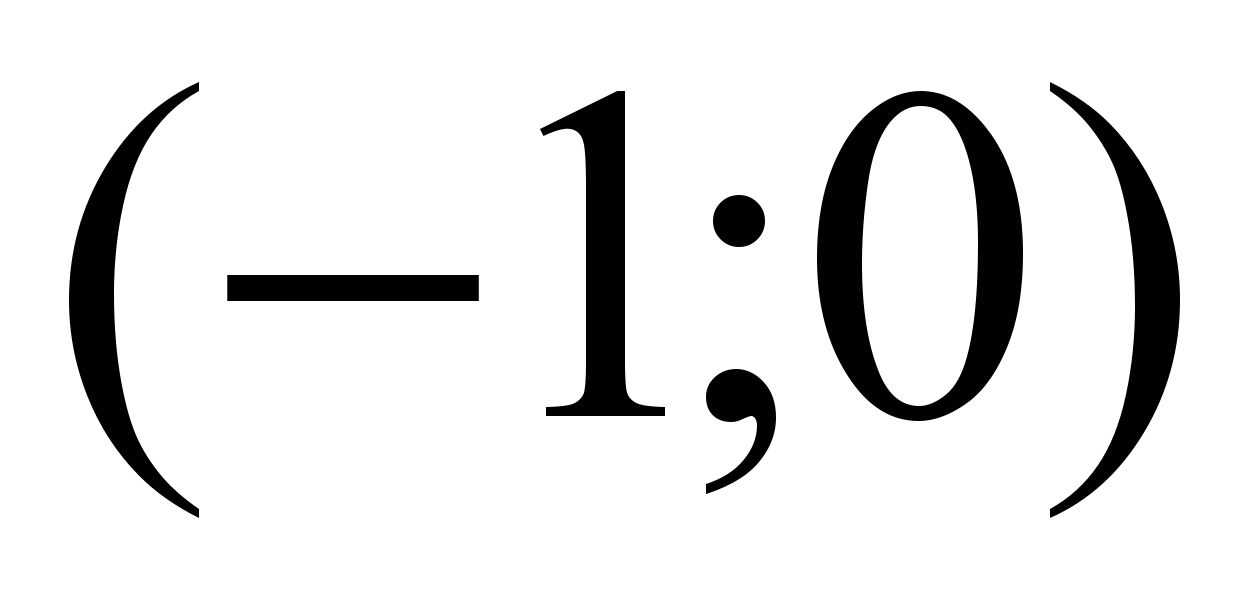 функция
функция 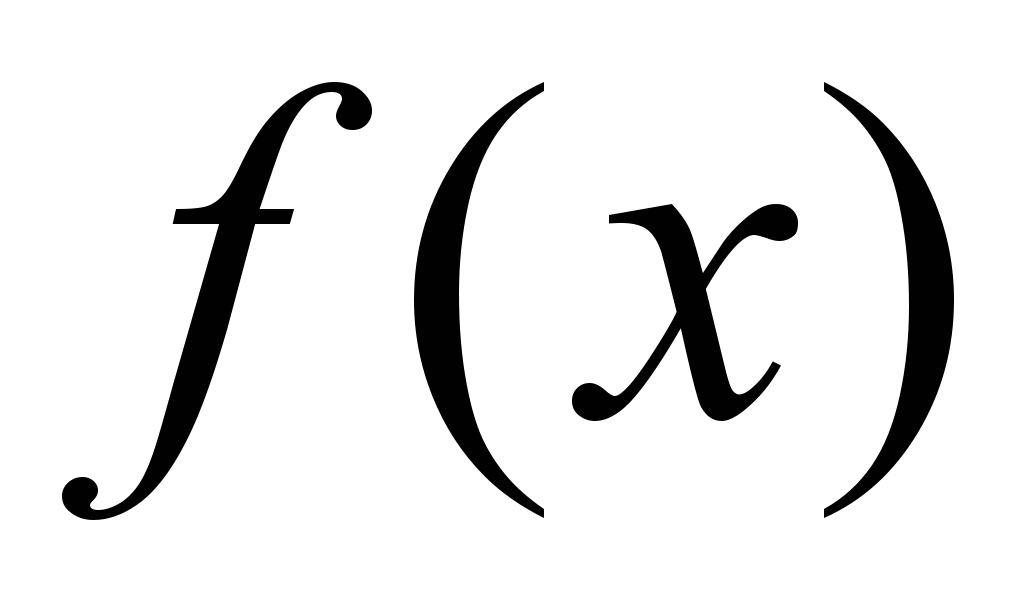 возрастает
возрастаетна промежутке
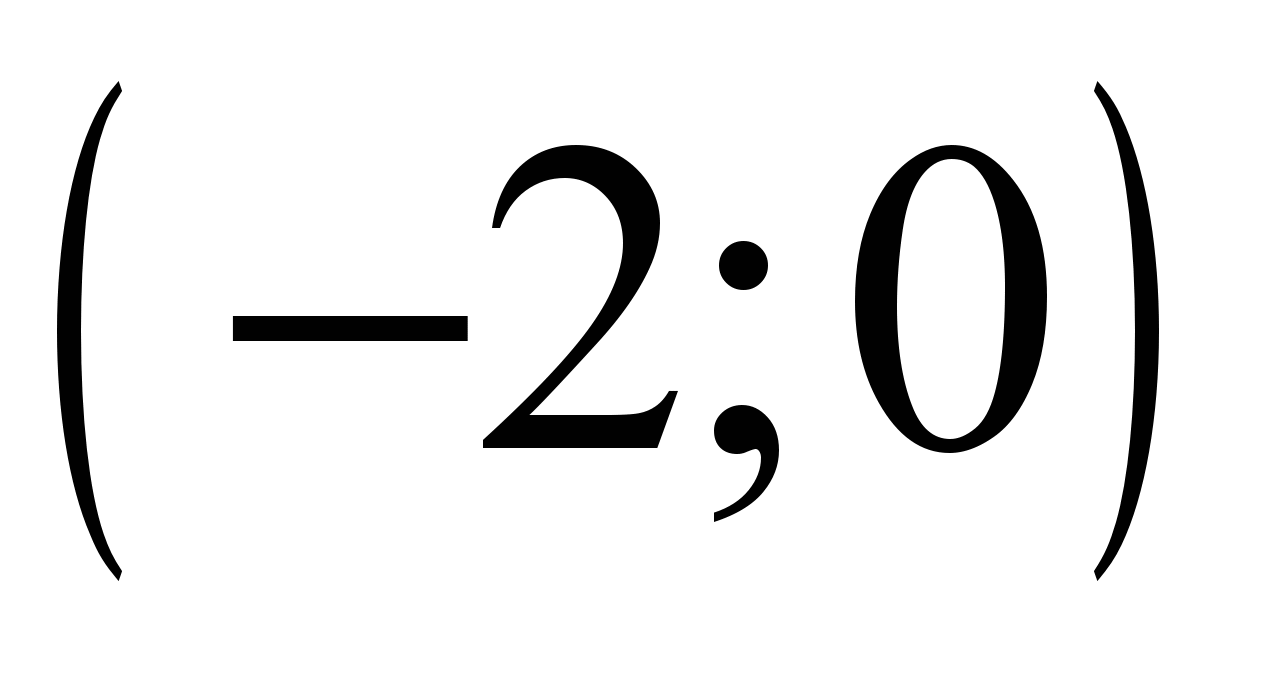 график функции
график функции 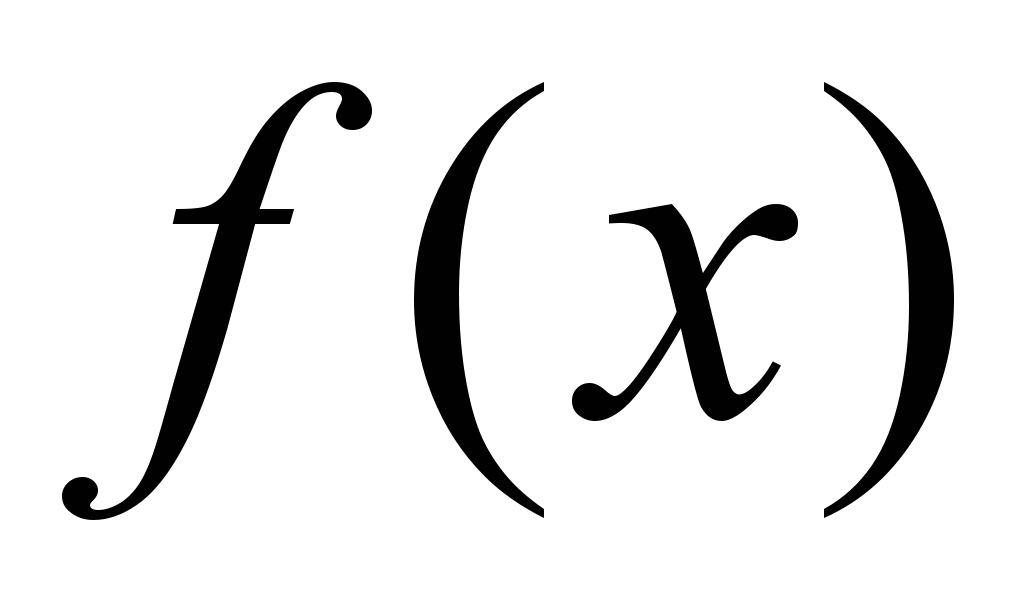 имеет точку перегиба
имеет точку перегибав точке
 функция
функция 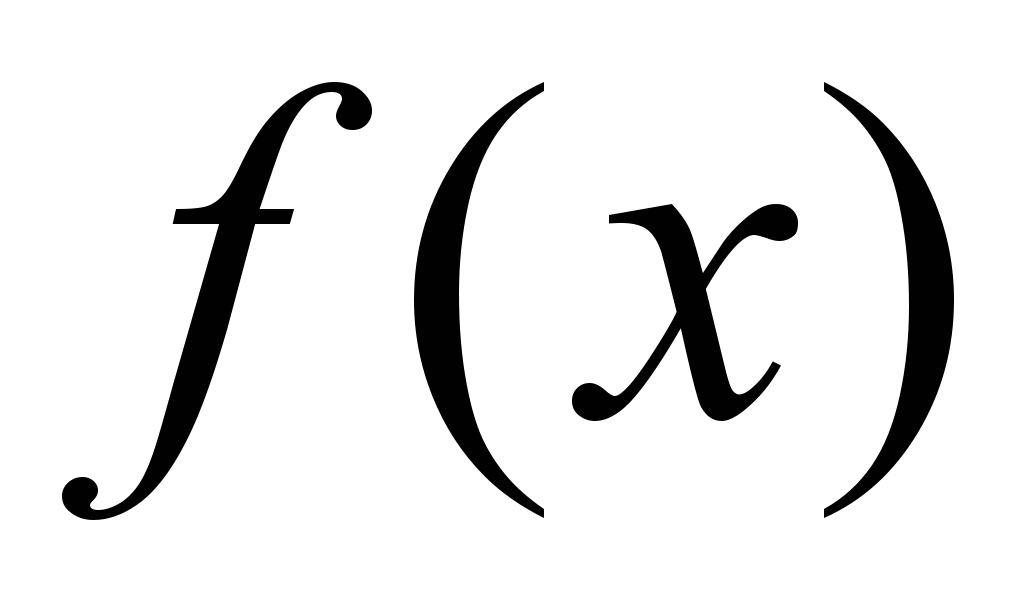 имеет максимум
имеет максимумна промежутке
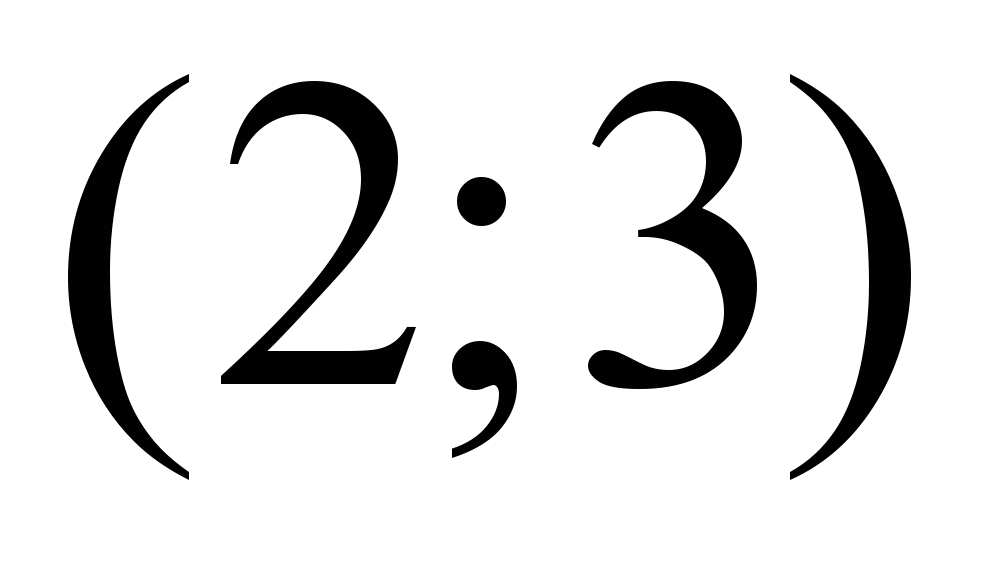 функция
функция 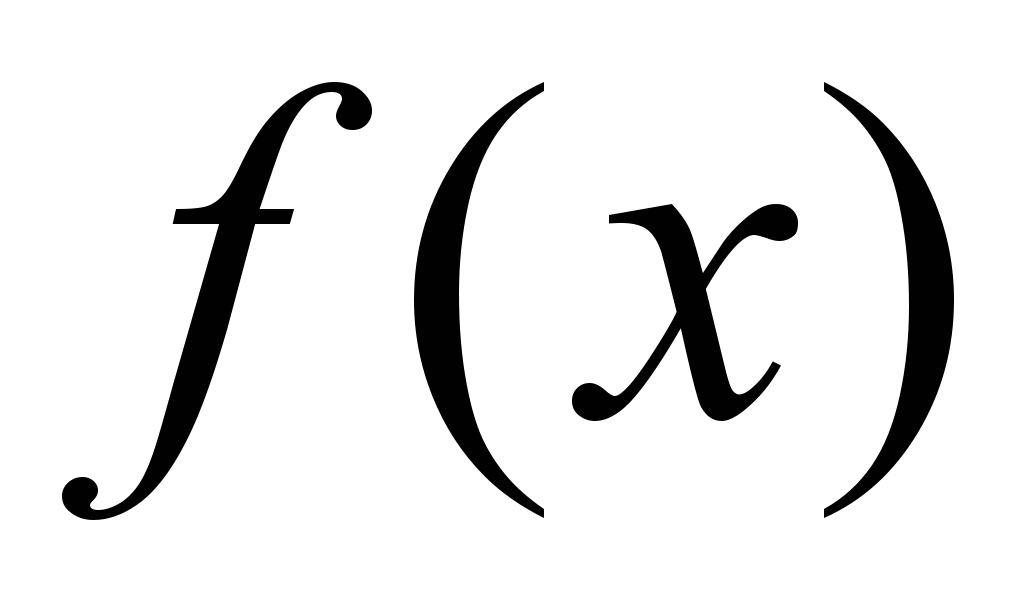 убывает
убываетТребуется выбрать правильные ответы.
Пусть функция
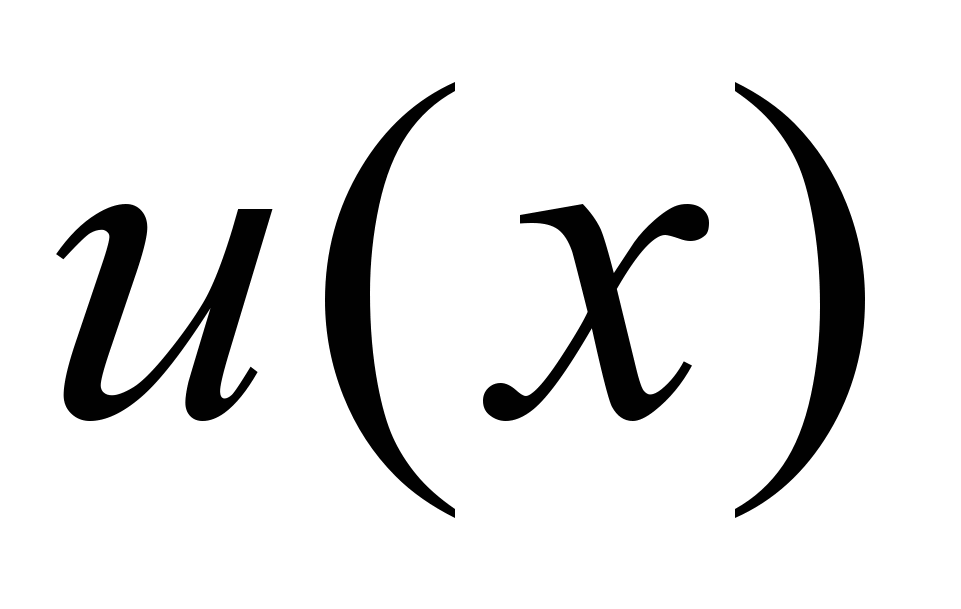 определена и ограничена в некоторой окрестности точки
определена и ограничена в некоторой окрестности точки  , а функция
, а функция 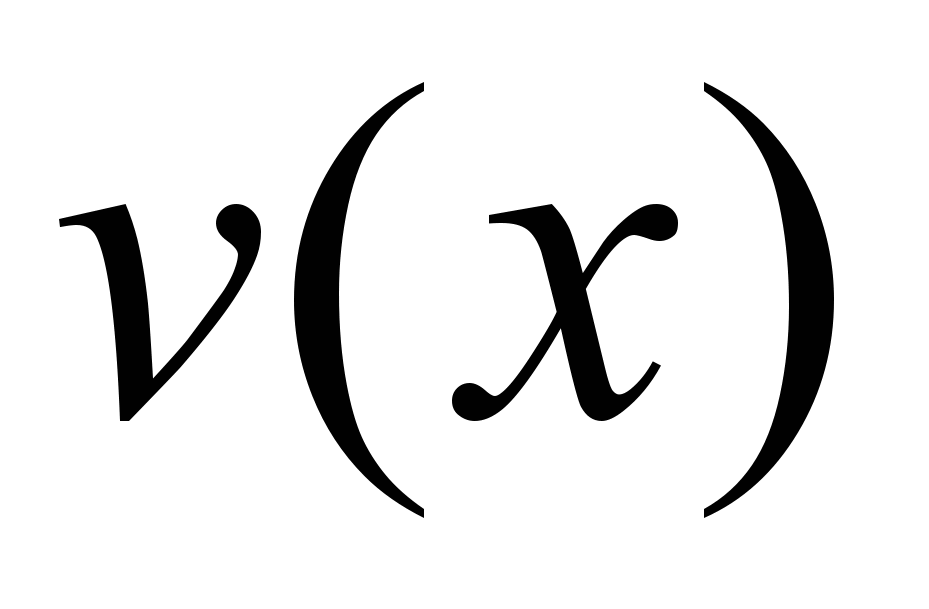 является бесконечно большой при
является бесконечно большой при 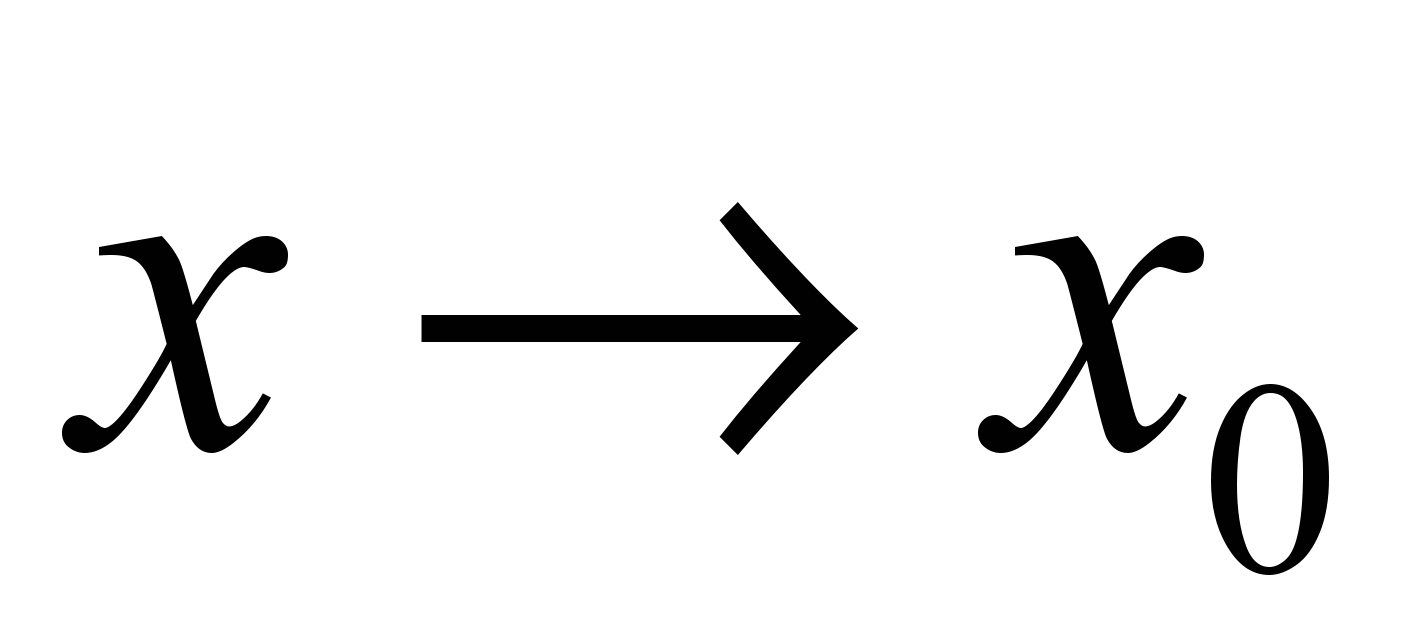 . Тогда при
. Тогда при 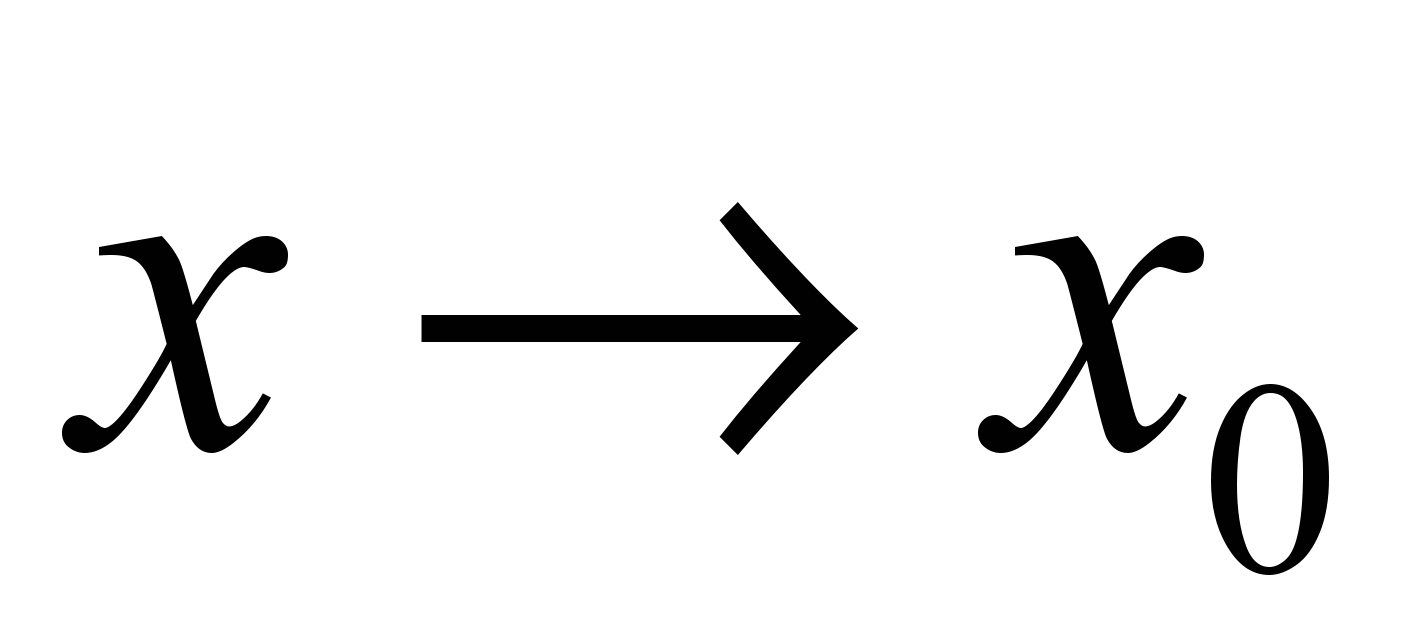 функция
функция 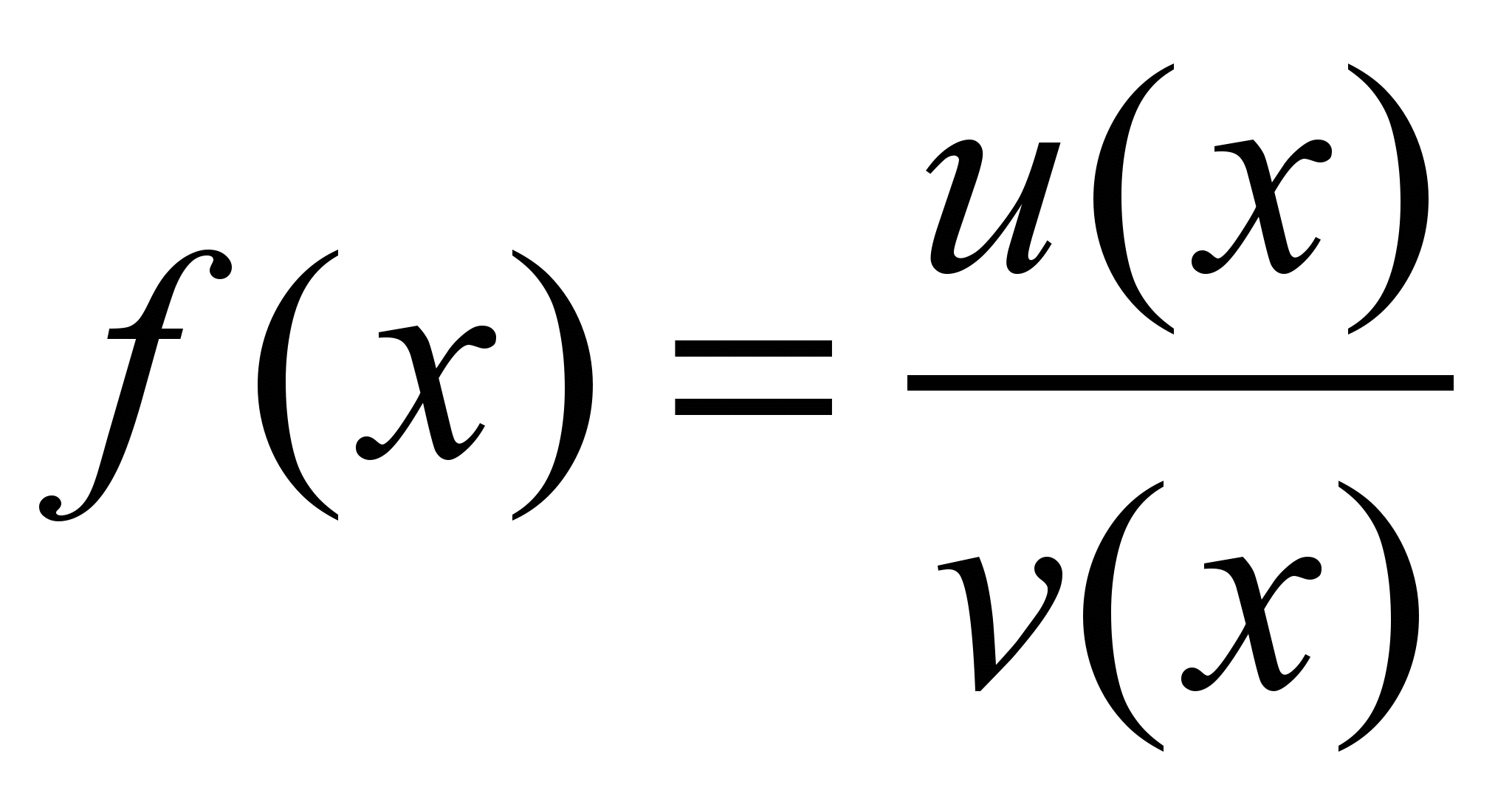 будет…
будет…А. бесконечно малая Б. бесконечно большая В. может не иметь предела Г. может иметь ненулевой предел
Требуется вычислить значение.
Для функции
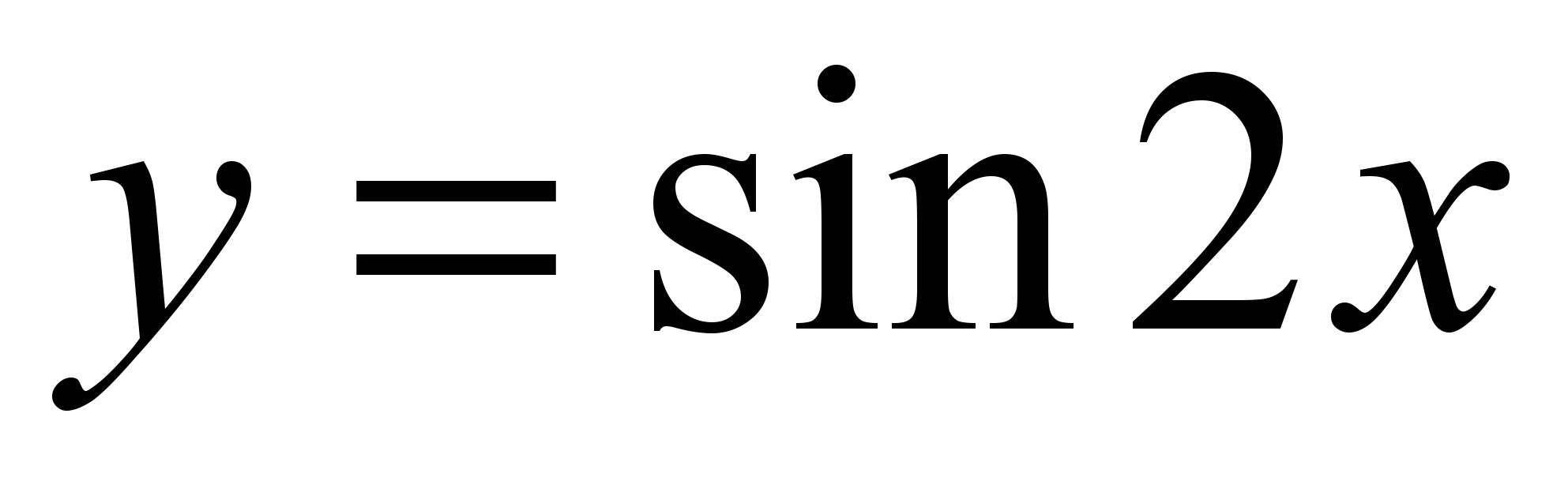 выписана формула Тейлора по степеням
выписана формула Тейлора по степеням  . Найти значение коэффициента при
. Найти значение коэффициента при  .
.Примеры задач и вопросов теста №4.
Требуется ответить да или нет на предлагаемые вопросы.
Пусть
 , Тогда верны следующие утверждения:
, Тогда верны следующие утверждения:Точка
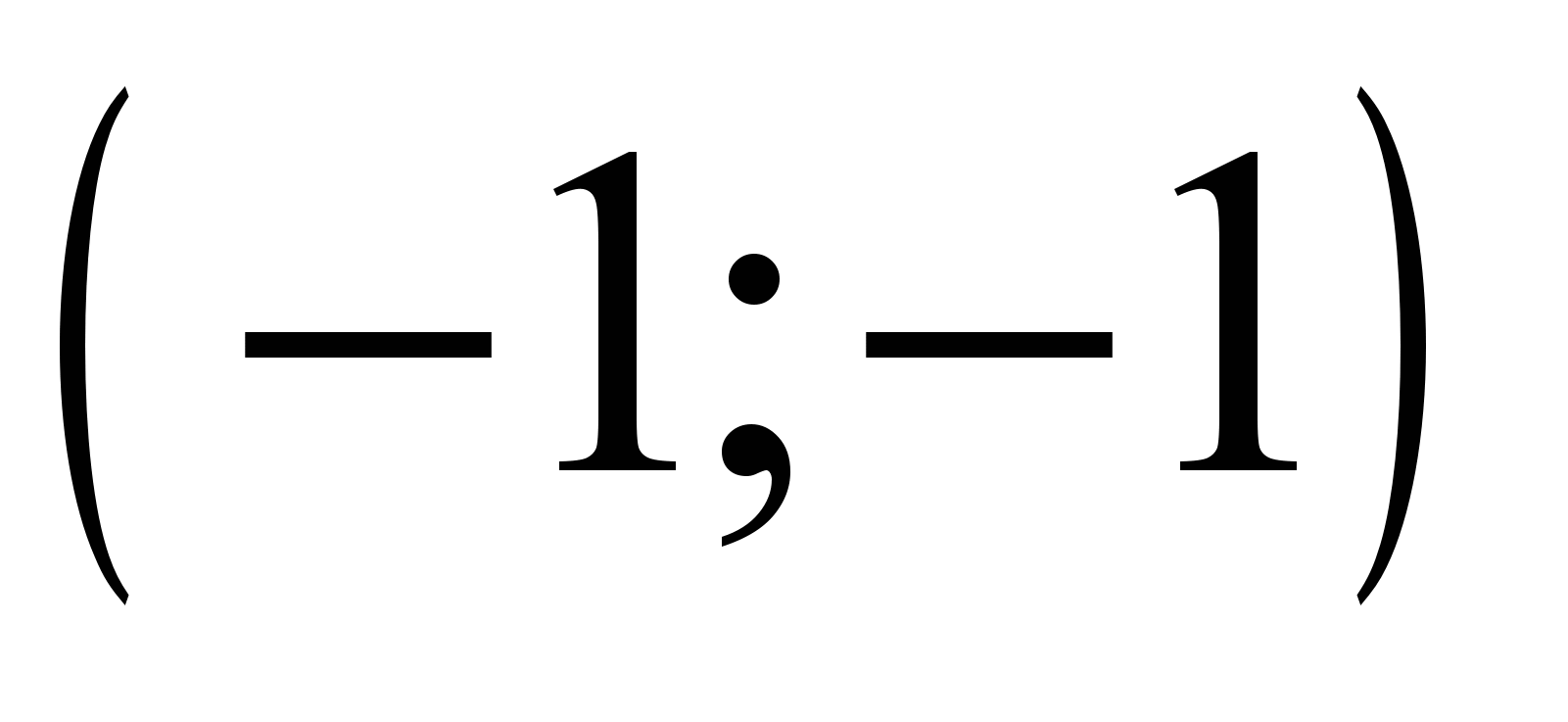 является точкой минимума функции
является точкой минимума функции  .
.Функция
 не имеет точек максимума.
не имеет точек максимума.Точка
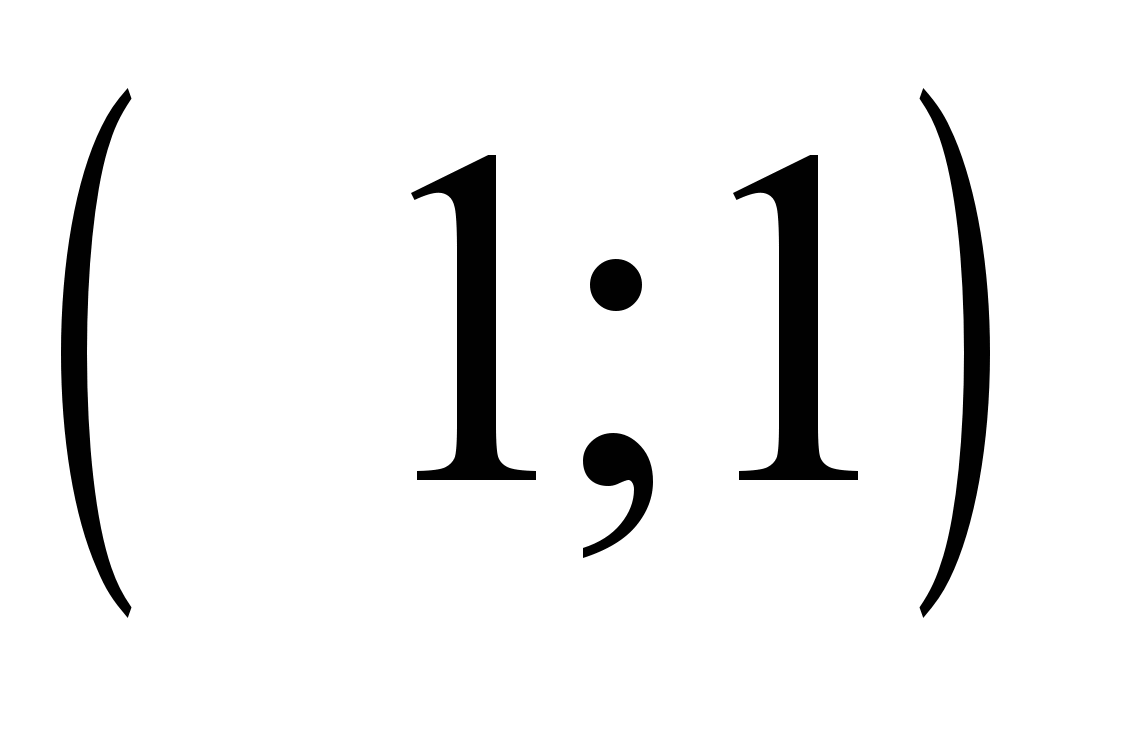 является стационарной точкой функции
является стационарной точкой функции  .
.Длина вектора - градиента функции
 в точке
в точке 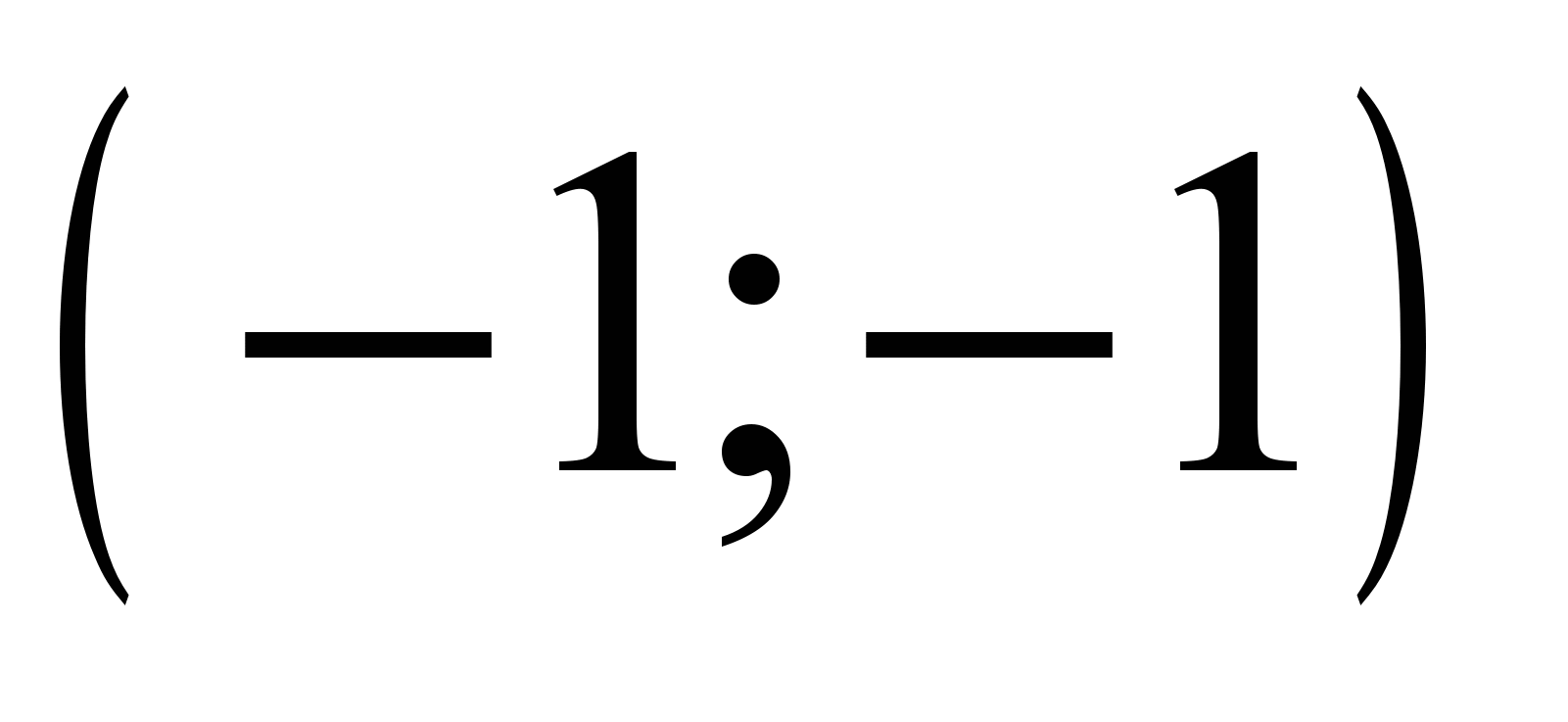 больше 1.
больше 1.Требуется выбрать правильные ответы.
Дан график функции
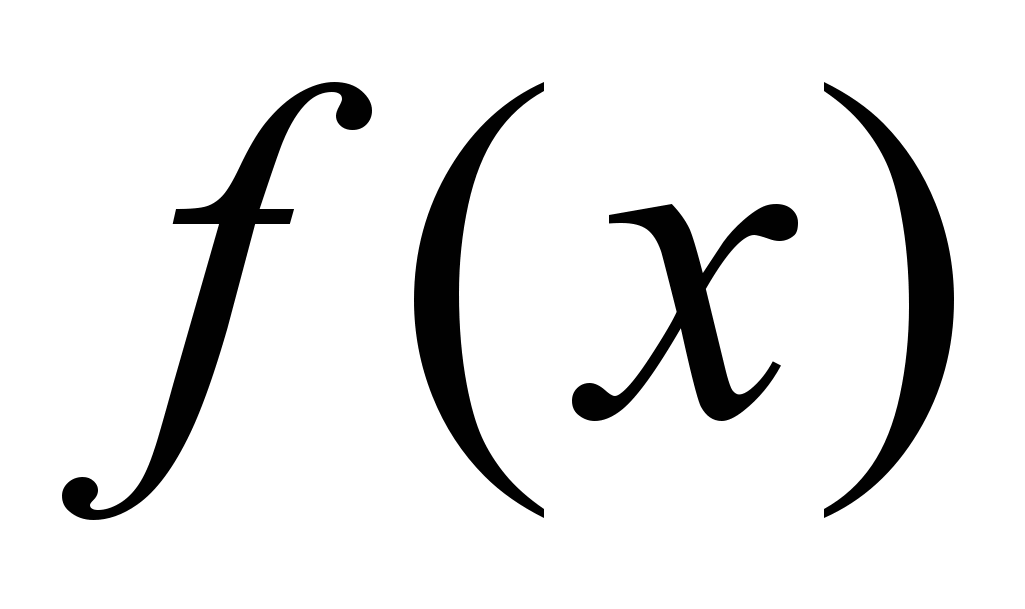 на отрезке:
на отрезке: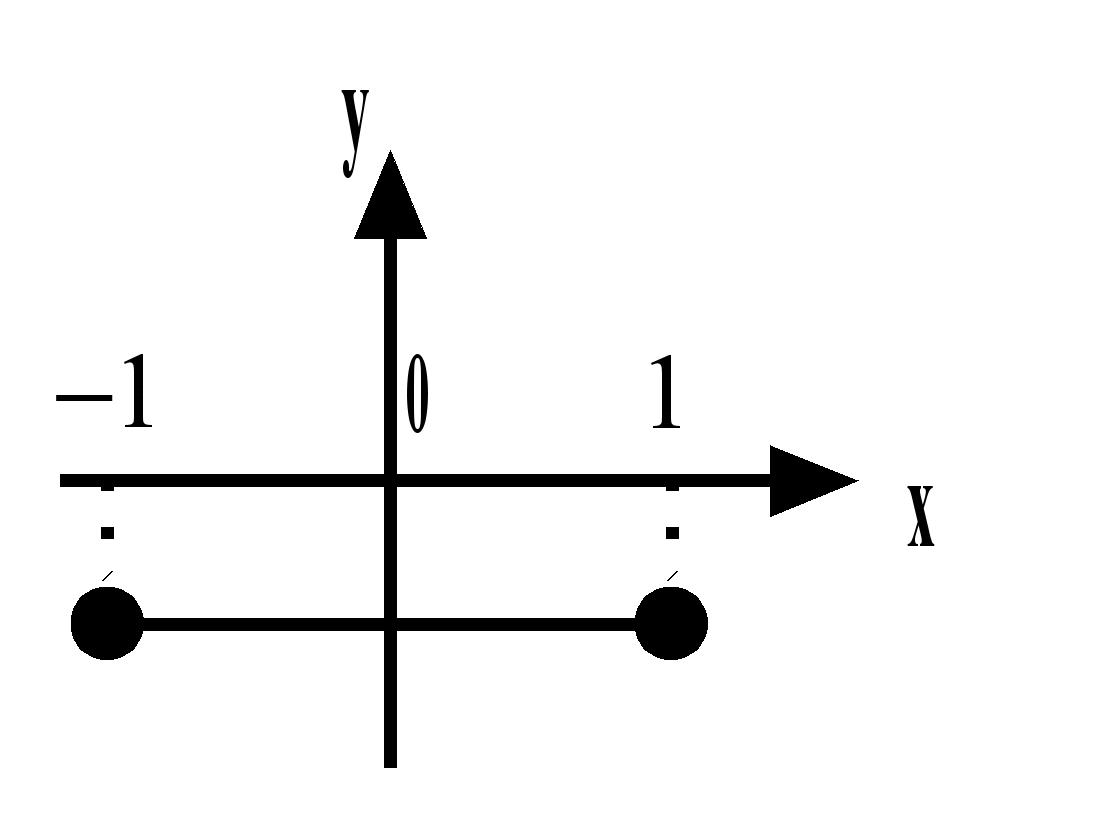
Тогда любая ее первообразная
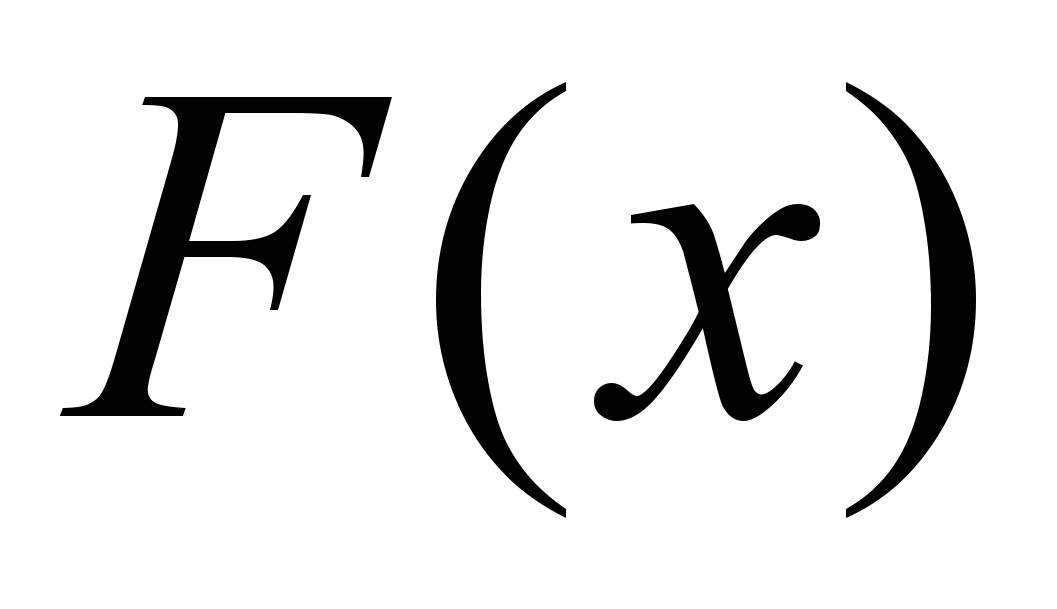 на этом отрезке принимает наименьшее значение в А. точке 1 Б. в точке
на этом отрезке принимает наименьшее значение в А. точке 1 Б. в точке  В. в точке 0 Г. в точках 1 и
В. в точке 0 Г. в точках 1 и  одновременно
одновременноТребуется вычислить значение.
Для функции
 значение интеграла
значение интеграла равно…
равно…Примеры задач контрольной работы №1.
1. Решить матричное уравнение:

- По формулам Крамера найти значение переменной
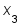 :
:

- Исследовать и решить систему линейных уравнений:
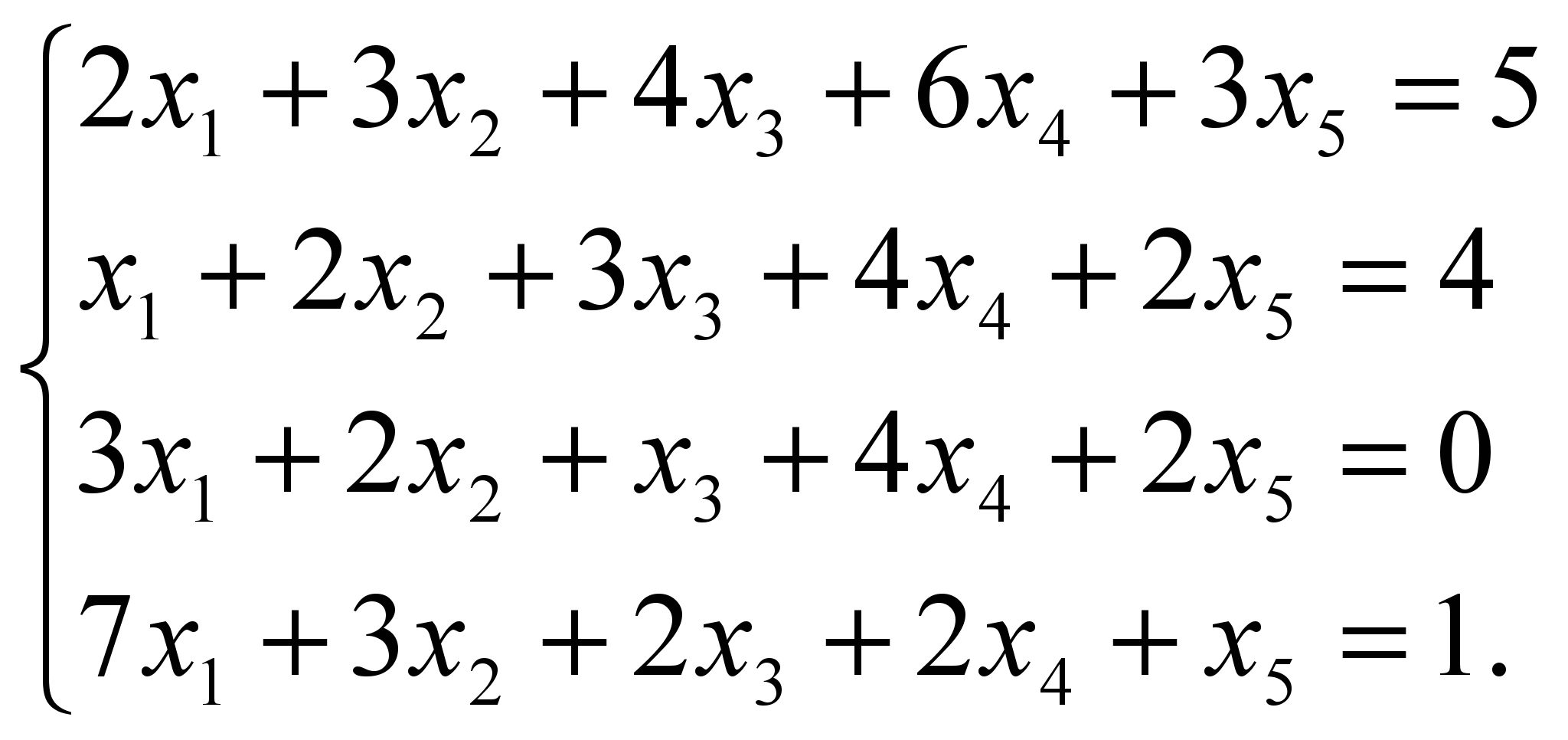
- Найти разложение вектора
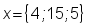 в базисе
в базисе
 .
.- Найти собственные числа и собственные векторы матрицы
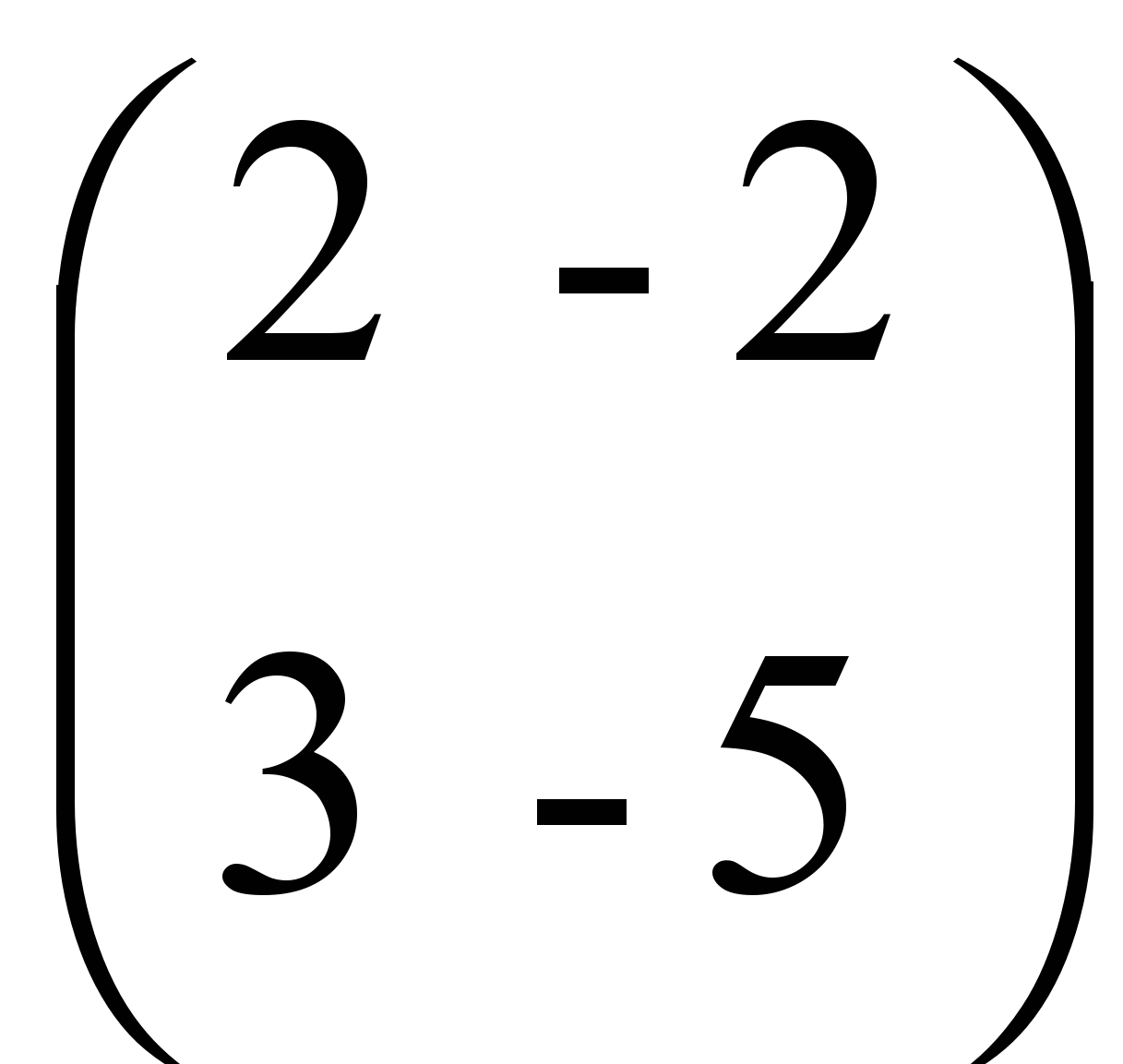 .
.
Примеры задач контрольной работы №2.
Задача №1. Изменить порядок интегрирования
 .
.Задача №2. Вычислить
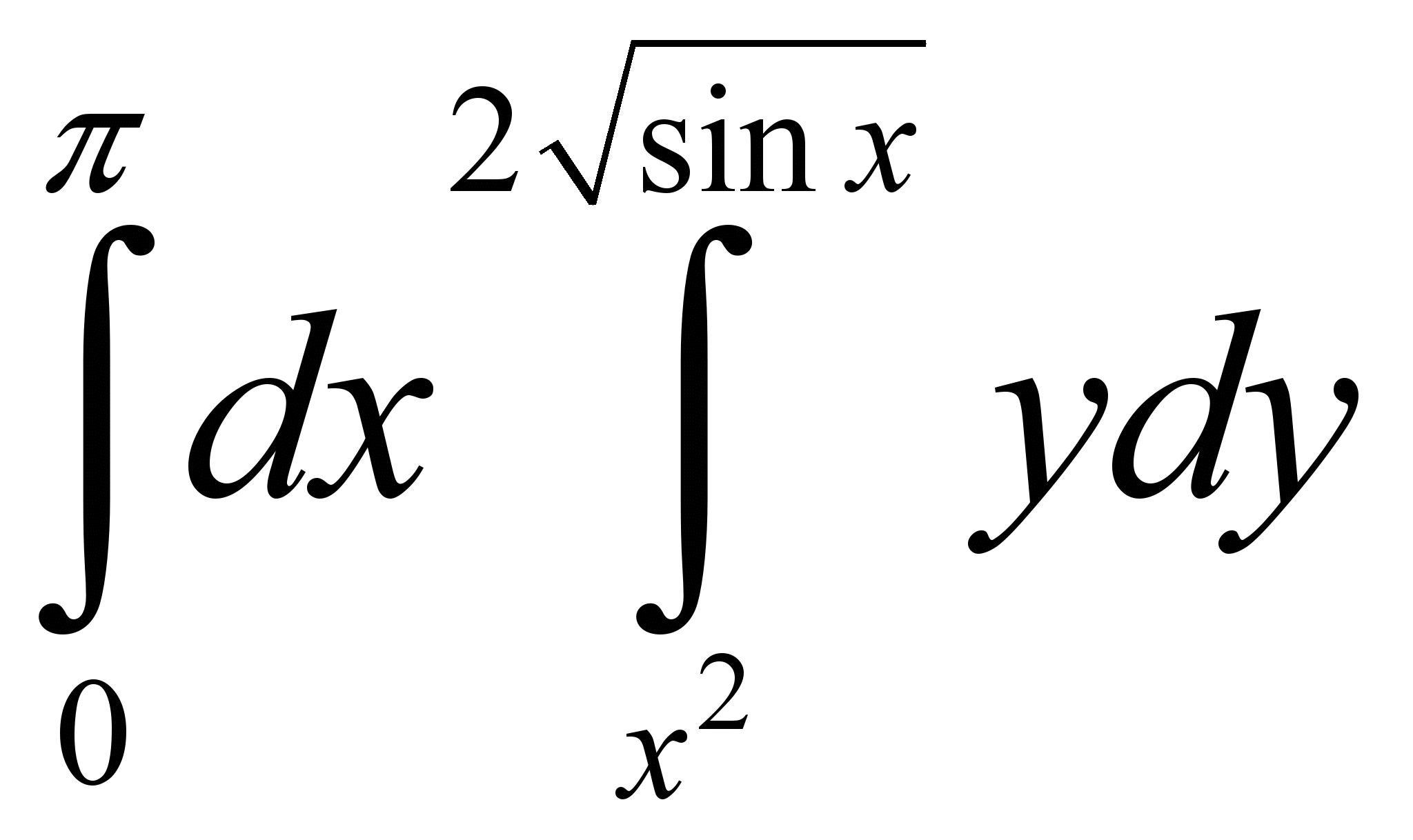 .
.Задача №3. Вычислить в полярных координатах
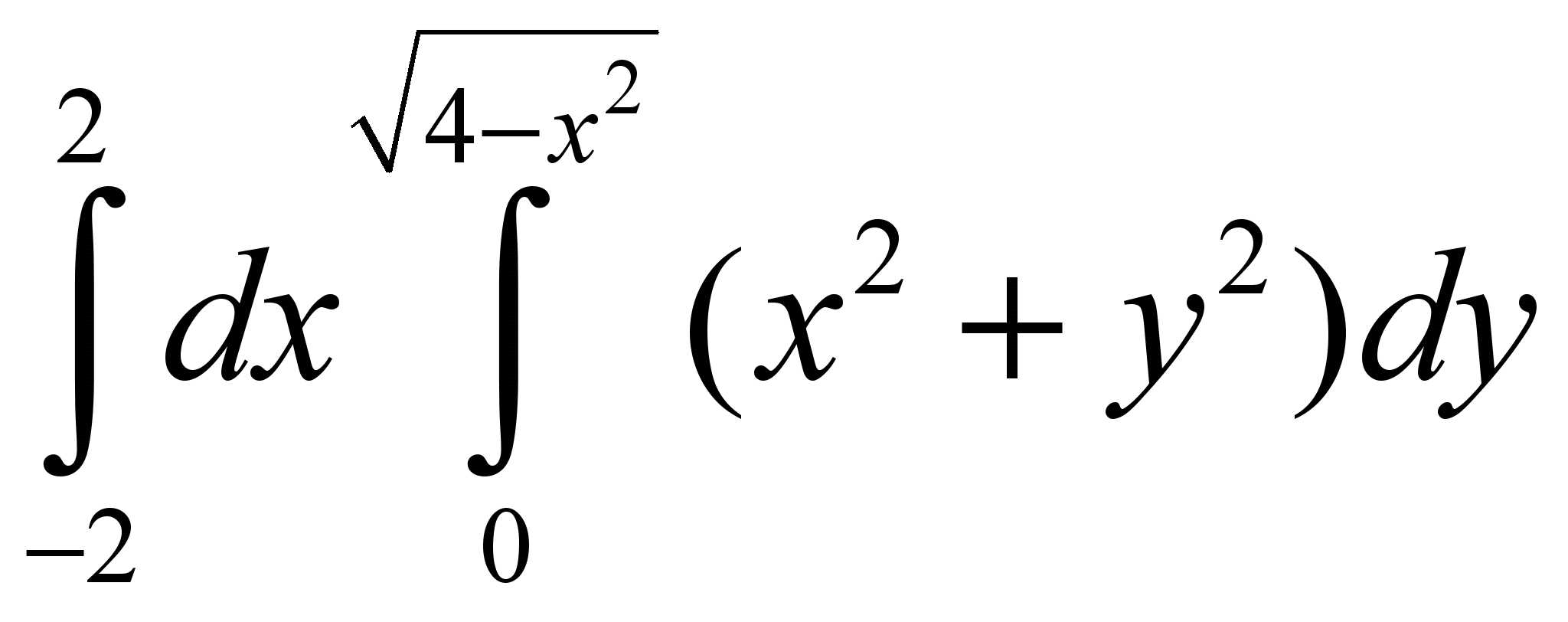 .
.Задача №4. Исследовать сходимость ряда
 .
.Разработчики:
СПбГУЭФ доцент В. Г. Дмитриев
СПбГУЭФ профессор Г. В. Савинов
Эксперты:
ЭМИ РАН директор Л. А. Руховец
СПбГМТУ профессор В. Б. Хазанов
