Geum.ru

Моу «Новоусманский лицей» Новоусманского муниципального района Воронежской области Устный журнал

Вид материалаУстный журнал

Содержание


1страница. Беседа «Математика и оборона страны».
Статистический контроль в военном производстве.
В. Келдыш
1.Задачу о максимальной даль­ности полета снаряда и задачу составления уравне­ния так называемой параболы безопасности.
2.Задача о параболе безопасности.
Крылов Алексей Николаевич
Курская битва
2.Кто рассчитал наиболее ­выгодную крутиз­ну нарезки стволов орудий, что позволило обеспечить кучность стрельбы и устойчи­вость
3.Кто выработал меры по выведении самолета из состояния «штопор»? (Келдыш)
9.Кто из математиков был «Главным теоретиком космонавтики», Президентом АН СССР? (Келдыш)
Подобный материал:
МОУ «Новоусманский лицей»

Новоусманского муниципального района

Воронежской области


Устный журнал


«Математика на службе армии»


Выполнили: учителя математики

Сухова З.А., Куликова Т.С.


Новая Усмань

2010г.

Устный журнал

«Математика на службе армии»

Цель:1)Воспитание чувства патриотизма, гордости за свою Родину.

2) Знакомство с некоторыми историческими фактами и математическими задачами, решение которых помогло победить в годы Великой Отечественной войны.

3) Формирование мировоззрения на математику- как на науку, прикладная особенность которой: математический аппарат, применяемый почти всеми другими науками.

4) Знакомство с учеными математиками, принимавших непосредственное участие в решении прикладных задач.

5) Формирование представлений о математике, как части общечеловеческой культуры, понимания значимости математики для общественного прогресса.


1страница. Беседа «Математика и оборона страны».

2страница. Баллада о математике.

3страница. Занимательные задачи.

4страница. Математическая викторина.


В наше время, чтобы строить

И машиной управлять,

Прежде нужно уже в школе

Математику узнать.

На войне ли современной,

В годы ль мирного труда,

При расчетах непременно

Математика нужна.


Открывают страницы ученики.


1 страница.

Прошло 66 лет со дня победы советского народа в Великой Отечественной войне. Неисчислимые жертвы понесла страна во имя независимости, свободы и общественных идеалов; миллионы погибших и раненых, страдания от голода, тысячи разрушенных городов и деревень, сотни тысяч угнанных на фашистскую каторгу. Несмотря ни на что советский народ выстоял и победил.

Размышляя сегодня об истоках нашей победы в Великой Отечественной войне, мы, прежде всего, обязаны отдать дань уважения нашим советским учителям. Ибо они помогли молодежи в короткое время получить те прочные знания, которые потребовались в страшные годы войны для быстрого создания передовой гражданской и военной техники, надежного овладения ею.

Интерес к знаниям был велик. Занимались в третью смену, при свечах, в полуразрушенных школах, после тяжелого трудового дня. Писали, используя каждый клочок бумаги, подчас и на газетах. Носили с собой в школу знаменитые «чернильницы - невыливайки». Учебников было мало, даже чаще всего один, поэтому приходилось много переписывать. Книги «ходили по кругу». Но главное - учились! Постоянная забота государства об обучении молодежи явилась одним из важных факторов, благодаря которым наша страна победоносно подошла к знаменательному дню- 9 мая 1945 года.

История военных лет показала, что большую роль в укреплении оборонной мощи нашей страны во время Великой Отечественной войны и после нее сыграла физика. А что можно сказать о математике?

Роль математики и математиков в военном деле велика. Математики нашей страны в период тягчайших испытаний проявили себя как подлинные патриоты, проявляли величайшее мужество, были храбрыми и расчетливыми воинами. Многие из тех, кто ушел на фронт, не возвратились. Страна потеряла огромное количество талантливой молодежи, которая могла бы стать гордостью отечественной науки.

Еще одним из факторов, приближавшим победу нашего народа, следует считать решения прикладных задач, которые осуществили в предвоенные годы и в годы войны советские математики. Они помогали успешно решать важнейшие практические вопросы освоения природных богатств, проблемы, связанные с созданием новой совершенной военной техники, с увеличением выпуска танков, самолетов и другой продукции, в которой так нуждался фронт.


Статистический контроль в военном производстве.

Одна из проблем, занимавшая многих математиков в то время, была проблема исключительной важности: проверка качества больших количеств однородных изделий. Ведь военные действия невозможны без патронов, снарядов, бомб, мин и т. д. причем все это необходимо в огромных количествах. Эта проблема со всей остротой возникла перед промышленностью уже впервые дни войны, поскольку прошла массовая мобилизация и квалифицированные рабочие стали солдатами. Им на смену пришли женщины и подростки без квалификации и рабочего опыта.





Изготовление деталей для снарядов

на оборонном заводе. Москва.

Некачественный патрон мог испортить ружье и принести вред стрелявшему, плохо сделанный снаряд разрывал пушку. Но проверка нередко требует намного больше того времени, что уходит на его изготовление. Тогда математики предложили использовать статистический метод контроля , что позволяло при проверке ничтожной доли изделий давать достаточно точные заключения о качестве всей партии. Через определенное время со станка берутся несколько (скажем, пять ) только что изготовленных изделий и замеряются параметры их качества. Если все эти параметры находятся в допустимых пределах, то производственный процесс продолжается, если же хотя бы одно изделие выходит за пределы допуска, то подается сигнал о необходимой переналадки станка или смене режущего инструмента. Какое отклонение параметра от номинала допустимо, чтобы вся партия была изготовлена качественно? Это требует специальных расчетов. После окончания войны выяснилось, что аналогичные исследования проводили математики США. Они подсчитали, что результаты их работы принесли за годы войны стране миллиардную экономию. То же самое можно сказать и о работе советских математиков и инженеров.

Среди математиков, занимавшихся этим вопросом, был А.Н. Колмогоров и его ученик Б.В. Гнеденко.


А.Н. Колмогоров


Эффективность стрельбы.

Добровольцем пошел в Армию профессор А.А.Ляпунов и, как и многие мехматовцы, стал артиллерийским офицером. Он не только храбро воевал, но и внес много ценного в правила стрельбы, используя свой опыт математика, которому свойственно искать самые лучшие решения. Его предложения позволили увеличить эффективность стрельбы.


Эту же проблему решал и академик А.Н. Колмого­ров. Используя свои работы в области теории вероятностей, он дал определение наиболее выгодного рассеяния артиллерий­ских снарядов.

Математическая суть проблемы состоит в следующем. При стрельбе по некоторой цели А, находящейся на земной поверхности, снаряды не попадают, вообще говоря, точно в точку прицеливания, а рассеиваются (см. рис. 1).




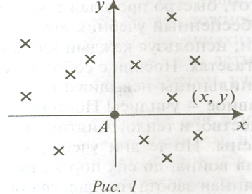
Возникает задача определения вероятности и или иного уклонения снаряда от центра цели. Если выбрать оси координат с началом в центре цели, то вопрос заключается в том, чтобы указать вероятность каждого возможного уклонения (х; у) снаряда от цели — возможных координат снаряда. Ясно, что уклонение снарядов от цели является результатом суммарного воздействия огромного количества зависящих от случая причин. Было показано, что уклонение снарядов подчиняется особому закону распределения вероятностей - двумерному нормальному закону. Эти результаты помогли повысить точность стрельбы и тем самым увеличить эффективность действия артиллерии.

Совершенствование военной техники.

Без предварительных математических исследований не создается ни одна техническая система и, чем сложнее, тем разнообразнее и шире ее математический аппарат. Для примера, крейсер представляет собой такую сложную техническую систему. Предварительно необходимо обеспечить живучесть корабля, надежность его управления, рассчитать влияние на устойчивость расположения различного рода масс- машин, орудий, торпедных аппаратов и т.д. Но и этого мало- требуется обеспечить связь со всеми боевыми единицами корабля, то есть создать эффективную систему управления кораблем и его оружием. Это лишь ничтожная доля тех задач, которые должен решить математик, прежде чем корабль начать строить. Но серьезные задачи необходимо решать и в период его эксплуатации- штурманские расчеты, расчеты стрельб и т.д.

Академик М. А. Лаврентьев за изучением пробивного действия взрывчатых веществ 1944г




Теория вероятностей ис­пользовалась и для определения наилуч­ших методов местонахождения самолетов и подводных лодок противника, для ука­зания путей, позволяющих избежать встречи с подводными лодками врага. На­пример, вставал такой вопрос: как лучше провести караван торговых судов при на­личии вражеских подводных лодок?


Если составить караван из большого числа су­дов, то вероятность встречи с подводны­ми лодками противника будет меньшей. Это с одной стороны. Но нельзя забывать и другое: увеличатся потери, если встреча большого каравана осуществится с под­водными лодками противника.

Тут математика пришла на помощь. Ее методами были оп­ределены размеры каравана судов и частота их отправления, при которых потери были бы наименьшими. Ученые-матема­тики помогли рассчитать, сколько нужно сделать одновремен­ных выстрелов по самолетам противника для того, чтобы иметь наибольшую вероятность попадания. Во всем этом большая заслуга академика А.Н. Колмогорова.

Во время Великой Отечественной войны появилась и та­кая важная проблема, как обеспечение кучности стрельбы и устойчивости снаря­дов при полете. Эту сложную математи­ческую задачу решил член-корреспондент АН СССР Н.Г. Четаев. Он рассчитал наиболее ­выгодную крутиз­ну нарезки стволов орудий, что позволило обеспечить кучность стрельбы и устойчи­вость снарядов при полете.





Война потребова­ла от авиации больших скоростей полетов са­молетов. Еще раньше авиаторы столкнулись с грозным явлением, которое возникало в самолетах, достигших больших скоростей,- так называемый флаттер, самовозбуждающиеся вибрации в моторах, которые часто вызывали катастрофы в воздухе. А в момент посадки скоростного самолета его колёса вдруг начинали вилять из стороны в сторону. Это явление, названное шимми, часто вызывало катастрофы на аэродромах.


. В. Келдыш -

президент Академии наук СССР,

главный теоретик космонавтики


М.В. Келдыш и его сотрудники исследовали причины флаттера шимми и создали математическую теорию, которая позволила своевременно защитить от этих явлений конструкции скоростных самолетов. Самолеты были обеспечены надежной защитой. Вибраций не стало. Наша авиация уже больше не знала случаев разрушения самолетов по причине неточного расчета их конструкций.

Работы В.В. Голубева по теории вихреобразования за обтекаемым в потоке телом, например, крылом или фюзеляжем самолета, помогли выработать меры по выведении самолета из состояния «штопор».

Великая Отечественная война выдвинула перед всеми видами деятельности огромное число новых проблем. Среди них были и такие, которым ранее не придавали значения. Например, до войны счи­талось, что в воздухе будут господствовать самоле­ты, летающие с большими скоростями и на боль­шой высоте. Но с началом войны оказалось, что нужны и тихоходные аэропланы, летающие на ма­лых высотах. А для них не было таблиц бомбомета­ния, поскольку никто не помышлял об их исполь­зовании в качестве бомбардировщиков. Пришлось срочно эти таблицы составлять, а для ускорения вычислений надо было вывести удобные формулы. В 1942 г. необходимые таблицы появились.

Их использовали пилоты и штурманы тихоход­ных самолетов У-2, служивших ночными бомбар­дировщиками. Экипажи этих маленьких, ничем не защищенных самолетов прославились умением не­заметно, почти бесшумно близко подлететь к по­зициям противника и точно их атаковать.

В 1942 г. коллектив математиков, руководимых С.Н.Бернштейном, разработал таблицы для определения местоположения судна по радиопеленгам. Таблицы ускоряли штурманские расчеты примерно в 10раз.

В блокадном Ленинграде ученые — математики и астрономы — написали исключительно важное пособие для авиации, флота и артиллерии — Большой астрономический ежегодник на 1943- 1945 гг. Во время работы над этим пособием треть его создателей погибла.

В 1941 г. многих выпускников механико-мате­матического факультета МГУ сразу после вручения им дипломов отправили на фронт техниками-лей­тенантами в основном в артиллерийские войска. Ходаков Владимир Алексеевич - оказался в их числе. В ходе реальных бо­евых действий решались сложные расчетные и оп­тимизационные задачи, о

которых можно расска­зать только на профессиональном уровне. Но про­стейшие «идеальные» задачи, в которых не учиты­ваются погодные или другие условия боя, могут быть понятны и школьнику, владеющему элемен­тарными знаниями механики и тригонометрии.

Рассмотрим две задачи, относящиеся к теории внешней баллистики:

1.Задачу о максимальной даль­ности полета снаряда и задачу составления уравне­ния так называемой параболы безопасности.

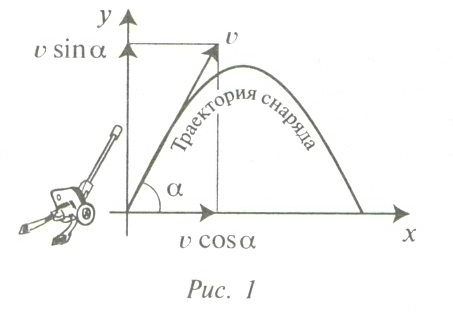
Задача о максимальной дальности полета снаря­да. Представим себе, что в начале координат стоит пушка (рис. 1), которая стреляет снарядами, выле­тающими из ствола со скоростью v.

Артиллерист может направить ствол пушки под любым углом α к горизонту

При разных углах α получаются разные траектории. Используя закон движения снаряда (механика) и уравнение линии траектории (математика), было доказано, что линией траектории снаряда является парабола, а на дальность полёта влияет лишь угол стрельбы α. Угол наибольшей дальности полёта снаряда равен 45





2.Задача о параболе безопасности.

Также было выведено уравнение семейства парабол и параболы безопасности, графики которых изображены на рисунке.





Оказывается, все параболы этого семейства касаются одной параболы. Она называется параболой безопасности. Выше неё самолетам летать безопасно (снаряды, выпущенные под любым углом из пушки, поднимутся не выше вершины параболы безопасности)


Видная роль в деле обороны нашей родины принадлежит выдающемуся мате­матику-академику А.Н. Крылову.


Крылов Алексей Николаевич

За время своей почти полувековой работы в Морской академии Крылов создал большое число трудов по теории кораблестроения, разработал теорию устойчивости корабля, то есть способность корабля возвращаться к состоянию равновесия после вынужденного выхода из него под влиянием внешних сил, а также установил строго научную теорию качки корабля на волнении и его плавучести. Он со­здал таблицу непотопляемости, по которой можно было рассчитать, как повлияет на корабль затопление тех или других отсе­ков, какие номера отсеков нужно затопить, чтобы ликвидировать крен и насколько это затопление может улучшить устойчивость корабля. Использование этих таблиц, спас­ло жизнь многих людей, помогло сберечь огромные материальные ценности.

Эти работы доставили Крылову мировую славу и способствовали установлению приоритета русской науки в этой области знания.

Из области прикладных наук большое значение имеют в артиллерии работы Крылова по вопросу о продольных и поперечных колебаниях орудийных стволов во время выстрела, а также его исследования о вращательном движении артиллерийского снаряда при его полете.

После войны на вооружении Военно-воздушных сил появились ракеты различ­ного назначения. В состав Военно-Морс­кого флота вошли новые атомные подвод­ные лодки - ракетоносцы, оснащенные баллистическими ракетами подводных стартов.





Это усложнило де­ятельность каждого командира и, в конечном счете, всю за­дачу управления войсками.





Командирам и солдатам на заметку:

 После войны на вооружении военно–воздушных сил появились ракеты различного назначения.
* В состав военно-морского флота вошли новые атомные подводные лодки – ракетоносцы, оснащенные баллистическими ракетами. * Оружие стало очень сложным, мощным и результативным, поэтому возросла мера ответственности за его применение.
* Точность попадания ракеты в цель во многом зависит от качества выполнения необходимых математических расчётов.
* Командиры должны иметь хорошие математические знания, уметь широко использовать вычислительные средства.
* В современной армии не только командиру, но и солдату, нужно владеть основами электротехники, радиотехники, хорошо знать математику.


2страница


Баллада о математике


Как воздух математика нужна,

Одной отваги мало.

Расчёты! Залп! И цель поражена

Могучими ударами металла.

И воину припомнилось на миг

Как школьником мечтал в часы ученья

О подвиге, о шквалах огневых,

О яростном порыве наступленья.

Но строг учитель был, и каждый раз

Он обрывал мальчишку резковато:

«Мечтать довольно! Повтори рассказ

О свойствах круга и углах квадрата!»

И воином любовь сбережена

К учителю далекому, седому.

Как воздух математика нужна

Сегодня офицеру молодому!


3страница

Занимательные задачи


1. Задача о партизанах.

Группу партизан в 68 человек во главе с учителем мате­матики Сидоренко внезапно окружил противник. Их привез­ли в родное село и закрыли в здании клуба, назначив на сле­дующий день суд. В центре клуба был зрительный зал, а вок­руг него 8 смежных между собой комнат с окнами на улицу. Командир противника поставил у четырех сторон здания ча­совых, а пленных партизан разместил в комнатах так, чтобы каждый часовой видел в окна 21 партизана одновременно (см. рисунок).




Приказав каждому часовому следить за тем, чтобы это число охраняемых им партизан не уменьшилось, командир назначил смену караула через 3 часа и ушел в штаб. Перед Сидоренко встали вопросы. Что делать? Как предупредить партизанский отряд, что село занято про­тивником? Как спасти свою группу от плена и смерти? Он знал, что под сценой зри­тельного зала есть подвал с выходом в сарай, где храни­лись декорации. Через этот ход можно было выйти. Од­нако, взяв из охраняемых комнат хотя бы одного чело­века, он мог вызвать тревогу, так как часовые непрерывно смотрели в окна и пересчи­тывали своих пленных. Сидоренко сообразил, что если в мо­мент смены караула сделать перестановку пленников в ком­натах, то незаметно для часовых он сможет каждый раз осво­бодить несколько человек, которые пройдут под сценой в са­рай, а затем - в отряд. Так и было сделано.

Во время смены караула Сидоренко перегруппировал партизан и освободил 8 человек, а затем 3 раза еще по 4 человека. Он подготовил и пятую группу из 4 человек, но в это время в село вошел предупрежденный партизанский от­ряд, он уничтожил противника и освободил всех остальных партизан.

Как Сидоренко размешал своих друзей по комнатам, что­бы освободить за пять приемов 24 человека, в то время как на глазах у каждого вновь заступившего на караул часового на каждой стороне здания всегда было по 21 партизану?

Решение.


1-ая перегруппировка 2-ая перегруппировка


-8 человек -4 человека



6
9
6

9



9

6
9
6



7
7
7

7




7

7
7
7





3-ая перегруппировка 4-ая перегруппировка


-4 человека -4 человека



8
5
8

5



5

8
5
8



9
3
9

3



3

9
3
9





2. Морская разведка.

а) Разведывательному кораблю (разведчику), двигавшему­ся в составе эскадры, дано задание обследовать район моря на 70 миль в направлении движения эскадры. Скорость эскад­ры - 35 миль в час, скорость разведчика - 70 миль в час. Определить, через сколько времени разведчик возвратится к эскадре.




Решение.

Обозначим искомое число часов через х.




Время, ч
Скорость, миль/ч
Путь, миль

Эскадра
х
35
35х

Разведчик
х
70
70х



Разведчик прошел вперед 70 миль и часть этого пути обратно до встречи с эскадрой, которая прошла остальную часть того же пути. Итого, они прошли вместе 140миль.

Имеем уравнение

35х + 70х = 140, откуда х =1⅓=1ч.20мин.


б) Разведчик получил приказ произвести разведку впере­ди эскадры по направлению ее движения и через 3 часа вер­нуться к эскадре. Через какое время после оставления эскад­ры разведывательный корабль должен повернуть назад, если его скорость 60 узлов, а скорость эскадры 40 узлов?

Решение.


Обозначим через х ч.время удаления разведчика.





Время, ч
Скорость, узлов/ч
Путь, узлов

Эскадра
х
40
40х

Разведчик
х
60
60х





60х-40х=20х-расстояние,на которое удалился разведчик


На обратный путь потребовалось ( 3-х ) ч.
Время, ч
Скорость, узлов/ч
Путь, узлов

Эскадра
3 - х
40
40(3-х)

Разведчик
3 - х
60
60(3-х)





Следовательно,

60(3-х)+40(3-х)=20х, х=2,5ч.


Разведчик должен изменить курс на обратный спустя 2ч. 30мин.


3. Шофер выполнял задание: 12 солдат одновременно до­ставить в пункт назначения, в 20 км от их места расположе­ния при помощи маленького автомобиля, вмещающего 4 че­ловека и движущегося со скоростью 20 км/ч. Скорость дви­жения солдат 4 км/ч. Шофер хорошо знал математику и зада­ние легко выполнил. Как?


4. Задача о переправе.

Небольшой отряд солдат подошел к реке, на берегу кото­рого была маленькая лодка и два мальчика. Как с помощью мальчиков и лодки отряд переправился на другой берег, если в лодку может сесть один солдат или два мальчика?

Решение. Сначала плывут 2 мальчика. Один остается на другом берегу, а второй возвращается и переправляется солдат. Затем мальчик с противоположного берега плывет обратно к отряду и забирает своего товарища, тот в свою очередь снова возвращается и переправляется второй солдат и т.д.


5. Мост через реку.

1.Двум воинским частям, расположенным на одном и том же берегу реки на разных расстояниях от нее, нужно срочно по одному мосту переправиться на другой берег реки. Где следует построить временный мост, чтобы он был на одина­ковом расстоянии от военных частей?


Ответ. На серединном перпендикуляре к отрезку, соединяющему две воинские части.


2.Воинской части, находящейся в пункте А нужно срочно переправиться на другой берег реки в пункт В.

А .

____________________________


___________________________


. В

Где следует построить временный мост PQ через реку, чтобы путь S=AP+PQ+QB был кратчайшим? Берега реки считаются параллельными прямыми, а мост, естественно, строится перпендикулярно берегам реки.

Решение. (см. Геометрия 8-9 А.Д. Александров, стр.300)


6. Великая Отечественная.
( удивительный квадрат)
Великая Отечественная.война началась 22 июня 1941 года. Узнать, сколько дней продолжалась война, поможет вам удивительный квадрат. Выберите из каждой строки и каждого столбца по одному числу, найдите сумму выбранных четырех чисел, и вы получите ответ на вопрос.

413
218
474
576

569
374
630
979

195
0
256
349

221
26
282
375



218+630+195+375 = 1418

7.Блокадный хлеб.

Перед наступлением на Ленинград Гитлер заявил: «Ленинград сам поднимет руки: он неминуемо падет, раньше или позже. Никто оттуда не освободится, никто не прорвется через наши линии. Ленинграду суждено умереть голодной смертью». Но это пророчество Гитлера не сбылось. В Ленинграде продолжали работать хлебозаводы, пекари продолжали печь хлеб.




Дочка надкусывает хлеб - на большее уже не хватает сил. Она умирает на глазах у мамы, на руках у сестренок. Это самая обычная смерть в голодном блокадном Ленинграде. Необычен поступок матери. Казалось... умерла дочка, но остались две другие. Их надо спасать. Хлеба теперь стало больше: 1/16 часть буханки вместо 1/24. Но мать поступает иначе. Она решает сохранить надкусанный ребенком кусочек хлеба как память. Она поняла, что сила духа ее, ее детей неизмеримо больше, чем маленький кусочек хлеба.


Из чего же состоял блокадный хлеб?



Поставьте разумные вопросы и ответьте на них.



Были и другие примеси и добавки, снижающие питательность хлеба. За все месяцы блокады было выработано при выпечке хлеба около 16 тысяч тонн пищевой целлюлозы.


8. Парад Победы


Прибывших на парад солдат планировали построить так, чтобы в каждом ряду стояло по 24человека. Но в действительности не все прибывшие смогли участвовать в параде и их перестроили так, чтобы число рядов стало на 2 меньше, а число человек в ряду на 26 больше нового числа рядов. Если бы все солдаты участвовали в параде, то их можно было бы построить так, чтобы число рядов было равно числу человек в ряду. Сколько солдат прибыло на парад?

Решение.

Пусть предполагаемое первоначально число рядов х, тогда число прибывших солдат 24х. После перестроения число рядов стало х-2, а число человек в ряду соответственно х+24. Число солдат после перестроения (х-2) (х+24).Получим 24х> (х-2) (х+24).Решая неравенство, получим х €(-6;8), так как х€N, то это числа от 1 до 7. Учитывая последнее предложение, делаем вывод, то из 24х должен извлекаться корень. 24*6=144.

Ответ: 144 солдата.


«Получил информацию- составь задачу»


К 1943 году Советские Вооруженные силы значительно окрепли организационно, повысилось их боевое мастерство, возрос моральный дух воинов. К лету этого года в составе действующей армии было

свыше 6 млн. 400 тыс. человек, 105 тыс. орудий и минометов, 2200 боевых установок полевой реактивной артиллерии, 10, 2тыс. танков и самоходно-артиллерийских установок, свыше 10 тыс. боевых самолетов

Курская битва - величайшее событие второй мировой и Великой Отечественной войны



В результате Курской битвы советские войска нанесли врагу такое поражение, от которого фашистская Германия уже не могла оправиться.

Всего с 19 ноября 1942 года по конец 1943 года фашистская Германия потеряла на советско-германском фронте около 2,6 млн. человек, почти 50 тыс. орудий и минометов, до 7 тыс. танков, более 14 тыс. боевых самолетов.


В одном из немецких комментариев говорилось: “После Сталинграда мы узнали, что уже не сможем выиграть войну, а после Курска убедились, что ее проиграли”


4страница.

Викторина


Узнай их имена

  • 1.Кто исследовал причины флаттера шимми и создал математическую теорию, которая позволила своевременно защитить от этих явлений конструкции скоростных самолетов? (М.В.Келдыш)
  • 2.Кто рассчитал наиболее ­выгодную крутиз­ну нарезки стволов орудий, что позволило обеспечить кучность стрельбы и устойчи­вость снарядов при полете? (Н.Г.Четаев)
  • 3.Кто выработал меры по выведении самолета из состояния «штопор»? (Келдыш)
  • 4.Кто автор первого в России учебника по арифметике? (Л.Ф.Магницкий)
  • 5.Кто дал определение наиболее выгодного рассеяния артиллерий­ских снарядов? (А.Н.Колмогоров)
  • 6.Кто предложил использовать статистический метод контроля, что позволило при проверке ничтожной доли изделий давать достаточно точные заключения о качестве всей партии? (Колмогоров)
  • 7.Кто из математиков изобрел тачку? (Паскаль)
  • 8.В честь какого ученого математика названа прямоугольная система координат? ( Рене Декарт)
  • 9.Кто из математиков был «Главным теоретиком космонавтики», Президентом АН СССР? (Келдыш)
  • 10.Кто из математиков создал таблицу непотопляемости кораблей? (Крылов)
  • 11.Кто из математиков создал школу русских математиков, успешно сочетая создание теории чисел с разработкой механических устройств и приборов? (П.Ф.Чебышев)
  • 12.Кого называли «добрым гением» Российской академии наук? (Л.Эйлер)
  • 13.Кто является основателем кибернетики? ( Норберт Винер)



Хвала математике


Идёт о математике молва,

Что она в порядок ум приводит.

Потому хорошие слова

Часто говорят о ней в народе.

Ты нам, математика, даешь

Для победы трудностей закалку.

Учится с тобою молодёжь

Развивать и волю, и смекалку.

И за то, что в творческом труде

Выручаешь в трудные моменты,

Мы сегодня искренне тебе

Посылаем шквал аплодисментов!


Список используемой литературы:


1. Гнеденко Б.В. «Математика и оборона страны». Журнал «Математика в школе» 1978/2

2. Гнеденко Б.В. «Математика и контроль качества продукции» М.: Знание,1984/11

3. Левшин Б.В. «Советская наука в годы Великой Отечественной войны» - М.: Наука, 1983

4. Геометрия 8-9. А.Д. Александров

5.Токарчук Н.П. « Предметная неделя математики», издательско-торговый дом

« Корифей», Волгоград.

6. Математики в годы Великой Отечественной войны.

works.tarefer.ru /50/100008/index.php

7. Воспитание учащихся на уроках математики.

/ festival.1september.ru /articles/21269/

8.Журнал «Квант» Гнеденко Б.В «Математика и математики в Великой Отечественной войне»

Kvant.mirror 1.mccme.ru/…/matematika i matematiki v velihtm.