Математические этюды. Часть 1

Вид материала

Документы

Содержание Немного об экспоненте, теории вероятностей и просто функции Сумасшедший математик бегает по психушке и всех пугает А другой сумасшедший математик отвечает радостно ОМ теории множеств Дорогой, ты математику любишь больше, чем меня! Пустым множеством Универсальное множество Парадоксы бесконечного Инструкция для тех, кто будет охотиться на льва! Теорема: лев точно в клетке. ВАЖНО: Нельзя ни в коем случае стоять посередине клетки, чтобы при обратном отображении не исчезнуть в бесконечности! ВАЖНО: поскольку проволока колючая, очень важно не отрезать ею кисточку хвоста! Многомерная логика Теорема Гёделя о неполноте. Любая формальная система аксиом содержит неразрешенные предположения» Математик, физик и социолог сидят в поезде и пересекают границу соседнего государства. На первом же поле они увидели двух черных

Подобный материал:

• Советский менталитет: Социальные этюды, 153.87kb.
• Список 1 класс. Этюды беренс Г. Соч. 70. 50 маленьких фортепианных пьес без октав №№1-30, 634.55kb.
• Филологические этюды: лингвистика, педагогика, методика, 1054.33kb.
• Методика получения математических моделей элементов. Математические модели, используемые, 28.81kb.
• Математические определения, 26.58kb.
• Примерная программа дисциплины "Математические методы финансового анализа", 464.29kb.
• Л. Н. Уланская ф 54 Филологические этюды: лингвистика, методика, страноведение (труды, 1628.91kb.
• План чтения лекции по учебной дисциплине «Математические методы» Раздел, 120.82kb.
• Рабочей программы учебной дисциплины математические методы и модели в экономике уровень, 37.32kb.
• Учебная программа дисциплины экономико-математические модели, 115.76kb.

Математические этюды. Часть 1.


В предыдущей статье «О математических символах» исследовался вопрос, о том, что среди чисел существуют объекты, которые могли бы нести собою идею Отца. Но числа с точки зрения математики – это объекты всего лишь одного из её разделов.

На сегодняшний день математику определяют как науку о структурах, порядке и отношениях, и этот взгляд далеко не новый. Почти 400 лет назад выдающийся математик и философ Рене Декарт писал: «К области математики относятся только те науки, в которых рассматривается либо порядок, либо мера, и совершенно не существенно, будут ли это числа, фигуры, звёзды, звуки или что-нибудь другое, в чём отыскивается эта мера. Таким образом, должна существовать некая общая наука, объясняющая всё относящееся к порядку и мере, не входя в исследование никаких частных предметов …»

В работе разговор пойдёт о структурах и отношениях. При глубоком взаимодействии с ними, каждый из «героев» рассказа превращается в символ, содержание которого соотнесёно с «самым главным». Для меня эти символы – проживание Отца во всём.


Немного об экспоненте, теории вероятностей и просто функции


Функция 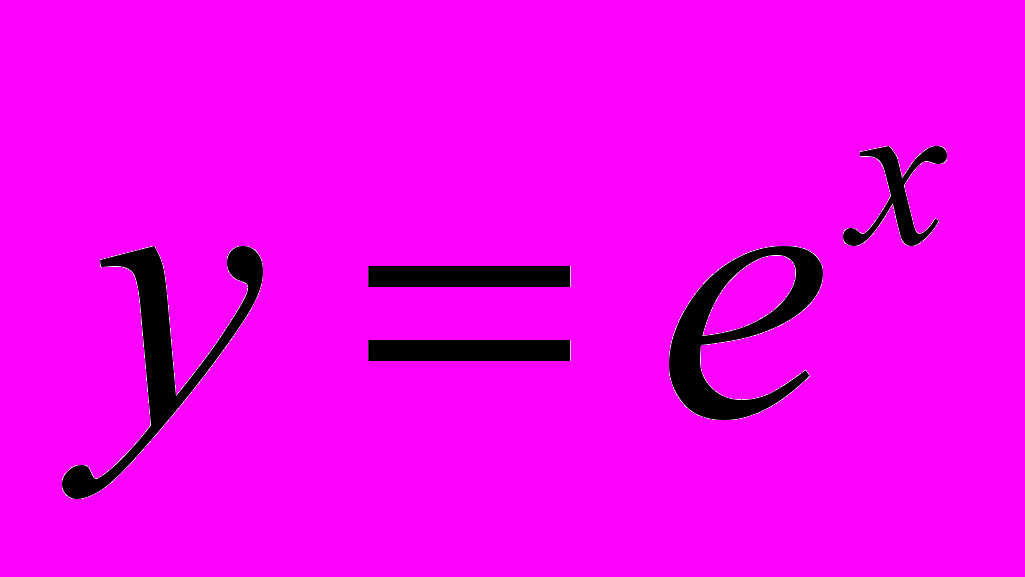, которая в математике носит название экспоненты, интересна по нескольким обстоятельствам. Часть из них была упомянута в предыдущей работе в главе Число е и логарифмы.

Экспонента – это единственная математическая функция, которая остаётся неизменной при дифференцировании и интегрировании. То есть,

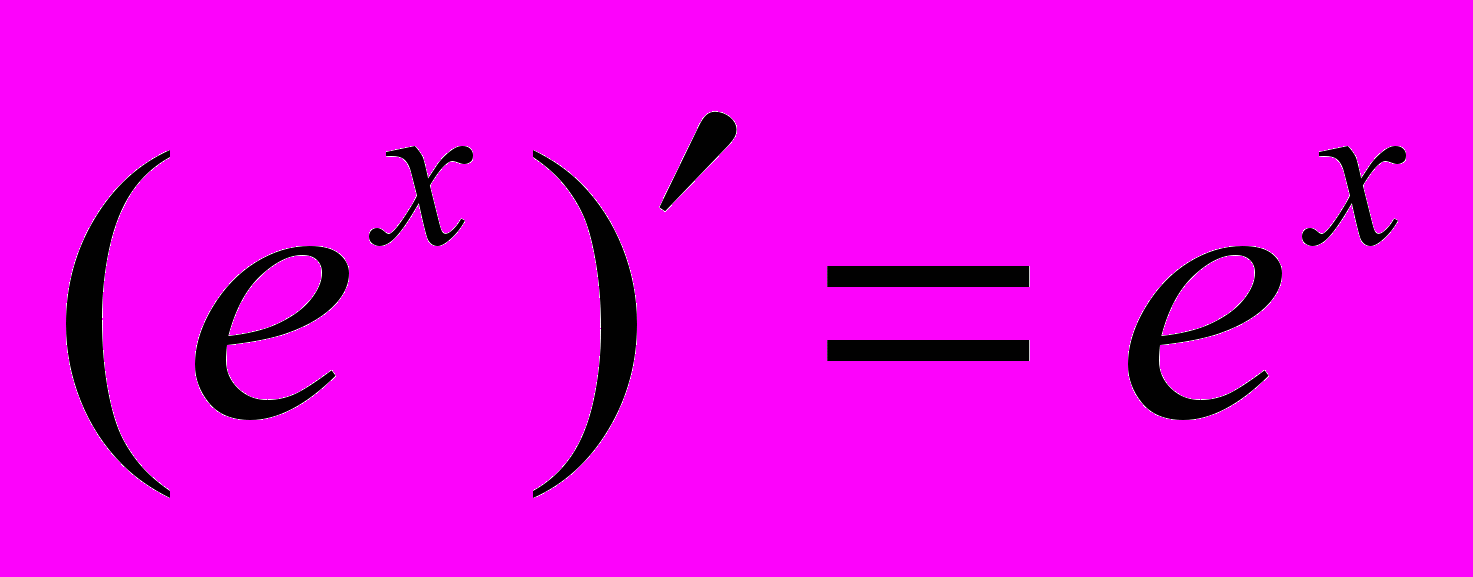, и с точностью до константы 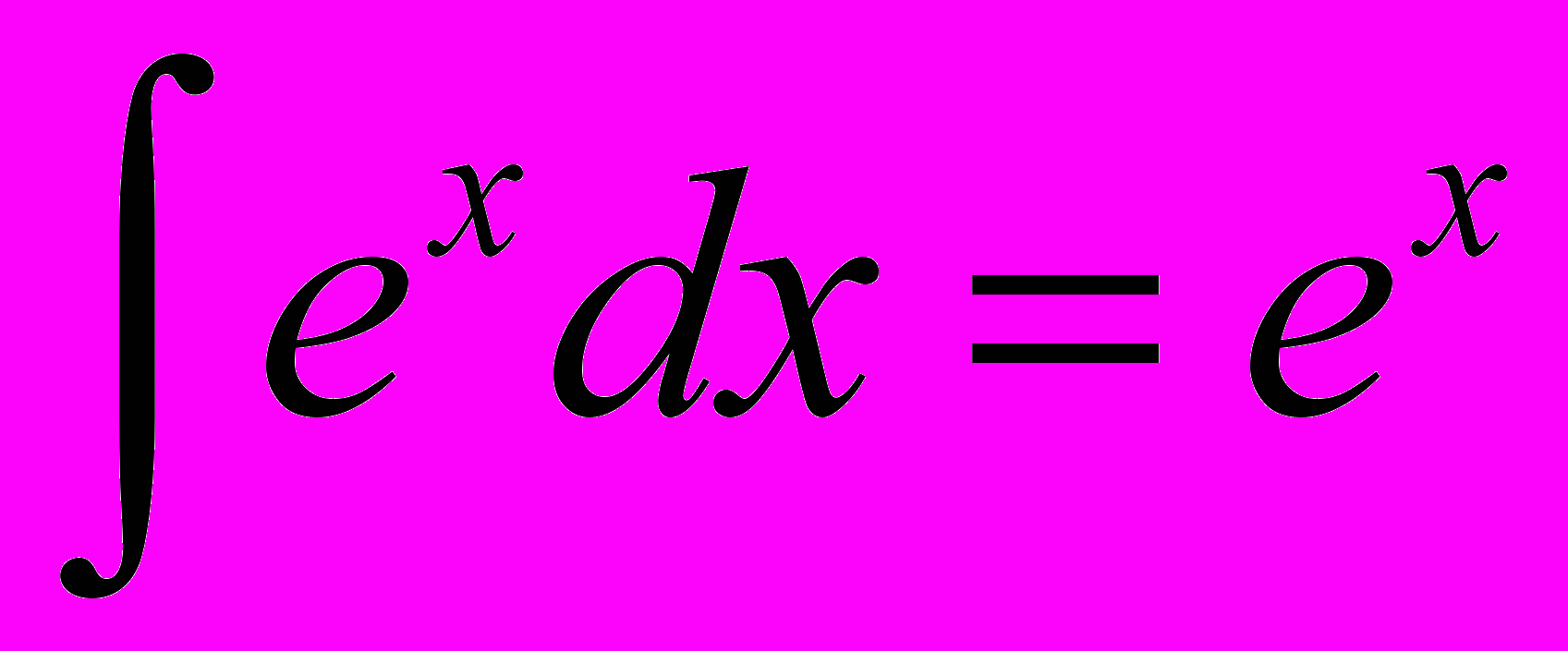. Ни одна другая функция не обладает таким удивительным свойством - не изменяться при таких «серьёзных» операциях, как взятие производной и интеграла. Причём, как дифференцирование, так и интегрирование можно повторять сколь угодное количество раз – экспонента всё равно останется экспонентой.

Сумасшедший математик бегает по психушке и всех пугает,

- Я тебя продифференцирую по x!

- Я тебя проинтегрирую по dx!

Все психи пугаются, прячутся под кровати, за тумбочки.

А другой сумасшедший математик отвечает радостно,

- Ха-ха-ха, а я !

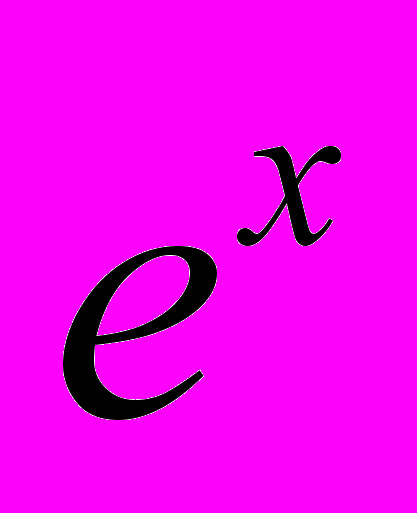Вообще, дифференцирование - штука удивительная, потому что именно оно приводит нас в область бесконечно малых – это раз, а это всегда интересно. А, во-вторых, предположительно, позволяет математически описать процесс перехода из огня в дух, и далее. А именно, производная от огня равна духу. Дифференцируя дух, мы получаем свет, и, наконец, .

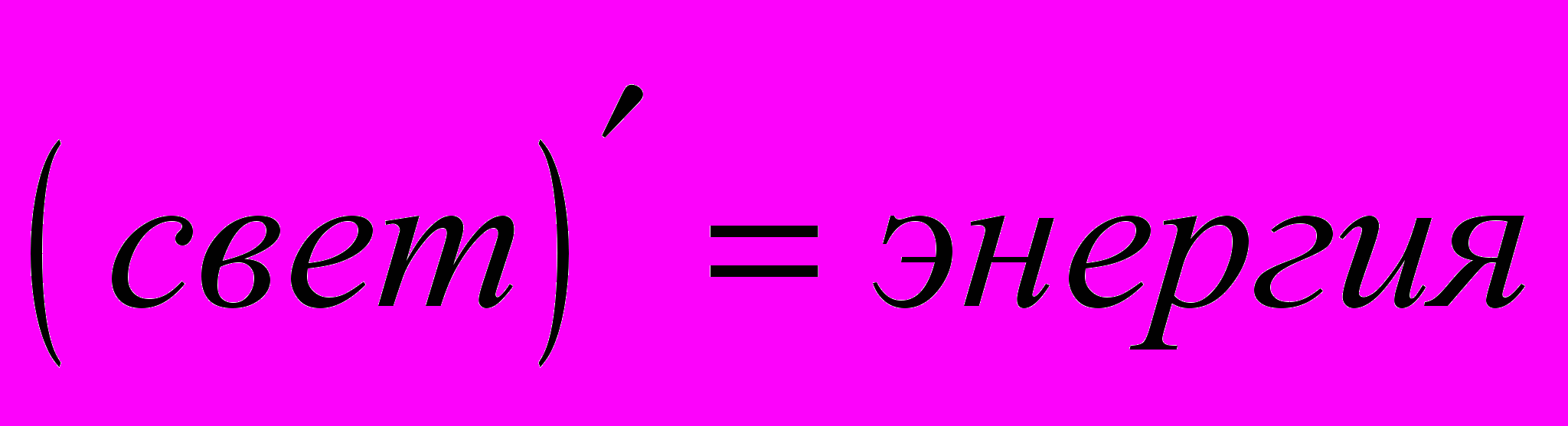Свойство оставаться неизменной при дифференцировании и интегрировании наводит на мысль, что если попробовать найти некую математическую функцию, которую можно было «сопоставить» Отцу, то лучшего кандидата, чем экспонента просто не найти. А если ещё вспомнить предположение астрономов о том, что вселенная расширяется по закону экспоненты …!

Экспоненту можно разложить в бесконечный степенной ряд (о бесконечных рядах речь пойдёт в следующей статье)

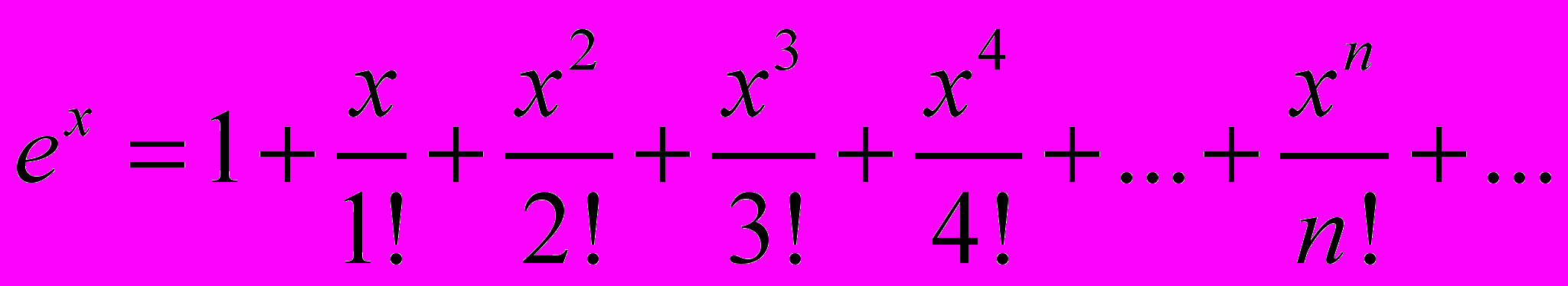, (1)

Если положить х=1, то мы получаем выражение для числа е.

Формула (1) незаменима с точки зрения вычислительных аспектов – когда калькулятору «нужно вычислить», например, 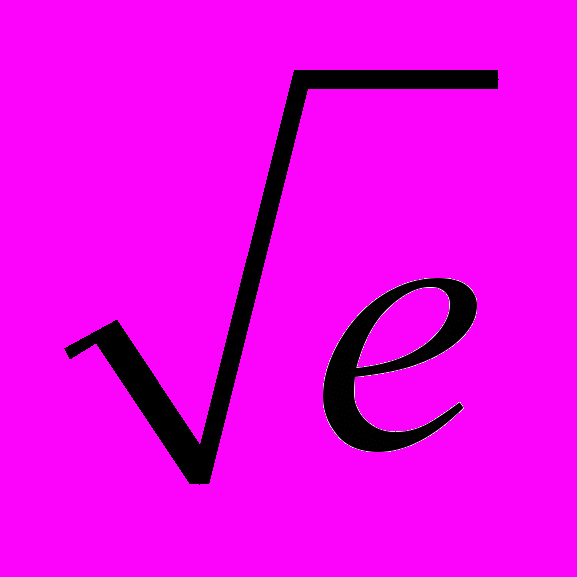, то он начинает работать по формуле (1), полагая, 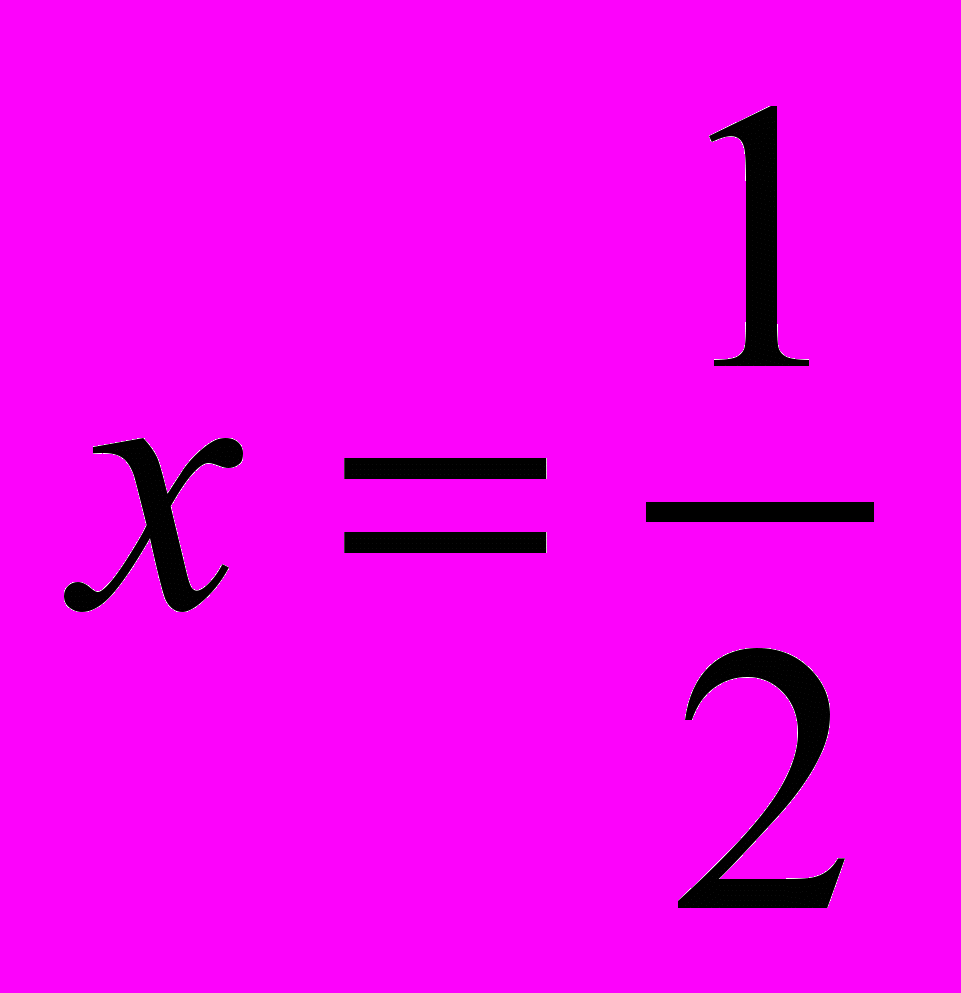, поскольку он «умеет» складывать и умножать, но не извлекать корни. И в зависимости от того, какая требуется точность вычисления, берётся то или иное количество членов ряда. Чем больше членов в разложении (1) взято, тем с большей точностью получается ответ, и тем ближе мы подходим к экспоненте.

В разложение экспоненты в виде ряда можно увидеть глубокий смысл, описывая процесс нашего пути к Отцу.

Первый член ряда – единица, некая данность, обусловленная нашим приходом в это воплощение, наше рождение в материи. И это главный член ряда. Следующий член ряда – х в первой степени – освоение первого физического присутствия, следующий член ряда – второе присутствие. И, чтобы выразить собою Отца, ты, говоря математически, складываешь соответствующие члены ряда, а по-другому – просто синтезируешь присутствия первое и второе. И ты уже приблизился, но «погрешность» такого приближения ещё велика. Затем ты освоил ещё одно присутствие, или сложил уже четыре слагаемых. И так далее. Ещё раз подчеркну, чем больше членов ряда удалось просуммировать или синтезировать, тем лучше или точнее приближение к экспоненте. Каждый член ряда (1) можно интерпретировать, как выражение соответствующего присутствия.

Ещё одно формула, связанная с экспонентой, немного в «мистическом» исполнении. С точки зрения математики речь идёт о функции комплексного переменного, и теперь в аргумент функции включается мнимая единица (см. Комплексные числа и мнимая единица). В идею этой изумительной формулы можно будет вникнуть, не обладая специальными знаниями, для этого достаточно одарить её пытливым, проникающим взглядом. Итак, формула Леонарда Эйлера

,

сочетание рационального и мистического. И не только. Несколько раз проводила эксперимент с аудиторией, которая только слышала о том, что существует такие понятия, как Инь и Ян, но не более того, спрашивая, какая, по их мнению, функция из правой части формулы – синус или косинус – соответствует Инь и Ян. Ответ всегда однозначный - косинус отождествляется с янским выражением, синус - с иньским. То есть, интуитивное представление о том, что есть математический инь и ян, существует у всех. (Кстати, косинус является чётной функцией, синус является нечётной функцией, что может служить прямым доказательством янского характера синуса и иньской выразимости косинуса). А если это так, то получается, что на формулу Эйлера имеет смысл посмотреть как на некое ДАО! Или как на математический комплексный ОМ!

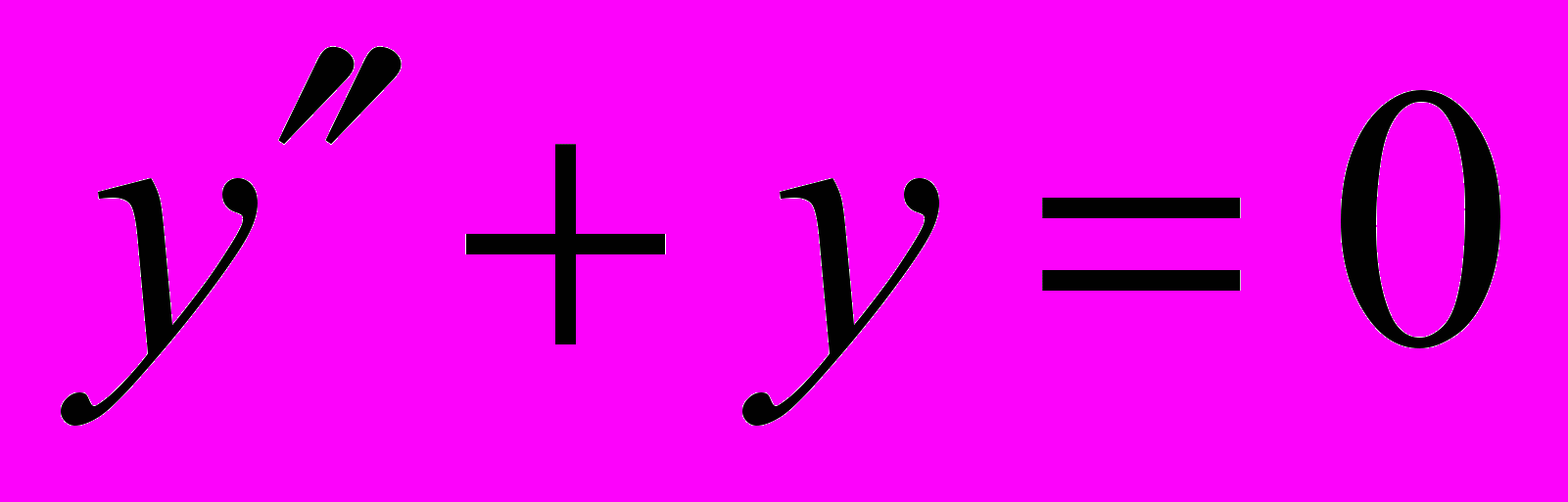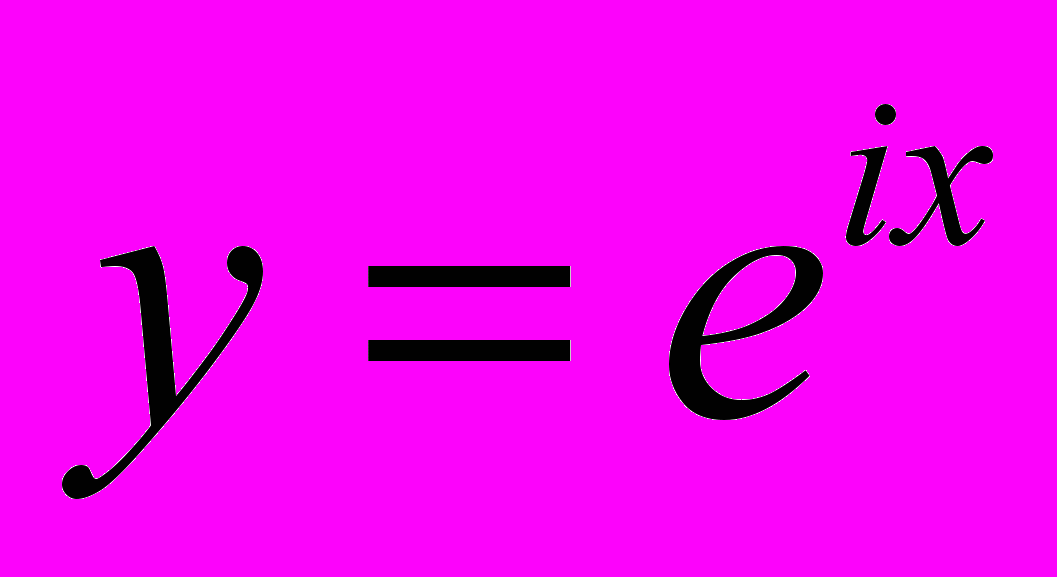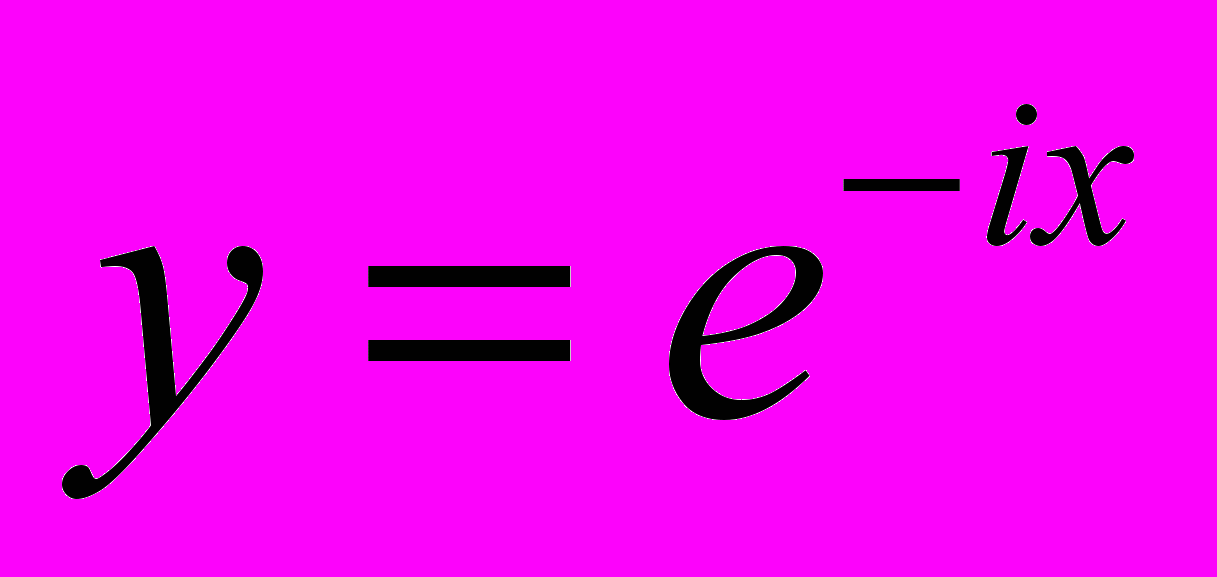И в этой же формуле – рационально-мистическая трактовка – в формуле мы находим мнимую единицу, а значит, выходим из области рационального, но решения, несмотря на это, оказываются совершенно рациональными. Пример: дифференциальное уравнение колебания маятника , (формула, известная всем из школьного курса, только там она написана через х), имеет два решения и . Присутствие мнимых величин в решениях кажется странными – все прекрасно знают, что маятник колеблется по закону синуса и косинуса. И это действительно получается, если в формуле (2) выделяется отдельно вещественная часть, и отдельно мнимая. И маятник колеблется совсем по-настоящему, несмотря на комплексные решения.

Теперь поищем экспоненту в другом разделе математики – теории вероятностей. Существует закон распределения случайной величины, называемый нормальным законом или Гауссовым. Закон имеет широчайший спектр применения, потому что является предельным. Это значит, что все остальные законы «стремятся» к нему. Законом Гаусса моделируются: погрешности измерений, рост живых организмов и т.д. и т.п. Функция распределения такой случайной величины содержит экспоненту, и этот факт указывает на «всеобъемлющий» характер закона.

Попробую объяснить на пальцах. Например, если взять всех чело ДИВО 31 Проявления женского пола, и измерить у них объём бедер, то результат можно записать в виде таблицы (бёдра от 80 до 85 см – столько-то человек, от 85 до 90 – столько-то человек, и т.д.). Рисуем график такой зависимости, откладывая по одной оси интервалы в см, по другой оси – количество человек. В результате получаются прямоугольники, приблизительно как на рис.1.




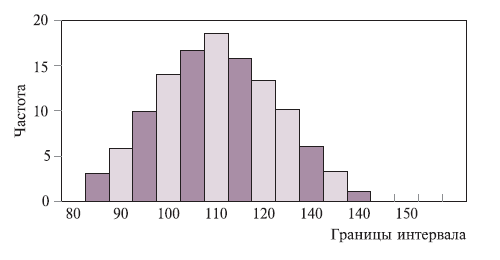
Рис. 1


Согласно рис.1 бёдра от 85 до 90 см – у трёх человек. От 90 до 95 – у шестерых. От 95 до 100 – десять человек, и т.д. Больше всего (18 человек) обладают размером бёдер от 110-до115 см. Полученные прямоугольники «огибаем» кривой.

Если бы мы провели такие же измерения бёдер, например, в ДИВО 28 Проявления, то результат, несмотря, на другое количество инь, будет очень напоминать предыдущую картинку. Точнее говоря, будет одинаковыми по форме кривые, которые огибают прямоугольники. Как происходит построение кривой по прямоугольникам показано на рис.2





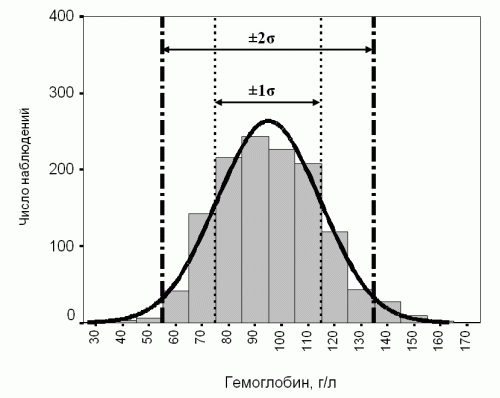
Рис.2

(не смущайтесь, что приведён «график с гемоглобином» – нормальный закон носит всеобщий характер).

Можно сказать, что нет ничего удивительного в том, что сравнивая объём бёдер, мы получаем одинаковые по виду кривые. Но оказывается, что, если мы проделаем измерения размеров обуви всех мужчин Санкт-Петербурга, а потом ширину плеч мужчин Киева, то кривая распределения будет оставаться такой же, как на рис 2. Она будет описываться одним и тем же уравнением, с разницей только в цифрах на графике. Этой кривой совершенно всё равно – бёдра это или ноги, в Киеве или в Санкт-Петербурге.

Все предыдущие примеры относились к «живой природы», которая, скорее всего, построена по математическому плану. Но если начать взвешивать все торты, на которых написано – вес 1 кг, испечённые сегодня во всех пекарнях города, а понятно, что они не будут весить ровно 1 кг, и считать количество тортов весом от 950 г до 955, потом от 955 до 960 и далее, а потом изображать эти величины на графике, картина огибающей кривой снова будет такой же.

Построенная таким образом кривая называется кривой Гаусса, в честь выдающего математика Гаусса, которого называют «королём математики».




Под кривой написано: «Нормальный закон выделяется в опыте человечества как одно из широчайших обобщений натуральной философии. Он служит как ведущий инструмент исследований в физических и социальных науках, медицине, сельском хозяйстве, технике. Это обязательное средство анализа и обработки данных, полученных наблюдениями и экспериментом».

Так вот, это «широчайшее обобщение» описывается при помощи экспоненты следующим образом



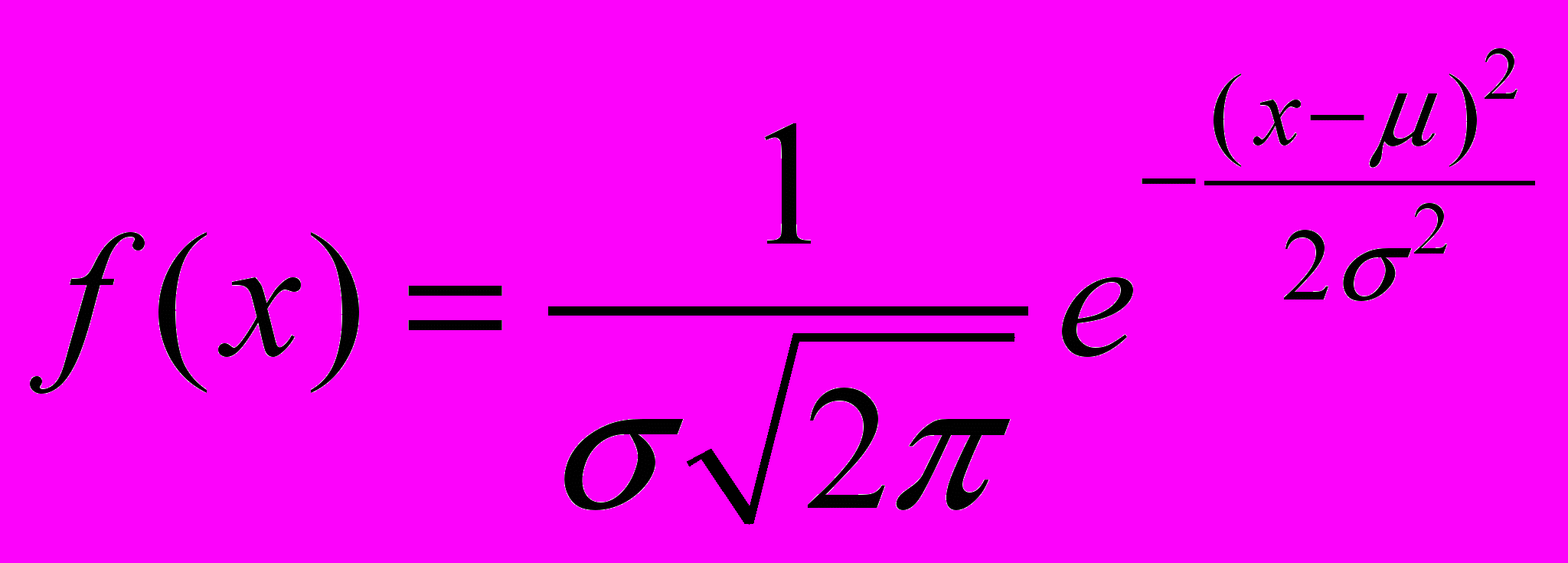
Не пугайтесь, пожалуйста. Самое главное, что следует заметить в этой формуле – в ней присутствует е в степени. (2)

Но это ещё не всё. В этой миленькой формуле, кроме 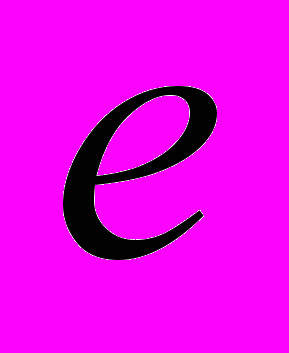, присутствует ещё и число Пи. А этот факт, вообще, с трудом поддаётся осмыслению. Причём тут число Пи, связанное с чем-то круглым – окружностями, кругами, сферами, и вычисление вероятности того, что подбросив монету 200 раз, орёл выпадет больше 110 раз? Можно пошутить и сказать, что монета круглая, поэтому там есть число Пи, но в случае с кубиком в формуле для плотности распределения Пи присутствует, а кубик меньше всего смахивает на что-то круглое. Здесь вспоминается математический анекдот на тему числа Пи: «Иррациональность Бога в том, что он не три-един, как все думают, а Пи-един».

И получается, что теория вероятностей доставляет приятные размышления о мироздании, начиная с того, что упомянутые случайные величины (например, вес «килограммового» торта) на самом деле случайными и не являются. Хотя основным объектом изучения этого раздела математики является именно случайная величина.

Остаётся вспомнить, что весь математический аппарат квантовой физики построен на волновой функции, которая непосредственно связана с плотностью вероятности. А любое обращение к квантовому описанию мира даёт огромные возможности, и позволяет элементарной частице быть и внутри какого-то объёма, и снаружи. В этом случае мы просто сравниваем вероятности, приписывая одному состоянию большую вероятность, чем другому.

И наконец, принцип неопределённости Гейзенберга тоже формулируется вероятностных терминах. Так что теория вероятностей в каком-то смысле удивительная область математики, которая говоря о некотором событии, оценивает лишь вероятность, с которой оно может произойти, но «позволяя» при этом ему и не происходить. И является, своего рода, ключом в квантовый мир.

Перед тем как перейти к понятию функции, которая обозначается буквой 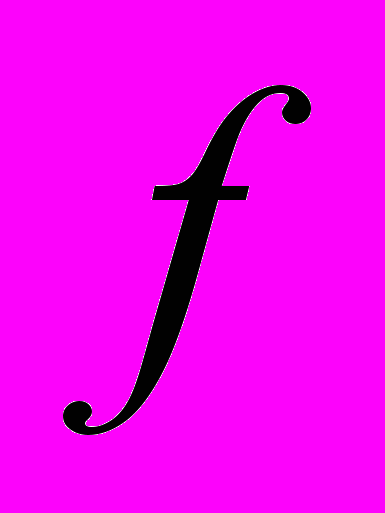, хочу поделиться мыслями об одном слове, которое начинается на такую же букву. Дело в том, что размышляя о функциях, в голову, прежде всего, приходило именно оно. Это английское слово Father, которое переводится на русский как Отец. Трактовку второй половины этого слова оставляю читателю на его вкус, для меня это, скорее всего, определённый артикль the, но первый слог Fa, надеюсь, все «переведут» одинаково.

А если взять определение функции, то это отображение, которое каждому элементу одного множества ставит в соответствие элемент другого, и как следует из названия, несёт некий Образ. Действительно, пусть Х - первое множество, У - второе множество, и есть правило, или закон, который каждому элементу из Х ставит в соответствие элемент из У. Это правило и будет называться функцией.

Позволю себе пример из советских времён (сейчас так быстро изменяются цены, что придумать пример из нынешнего времени проблематично). Тогда, на улицах города стояли автоматы с газированной водой. Вода без сиропа стоила 1 копейку, в то время как за газировку с сиропом надо было заплатить 3 копейки. Так вот, множество Х – это множество, состоящее из двух элементов – монета в 1 копейку и монета в 3 копейки. Стакан газировки без сиропа, и стакан газировки с сиропом – составляют множество У. Тогда функция – это правило, которое 1 копейке ставит в соответствие воду без сиропа, и 3 копейкам – воду с сиропом, или, по-другому, отображает копейки в питьё. При этом множество Х называется Прообразом, а множество У - Образом. То есть, У - это образ множества Х.

На этом моменте рассказ о функциях прерывается, потому что знакомых слов уже достаточно, чтобы читатель попробовал сложить для себя математические наброски на тему Образа Отца и связи функции и образа Отца, помня о том, что функция – это правило или закон.

Отмечу, что функция как позиция Слова Отца, и функция в контексте пятёрки (ЕНФ), в данном разделе не затрагиваются, но, возможно, для предложенного размышления это упоминание будет весьма уместным.


ОМ теории множеств


В этой главе речь пойдёт о теории множеств, двух математических действиях, и двух знаках, выражающих эти действия, 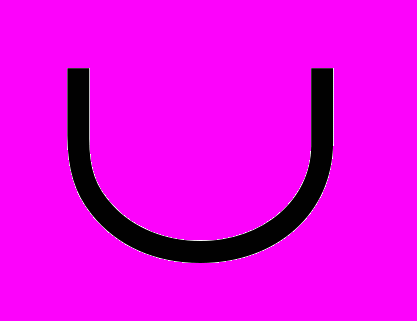и _.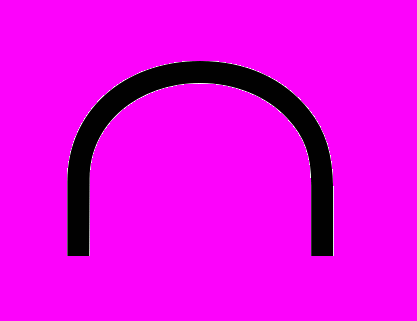

Начнём с первого. Дело в том, что не все математические объекты можно складывать. Если мы говорим, например, о числах, то их сложить можно, и понятно, «чем» окажется результат, это будет снова число. (Три плюс пять будет равно восьми). Но как только мы переходим к другим математическим категориям, то операция сложения теряет смысл. Не совсем ясно, что получится, если сложить два множества, два события, две геометрические фигуры. Зато мы можем их единять или объединять.

Мно́жество — одно из ключевых понятий математики. Оно является аксиоматическим, то есть, не может быть сведено к другим, а значит, и не имеет определение. Можно дать описание множества, например, в формулировке выдающего немецкого математика Георга Кантора: «Под «множеством» мы понимаем соединение в некое целое M определённых хорошо различимых предметов нашего созерцания или нашего мышления, которые будут называться «элементами» множества M». Это как раз то, о чём говорил Декарт – безразлично, звёзды это, или фигуры, или звуки.

Примеры. Множество - множество чело Владыки Иосифа, служащие в ДИВО 31 Проявления. Множество В – множество ведущих огня того же ДИВО. Объедине́нием мно́жеств будет называться множество, содержащее в себе все элементы и первого и второго множеств, и это новое множество будет обозначаться следующим образом 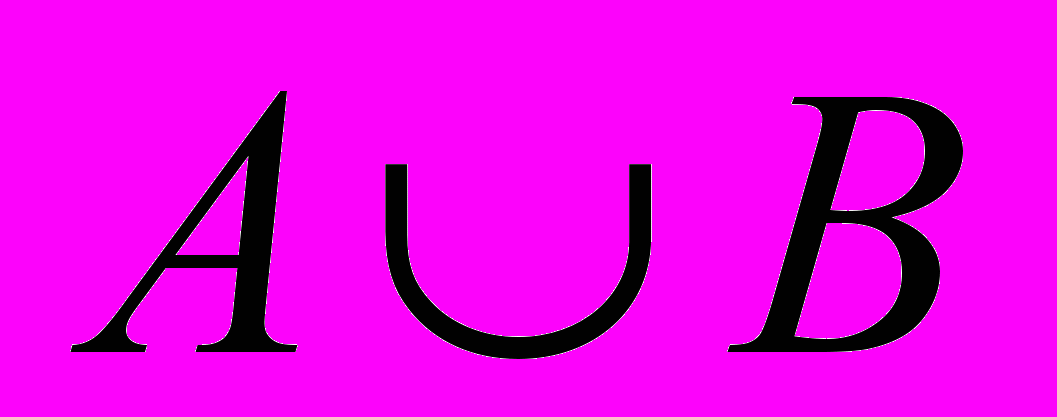. Причём, некоторые элементы первого и второго множества могут совпадать – естественно предположить, что найдётся ведущий огня, ведущим Владыкой которого является ИВ Владыка Иосиф.

– Дорогой, ты математику любишь больше, чем меня!

– Конечно нет, как ты могла такое подумать!

– Докажи!

– Пусть А – множество любимых объектов…

В разговоре о множествах не обойтись без двух специальных множеств, которые являются обобщением нуля и бесконечности в теории множеств.

Пустым множеством называется множество, в котором нет ни одного элемента, и для его обозначения используется символ перечёркнутого нуля . Это действительно нуль теории множеств. Пусть, например, С - множество 64-ричных человеков Санкт-Петербурга, которые имеют развитые 63 части. Очевидно, что на сегодняшний момент .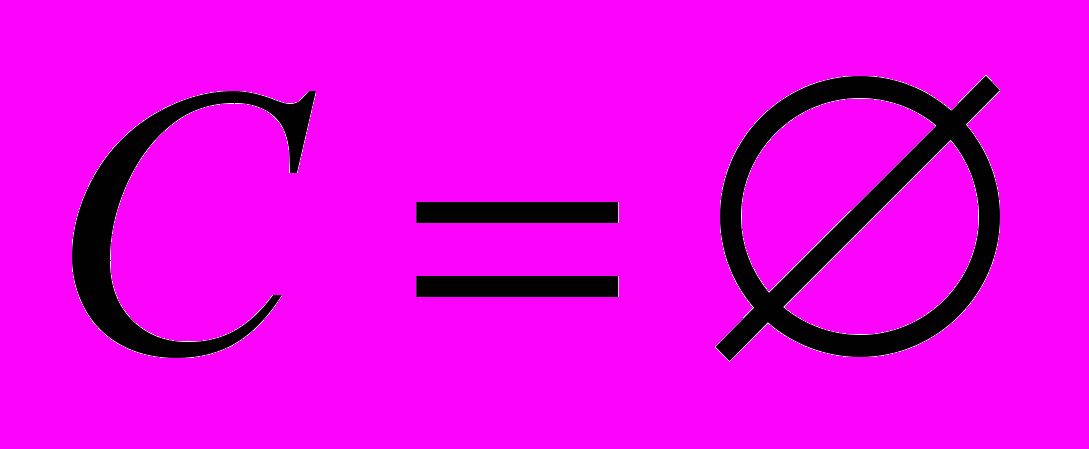

Универсальное множество в математике это множество, содержащее все мыслимые объекты. Универсальное множество обычно обозначается U (от англ. universe). Самое замечательное, что оно единственно! Так и хочется воскликнуть, вот же Он, Отец! И уже даже в физическом мире шестой расы, так как «мыслимые объекты» пятой расы, могли быть отнесены к тонкому миру, а теперь это уже чистая физика. Единственное, что дальше Универсума, судя по названию, пройти не получилось, но тут надо быть снисходительными – обозначение вводилось уже много лет назад, ещё в «разгар» 5 расы, когда Отец действительно управлял Планетой из Универсума. Обращаю внимание, что написание латинской буквы U напоминает знак объединения.

Посмотрим, какими свойствами обладает операция объединения





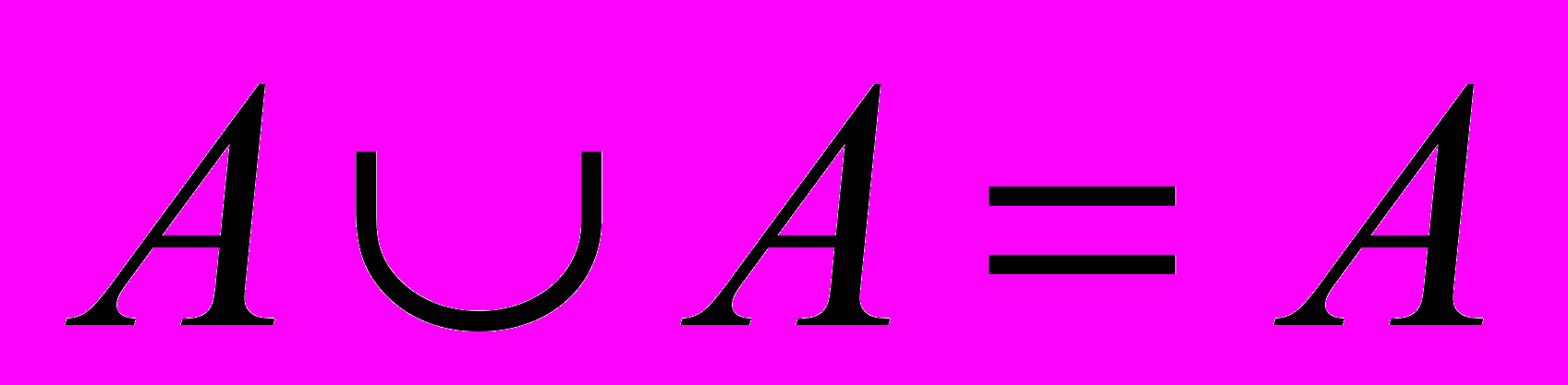
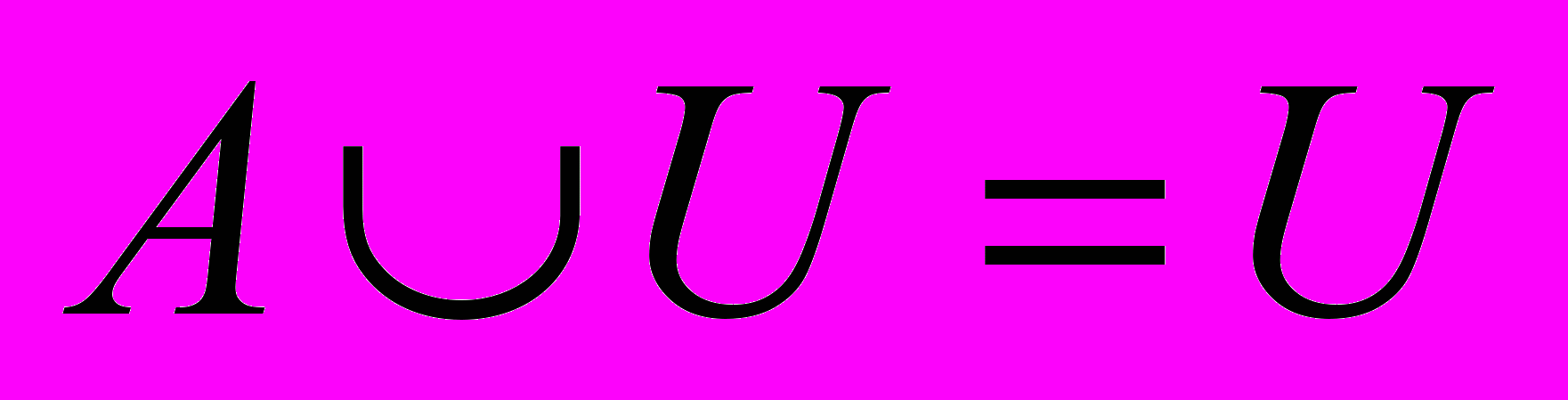
Пусть А – множество, состоящее из одного элемента – Человека. А={Человек}. Тогда первое свойство говорит о том, что ты можешь единяться сам с собой сколько хочешь, но ничего нового при этом не получается. А вот если ты единяешься с Отцом – тогда смотри второе свойство ….

Теперь о пересечении множеств. Пересечением двух множеств будет называться множество, элементами которого являются объекты, принадлежащие и первому, и второму множеству, и обозначать знаком 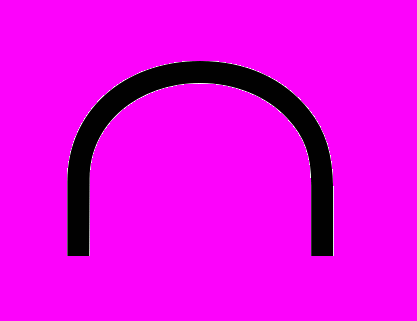. В нашем примере с множествами А и В, их пересечением будет являться множество ведущих огня ДИВО 31 Проявления, ведущим Владыкой которых является ИВ Владыка Иосиф.

Если изображать действия над множествами геометрически, то картинки получатся такими:




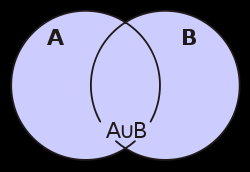
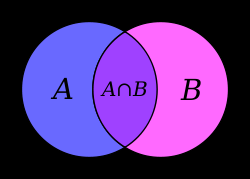
Знаку объединения соответствует союз или, так как в результате получается множество, состоящее из элементов или А, или В. Пересечению отвечает союз и – в нём (пересечении) присутствую элементы, принадлежащие и А, и В.

Так вот, нарисованные один над другим, два знака – объединения и пересечения – как будто устремляются навстречу друг другу, неся собою некий дух, ведь даже по названию сейчас идёт речь о действиях с множествами, а действие, несёт заряд духа. И становясь уже символами, складывают собой новую цельность, и рождают, если так можно назвать, математический ОМ теории множеств.





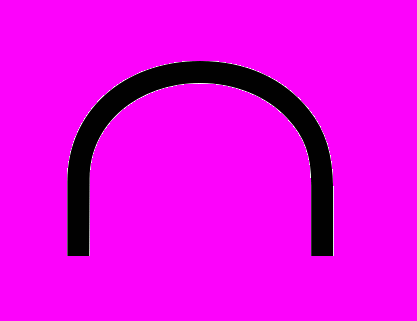
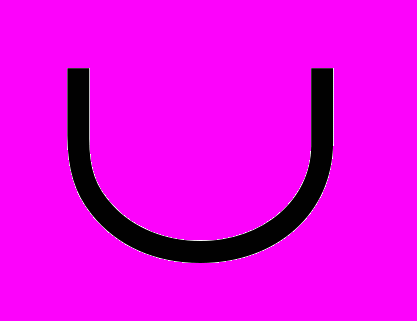
В связи с этим возникает вопрос, а где же волнистая линия, соединяющая или наоборот, отделяющая две половины, которым надлежит быть соединёнными.




Есть предположение, что и это совсем рядом и близко. Дело в том, что элементы множества принято записывать в фигурных скобках. Например, множество D, состоящее из груши, сосиски и бегемота, записывают так

D= {груша, сосиска, бегемот},

то есть, элементы множества обрамляются фигурными скобками. С учётом того, что базовые обозначения в математике весьма лаконичны и просты, появление «фигурностей» в самом базовом математическом объекте требует объяснения. На мой взгляд,

фигурная скобка







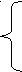
представляет собой две волнистых линии, зеркально отражённых друг от друга, словно напоминая слова Гермеса Трисмегиста «то, что наверху, подобно тому что внизу».


Парадоксы бесконечного

Пока элементов множества не много, теория даёт чудесные результаты. Мы имеем возможность сравнивать множества и определять классы эквивалентных множеств. Когда два конечных множества будут эквивалентны? Тогда, когда они имеют одинаковое количество элементов. Или, когда можно установить правило, по которому каждому элементу одного множества ставится в соответствие единственный элемент другого, и наоборот. (Последнее утверждение фактически является определением функции). Например, множество А={a,2b,7c} эквивалентно множеству В={3a,6b,21c}, потому что каждый элемент второго множества получается умножением на 3 каждого элемента первого множества. Обозначается этот факт волнистой линией, которая недавно упоминалась,

Но как только множество становится бесконечным, ситуация, можно сказать, выходит из-под контроля – начинают возникать парадоксы, причём давно сформулированные. Самые первые из дошедших до нас – апории Зенона. Например, о том, что Ахиллес никогда не догонит черепаху. «Допустим, Ахиллес бежит в десять раз быстрее, чем черепаха, и находится позади неё на расстоянии в тысячу шагов. За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползёт сто шагов. Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху»

В восточном варианте, приписываемом Гунсунь Луну, парадокс звучит так: «Если от палки [длиной] в один чи ежедневно отнимать половину, это не завершится и через 10000 поколений».

Бесконечность – это та область, в которой законы формальной логики перестают выполняться. Здесь, наверное, прослеживается параллель с классической механикой, которая хорошо описывает свойства мира до определённого масштаба, а потом становится неверной, и вступает в силу квантовомеханическое описание реальности. То же самое происходит при подходе к бесконечности, когда мы приближаемся к категориям бесконечно большой величины и бесконечно малой (о «взаимообратности» нуля и бесконечности см. Нуль и единица ).

Ещё Аристотель выделил в понятии бесконечности два аспекта – потенциальную и актуальную, подразумевая под последней реальность существования бесконечных вещей. Но при этом актуальную бесконечность принимать сам отказался. И понадобилось около 20 веков, чтобы появился учёный, который дал жизнь актуальной бесконечности. Этим учёным оказался Георг Кантор, между прочим родившийся и проведший детские годы в Петербурге. Так что Петербург – это не только колыбель революции, это ещё и колыбель актуальной бесконечности. Современная физика только приближается к бесконечности такого вида понятием сингулярности в теории чёрных дыр и большого взрыва.

Само слово «бесконечность» несёт алфавитную «проблему», поскольку первый слог этого слова является причиной того, что в Синтезе оно почти не произносится. Но в математике его невозможно не употреблять.

Если брать английское название бесконечности, то оно более удачное – infinity. С учётом перевода слова finite – конечный, дословно можно было бы перевести как вконечность, что, по сути, очень глубоко. Но всё сложилось, как сложилось, поэтому попробую вложить новый смысл в знакомое слово. Может, будем считать, что мы постигаем «логику» бесконечности, которая несёт собою идею Отца, и бес кончается, завершается, его больше нет, и уже невозможна никакая манипуляция? Единственное, что эту логику надо действительно постичь.

Кстати, к вопросу о логике и логической сфере мысли. Часто приходится слышать, что у человека уже легко работают больше 8 сфер мысли. Проверь себя и разреши известный со времен Древней Греции парадокс лжеца. «То, что я пишу сейчас в кавычках – ложно». (Если я написала правду, то это противоречит тому, в чём состояло утверждение. Но если то, что я написала ложно, означает, что у меня должна быть написана правда.) Если вы не запутались ещё до конца, вопрос в следующем – выражение в кавычках истинно или ложно?

Следующий наш шаг – в сторону бесконечных множеств. Самое просто бесконечное множеств это числа 1,2,3,4,… . Вопрос – а какое множество «больше» {1,2,3,4,….} или {2,4,6,8,……}? Обращаю внимание, что все числа второго множества содержатся в первом. Часть меньше целого? Или всё-таки равна? Ведь все числа второго множества получены в результате умножения на два чисел первого множества …

Ещё один парадокс бесконечности – парадокс Тристрама Шенди. В романе Стерна «Жизнь и мнения Тристрама Шенди, джентльмена» герой обнаруживает, что ему потребовался целый год, чтобы изложить события первого дня его жизни, и еще один год понадобился, чтобы описать второй день. В связи с этим герой сетует, что материал его биографии будет накапливаться быстрее, чем он сможет его обработать, и он никогда не сможет её завершить. Теперь я утверждаю, — возражает на это Бертран Рассел, которому и принадлежит этот парадокс — что если бы он жил вечно, и его работа не стала бы ему в тягость, даже если бы его жизнь продолжала быть столь же богатой событиями, как вначале, то ни одна из частей его биографии не осталась бы ненаписанной.

Продолжаем задавать вопросы по бесконечным множествам. А как можно описать множество {1,2,3,4,…}, если в нём бесконечное множество элементов. А множество точек на отрезке [0,1] «больше»? Или по-другому, а чего больше – натуральных чисел или точек внутри маленького отрезка, и вообще, можно ли их сравнивать.

Вернёмся к эквивалентности. Будем говорить, что два эквивалентных множества имеют одинаковую мощность или одинаковое кардинальное число. Это означает, что каждому множеству ставится в соответствие некая «штучка» так, что эквивалентным множествам соответствует одна и та же «штучка». Вот эта «штучка» и называется кардинальным числом или мощностью множества. Такое несерьёзное определение говорит о том, чем должно быть кардинальное число, попытка дать строгое определение не приведёт к успеху. Отношения между кардинальными числами есть удобный способ выражения отношений между множествами. Мощность множества или кардинальное число множества — это обобщение понятия количества элементов множества, которое имеет смысл для всех множеств, включая бесконечные.

Итак, пустое множество имеет мощность равную нулю. Множества {2,5,8,11} и {Душа, Престол, Вера, Ум} имеют одинаковое кардинальное число равное четырём, поскольку содержат по четыре элемента.

Самому простому из всех бесконечных множеств – множеству натуральных чисел N={1,2, 3,….. }, следуя за Кантором, припишем мощность – алеф-нуль.

Алеф это первая буква семитских алфавитов (финикийского, еврейского, арабского и др.). Необходимость прибегнуть к другому алфавиту с одной стороны обусловлена тем, что ко времени, когда Кантор занялся разработкой теории множеств, а это конец 19 века, многие буквы латинского алфавита и греческого были уже заняты под какие-то базовые математические обозначения. Но с другой стороны, Кантор не мог не чувствовать значимость кардинальных чисел и появление еврейского варианта буквы альфа отнюдь не случайно. Все буквы в иврите имеют числовое значение. В древности евреи, как и многие другие народы, не использовали для счёта цифры — и записывали числа буквами. Такой заменой пользуются до сих пор в религиозных текстах, в календаре и даже в современной разговорной речи на иврите. Числовое значение (гематрия) буквы «Алеф» — 1. В мистической символике это число выражает единство всего сущего. В каббале эта буква обозначает Эйн-соф (ивр. אינסוף‎) — безграничную, чистую божественность. Выглядит эта буква так



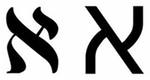
Тогда получается, что все эквивалентные множества имеют такое же кардинальное число, и значит, множества, элементы которых можно пронумеровать 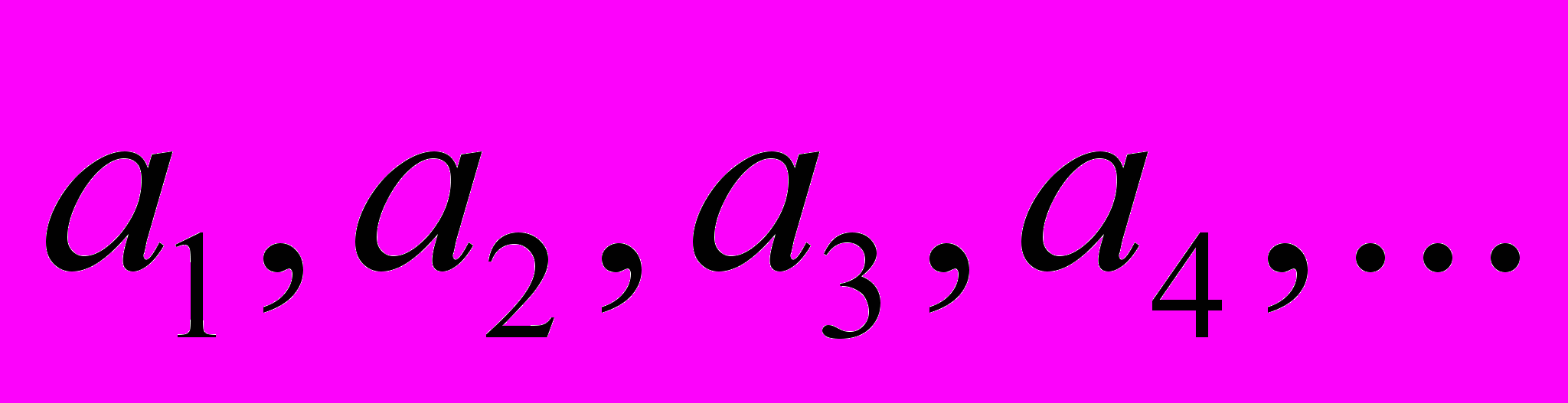имеют мощность алеф-нуль. Приведу примеры таких множеств

1, 2, 3, 4,…, n, ……

2, 4, 6, 8,…., 2n, …..



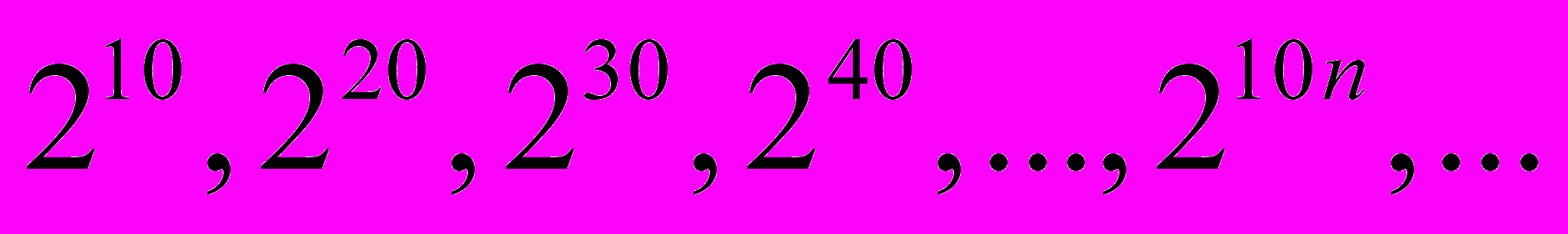
Все три множества имеют одинаковую мощность, равную алеф-нуль. Последняя последовательность содержит числа, которые очень редко распределены на множестве натуральных чисел, тем не менее, мощность соответствующего множества совпадает с мощностью N. Это нарушение аксиомы «totus parte majus» (целое больше части) является одним из парадоксов бесконечности, к которым просто следует привыкнуть. Это одна из изюминок логики бесконечности.

Следующий шаг в следующую бесконечность, и примеры становятся ещё ярче и выразительней. Множество точек отрезка [1,2] и отрезка [10 000, 20 000] имеют одинаковое кардинальное число, (существует функция у=10 000х, которая преобразует элементы одного множества в другое). Эти два множества оказываются эквивалентными или равномощными, хотя второй отрезок длиннее первого в 10 тысяч раз.

Идём дальше и сравниваем отрезок 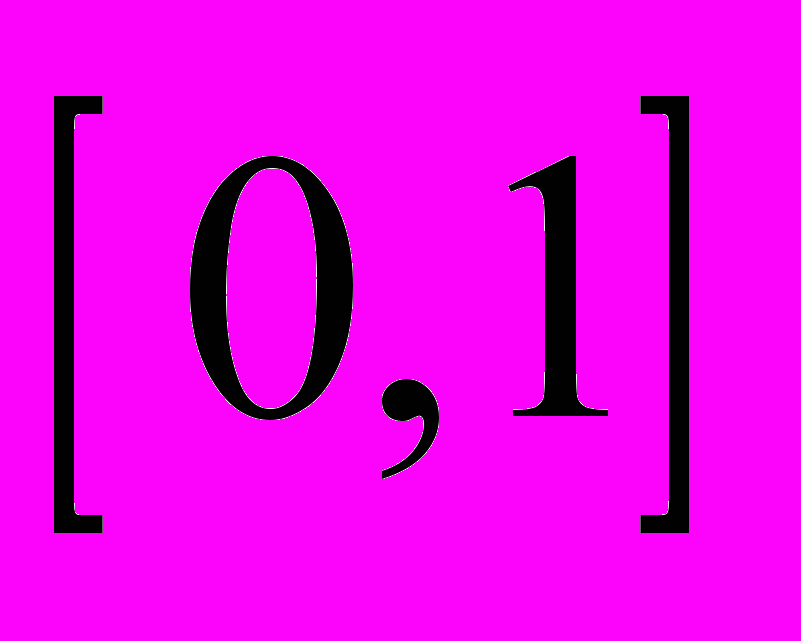и ВСЮ числовую прямую, то есть, интервал (-∞,∞) и отрезок 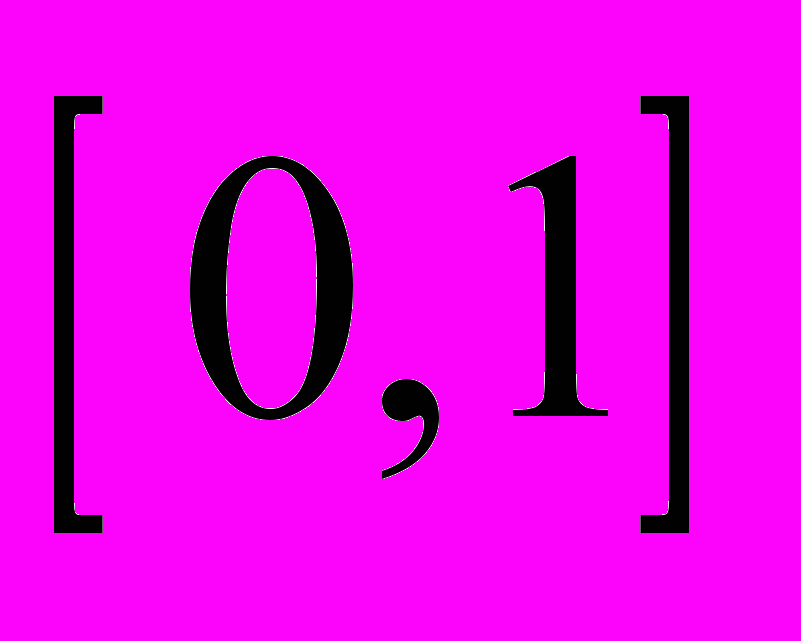. Они тоже эквивалентны!!! ОБА множества имеют одинаковое кардинальное число.

Для доказательства этого утверждения достаточно привести функцию, которая отобразила бы одно множество в другое. Её несложно придумать, учитывая, что , 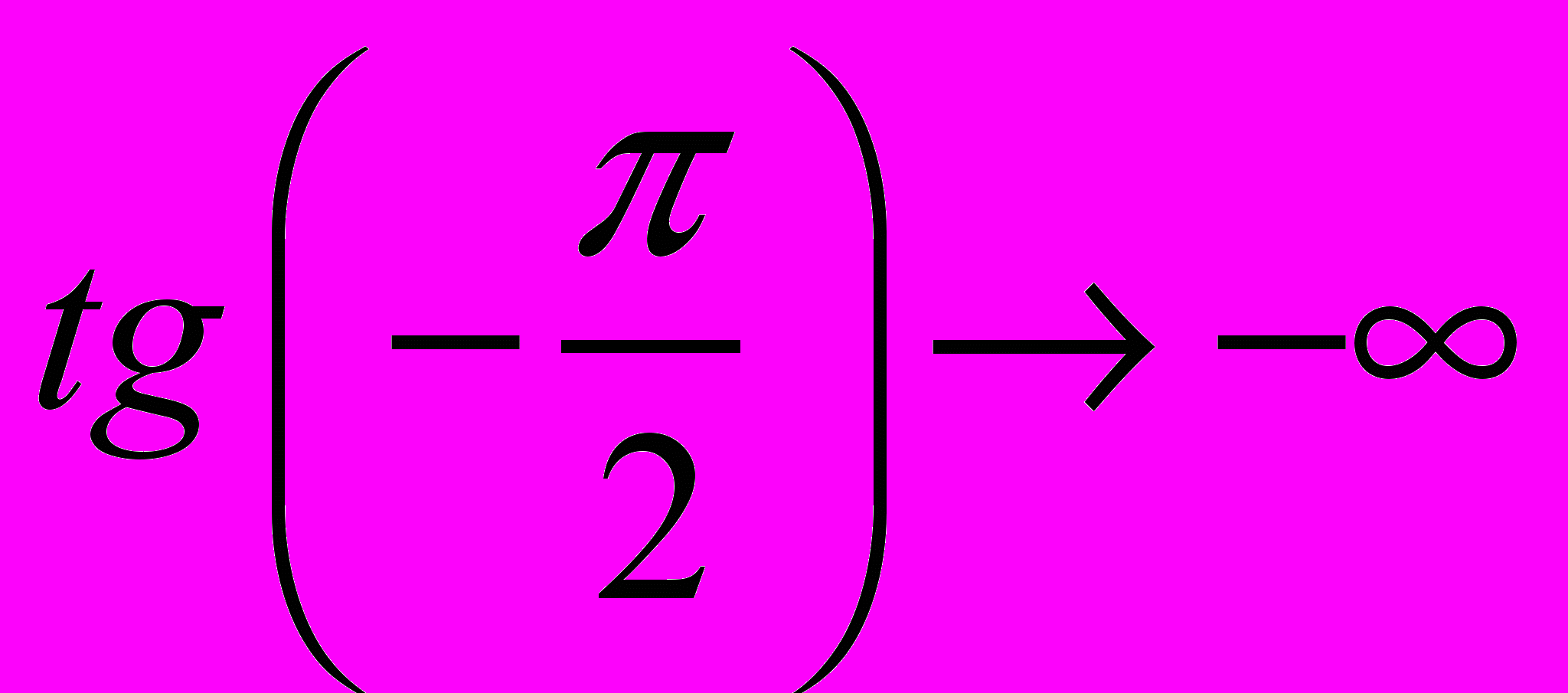. Искомое преобразование имеет вид 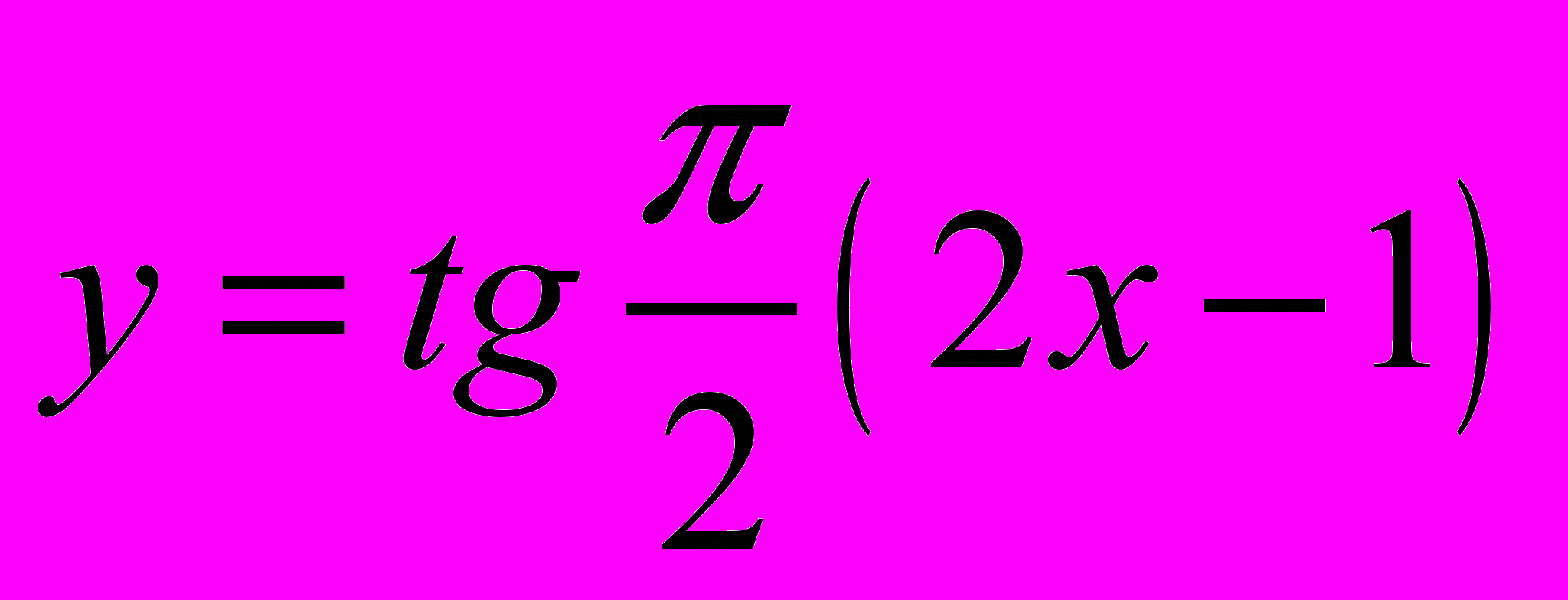. Чтобы проверить, достаточно подставить точки 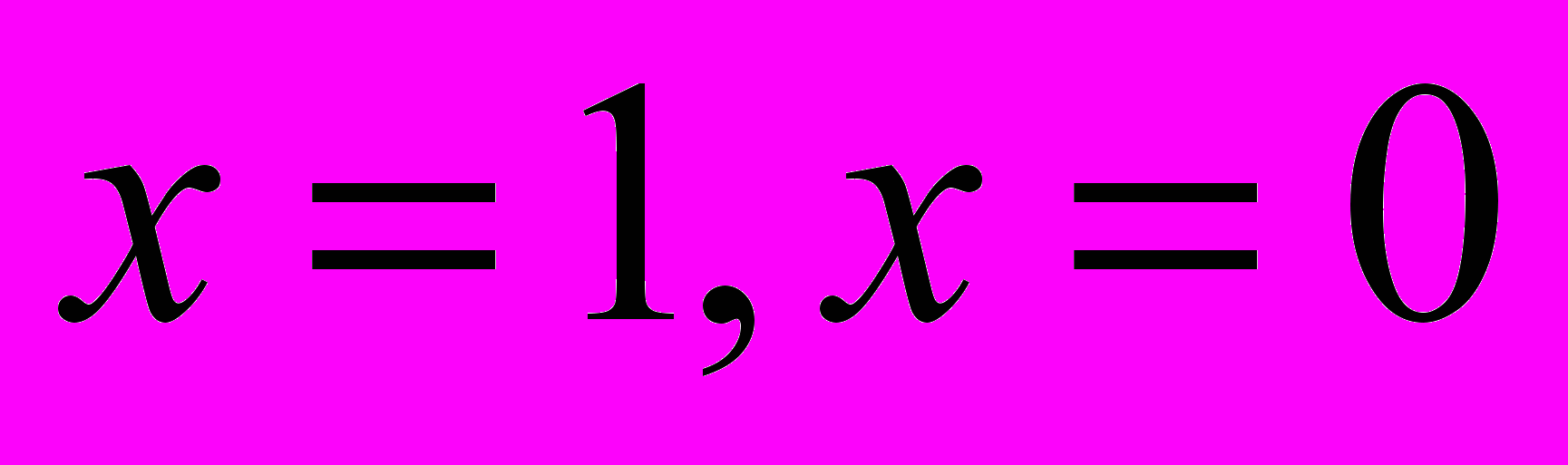в выражение для 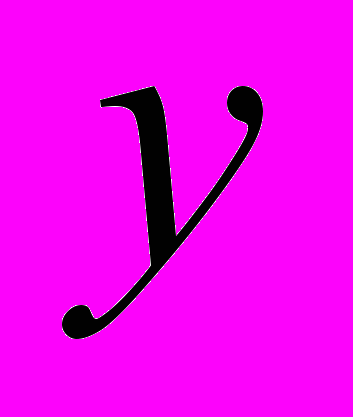, и вспомнить, что тангенс является непрерывной функцией на отрезке )


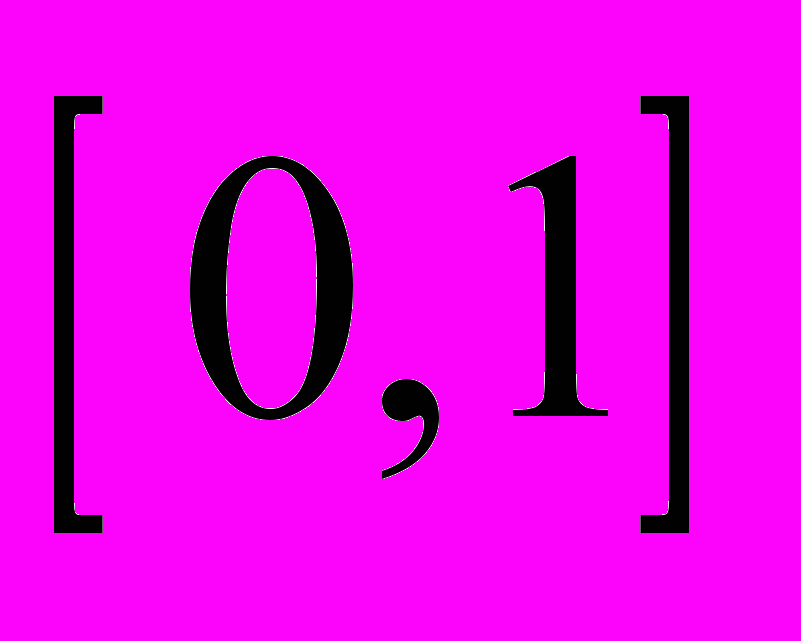Итак, вся бесконечная прямая, и маленький её отрезочек – эквивалентные множества. Ну как тут не вспомнить Гермеса с законом «часть подобна целому»!

Кантор показал, что такое свойство – эквивалентность множества его правильной части – основная характеристика бесконечного множества, то есть, именно то, что отличает его от множества конечного.

Интуитивно ясно, множество всех точек прямой существенно отличается от множества натуральных чисел, и Кантор назвал мощность такого множества – алеф. По-другому она называется мощностью континуума. Поэтому бесконечный интервал (-∞,∞) имеет мощность алеф. И как это ни странно звучит, конечный промежуток 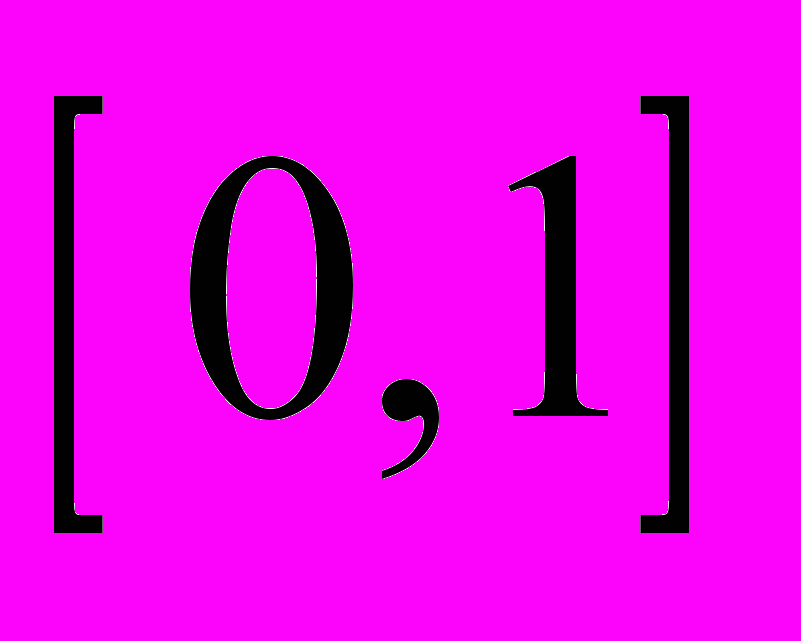обладает такой же мощностью.

И «бесконечность» приобретает новый смысл, как глубина или тайна, которая заложена в конечном, соответствуя английской версии этого слова. Бесконечность перестает быть безразличным отрицанием конечного и становится присущей ему внутренне. Конечное рацио и мистика бесконечного снова оказываются рядом друг с другом.

Попробуем в рамках теории множеств ответить на вопрос «почему в Синтезе основные числовые выражения базируются на степенях двойки – 16, 32, 64, 128, 256,…?». Возьмём множество, состоящее из трёх элементов {a,b,c}, и попробуем найти все возможные его подмножества. Перечисляем: оно само – {a,b,c}, множества, состоящие из двух элементов – {a,b},{a,c},{b,c}, из одного – {a},{b},{c}, и наконец, пустое множество. Всего 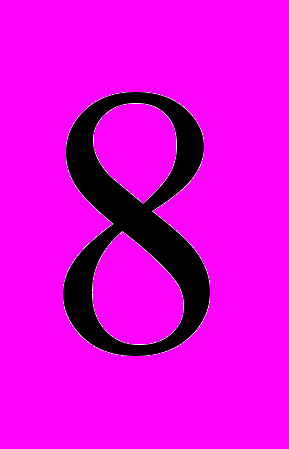или 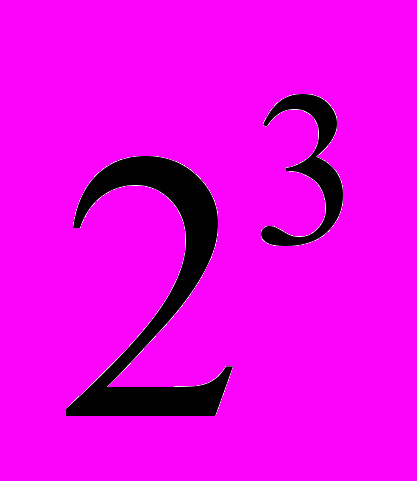. Если взять множество из четырёх элементов, то подмножеств окажется ровно 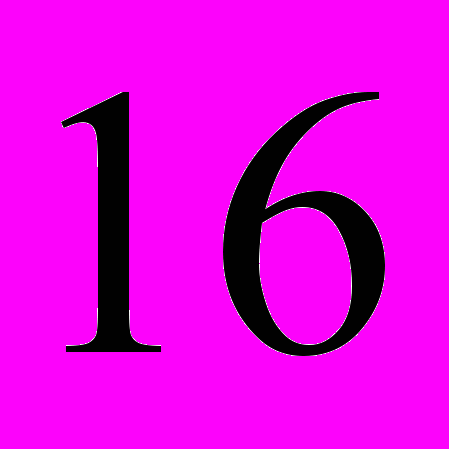или 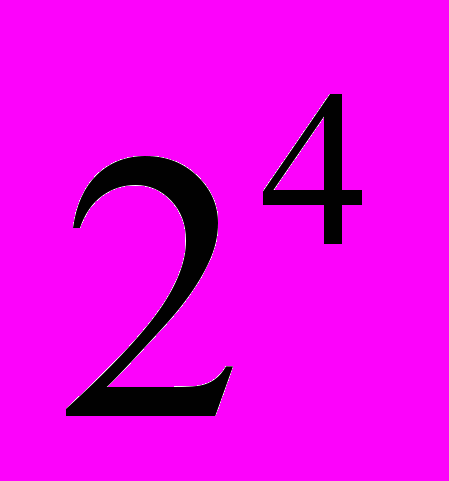. Вероятно поэтому, «четверица» Новой эпохи {огонь, дух свет, энергия} рождает 16-ричного человека.

Множество, содержащее 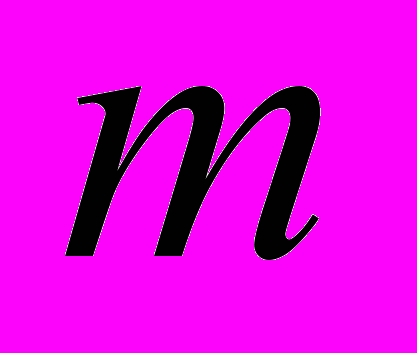элементов, будет иметь 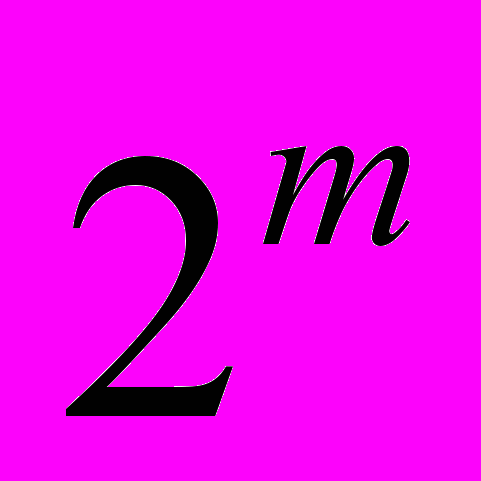подмножеств или составных частей.

Если сравнивать само множество и множество всех подмножеств, то первое имеет 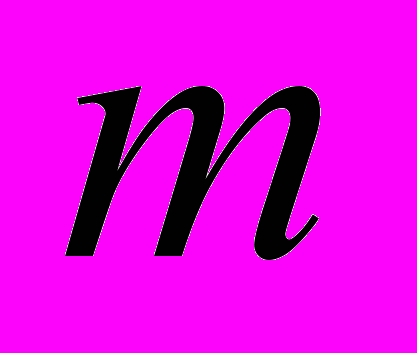элементов, а второе – 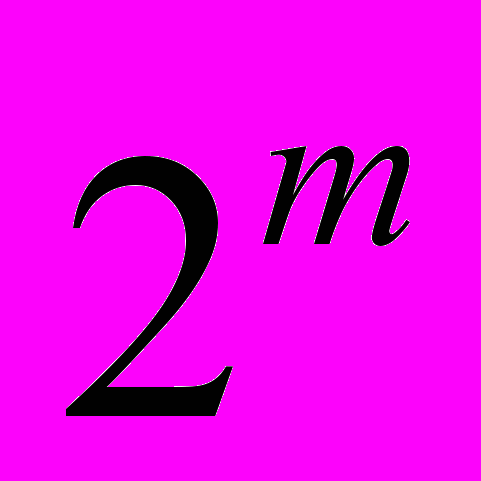. И поскольку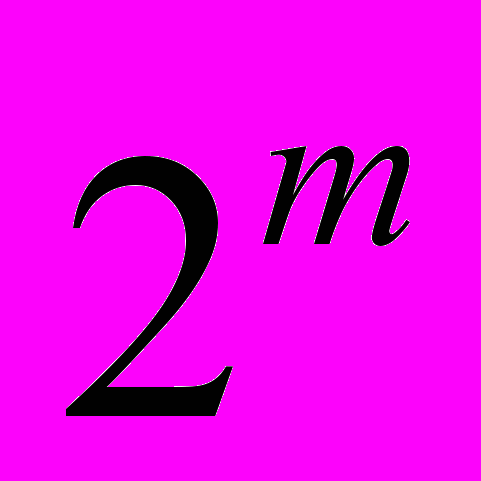больше 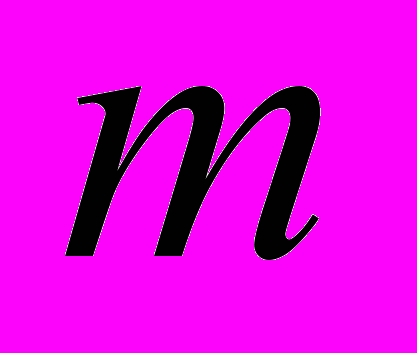, то множество всех подмножеств очевидно мощнее самого множества.

Этот факт порождает ещё один замечательный парадокс бесконечности – парадокс Кантора. Он говорит о том, что не существует максимального кардинального числа. В самом деле: пусть оно существует и равно μ. Но тогда, с учётом сказанного ранее 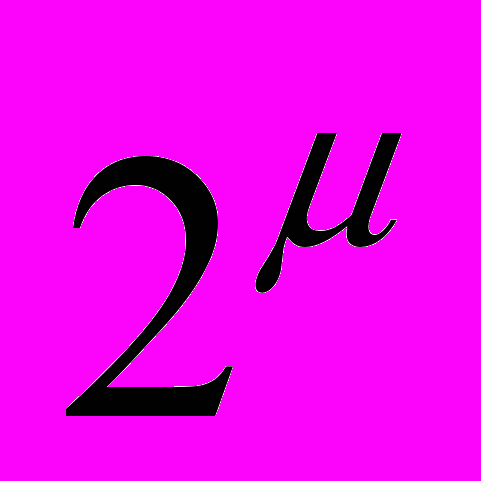больше, чем , поскольку множество всех подмножеств мощнее самого множества.


Резюмируем, что мы узнали о бесконечных множествах к настоящему моменту. Существует первый тип бесконечных множеств, «похожих» на натуральные числа. Мощность такого множества равна алеф-нуль. Второй тип бесконечных множеств – множества типа континуум (или все числа на прямой), мощность которых равна алеф. Оказывается, что этими двумя величинами – алеф и алеф-нуль – описываются все мыслимые бесконечные множества, причём алеф и алеф-нуль связаны равенством



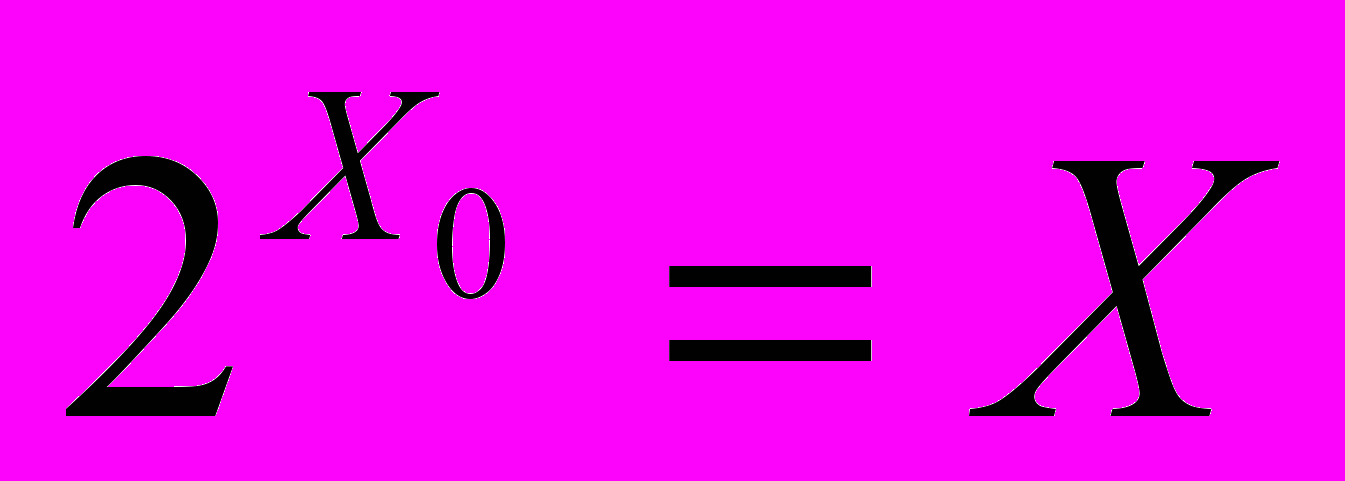
(возможности программы, которой я пользуюсь при вставке математических формул, не позволяют записать букву алеф, поэтому здесь для обозначения алеф-нуль и алеф использованы символы 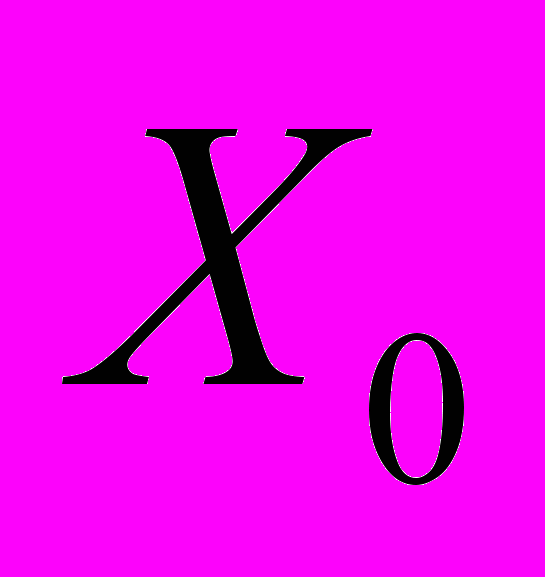и 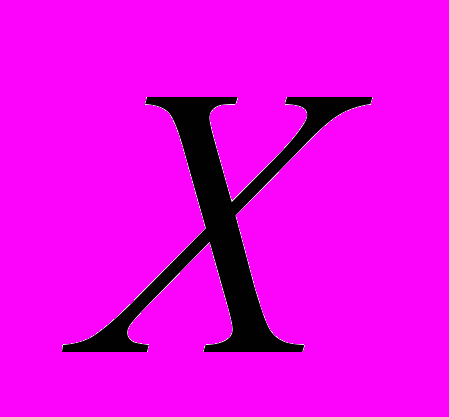соответственно).

Кантор высказал предположение о том, что алеф есть ближайшая к алеф-нуль по величине мощность. Это предположение носит название континуум-гипотезы и остаётся недоказанным уже более 100 лет.

Все конечномерные и счётномерные пространства имеют одинаковую мощность алеф – вне зависимости от того какое пространство – двумерное, пятимерное, или ещё какое-нибудь мерное.

Кстати, если попробовать определить, что такое пространство, то математически это будет выглядеть как множество с некой дополнительной структурой, и значит, любые пространства можно описывать в рамках теории множеств.

До этого момента мы рассматривали множества, не беспокоясь о том, существуют ли какие-либо отношения между элементами множества, или, как элементы расставлены внутри множества. К примеру, берём множество, составленное из слона, муравья и лебедя. Вначале я хочу, чтобы элементы внутри множества распределились в порядке размера, от меньшего к большему. Тогда, очевидно, это множество принимает вид {муравей, лебедь, слон}. А теперь задача другая – расположить их же, в цветовой гамме от светлого к тёмному. В этих предположениях множество из тех же элементов становится другим {лебедь, слон, муравей}, и мы можем говорить об отношениях порядка. Как только отношения порядка заданы, множество становится упорядоченным. Причём эта упорядоченность бывает разная – говорят о множествах вполне упорядоченных, частично упорядоченных.

Например, частично упорядоченным множеством называется множество, на котором определено отношение частичного порядка. Неформально можно сказать, что это отношение вводит некую иерархию элементов множества, выстраивая зависимость между ними. При этом такое отношение необязательно должно быть отношением линейного порядка, то есть не все элементы «сравнимы». Одним словом, как только мы выходим на вопросы упорядоченности, получается очень иерархическая история о множествах.

Когда мы начинаем сравнивать бесконечные множества, мы включаем отношения порядка, и понятие мощности, в общем-то, для этого и нужно. Самое маленькие бесконечные множества – это множества мощности алеф-нуль. Множества побольше – множества мощности алеф. И ещё больше, прямо как в сказке про трёх медведей, множества мощности .

Снова возвращаюсь к рациональному и мистическому. В предыдущей работе мы обсудили, что существуют числа рациональные. Так вот, эти числа образуют пространство, которое так и называется – пространство рациональных чисел – Q. Это те числа, которыми мы пользуемся в повседневной жизни. Всё было бы хорошо, но пространство Q оказывается неполным. (Полнота пространства означает, что каждая фундаментальная последовательность сходится). Если мы произведём процедуру пополнения пространства, то есть, добавим все иррациональные числа, которые «живут» между рациональными, только в этом случае достигается полнота. Результатом пополнения пространства будет множество всех вещественных чисел, то есть, вся числовая прямая. Таким образом, математически устанавливается, что полноты можно достичь только в синтезе рационального и иррационального, рационального и мистического.

И немного математического дзена. Математики разных направлений решают одну и ту же проблему.


Инструкция для тех, кто будет охотиться на льва!


Гильбертов метод

В пустыне устанавливаем клетку и вводим следующие аксиомы:

аксиома 1) Множество львов не пустое множество;

аксиома 2) Если есть множество львов в пустыне, то один из них точно находится в клетке.

Заключение: если 1) правильно и действительно следующее: «если 1, то 2», то 2) тоже правильно.

Теорема: лев точно в клетке.


Геометрический метод

Устанавливаем цилиндрическую клетку в пустыне.

1) Лев в клетке. Решение тривиально.

2) Лев находится снаружи клетки. Заходим в клетку и делаем непрерывное обратное отображение стенок клеток. Тогда лев попадёт внутрь клетки, а мы сами окажемся снаружи.

ВАЖНО: Нельзя ни в коем случае стоять посередине клетки, чтобы при обратном отображении не исчезнуть в бесконечности!


Метод Больцано-Вейерштрасса

Делим пустыню с севера на юг колючей проволокой. Лев будет находиться либо в её восточной или западной части. Мы предполагаем, что он находится в западной. Делим западную часть с востока на запад. Лев может находиться либо в северо-западной, либо в юго-западной. Предполагаем, что находится в северо-западной. Таким образом, продолжаем делить всю пустыню. При этом диаметр рассматриваемых областей будет монотонно стремиться к 0. Поэтому в конечном итоге лев будет окружён проволокой вплотную со всех сторон.

ВАЖНО: поскольку проволока колючая, очень важно не отрезать ею кисточку хвоста!


Метод функционального анализа

Пустыня - сепарабельное пространство, поэтому содержит счётное, всюду плотное множество, из которого можно выбрать какую-то последовательность. Она будет иметь поточечную сходимость ко льву. Остаётся только взять клетку и следуя этим точкам, максимально близко приблизиться ко льву.


Топологический метод

Рассмотрим льва как тор. Перенесём пустыню в 4-мерное пространство. Отсюда является возможным так деформировать пустыню, что при обратном переносе в 3-мерное лапы льва будут скручены вокруг точек пересечения. Но тогда он беспомощен.


Многомерная логика


Логику мы не знаем совершенно, и чаще всего, уверены в обратном. Кто не согласится со мной, отправлю к статье Логика в Википедии. Там достаточно посмотреть раздел «Основные понятия», и кликнуть, например, на статью силлогизм. Или просто набрать «категорический силлогизм». Очень милая статья …. А четвёртая сфера мысли должна брать такое играючи!

Вскоре после того, как были открыты парадоксы бесконечного (конец 19 в), крупнейшие математики и логики пришли к тому, что антиномии типа парадокса Кантора, не являются следствием логических ошибок в объяснениях, а представляют собой новый мыслительные проблемы. Найти для них логическое оправдание смог только один человек – русский мыслитель и логик Николай Васильев. Его роль в логике можно сравнить с ролью Лобачевского в геометрии, с той разницей, что идеи Лобачевского были приняты сразу, о логика Васильева была оставлена в забвении на 80 лет.

Лобачевский положил начало неклассической геометрии, а Васильеву пришлось создать неклассическую, «воображаемую» логику (Лобачевский тоже называл свою геометрию воображаемой).

Существуют аксиомы геометрии, существуют аксиомы логики. В геометрии Лобачевского всего одна аксиома о параллельности прямых заменена на другую – и в результате совершенно другая геометрия, абсолютно другая картина мироздания. А изменён всего один параметр. Аксиома Евклида

«Через точку, не лежащую на данной прямой, проходит не более одной прямой, лежащей с данной прямой в одной плоскости и не пересекающей её»

заменяется на аксиому

«Через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её»

Раз это так, то какое-нибудь логическое предположение тоже может быть отброшено, заменено другим и тогда неминуемо должно получиться нечто совершенно новое.

Все аксиомы логики не могут быть абсолютными. Например, утверждение «все треугольники имеют три угла» может быть истинным, в то время как «сумма углов треугольника равна 180 градусам» таковым не будет (в геометрии Лобачевского сумма углов треугольника не равна 180градусам, так как треугольник «лежит на сфере»).

Отсюда – вывод о множественности логических систем и возможность воображаемой (неаристотелевой) логики. «Предметом воображаемой логики, - пишет Васильев - будет мир, отличный от привычного нам, в том мире, где истинна одна логика, друга – ложна. В мире с иными физическими законами должны быть иные естественные законы мышления, существа с иной интеллектуальной организацией, и, стало быть, с другими логическими законами».

Традиционная аристотелева логика учит о четырёх основных законах мышления:

- тождества (предмет суждения должен оставаться тождественным самому себе в этом суждении);

- противоречия (два противоречащих либо противоположных суждения не могут быть одновременно истинными. По крайней мере одно из них необходимо ложно);

- исключённого третьего (из двух высказываний — «А» или «не А» — одно обязательно является истинным;

- достаточного основания.

Закон противоречия не позволяет одновременно существовать утвердительному и отрицательному суждению. Этим законам изгоняется из нашего мира противоречие. А почему не предположить, что во Вселенной, в безграничном её многообразии есть такие миры, в которых существуют противоречивые вещи, - так рассуждает Васильев, и строит воображаемую логику, освобождая её от закона противоречия.

Закон исключённого третьего - или так, или не так, другого не дано – исключает всякую третью форму суждения. Благодаря этим законам классическая логика имеет дело только с утвердительными и отрицательными суждениями. Поэтому, может быть, попробовать отойти и от этого закона? И тогда мы сразу, законодательно, отходим от деления на хорошо – плохо, а другого не бывает, а значит, поднимаемся выше «шестёрки»?

Васильев предложил два типа интерпретации логики – чисто эмпирическую и метафизическую, фактически выделив Отцовский и Материнские аспекты логики. Метафизическую часть он назвал металогикой.

И логика предстала в двух ипостасях – логика вещей, логика Матери, в которой действуют законы классической логики, и логики понятий или металогика. И последняя с необходимостью потребовала закона несамопротиворечия и закона исключённого четвёртого.

Закон несамопротиворечия вытекает из закона противоречия, как бы, усиляя его. Ведь одно дело, когда запрещается существование двух несовместимых признаков в предмете, а другое – когда провозглашается, что одно высказывание не может быть одновременно истинным и ложным. В воображаемой логике первое отбрасывается, а второе сохраняет силу для любой мыслимой логической системы.

Закон исключённого четвёртого подразумевает, что теперь существует три формы суждения – утвердительное, отрицательное, и комбинация утвердительного и отрицательного (индифферентное суждение) вида «S суть Р и не Р».

В таком варианте возможности новой логической системы оказываются огромными. Наверное, поэтому и говорится о том, что логическая мысль 5-ой расы отдыхает перед логической мыслью 6-ой.

Более 100 лет назад Васильев писал: «Мы должны внести в логику идею бесконечности, великую идею нового времени с её бесконечно большим – вселенной, с её бесконечно малым математического анализа. В логике всегда не хватало бесконечности, маленькой и замкнутой была она со своими 19 модусами силлогизма и 4-мя правилами индукции. Нужно расширить её пределы, удостовериться в бесконечности возможных логических систем. Тот, кто удостоверится в этом, будет испытывать ощущение Джордано Бруно, когда впервые в его воображении предстала бесконечность физической Вселенной, когда разлетелись вдребезги хрустальные сферы неба».

Остаётся предположить, что когда-нибудь закон исключённого четвёртого тоже окажется недостаточным, и нам придётся осваивать новую «логическую мерность», входя в закон исключённого пятого, разворачивая новые многомерные логики…

Теорема Гёделя о неполноте.

В 1900 в Париже на Всемирной конференции математиков Давид Гильберт сформулировал задачи, которые предстояло решить ученым-теоретикам наступающего ХХ века. Под вторым номером значилась одна из тех простых задач, ответ на которые кажется очевидным, пока не копнешь немножечко глубже. Говоря современным языком, это был вопрос: самодостаточна ли математика?

Вторая задача Гильберта – необходимость строго доказать, что система аксиом, — совершенна и полна, то есть, позволяет математически описать всё сущее. (Аксиома – это то, что принимается за основу без доказательств). Надо было доказать, что можно задать такую систему аксиом, что они будут, во-первых, взаимно непротиворечивы, а во-вторых, из них можно вывести заключение относительно истинности или ложности любого утверждения.

Берём уже знакомый пример. В рамках евклидовой геометрии можно безоговорочно доказать, что утверждение «сумма углов треугольника равна 180°» истинно, а утверждение «сумма углов треугольника равна 137°» ложно. Если говорить по существу, то в Евклидовой геометрии любое утверждение, либо ложно, либо истинно, и третьего не дано – закон исключённого третьего. И в начале ХХ века математики наивно полагали, что такая же ситуация должна наблюдаться в любой логически непротиворечивой системе. В 1931 году венский математик Курт Гёдель опубликовал короткую статью, которая перевернула мир «математической логики».

Возьмем любое утверждение типа: «Предположение № 8 в данной системе аксиом логически недоказуемо» и назовем его «утверждением A». Так вот, Гёдель доказал удивительное свойство любой системы аксиом:

«Если можно доказать утверждение A, то можно доказать и утверждение не-A».

Иными словами, если можно доказать справедливость утверждения «предположение 8 недоказуемо», то можно доказать и справедливость утверждения «предположение 8 доказуемо». То есть, возвращаясь к формулировке второй задачи Гильберта, если система аксиом полна (то есть, любое утверждение в ней может быть доказано), то она противоречива.

Единственным выходом из такой ситуации остается принятие неполной системы аксиом. Это значит, приходиться мириться с тем, что в контексте любой логической системы у нас останутся утверждения «типа А», которые являются заведомо истинными или ложными, — и мы можем судить об их истинности лишь вне рамок принятой нами аксиоматики. Если же таких утверждений не имеется, значит, наша аксиоматика противоречива, и в ее рамках неизбежно будут присутствовать формулировки, которые можно одновременно и доказать, и опровергнуть.

Итак, формулировка первой, или слабой теоремы Гёделя о неполноте: « Любая формальная система аксиом содержит неразрешенные предположения».

Но на этом Гёдель не остановился, сформулировав и доказав вторую, или сильную теорему Гёделя о неполноте: «Логическая полнота (или неполнота) любой системы аксиом не может быть доказана в рамках этой системы. Для ее доказательства или опровержения требуются дополнительные аксиомы (усиление системы)».


Теорема Гёделя относится к величайшим открытиям ХХ века, в одном ряду с теорией относительности и квантовой механикой. Считается, что вместе с принципом неопределённости Гейзенберга, теорема Гёделя о неполноте перевернули все основания науки. Споры о «теории противоречивости бытия», как её иногда называют, не утихают и по сей день. Так что любителям логики и специалистам по четвёртой сфере мысли есть, что почитать и о чём поразмышлять. И каждый сделает свои выводы, как в следующей истории:


Математик, физик и социолог сидят в поезде и пересекают границу соседнего государства. На первом же поле они увидели двух черных овечек.

Социолог говорит:

– Можно сделать заключение, что в этой стране все овцы черного цвета.

Физик с сомнением покачал головой и возразил:

– Этого нельзя сказать. Самое большее, что можно утверждать – в этой стране минимум две овцы черного цвета.

На это математик, улыбаясь, заметил:

– И этого тоже нельзя утверждать! Однозначно можно сказать, что в этой стране две овцы черного цвета с одной стороны!


Продолжение следует.


Полякова Оксана, ДИВО 31 Про

Июль 2011