Geum.ru

Исследование характеристик систем массового обслуживания с простейшим входящим потоком заявок и произвольными потоками обслуживания 29

Вид материалаИсследование

Содержание


4.2Исследованиефункции штрафа для систем, состоящих из нескольких обслуживающих устройств
Подобный материал:
1   ...   5   6   7   8   9   10   11   12   13

4.2Исследованиефункции штрафа для систем, состоящих из нескольких обслуживающих устройств



Исследуем поведение функции штрафа E для системы, состоящей из нескольких последовательных устройств. Например, проведем анализ совокупности агрегатов типа процессор-память и накопитель на жестком магнитном диске.

С
труктурная схема системы в терминах имитационной модели представлена на рисунке 4.3.

Рисунок 4.3 – имитационная модель системы, состоящей из двух последовательных устройств.

Для проведения вычислительного эксперимента допустим, что время поступления заявок в систему распределено равномерно на интервале от 9 до 11 секунд. Штраф за простой заявки в очереди составляет 5 у.е./секунду. Обслуживание требований осуществляется устройствами 1 и 2. Закон распределения времени обслуживания – равномерный.

Функция штрафа в данном случае имеет вид:



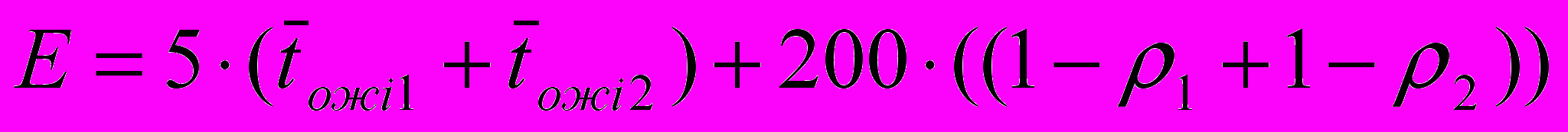
Рассмотрим процесс чтения данных с магнитного носителя и их последующей обработки. Предположим, что время обработки информации в несколько раз меньше времени чтения (длительность обработки распределена равномерно на интервале от 2 до 4 секунд). Исследуем поведение функции штрафа при изменении минимального и максимального времени обслуживания первого прибора от. Результаты исследования представлены в таблице 4.3.


Таблица 4.3 – Результаты исследований при tср1>tср2

tmin1
tmax1
Длина очереди1
Длина очереди2
1
2
Штраф

9,000
11,000
3,413
0,384
0,999
0,299
474,883

8,950
10,950
1,185
0,315
0,996
0,300
200,519

8,900
10,900
0,685
0,355
0,988
0,300
173,745

8,850
10,850
0,657
0,336
0,986
0,301
171,706

8,800
10,850
0,512
0,318
0,967
0,299
170,345

8,750
10,750
0,421
0,356
0,961
0,301
168,254

8,700
10,700
0,395
0,324
0,957
0,300
170,324

8,600
10,600
0,374
0,346
0,953
0,301
171,005

8,500
10,500
0,369
0,333
0,949
0,299
171,499



Анализ данных таблицы 4.3 показывает, что в этом случае функция штрафа целиком определяется загрузкой первого прибора. Исследуем поведение функции штрафа в процессе записи данных на магнитный диск (Таблица 4.4). В этом случае время работы первого прибора в несколько раз меньше времени работы второго прибора.


Таблица 4.4 – исследование поведения функции штрафа при tср1ср2

tmin2
tmax2
Штраф

9,000
11,000
695,346

8,950
10,950
173.548

8,900
10,900
158,816

8,800
10,850
151,845

8,700
10,700
150,661

8,600
10,600
151,39

8,500
10,500
152,93


С
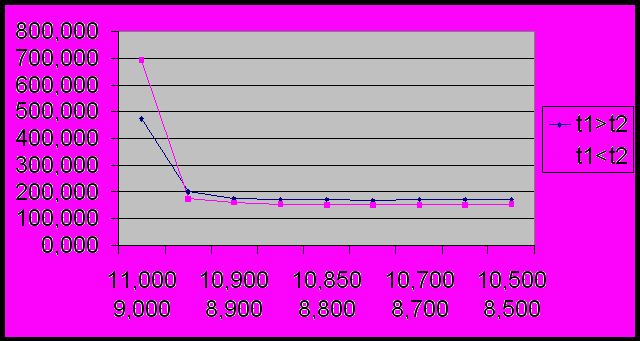
овмещенный график результатов экспериментов показан на рисунке 4.4.

Рисунок 4.4 – Результаты экспериментов по исследованию поведения функции штрафа E для системы из двух устройств.


Как видно из графика функция штрафа достигает экстремума в одной точке и в первом и во втором случае. Однако ее абсолютное значение меньше для случая, когда первым в цепочке находится более быстродействующий прибор.

Проанализируем каким образом величина отклонения влияет на функцию штрафа. При этом предположим, что среднее время чтения и обработки данных равны. Результаты исследования даны в таблице 4.5. Анализ результатов таблицы показывает, что уменьшение величины отклонения приводит к уменьшению функции штрафа, при этом уменьшение величины отклонения времени обслуживания в работе первого прибора приводит к большой скорости спада функции, нежели для второго.


Таблица 4.5 – результаты экспериментов при равном среднем времени обслуживания и различной величине отклонения.

tmin1
tmax1
tmin2
tmax2
Штраф

9
11
9
11
20,315

9,3
10,7
9
11
18,463

9,5
10,5
9
11
17,029

9,7
10,3
9
11
15,355

9
11
9,3
10,7
19,968

9
11
9,5
10,5
17,832

9
11
9,7
10,3
17,475