–Ш—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є–µ —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї —Б–Є—Б—В–µ–Љ –Љ–∞—Б—Б–Њ–≤–Њ–≥–Њ –Њ–±—Б–ї—Г–ґ–Є–≤–∞–љ–Є—П —Б –њ—А–Њ—Б—В–µ–є—И–Є–Љ –≤—Е–Њ–і—П—Й–Є–Љ –њ–Њ—В–Њ–Ї–Њ–Љ –Ј–∞—П–≤–Њ–Ї –Є –њ—А–Њ–Є–Ј–≤–Њ–ї—М–љ—Л–Љ–Є –њ–Њ—В–Њ–Ї–∞–Љ–Є –Њ–±—Б–ї—Г–ґ–Є–≤–∞–љ–Є—П 29
| –Т–Є–і –Љ–∞—В–µ—А–Є–∞–ї–∞ | –Ш—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є–µ |
- –£—В–≤–µ—А–ґ–і–∞—О, 89.56kb.
- –Ч–∞–і–∞—З–Є —В–µ–Њ—А–Є–Є –Љ–∞—Б—Б–Њ–≤–Њ–≥–Њ –Њ–±—Б–ї—Г–ґ–Є–≤–∞–љ–Є—П. –Ъ–ї–∞—Б—Б–Є—Д–Є–Ї–∞—Ж–Є—П —Б–Є—Б—В–µ–Љ –Љ–∞—Б—Б–Њ–≤–Њ–≥–Њ –Њ–±—Б–ї—Г–ґ–Є–≤–∞–љ–Є—П, 38.01kb.
- –Ч–∞–і–∞—З–Є —В–µ–Њ—А–Є–Є –Љ–∞—Б—Б–Њ–≤–Њ–≥–Њ –Њ–±—Б–ї—Г–ґ–Є–≤–∞–љ–Є—П (—В–Љ–Њ). –Ґ–Є–њ—Л —Б–Є—Б—В–µ–Љ –Љ–∞—Б—Б–Њ–≤–Њ–≥–Њ –Њ–±—Б–ї—Г–ґ–Є–≤–∞–љ–Є—П (—Б–Љ–Њ), 95.6kb.
- –Ю—Б–љ–Њ–≤–љ—Л–µ —Б–≤–µ–і–µ–љ–Є—П –Є–Ј —В–µ–Њ—А–Є–Є –Љ–∞—Б—Б–Њ–≤–Њ–≥–Њ –Њ–±—Б–ї—Г–ґ–Є–≤–∞–љ–Є—П, 47.41kb.
- –†–∞–±–Њ—З–µ–є –њ—А–Њ–≥—А–∞–Љ–Љ—Л –і–Є—Б—Ж–Є–њ–ї–Є–љ—Л ¬Ђ–Т–≤–µ–і–µ–љ–Є–µ –≤ —В–µ–Њ—А–Є—О —Б–Є—Б—В–µ–Љ –Љ–∞—Б—Б–Њ–≤–Њ–≥–Њ –Њ–±—Б–ї—Г–ґ–Є–≤–∞–љ–Є—П¬ї –њ–Њ –љ–∞–њ—А–∞–≤–ї–µ–љ–Є—О, 20.17kb.
- –Т–≤–µ–і–µ–љ–Є–µ –≤ —В–µ–Њ—А–Є—О –Љ–∞—Б—Б–Њ–≤–Њ–≥–Њ –Њ–±—Б–ї—Г–ґ–Є–≤–∞–љ–Є—П, 10.41kb.
- –°–Є—Б—В–µ–Љ—Л –Љ–∞—Б—Б–Њ–≤–Њ–≥–Њ –Њ–±—Б–ї—Г–ґ–Є–≤–∞–љ–Є—П, 754.03kb.
- 2 –Ш–Љ–Є—В–∞—Ж–Є–Њ–љ–љ–Њ–µ –Љ–Њ–і–µ–ї–Є—А–Њ–≤–∞–љ–Є–µ —Б–Є—Б—В–µ–Љ –Љ–∞—Б—Б–Њ–≤–Њ–≥–Њ –Њ–±—Б–ї—Г–ґ–Є–≤–∞–љ–Є—П, 29.08kb.
- –Ъ–Њ–Љ–њ—М—О—В–µ—А–љ–Њ–µ –Љ–Њ–і–µ–ї–Є—А–Њ–≤–∞–љ–Є–µ –Љ–∞—Б—Б–Њ–≤–Њ–≥–Њ –Њ–±—Б–ї—Г–ґ–Є–≤–∞–љ–Є—П –Ї–ї–Є–µ–љ—В–Њ–≤ –љ–∞ —Д–∞—А–Љ–∞—Ж–µ–≤—В–Є—З–µ—Б–Ї–Њ–Љ —А—Л–љ–Ї–µ, 202.1kb.
- –Ч–∞–і–∞–љ–Є–µ –і–ї—П –≤—Л–њ–Њ–ї–љ–µ–љ–Є—П –Ї—Г—А—Б–Њ–≤–Њ–є —А–∞–±–Њ—В—Л –њ–Њ —Н–Љ–Љ–Є–Ь –і–ї—П —Б—В—Г–і–µ–љ—В–Њ–≤ 2 –Ї—Г—А—Б–∞ –Ј–∞–Њ—З–љ–Њ–≥–Њ –Њ–±—Г—З–µ–љ–Є—П, 277.53kb.
3.4 –Ю–њ—А–µ–і–µ–ї–µ–љ–Є–µ —Б—В–∞—В–Є—Б—В–Є—З–µ—Б–Ї–Є—Е —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї —Б–Є—Б—В–µ–Љ—Л
–Т —А–∞–Ј—А–∞–±–Њ—В–∞–љ–љ–Њ–є –њ–ї–∞—В—Д–Њ—А–Љ–µ –Њ–њ—А–µ–і–µ–ї—П—О—В—Б—П —Б–ї–µ–і—Г—О—Й–Є–µ —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–Є –Љ–Њ–і–µ–ї–Є—А—Г–µ–Љ–Њ–є —Б–Є—Б—В–µ–Љ—Л: —Б—А–µ–і–љ–µ–µ –≤—А–µ–Љ—П –њ—А–µ–±—Л–≤–∞–љ–Є—П –Ј–∞—П–≤–Ї–Є –≤ —Б–Є—Б—В–µ–Љ–µ, —Б—А–µ–і–љ—П—П –і–ї–Є–љ–∞ –Њ—З–µ—А–µ–і–Є —Б–Є—Б—В–µ–Љ—Л –Є —Б—А–µ–і–љ–µ–µ –≤—А–µ–Љ—П –≤—А–µ–Љ—П –Њ–±—А–∞–±–Њ—В–Ї–Є –Ј–∞—П–≤–Ї–Є –і–ї—П –Ї–∞–ґ–і–Њ–≥–Њ –Њ–±—Б–ї—Г–ґ–Є–≤–∞—О—Й–µ–≥–Њ —Г—Б—В—А–Њ–є—Б—В–≤–∞. –Я–Њ –Њ–Ї–Њ–љ—З–∞–љ–Є–Є –Љ–Њ–і–µ–ї–Є—А–Њ–≤–∞–љ–Є—П –Ј–љ–∞—З–µ–љ–Є—П –њ–µ—А–µ—З–Є—Б–ї–µ–љ–љ—Л—Е –≤—Л—И–µ —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї —Б–Њ—Е—А–∞–љ—П—О—В—Б—П –≤ —Д–∞–є–ї–µ Stat.rez.
–Ф–ї—П –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П —Б—А–µ–і–љ–µ–≥–Њ –≤—А–µ–Љ–µ–љ–Є –њ—А–µ–±—Л–≤–∞–љ–Є—П –Ј–∞—П–≤–Ї–Є –±—Л–ї–∞ –≤–≤–µ–і–µ–љ–∞ –њ–µ—А–µ–Љ–µ–љ–љ–∞—П TimeRequestInSystem (—В–Є–њ–∞ Real). –Т –Љ–Њ–Љ–µ–љ—В –љ–∞—З–∞–ї–∞ –Љ–Њ–і–µ–ї–Є—А–Њ–≤–∞–љ–Є—П –Ј–љ–∞—З–µ–љ–Є–µ –њ–µ—А–µ–Љ–µ–љ–љ–Њ–є TimeRequestInSystem —А–∞–≤–љ–Њ 0. –Т –Љ–µ—В–Њ–і–µ PutReqest –Ї–Њ–Љ–њ–Њ–љ–µ–љ—В–∞ TTerminator –Ї –Ј–љ–∞—З–µ–љ–Є—О TimeRequestInSystem –њ—А–Є–±–∞–≤–ї—П–µ—В—Б—П –≤—А–µ–Љ—П –њ—А–µ–±—Л–≤–∞–љ–Є—П –≤ —Б–Є—Б—В–µ–Љ–µ –Ј–∞—П–≤–Ї–Є –Њ–±—Б–ї—Г–ґ–µ–љ–љ–Њ–є –Ї–Њ–Љ–њ–Њ–љ–µ–љ—В–Њ–Љ –≤ —Б–Є—Б—В–µ–Љ–µ (—А–∞–Ј–љ–Њ—Б—В—М —В–µ–Ї—Г—Й–µ–≥–Њ –Љ–Њ–і–µ–ї—М–љ–Њ–≥–Њ –≤—А–µ–Љ–µ–љ–Є –Є –≤—А–µ–Љ–µ–љ–Є –њ–Њ—Б—В—Г–њ–ї–µ–љ–Є—П –Ј–∞—П–≤–Ї–Є –≤ —Б–Є—Б—В–µ–Љ—Г). –Я–Њ –Њ–Ї–Њ–љ—З–∞–љ–Є–Є –Љ–Њ–і–µ–ї–Є—А–Њ–≤–∞–љ–Є—П —Б–Є—Б—В–µ–Љ—Л –Ј–љ–∞—З–µ–љ–Є—П –њ–µ—А–µ–Љ–µ–љ–љ—Л—Е TimeRequestInSystem –≤—Б–µ—Е –Ї–Њ–Љ–њ–Њ–љ–µ–љ—В–Њ–≤ —В–Є–њ–∞ TTerminator, –Њ–њ—А–µ–і–µ–ї–µ–љ–љ—Л—Е –≤ —Б–Є—Б—В–µ–Љ–µ, —Б—Г–Љ–Љ–Є—А—Г—О—В—Б—П, –Є –њ–Њ–ї—Г—З–µ–љ–љ–∞—П —Б—Г–Љ–Љ–∞ –і–µ–ї–Є—В—Б—П –љ–∞ –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ –Ј–∞—П–≤–Њ–Ї, –Њ–±—Б–ї—Г–ґ–µ–љ–љ—Л—Е —Б–Є—Б—В–µ–Љ–Њ–є. –Я–Њ–ї—Г—З–µ–љ–љ–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ —П–≤–ї—П–µ—В—Б—П —Б—А–µ–і–љ–Є–Љ –≤—А–µ–Љ–µ–љ–µ–Љ –њ—А–µ–±—Л–≤–∞–љ–Є—П –Ј–∞—П–≤–Ї–Є –≤ —Б–Є—Б—В–µ–Љ–µ.
–°—А–µ–і–љ—П—П –і–ї–Є–љ–∞ –Њ—З–µ—А–µ–і–Є —Б–Є—Б—В–µ–Љ—Л –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П —Б–ї–µ–і—Г—О—Й–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ: –њ—А–Є –њ–Њ—Б—В—Г–њ–ї–µ–љ–Є–Є –Њ—З–µ—А–µ–і–љ–Њ–є –Ј–∞—П–≤–Ї–Є –≤ –Њ—З–µ—А–µ–і—М –Є –≤—Л—Е–Њ–і–µ –Ј–∞—П–≤–Ї–Є –Є–Ј –Њ—З–µ—А–µ–і–Є –≤ –њ–µ—А–µ–Љ–µ–љ–љ—Г—О FsumLength –Ј–∞–љ–Њ—Б–Є—В—Б—П –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ —Н–ї–µ–Љ–µ–љ—В–Њ–≤ –≤ –Њ—З–µ—А–µ–і–Є, –≤ –њ–µ—А–µ–Љ–µ–љ–љ–Њ–є FRequestCount —Д–Є–Ї—Б–Є—А—Г–µ—В—Б—П –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ –Ј–∞—П–≤–Њ–Ї, –њ—А–Њ—И–µ–і—И–Є—Е —З–µ—А–µ–Ј –Њ—З–µ—А–µ–і—М. –Я–Њ –Њ–Ї–Њ–љ—З–∞–љ–Є–Є –Љ–Њ–і–µ–ї–Є—А–Њ–≤–∞–љ–Є—П —Б–Є—Б—В–µ–Љ—Л –≤—Л—З–Є—Б–ї—П–µ—В—Б—П —Б—А–µ–і–љ—П—П –і–ї–Є–љ–∞ –Ї–∞–ґ–і–Њ–є –Њ—З–µ—А–µ–і–Є –Є –Ј–љ–∞—З–µ–љ–Є–µ —Б—А–µ–і–љ–µ–є –і–ї–Є–љ—Л —Г—Б—А–µ–і–љ—П–µ—В—Б—П –њ–Њ –Ї–Њ–ї–Є—З–µ—Б—В–≤—Г —Н–ї–µ–Љ–µ–љ—В–Њ–≤ —В–Є–њ–∞ –Њ—З–µ—А–µ–і—М.
–Ф–ї—П –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П —Б—А–µ–і–љ–µ–≥–Њ –≤—А–µ–Љ–µ–љ–Є –Њ–±—А–∞–±–Њ—В–Ї–Є –Ј–∞—П–≤–Ї–Є –Њ–±—Б–ї—Г–ґ–Є–≤–∞—О—Й–Є–Љ —Г—Б—В—А–Њ–є—Б—В–≤–Њ–Љ –≤ –њ–µ—А–µ–Љ–µ–љ–љ–Њ–є FAllWorkTime —Б—Г–Љ–Љ–Є—А—Г—О—В—Б—П –≤—А–µ–Љ–µ–љ–∞ –Њ–±—А–∞–±–Њ—В–Ї–Є –Ј–∞—П–≤–Њ–Ї —Г—Б—В—А–Њ–є—Б—В–≤–Њ–Љ. –Я–Њ –Њ–Ї–Њ–љ—З–∞–љ–Є–Є –Љ–Њ–і–µ–ї–Є—А–Њ–≤–∞–љ–Є—П –Ј–љ–∞—З–µ–љ–Є–µ FAllWorkTime –і–µ–ї–Є—В—Б—П –љ–∞ –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ –Ј–∞—П–≤–Њ–Ї, –Њ–±—А–∞–±–Њ—В–∞–љ–љ—Л—Е —Г—Б—В—А–Њ–є—Б—В–≤–Њ–Љ –Ј–∞ –њ–µ—А–Є–Њ–і –Љ–Њ–і–µ–ї–Є—А–Њ–≤–∞–љ–Є—П.
–Я—А–Є –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ—Б—В–Є –њ–Њ–ї—Г—З–µ–љ–Є—П –і—А—Г–≥–Є—Е —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї –Љ–Њ–і–µ–ї–Є—А—Г–µ–Љ–Њ–є —Б–Є—Б—В–µ–Љ—Л, –њ–Њ–ї—М–Ј–Њ–≤–∞—В–µ–ї—М –Љ–Њ–ґ–µ—В –≤–љ–µ—Б—В–Є –Є–Ј–Љ–µ–љ–µ–љ–Є—П –≤ –Њ–њ–Є—Б–∞–љ–Є–µ –Љ–µ—В–Њ–і–Њ–≤ –Њ–±—К–µ–Ї—В–Њ–≤.
^
4–Ш–°–°–Ы–Х–Ф–Ю–Т–Р–Э–Ш–Х –°–Ґ–Р–¶–Ш–Ю–Э–Р–†–Э–Ю–У–Ю –†–Х–Ц–Ш–Ь–Р –°–Ь–Ю –° –Я–†–Ю–Ш–Ч–Т–Ю–Ы–ђ–Э–Ђ–Ь–Ш –Я–Ю–Ґ–Ю–Ъ–Р–Ь–Ш –°–Ю–С–Ђ–Ґ–Ш–Щ
–Т –љ–∞—Б—В–Њ—П—Й–µ–Љ —А–∞–Ј–і–µ–ї–µ —Б –њ–Њ–Љ–Њ—Й—М—О —А–∞–Ј—А–∞–±–Њ—В–∞–љ–љ–Њ–є —Б–Є—Б—В–µ–Љ—Л –Є–Љ–Є—В–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ –Љ–Њ–і–µ–ї–Є—А–Њ–≤–∞–љ–Є—П –Љ—Л –Є—Б—Б–ї–µ–і—Г–µ–Љ –њ–Њ–≤–µ–і–µ–љ–Є–µ —А–∞–Ј–ї–Є—З–љ—Л—Е –°–Ь–Ю –≤ —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–Љ —А–µ–ґ–Є–Љ–µ –і–ї—П –њ—А–Є–Њ—А–Є—В–µ—В–љ–Њ–є –Є –±–µ—Б–њ—А–Є–Њ—А–Є—В–µ—В–љ–Њ–є –і–Є—Б—Ж–Є–њ–ї–Є–љ—Л –Њ–±—Б–ї—Г–ґ–Є–≤–∞–љ–Є—П.
^
4.1–Ш—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є–µ –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є —Д—Г–љ–Ї—Ж–Є–Є —И—В—А–∞—Д–∞ –Њ—В –Ј–∞–Ї–Њ–љ–∞ —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П –≤—А–µ–Љ–µ–љ–Є –Њ–±—Б–ї—Г–ґ–Є–≤–∞–љ–Є—П
–Ш—Б—Б–ї–µ–і—Г–µ–Љ, –Ї–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ —Д—Г–љ–Ї—Ж–Є—П —И—В—А–∞—Д–∞, –Њ–њ—А–µ–і–µ–ї—П–µ–Љ–∞—П —Б –њ–Њ–Љ–Њ—Й—М—О –≤—Л—А–∞–ґ–µ–љ–Є—П 1.1, –Ј–∞–≤–Є—Б–Є—В –Њ—В –Ј–∞–Ї–Њ–љ–∞ —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П –≤—А–µ–Љ–µ–љ–Є –Њ–±—Б–ї—Г–ґ–Є–≤–∞–љ–Є—П. –Ф–ї—П —Н—В–Њ–≥–Њ —А–∞—Б—Б–Љ–Њ—В—А–Є–Љ –Є–Љ–Є—В–∞—Ж–Є–Њ–љ–љ—Г—О –Љ–Њ–і–µ–ї—М –њ—А–Њ—Ж–µ—Б—Б–Њ—А–љ–Њ–≥–Њ –±–ї–Њ–Ї–∞, –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–љ—Г—О –љ–∞ —А–Є—Б—Г–љ–Ї–µ 1.3.
–Я
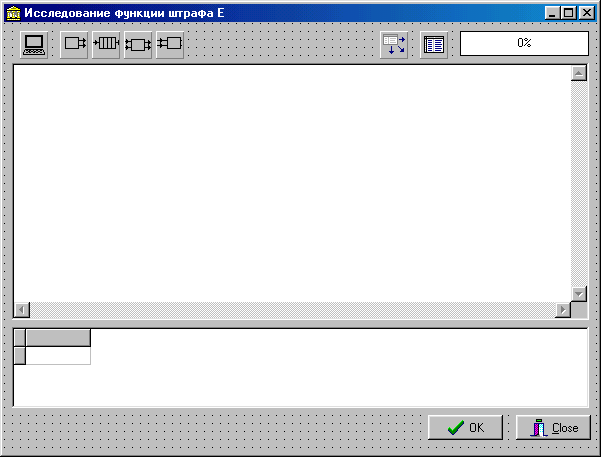
—А–Є —Н—В–Њ–Љ –±—Г–і–µ–Љ –њ—А–µ–і–њ–Њ–ї–∞–≥–∞—В—М, —З—В–Њ –њ–Њ—В–Њ–Ї –Ј–∞—П–≤–Њ–Ї, –њ–Њ—Б—В—Г–њ–∞—О—Й–Є—Е –≤ —Б–Є—Б—В–µ–Љ—Г –Є–Ј–≤–љ–µ, —П–≤–ї—П–µ—В—Б—П –њ—А–Њ—Б—В–µ–є—И–Є–Љ. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –≤ —Б–Њ—Б—В–∞–≤ –Є–Љ–Є—В–∞—Ж–Є–Њ–љ–љ–Њ–є –Љ–Њ–і–µ–ї–Є (—А–Є—Б—Г–љ–Њ–Ї 4.1) –≤—Е–Њ–і—П—В —Б–ї–µ–і—Г—О—Й–Є–µ –Ї–Њ–Љ–њ–Њ–љ–µ–љ—В—Л:
–†–Є—Б—Г–љ–Њ–Ї 4.1 вАУ –Ш–Љ–Є—В–∞—Ж–Є–Њ–љ–љ–∞—П –Љ–Њ–і–µ–ї—М –њ—А–Њ—Ж–µ—Б—Б–Њ—А–љ–Њ–≥–Њ –±–ї–Њ–Ї–∞ –≤ —В–µ—А–Љ–Є–љ–∞—Е —Б–Є—Б—В–µ–Љ—Л –Є–Љ–Є—В–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ –Љ–Њ–і–µ–ї–Є—А–Њ–≤–∞–љ–Є—П
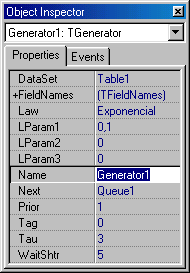
–У–µ–љ–µ—А–∞—В–Њ—А –Ј–∞—П–≤–Њ–Ї TGenerator. –Э–∞ —Б—В—А–∞–љ–Є—Ж–µ —Б–≤–Њ–є—Б—В–≤ –Ї–Њ–Љ–њ–Њ–љ–µ–љ—В–∞ (—А–Є—Б—Г–љ–Њ–Ї 4.2 (–∞) —Г–Ї–∞–Ј—Л–≤–∞–µ–Љ, —З—В–Њ –Ј–∞–Ї–Њ–љ —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П –≤—А–µ–Љ–µ–љ–Є –Њ–±—Б–ї—Г–ґ–Є–≤–∞–љ–Є—П –Ј–∞—П–≤–Ї–Є —П–≤–ї—П–µ—В—Б—П —Н–Ї—Б–њ–Њ–љ–µ–љ—Ж–Є–∞–ї—М–љ—Л–Љ, –Є–љ—В–µ–љ—Б–Є–≤–љ–Њ—Б—В—М –њ–Њ—В–Њ–Ї–∞ вАУ 10 –Ј–∞—П–≤–Њ–Ї/—Б–µ–Ї—Г–љ–і—Г, —И—В—А–∞—Д –Ј–∞ –њ—А–Њ—Б—В–Њ–є –Ј–∞—П–≤–Ї–Є –≤ –Њ—З–µ—А–µ–і–Є вАУ 5 —Г.–µ./—Б–µ–Ї—Г–љ–і—Г.
–∞) –±)
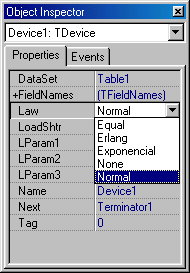
–†–Є—Б—Г–љ–Њ–Ї 4.2 вАУ –Ф–Є—Б–њ–µ—В—З–µ—А —Б–≤–Њ–є—Б—В–≤ –Љ–Њ–і–µ–ї–Є—А—Г—О—Й–Є—Е –Ї–Њ–Љ–њ–Њ–љ–µ–љ—В–Њ–≤: –∞)–≥–µ–љ–µ—А–∞—В–Њ—А —В—А–µ–±–Њ–≤–∞–љ–Є–є; –±) –Њ–±—Б–ї—Г–ґ–Є–≤–∞—О—Й–Є–є –њ—А–Є–±–Њ—А.
–Э–∞ —А–Є—Б—Г–љ–Ї–µ 4.2 (–±) –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ –і–Є—Б–њ–µ—В—З–µ—А —Б–≤–Њ–є—Б—В–≤ –Ї–Њ–Љ–њ–Њ–љ–µ–љ—В–∞ —В–Є–њ–∞ ¬Ђ–Њ–±—Б–ї—Г–ґ–Є–≤–∞—О—Й–Є–є –њ—А–Є–±–Њ—А¬ї. –° –њ–Њ–Љ–Њ—Й—М—О —Б–≤–Њ–є—Б—В–≤–∞ ¬ЂLaw¬ї –Љ—Л –±—Г–і–µ–Љ –Ј–∞–і–∞–≤–∞—В—М –≤–Є–і —Д—Г–љ–Ї—Ж–Є–Є —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П –Є –µ–≥–Њ –њ–∞—А–∞–Љ–µ—В—А—Л —В–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, —З—В–Њ–±—Л –Ј–љ–∞—З–µ–љ–Є—П –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–≥–Њ –Њ–ґ–Є–і–∞–љ–Є—П –Є –Њ—В–Ї–ї–Њ–љ–µ–љ–Є—П —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–Њ–≤–∞–ї–Є –±—Л –њ–∞—А–∞–Љ–µ—В—А–∞–Љ —Н–Ї—Б–њ–Њ–љ–µ–љ—Ж–Є–∞–ї—М–љ–Њ–≥–Њ –Ј–∞–Ї–Њ–љ–∞. –Я—А–Є–Љ–µ—А —И—В—А–∞—Д –Ј–∞ –љ–µ–і–Њ–≥—А—Г–Ј –њ—А–Њ—Ж–µ—Б—Б–Њ—А–∞ —А–∞–≤–љ—Л–Љ 200 —Г.–µ/—Б–µ–Ї—Г–љ–і—Г.
–Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, —И—В—А–∞—Д–љ–∞—П —Д—Г–љ–Ї—Ж–Є—П –Є–Љ–µ–µ—В –≤–Є–і:
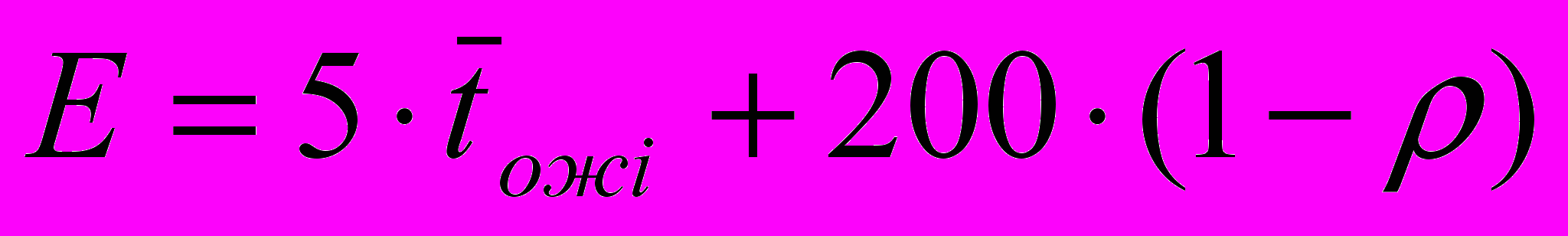 ,
,–≥–і–µ пБ≤ - –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В –Ј–∞–≥—А—Г–Ј–Ї–Є –њ—А–Њ—Ж–µ—Б—Б–Њ—А–∞.
–†–µ–Ј—Г–ї—М—В–∞—В—Л —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–Њ–≤ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ—Л –≤ —В–∞–±–ї–Є—Ж–µ 4.1. –Р–љ–∞–ї–Є–Ј –њ–Њ–≤–µ–і–µ–љ–Є—П —Д—Г–љ–Ї—Ж–Є–Є —И—В—А–∞—Д–∞ –њ–Њ–Ї–∞–Ј—Л–≤–∞–µ—В, —З—В–Њ —В–Њ—З–Ї–∞ —Н–Ї—Б—В—А–µ–Љ—Г–Љ–∞ —Б–Љ–µ—Й–∞–µ—В—Б—П –≤ –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є –Њ—В —Е–∞—А–∞–Ї—В–µ—А–∞ –Ј–∞–Ї–Њ–љ–∞ —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –њ—А–µ–і–њ–Њ–ї–Њ–ґ–µ–љ–Є–µ –Њ –њ—А–Њ—Б—В–µ–є—И–µ–Љ —Е–∞—А–∞–Ї—В–µ—А–µ –њ–Њ—В–Њ–Ї–∞ –Љ–Њ–ґ–љ–Њ –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞—В—М –ї–Є—И—М –і–ї—П –њ—А–Є–±–ї–Є–Ј–Є—В–µ–ї—М–љ–Њ–є —В–µ–Њ—А–µ—В–Є—З–µ—Б–Ї–Њ–є –Њ—Ж–µ–љ–Ї–Є –њ–Њ–ї–Њ–ґ–µ–љ–Є—П –Њ–њ—В–Є–Љ—Г–Љ–∞ —Д—Г–љ–Ї—Ж–Є–Є E.
–Ґ–∞–±–ї–Є—Ж–∞ 4.1 вАУ –†–µ–Ј—Г–ї—М—В–∞—В—Л —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–Њ–≤ –Љ–Њ–і–µ–ї–Є—А–Њ–≤–∞–љ–Є—П –њ–Њ–≤–µ–і–µ–љ–Є—П –°–Ь–Ю –Є–Ј –Њ–і–љ–Њ–≥–Њ –њ—А–Є–±–Њ—А–∞ –њ—А–Є —А–∞–Ј–ї–Є—З–љ—Л—Е –Ј–∞–Ї–Њ–љ–∞—Е –≤—А–µ–Љ–µ–љ–Є –Њ–±—Б–ї—Г–ґ–Є–≤–∞–љ–Є—П
| tcp | –≠–Ї—Б–њ–Њ–љ–µ–љ. | –®—В—А–∞—Д | –†–∞–≤–љ–Њ–Љ–µ—А–љ—Л–є | –®—В—А–∞—Д | –Э–Њ—А–Љ–∞–ї—М–љ—Л–є | –®—В—А–∞—Д | ||
| | пБђ | | Min | Max | | M | пБ≥ | |
| 10,000 | 0,100 | 2752,600 | 9,684 | 10,316 | 2426,450 | 10,000 | 0,316 | 2480,647 |
| 9,090 | 0,110 | 606,108 | 8,759 | 9,423 | 278,495 | 9,090 | 0,332 | 257,739 |
| 8,333 | 0,120 | 240,707 | 7,987 | 8,680 | 142,859 | 8,333 | 0,346 | 148,639 |
| 7,692 | 0,130 | 174,080 | 7,332 | 8,053 | 111,447 | 7,692 | 0,361 | 104,173 |
| 7,142 | 0,140 | 148,672 | 6,769 | 7,517 | 98,957 | 7,142 | 0,374 | 100,433 |
| 6,666 | 0,150 | 133,670 | 6,279 | 7,054 | 101,159 | 6,666 | 0,387 | 98,459 |
| 6,250 | 0,160 | 128,730 | 5,850 | 6,650 | 102,196 | 6,250 | 0,400 | 100,473 |
| 5,880 | 0,170 | 125,410 | 5,470 | 6,295 | 105,055 | 5,880 | 0,412 | 102,912 |
| 5,550 | 0,180 | 124,010 | 5,131 | 5,980 | 106,148 | 5,550 | 0,424 | 106,085 |
| 5,260 | 0,190 | 123,012 | 4,827 | 5,699 | 108,302 | 5,260 | 0,436 | 110,054 |
| 5,000 | 0,200 | 124,280 | 4,553 | 5,447 | 113,431 | 5,000 | 0,447 | 113,796 |
| 4,760 | 0,210 | 126,790 | 4,304 | 5,220 | 115,178 | 4,760 | 0,458 | 115,807 |
| 3,846 | 0,260 | 128,310 | 3,336 | 4,356 | 128,140 | 3,846 | 0,510 | 128,085 |
–У—А–∞—Д–Є–Ї —Д—Г–љ–Ї—Ж–Є–Є —И—В—А–∞—Д–∞ E(tcp) –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ –љ–∞ —А–Є—Б—Г–љ–Ї–µ 4.3. –Ю—Б—М –Ј–љ–∞—З–µ–љ–Є–є –Є–Љ–µ–µ—В –ї–Њ–≥–∞—А–Є—Д–Љ–Є—З–µ—Б–Ї–Є–є –Љ–∞—Б—И—В–∞–±. –Ш–Ј –≥—А–∞—Д–Є–Ї–∞ –≤–Є–і–љ–Њ, —З—В–Њ –ї–Є–љ–Є—П —Г—А–Њ–≤–љ—П —Д—Г–љ–Ї—Ж–Є–Є —И—В—А–∞—Д–∞ –і–ї—П —Н–Ї—Б–њ–Њ–љ–µ–љ—Ж–Є–∞–ї—М–љ–Њ–≥–Њ –Ј–∞–Ї–Њ–љ–∞ –Є–Љ–µ–µ—В –Ј–љ–∞—З–Є—В–µ–ї—М–љ–Њ –Љ–µ–љ—М—И–Є–є –њ—А–Њ–≥–Є–±, —З–µ–Љ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ –ї–Є–љ–Є–Є –і–ї—П —А–∞–≤–љ–Њ–Љ–µ—А–љ–Њ–≥–Њ –Є –љ–Њ—А–Љ–∞–ї—М–љ–Њ–≥–Њ –Ј–∞–Ї–Њ–љ–∞ —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є–є. –Т –љ–∞—З–∞–ї—М–љ–Њ–є –Є –Ї–Њ–љ–µ—З–љ–Њ–є —В–Њ—З–Ї–µ –Ј–љ–∞—З–µ–љ–Є—П —Д—Г–љ–Ї—Ж–Є–Є —И—В—А–∞—Д–∞ –њ—А–∞–Ї—В–Є—З–µ—Б–Ї–Є —Б–Њ–≤–њ–∞–і–∞—О—В.
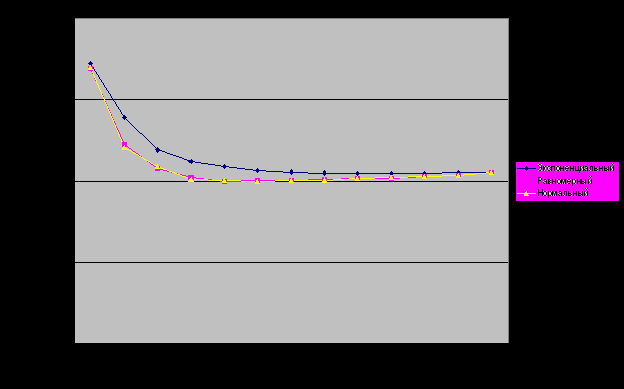
–†–Є—Б—Г–љ–Њ–Ї 4.3 вАУ –У—А–∞—Д–Є–Ї –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є —Д—Г–љ–Ї—Ж–Є–Є —И—В—А–∞—Д–∞ E –Њ—В —Б—А–µ–і–љ–µ–≥–Њ –≤—А–µ–Љ–µ–љ–Є –Њ–±—Б–ї—Г–ґ–Є–≤–∞–љ–Є—П —В—А–µ–±–Њ–≤–∞–љ–Є–є tcp –њ—А–Є —А–∞–Ј–ї–Є—З–љ—Л—Е –Ј–∞–Ї–Њ–љ–∞—Е –≤—А–µ–Љ–µ–љ–Є –Њ–±—Б–ї—Г–ґ–Є–≤–∞–љ–Є—П
–Ґ–∞–±–ї–Є—Ж–∞ 4.2 вАУ —А–µ–Ј—Г–ї—М—В–∞—В—Л —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–Њ–≤ –њ—А–Є —А–∞–Ј–ї–Є—З–љ—Л—Е –Ј–љ–∞—З–µ–љ–Є—П—Е –Њ—В–Ї–ї–Њ–љ–µ–љ–Є—П пБ≥
| –†–∞–≤–љ–Њ–Љ–µ—А–љ—Л–є | | –Э–Њ—А–Љ–∞–ї—М–љ—Л–є | ||
| Min | Max | –®—В—А–∞—Д | Sigma | –®—В—А–∞—Д |
| 7,042 | 7,242 | 101,729 | 0,100 | 99,120 |
| 6,942 | 7,342 | 100,302 | 0,200 | 99,447 |
| 6,842 | 7,442 | 102,334 | 0,300 | 98,970 |
| 6,742 | 7,542 | 102,585 | 0,400 | 98,150 |
| 6,642 | 7,642 | 101,498 | 0,500 | 98,946 |
| 6,542 | 7,742 | 101,159 | 0,600 | 98,459 |
| 6,442 | 7,842 | 101,136 | 0,700 | 99,005 |
| 6,342 | 7,942 | 102,088 | 0,800 | 98,312 |
| 6,242 | 8,042 | 101,268 | 0,900 | 99,404 |
| 6,142 | 8,142 | 101,533 | 1,000 | 98,003 |
–Т —В–Њ –ґ–µ –≤—А–µ–Љ—П –Ј–љ–∞—З–µ–љ–Є–µ —Д—Г–љ–Ї—Ж–Є–Є —И—В—А–∞—Д–∞ E –њ—А–∞–Ї—В–Є—З–µ—Б–Ї–Є –љ–µ –Ј–∞–≤–Є—Б–Є—В –Њ—В –Ј–љ–∞—З–µ–љ–Є—П —Б—А–µ–і–љ–µ–≥–Њ –Њ—В–Ї–ї–Њ–љ–µ–љ–Є—П пБ≥ –Є –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П –Є—Б–Ї–ї—О—З–Є—В–µ–ї—М–љ–Њ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є–Љ –Њ–ґ–Є–і–∞–љ–Є–µ–Љ –≤—А–µ–Љ–µ–љ–Є –Њ–±—Б–ї—Г–ґ–Є–≤–∞–љ–Є—П. –≠—В–Њ —Г—В–≤–µ—А–ґ–і–µ–љ–Є–µ –њ–Њ–і—В–≤–µ—А–ґ–і–∞–µ—В—Б—П —А–µ–Ј—Г–ї—М—В–∞—В–∞–Љ–Є —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–Њ–≤, –њ—А–Є–≤–µ–і–µ–љ–љ—Л—Е –≤ —В–∞–±–ї–Є—Ж–µ 4.2.
–Ю—В–Ї–∞–ґ–µ–Љ—Б—П –Њ—В –њ—А–µ–і–њ–Њ–ї–Њ–ґ–µ–љ–Є—П –Њ –њ—А–Њ—Б—В–µ–є—И–µ–Љ —Е–∞—А–∞–Ї—В–µ—А–µ –њ–Њ—В–Њ–Ї–∞ –Є –Є—Б—Б–ї–µ–і—Г–µ–Љ –њ–Њ–≤–µ–і–µ–љ–Є–µ —Б–Є—Б—В–µ–Љ—Л –≤ —В–Њ–Љ —Б–ї—Г—З–∞–µ, –µ—Б–ї–Є –≤—А–µ–Љ—П –њ–Њ—Б—В—Г–њ–ї–µ–љ–Є—П –Ј–∞—П–≤–Њ–Ї –≤ —Б–Є—Б—В–µ–Љ—Г —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Њ –њ–Њ —А–∞–≤–љ–Њ–Љ–µ—А–љ–Њ–Љ—Г –Ј–∞–Ї–Њ–љ—Г (—В–∞–±–ї–Є—Ж–∞ 4.3).
–Ґ–∞–±–ї–Є—Ж–∞ 4.3 вАУ –Ј–љ–∞—З–µ–љ–Є—П —Д—Г–љ–Ї—Ж–Є–Є —И—В—А–∞—Д–∞ –њ—А–Є –Є–Ј–Љ–µ–љ–µ–љ–Є–Є —Б—А–µ–і–љ–µ–≥–Њ –Њ—В–Ї–ї–Њ–љ–µ–љ–Є—П –≤—А–µ–Љ–µ–љ–Є –Њ–±—Б–ї—Г–ґ–Є–≤–∞–љ–Є—П
| tmin | tmax | –®—В—А–∞—Д |
| 9 | 11 | 10,101 |
| 9,2 | 10,8 | 8,9 |
| 9,5 | 10,5 | 7,5 |
| 9,7 | 10,3 | 7,11 |
–Р–љ–∞–ї–Є–Ј —А–µ–Ј—Г–ї—М—В–∞—В–Њ–≤ –њ–Њ–Ї–∞–Ј—Л–≤–∞–µ—В, —З—В–Њ –≤ –і–∞–љ–љ–Њ–Љ —Б–ї—Г—З–∞–µ –Ј–љ–∞—З–µ–љ–Є–µ —Д—Г–љ–Ї—Ж–Є–Є —И—В—А–∞—Д–∞ —Г–Љ–µ–љ—М—И–∞–µ—В—Б—П –њ–Њ –Љ–µ—А–µ —Г–Љ–µ–љ—М—И–µ–љ–Є—П –Є–љ—В–µ—А–≤–∞–ї–∞ –њ—А–Є –љ–µ–Є–Ј–Љ–µ–љ–љ–Њ–Љ —Б—А–µ–і–љ–µ–Љ –≤—А–µ–Љ–µ–љ–Є –Њ–±—Б–ї—Г–ґ–Є–≤–∞–љ–Є—П.
