Лекция Понятия множества и элементы множества. Способы задания множеств
| Вид материала | Лекция |
- Вопросы к экзамену «дискретная математика» (пм-91), 26.54kb.
- Для кафедр пм и к вопросы по курсу «Дискретная математика». 19. 05. 2010г, 52.29kb.
- Словесное задание. Перечислением элементов (для конечных множеств) Указание характеристического, 49.85kb.
- Введение в общую топологию и топологическую алгебру, 25.85kb.
- Математика, 87.27kb.
- Α Множество всех подмножеств данного множества называется булеаном данного множества., 83.26kb.
- Задание бинарных отношений графами. Теорема Эйлера о необходимых и достаточных условиях, 22.76kb.
- Введение в математическую логику, 29.8kb.
- История чисел и вычислений содержание: Стр, 310.33kb.
- Лекция Функция распределения, 62.64kb.
Задания для самостоятельной работы по теме 6:
1
. В каждом из следующих умозаключений выделите посылки и заключение, проверьте правильность умозаключений с помощью кругов Эйлера: а) Все учащиеся нашего класса в каникулы ходили в театр. Петя не был в театре в дни каникул. Следовательно, Петя – учащийся не нашего класса. б) Все деревья – растения. Сосна – дерево. Значит, сосна – растение. в) Каждый учащийся нашего класса занимается в каком-то кружке. Петя занимается в кружке по рисованию. Следовательно, Петя учится в нашем классе. г) Все антилопы стройные. Стройные животные радуют глаз. Все антилопы радуют глаз.
А)
Б
) 
2. Выделите логическую форму умозаключений, приведенных в № 1, и укажите те из них, которые построены по правилу:
а) отрицания;
б) заключения;
в) силлогизма.
3. Сделайте выводы из каждой пары посылок, если это возможно.
а) Некоторые деревья зеленые и летом и зимой. Береза – дерево.
б) Мальчики и девочки второго класса пойдут гулять. Галя – ученица этого класса.
в) Все, кто имеет пятерки по математике, будут участвовать в олимпиаде. Лена имеет пятерки по математике и по русскому языку.
г) Все, кто имеет пятерки по математике, будут участвовать в олимпиаде. Лена имеет пятерки по математике или по русскому языку.
Лекция 7. Неполная индукция и аналогия. Равномощные множества.
Неполная индукция – это умозаключение, в котором на основании того, что некоторые объекты класса обладают данным свойством, делается вывод о том, что этим свойством обладают все объекты данного класса.
Например, можно измерить противоположные стороны у нескольких прямоугольников. Окажется, что они в каждом случае равны друг другу. Можно сделать вывод, что у всех прямоугольников противоположные стороны равны. Тем не менее, этот факт требует доказательства.
Неполная индукция не является дедуктивным умозаключением и может привести к ошибочным выводам. Например, рассмотрим такие выражения: 2 + 5 и 2·5, 4 + 3 и 4·3, 6 + 8 и 6·8. Видим, что 2 + 5 < 2·5, 4 + 3 < 4·3, 6 + 8 < 6·8. Можем утверждать, что сумма натуральных чисел меньше их произведения. Но вывод ложен, так как можно привести контрпример: 1 + 5 > 1·5.
Часто используют рассуждения по аналогии . Под аналогией понимают умозаключение, в котором на основании сходства двух объектов в некоторых признаках и при наличии дополнительного признака у одного из них делается вывод о наличии такого же признака у другого объекта.
Например, известно, что двузначное число можно представить в виде суммы десятков и единиц, тогда трехзначное число аналогично представляется в виде суммы сотен, десятков и единиц. Аналогия не всегда приводит к правильным выводам. Так, например, на основании того, что число делится на 6, если оно делится на 2 и на 3, можно сделать аналогичный вывод: число делится на 8, если оно делится на 2 и на 4. Однако пример числа 12 говорит о том, что это не так.
Задания для самостоятельной работы по теме 7:
1. Сделайте вывод, если возможно:
0+1=1, 2+3=5, 3+4=7, 4+5=9, 5+6=11, 6+7=13, 7+8=15 и т.д.
22*2:2=22, 14*7:7=14, 56*8:8=56 и т.д.
74-47=27, 52-25=27, 63-36=27
2. Преврати «род» в «вид» составив цепочку слов: род - … - … - вид. Каждое последующее слово должно отличаться от предыдущего только одной буквой. Аналогично:
А) МУХА-МУРА-ТУРА-ТАРА-ПАРА-ПАРК-ПАУК-ПАУТ-ПЛУТ-ПЛОТ-СЛОТ-СЛОН
муха-мура-мара(разновидность тумана)-пара-парк-паук-каук(тёплая одежда у эскимосов)-каюк-каик(турецкое судно)-клик-клин-клон-слон
муха-мура-фура-фора-кора-корн-коан-клан-клон-слон
Б) Каша –кара-карт-корт - торт.
В) Мрак — брак — брус — трус — трос — трон — урон — урок — срок — сток — стон — стан — стая — свая — сват — свет
Мрак – трак-трек-трюк-крюк- урюк-урок-срок- сток — стон — стан — стая — свая — сват — свет
3. Почему следующее рассуждение по неполной индукции приводит к неправильному выводу: рассмотрим квадрат со стороной 1 см и измерим его углы. Все они равны 90 градусам. Проделаем тоже с квадратами, у которых другая длина сторон. Убедимся, что все углы у них будут равны 90. Вывод: все четырехугольники с равными сторонами имеют углы 90 градусов.
Лекция 8. Соответствия между элементами двух множеств. Определение соответствия между элементами двух множеств. Взаимно однозначные соответствия.
Соответствием между множествами Х и Y называется всякое подмножество произведения этих множеств.
Соответствие можно задавать как любое множество, т.е. либо перечислив все пары элементов, находящихся в данном соответствии, либо указав характеристическое свойство элементов этого подмножества. Например, соответствие между множествами Х = {2, 4, 6, 8} и Y = {3, 5, 7} можно задать:
1) при помощи предложения с двумя переменными: а < b при условии, что а ∈ Х, b∈Y;
2) перечислив пары чисел, принадлежащих подмножеству декартова произведения Х хY: { (2,3), (2,5), (2,7), (4,5), (4,7), (6,7)}. К этому способу задания относят также задание соответствия при помощи графа (рис. 1).
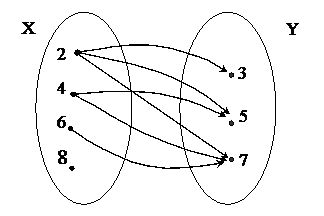
Рис. 1
Соответствие между числовыми множествами можно изобразить при помощи графика в прямоугольной системе координат.
Соответствия принято обозначать буквами P, S, T, R и др. Множество Х называется областью отправления соответствия, а множество Y – областью прибытия соответствия. Если элемент х находится в соответствии R с элементом у , то пишут x R y или ( х , у )∈ R.
Каждому элементу а ∈Х сопоставим подмножество R( а ) в Y, состоящее из всех элементов у∈Y таких, что ( а , у )∈R: R( а ) = { у | ( а , у )∈ R}. Это множество называют образом элемента а при соответствии R.
Каждому элементу b∈Y сопоставим подмножество R -1 ( b ) элементов из Х таких, что ( х , b ) ∈ R: R -1 ( b ) = { х|( х , b ) ∈R }. Это множество называют полным прообразом элемента b при соответствии R.
Подмножество А⊂Х, состоящее из элементов х , имеющих образы в множестве Y, называют областью определения соответствия R. Подмножество В⊂Y, состоящее из элементов y , имеющих непустые прообразы в множестве Х, называют множеством значений соответствия R.
Пусть S – соответствие между множествами Х и Y. Соответствие S -1 между множествами Y и Х называется обратным данному, если у S -1 х тогда и только тогда, когда х S у .
Соответствия S и S -1 называют взаимно обратными . Граф соответствия S -1 получается из графа соответствия S изменением направления всех стрелок.
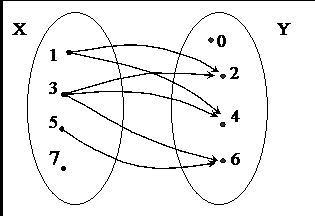рис 2. П р и м е р 1. Соответствие R между множествами X и Y задано при помощи графа (рис. 2). а) Укажите область отправления, область прибытия, область определения и множество значений соответствия R. б) Задайте это соответствие, перечислением пар чисел. в) Постройте график соответствия R в прямоугольной системе координат. г) Найдите соответствие R -1 , обратное данному, и постройте его график.
Р е ш е н и е. а) Из рисунка следует, что областью отправления данного соответствия R является множество Х = {1, 3, 5, 7}, а областью прибытия – множество Y = {0, 2, 4, 6}. Область определения образуют те числа из множества Х, от которых выходит хотя бы одна стрелка, т.е. А = {1, 3, 5}. В множество значений входят те элементы из множества Y, к которым идет хотя бы одна стрелка. Это множество В = {2, 4, 6}.
б) Каждая пара чисел, входящая в данное соответствие, на графе соединена стрелкой, поэтому в виде пар соответствие R можно записать так: {(1,2), (1,4), (3,2), (3,4), (3,6), (5,6)}.
в) График соответствия R в прямоугольной системе координат изображен на рис. 3.
г) Так как граф соответствия R -1 получается из графа соответствия R изменением направления стрелок, то соответствие R -1 можно получить из соответствия R, поменяв местами компоненты в парах: R -1 = {(2,1), (4,1), (2,3), (4,3), (6,3), (6,5)}. График обратного соответствия R -1 в прямоугольной системе координат изображен на рис. 4.
П р и м е р 2. Даны два множества: А = {-1, -2, -3, 1, 2, 3, 0}, N – множество натуральных чисел. Поставим в соответствие каждому числу а Î А его квадрат. Выпишите все пары, принадлежащие соответствию. Найдите образ элементов -2 и 0. Найдите полный прообраз 9.
Р е ш е н и е. Найдем множество пар, входящих в данное соответствие: {(-1, 1), (-2, 4), (-3,9), (1, 1), (2, 4), (3, 9)}. Пара (0, 0) в соответствии не присутствует, так как 0 не является натуральным числом. Образом элемента -2 будет число 4 (вторая компонента пары (-2, 4)), число 0 имеет пустой образ. Полным прообразом числа 9 будет множество {-3, 3}.
П р и м е р 3. Соответствие R задано с помощью пар (1, 2), (0, 0), (2, 4), (-1, -2), (-2, -4). Найдите область определения и множество значений этого соответствия. Какой формулой задается это соответствие?
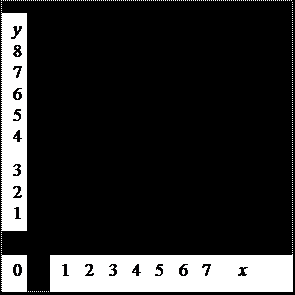
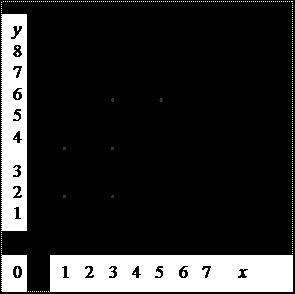Рис. 3 Рис. 4Р е ш е н и е. В область определения Х входят первые компоненты пар соответствия, поэтому Х = {0, 1, 2, -1, -2}. Множество значений Y соответствия R составляют вторые компоненты пар соответствия, значит, Y = {0, 2, 4, -2, -4}. Замечаем, что вторая компонента в каждой паре получается из первой умножением на число 2, следовательно, данное соответствие можно задать с помощью формулы y = 2 x .
Задания для самостоятельной работы по теме 8:
1. Укажите соответствия, существующие между элементами множеств А и В, если: а) А – множество отрезков, В – множество чисел; б) А - множество треугольников, В – множество окружностей.
2. Даны два множества: А = {-1, -2, -3, 1, 2, 3, 0}, N – множество натуральных чисел. Поставим в соответствие каждому числу а∈А его квадрат. Выпишите все пары, принадлежащие соответствию. Найдите образ элементов -2 и 0. Найдите полный прообраз 9.
Лекция 9. Отношения между элементами одного множества. Способы задания отношений. Свойства отношений.
В процессе обучения дошкольникам часто приходится рассматривать элементы одного множества и устанавливать отношения между ними
- Сравнивать по величине;
- Подбирать одинаковые:
- Выстраивать сериационный ряд;
- Упорядочивать карточки.
В математике изучают взаимосвязи между числами («быть больше», «следовать за», «быть меньше на один»), в геометрии рассматривают отношения равенства, пересечения, параллельности и др. Чаще всего дошкольники сталкиваются с отношениями между двумя объектами. Такие отношения называют бинарными.
Способы задания отношений:
1. Указывается характеристическое свойство всех пар элементов, находящихся в этом отношении. При этом характеристическое свойство представляет собой предложение с двумя переменными.
2 .Перечисляют все пары элементов, взятых из множества и связанных этим отношением.
Приведем пример: дано множество Х= [1,2,3,4,5]. Его элементы связаны отношением «быть больше на 1» т.е. отношение задано с помощью предложения «число х больше числа у на 1» или это отношение можно задать , перечислив все пары чисел (2,1),(3,2), (4,3), (5,4).
В математике отношения между двумя элементами часто записывают с помощью символов: х> у, а ll в, у=3х,c ⊥ d.
В математике изучают большое разнообразие отношений. Их классифицируют по свойствам. Пусть R некоторое отношение на множестве Х, а х, у, z- любые его элементы. Если элемент х находится в отношении R с элементом у, то пишут хRу.
Свойства отношений:
1.Рефлексивность: каждый элемент множества находится в этом отношении с самим собой(«параллельность», «равенство»).
| R рефлексивно <-> x R x |
2 . Симметричность: если из того, что элемент х находится в данном отношении с элементом у, следует, что элемент у находится в этом отношении с элементом х («параллельность», «перпендикулярность», «равенство». «быть родственником»).
R симметрично <-> x R y => y R x
3 . Антисимметричность : если из того, что х находится в данном отношение с элементом у и х≠ у, следует, что элемент у в том отношении с х не находится («больше», «меньше»,»длиннее»,»короче»).
R антисимметрично <-> x R y и x≠ y => y R x
4. Транзитивность: если из того, что элемент х находится в данном отношении с элементом у, а элемент y находится в этом отношении с элементом z следует, что элемент х находится в данном отношении с элементом z («больше», «выше», «старше»,»равно», «параллельно»).
R транзитивно <-> x R y и y R x => x R z
Одно и то же отношение может обладать несколькими свойствами. Например отношение «равно»- рефлексивно, симметрично. Транзитивно, а отношение «больше»- антисимметрично и транзитивно.
Определение: если отношение рефлексивно, симметрично и транзитивно. То оно является отношением эквивалентности.
Если на множестве Х задано отношение эквивалентности, то оно определяет разбиение этого множества на классы и наоборот, любое разбиение множества Х на классы определяет на этом множестве отношение эквивалентности. Например, выполни задание «разложи мячи так, чтобы в каждой коробке были мячи одного цвета».
Определение: если отношение транзитивно и антисимметрично, то оно называется отношением порядка («больше», «длиннее»,»следовать»).
Эти отношения упорядочивают элементы множества.
Множества с заданным на нем отношением порядка называется упорядоченным множеством.
Например, выполняя задание: разложи полоски по ширине от самой узкой до самой широкой дети упорядочивают элементы множеств полосок с помощью отношения «быть шире».
Вообще, отношения эквивалентности и порядка играют большую роль в формировании у дошкольников правильных представлений о классификации и упорядочивании множеств.
Задания для самостоятельной работы по теме 9:
1. Приведите примеры отношений, существующих между: а) людьми; б) натуральными числами; в) треугольниками; г) множествами.
2
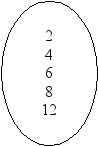
. Отношение Р – «больше», Т – «больше на 2» и Е – «больше в 2 раза» заданы на множестве А = {2, 4, 6, 8, 12}. Постройте графы данных отношений. 
3. Отношение S – «больше», Т – «больше на 3» и Q – «больше в 3 раза» заданы на множестве А = {2, 4, 5, 8, 9, 12, 15}. Постройте графы данных отношений.
4. На множестве Х = {0, 1, 2, 3} задано отношение S = {(0,0), (1,1), (2,2) (3,3), (0,1), (1,2), (0,2), (1,0), (2,1), (2,0)}. Постройте граф этого отношения, определите свойства отношения.
5. Отношение Т – «не короче» задано на множестве отрезков с длинами {4 см, 5 см , 18 см , 10 см}. Докажите, что отношение Т – отношение порядка.
6. На множестве Х= {3,4, 5, 6, 7} задано отношение «x