И в авторской редакции. Удк 536. 7 +"7"+ (201) +53+57 +577. 4+211 Вейник А. И., «Термодинамика реальных процессов», Мн.: "Навука I тэхнiка", 1991. 576 с. Isbn 5-343-00837. Вмонографии приводятся ряд новых закон

Вид материала

Закон

Содержание 2. Условия нарушения закона сохранения количества движения. 3. Возникновение внутренней силы в устройствах типа БМ-28. А тело имеет большую скорость  4. Устройства БМ-29 и БМ-30. 5. Устройства типа БМ-33. Р" , действующая со стороны оси гироскопа 1 6, вращающийся на оси 7 6. Устройства типа БМ-34. 7. Устройства типа БМ-35.

Подобный материал:

• Впервые в авторской редакции, 9591.86kb.
• Конспект лекций Кемерово 2004 удк: 637. 992, 2553.59kb.
• Хавронюк Микола Іванович удк 343 (4: 447) Кримінальне закон, 3077.54kb.
• М. М. Ничипорчук национальный исследовательский ядерный университет «мифи» моделирование, 9.59kb.
• Удк [544. 77: 577. 112. 824]: 535, 64.03kb.
• Хавронюк Микола Іванович удк 343 (4: 447) кримінальне закон, 684.97kb.
• Учебное пособие и Учебный словарь-минимум по религиоведению. М.: Гардарики, 2000. 536, 8576.03kb.
• Учебное пособие и Учебный словарь-минимум по религиоведению. М.: Гардарики, 2000. 536, 8588.39kb.
• И. А. Бунин принадлежал к тем реалистам рубежа веков, которым была дорога сущность, 164.9kb.
• Формирование гендерного подхода к обучению и воспитанию учащихся в школе 343, 102kb.

Глава ХXI. Теоретические прогнозы ОТ:

«движение за счет внутренних сил».


1. Условия нарушения третьего закона Ньютона.


Описанные простые явления в совокупности с семью нача­лами ОТ позволяют сделать большое множество прог­нозов, поддающихся непосредственной эксперименталь­ной проверке и одновременно не вытекающих из совре­менных теоретических представлений или даже противоречащих им. Вполне естественно, что наибольшее число интереснейших и принципиально важных теоретических выводов следует из новых, неизвестных ранее начал ОТ - второго, третьего, четвертого и седьмого. Однако новые знания и идеи приходят не только от новых законов: как это звучит ни парадоксально, весьма любопытные прогнозы можно извлечь также из того, что отсутствует в ОТ, - речь идет об энтропии и втором законе термодинамики, которых природа и ОТ не знают; одновременно в ОТ отсутствуют и все запреты второго закона.

Выше упоминались многие опытные факты, подтверждаю­щие выводы ОТ, однако мне представляется, что для торжества новой парадигмы важно получить такие принципиально важ­ные выводы, которые бы однозначно, ясно и недвусмысленно опрокидывали старую парадигму и приводили бы к опытам, находящимся в прямом противоречии с традиционными пред­ставлениями. Соответствующие опыты в науке принято имено­вать решающими экспериментами, ибо Его Величество Экспе­римент - это единственный верховный судья, кто способен и должен решать споры между парадигмами и теориями и опре­делять их судьбы.

Из всего арсенала средств ОТ я отобрал три наиболее наглядные, неожиданные и убедительные новые проблемы, которые задействовал в своих решающих экспериментах. Первая связана с нетрадиционным определением времени (и пространства). О времени с упоминанием экспериментов уже говорилось в гл. XVIII, говорится в настоящей и следую­щей, а также в некоторых других главах. Остальные две про­блемы подсказаны «Указаниями по составлению заявки на открытие» Государственного комитета Совета Министров СССР по делам изобретений и открытий. В «Указаниях» говорит­ся: «4. Не принимаются к рассмотрению в качестве заявок на открытия материалы, в которых описаны... д) ...движение за счет внутренних сил, получение КПД устройств, равного или более единицы и т.д.» Движение за счет внутренних сил нарушает известный закон сохранения количества движения механики Ньютона, а КПД, равный единице (100%), - второй закон термодинамики Клаузиуса.

Мне представляется, что нарушить запреты «Указаний», содержащих квинтэссенцию современных теоретических пред­ставлений, - это самый убедительный решающий эксперимент. Именно поэтому я без сожалений потратил на решение указан­ной проблемы более 35 лет. В гл. XXIII и XXIV описаны устрой­ства, преобразующие теплоту окружающей среды в электро­энергию и работу с КПД 100%. В настоящей главе теорети­чески решается задача создания нескомпенсированной силы внутри изолированной системы, соответствующие эксперименты описаны в следующей главе.

В уравнении закона сохранения количества движения (315), как и в уравнении (312), масса m и пространство х под­чиняются закону сохранения. Следовательно, нарушить закон (315) можно только в том единственном случае, если повлиять на оставшуюся величину  - ход реального времени, сделав его различным на взаимодействующих телах.

Из общего уравнения состояния (308) видно, что это можно сделать с помощью всех наличных степеней свободы системы. Однако для упрощения и наглядности рассуждений ограничимся группой механических явлений, которые сами помогут нам нарушить свои собственные механические законы. С этой целью отбросим в уравнении (308) хрональный, вермический, электрический и магнитный экстенсоры. Остаются три: кинетический, кинетовращательный и колебательный, влияющие на хронал, а следовательно, и на ход реального времени через коэффициенты Α₁₂ , Α₁₃ и А₁₄ . Числовые значения этих коэффициентов нам не известны, но мы твердо знаем, что благодаря универсальному взаимодействию они нулю не равны и, следовательно, с их помощью вполне можно подей­ствовать на величину d.

При качественном анализе первой строчки уравнения (308) вместо изменений экстенсоров можно воспользоваться измене­ниями сопряженных с экстенсорами интенсиалов, ибо связь между этими величинами отличается наибольшей интенсив­ностью, остальные величины влияют менее существенно и мы их не будем учитывать. Тогда интересующая нас зависимость примет вид

d = (Α₁₂/ Α₂₂)d² + (Α₁₃/ Α₃₃)d² + (Α₁₄/ Α₄₄)d² + ... (328)

или в идеальном случае, когда А = const,

 = (Α₁₂/ Α₂₂)² + (Α₁₃/ Α₃₃)² + (Α₁₄/ Α₄₄)² + ... (329)

Из уравнения (328) видно, что изменение (приращение) хронала тем выше, чем сильнее изменяются (наращиваются) квадраты скорости тела и частот его вращения и колебания. В свою очередь приращения скорости и частот представляют собой соответствующие ускорения. Следовательно, на при­ращение хронала, а значит, и на приращение хода реального времени (см. второе равенство (237)) очень большое влияние оказывают разного рода ускорения системы. Напомню, что в данном случае приращение хода реального времени d есть именно ускорение этого хода, а не малая длительность d. Все сказанное легче себе представить, если левую и правую части уравнения (328) разделить на малый отрезок времени d (или dt), для наглядности то же самое можно проделать и со вторым равенством (237).

Весьма интересно также уравнение (329). Согласно этому уравнению, высоким скоростям движения и частотам вращения и колебания тела отвечают большие значения хронала и малые значения хода реального времени (см. первое равенство (237)). При малых скоростях и частотах, наоборот, хронал невелик, а скорость хода реального времени высока.

Применим изложенные соображения к процессу соударения двух тел - первого и второго, на которых реальное время течет с разными скоростями. С помощью уравнений (328) и (329) мы теперь вполне можем создать необходимую разность скоростей. Если для постороннего (внешнего) наблюдателя длительность соударения равна d (или dt), то наблюдатель, находящийся на первом теле, зафиксирует по своим часам длительность d₁ , а находящийся на втором теле - длитель­ность d₂ . Для определенности предположим, что

d₁ > d₂

Обратимся теперь к уравнению второго закона Ньютона (312), связывающему силу Р_х с ходом реального времени d на телах. Легко видеть, что сила Р_х2 , действующая со сто­роны второго тела на первое, превышает силу Р_х1 , действующую со стороны первого тела на второе, то есть

Р_х2 > Р_х1

ибо в первом случае знаменатель правой части формулы (312) меньше, чем во втором.

Следовательно, в процессе соударения двух тел с разным ходом времени на них образуется нескомпенсированная сила

Р_хв = Р_х2 - Р_х1  0 (330)

Условно будем называть эту силу, вызванную хрональными причинами, внутренней, ибо она возникает внутри полностью изолированной системы и действует на окружающую среду. Если ход, времени на телах одинаков, то сила Р_хв = 0, то есть сила действия равна силе противодействия.

Мы пришли к совершенно замечательному результату: если на соударяющихся телах время течет с разной скоростью, то сила действия по абсолютной величине не равна силе проти­водействия. Таковы условия, необходимые и достаточные для нарушения третьего закона механики Ньютона. При этом сила всегда меньше со стороны того тела, на котором больше ско­рость хода реального времени, и наоборот. Таков теоретический прогноз ОТ. Он в равной мере касается микромира (элемен­тарных частиц, атомов, молекул), макромира (привычных нам тел), мега- и более грубых миров (планет, звезд, галактик и т.д.). Следует также добавить, что гравитационное взаимо­действие планет, звезд и галактик тоже можно рассматривать как удар, только мягкий, причем на всех подобного рода телах ход реального времени, как правило, не одинаков со всеми вытекающими отсюда пикантными последствиями [ТРП, стр.413-416].


2. Условия нарушения закона сохранения количества движения.


Несоблюдение в определенных условиях третьего закона Нью­тона автоматически решает проблему нарушения закона сохра­нения количества (и момента количества) движения.

Действительно, из-за разного хода времени и нарушения третьего закона на тела действуют неодинаковые импульсы, причем

Р_х2 d₂ > Р_х1 d₁

Это объясняется тем, что в уравнение (312) сила входит в пер­вой, степени, а ход времени - в квадрате. Поэтому ускорен­ный ход времени на первом теле не в состоянии скомпенсиро­вать уменьшение первой силы. Например, если первый ход больше второго в 2 раза, то первая сила окажется меньше второй в 4 раза. В результате импульс первой силы будет в 2 раза меньше импульса второй.

Импульсы сил равны изменениям соответствующих коли­честв движения (см. формулу (315)), поэтому

d(m)₁ < d(m)₂

Это значит, что суммарное количество движения двух тел до взаимодействия (m)’ оказывается не равным суммарному количеству движения тех же тел после взаимодействия (m)”, причем

(m)’ > (m)” (331)

ибо первое тело теряет часть своего импульса в ходе взаимо­действия.

Следовательно, при механических взаимодействиях тел с разным ходом времени нарушается не только третий закон Ньютона, но и закон сохранения количества движения (им­пульса) (см. уравнения (330) и (331)). Все сказанное относит­ся также к закону сохранения момента количества движения и к упомянутому в параграфе 14 гл. XV закону сохранения количества вибродвижения. В результате взаимодействия воз­никает нескомпенсированная внутренняя сила Р_хв , направлен­ная в сторону тела с ускоренным ходом времени; это же тело обладает заниженным количеством движения; суммарное коли­чество движения обоих тел после взаимодействия тоже умень­шается. На практике соответствующая ситуация возникает, например, при бета-распаде ядер, где замедленным ходом вре­мени располагает быстро движущаяся бета-частица.

В приведенных рассуждениях величины d₁ , d₂ и dt харак­теризуют ход реального времени на первом и втором телах, а также ход эталонного времени; они могут быть равны дли­тельности взаимодействия (удара) или быть пропорциональ­ными этой длительности. В общем случае имеет место соотно­шение

d₁  d₂  dt (332)

Это неравенство определяет условия нарушения третьего зако­на Ньютона и закона сохранения количества движения. Воз­никающие нарушения тем значительнее, чем больше различа­ются между собой указанные величины.

Для нас привычными являются случаи, когда ход реального времени на взаимодействующих телах практически одинаков и его можно принять равным ходу эталонного времени. Это соответствует условию

d₁  d₂  dt (333)

при котором упомянутые законы практически сохраняют свою силу. Именно при подобных условиях выполняли свои опыты Рен, Мариотт, Ньютон и другие авторы.

Таковы выводы-прогнозы ОТ. Они в корне противоречат существующим представлениям и поэтому ставят вопрос жест­ко: быть или не быть ОТ. Для реализации в опыте этих выводов я рассмотрю несколько схем механических устройств, в кото­рых возникает нескомпенсированная внутренняя сила и кото­рые получили наименование безопорных движителей (БМ) [ТРП, стр.416-418].


3. Возникновение внутренней силы в устройствах типа БМ-28.


При выборе соответствующих устройств я буду руководство­ваться идеей, чтобы они отличались наибольшей простотой, наглядностью и доступностью. Это обстоятельство мне пред­ставляется крайне важным: я придаю особое значение тому, чтобы каждый желающий мог легко повторить эксперимент и убедиться в правильности выводов ОТ. Принципиальная схема механического БМ описана в книге [21, с.214]. Простей­шим устройством подобного рода могут служить, как уже говорилось, два соударяющихся тела. Однако удар - это слишком грубый процесс, другой недостаток простого удара - его однократность.

Очевидно, что надо осуществить непрерывный круговой процесс изменения состояния движения тела, повторять его быстро и многократно, тогда получится безостановочно дей­ствующая внутренняя сила, которую нетрудно измерить. На­пример, соответствующий процесс возникает в случае мягкого удара, если заставить тело двигаться с переменной скоростью по схеме, показанной на рис. 17, а.





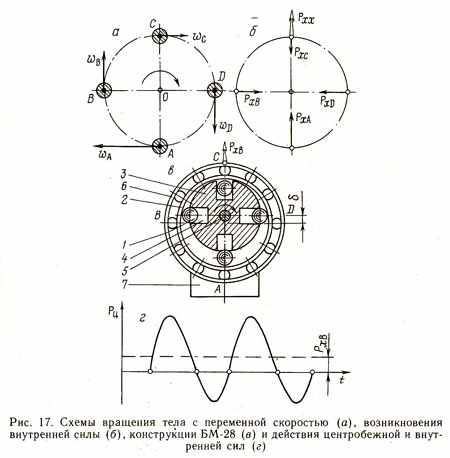
Для конкретности предположим, что в зоне А тело имеет большую скорость _А , в зоне С - малую _С , а в зонах В и D - промежуточную _В и _D , ибо в зоне В тело тормозится, а в зоне D разгоняется и затем вновь приходит в исходное состояние А. Чтобы детально проанализировать силовую ситуацию в этих условиях, надо знать закон изменения скорости и интегрировать процесс по всей окружности. Однако для грубого качественного анализа вполне достаточно ограничиться рассмотрением лишь четырех наибо­лее характерных зон – А, В и С и D.

В зонах А и С скорости изменяются мало, поэтому ускоре­ниями можно пренебречь и ориентироваться на первое равен­ство (237) и уравнение (329). Согласно этим уравнениям, центробежная сила тела в зоне А претерпевает максимальное хрональное уменьшение на величину Р_хА , а в зоне С - минимальное на величину Р_хС (рис. 17, б). Реакция опоры, не имею­щей такой высокой скорости, как тело, испытывает пренебре­жимо малые хрональные изменения. Поэтому в системе появляется за цикл (за один оборот) нескомпенсированная внутренняя (хрональная) сила Р_хх = Р_хА - Р_хС , действующая со стороны опоры и направленная вверх.

Что касается зон В и D, то здесь на эффект скоростного ослабления центробежной силы накладывается также эффект, обусловленный ускорением. О последнем эффекте можно судить по второму равенству (237) и уравнению (328). При симмет­ричном процессе скорости и ускорения в зонах В и D одинаковы по величине и противоположны по знакам, поэтому нескомпенсированные силы гасят друг друга (Р_хВ = - Р_хD ). В результате равнодействующая всех четырех сил за цикл остается равной Р_хх .

На первый взгляд может показаться, что эта сила должна быть направлена вниз, то есть в сторону, где скорость и центро­бежная сила тела максимальны. Чтобы такого ощущения не возникало, надо не упускать из виду, что речь идет не о самой центробежной силе Р_ц , а только о ее хрональном уменьшении, избыточные же по отношению к хрональным силы благополуч­но гасятся внутри системы. При этом направление хрональной силы Р_хх от направления вращения тела не зависит, оно целиком определяется относительной ориентацией максималь­ной и минимальной скоростей: сила Р_хх всегда направлена в сторону минимальной скорости. Это важно помнить при обсуждении опытных данных.

На примере группы механических явлений (и БМ) полезно еще раз оговорить разницу, существующую между малой скоростью хода (малым ходом, малым отрезком) реального времени d, входящей в уравнения (312), (315) и т.д., и уско­рением (изменением, приращением) хода реального времени d, входящим во второе равенство (237). Ускорение хода времени всегда обусловлено только изменением (приращением) хронала (второе равенство (237) и уравнение (328)), а ско­рость хода времени обычно рассматривается при постоянном значении хронала или приводится к нему, то есть к постоян­ному ходу реального или эталонного времени.

Описанный круговой процесс можно осуществить с помощью самых различных механизмов. Например, можно применить простейшее устройство БМ-28 (рис. 17, в), в котором шарики, ролики или стерженьки 1 катятся или скользят по кольцу 2, скрепленному с корпусом электродвигателя 7 [9, с.44]. Водилом служит диск 3 с отверстиями 4, насаженный на вал 5 двигателя. Ось кольца 2 смещена относительно оси двигате­ля на величину . При равномерном вращении двигателя в зоне А шарики катятся на большем радиусе, чем в зоне С, поэтому обладают большей скоростью. Для общего повышения скорости шариков путем уменьшения их трения о кольцо в ка­честве последнего целесообразно использовать соответствую­щий шариковый или роликовый подшипник, состоящий из подвижного кольца 2 и неподвижного 6.

Если бы хрональный эффект отсутствовал, тогда центробеж­ная сила Р_ц изменялась бы симметрично относительно нулевой линии, изображенной на графике рис. 17, г горизонтальными штрихами, а все устройство работало бы как обыкновенный вибратор. Наличие хронального эффекта приводит к появлению нескомпенсированной силы Р_хВ , направленной вверх, что равносильно смещению на графике нулевой линии вниз. Вообще, в данном устройстве сила Р_хВ всегда ориентирована в сторону, обратную эксцентриситету  кольца, и при перемене направле­ния вращения мотора не изменяется. Эту силу нетрудно изме­рить на достаточно чувствительных технических, аналитических или крутильных весах, она вызывает уменьшение веса работаю­щего устройства. Величина силы зависит от числа оборотов, эксцентриситета, числа и массы шариков, радиуса кольца 2 и т.д. При нулевом эксцентриситете нескомпенсированная внутренняя сила обращается в нуль, так как в условиях равно­мерного движения шариков все силы - центробежные и внут­ренние - гасят друг друга [ТРП, стр.418-421].


4. Устройства БМ-29 и БМ-30.


Необходимый круговой процесс можно осуществить также с помощью гироскопа, представляющего собой тело, вращаю­щееся вокруг некоторой оси. Но с целью получения хронального эффекта гироскопу надо придать дополнительное пере­мещение (колебание) с переменной скоростью. При этом гироскоп можно использовать двумя различными способами - путем колебаний поперек (БМ-29) или вдоль (БМ-30) оси вращения, а сами колебания должны быть несимметричными: в одном направлении гироскоп надо перемещать с большой скоростью, а в обратном - с малой. В результате отдельные точки тела будут двигаться с переменной за цикл скоростью, то есть будет совершаться круговой процесс, и возникнет описанный выше нескомпенсированный силовой хрональный эффект.

Н
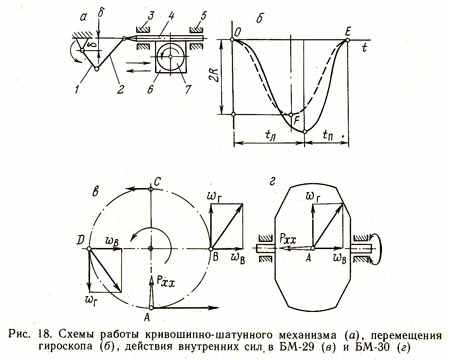
еодинаковое по скорости прямого и обратного движений контролируемое перемещение вращающегося гироскопа можно проще всего задать с помощью кривошипно-шатунного или эксцентрикового механизма, в котором ось вращения криво­шипа (эксцентрика) смещена на величину δ относительно линии перемещения гироскопа (рис. 18, а). Гироскоп 7, заклю­ченный в кожух 6, прикреплен к ползушке 4, которая двигает­ся вправо и влево вдоль направляющих 3 и 5. Если кривошип 1 вращается в сторону, показанную стрелкой, то гироскоп переме­щается вправо быстрее, чем влево. Разница в прямой и обрат­ной скоростях тем выше, чем больше смещение  и радиус R кривошипа и меньше длина 1 шатуна 2. При  = 0 движение гироскопа является симметричным и обсуждаемый эффект не возникает: этот случай на рис. 18, б изображен штриховой линией, которая показывает смещение гироскопа от крайне правого положения (точка 0) до крайне левого (точка F) на величину 2R и затем вновь до конца направо (точка Е).

При   0 процесс описывается несимметричной сплошной линией, при этом несколько возрастает амплитуда колебаний и увеличивается длительность t_л движения гироскопа влево по срав­нению с длительностью t_п его движения вправо, именно по­этому скорость справа больше, чем слева.

Если гироскоп колебать поперек оси вращения, то скорость точек А и С обода будет изменяться по величине, а точек В и D - по величине и направлению (рис. 18, в). На рисунке показана только большая скорость wв перемещения гироскопа вправо, от нее зависит количественная сторона эффекта, ско­рость вращения самого гироскопа _В во всех точках А, В, С и D одинакова. Наибольший вклад в эффект дают точки А и С, движущиеся с различными суммарными скоростями, причем точка А обладает скоростью _г + _В , а точка С - скоростью _г - _В . Возникает нескомпенсированная за цикл колебания (оборот кривошипа) хрональная сила Р_хх , направленная вверх, то есть поперек линии вибраций, в сторону зоны с наи­меньшей скоростью движения. При изменении направления вращения гироскопа сила Р_хх изменяет свое направление на обратное, то же самое происходит при изменении направления вращения кривошипа.

Если гироскоп колебать вдоль оси вращения (рис. 18, г), то все его точки одновременно примут участие в дополнитель­ном колебательном движении со скоростью _В . В результате возникает нескомпенсированная хрональная сила Р_хх , направ­ленная вдоль оси, в сторону меньшей суммарной скорости движения точек гироскопа, а значит, и ползушки, то есть в сторону, противоположную максимальной скорости _В , при­чем направление силы не зависит от направления вращения гироскопа, а целиком определяется направлением вращения кривошипа. При продольном колебании гироскопа эффект должен получиться заметно выше, чем при поперечном, так как в первом случае в процессе одновременно принимает участие большее количество метрического вещества [ТРП, стр.421-423].


5. Устройства типа БМ-33.


Методом вращения тел можно создать множество различных вариантов БМ. В настоящей главе я упомяну еще три вариан­та, которые являются частными случаями общей схемы, изобра­женной на рис. 19, а и б. Маховик (гироскоп) 1 вращается в подшипниках 2 и 4 на оси 3, которая в свою очередь вращает­ся вокруг оси 5 (направление вращения показано стрелками). Гироскопический момент на плече L дает несимметричную пару сил Ρ_х’ и Р_х", причем разность

Р_хВ = Ρ_х’ + Р_х"

представляет собой интересующую нас нескомпенсированную внутреннюю силу.





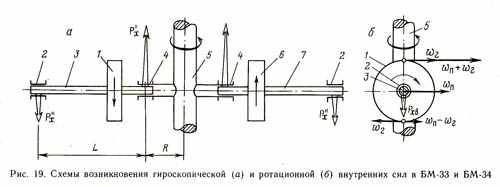
Действительно, согласно уравнению третьего начала ОТ (308), хронал со скоростью возрастает и, следовательно, сила Р" , действующая со стороны оси гироскопа 1 на подшипник 2, хронально ослабляется тем значительнее, чем выше скорость этого подшипника вокруг оси 5 по сравнению со скоростью подшипника 4. Поэтому с увеличением плеча L и уменьшением радиуса R хрональный эффект растет. Гироскопические силы, а значит, и хрональный эффект тем выше, чем больше момент инерции маховика и частота вращения осей 3 и 5, ибо момент гироскопических сил определяется произведением момента инерции маховика и угловых скоростей вращения осей 3 и 5, а момент инерции маховика пропорционален радиусу послед­него в четвертой степени. В условиях рис. 19, а нескомпенси­рованная (внутренняя, хрональная) сила Р_хВ направлена вверх. Если изменить направление вращения оси 3 или 5, то хрональная сила изменит свое направление на обратное. Если одновременно изменить оба направления вращения, то неском­пенсированная сила останется неизменной. Таковы теоретичес­кие прогнозы ОТ. По этому принципу работают устройства типа БМ-33, они основаны на эффекте возникновения гиро­скопических сил.

Для устранения дисбаланса целесообразно симметрично к первому расположить второй точно такой же гироскоп 6, вращающийся на оси 7 в противоположную сторону, как показано на рисунке, ибо если оба гироскопа вращать в оди­наковом направлении, то возникающие моменты погасят друг друга и нескомпенсированная сила обратится в нуль. Более того, для взаимной компенсации крутящего момента от двига­телей целесообразно использовать не два, а четыре гироскопа, вращающихся в разные стороны, и синхронизировать частоты их вращения с помощью системы шестеренок (см. параграф 5 гл. XXII), причем минимальное число моторов равно двум, по числу осей 5, а максимальное - шести, по одному на каж­дую из шести осей.

Принципиальное преимущество такой схемы БМ заклю­чается в том, что в процессе создания нескомпенсированной силы принимает участие одновременно вся масса гироскопа и этот процесс осуществляется непрерывно, а не периодически, как в БМ-28, БМ-29 и БМ-30. В результате устраняются неиз­бежные вибрации, что многократно увеличивает эффективность данной схемы по сравнению с предыдущими - позволяет резко повысить частоту вращения и т.д. [ТРП, стр.423-425].


6. Устройства типа БМ-34.


Интересно, что на схеме рис. 19, а действует еще одна неском­пенсированная сила, обусловленная сложением переносной ско­рости маховика ш_п при его вращении вокруг оси 5 со скоростями различных точек маховика w_r в связи с его одновременным вращением вокруг оси 3 (рис. 19, б). В верхней точке маховика эти скорости суммируются, а в нижней вычитаются. В резуль­тате возникает непрерывно действующая нескомпенсированная внутренняя сила Р_хВ , направленная вниз, в сторону малой суммарной скорости. По этому принципу работают ротацион­ные устройства типа БМ-34. Эта схема напоминает прежнюю, изображенную на рис. 18, в. При изменении направления вращения маховика 1 или оси 5 хрональная сила изменяет свое направление на обратное. Если одновременно изменить оба направления вращения, то сила останется неизменной. Для устранения дисбаланса и компенсации крутящего мо­мента целесообразно добавить второй маховик справа и еще одну такую же пару маховиков, вращающихся в противопо­ложном направлении (как в БМ-33).

Необходимо отметить, что силы Р_хВ в ротационном хрональном эффекте у БМ-34 и в гироскопическом эффекте у БМ-33 всегда действуют одновременно и направлены в прямо проти­воположные стороны, то есть стараются погасить одна другую. Чтобы выделить ротационный эффект и ослабить гироскопи­ческий, надо пойти по пути максимального увеличения радиуса R и снижения плеча L до возможного минимума [ТРП, стр.425-426].


7. Устройства типа БМ-35.


Любопытно, что схема рис. 19, а содержит помимо гироскопи­ческого (основной в БМ-33) и ротационного (основной в БМ-34) также еще третий хрональный силовой эффект, который условно будем именовать смерчевым; он реализует­ся в устройствах типа БМ-35.

Самое простое устройство БМ-35, в котором создается нескомпенсированная внутренняя сила, нарушающая закон сохранения количества движения, представляет собой обыкно­венный маховик или любое другое тело, вращающееся вокруг какой-либо оси. В качестве схемы его действия можно восполь­зоваться рис. 19, б, если отбросить ось 5, а создаваемую ею переносную скорость _n заменить скоростью движения данной точки Земли _З вокруг собственной оси (на широте Минска эта скорость равна около 0,3 км/с), вокруг Солнца (около 30 км/с), вокруг центра Галактики вместе с Солнцем (около 250 км/с) и т.д. Абсолютная скорость данной точки Земли _з в мировом пространстве с одной стороны гироскопа склады­вается со скоростью его вращения _т , а с другой вычитается. Хрональная сила Р_хВ , как всегда, смотрит в сторону от большей скорости к меньшей. Если изменить направление вращения гироскопа (или движения Земли), то сила изменит свое направ­ление на обратное, при одновременном изменении обоих на­правлений сила не изменится. Непрерывное действие этой силы должно отличаться от двух предыдущих случаев периоди­ческими суточными, годичными и т.п. колебаниями в связи с соответствующими периодическими изменениями скорос­ти _З .

Если попеременно ориентировать ось гироскопа в разных направлениях, например, с помощью подвеса Кардана и управляющей ЭВМ, то максимальное значение хрональной силы укажет направление и величину абсолютной скорости данной точки Земли в данный момент времени, даже если сидеть в закрытой каюте корабля. Кстати, установить абсолютную скорость можно также с помощью любого из слагаемых уравнения (308).

Поскольку всякое соответствующим образом ориентиро­ванное на Земле вращающееся тело создает обсуждаемую нескомпенсированную силу, постольку от нее не свободны и устройства типа БМ-33 и БМ-34. Однако при наличии двух осей 5, вращающихся в противоположные стороны, смерчевые силы гасятся внутри этих устройств. Смерчевый эффект получил свое наименование от машины БМ-35, которая является на­глядной моделью смерча. Его хрональное поле, усиленное эффектами трения, заряжает предметы, животных и даже целые дома, они отталкиваются от земли и иногда плавно перено­сятся хрональными силами и ветром на большие расстояния (см. параграфы 24 гл. XVIII и 6 гл. XXII).

Таковы вкратце некоторые конкретные принципиально важ­ные выводы-прогнозы ОТ. Они носят качественный характер, так как мы пока не знаем числовых значений коэффициентов состояния в уравнении (308). Однако уже сам факт наруше­ния в запланированных экспериментах третьего закона Нью­тона и закона сохранения количества движения независимо от количественной стороны этого нарушения должен будет свидетельствовать о справедливости основных положений ОТ. Обратимся теперь к описанию соответствующих эксперимен­тальных результатов [ТРП, стр.426-427].