Русской народной сказки

Вид материала

Документы

Подобный материал:

• Календарный план фронтальных занятий по развитию связной речи детей 6-7 лет с онр, 92.77kb.
• Разработка урока чтения по теме: «Устное народное творчество», 30.92kb.
• Цель: Ознакомить детей с жанром русской народной сказки, 48kb.
• Ноу средняя общеобразовательная школа «Росинка», 365.73kb.
• Сценарий русской народной сказки «Колобок», 109.2kb.
• Кейс. 5 класс. Литература, 17.71kb.
• Присказка и зачин как жанровые характеристики русской и британской народной сказки, 13.02kb.
• Особенности литературной сказки. Сказки Г. Х. Андерсена, 84.48kb.
• Задачи: Ознакомить детей с персонажами сказки, их действиями; Способствовать развитию, 54.06kb.
• Русская народная сказка, 402.56kb.

1. Прочтите название русской народной сказки:
   

2. В квартирах №№ 1, 2, 3 жили белый, черный и рыжий котята. Черный котенок не жил в № 1 и № 2. в квартире № 1 не жил белый котенок. В какой квартире жил каждый котенок?
   
3. Имеется 2 замка и 2 ключа к ним. Взяли ключ и проверили, подходит ли  он к одному из замков. Достаточно ли этой проверки, чтобы узнать от какого замка каждый ключ?
   
4. Посмотрите на слова аппетит, мозги, нежности, холод и решите, кто лишний:
   

(А) собака; (Б) кошка; (В) волк;

(Г) телёнок; (Д) курица.

5. Какое из этих слов по смыслу лишнее?
   

(А) волкодав; (Б) борзая; (В) пудель;

(Г) собака; (Д) овчарка.

6. Я положил в сумку: надувной матрас, плавки, полотенце, книжку, кастрюлю.Угадайте, куда я собрался, если одну вещь я взял по ошибке.
   

(А) в гости; (Б) в школу; (В) на пляж;

(Г) в бассейн; (Д) в кино.

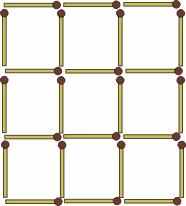
7. Из этой же фигуры так извлеките 8 спичек, не трогая других, чтобы оставшиеся спички составили 4 одинаковых квадрата.
   

8. Метаграммы
   

Первую метаграмму (meta - между, gramma - буква) 29 марта 1879 года поместил в журнале «Ярмарка тщеславия» английский писатель, математик и логик Л. Кэрролл, написавший популярные сказки «Алиса в стране чудес» и «В Зазеркалье».

Российская история метаграммы пока изучена недостаточно, однако известны своими оригинальными метаграммами Р. Вердин, О. Степанов, Е. Ефимовский.

Метаграмма - это загадка, в которой зашифрованы различные слова, состоящие из одного и того же числа букв. Разгадав одно из слов метаграммы, нужно заменить в нём одну букву так, чтобы получилось новое слово по смыслу загадки, например, из слова «липа», заменив «П» на «С», получаем другое слово - «лиса». Аналогично: «сазан - фазан», «цапля - капля», «карта - парта», «сайка - чайка - байка - майка».

Разгадайте метаграммы:


С «Г» - её на винт накрутят,
С «Л» - конечно, лает,
С «М» - одежда, но не греет,
С «3» - от волка убегает


С буквой «Т» -
Весенний месяц это,
А вот с «С» -
Огромная планета.

9. Двое одновременно подошли к реке. Лодка, на которой можно переправиться, выдерживает только одного человека. И все же без посторонней помощи каждый переправился на этой лодке на другой берег. Как им это удалось?
   
10. Числовой ребус:
    

КТО + КОТ = ТОК