Информатика. Лекции. Краткая история компьютерной техники Первые компьютеры: Z3, Colossus, eniac

Вид материала

Содержание

Структурированный алгоритм
Теорема (о структурировании)
Свойства модулей

Подобный материал:

1 ... 9 10 11 12 13 14 15 16 ... 19

Пример. Результаты применения этих функций: sqrt(9) = 3, abs(–5) = 5, sin(0) = 0, cos(0) = 1, ln(1) = 0, exp(1 ) =e, 23 mod 5 = 3, 20 mod 5 = 0, 23 div 5 = 4, 20 div 5 = 4, int(2.7) = 2, int(2) = 2, rnd(0) = 0.231356, length(‘информ’) = 6.

Порядок выполнения операций (старшинство операций – по убыванию) в языке Паскаль:

вычисление выражений в скобках;
вычисление стандартных функций;
умножение и деление (обозначаются "*" и "/");
сложение и вычитание (обозначаются "+" и "–").

Пример. Выражение b*c + (d/t*(v/n/m))*sin(x) вычисляется в следующем порядке (слева направо): v/n, (v/n)/m, d/t, (d/t)*(v/n/m), sin(x), b*c, (d/t*(v/n/m))*sin(x), b*c+(d/t*(v/n/m))*sin(x) и эквивалентно математическому выражению:

.

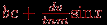Рассмотрим базовые простые команды языка Паскаль.

Команда описания (заголовка) алгоритма (программы) :

Program <имя алгоритма>;,

где <имя алгоритма> – имя, задаваемое составителем программы (краткое, полное, грамотное отражение сути алгоритма).

Ввод – команда ввода в рассмотрение (в тело алгоритма) тех или иных входных параметров:

Read (<список вводимых параметров>);

или

ReadLn (<список вводимых параметров>);.

Первая команда вводит данные с текущей позиции экрана (где стоит курсор), вторая – с новой строки экрана.

Вывод – команда вывода на экран тех или иных входных или выходных параметров алгоритма:

Write (<список выводимых параметров>);

или

WriteLn (<список выводимых параметров>);.

Первая команда выводит данные с текущей позиции экрана (где стоит курсор), вторая – с новой строки экрана.

Присваивание – команда изменения текущего значения переменной вида:

<идентификатор> := <выражение>;,

где <идентификатор> соответствует имени переменной, <выражение> – корректно записанное выражение. Знак ":=" означает последовательное выполнение двух действий: определение текущего значения <выражения> и замена текущего значения переменной, имя которой задано <идентификатором>, на новое значение, равное значению <выражения>.

Команда начала алгоритма (блока) – команда Begin.
Команда завершения алгоритма (блока) – команда End.
Команда вставки комментариев в текст алгоритма имеет вид:

<комментируемое в программе> <текст комментария>.

Комментировать можно любой объект в программе. Обычно комментируют переменную, структуру данных, команду, группу команд.

Различают три базовые алгоритмические структуры: следование, ветвление, повторение.

Структура следование состоит из двух команд с указанной очередностью их выполнения и имеет вид:
<команда – предшественник>;
<команда – преемник>.

Структура типа ветвления в полной форме состоит из некоторого условия, проверяемого на истинность при выполнении структуры, команды, выполняемой при выполнении проверяемого условия, и команды, выполняемой при невыполнении условия. Структура имеет вид
if <условие>
then <команда, выполняемая при выполнении условия>
else <команда, выполняемая при невыполнении условия>;.

Ключевые (служебные) слова Паскаля – if (если), then (то), else (иначе). Ключевые слова нельзя изменять, заменять, так как их эталоны закреплены в переводчике с языка Паскаль (о нем подробнее – ниже).

Пример. Команда вида

if (х>y) { если текущее значение х больше текущего значения y, }

then у := х { то текущее значение у полагаем равным текущему значению х, }

else x:= y; { иначе (при х <= y) текущее значение x заменяем на текущее значение y }.

Структура типа ветвления в неполной форме – частный случай ветвления в полной форме, в которой, при невыполнении условия, управление просто передается следующей команде и больше никаких действий команда ветвления не осуществляет. Эта структура имеет вид

if <условие>

then <команда, выполняемая при исполнении условия>; .

Структура повторения (цикл) служит для компактной записи одного и того же набора команд, повторяемых для различных значений параметров команд.

Структура повторения типа "пока (while)" записывается в виде:

while <условие продолжения повторения> do

<повторяемая команда>;

или

while <условие продолжения повторения> do

begin

<повторяемая команда номер 1>;

<повторяемая команда номер 2>;

. . .

<повторяемая команда номер N>

end;.

Ключевые слова Паскаля – while (пока), do (выполнять), begin (начало), end (конец).

Телом цикла называется последовательность повторяемых команд, которая может быть и пустой (редко встречаемый случай).

Часть команды цикла "while <условие продолжения повторения>" – заголовок цикла.

Данный цикл выполняется по правилу: если условие повторения для текущих его параметров не выполнено, то повторение команд (тела) цикла на этом завершается; если же оно выполнено, то выполняется тело цикла и опять проверяется условие повторения команд тела цикла.

Пример. Пусть необходимо находить сумму всех нечетных элементов натурального ряда чисел до тех пор, пока эта сумма не превысит значение n. Слагаемое, при котором эта сумма превысит n – включать в сумму.

"Забудем" временно чисто математическое решение этой задачи – с использованием суммы арифметической прогрессии с шагом 2. Алгоритмпрограмма) имеет вид

Program Summa;

Uses Crt; { подключение библиотеки ввода/вывода на экран "в звуке и цвете"}

Var i, n, s: real;

{ для ряда чисел 1, 3, 5, …, }

{ найти и выдать сумму s всех первых чисел ряда, для которых впервые s > n }

Begin

ClrScr; { команда очистки экрана (от данных предыдущей задачи) }

ReadLn (n); { ввод входного параметра }

s:=1; { начальное значение суммы до входа в цикл }

i:=1; { количество просуммированных чисел в начале }

while (s<=n) do { заголовок цикла (проверка условия выхода из цикла) }

begin

i:=i+2; { находим новое слагаемое }

s:=s+i { добавили к предыдущему значению суммы новое слагаемое }

end;

WriteLn (‘Вычисленная сумма равна ’, s); { вывод результата }

End.

Вторая форма повторения – цикл типа "до" (for), которая имеет вид

for <переменная> := <начальное значение переменной> to <конечное ее значение> do

<команда>;

или

for <переменная> := <начальное значение переменной> to <конечное ее значение> do

begin

<повторяемая команда номер 1>;

<повторяемая команда номер 2>;

. . .

<повторяемая команда номер N>

end;.

Здесь <переменная> – имя, идентификатор пересчитываемой переменной.

Ключевые слова Паскаля – for (для), to (к).

Этот цикл выполняется по правилу: для начального значения переменной выполняются команды тела цикла по порядку и затем проверяется, превысило ли текущее значение переменной ее заданного конечного значения; если превысило – цикл заканчивается, иначе значение переменной увеличивается на единицу и снова повторяется тело цикла и т.д.

Пример. Необходимо вычислить среднюю стоимость единицы всех n видов товаров (единица измерения – одна и та же, например, тонна), если стоимость единицы каждого товара увеличивается на 10, а наименьшая стоимость единицы товара равна 2. Если "забыть" временно лучшее, "чисто математическое" решение этой задачи, то алгоритм будет иметь вид

Program ST;

Uses Crt { подключение библиотеки ввода/вывода на экран "в звуке и цвете"}

Var i, n, s: real;

{ стоимость единицы товара дается рядом n чисел вида: 2, 12, 22, 32, … }

{ найти и выдать среднюю стоимость s всех n товаров s }

Begin

ClrScr { команда очистки экрана (от данных предыдущей задачи) }

ReadLn (n); { ввод входного параметра }

s:=0; { начальное значение суммы до входа в цикл }

x:=2; { начальное значение стоимости товара – стоимость первого товара }

for i:=1 to n do { заголовок цикла (проверка условия выхода из цикла) }

begin

s:=s+x; { находим новую сумму товаров }

x:=x+10 { находим стоимость следующего товара }

end;

WriteLn (‘Вычисленная средняя стоимость товаров равна ’, s/n, f: 5:5); { вывод результата }

End.

Рассмотрим примеры алгоритмизации (программирования) задач на языке Паскаль.

Пример. Составим алгоритм вычисления факториала заданного натурального числа n, то есть произведения n! = 1 • 2 • 3 • … • (n – 1)•n c использованием рекуррентной формулы n! = (n – 1)! • n. Опишем метод решения. Для этого заметим цепочку справедливых равенств:

1! = 1, 2! = 1 • 2 = 1! • 2, 3! = 1 • 2 • 3 = 2! • 3, …, m ! =1 • 2 • 3 • … • (m – 1)•m = (m – 1)! •m.

Следовательно, для вычисления факториала m! необходимо факториал (m – 1)! домножить на m, где m = 1, 2, …, n. Программа на Паскале имеет вид

Program Factorial;

Uses Crt;

Var n, f, i: integer;

{ дано натуральное число n }

{ найти и выдать произведение всех натуральных чисел до n включительно }

Begin

ClrScr;

WriteLn('Введите число n : '); { приглашение к вводу входного параметра }

ReadLn(n); { ввод входного параметра }

f:=1; { начальному значению f присваивается 1, то есть 1!=1 }

for i:=1 to n do { цикл умножения текущего произведения f на текущее i }

f:=f*i; { предыдущее значение факториала умножаем на текущее значение i }

WriteLn('Полученный результат f : ',f); { вывод результата }

End.

Пример. Составим алгоритм перевода заданного десятичного натурального числа n в двоичную систему. Метод решения определяется процедурой перевода – последовательными делениями числа n на 2 и последующим сбором остатков от деления. Если последовательно выдавались с равные 1,0,1,0,0,1, то двоичное изображение c равно 100101. Алгоритм имеет вид

Program S10-S2;

Uses Crt;

Var n, a, i, c: integer;

{ дано десятичное натуральное число }

{ выдать последовательно цифры его двоичного изображения }

Begin

ClrScr;

WriteLn('Введите переводимое число : '); { приглашение к вводу входного параметра }

ReadLn(n); { ввод входного параметра }

WriteLn('Полученное двоичное число от конца :'); { выдача "шапки" к результату }

i:=0; { начинаем с младшего, нулевого разряда }

while (n>0) do { цикл деления числа и получаемых частных (пока делится) }

begin

i:=i+1; { переход к следующему делению }

c:=n mod 2; { находим очередной остаток от деления на 2}

n:=n div 2; { находим очередное частное от целочисленного деления }

write(c) { выдаем новую двоичную цифру }

end;

End.

Нисходящим проектированием алгоритмов, проектированием алгоритмов "сверху вниз" или методом последовательной (пошаговой) нисходящей разработки алгоритмов называется такой метод составления алгоритмов, когда исходная задача (алгоритм) разбивается на ряд вспомогательных подзадач (подалгоритмов), формулируемых и решаемых в терминах более простых и элементарных операций (процедур). Последние, в свою очередь, вновь разбиваются на более простые и элементарные, и так до тех пор, пока не дойдём до команд исполнителя. В терминах этих команд можно представить и выполнить полученные на последнем шаге разбиений подалгоритмы (команд системы команд исполнителя).

Восходящий метод , наоборот, опираясь на некоторый, заранее определяемый корректный набор подалгоритмов, строит функционально завершенные подзадачи более общего назначения, от них переходит к более общим, и так далее, до тех пор, пока не дойдем до уровня, на котором можно записать решение поставленной задачи. Этот метод известен как метод проектирования "снизу вверх".

Структурные принципы алгоритмизации (структурные методы алгоритмизации) – это принципы формирования алгоритмов из базовых структурных алгоритмических единиц (следование, ветвление, повторение), используя их последовательное соединение или вложение друг в друга с соблюдением определённых правил, гарантирующих читабельность и исполняемость алгоритма сверху вниз и последовательно.

Структурированный алгоритм – это алгоритм, представленный как следования и вложения базовых алгоритмических структур. У структурированного алгоритма статическое состояние (до актуализации алгоритма) и динамическое состояние (после актуализации) имеют одинаковую логическую структуру, которая прослеживается сверху вниз ("как читается, так и исполняется"). При структурированной разработке алгоритмов правильность алгоритма можно проследить на каждом этапе его построения и выполнения.

Теорема (о структурировании). Любой алгоритм может быть эквивалентно представлен структурированным алгоритмом, состоящим из базовых алгоритмических структур.

Одним из широко используемых методов проектирования и разработки алгоритмов (программ) является модульный метод (модульная технология).

Модуль – это некоторый алгоритм или некоторый его блок, имеющий конкретное наименование, по которому его можно выделить и актуализировать. Иногда модуль называется вспомогательным алгоритмом, хотя все алгоритмы носят вспомогательный характер. Это название имеет смысл, когда рассматривается динамическое состояние алгоритма; в этом случае можно назвать вспомогательным любой алгоритм, используемый данным в качестве блока (составной части) тела этого динамического алгоритма. Используют и другое название модуля – подалгоритм. В программировании используются синонимы – процедура, подпрограмма.

Свойства модулей:

функциональная целостность и завершенность (каждый модуль реализует одну функцию, но реализует хорошо и полностью);
автономность и независимость от других модулей (независимость работы модуля-преемника от работы модуля-предшественника; при этом их связь осуществляется только на уровне передачи/приема параметров и управления);
эволюционируемость (развиваемость);
открытость для пользователей и разработчиков (для модернизации и использования);
корректность и надежность;
ссылка на тело модуля происходит только по имени модуля, то есть вызов и актуализация модуля возможны только через его заголовок.

Свойства (преимущества) модульного проектирования алгоритмов:

возможность разработки алгоритма большого объема (алгоритмического комплекса) различными исполнителями;
возможность создания и ведения библиотеки наиболее часто используемых алгоритмов (подалгоритмов);
облегчение тестирования алгоритмов и обоснования их правильности ;
упрощение проектирования и модификации алгоритмов ;
уменьшение сложности разработки (проектирования) алгоритмов (или комплексов алгоритмов);
наблюдаемость вычислительного процесса при реализации алгоритмов.

Тестирование алгоритма – это проверка правильности или неправильности работы алгоритма на специально заданных тестах или тестовых примерах – задачах с известными входными данными и результатами (иногда достаточны их приближения). Тестовый набор должен быть минимальным и полным, то есть обеспечивающим проверку каждого отдельного типа наборов входных данных, особенно исключительных случаев.

Пример. Для задачи решения квадратного уравнения ax² + bx + c = 0 такими исключительными случаями, например, будут: 1) a = b = c = 0; 2) a = 0, b, c – отличны от нуля; 3) D = b² – 4ac < 0 и др.

Тестирование алгоритма не может дать полной (100%-ой) гарантии правильности алгоритма для всех возможных наборов входных данных, особенно для достаточно сложных алгоритмов.

Полную гарантию правильности алгоритма может дать описание работы и результатов алгоритма с помощью системы аксиом и правил вывода или верификация алгоритма.

Пример. Составим алгоритм нахождения числа всех различных двоичных сообщений (двоичных последовательностей) длины n битов, используя при этом не более одной операции умножения, и докажем правильность этого алгоритма. Вначале найдем число всех таких сообщений. Число двоичных сообщений длины 1 равно 2 = 2¹ (это "0" и "1"), длины 2 равно 4 = 2² ("00", "01", "10", "11"). Отправляясь от этих частных фактов, методом математической индукции докажем, что число различных сообщений длины n равно 2ⁿ . Этот индуктивный вывод докажет правильность алгоритма.

Пусть это наше утверждение верно для n = k. Тогда для n = k + 1 получаем, что добавление каждого бита (0 или 1) к любому из 2^k сообщений длины k приведет к увеличению числа сообщений в 2 раза, то есть их число будет равно 2 x 2^k = 2^k+1 , что и доказывает наше индуктивное предположение.

Составим теперь алгоритм вычисления числа x = 2ⁿ с использованием операции умножения только один раз.

Прологарифмируем последнее равенство. Получим ln(x) = ln(2ⁿ) = n ln(2) .

Используя равенство exp(ln(x)) = x, получим, что exp(ln(x)) = x = exp(n ln(2)).

Остается теперь записать простейший алгоритм вычисления числа x.

Program Power;

Uses Crt;

Var x: real;

n: integer;

Begin

ClrScr;

WriteLn('Введите длину в битах n ='); { приглашение к вводу входного параметра }

ReadLn(n); { ввод входного параметра }

x:=exp(n*ln(2)); { вычисление степени }

WriteLn('количество сообщений равно: ', int(x+0.5)); { вывод х с округлением }

End.

Для несложных алгоритмов грамотный подбор тестов и полное тестирование может дать полную картину работоспособности (неработоспособности).

Трассировка – это метод пошаговой фиксации динамического состояния алгоритма на некотором тесте. Часто осуществляется с помощью трассировочных таблиц, в которых каждая строка соответствует определённому состоянию алгоритма, а столбец – определённому состоянию параметров алгоритма (входных, выходных и промежуточных). Трассировка облегчает отладку и понимание алгоритма.

Процесс поиска и исправления (явных или неявных) ошибок в алгоритме называется отладкой алгоритма.

Некоторые (скрытые, труднообнаруживаемые) ошибки в сложных программных комплексах могут выявиться только в процессе их эксплуатации, на последнем этапе поиска и исправления ошибок – этапе сопровождения. На этом этапе также уточняют и улучшают документацию, обучают персонал использованию алгоритма (программы).

Пример. Определим функцию фрагмента алгоритма вида на тесте n=2; x[1]=4; x[2]=9:

k:=1;

s:=x[1];

for i:=1 to n

if (s
then begin

s:=x[i]

k:=i

end;

writeln (k);

Если выписать трассировочную таблицу вида

i	S	x[i]	K	s	i<=n
1	4	4	1	Нет	Да
2	4	9	2	Да	Да
3	—	—	—	—	Нет

то функция алгоритма становится более понятной – эта функция состоит в нахождении индекса максимального элемента ряда.

В заключение данного раздела приведем общую структуру алгоритмического обеспечения. Критерии, по которым алгоритмы могут быть классифицированы, бывают разными, поэтому предлагаемая ниже схема отражает основные элементы структуры и в некоторых случаях является условной, в том смысле, что блоки приведенной на рис. 9.1 структуры могут "перекрываться".

Blog

Информатика. Лекции. Краткая история компьютерной техники Первые компьютеры: Z3, Colossus, eniac

Содержание