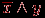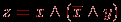Информатика. Лекции. Краткая история компьютерной техники Первые компьютеры: Z3, Colossus, eniac
| Вид материала | Лекции |
СодержаниеОсновы математической логики |
- Лекция Развитие компьютерной техники, 430.69kb.
- 1. Что такое информатика?, 205.32kb.
- Положение о проведении Всероссийского игрового конкурса «Кит компьютеры, информатика,, 59.05kb.
- Учебной дисциплины «Компьютерная графика» для направления 010400 «Прикладная математика, 36.03kb.
- Урок подготавливается и проводится учителем информатики совместно с учителем предметником, 138.11kb.
- Врассказе «Краткая история парикмахерского дела», 191.64kb.
- Передача информации между компьютерами существует, наверное, с самого момента возникновения, 65.58kb.
- Характеристика предмета «Радиоприемные устройства», взаимосвязь с другими, 3189.29kb.
- Реферат по информатике История вычислительной техники, 158.06kb.
- Общие принципы построения вычислительных сетей, 1480.56kb.
Основы математической логики Информатика, как было рассмотрено выше, изучает знаковые (алфавитные) системы. Алгебра – наиболее адекватный математический аппарат описания действий в них, поэтому алгебраический аппарат наилучшим образом подходит для описания информационных систем общей природы, отвлеченно от их предметной направленности. Информационные процессы хорошо формализуются с помощью различных алгебраических структур. Алгеброй A называется некоторая совокупность определенных элементов X, с заданными над ними определенными операциями f (часто определяемые по сходству с операциями сложения и умножения чисел), которые удовлетворяют определенным свойствам – аксиомам алгебры . Операция f называется n-местной, если она связывает n операндов (объектов – участников этой операции). Совокупность операций алгебры A называется ее сигнатурой , а совокупность элементов алгебры – носителем алгебры. Утверждение (высказывательная форма) – основная единица, неделимая с точки зрения отражения смысла информации (семантики). Высказывание – некоторое повествовательное утверждение, про которое можно однозначно сказать ("сразу посмотрев на него"), истинно оно или ложно. Эти два значения всевозможных высказываний обозначаются "истина" и "ложь", "true" и "fаlse" или "1" и "0". Переменная, значениями которой могут быть лишь значения "1" или "0", называется логической переменной или булевой переменной. Пример. Рассмотрим словосочетания:
Высказывание должно быть однозначно истинным или однозначно ложным, поэтому высказываниями являются только утверждения 1), 4), 6). Пример. Не является высказыванием и "парадокс лжеца" (Эвбулид, учитель Демосфена, около 350 лет до н.э.): "То, что я сейчас утверждаю, – ложно", ибо если оно истинно – то оно ложно, а если допустить, что оно ложно, то оно истинно. Это неопределенная высказывательная форма. Аналогичный пример принадлежит известному математику, логику Гёделю (1931 г.): "То, что утверждается в этом предложении, не может быть доказано". Если его можно опровергнуть, то его нельзя доказать, а если его можно опровергнуть, то его можно доказать. Предложения такого рода не могут быть доказаны или опровергнуты в пределах того языка (той теории, алгебры), с помощью которой они сформулированы. Известны многие подобные парадоксы. Рассматривая высказывания, мы не обращаем внимания на их внутреннюю структуру и можем разлагать их на структурные части, равно как и объединять их. Пример. Построим из ниже заданных простых высказываний составные, сложные высказывания, принимающие значение "истина", "ложь":
Истинным будет, например, сложное высказывание: "Зима – холодное время года и зимой носят пальто", а ложным будет, например, высказывание: "Некоторые ходят в пальто, поэтому на улице зима". Придумайте другие примеры. Предикат – высказывательная форма с логическими переменными (множество значений этих переменных вполне определено), имеющая смысл при любых допустимых значениях этих переменных. Количество переменных в записи предиката называется его местностью. Простые высказывания или предикаты не зависят от других высказываний или предикатов ("не разбиваемы на более простые"), а сложные – зависит хотя бы от двух простых. Пример. Выражение "х = у" – предикат, "х > 5" – предикат, а "7 > 5" – высказывание. Утверждение "Хорошо" не является высказыванием, утверждение "Оценка студента А по информатике – хорошая" – простое высказывание, утверждение "Вчера была ясная погода, я был вчера на рыбалке" – сложное высказывание, состоящее из двух простых. Логической (булевой) функцией f(х) называется некоторая функциональная зависимость, в которой аргумент х – логическая переменная с заданным множеством изменений аргумента, а значения функции f(x) берутся из двухэлементного множества R(f) = {1,0}. Пример. Заданы предикаты вида р = "число х делится нацело на 3" и q = "у – день недели". Найдем множество истинности предикатов р и q, если 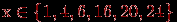 , , 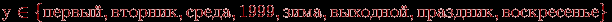 . Получаем, что . Получаем, что 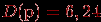 , , 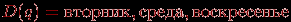 . . Множество логических переменных 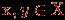 с определенными над ним операциями: с определенными над ним операциями: 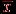 – отрицания или инверсии, – отрицания или инверсии, 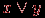 – логического сложения или дизъюнкции , – логического сложения или дизъюнкции , 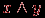 – логического умножения или конъюнкции называется алгеброй предикатов (и высказываний) , если эти операции удовлетворяют следующим аксиомам: – логического умножения или конъюнкции называется алгеброй предикатов (и высказываний) , если эти операции удовлетворяют следующим аксиомам:
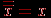
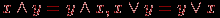
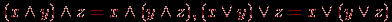
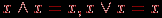
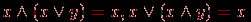
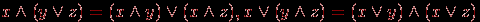


 Из этих аксиом следует ряд полезных соотношений, например, 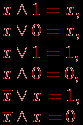 Три базовые операции алгебры предикатов определяются таблицей их значений, так как в алгебре предикатов из-за дискретности значений логических функций часто используется табличная форма задания функции. Булеву функцию n переменных можно полностью определить таблицей из 2n строк. Итак, эти операции определяются совмещенной таблицей значений вида
Такая таблица всех значений некоторой логической функции называется таблицей истинности этой функции. Пример. Составим таблицу истинности функции  . Эта таблица имеет вид . Эта таблица имеет вид
Следовательно, функция тождественно-истинна. Это можно было доказать (проверить) и с помощью аксиом: 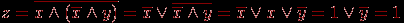 Пример. Заполним таблицу истинности трехместной логической функции  . Эта таблица имеет вид . Эта таблица имеет вид
|