Информатика. Лекции. Краткая история компьютерной техники Первые компьютеры: Z3, Colossus, eniac
| Вид материала | Лекции |
СодержаниеНорберт Винер Клод Шеннон Загадка памятника пионеру информации Системы счисления и действия в них Основание системы |
- Лекция Развитие компьютерной техники, 430.69kb.
- 1. Что такое информатика?, 205.32kb.
- Положение о проведении Всероссийского игрового конкурса «Кит компьютеры, информатика,, 59.05kb.
- Учебной дисциплины «Компьютерная графика» для направления 010400 «Прикладная математика, 36.03kb.
- Урок подготавливается и проводится учителем информатики совместно с учителем предметником, 138.11kb.
- Врассказе «Краткая история парикмахерского дела», 191.64kb.
- Передача информации между компьютерами существует, наверное, с самого момента возникновения, 65.58kb.
- Характеристика предмета «Радиоприемные устройства», взаимосвязь с другими, 3189.29kb.
- Реферат по информатике История вычислительной техники, 158.06kb.
- Общие принципы построения вычислительных сетей, 1480.56kb.
Интересные факты Норберт Винер «Отец кибернетики» Норберт Винер родился 26 ноября 1894 годв а Колумбии, США. Родители Норберта, были выходцами из России. Отец Норберта, Лео Винер, был профессором славянских языков и литературы Гарвардского университета. С четырех лет Норберт научился читать и почти с этого же возраста стал увлекаться научной литературой самого различного характера. К семи года у Норберта уже был опыт чтения книг Дарвина, Кингли, Шарко и других. Отец разработал для маленького Норберта весьма напряженную программу домашнего обучения: мальчик должен был изучать различные языки и заниматься математикой. После окончания в 1906 году начальной школы Норберт поступил в Тафтс-колледж, который он окончил в 1909 году и получил звание бакалавра. После этого Норберт слушает лекции в Гарвардском (1909–1913 года) и Корнуэльском (1910 год) университетах. В возрасте 18 лет Винер защити в Гарвардском университете диссертацию по философии математики на степень доктора философии. После окончания университетского курса Гарвардский университет предоставил Н. Винеру стипендию для поездки за границу. Н. Винер использовал эту возможность, чтобы побывать в Англии — в Кембридже (1913–1915 года) и в Германии — в Геттингене (1914 год). В 1919 году Винер получил должность ассистента на кафедре математики Массачусетского института. В этот период им были написаны статьи о броуновском движении, в которых была раскрыта возможность совместного использования лебеговой техники интегрирования и статистической физики Гиббса. В период в 1919 по 1932 год Винером был написан ряд статей по теории банаховых пространств, теории потенциала, теории функций действительного переменного и по другим проблемам различных разделов математик и физики. Во время второй мировой войны Винер под руководством В. Буша участвовал в разработке и применении электронной вычислительной машины для баллистических расчетов. Задачи управления артиллерийским огнем заставляют Винера заняться теоретическими и экспериментальными исследованиями, непосредственно связанными с теорией автоматического управления. К этому моменту у Винера уже возникли соображения об общности принципа отрицательной обратной связи как для систем автоматического регулирования, так и для живых организмов. Эти идеи, поддержанные нейрофизиологом доктором Розенблютом, явились началом формирования кибернетической концепции Винера, которая была позднее изложена в книгах «Кибернетика» и «Кибернетика и общество». Под непосредственным влиянием идей Винера о сущности информации и энтропии и их роли в организованных системах развивались также работы, приведшие к созданию теории информации. Кроме работ по кибернетике, Н. Винеру принадлежат фундаментальные исследования по теории вероятностей и по теории интеграла Фурье и его приложений. Умер Норберт Винер 19 марта 1964 года. Клод Шеннон Клод Шеннон родился в 1916 году в небольшом американском городке. Став студентом Мичиганского университета, Шеннон специализировался одновременно и на математике, и на электротехнике. По каждому из направлений он получил по одному диплому бакалавра. Как известно, мир тесен. И если с В. Бушем Винер работал во время второй мировой войны, то Клод Шеннон еще в 30-е годы работал и учился под его началом. В конце 20-х годов прошлого века Вэннивер Буш, магистр Массачусетского технологического института, приступил к созданию своего дифференциального анализатора — механического устройства, предназначенного для решения сложных дифференциальных уравнений. Анализатор был построен в 1930 году, а оператором на этом устройстве работал Клод Шеннон. Одновременно с работой на анализаторе Шеннон начал работу над диссертацией, тему которой ему подсказал сам Вэннивер Буш, предложивший изучить логическую схему дифференциального анализатора. Шеннон, который, в отличие от многих инженеров того времени, был хорошо знаком с двоичной булевой алгеброй, доказал в диссертации, которую защитил в 1940 году, что работу переключателей и реле — элементная база дифференциального анализатора Буша — можно моделировать посредством булевой алгебры. «Просто так случилось, что никто другой не был знаком с этими обеими областями одновременно», — комментировал позднее свое открытие Шеннон. Хотя, стоит сказать, не один Шеннон смог сделать подобное открытие. Русский ученый В.И. Шестаков в тоже самое время пришел к аналогичным выводам, как это часто бывает в истории науки, когда два ученых независимо друг от друга формулируют одни и те же результаты (вспомним тех же Котельникова и Найквиста). В 1941 году Клод Шеннон поступил в Bell Laboratories и в годы войны занимался разработкой криптографических систем, что позднее помогло ему в работах по созданию методов кодирования и коррекции ошибок. Тогда-то Шеннон и начал размышлять над идеями, которые позднее вылились в теорию информации. А исходным пунктом в его размышлениях явилась проблема улучшения передачи информации по телеграфному или телефонному каналу, зашумленному сторонними электрическими сигналами. В 1948 году Клод Шеннон выпустил работу под названием «Математическая теория связи», которую позднее назвали «величайшей работой в анналах технической мысли», а его интуицию первооткрывателя по значимости сравнили с работами Эйнштейна. Сам Шеннон в ответ заметил: «Я всегда следовал своим интересам, не думая ни о том, во что они мне обойдутся, ни об их ценности для мира. Я потратил уйму времени на совершенно бесполезные вещи». В 50-х годах прошлого века Шеннон сформулировал теорему о пропускной способности зашумленных каналов связи, опередив свое время на многие годы и создав предпосылки для развития «информационного века». Теория Шеннона привела нас из мира аналоговых средств сообщения в мир цифровых коммуникаций, который мы знаем сейчас. Без Клода Шеннона не было бы спутниковых коммуникаций, сотовых телефонов, электронной почты, компакт-дисков, цифрового телевидения. Но не было бы и маленькой механической мыши, которая до сих пор сидит в лабиринте на полу в комнате Элизабет Шеннон. Загадка памятника пионеру информации При поддержке Общества теории информации IEEE Information Theory Society шесть памятников Клоду Шеннону (Claude Elwood Shannon) работы Евгения Дауба (Eugene Daub) были установлены в шести различных местах Соединенных Штатов:
Открыты они были также в разное время. Одно из самых «массовых» открытий было 9 ноября 2001 года в Мичиганском Университете, на котором присутствовали около двухсот членов Общества Мичиганского Университета. Однако, пожалуй самое «важное» из них произошло годом раньше, 6 октября 2000 года в родном городе Клода Шеннона — Гейлорде (Gaylord, Michigan). Памятник, который открыли жена Клода Шеннона Элизабет и скульптор Евгений Дауб, установили в Парке Шеннона, который ранее заложили в честь знаменитого горожанина. В этом же парке стоит и дом, который построил отец Клода Шеннона, и в котором тот провел свое детство. Отличительной особенностью статуи является лист бумаги, который бронзовый Шеннон держит в своей левой руке. На этом листке написана его знаменитая формула: C = W log((P+N)/N). Наличие нескольких памятников одного скульптора, установленных в разных местах и открытых в разное время, привело к чудовищной неразберихе в информационных кругах. То, что знаменитый «бронзовый листок бумаги» «переложили» в другую руку — меньшая из встречающихся неточностей. Самой же вопиющей и просто ужасающей ошибкой, при этом и самой часто встречающейся, стало распространенное выражение «покрывало с памятника сняла вдова», хотя на момент открытия — 6 октября 2000 года — Клод Шеннон еще был жив! К сожалению, как это часто бывает с по-настоящему великими людьми, Умер Клод Шеннон всеми забытый в массачусетском доме для престарелых 1 марта 2001 года после продолжительной болезни в возрасте 84 лет. Но все же достаточно поздно для того, чтобы не спешить называть его жену «вдовой». Системы счисления и действия в них Алфавит Х из р символов и правила записи (изображения) и обработки чисел с помощью символов этого алфавита называются системой счисления (нумерацией) с основанием р. Число х в системе с основанием р обозначается как (х)р или хр . Любая система счисления – это система кодирования числовых величин (количеств), позволяющая выполнять операции кодирования и декодирования, то есть по любой количественной величине однозначно находить его кодовое представление и по любой кодовой записи – восстанавливать соответствующую ей числовую величину. Все системы счисления строятся по общему принципу: определяется величина р – основание системы, а любое число х записывается в виде комбинации степеней веса р от 0-й до n-й степени следующим образом: (x)10 = xnpn + xn–1pn–1 + ... + x1p1 + x0p0 . Наиболее используемые в информатике системы счисления, кроме, естественно, десятичной, – это: 1) двоичная, над алфавитом Х = {0,1}; 2) восьмеричная, над Х = {0, 1, 2, 3, 4, 5, 6, 7}; 3) шестнадцатеричная, над Х = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, Е, F}, где символы А, В, С, D, Е, F имеют, соответственно, десятичные веса 10, 11, 12, 13, 14, 15. Пример. 11012 = 1 x 23 + 1 x 22 + 0 x 21 + 1 x 20 = 8 + 4 + 1 = 1310 , 1578 = 1 x 82 + 5 x 81 + 7 x 80 = 64 + 40 + 7 = 11110 , A6F16 = 10 x 256 + 6 x 16 + 15 x 1 = 267110 . В большинстве систем счисления вес цифры (или символа алфавита) зависит от ее места в записи числа или слова. Такая система счисления называется позиционной ; в противном случае система называется непозиционной . Пример. Непозиционная система – древняя римская система записи чисел с алфавитом вида Х={I (1), V (5), Х (10), L (50), С (100), D (500), М (1000)}, где в скобках указаны веса символов (не зависящие от позиции символа). Примеры римских чисел (в скобках – обычные десятичные эквиваленты): III (3), IV (4), V (5), VI (6), IX (9), XI (11), DCL (650). Запись числа в этой системе получается двусторонней конкатенацией, причем правая конкатенация ассоциируется с добавлением, а левая конкатенация – с убавлением (например, IV и VI). Поразрядное же выполнение арифметических операций не имеет места (например, XIV + IV = XVIII ). Для изображения десятичных дробей используется подобная формула разложения по степеням основания. Пример. 110,0012 = 1x22 + 1 x 21 + 0 x 20 + 0 x 2-1 + 0 x 2-2 + 1 x 2-3 = 6,12510 ; A,B16 = A x 160 + B x 16-1 = 10 x 1 + 11 x 0,0625 = 10,687510 . Процедура перевода десятичных чисел в р-ную систему счисления:
Пример. Найти: 12,810 = ?2 . Решение:
Пример. Найдем 29,2510 = ?8 . Решение имеет вид 1) 2910 = 358 ; 2) 0,2510 = 0,28 ; 3) 29,2510 = 35,28 . Пример. Найдем 79,2610 = ?16 . Решение: 1) 7910 = 4F16 ; 2) 0,2610 = 0,4016 ; 3) 79,2610 = 4F,416 . При переводе дробной части мы ограничились нахождением двух значащих цифр после запятой, ибо перевод точно сделать невозможно. Для перевода из 2-ной в 8-ную и наоборот, из 2-ной в 16-ную и наоборот, из 8-ной в 16-ную и обратно, используется таблица следующего вида:
При переводе в 8-ную систему или из нее необходимо группировать в тройки биты, а при переводе в 16-ную или из нее – группировать их в четверки битов. Можно добавлять, если нужно, незначащие нули (слева от целой части и справа от мантиссы) или отбрасывать их. Пример. Рассмотрим переводы в смешанных системах.
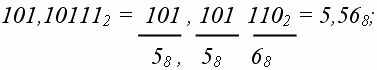
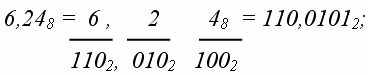
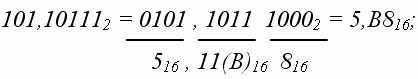
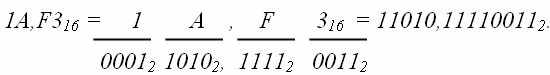 Сложение в двоичной системе счисления осуществляется по правилам 0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1, 1 + 1 = 210 = 102 (единица идет в старший разряд). Таблица вычитания в двоичной системе счисления имеет вид 0 – 0 = 0, 1 – 0 = 1, 1 – 1 = 0, 0 – 1 = 10 – 1 = 1 (единицу забираем у старшего разряда). Таблица умножения в двоичной системе счисления имеет вид 0 x 0 = 0, 0 x 1 = 0, 1 x 0 = 0, 1 x 1 = 1. Таблица деления в двоичной системе счисления имеет вид 0 : 0 = не определено, 1 : 0 = не определено, 0 : 1 = 0, 1 : 1 = 1. Обратным кодом числа в системе с основанием р называется число в этой системе, получаемое заменой цифры, символа в каждом разряде числа на его дополнение до максимальной цифры в системе (то есть до р – 1). Дополнительный код = обратный код + единица в младшем разряде. Пример.
01100  обратный код этого двоичного числа, обратный код этого двоичного числа, 01101  дополнительный код этого двоичного числа; дополнительный код этого двоичного числа;
321  дополнительный код; дополнительный код;
57  дополнительный код. дополнительный код. Вычитание с помощью дополнительного кода: найти дополнительный код вычитаемого такой же разрядности, как и уменьшаемое, и сложить этот код с уменьшаемым. Результатом вычитания будет полученная сумма без учета старшего разряда (отбрасывается). Пример. Выполним вычитание напрямую и через сложение (через дополнительный код): 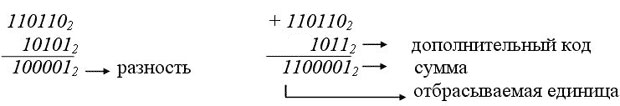 Целые числа в математике и их аналоги в n-разрядных арифметиках тождественны (по количеству) в рамках их представления с этой разрядностью. При этом можно отметить основные отличия представления чисел в поле памяти человека и в поле памяти n-разрядной арифметики:
С точки зрения обычной арифметики, например, в интервале (–1; 1) имеется бесконечное множество "плотно" расположенных точек, причем в любой окрестности каждой такой точки имеется хотя бы одна точка из этого множества. Такую арифметику называют часто регулярной арифметикой. Машинная же арифметика имеет следующие особенности. Она нерегулярна – точки интервала сгущаются около нуля; кроме того, в этом интервале точка х "изолирована" – если взять любую ее окрестность (х – а; х + а), где а – число, которое не превосходит машинного нуля (наименьшего представимого в машине числа), то в этом интервале нет других точек (отличных от х). Говоря языком теории вероятности, плотности распределения чисел в регулярной и нерегулярной арифметике – различны, как, впрочем, плотности распределения целых и вещественных чисел в одной и той же арифметике. Множество вещественных чисел в машинной арифметике представляется как подмножество (определяемое разрядностью арифметики) множества рациональных чисел. Есть и другие особенности этих множеств (связанные, например, с выполнением операций), но указанные выше особенности – основные. Различия в представлении чисел в обычной и в машинной (n-разрядной) арифметике ограничивают как "математические" возможности компьютера, так и "компьютерные" возможности математики, использование математических методов, алгоритмов в компьютерах. Нужно всегда иметь в виду, что точность в теоретической математике – понятие абстрактное, и в практической математике может возникать иллюзия точности там, где ее на самом деле нет, – если нет корректной договоренности о пределах возможных значений неизбежных погрешностей в рамках рассматриваемых вычислительных ресурсов, например, трудоемкости и времени, а также не оговорена стратегия управления этой погрешностью. Так как диапазон n-разрядных чисел системы счисления с основанием p находится в пределах 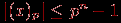 , то для представления дробных чисел этот диапазон еще снижается, поскольку часть разрядов необходимо отвести под изображение мантиссы. Таким образом, имеются так называемые "зоны нечувствительности" форм представления чисел в n-разрядных арифметиках. , то для представления дробных чисел этот диапазон еще снижается, поскольку часть разрядов необходимо отвести под изображение мантиссы. Таким образом, имеются так называемые "зоны нечувствительности" форм представления чисел в n-разрядных арифметиках. В 1937 году Конрадом Цузе для увеличения диапазона чисел, представимых в арифметике двоичных чисел, а также для повышения точности этого представления чисел было предложено представление чисел в плавающей, нормализованной форме – число x представляется в виде: 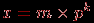 , где m – мантисса числа, k – целый порядок числа, , где m – мантисса числа, k – целый порядок числа, 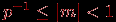 . . Пусть даны два числа: 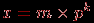 и и 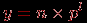 ( ( ). Тогда можно проверить, что результаты выполнения операций будут равны: ). Тогда можно проверить, что результаты выполнения операций будут равны: 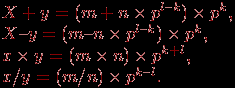 Если из n разрядов, отводимых под изображение чисел, m двоичных разрядов отвести под мантиссу, k – под порядок, один разряд – под знак числа и один разряд – под знак порядка (например, 0 – плюс, 1 – минус), то диапазон представимых в форме с плавающей запятой чисел резко увеличивается (m + k + 2 = n): 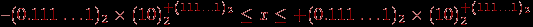 (многоточие соответствует k единицам). Числа, меньшие нижней границы положительных чисел и большие верхней границы отрицательных чисел, считаются равными нулю, не различаются между собой. Числа, большие верхней границы положительных чисел, полагаются равными положительной бесконечности (меньшие нижней границы отрицательных – отрицательной бесконечности). Сравнение двух разных по величине чисел в арифметике с ограниченной разрядностью может поэтому приводить к неверному результату, как и сравнение двух равных в таких системах чисел с точки зрения математической. Такое представление очень удобно для хранения в ЭВМ, так как на самом деле необходимо хранить не само число, а его знак, мантиссу, порядок и знак порядка, и все операции с числами сводятся к операциям с этими объектами. Операции же с этими объектами просты: сравнение знаков, увеличение, уменьшение порядка, сложение мантисс, нормализация, то есть в конечном итоге сводятся к достаточно просто реализуемым операциям сдвига, выравнивания, сравнения разрядов. Пример. Вычислить наибольшее и наименьшее 5-разрядное целое число в системе счисления с основанием 3. Наибольшее целое n-разрядное число, которое возможно записать в системе счисления с основанием р, равно: 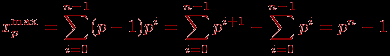 Наименьшее целое n-разрядное число в этой системе равно  Таким образом, в системе счисления с основанием 3 и числом разрядов 5 представим диапазон следующих чисел: 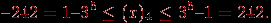 Формулам можно придать более компактный вид. Например, для двоичной системы 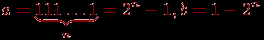 а в восьмеричной системе счисления эти числа 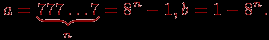 К "неудобствам" этой формы представления чисел можно отнести возможность возникновения следующих "особо опасных" ситуаций:
Есть много различных способов (часто искусственных) формирования систем чисел. Пример. В факториальной системе счисления целые числа записывают линейной комбинацией факториалов, например,  . Эта система (условно) позиционна. Так как 0! = 1! = 1, то два младших разряда n-разрядного числа . Эта система (условно) позиционна. Так как 0! = 1! = 1, то два младших разряда n-разрядного числа  в разложении этого числа по факториалам представимы как в разложении этого числа по факториалам представимы как  и поэтому веса этих разрядов не зависят от позиции (поэтому при и поэтому веса этих разрядов не зависят от позиции (поэтому при  это число можно считать непозиционным лишь условно). Формула перевода из факториальной системы счисления в десятичную систему: это число можно считать непозиционным лишь условно). Формула перевода из факториальной системы счисления в десятичную систему: 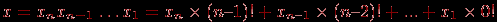 История развития систем счисления достаточно интересна. Приведем лишь некоторые факты. Счет вначале велся с помощью пальцев рук (пятерками и затем – десятками). В некоторых странах сохранился счет с основанием 12 (например, Великобритания – 12 шиллингов) и 20 (например, Франция – "quatre–vingts" или "четыре-двадцать" то есть 80; у древних адыгов счет велся аналогично: "тощIищ", то есть "двадцать-три" – 60) и др. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 , располагающееся на числовой оси равномерно и плотно, представляется в n-разрядной арифметике множеством с неравномерной плотностью (сгущение у нуля и сжатость со стороны меньших чисел);
, располагающееся на числовой оси равномерно и плотно, представляется в n-разрядной арифметике множеством с неравномерной плотностью (сгущение у нуля и сжатость со стороны меньших чисел);