Информатика. Лекции. Краткая история компьютерной техники Первые компьютеры: Z3, Colossus, eniac

Вид материала

Содержание

Базовые алгоритмические основы
Обычная запись

Подобный материал:

1 ... 8 9 10 11 12 13 14 15 ... 19

Пример. Изобразим графически множество истинности двухместного предиката вида р(х,у) = "модуль числа х равен модулю числа у", если задана область изменения аргументов:

. Имеем соотношение

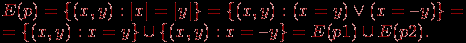
Смысл предикатов р1(х,у) и р2(х,у) очевиден. Множество изображается графиком функции y=|x|, который дан на рис. 5.1:

Рис. 5.1. График функции y = |x|

Кроме указанных трех базовых операций можно с их помощью ввести еще следующие важные операции алгебры предикатов (можно их назвать небазовыми операциями):

импликации: ;
эквиваленции: .

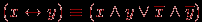Операции импликации и эквиваленции, хотя и являются часто используемыми, но не базовые, ибо они определяемы через три введенные выше базовые операции. Нетрудно определить их таблицы истинности (проделайте это самостоятельно с помощью правых частей приведенных равенств).

При выполнении логических операций в компьютере они сводятся к поразрядному сравнению битовых комбинаций. Эти операции достаточно быстро (аппаратно) выполняемы, так как сводятся к выяснению совпадения или несовпадения битов.

В логических формулах определено старшинство операций, например: скобки, отрицание, конъюнкция, дизъюнкция (остальные, небазовые операции пока не учитываем).

Всегда истинные формулы называют тавтологиями .

Логические функции эквивалентны, если совпадают их таблицы истинности, то есть совпадают области определения и значения, а также сами значения функции при одних и тех же наборах переменных из числа всех допустимых значений. Если это совпадение происходит на части множества допустимых значений, то формулы называются эквивалентными лишь на этой части (на этом подмножестве).

Задача упрощения логического выражения состоит в преобразовании его к более простому (по числу переменных, операций или операндов) эквивалентному выражению. Наиболее простой вид получается при сведении функции к постоянной – 1 (истина) или 0 (ложь).

Пример. Упростим:

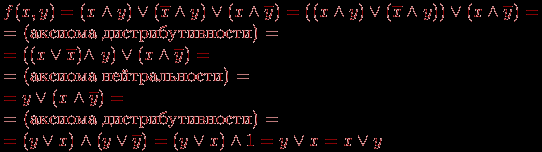
Задача доказательства равенства двух логических выражений (функций) состоит в установлении эквивалентности этих функций на некотором множестве значений всех переменных, входящих в данную функцию.

Пример. Докажем равенство логических выражений:

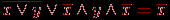Используя аксиомы алгебры предикатов, получаем равенства

Левая часть равенства приведена к правой части, то есть данное равенство доказано полностью.

Такие задачи решаются с помощью аксиом алгебры предикатов одним из следующих способов:

правая часть равенства приводится к левой части;
левая часть равенства приводится к правой части;
обе части равенства приводятся к третьему выражению.

Логические функции позволяют эффективно решать так называемые инфологические (информационно-логические) задачи, доказывать утверждения.

Информационно-логическая (инфологическая) задача – это задача, в которой необходимо установить некоторые информационные или логические связи и сделать необходимые причинно-следственные логические выводы. Эти задачи возникают в различных областях и часто являются плохо формализованными и структурированными. Их нужно хорошо формализовать и структурировать. Насколько хорошо будет возможно это сделать – настолько хорошо и полно будет решена рассматриваемая проблема или задача. Рассмотрим пример информационно-логической задачи (например, решаемой следователем, знакомым с алгеброй предикатов).

Пример. Брауну, Джонсу и Смиту предъявлено обвинение в соучастии в ограблении банка. В ходе следствия Браун сказал, что преступники были на синем "Бьюике", Джонс сказал, что это был черный "Крайслер", Смит утверждал, что это был "Форд", но не синий. Каждый указал неправильно либо марку, либо цвет автомобиля. Определим истинный цвет и истинную марку автомобиля. Рассмотрим простые высказывания вида: х = "машина – синяя", у = "машина – Бьюик", z = "машина – черная", u = "машина – Крайслер", v = "машина – Форд". На их основе высказывание Брауна можно записать в виде сложного логического выражения вида

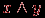, высказывание Джонса – в виде

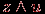, а высказывание Смита – в виде

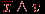. Так как в каждом из этих выражений одна из переменных принимает значение "истина", то истинны и дизъюнкции вида:

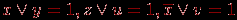. По определению конъюнкции,

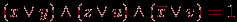. Это выражение мы взяли из-за однозначности равенства 1 конъюнкции и неоднозначности (многовариантности) его равенства нулю. Упростим выражение: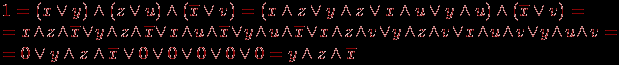

Мы использовали тот факт, что одновременно не могут быть истинными два высказывания относительно цвета или два высказывания относительно марки машины. Так как конъюнкция истинна только тогда, когда

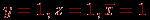, то заключаем, что автомобиль был черным "Бьюиком".

Законы алгебры высказываний и предикатов сходны с правилами, по которым человек делает умозаключения, доказывает, мыслит.

Пример. Операции конъюнкции, дизъюнкции, отрицания алгебры высказываний – аналоги союзов "и", "или", приставки "не", используемых (возможно, интуитивно) при выражении мысли человеком.

Чтобы переложить на ЭВМ работы мыслительного характера, эти правила необходимо строго сформулировать, формализовать. Это позволяет осуществить алгебра логики. Приведем некоторые аксиомы логики – науки, изучающей методы доказательства и опровержения утверждений.

Аксиома исключения третьего : либо имеет место высказывание, либо его отрицание.
Аксиома противоречия : высказывания и его отрицание не могут иметь места одновременно.
Аксиома двойного отрицания : двукратное отрицание какого-либо утверждения равносильно исходному утверждению.
Аксиома тождества : всякое высказывание тождественно самому себе.

Если высказывания x и y связаны друг с другом отношением

, то говорят, что высказывание y следует из высказывания x (или y – следствие x); если множество истинности Х высказывания х содержит множество истинности Y высказывания y, то высказывание x – условие, высказывание y – заключение, а само соотношение

– вывод.

Доказательство формальных математических утверждений (теорем) – последовательность корректных выводов, ведущих от условия к заключению. Алгебра логики помогает доказывать теоремы (дает общие подходы и методы доказательства).

Общий подход к доказательству теорем методом от противного, обратных и противоположных теорем можно формализовать с помощью алгебры логики.

Базовые алгоритмические основы

"Алгоритм" является базовым основополагающим понятием информатики, а алгоритмизация (программирование) – основным разделом курса информатики (ядром курса). Понятие алгоритма, как и понятие информации, точно определить невозможно. Поэтому встречаются самые разнообразные определения – от "наивно-интуитивных" ("алгоритм – это план решения задачи") до "строго формализованных" (нормальные алгоритмы Маркова).

В качестве рабочего определения алгоритма возьмем следующее определение.

Алгоритм – это упорядоченная совокупность точных (формализованных) и полных команд исполнителю алгоритма (человек, ЭВМ), задающих порядок и содержание действий, которые он должен выполнить для нахождения решения любой задачи из рассматриваемого класса задач.

Алгоритм удовлетворяет следующим основным свойствам:

Конечность (дискретность) команд и выполняемых по ним действий алгоритма.
Выполнимость в определенной операционной среде (в определенном классе исполнителей).
Результативность отдельных команд и всего алгоритма.
Применимость алгоритма ко всем возможным входным данным конкретного класса задач.
Определенность (детерминированность) команд и всего алгоритма для всех входных данных.
Формализованное, конструктивное описание (представление) команд алгоритма.
Минимальная полнота системы команд алгоритм.
Непротиворечивость любых команд алгоритма на любом наборе входных данных.

Любой алгоритм ориентирован на некоторый общий метод решения класса задач и представляет собой формализованную запись метода, процедуры.

Алгоритм, записанный на некотором алгоритмическом, формальном языке, состоит из заголовка алгоритма (описания параметров, спецификаций класса задач) и тела алгоритма (последовательности команд исполнителя, преобразующих входные параметры в выходные).

Для записи, исполнения, обмена и хранения алгоритмов существуют различные средства, языки, псевдокоды – блок-схемы, структурограммы (схемы Нэсси-Шнайдермана), Р-схемы, школьный алгоритмический язык (ШАЯ), различные языки программирования.

В качестве языка описания алгоритмов нами используется далее язык программирования Паскаль, так как он наиболее подходит для целей обучения и часто (обоснованно) используется в обучении.

На алгоритмическом языке Паскаль любой алгоритм простой (не модульной, не составной) структуры имеет следующий стандартный вид:

Program <имя (заголовок) алгоритма>;

Uses <список подключаемых библиотек, если они нужны>; { комментарии, если нужны }

Label <список меток (имен участков программ), если они нужны>; { комментарии }

Const <список констант (не изменяемых величин), если они нужны>; { комментарии }

Type <список имен и типов структур данных, если они нужны>; { комментарии }

Var <список имен и типов переменных, если они нужны>; { комментарии }

{ < условия задачи и применимости алгоритма > }

{ < цель составления и выполнения алгоритма > }

Begin

<команды ввода входных данных, если они нужны>; { комментарии }

<тело алгоритма (команды управления и преобразования алгоритма)>; { комментарии }

<команды вывода результатов (выходных данных), если они нужны>; { комментарии }

End.

Пример. Программа вычисления объема v правильного цилиндра с радиусом основания r и высотой h.

Program VСil;

Uses Crt { подключение библиотеки ввода/вывода на экран "в звуке и цвете" }

Const pi = 3.14;

Var r, h, v: real;

{ для правильного цилиндра с радиусом основания r и высотой h }

{ вычислить и выдать на экран значение его объема v }

Begin

ClrScr; { команда очистки экрана (от данных предыдущей задачи) }

ReadLn (r, h); { ввод входных параметров }

v:=pi*r*r*h; { вычисление объема по формуле для цилиндра }

WriteLn (‘Вычисленный объем цилиндра равен ’, v) { вывод результата }

End.

Приведем таблицу наиболее часто используемых в языке Паскаль функций и процедур.

Обычная запись	Паскаль
Квадрат числа х	sqr(x)
Корень квадратный из x	sqrt (x)
Модуль \|х\|	abs (x)
sin x	sin(x)
cos x	cos(x)
tg x	tg(x)
ctg x	ctg(x)
arcsin x	arcsin (x)
arccos x	arccos(x)
arctg x	arctg(x)
Натуральный логарифм ln x	ln(x)
Степень числа е = 2, 7... или е^x	exp(x)
Остаток от деления целого х на целое у	x mod y
Частное от деления целого х на целое y	x div y
Целая часть числа х (вещественного)	int(x)
Случайное число от 0 до х	rnd(x)
Длина текста х в символах	length (x)

Blog

Информатика. Лекции. Краткая история компьютерной техники Первые компьютеры: Z3, Colossus, eniac

Содержание