Магазины электрических ве­личин

• Рабочей программы дисциплины Электроэнергетические системы и сети по направлению подготовки, 21.71kb.
• Отчет по лабораторной работе должен содержать: наименование работы и номер, схемы, 365.83kb.
• Экзаменационные вопросы по курсу «Электротехника и электроника», 23.91kb.
• Бизнес-план магазина товаров для детей Содержание, 138.19kb.
• 1. Основные понятия и обозначения электрических величин и элементов электрических цепей., 277.03kb.
• Цифровой вольтметр щ-304, 137.06kb.
• Телемеханики, 26.01kb.
• Отдел метрологического обеспечения измерений электрических величин, 42.58kb.
• Курсовая работа по курсу «основы физических измерений», 226.86kb.
• Теория электрических цепей (часть, 63kb.

МОЛЕКУЛЯРНЫЙ ГЕНЕРАТОР, первый квант. генератор, в к-ром эл.-магн. колебания СВЧ генерировались за счёт вынужденных квант. перехо­дов молекул NH3 (см. Квантовая электроника). М. г. был создан в 1954 Н. Г. Басовым и А. М. Прохоровым (СССР) и независимо от них Ч. Таунсом, Дж. Гордоном и X. Цайгером (США). Оба варианта М. г. работали на пучке молекул аммиака NH3 (см. Молекулярные и атомные пучки) И генерировали эл.-магн. колебания с частотой 24840 МГц (=1,24 см). Молекулы NH3, обладающие элект­рич. дипольным моментом, пролетая через неоднородное электрич. поле, по-разному отклоняются этим полем в зависимости от их энергии (см. Штарка эффект). В первом М. г. сортирующая система представляла собой квадрупольный конденсатор, состоящий из четырёх параллельных стержней спец. формы, соединённых а — Квадрупольный конденсатор; б — кон­фигурация электрич. поля (стрелки — сило­вые линии). попарно с высоковольтным выпря­мителем (рис., а). Электрич. поле (рис., б) такого конденсатора неодно­родно и вызывает искривление траек­торий молекул, летящих вдоль его оси. Молекулы NH3, находящиеся в верх. энергетич. состоянии, откло­няются к оси конденсатора и попа­дают внутрь объёмного резонатора. Молекулы, находящиеся в ниж. энер­гетич. состоянии, отбрасываются в стороны. Попадая внутрь резонатора, возбуждённые молекулы излучают под воздействием эл.-магн. поля резона­тора, фотоны остаются внутри резона­тора, усиливая его поле и увеличивая вероятность вынужденного излучения для молекул, пролетающих позже (обратная связь). Если вероятность вынужденного излучения фотона больше, чем вероятность его погло­щения в стенках резонатора, то интен­сивность эл.-магн. поля резонатора на частоте перехода быстро возрастает за счёт внутр. энергии молекул. Воз­растание прекращается, когда поле в резонаторе достигает величины, при к-рой вероятность вынужденного ис­пускания становится столь большой, что за время пролёта резонатора успе­вает испустить фотон как раз поло­вина молекул пучка. При этом для пучка в целом вероятность поглоще­ния становится равной вероятности вынужденного испускания (насыще­ние). Мощность, генерируемая М. г. на пучке молекул NH3~10-8 Вт; ста­бильность частоты  колебаний /~10-7—10-11. Выли созданы М. г. и на др. дипольных молекулах, с  в диапазоне сантиметровых и мил­лиметровых волн. • Ораевский А. Н., Молекулярные генераторы, М., 1964. М. Е. Жаботинский. МОЛТЕРА ЭФФЕКТ, эмиссия эл-нов в вакуум из тонкого диэлектрич. слоя на проводящей подложке при на­личии сильного ' электрич. поля (106 В/см) в слое. Открыт амер. радио­инженером Л. Молтером (L. Malter) в 1936 в слое Al2O3+Cs2O на Al. Эмиссионный ток быстро растёт с рос­том анодного напряжения. М. э. обу­словлен наличием сильного электрич. поля в слое, что приводит к авто­электронной эмиссии из подложки в слой, к «разогреву» эл-нов и к удар­ной ионизации в основной толще слоя. Основное падение напряжения сосредоточивается вблизи подложки. В результате часть быстрых эл-нов вылетает в вакуум. В пористых слоях М. э. обусловлен также лавинной ударной ионизацией, развивающей­ся в порах; эл-ны вылетают преим. из пор. • См. лит. при ст. Электронная эмиссия. Б. С. Кульварская. МОЛЬ (моль, mol), ед. СИ кол-ва в-ва. В 1 М. содержится столько молекул (атомов, ионов или к.-л. др. структур­ных элементов в-ва), сколько атомов содержится в 0,012 кг 12С (нуклида углерода атомной массой 12), см. Авогадро постоянная. МОМЕНТ ИНЕРЦИИ, величина, ха­рактеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступат. движении. В механике различают М. и. осевые и центробежные. Осе­вым М. и. тела относительно оси z наз. величина, определяемая равенст­вом: 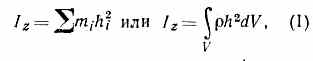где mi — массы точек тела, hi — их расстояния от оси z, a  — массовая плотность, V — объём тела. Вели­чина Iz явл. мерой инертности тела при его вращении вокруг оси (см. Вращательное движение). Осевой М. и. можно также выразить через линейную величину r, наз. радиусом инерции, по формуле Iz=Mr2, где М — масса тела. Размерность М. и.— L2M; а единицы — кг•м2 или г•см2. Центробежным М. и. относительно системы прямоугольных осей х, у, z, проведённых в точке О, наз. вели­чины, определяемые равенствами: или же соответствующими объёмными интегралами. Эти величины явл. ха­рактеристиками динамич. неуравнове­шенности тел. Напр., при вращении тела вокруг оси z от значений Ixz и Iyz зависят силы давления на подшипники, в к-рых закреплена ось. М. п. относительно параллельных осей z и z' связаны соотношением: lz=l'z + Md2 (3) где z' — ось, проходящая через центр масс тела, а d — расстояние между осями. М. и. относительно любой проходя­щей через начало координат О оси О1 с направляющими косинусами , ,  находится по ф-ле: IOl=Ix2+Iy2+Iz2-2Ixy-2Iyz-2Izx. (4) Зная шесть величин Ix, Iy Iz, Iху, Iyz, Izx, можно последовательно, ис­пользуя ф-лы (4) и (3), вычислить всю совокупность М. и. тела относи­тельно любых осей. Эти шесть вели­чин определяют т. н. тензор инерции тела. Через каждую точку тела можно провести три такие взаимно-перпендикулярные оси, наз. главными осями инерции, для к-рых Ixy=Iyz=Izx=0 Тогда, зная главные оси инерции и М. п. относительно этих осей, можно определить М. и. тела относительно любой оси. М. п. тел сложной конфигурации обычно определяют эксперименталь­но. Понятием о М. и. широко поль­зуются при решении многих задач механики и техники, • Фаворин М. В., Моменты инерции тел. Справочник, М., 1970; Г е р н е т М. М., Р а т о б ы л ь с к и й В. Ф., Определение моментов инерции, М., 1969. См. также лит. при ст. Механика. С. М. Тарг. МОМЕНТ КОЛИЧЕСТВА ДВИЖЕ­НИЯ (кинетический момент, угловой момент), одна из мер механич. движе­ния материальной точки или системы. Особенно важную роль М. к. д. играет при изучении вращат. движения. Как и для момента силы, различают М. к. д. относительно центра (точки) и относительно оси. Для вычисления М. к. д. К мате­риальной точки относительно центра О или оси z справедливы все ф-лы, приведённые для вычисления момента силы, если в них заменить вектор F вектором количества движения mv. Т. о., KO=[r•mv], где r — радиус-вектор движущейся точки, проведён- 437 ный из центра О, а Kz равняется проек­ции вектора ko на ось z, проходящую через точку О. Изменение М. к. д. точки происходит под действием мо­мента m,O(F) приложенной силы и определяется теоремой об изменении М. к. д., выражаемой ур-нием dKO/dt=mO(F). Когда mO(F)=0, что, напр., имеет место для центр. сил, движение точки подчиняется площа­дей закону. Этот результат важен для небесной механики, теории движения ИСЗ, косм. летат. аппаратов и др. Главный М. к. д. (или кинетич. мо­мент) механич. системы относительно центра О или оси z равен соответст­венно геом. или алгебр. сумме М. к. д. всех точек системы относительно того же центра или оси, т. е. ko=koi, kz=Kzi. Вектор ko может быть определён его проекциями Kx, Ky, Kz на координатные оси. Для тела, которое вращается вокруг неподвиж­ной оси z с угловой скоростью , Kx=-Ixz, Ky=-Iyz, Kz=Iz, где Iz — осевой; a Ixz, Iyz — цен­тробежные моменты инерции. Если ось z является гл. осью инерции для начала координат О, то ko=iz. Изменение гл. М. к. д. системы про­исходит под действием только внеш. сил и зависит от их гл. момента MeO. Эта зависимость определяется теоре­мой об изменении гл. М. к. д. системы, выражаемой ур-нием dKO/dt=MeO. Аналогичным ур-нием связаны мо­менты Kz и Меz относительно оси z. Если MeO=0 или Mez=0, то соответст­венно КO или Kz будут величинами постоянными, т. е. имеет место закон сохранения М. к. д. (см. Сохранения законы). Т. о., внутр. силы не могут изменить М. к. д. системы, но М. к. д. отд. частей системы или угловые ско­рости под действием этих сил могут изменяться. Напр., у вращающегося вокруг вертикальной оси z фигуриста (или балерины) величина Kz=Iz будет постоянной, т. к. практически Mez=0. Но, изменяя движением рук или ног значение момента инерции lz, фигурист может изменять угловую скорость со. Понятое о М. к. д. ши­роко используется в динамике тв. тела, особенно в теории гироскопа. Размерность М. к. д.— L2MT--1, a единицы — кг•м2/с, г•см2/с. М. к. д. обладают также эл.-магн., гравитац. и др. физические поля. Большинству элем. ч-ц присущ собственный, внутр. М. к. д.— спин. Большое значение М. к. д. имеет в квантовой механике. • См. лит. при ст. Механика. С. М. Тарг. МОМЕНТ ОРБИТАЛЬНЫЙ, см. Орбитальный момент. МОМЕНТ СИЛЫ, величина, характе­ризующая вращат. эффект силы при действии её на тв. тело; одно из осн. понятий механики. Различают М. с. относительно центра (точки) и отно­сительно оси. М. с. относительно центра О — вели­чина векторная. Его модуль MO=Fh, где F — модуль силы, a h — плечо, т. е. длина перпендикуляра, опу­щенного из О на линию действия силы (рис.); направлен вектор МO перпендикулярно плоскости, прохо­дящей через центр О и силу ¥ в сто­рону, откуда поворот, вызываемый силой, виден про­тив хода часо­вой стрелки (в правой системе координат). С по­мощью векторно­го произведения М. с. выражает­ся равенством MO=[r•F], где r — радиус-век­тор, проведён­ный из О в точку приложения си­лы. Размерность М. с. — L2MT2, единицы — Н•м, дин•см или кгс•м. М. с. относительно оси — величина алгебраическая, равная проекции на эту ось М. с. относительно любой точки О оси или же численной вели­чине момента проекции Fxy силы F на плоскость ху, перпендикулярную оси z, взятого относительно точки пересечения оси с плоскостью. Т. е. Mz= МOcos=Fxyh1 или Mz= -Fxyh1. Знак минус (последнее выражение) берётся, когда поворот силы F с поло­жит. направления оси z виден по ходу часовой стрелки (тоже в правой систе­ме). М. с. относительно осей х, у, z могут также вычисляться по ф-лам: Mx=yFz-zFy, My=zFx-xFz, Mz=xFy-yFx, где Fx, Fy, Fz — проекции силы F на оси; х, у, z — координаты точки А приложения силы. Если система сил имеет равнодейст­вующую, то её момент вычисляется по Вариньона теореме. • См. лит. при ст. Механика. С. М. Тарг. МОНОКРИСТАЛЛ, кристаллич. ин­дивид, имеющий во всём объёме еди­ную кристаллич. решётку (см. Крис­таллы). Внеш. форма М. определяется их ат. структурой и условиями крис­таллизации: в равновесных условиях М. приобретают хорошо выраженную естеств. огранку. Примеры хорошо огранённых природных М.— кварц, каменная соль, исландский шпат, ал­маз, рубин. М. могут не иметь пра­вильной огранки (напр., закруглён­ные искусственно выращиваемые «були» рубина, М. кремния). Многие М. обладают особыми физ. св-вами: алмаз очень твёрд, сапфир, кварц, флюорит — исключительно прозрачны, нитевидные кристаллы ко­рунда рекордно прочны. Многие М. чувствительны к внеш. воздействиям (света, механич. напряжений, магн. и электрич. полей, радиации и др.). Поэтому они применяются в качестве разного рода преобразователей в ра­диоэлектронике, квантовой электро­нике, акустике и др. В связи с этим возникла потребность в М. разных 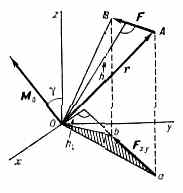размеров и форм: от микрокристаллов, плёнок и нитевидных кристаллов ве­сом в неск. мг до крупных М. весом в десятки кг. Первоначально исполь­зовались природные М. кварца, флю­орита, корунда, алмаза и др. Однако они содержат большое кол-во дефек­тов. Поэтому появилась необходи­мость искусств. выращивания М. При этом было создано множество ценных М., не имеющих природных аналогов (см. Синтетические кристаллы). МОНОМОЛЕКУЛЯРНЫЙ СЛОЙ (мо­нослой), слой в-ва толщиной в одну молекулу на поверхности раздела фаз. Образуется при адсорбции, поверх­ностной диффузии и в результате ис­парения растворителя из раствора, содержащего летучий компонент. Осо­бый интерес представляют М. с. по­верхностно-активных веществ на по­верхности жидкости, резко изменяю­щие её св-ва; они могут образовы­ваться за счёт адсорбции из газовой фазы или из раствора. В газооб­разных М. с. расстояние между молекулами велико по сравнению с их размерами, поэтому межмол. вз-ствие практически отсутствует. Конден­сированные М. с. имеют пре­дельно плотную упаковку молекул. Так, углеводородные цепи с полярной группой на конце располагаются в кон­денсированных М. с. в виде «часто­кола», занимающего всю площадь по­верхности раздела фаз. Каждая моле­кула в таком «частоколе» расположена перпендикулярно или наклонно по­верхности и независимо от длины мо­лекулы занимает площадь в 20— 25 Å2. Высокомол. линейные молекулы, как правило, образуют М. с. с гори­зонт, ориентацией макромолекул. М. с. могут проявлять поверхностную вяз­кость и прочность, сильно отличаю­щиеся от соответствующих хар-к объём­ных фаз. Структура и св-ва М. с. влияют на процессы массопереноса (диффузию, испарение), катализа, трения, адгезии и коррозии. От состояния М. с. часто определяющим образом зависит устой­чивость высокодисперсных систем: эмульсий, суспензий, золей. Сущест­венна роль М. с. в разнообразных биол. структурах (напр., биол. мемб­ранах). МОНОПОЛЬ ДИРАКА, то же, что магнитный монополь. МОНОПОЛЬНЫЙ МАСС-СПЕКТРО­МЕТР, устройство, в к-ром разделение ионов по величине отношения массы к заряду происходит в переменном электрич. поле, создаваемом цилиндрич. стержнем и заземлённым уголко­вым электродом. См. Масс-спектро­метр. МОНОХРОМАТИЧЕСКИЙ СВЕТ, монохроматическое излучение в диапа­зоне частот, непосредственно воспри­нимаемых человеч. глазом (см. Свет). МОНОХРОМАТИЧЕСКОЕ ИЗЛУЧЕ­НИЕ (от греч. monos — один, единый и chroma — цвет), электромагнитное 438 излучение одной определённой и строго постоянной частоты. Происхождение термина «М. и.» связано с тем, что различие в частоте световых волн воспринимается человеком как различие в цвете. Однако по своей природе электромагнитные волны ви­димого диапазона, лежащие в интер­вале 0,4—0,7 мкм, не отличаются от эл.-магн. волн др. диапазонов (ИК, УФ, рентгеновского и т. д.), по отно­шению к к-рым также используют тер­мин «монохроматический» (одноцвет­ный), хотя никакого ощущения цвета эти волны не дают. Теория эл.-магн. излучения, осно­ванная на Максвелла уравнениях, опи­сывает любое М. и. как гармонич. ко­лебание, происходящее с неизменной амплитудой и частотой в течение бес­конечно долгого времени. Плоская монохроматич. волна эл.-магн. излу­чения служит примером полностью когерентного поля (см. Когерент­ность), параметры к-рого неизменны в любой точке пр-ва и известен закон их изменения во времени. Однако процессы излучения всегда ограничены во времени, а потому понятие М. и. явл. идеализацией. Реальное естеств. излучение обычно представляет собой сумму нек-рого числа монохроматич. волн со случайными амплитудами, частотами, фазами, поляризацией и направлением распространения. Чем уже интервал, к-рому принадлежат частоты наблюдаемого излучения, тем оно монохроматичнее. Так, излуче­ние, соответствующее , отд. линиям спектров испускания свободных ато­мов (напр., атомов разреженного газа), очень близко к М. и. (см. Атомные спектры); каждая из таких линий соответствует переходу атома из со­стояния т с большей энергией в со­стояние и с меньшей энергией. Если бы энергии этих состояний имели строго фиксированные значения Еm и Еn, атом излучал бы М. и. частоты vmn= (Еm-En)/h. Однако в состояниях с большей энергией атом может нахо­диться лишь малое время t (обычно 10-8 с — т. н. время жизни на энергетич. уровне), и согласно неопределённостей соотношению для энергии и времени жизни квант. состояния (E•th) энергия, напр. состояния га, может иметь любое значение между Еm+E и Еm-Е. Поэтому излуче­ние каждой линии спектра соответст­вует интервалу частот vmn=E/h=1/t (подробнее см. в ст. Ширина спектральных линий). Т. к. идеальным М. и. не может быть по самой своей природе, то обычно монохроматическим считается излучение с узким спектр. интервалом, к-рый можно приближённо характеризовать одной частотой (или длиной волны). Приборы, с помощью к-рых из реального излучения выделяют узкие спектр. интервалы, наз. монохроматорами. Чрезвычайно высокая монохроматичность характерна для из- лучения нек-рых типов лазеров (ши­рина спектр. интервала излучения достигает величины 10-6 Å, что зна­чительно уже, чем ширина линий ат. спектров). • Б о р н М., Вольф Э., Основы оп­тики, пер. с англ., 2 изд., М., 1973; Калитеевский Н. И., Волновая оптика, 2 изд., М., 1978. Л. Я. Капорский. МОНОХРОМАТОР, спектральный оптич. прибор для выделения узких участков спектра оптического излучения. М. состоит (рис.) из входной щели 1, освещаемой источником излу­чения, коллиматора 2, диспергирую­щего элемента 3, фокусирующего объектива 4 и выходной щели 5. Диспергирующий элемент простран­ственно разделяет лучи разных длин волн Я, направляя их под разными углами , и в фокальной плоскости объектива 4 образуется спектр — со­вокупность изображений входной щели в лучах всех длин волн, испус­каемых источником. Нужный участок спектра совмещают с выходной щелью поворотом диспергирующего элемен­та; изменяя ширину щели 5, меняют спектр, ширину  выделенного уча­стка. Диспергирующими элементами М. служат дисперсионные призмы и диф­ракционные решётки. Их угл. диспер­сия D=/ вместе с фокусным рас­стоянием f объектива 4 определяет л и н е й н у ю д и с п е р с и ю l/=D•f ( — угл. разность на­правлений лучей, длины волн к-рых отличаются на ; l — расстояние в плоскости выходной щели, разделяю­щее эти лучи). Призмы дешевле решё­ток в изготовлении и обладают боль­шой дисперсией в УФ области. Однако их дисперсия значительно умень­шается с ростом К, и для разных об­ластей спектра необходимы призмы из разных материалов. Решётки свободны от этих недостатков, имеют пост. высо­кую дисперсию во всём оптич. диапа­зоне и при заданном пределе разреше­ния позволяют построить М. с су­щественно большей светосилой, чем призменный М. Кроме дисперсии, качество М. опре­деляют его разрешающая способность и светосила. Раз­решающая способность М., как и лю­бого др. спектр. прибора, равна /()*, где ()*— наименьшая разность длин волн, ещё различимая в выходном из­лучении М.; она тесно связана с его аппаратной функцией, к-рую можно представить как распределение потока лучистой энергии по ширине изобра­жения входной щели, освещаемой узко монохроматическим излучением. Светосила М. показывает, какая часть лу­чистой энергии, испускаемой источни­ком в выделенном М. интервале , проходит через М. Она зависит от геом. хар-к М. (в частности, от разме­ров щелей и диспергирующего эле­мента) и от потерь на отражение и по­глощение в оптич. системе М. Объективы М. (коллиматорный и фокусирующий) могут быть линзо­выми и зеркальными. Зеркальные объективы пригодны в более широком спектр. диапазоне, чем линзовые, и, в отличие от последних, не требуют перефокусировки при переходе от од­ного выделяемого участка спектра к другому. Это особенно удобно в не­видимых для глаза УФ и ИК областях спектра, где и применяется преим. зеркальная оптика. М. явл. важнейшей составной час­тью источников монохроматич. осве­щения, а также с п е к т ро ф о т о м е т р о в. В спектрофотометрии особенно важно избежать попадания в выходную щель М. рассеянного света с длинами волн, далёкими от выделяемого участка спектра. С этой целью часто применяют два М., кон­структивно объединённых так, что выходная щель первого из них служит входной щелью второго. Одно из преимуществ таких двойных М.— их повышенная дисперсия. • Топорец А. С., Монохроматоры, М., 1955; Пейсахсон И. В., Оптика спектральных приборов, Л., 1970. А. П. Гагарин.