1. Основные понятия и обозначения электрических величин и элементов электрических цепей. Ток напряжение и энергия электрической цепи

Вид материала

Документы

Содержание Ток – это скорость изменения заряда по времени: i=dq/dt. Напряжение 2.Источники и приемники электрической энергии. Пассивные и активные элементы электрических цепей. 3.Классификация электрических цепей. Топологические понятия теории электрических цепей. Ветвь – цепь, соединяющая 2 узла. Ветви содержащие >1 эл-та, наз-ся сложными. Если наоборот – простые. Контур 4.Законы Кирхгофа. Основные принципы и теоремы теории цепей и их применение для анализа. Принцип суперпозиции. 5.Методы анализа и расчета линейных электрических цепей. Цепи постоянного тока. Методы токов и напряжений ветвей. 6.Методы контурных токов и узловых напряжений. 7.Преобразования цепей и их применение для анализа 2.Преобразование параллельных GJ-ветвей. Переменный ток Активное, реактивное и полное сопротивление ЭЦ 9.Фазовые соотношения между током и напряжением. Мощность в цепях переменного тока. 32.Источники вторичного электропитания. 10.Анализ цепей при гармоническом воздействии. 11.Комплексные схемы замещения идеальных элементов электрических цепей. Законы Кирхгофа в комплексной форме. Комплексные схемы замещения идеальных эл-тов 12.Частотные свойства цепей переменного тока. Методы построения схемных функций. 13. Явление резонанса. Последовательный, параллельный колебательные контуры. 14. Явление резонанса. Сложный колебательный контур. ... Полное содержание

Подобный материал:

• Экзаменационные вопросы по курсу «Электротехника и электроника», 23.91kb.
• Теоретические вопросы дисциплины «Теоретические основы электротехники»,, 28.22kb.
• Магистерская программа 140400. 91 «Силовые электронные и микропроцессорные аппараты», 37.41kb.
• Контрольная работа выполняется на тему «Основные законы теории цепей, анализ установившегося, 35.6kb.
• Вопросы для подготовки к экзамену теоретические основы электротехники, 19.46kb.
• Программа вступительных экзаменов в магистратуру по специальности 6М071800 «Электроэнергетика», 590.06kb.
• Тема: «Основные определения теории электрических цепей», 125.43kb.
• Теория электрических цепей (часть, 63kb.
• Учебная программа Дисциплины р4 «Теория электрических цепей» по направлению 010300, 234.27kb.
• Отдел метрологического обеспечения измерений электрических величин, 42.58kb.

1.Основные понятия и обозначения электрических величин и элементов электрических цепей. Ток напряжение и энергия электрической цепи. 3 осн. эл-та: 1)емкостной эл-т. происходит запасание энергии и преобразование её в электрич. 2)индуктивный эл-т. – 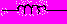происх. запасание энергии и преобр. электромагнитной энергии в магнитную. 3)резистивный эл-т. происх. необратимое преобр. электромагн. энергии в другие виды. + ист. тока и напряжения . Ток – это скорость изменения заряда по времени: i=dq/dt. Напряжение – количество энергии, затрачиваемой на перемещение единицы заряда из одной точки в другую: u=dw/dt, где w-энергия. 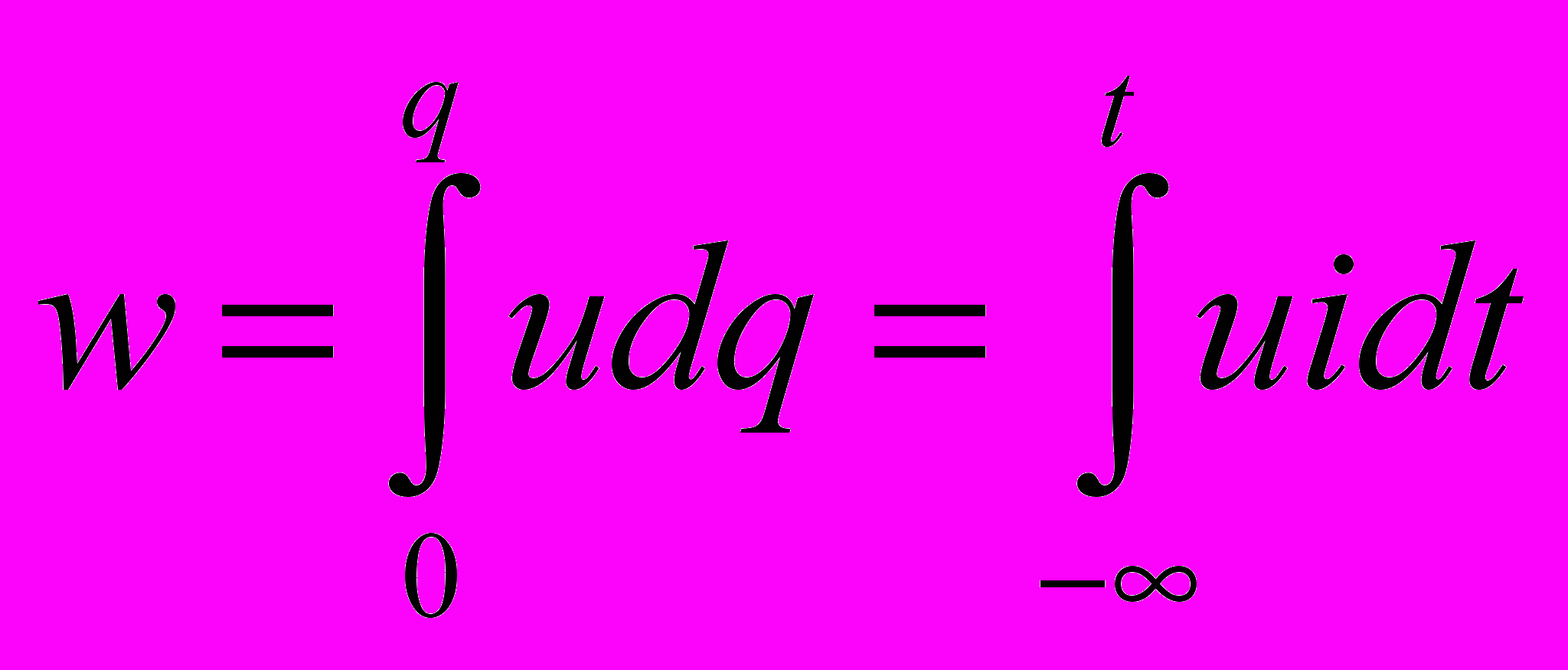p-мощность, p=dw/dt=UI У источников энергии мощность отрицательная, у приёмников – положительная.	2.Источники и приемники электрической энергии. Пассивные и активные элементы электрических цепей. Источник – это эл-т электрич. цепи, снабжающий её ЭМ-энергией. Независимые ист.: Источник напряжения – это эл-т с 2 выводами, напряжение м/у кот. задано в виде нек. ф-ции времени,не зависящей от тока. Источник тока – это эл-т цепи, ч-з выводы кот. протекает ток с заданным законом изменения независимо от напряжения м/у выводами. Зависимые: ист. напряжения, управляемый напряжением(ИНУН – Uист.=к*Uвх. и т.д.), ИТУН, ИНУТ, ИТУТ. Приёмник – эл-т потребляющий, запасающий или преобразующий ЭМ-энергию. Все источники явл. активными, приемники – пассивными эл-тами. 3 осн. пасс. эл-та: 1)емкостной эл-т. происходит запасание энергии и преобразование её в электрич. I(t)=C*dU/dt; 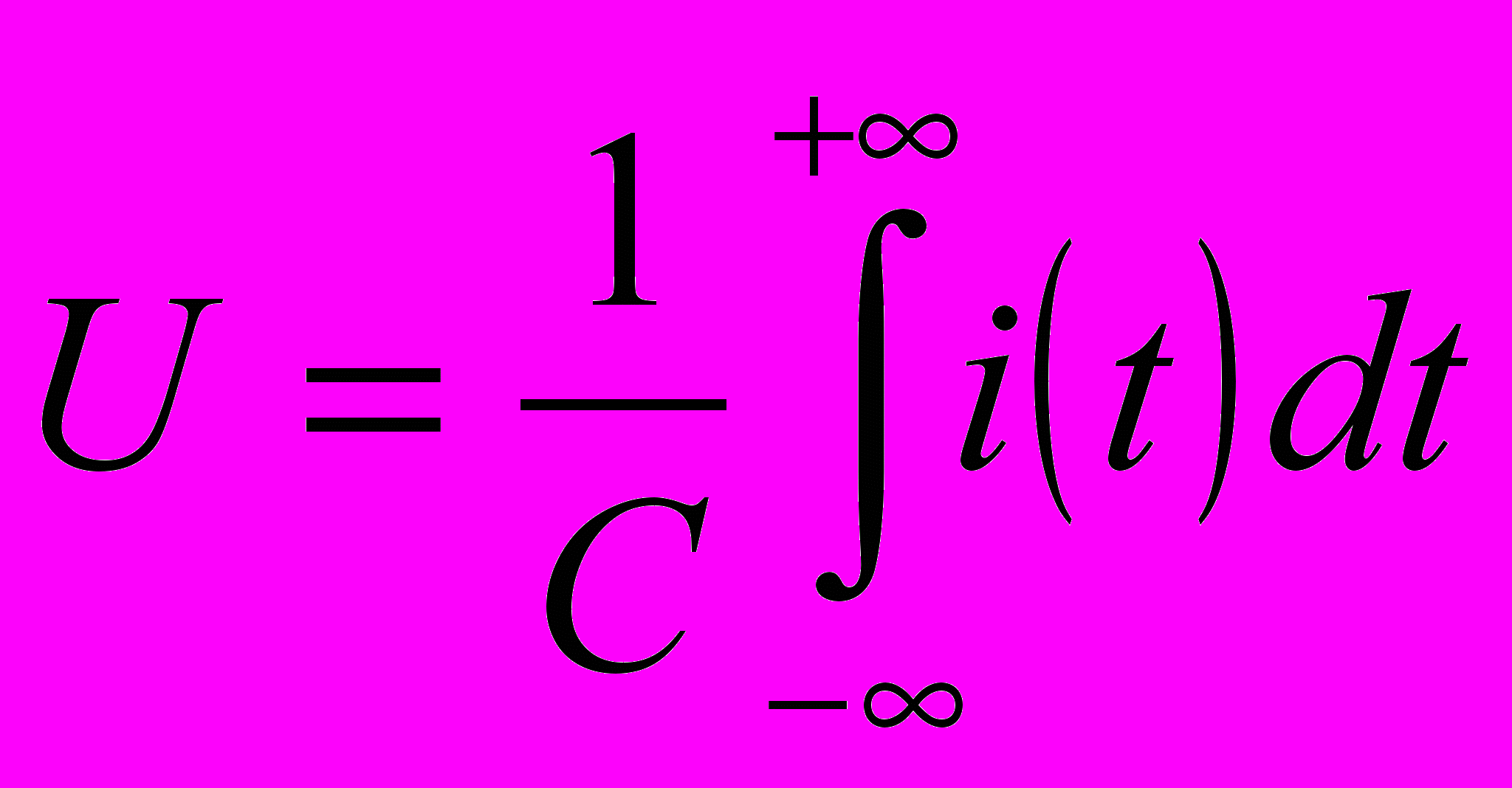2)индуктивный эл-т. - происх. запасание энергии и преобр. электромагнитной энергии в магнитную.U=L*di/dt; 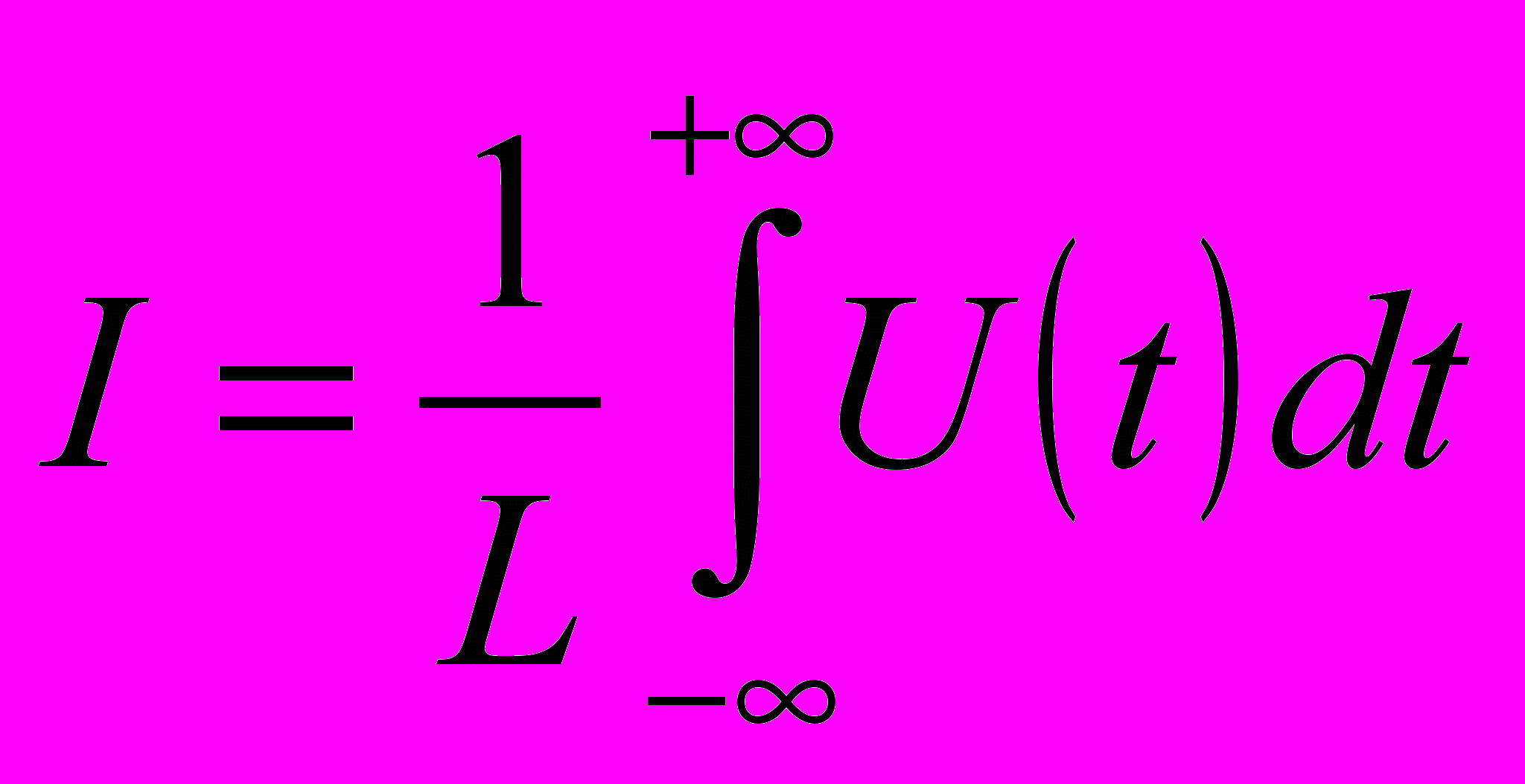3)резистивный эл-т. происх. необратимое преобр. электромагн. энергии в другие виды.U=RI; I=GU	3.Классификация электрических цепей. Топологические понятия теории электрических цепей. Электрическая цепь – система соед. м/у собой электро-радио эл-тов и компонентов (проводящие, полупроводниковые и диэлектр. устройства), предн. для преобр. электроэнергии. 1) с сосред. параметрами (эл-ты не имеют геометрических размеров); 2)с распред. параметрами (параметры эл-тов зависят хотя бы от 1 пространственной координаты). Топология ЭЦ: раздел ТЭЦ, занимающийся конфигурацией ЭЦ вне зависимости от их элементного состава. Граф –условное изображение ЭЦ без учёта без учёта её элементного состава, состоит из узлов и ветвей. Узел – т. соединения 2 и более ветвей. Ветвь – цепь, соединяющая 2 узла. Ветви содержащие >1 эл-та, наз-ся сложными. Если наоборот – простые. Контур – это совокупность ветвей, двигаясь по кот., можно прийти из 1 точки к ней же самой. Простой контур – не содержит вложенных контуров. Сложный контур – наоборот. Дерево графа – подграф эл. цепи, обл. след. св-вами: 1)дерево графа содержит то же кол-во узлов, что и основной граф=q. 2)граф сод. q-1 ветвь 3)граф не сод. контуров. 4)граф неразрывен	4.Законы Кирхгофа. Основные принципы и теоремы теории цепей и их применение для анализа. Законы явл. топологическими – не зависят от элементного состава. 1.Закон для токов: алгебр. сумма токов (сумма с учётом условного положительного направления) в любом узле ЭЦ=0. , где ik – ток в к-й ветви, а знак +/- берётся из расчёта, совпадает ли направление тока в контуре и в источнике. 2.Закон для напряжений: алгебр. сумма(с учётом направления обхода контура и направлений напряжений) напряжений в люб. контуре ЭЦ=0. - для люб. контура сумма произведений силы тока на сопротивление узла с учётом направления тока в контуре равна общему напряжению в контуре. Следствия: Принцип суперпозиции. Если ЭЦ сод. несколько ист. энергии, то люб. отклик м.б. получен в виде суммы откликов при воздействии каждого из них в отд.: A1(X1+X2)=B1+B2 где А – матрица параметров, Х1, Х2 – матрица источников. В1, В2 – отклики. При построении решения ЭЦ исходная ЭЦ превращается в несколько ЭЦ с одним источником энергии. При этом источники тока разрываются. а источники напряжения закорачиваются. Теорема компенсации: Люб. из пассивных эл-тов м.б. замещен ист. тока или напряжения, если он повторяет направление тока на этом эл-те. Принцип взаимности: применим только для планарных (без пересечений) цепей с пассивными эл-тами. Если в 1 из ветвей ЭЦ поместить ист. напряжения, то ток, возникающий в др. ветви, будет с точностью до знака= току первой ветви. Теорема об эквивалентном генераторе: Если ЭЦ м.б. представлена в виде измеримой и неизмеримой части, то неизмеримая часть м.б. представлена в виде эквивалентного генератора.	5.Методы анализа и расчета линейных электрических цепей. Цепи постоянного тока. Методы токов и напряжений ветвей. Режим ЭЦ вкл. в себя: U,i – напряжения и токи на ветвях ЭЦ, р – мощность цепи, w- энергия цепи. Задача анализа ЭЦ состоит в нахождении её режима. Для этого составляют n=2р уравнений, шде р – кол-во ветвей ЭЦ. Из них n­­­­­1=q-1 (где q - кол-во узлов) – кол-во ур-й по 1 з. Кирхгофа. n2=p-q+1 –кол-во ур-й по 2 з. Кирхгофа. Алгоритм: 1)систему интегро-диф. ур-й приводят к 1 ДУ с порядком k.Оно имеет ед. р-е предст. в виде 2 частей: Uсв – общее р-е описывает свобоную составляющую системы. Переходн процесс возникает, когда быстро меняется 1 из сост. ЭЦ. Uвс – частное р-е описывает вынужденную сост. Условия протекания пост. токов и формирования пост. напряжения, производимого в ЭЦ: сопротивления, ист.тока и напряжения не изменяются, индуктивности закорачиваются, ёмкости разрываются. Методы анализа: 1)метод токов ветвей: В кач. базовых ветвей исп. ветви типа RE. (последовательно соединённые ист. напряжения и резистивные эл-ты). При этом строятся ур-я по 1 и 2 з-нам Кирхгофа: U=RI-E. Искомый эл-т – I. 2)Метод напряжений: в кач-ве базовых исп. GJ-ветви(параллельно соединённые ист. тока и эл-ты проводимости). При этом строятся ур-я по 1 и 2 з-нам Кирхгофа: I=GU-J. 3) Комбинированный метод: исх. схема не преобразовывается, исп. ур-я и того, и др. типа.
6.Методы контурных токов и узловых напряжений. Контурный ток – это независимый ток, кот. протекает в независимом контуре. Фиктивный ток, в отл. от токов ветвей. Является суммой токов ветвей, входящих в контур с учётом их совпадения с направлением обхода. Ф-ла, по кот. строится сист. ур-й: ZI=E, где Z –матрица сопротивлений эл-тов, входящих в контур, I – искомый столбец токов контура, E – столбец ЭДС источников. По диагонали матрицы сопротивления расположены собственные контурные сопротивления. В остальных ячейках таблицы – межконтурные сопр. Затем возвр. к вычислению реальных токов. Метод нужен для упрощения. Узловое напряжение – это потенциал узла по отн. к узлу с нулевым потенциалом. Метод узловых напряжений: 1)преобразуем все сопротивления в проводимости(GJ). 2) Вводим узловые напряжения –по ф-ле GU=J. Получаем матрицу проводимости: по диагонали расположены собственные проводимости узлов, ост. эл-ты -межузловые проводимости (только прямые). Общий алгоритм: 1)Построение схемы замещения для выбранного метода; 2)Определение фиктивных значений токов и напряжений; 3)составление СУ; 4)Р-е СУ известными методами; 5)Возврат от фиктивных токов и напряжений к фактическим.	7.Преобразования цепей и их применение для анализа Преобразование ЭЦ – изменение конфигурации ЭЦ с изменением числа ветвей. Эквивалентное преобразов. – токи инапряжения полученной цепи не изменяются относительно первоначальных. Неэквивалентное пр. – изменяются. 1.Преобразование последовательных RE-ветвей. При преобразовании посл. RE-ветвей мн-во ист. напряжения и резистивных эл-тов м.б. заменено 1 эл-том и 1 источником. При этом параметры соотв. равны: 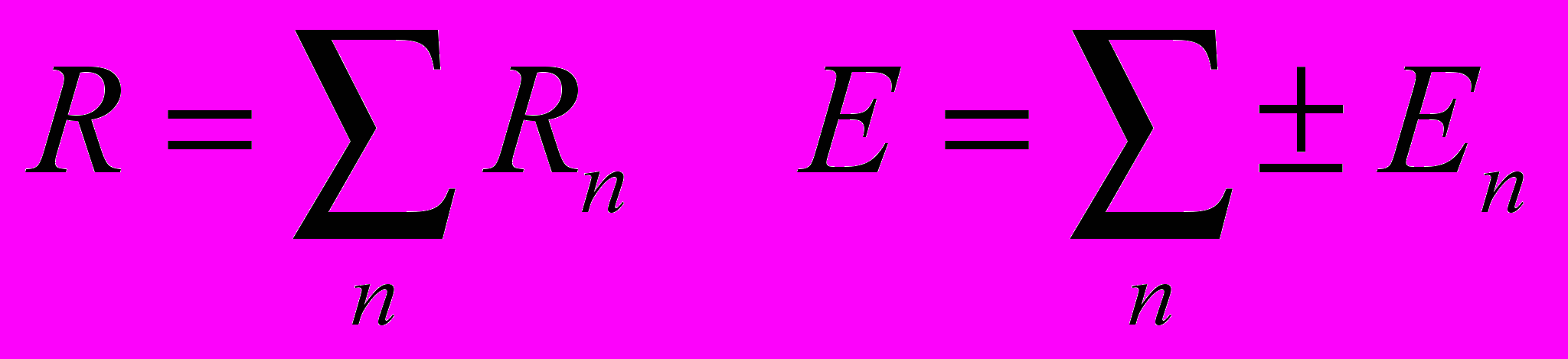2.Преобразование параллельных GJ-ветвей. Аналогично предыдущему мн-во пар.соед.GJ-ветвей м.б. заменено 1 ист. напряж. и 1 проводимостью. Параметры: 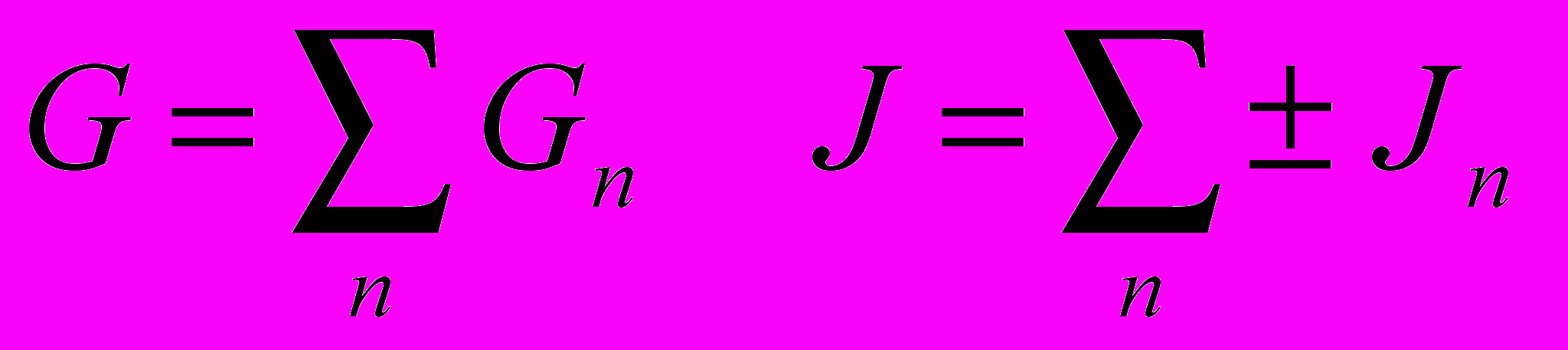3,4.Преобразования пар. RE-ветвей и послед. GJ-ветвей. 2 паралл-вкл. RE-ветви м.б. преобразованы в 1 последов. RE-ветвь. Послед.-вкл. GJ-ветви м.б. преобразованы в 1 GJ-ветвь. Порядок преобр.1.RnEn=>GnJn; 2.GnJn=>GJ; 3.GJ=>RE 5,6.Преобразования «Звезда-Треугольник»,»Треугольник-Звезда». Сопротивление ветви трехлучевой звезды =произведению смежных ветвей треугольника, деленному на сумму сопр. всех его ветвей. Проводимость стороны треугольника =произведению проводимости смежных ветвей звезды, дел. на их сумму.	8.Способы представления синусоидальных функций. Мгновенное, среднее и действующее значение синусоидального тока. Активное. Реактивное и полное сопротивление цепи. Векторные диаграммы. Переменный ток –ток, амплитуда и направление кот. изменяются во времени. Периодический ток и напряжение – ток и напряжение, значения и направление кот. повторяются с течением опр. промежутка времени. Т-период, 1/Т –частота. 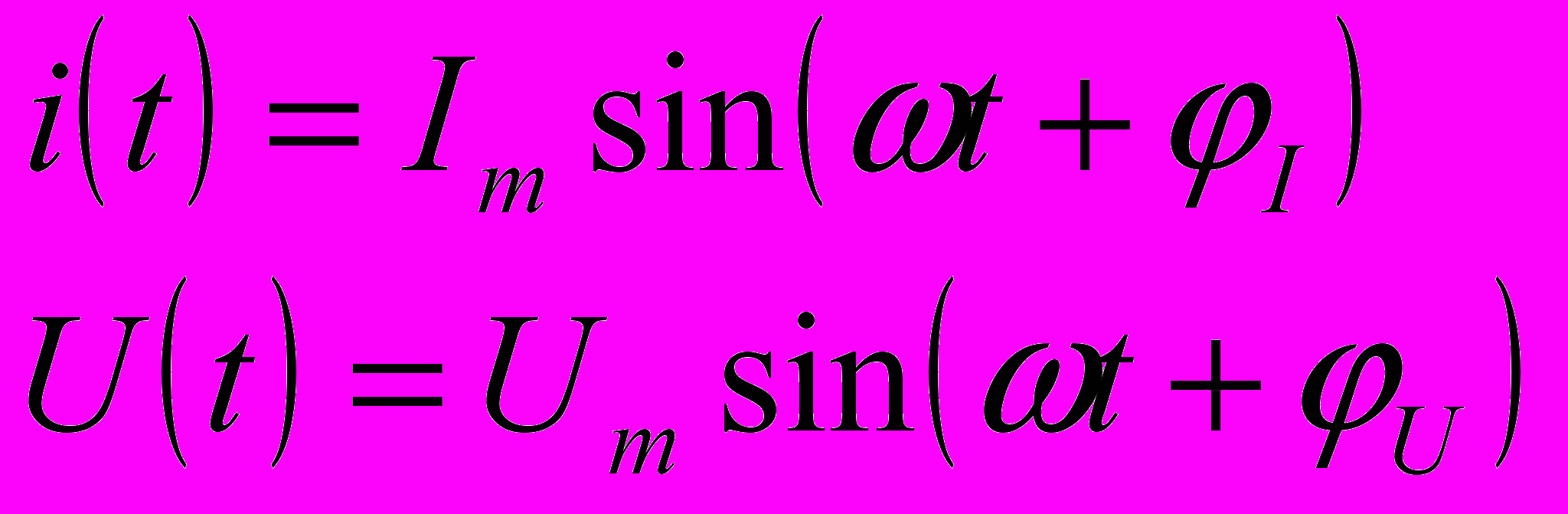Где φI, φU – соотв. фаза по току и напряжению. В каждый момент времени ток и напряжение принимают мгновенные значения. φI-φU=Δφ – разность фаз. Среднее для ф-ции: 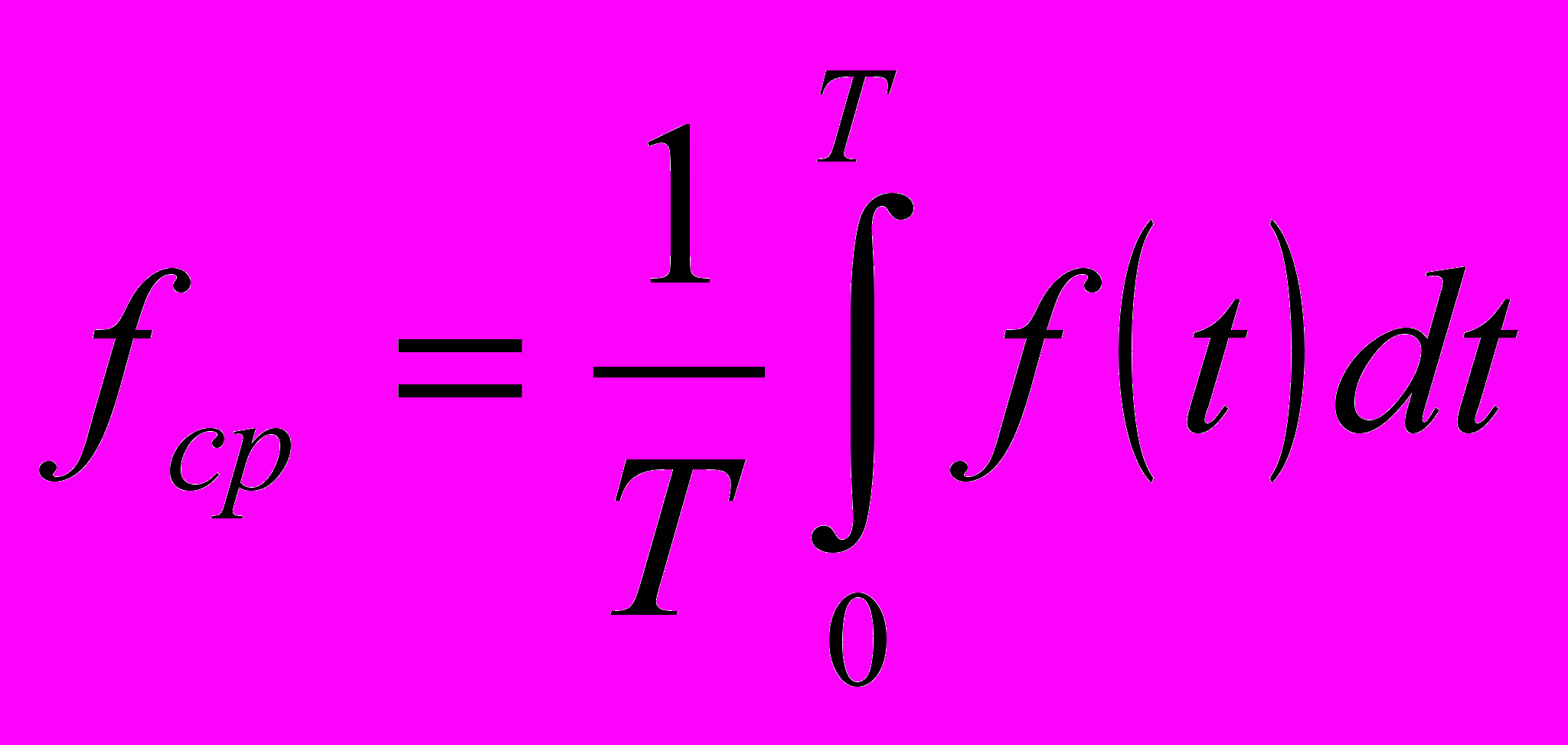Переменный ток- ток, ср.значение кот.за период=0. Поэтому ср.значение берётся за ½ Т. Действующее значение – такое постоянное знач., при кот. мощность отдаваемая/принимаемая системой была бы равна мощности, отд./прин. системой при синусоидальном воздействии. 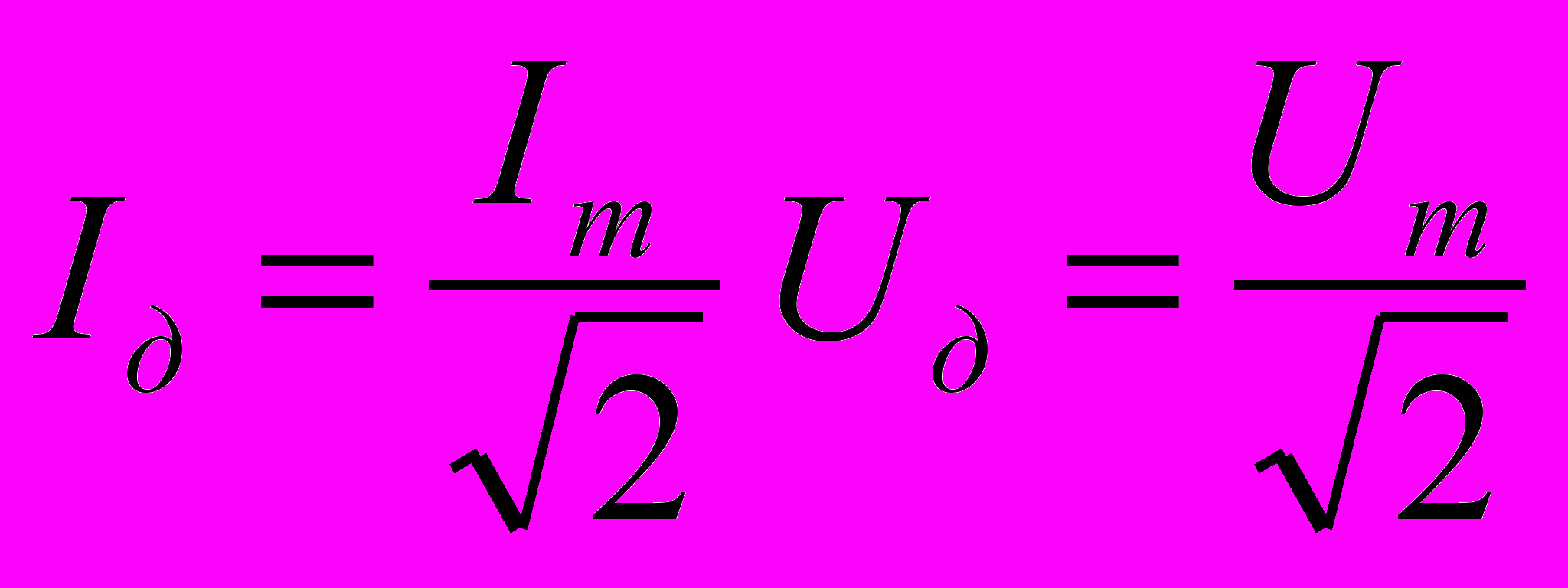Активное, реактивное и полное сопротивление ЭЦ. Полное сопр. цепи: Z=R+jX, где R-активное(необратимые преобразования), Х-реактивное сопр.(обратимые преобр.). Векторные диаграммы: строится график полного сопротивления по действительной оси R и мнимой Х. Можно исп. комплексную проводимость: Y=G+jB	9.Фазовые соотношения между током и напряжением. Мощность в цепях переменного тока. 1 Резистивный эл-т: U(t)=i(t)*R; I(t)=(Um/R)/sin(wt). Сдвига фаз не происходит. 2. Индуктивность. U(t)=L*(di(t)/dt); Z(t)=Zmsin(wt); Uвн опережает I на 3.Ёмкость. i(t)=C*(dU/dt). Z опережает U на Мощность: P(t)=UmIm­­sinωt*sin(ωt+φ) действующее значение мощности: UmIm – активная мощность системы. Q –реактивная мощность, S –полная мощность. P=S cos φ; Q=S sin φ. 32.Источники вторичного электропитания. Выпрямитель, вентиль – выпрямительный диод. Однополупериодная и двухполупериодная(мостовая, диодный мост). Вместо диодов можно использовать тиристоры. Управляемые выпрямители – когда нужно полностью отключить пропуск, включаем тиристор только при фазе 180. Фильтры – сглаживают пульсации на выходе выпрямителя, характеризуются коэффициентом сглаживания. Чем выше коэфф., тем эффективнее фильтр. 1) Емкостные. 2)  3) Г-образный 1. 4) Г-образный 2. 5) П-образный. Стабилизатор – поддерживает уровень выходного напряжения и тока в относительно неизменном состоянии. Преобразователи напряжения – инвертные(пост. – перем.), конверторы (переем. – пост.).	10.Анализ цепей при гармоническом воздействии. Цепь произвольной конфигурации, содержащая R, C, L, гармонические источники i(t),U(t). 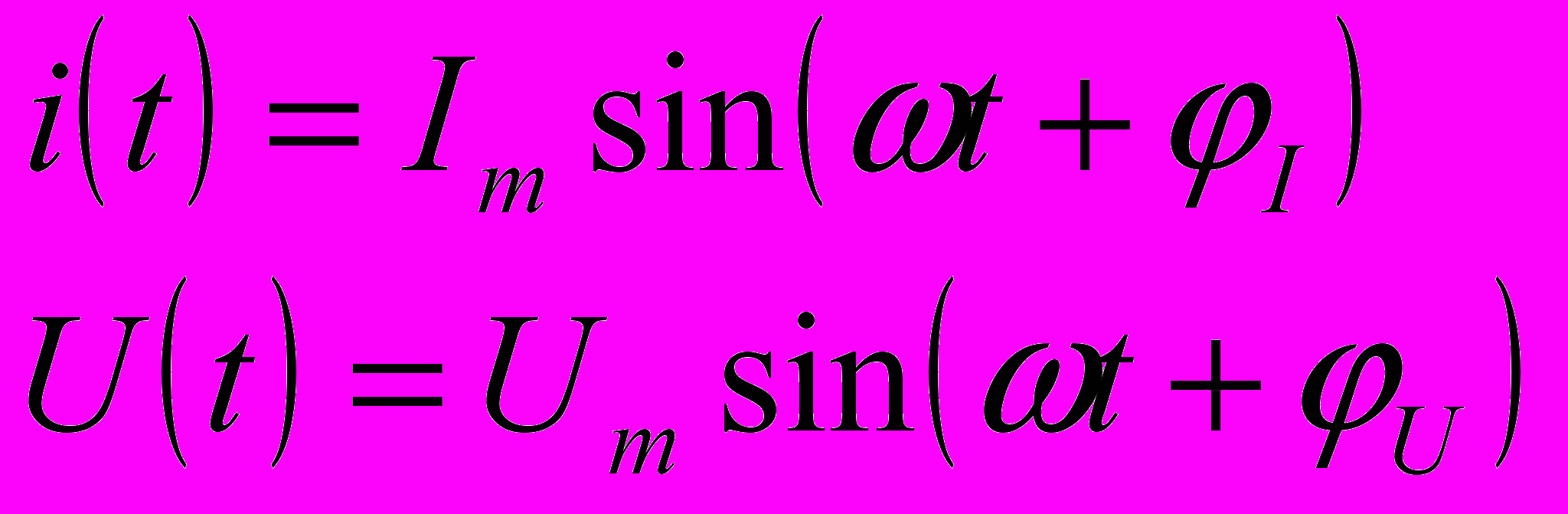Цель анализа: определить режим ЭЦ. Ограничения: 1) ω=const – режим установившийся. 2)элементы идеальные. Метод комплексных амплитуд: 1)Построение комплексной схемы замещения исх. ЭЦ; 2)Анализ комплексной схемы замещения любыми изв. методами, результатом кот. явл. параметры режима цепи, записанные ч-з комплексные числа. 3)Возврат с комплексной на временную плоскость посредством ф-лы Эйлера: eij=cosα+jsinα Um= Um eiju Im= Im eiji
11.Комплексные схемы замещения идеальных элементов электрических цепей. Законы Кирхгофа в комплексной форме. Законы Кирхгофа в комплексной форме: 1)В установившемся синусоидальном режиме сумма комплексных амплитуд токов в узле электрической цепи равна нулю.ΣIm=0 2)В установившемся синусоидальном режиме сумма комплексных амплитуд напряжений в контуре равна нулю. ΣUm=0 Комплексные схемы замещения идеальных эл-тов: 1)Резистивный эл-т: Im=GUmejφu=YUm где G- проводимость, Y – компл.проводимость. Мгновенная мощность: p=(RI2/2)*(1+cos2(ωt+φU)) Активная мощность: P=RI2 Действующее значение переменного тока: P=UI 2)Индуктивный эл-т. Um=jωLIm=xLIm=ZLIm, где xL=ωL=Um/Im – индуктивное сопротивление. Обратная величина -индуктивная проводимость, ZL –комплексное сопротивление. Мощность: p=-UIsin2(ωt+φI) 3)Ёмкостной эл-т. Im=ωCUm Компл. сопротивление и проводимость: ZC=1/jωC; YC=jωC; Мощность: p=-UIsin2(ωt+ φI)	12.Частотные свойства цепей переменного тока. Методы построения схемных функций. Схемная ф-ция – зависит от отклика и воздействия токов или напряжений. Если есть зависимость токов от частоты. 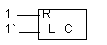Схема обл. 2 входами, м/у кот. может появляться напряжение. Комбинации: 1)U/I=Z – входное сопротивление. 2)I/U- входная проводимость. U,I –зависят от частоты.Классы схемных ф-ций: 1)U2/U1 =Ku1,2 – безразмерный коэф. передачи = схемная ф-ция. 2)i1/i2=Ki1,2; 3)Перекрёстные взаимодействия: U2/i1=Z1,2 –передаточное сопротивление. U1/i2=Z2,1 4)Передаточная проводимость: i2/U1=Y21, i1/U2=Y12 Методы построения сх.ф-ций: 1)Построения ур-й: а)Люб. способом построить систему ур-й (параметрических или комплексных) и свести её к одному. б)Построить СУ по люб. методу анализа, в кот. в явном виде присутствуют отклики и воздействия. в)Р-е полученной СУ люб.способом. г)Преобразование и нахождение искомых величин для схемных ф-ций. 2)Метод преобразований: Всю ЭЦ необх. свести к 1 или 2 эл-там, на кот. организуется схемная ф-ция. Для входных сх. ф-ций – 1 эл-т, для передаточных – больше. После преобразований должна получиться сх.ф-ция, явно зависящая от частоты. 3)Топологический метод: основан на граф. построении сх.ф-ций и граф. комбинации ид.эл-тов.	13. Явление резонанса. Последовательный, параллельный колебательные контуры. Резонанс – это полная компенсация (уничтожение) реактивного сопротивления внутри колебательной системы. В эл. схеме: Z(jω) = R + jX. Резонанс – когда X = 0. Условия возникновения: 1) при некотором φ -> XL = XC; 2) сдвиг фаз между током и напряжением отсутствует. Типы резонанса:1) р. токов(в параллельных),2) р. напряжений (в последовательных системах). Типы колебательных контуров: 1)параллельные, 2)последовательные, 3)смешанные. В простом последовательном контуре: Z(jω) = R + j(ωL – 1/ωC). Резонансная частота контура: Характеристическое сопротивление индуктивного контура: ρ=1/(ω0С). Добротность =коэф. передачи по напряжению при резонансной частоте ω0. Q= ρ/R, где R – активное, а ρ – реактивное сопротивление в сети. Затухание d –обратная величина.	14. Явление резонанса. Сложный колебательный контур. Резонанс – это полная компенсация (уничтожение) реактивного сопротивления внутри колебательной системы. В эл. схеме: Z(jω) = R + jX. Резонанс – когда X = 0. Условия возникновения: 1) при некотором φ -> XL = XC; 2) сдвиг фаз между током и напряжением отсутствует. Типы резонанса: р. токов, р. напряжений. Типы колебательных контуров: параллельные, последовательные, смешанные.	15.Понятие об электрических цепях с индуктивной связью. Индуктивные элементы (катушки) взаимодействуют друг с другом. Коэффициент воздействия одной на другую наз. взаимоиндуктивностью М. В уравнениях от каждой катушки она учитывается так же, как и обычная индуктивность. М=К*корень(L1*L2), где К – геометрический коэф. связи, зависящий от взаимного расположения катушек. В зависимости от направления тока в катушках включение может быть согласным (ток протекает однообразно) или встречным. Катушки включаются последовательно, иначе нет смысла – они могут быть заменены на одну. Для описания магнитных систем применимы законы Ома и Кирхгофа.
16.Расчет цепей содержащих взаимоиндуктивности. Алгоритм анализа 1) определить тип включения катушки (согласное/встречное); 2) построить сх. замещения цепи в комплексной форме; 3) постр. системы ур-ий для взаимоинд. катушек; 4) постр. общую систему ур-ий; 5) решить систему; 6) определить параметры режимов элементов или самой цепи;	17.Понятие о линейных четырехполюсниках. Первичные параметры. Вторичные параметры. Четырехполюсник – представление различных устройств электротехники в виде черного ящика, который хар-ся только входными параметрами. Бывают: 1) линейные (содержат только линейные эл-ты) и нелинейные; 2) активные (содержат источники энергии) и пассивные. Модель ч.: Y = FX. X – столбец воздействий, Y – откликов, F – матрица первичных параметров. Вторичные параметры – это: 1) характеристическое сопротивление Z0 (на которое нагружаются выходы ч.); 2) передаточная хар-ка (коэф. передачи) U2/U1.	18.Понятие о линейных четырехполюсниках. Схемы замещения четырехполюсников. Соединение четырехполюсников. Четырехполюсники могут моделироваться стандартными схемами замещения, но при этом последние должны содержать все ветви, кот. реализуют вх. и вых. воздействия. Основные схемы: Г-образная, П-обр., Т-обр., Н-образная. Соединия четырехполюсников: 1) каскадное (выходы одного ко входам другого) 2) последовательное 3) параллельное 4) последовательно-паралл. 5) паралл-посл.	19.Расчет электрических цепей при периодических несинусоидальных воздействиях. Пусть f(t)- негармоническая ф-ция, имеет кон. число кон. разрывов. Тогда её можно разложить в ряд Фурье: f(t)=A0+A1sin(ωt+φ1)+…+ Aksin(kωt+φk), где ω – задано, 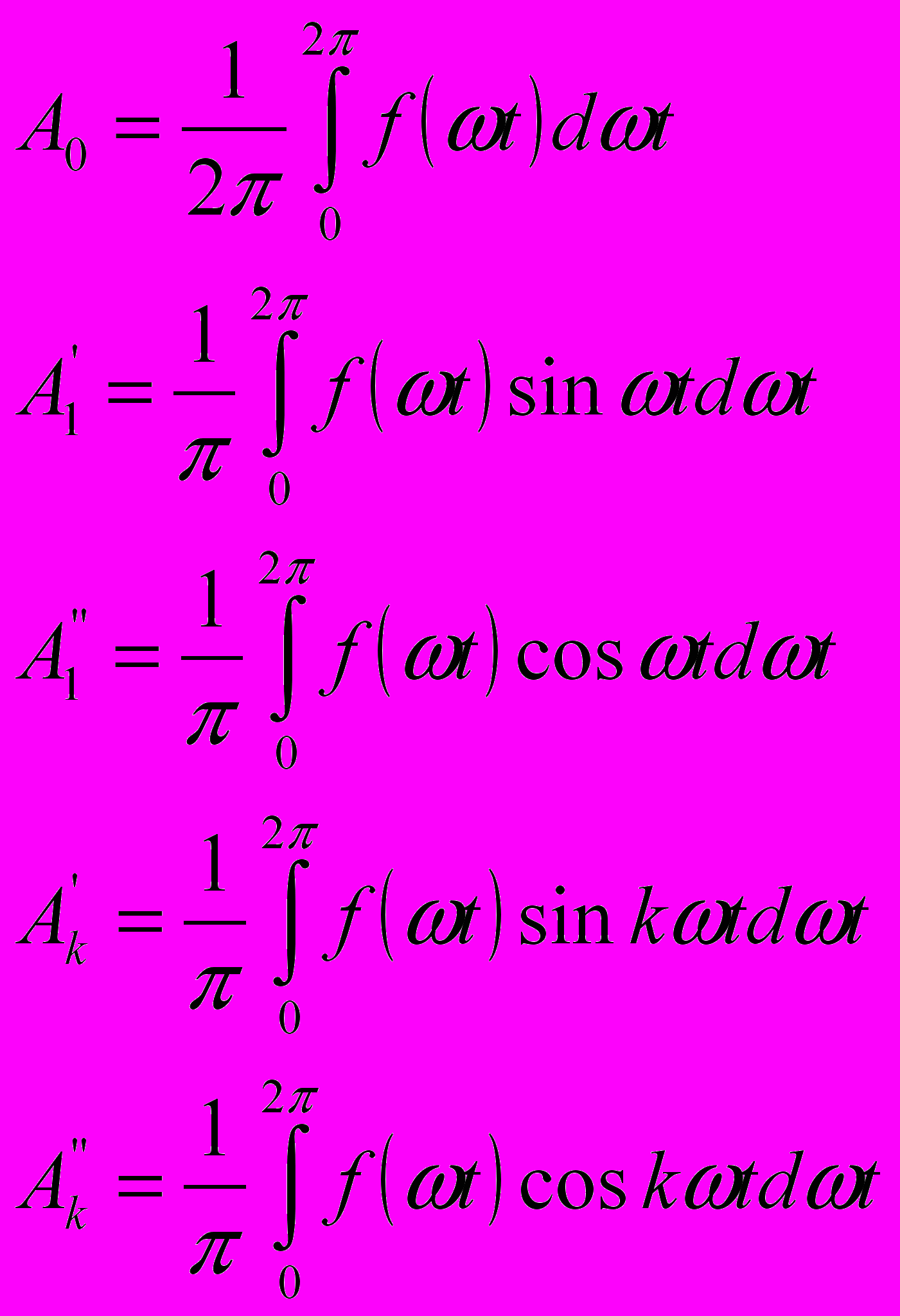Правила симметрии: 1)Если ф-ция симметрична отн. оси абсцисс со сдвигом на полпериода, то в разложении отсутствует постоянная сост. А0; 2)Если ф-ция симм. отн. оси ординат, то в разл. отс. синусы. 3)Если ф-ция симм. отн. еачала координат, то в разл отс. косинусы. Алгоритм решения: 1)Разложение ф-ции в ряд Фурье; 2)Построение схемы замещения исх. ЭЦ для люб. гармон. сост. 3)Р-е всех задач анализа схемы замещения исх. цепи при значениях гармоник. 4)Представление р-я в виде суммы р-й на всех гармониках. 2)Если ф-ция симм. отн. оси ординат, то в разл. нии отс.	20.Переходные процессы в электрических цепях. Постановка задачи. Математическая модель. Классический метод анализа. Пусть в ЭЦ присутствуют:R,L,C, ист.тока, ист. напряжения, зависимые источники, ключ-> Характеризуется временем коммутации(замыкания-размыкания – если стремится к 0->ключ –идеальный эл-т).М.б. на замыкание и на размыкание. Обозначение: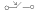Если на размыкание, стрелка наоборот. При размыкании ключа в ЭЦ начинается переходный процесс. Математическая модель переходного процесса: (в качестве базы исп. законы Кирхгофа и изв. методы анализа): 1)преобразование системы интегро-диф. ур-й к 1 ур-ю k-го порядка: 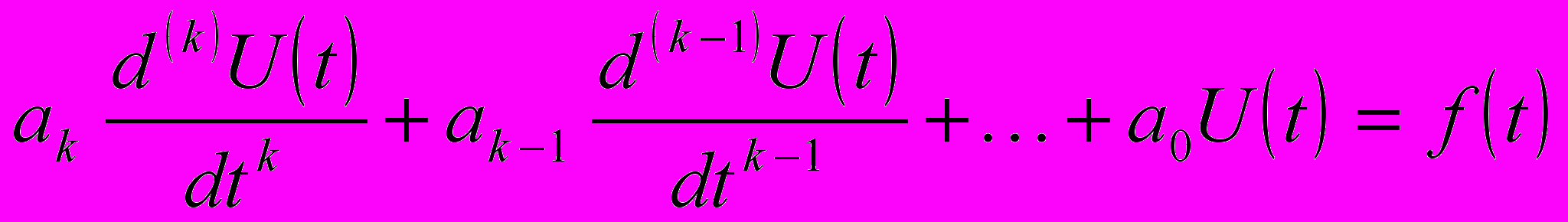U(t)=Uop(t)+Uчр(t), где Uop(t) – общее р-е, Uчр(t) – частное р-е. Для однозначного р-я нужно знать все производные ф-ции U начиная с k-ой, и что все коэф. зависят от R,L,С. Если параметры эл-тов зависят от времени, то р-е м.б. только численными методами. Если R,L,C=CONST, то р-е производится станд. методами теории инт. и ДУ. Классический метод анализа: цель: определить свободную составляющую(не зависит от источников, общее р-е) и вынужденную(частное р-е).
21.Переходные процессы в электрических цепях. Алгоритм классического метода анализа. Постановка задачи расчета цепей первого порядка. Алгоритм: 1)Определение общего вида Ucв(t)=Akepkt – свободной составляющей. 2)Вынужденная сост. повторяет ф-цию источника по принципу суперпозиции (если источников много). 3)На базе предложенного р-я определить все константы pk, кот. определяются на основе характеристического ур-я или по топологии ЭЦ. 4)На основании полученных pk определить константы Ak, кот. определяются из начальных условий для искомой ф-ции и её производных.(t=0,t≥tk). 4)Запись общего вида р-я с учётом определённых констант. Построение характеристического ур-я: 1) Построение схемы замещения исх. ЭЦ. Схема д.б. операторной с учётом некоторых особенностей: => Короткое замыкание => Разрыв. => то же самое 1/СР L/P Ключ на замыкание => короткое замыкание. Ключ на размыкание => разрыв. 2)Построение входного операторного сопротивления(при этом необх. разорвать люб. из полученных в результате операторного замещения ЭЦ).Входное сопротивление строится отн. незамкнутого ключа 3)Z(p)=0 – находим все корни рк, кот. будут явл. корнями характ. ур-я. Постановка задачи расчёта цепей 1 порядка: Для начала анализа необх. установить, какие эл-ты присутствуют: а)R; б)U(t), i(t)+зависимые ист. и ключи. в)tk г)С(t)- реактивные эл-ты. Кол-во – люб., но все- линейно зависимы (можно преобразовать к 1 эл-ту). Цепь 1-го порядка сод. 1 реактивный эл-т.	22.Переходные процессы в электрических цепях. Анализ цепей первого порядка. алгоритм анализа: 1)a1*dU(t)/dt + a0U(t)=f(t) Начальные условия: U(0)=0; i(t); U(t)=Uсв(t)+Uвс(t); Ucв(t)=A*ept 2)Определить: Uвс(t). 3)p=a0/a1 4)U(0)=Ae-a0/a1+Uвс(0) В момент t=0 происходит изменение энергетических состояний: U(0-) сразу до U(0+) и сразу после -коммутатор. Переменные состояния не изменяются мгновенно. iL(0-) =iL(0+); UC(0-)=UC(0+). 5)Для люб. ЭЦ 1-го порядка р-е имеет общий вид: U(t)=(U0-Uвс(0))e*(-a0/a1)+Uвс(t) Все параметры режима ЭЦ опр. на основе этого ур-я. При анализе ЭЦ 1 порядка с гармоническими источниками переходные формы процесса описываются стандартной формой р-я ур-й 1 порядка. Вынужденная сост. описывается гармонической ф-цией ист. Переходный процесс описывается суммой экспоненциальной и гармонических составляющих.	23.Переходные процессы в электрических цепях. Анализ цепей второго порядка. Система 2 порядка представляет собой ЭЦ, сод. 2 типа эл-тов:ёмкость и индуктивность. Для её описания необх. построить систему ДУ: a2d2U/dt + a1dU/dt+a2U=f(t) Р-е сост. из вынужденной и своб. составляющих. Условия: должны быть определены t=0, U(0), U’(0), иначе не будет однозначного р-я. Рассмотрим 4 типа р-я. Цель: найти i(t), U(t). U(t)=Uсв(t)+Uвс(t). Вынужденная сост. опр. ф-циями источника. U(t)=Aept; p2+2δp+ω2=0, где δ – затухание. Решения: 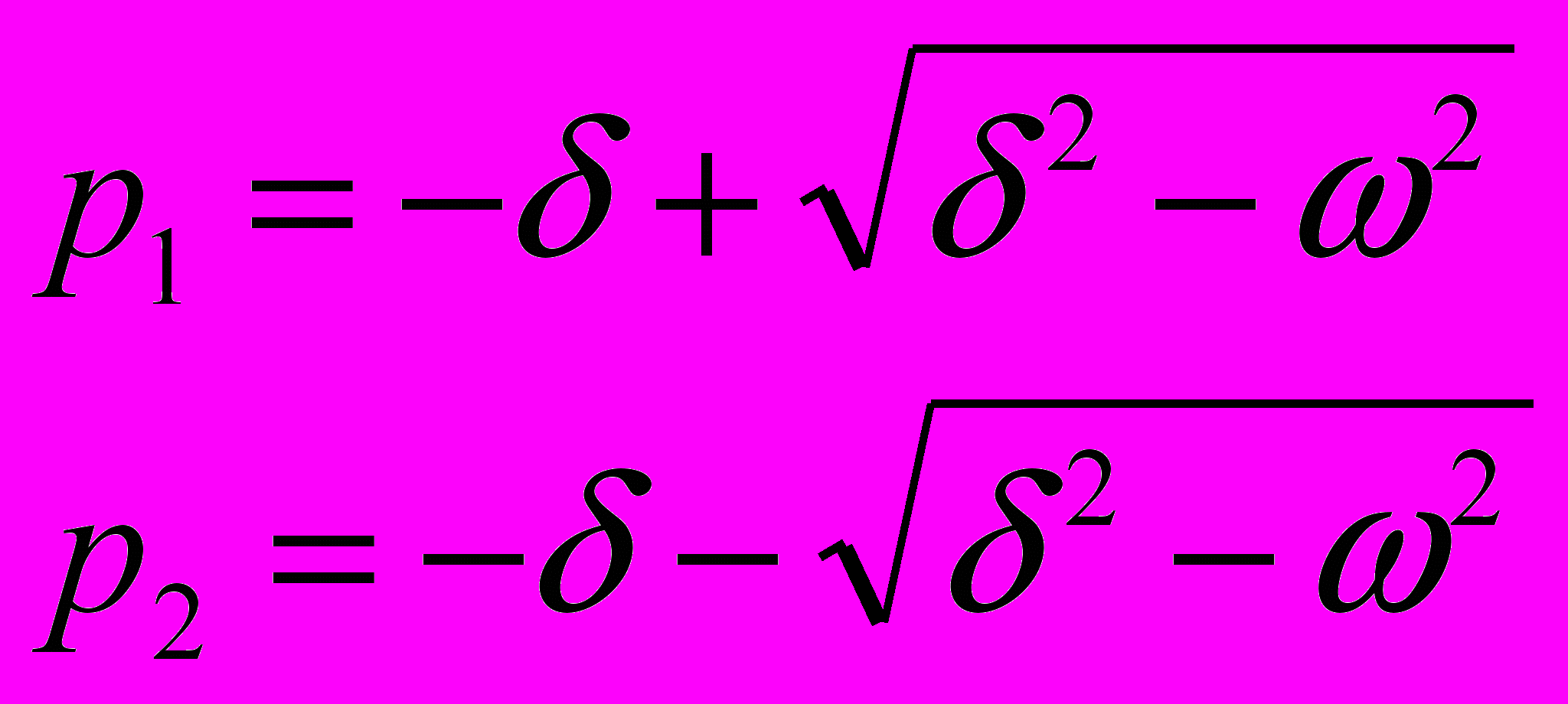1) δ2> ω2; p1≠p2; Колебаний не будет. 2)δ2< ω2; p1≠p2; p1=- δ+jωсв; p2=- δ-jωсв; Затухающая синусоида. 3) δ2= ω2; p1=p2=- δ; Критический режим. 4) δ2=0; p1=p2=jω; Колебания с резонансной частотой. 5) δ2<< ω2;напр., ист. постоянного напряжения. Режим самогенерации. Эл энергия переходит в магнитную с минимальными потерями.	24.Операторный метод анализа электрических цепей. Оператор Лапласа явл. интегральным. Он преобразует ф-цию f(t) к виду F(р), где Р=а+jb. f(t) – оригинал, F(р) – изображение, р€С. f(t) Не должна иметь разрывов 2 рода. 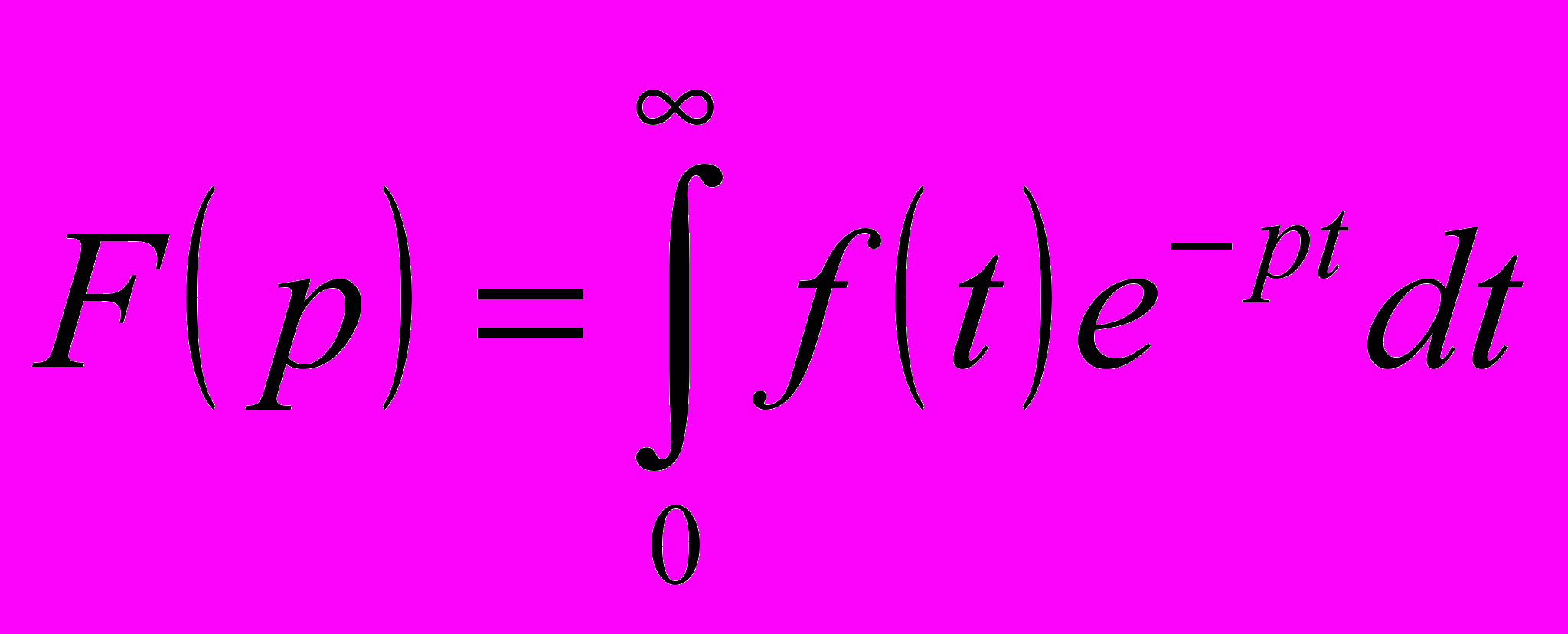-выход из плоскости времени. Происходит преобразование элементного уровня в усл.-граф. изображение. Алгоритм: 1)Построить операторную схему замещения исх. ЭЦ (каждый эл-т формируется за счёт интегрального преобразования Лапласа). 2)Формулировка и р-е задачи на операторной плоскости. 3)Возврат с плоскости опер. изображений на плоскость временных зависимостей. Операторные преобразования осн.эл-тов ЭЦ: 1) E0 E(p)=E0/p; J(p)=J0/p 3) E(t)=Emejωt – источник напряжения, зависящий от времени. E(p)=Em/jω-p 4)R U(p)=RI(p) Законы Ома инвариантны по отн. к операторному методу. 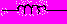5) U(t)=L*di(t)/dt U(p)=-Li0+pL(p); При применении преобразования Лапласа к реактивным эл-там в схеме замещения появл. источники пост. тока и напряж. кот. характеризуют переменное сост. на этих эл-тах. 6) U(t)=C*dU(t)/dt i(p)=-CU0+CpU(p) При преобразовании пассивных эл-тов ЭЦ в схеме должны присутствовать операторные сопр. Следствия из законов Кирхгофа явл. справедливыми на плоскости разложения a+jb. Обратное преобр. Лапласа:	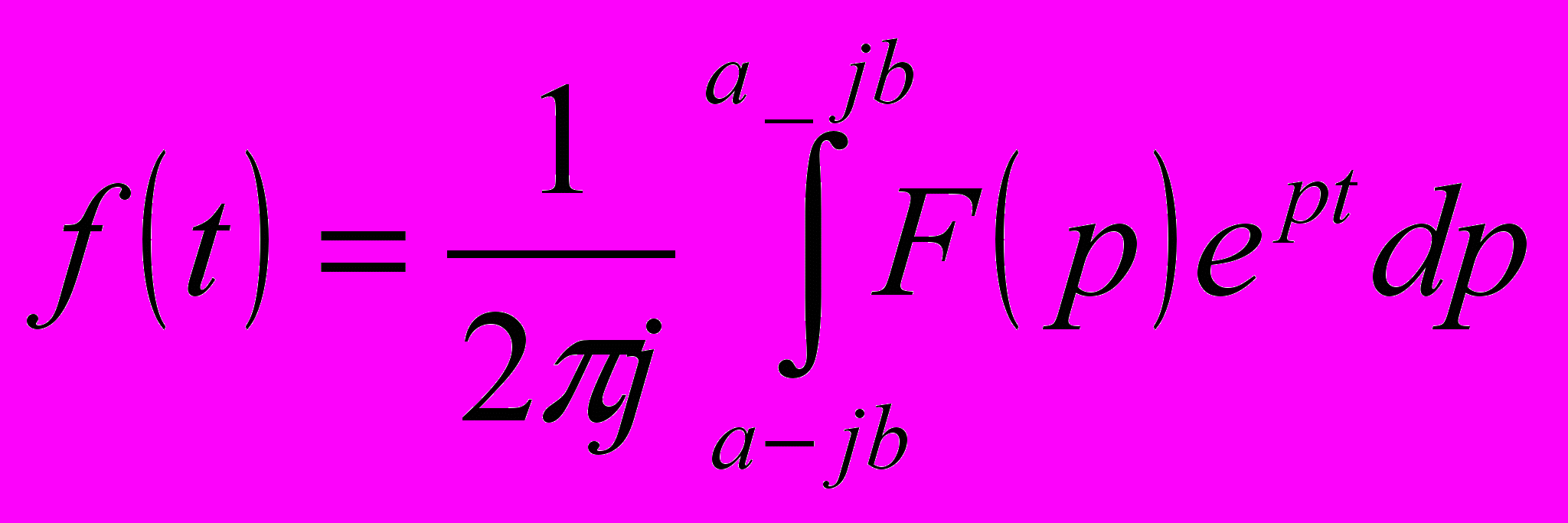25.Анализ и расчет электрических цепей с нелинейными элементами. Нелинейные резистивные элементы. Методы описания характеристик. R=R0+R(U;L), где R(U;L)- динамическое сопротивление. Люб. эл-т приводит к тому, что зависимость тока и напряжения становится нелинейной. Методы описания характеристик нелинейных эл-тов: 1)топологические; 2)аналитические: 3)численные; Описание нелинейной хар-ки: 1)табличное(таблица токов и напряжений); 2)аналитическое: описание с помощью станд. ф-ций; 2 методики: 1)Интерполяция: табличное описание ф-ции с помощью зависимости. Решаем, получаем таблицу коэф., кот. характеризует систему. 2)минимизация: а)выбор исх. фции.Сравн результатов с эксп. данными. б)f(U1)-U1=Δ1 и т.д. – невязки показывают разницу исх. и эксп. ф-ций. в)стоится целевая ф-ция: 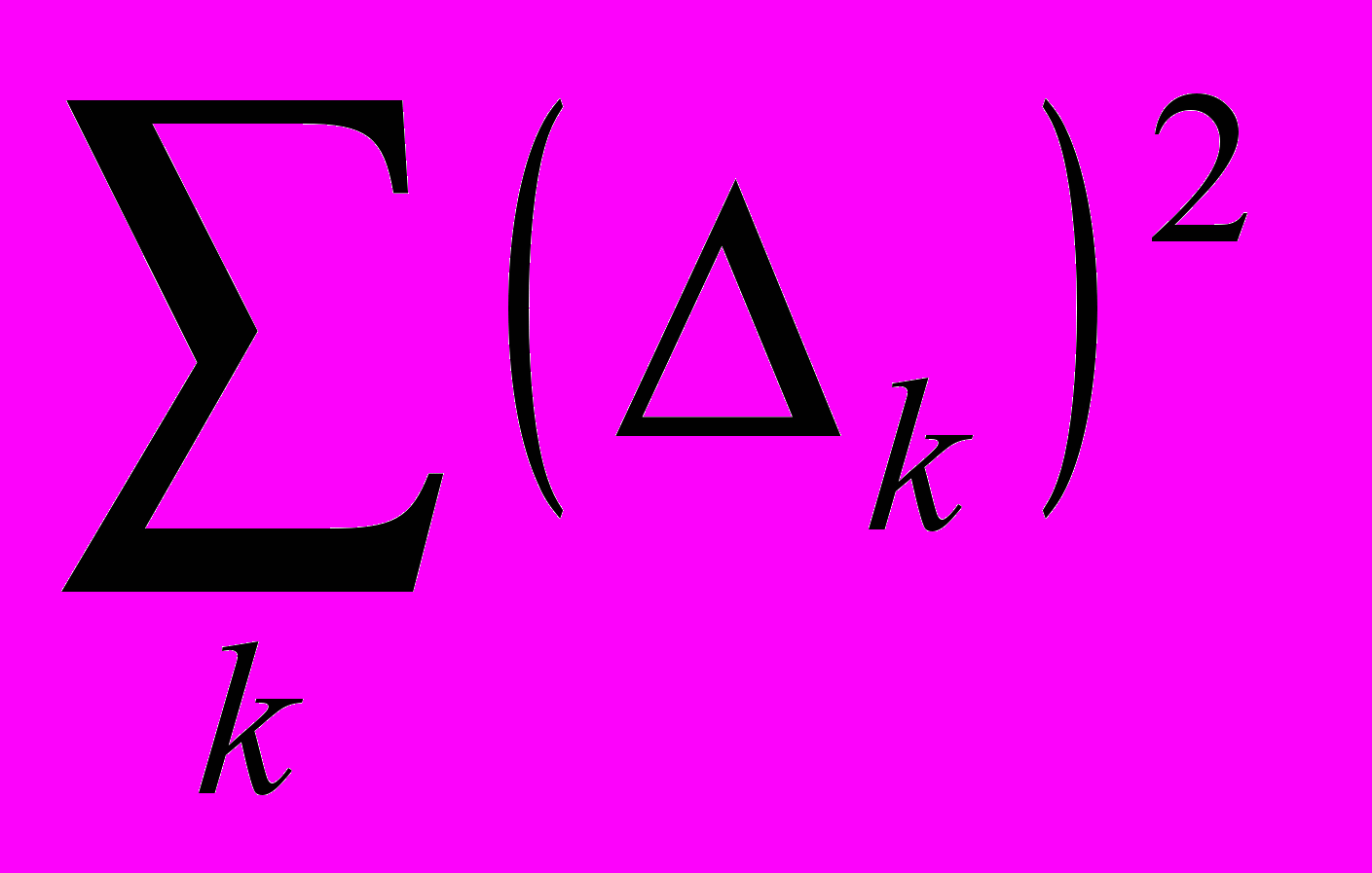-сумма по модулю всех невязок. г)минимизируется. д)коррекция получившейся ф-ции.
26.Расчет нелинейных цепей содержащих резистивные элементы. 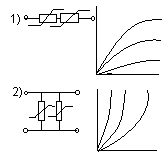R R1 R2 R1 R2 R1 R2 R1 R2 R Складываем по точкам. 31.Полевые транзисторы. Тиристоры и оптоэлектронные приборы. Полевые транзисторы – основаны на положительности всего лишь одного типа носителей заряда и представляют собой управляемые сопротивления. 1) Полевые транзисторы с управляющим p-n переходом. 2) Полевые транзисторы с индуцированным 3) Полевые транзисторы со встроенным Тиристоры – тройной p-n переход.	27.Анализ активных цепей. Активные цепи – ЭЦ, эл-ты кот. моделируются с помощью зависимых ист. энергии. 2 метода: 1)Метод контурных токов(используется ист. напряжения, упр. током); 2)метод узловых напряжений(исп. ист. тока упр. напряжением). Алгоритм: 1)Определить метод =тип источника. 2) при необходимости произвести преобразование нерегулярных ист. в регулярные. Исходный ист. д.б. не идеальным – нужно добавить сопротивление. U=ZI I ZU ZI U=ZI I I=Uупр/ZI; U=ZUу­/ZI; G=1/ZU; Y=U/ZU а)преобразовать нерегулярные ист. в регулярные. б)построение схемной модели активного эл-та. в)реализуем построения схемы замещения исх. ЭЦ с учётом схемной модели активного эл-та. 4)построение ур-й по люб. выбранному методу; 5)р-е	28.Элементная база современных электронных устройств. Электронные приборы. Электронные лампы. Электронные приборы – это приборы, основанные на эффектах, связанных с перемещением носителей зарядов в вакууме, газе, жидкостях и твёрдых телах под воздействием различного вида полей и излучений (электрические, магнитные, акустические поля, оптическое и радиационное излучение и их комбинации). Общая схема функционирования: управляющая ф-ция c(t), кот. отображает способ преобразования энергии, подаётся на электронный прибор, кот. сост. из: 1)Источник(энергии), 2)Преобразователь (реализует ф-цию f(t)=k*c(t)), 3)потребитель энергии. Энергия, затрачиваемая на управление, д.б. во много раз < чем энергия передачи. Отн. энергии передачи к энергии упр. определяет эффективность прибора. Если энергия упр.>энергии передачи прибор считается неэффективным. Вакуумные приборы(электронные лампы) – носители заряда – электроны. Источники электронов – металлы с невысокой работой выхода. Для создания потока электронов исп. следующие методы: 1)нагревание(>>распространён); 2)бомбардировка радиационными частицами; 3)Освещение. 1-вакууная колба, 2-анод(приёмник электронов), 3-сетка(если добавить, получится триод), 4- металл(катод), 5-нагреватель(спираль). Сетка позволяет увеличивать/уменьшать сигнал в зависимости от направления тока, т.е. создаёт ф-цию управления.	29.Газоразрядные приборы. Физические основы работы полупроводниковых электронных приборов. Газоразрядные приборы – кр.электронов, носителями заряда в них явл. и ионы газа, т.к. в отл. от вакуумных ламп, они заполнены инертным газом. За счёт действия поля электроны ускоряются, а при их столкновении с молекулами газа начинается ионизация и происходит отдача энергии в виде квантов света. При включении ионизация сначала сущ. в виде тлеющего разряда, а потом переходит в дуговой. Лампа изнутри покрыта люменфором, кот. преобразует ультрафиолет в белый цвет. Полупроводниковые приборы: их осн. ф-ция – управление параметрами. Полупроводники:1)Объёмные эффекты=>Датчики Холла(изменение подвижности носителей заряда в магн. поле). Минус – слабо реализована управляющая ф-ция. 2)Контактные явления(на границе раздела 2 твёрдых тел). М.б. исп. разл. типы контактов: м/у металлом и полупроводником; м/у полупроводником и диодом; м/у 2 полупроводниками с разл. типами носителей зарядов(у одного избыток – надо вводить донорные примеси, валентность кот. > чем у полупроводника; а у другого – недостаток – надо вводить акцепторные примеси, вал. кот. < чем у полупроводника). В результате контактной разности потенциалов на границе раздела 2 сред образуется область пространственного заряда(ОПЗ). Подключим ист. энергии: если на одном конце +, на др. - , то ОПЗ уменьшится и будет ток. А если наоборот – ОПЗ увел., закрытый pn-переход, тока нет. Т.е. пропукание тока только в 1 направлении. In=Iдиффузионныйexp(qUвнеш/kT)-I0 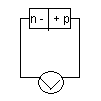Ip=Iдиффузионныйexp (-qUвнеш/kT)-I0	30.Диоды. Биполярные транзисторы. 1) Выпрямительные – эффект пропускания тока в одном направлении. 2) Импульсные – предназначены для импульсной техники, обладают односторонней проводимостью. 3) Стабилитропы – включаются в обратном смещении, при определенных условиях наступает пробой p-n перехода, наблюдается увеличение тока при почти неизменном напряжении. 4) Варикаты - диоды, включаемые в напряжения и представляющие собой управляемые конденсаторы в зависимости от напряжения. 5)  Туннельные диоды – используются в качестве высокочастотных генераторов, для защиты от перегрузок (токовая защита). 6) СВЧ-диоды – в области пространства зарядов носители не накапливаются, фильтрация ВЧ-сигналов. 7) Лавинопролетные – реализованы лавинной пробой,(так же как в стабилитропах), и лавина, движущаяся от анода к катоду, сопротивление диода мало, используются в генераторной технике. 8)  Диоды Ганжа – пакет перемещения от анода к катоду со скоростью ~105м\с, меняя длину полупроводника р, регулируя частоту. 9) Диоды Шоттки – как обычные диоды, быстродействующие(квази-р-область, инверсная область). Транзисторы 1) Биполярные. Коллектор База управления Эмиттер(содержит >кол-во примесей)