Магазины электрических ве­личин

Вид материала

Документы

Содержание Маха конус Конус Маха, возни­кающий от точечно­го источника воз­мущений в сверх­звуковом потоке. Маха число МАХЕ (единица Махе) Рис. 1. Маятники: а — круговой математи­ческий; б — физический. Математический маятник. С будет описывать на сфере радиуса l Физический маятник. К на продолжении прямой ОС Рис. Схема МОП-транзистора. Медленные нейтроны Шредин­гера уравнением. Зависимость потен­циальной энергии межатомного вз-ствия U(r) от межъядерного расстояния r.  — глубина потенциаль­ной ямы, r В. Г. Дашевский, А. И. Китайгородский.

Подобный материал:

• Рабочей программы дисциплины Электроэнергетические системы и сети по направлению подготовки, 21.71kb.
• Отчет по лабораторной работе должен содержать: наименование работы и номер, схемы, 365.83kb.
• Экзаменационные вопросы по курсу «Электротехника и электроника», 23.91kb.
• Бизнес-план магазина товаров для детей Содержание, 138.19kb.
• 1. Основные понятия и обозначения электрических величин и элементов электрических цепей., 277.03kb.
• Цифровой вольтметр щ-304, 137.06kb.
• Телемеханики, 26.01kb.
• Отдел метрологического обеспечения измерений электрических величин, 42.58kb.
• Курсовая работа по курсу «основы физических измерений», 226.86kb.
• Теория электрических цепей (часть, 63kb.

МАХА КОНУС, конич. поверхность, ограничивающая в сверхзвуковом потоке газа область, в к-рой сосре­доточены звуковые волны (возмущения), исходящие из точечного источ­ника возмущений А (рис.).



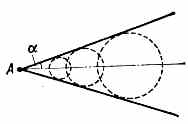
Конус Маха, возни­кающий от точечно­го источника воз­мущений в сверх­звуковом потоке.


В однород­ном сверхзвуковом потоке газа угол а между образующими М. к. и его осью наз. углом Маха; он связан с Маха числом М соотношением sin =1/M.

МАХА ЧИСЛО [по имени австр. учёного Э. Маха (Е. Mach)] (M-число), характе­ристика течения газа с большими ско­ростями, равная отношению скорости течения v к скорости звука а в той же точке потока; М= v/a. Когда тело дви­жется в газе, М. ч. равно отношению скорости тела к скорости звука в этой среде. М. ч. служит одним из осн. подобия критериев в гидроаэромеха­нике и явл. мерой влияния сжимае­мости газа на его движение. При М <<1 газы можно считать несжима­емыми. В воздухе сжимаемость необ­ходимо учитывать при скоростях v>100 м/с, к-рым соответствует число М>0,3. При М<1 течение наз. до­звуковым, при М=1 — звуковым, а при М>1 — сверхзвуковым течением. В области течений с М>5 (т. н. гиперзвуковые течения) ста­новятся существенными физико-хим.

398


превращения в газе, сжимаемом в ударной волне или тормозящемся в пограничном слое.

МАХЕ (единица Махе) (махе, ME), устаревшая внесистемная единица концентрации радиоактивных нуклидов. Была введена австр. физиком Г. Махе (Н. Mache). Иногда применя­ется в дозиметрии минеральных вод, лечебных грязей и т. п.; в М. указы­вают концентрацию в воде или в воз­духе радона. 1 махе=3,64 эман=3,64•10^-10кюри/л=13,47•10³ Бк/м³.

МАЯТНИК, твёрдое тело, совершаю­щее под действием приложенных сил колебания около неподвижной точки или вокруг оси. Обычно под М. пони­мают тело, совершающее колебания под действием силы тяжести; при этом ось М. не должна проходить через центр тяжести тела. Простейший М. состоит из небольшого массивного груза С, подвешенного на нити (или лёгком стержне) длиной l. Если счи­тать нить нерастяжимой и пренебречь размерами груза по сравнению с дли­ной нити, а массой нити по сравнению



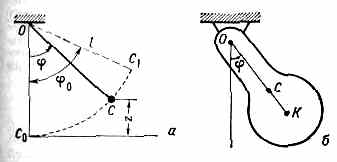
Рис. 1. Маятники: а — круговой математи­ческий; б — физический.


с массой груза, то груз на нити можно рассматривать как материальную точ­ку, находящуюся на неизменном рас­стоянии l от точки подвеса О (рис. 1, а). Такой М. наз. м а т е м а т и ч е с к и м. Если же колеблющееся тело нельзя рассматривать как материаль­ную точку, то М. наз. ф и з и ч е с к и м.

Математический маятник. Если М., отклонённый от равновесного поло­жения c₀, отпустить без нач. ско­рости или сообщить точке С скорость, направленную перпендикулярно ОС и лежащую в плоскости нач. отклоне­ния, то М. будет совершать колеба­ния в одной вертикальной плоскости и точка С будет двигаться по дуге окружности (плоский, или круговой математич. М.). В этом случае поло­жение М. определяется одной коорди­натой, напр, углом отклонения  от положения равновесия. В общем слу­чае колебания М. не являются гармо­ническими; их период Т зависит от амплитуды. Если же отклонения М. малы, он совершает колебания, близ­кие к гармоническим, с периодом:

Т=2(l/g),

где g — ускорение свободного паде­ния; в этом случае период Т не зави­сит от амплитуды, т. е. колебания изохронны.

Если отклонённому М. сообщить нач. скорость, не лежащую в плоскости

начального отклонения, то точка С будет описывать на сфере радиуса l кривые, заключённые между двумя параллелями z=z₁ и z=z₂ (рис. 2, а), где значения z₁ и z₂ зависят от нач. условий (сферический М.). В ча­стном случае, при z₁=z₂ (рис. 2, б) точка С будет описывать окружность в горизонтальной плоскости (кони­ческий М.). Интерес представляет ещё циклоидальный маятник, коле­бания к-рого изохронны при любой величине амплитуды.



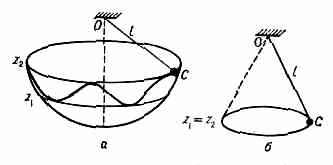
Рис. 2. Маятники: а — сферический; б — конический.

Физический маятник. М. представ­ляет собой тв. тело, совершающее под действием силы тяжести колебания вокруг горизонтальной оси подвеса (рис. 1, б). Движение такого М. вполне аналогично движению кругового математич. М. При малых углах отклоне­ния  М. также совершает колебания, близкие к гармоническим, с периодом:

Т=2(I/Mgl),

где I — момент инерции М. относи­тельно оси подвеса, l — расстояние от оси подвеса О до центра тяжести С, М — масса М. Следовательно, период колебаний физ. М. совпадает с перио­дом колебаний такого математич. М., к-рый имеет длину l₀=I/Мl. Эта длина наз. приведённой длиной данного физ. М.

Точка К на продолжении прямой ОС, находящаяся на расстоянии l₀ от оси подвеса, наз. центром качаний физ. М. При этом рас­стояние ОK=l₀ всегда больше, чем ОС=l, Точка О оси подвеса М. и центр качания обладают св-вом взаим­ности; если ось подвеса сделать про­ходящей через центр качаний, то точ­ка О прежней оси подвеса станет но­вым центром качаний и период колеба­ний М. не изменится. Это св-во вза­имности используется в оборотном маятнике для определения приведён­ной длины l₀; зная l₀ и Т, можно найти значение g в данном месте.

Св-вами М. широко пользуются в разл. приборах: в часах, в приборах для определения ускорения силы тя­жести, ускорений движущихся тел, колебаний земной коры, в гироскопич. устройствах, в приборах для эксперим. определения момента инерции тел и др. См. также Фуко маятник.

• Бухгольц Н. Н., Основной курс тео­ретической механики, 9 изд., ч. 1, 6 изд., ч. 2, М., 1972; Т а р г С. М., Краткий курс теоретической механики, 9 изд., М., 1974, гл. 28; X а й к и н С. Э., Физические осно­вы механики, 2 изд., М., 1971, гл. 13.

С. М. Тарг.

МГД-ГЕНЕРАТОР, то же, что магнитогидродинамический генератор.

М — Д — П-СТРУКТУРА (структура металл — диэлектрик — полупровод­ник), конденсатор, состоящий из пла­стины полупроводника, слоя ди­электрика и металлич. электрода. При зарядке конденсатора электропро­водность полупроводника изменяется вблизи границы раздела с диэлектри­ком вследствие изменения концент­рации носителей заряда. На этом основана работа ряда приборов.



Рис. Схема МОП-транзистора.


Наиболее распространён кремниевый МОП-т р а н з и с т о р (металл — окисел металла — полупроводник). На подложке Si р-типа (рис.) окисле­нием создаётся тонкий диэлектрич. слой двуокиси SiО₂ (толщиной 1000 Å) и наносится металлич. электрод (з а т в о р). Под поверхностью диэлектри­ка в Si р-типа создаются на нек-ром: расстоянии друг от друга две области с электронной проводимостью, к к-рым подводятся металлич. контакты (исток и сток). Если к затвору приложить положит. потенциал, то все эл-ны под ним в Si (р) притянутся к тонкому слою диэлектрика, создав там проводящий инверсионный слой n-типа. В результате между стоком и истоком образуется канал, по к-рому течёт ток. Подобная система эквива­лентна вакуумному триоду (исток — катод, сток — анод, затвор — сетка). Она может служить также элементом памяти. Для этого диэлектрик дела­ется двухслойным — тонкий слой SiО₂ и нитрида кремния. Электрич. заряд, введённый в Si, можно (с помо­щью нек-рых физ. процессов) перевести из Si в ловушки на границе окисел — нитрид. В этих ловушках заряд сохра­няется длительно после снятия напря­жения между затвором и подложкой (запоминание). Это состояние можно считывать по изменению свойств приповерхностной области подложки. М — Д — П-с.— один из базовых элементов твердотельной электроники. Они служат также для изучения по­верхностных свойств полупроводни­ков (вблизи его границы с диэлектри­ком).

• Мейндл Дж., Элементы микроэлек­тронных схем, «УФН», 1979, т. 127, в. 2; 3 и С. М., Физика полупроводниковых при­боров, М., 1973.

399


МЕГА... (от греч. megas — большой), приставка к наименованию единицы физ. величины для образования наименования кратной единицы, рав­ной 10⁶ исходных единиц. Сокр. обоз­начение — М. Пример: 1 МВт (мега­ватт) = 10⁶ Вт.

МЕДЛЕННЫЕ НЕЙТРОНЫ, нейтро­ны с кинетич. энергией менее 100 кэВ. См. Нейтронная физика.

МЕЖАТОМНОЕ ВЗАИМОДЕЙСТВИЕ, взаимодействие между атомами как свободными, так и входящими в со­став одной или разных молекул, кри­сталлов и т. д. М. в. может быть к о в а л е н т н ы м, и о н н ы м, м е т а л л и ч е с к и м, типа в о д о р о д н о й с в я з и и в а н-д е р - в а а л ь с о в ы м. Первые три типа М. в. явл. причиной образования химиче­ских связей в молекулах, атомных и ионных кристаллах, металлах и спла­вах; водородные связи могут образовы­ваться внутри молекул и между раз­ными молекулами в случае, когда между двумя электроотрицат. атома­ми располагается злектроположит. атом Н; ван-дер-ваальсовы М. в. обус­ловливают межмолекулярное взаимо­действие, а также ответственны за нек-рые св-ва молекул (напр., за существование разл. конформеров; см. Изомерия молекул). Энергия ковалентного, ионного и металлич. М. в. ~10² кДж/моль, энергия водородной связи ~10—50 кДж/молъ и энергия ван-дер-ваальсова М. в. ~0,1—1 кДж/моль.

Помимо указанной классификации, М. в. часто делят на валентные и невалентные. К валентным М. в. относят ковалентные, ионные и металлические, а к невалентным — ван-дер-ваальсовы М. в. Вз-ствие типа водородной связи считают либо сла­бым валентным, либо занимающим промежуточное положение между ва­лентным и невалентным М. в. Нева­лентное М. в. может включать не толь­ко чисто ван-дер-ваальсово притяже­ние и отталкивание атомов, но также индукционное и поляризационное, электростатич. и др. М. в. Энергия невалентного М. в. по крайней мере на два порядка меньше энергии ва­лентного М. в.

Ковалентное М. в. возникает в ре­зультате обобществления валентных эл-нов парой соседних атомов. Пони­жение энергии в этом случае выража­ется в обменных интегралах, поэтому Ковалентное межатомное взаимодей­ствие часто называют обменным (см. Обменное взаимодействие). Ковалент­ное М. в. является причиной сущест­вования молекул простых газов (Н₂, Сl₂ и пр.), разл. соединений (Н₂O, NH₃ и пр.), многочисл. органич. мо­лекул (СН₄, Н₃С—СН₃ и пр.), а так­же атомных кристаллов (различных модификаций фосфора и серы, графи­та и пр.).

Ионное М. в. обусловлено переносом валентных эл-нов с одного атома на другой и электростатич. вз-ствием образовавшихся в результате этого переноса ионов. Оно характерно для соединений металлов с наиболее ти­пичными металлоидами (напр., NaCl, СаСl₂, Аl₂O₃), а также для ионных кристаллов (NaCl, CsCl и пр.). М. в. в ионных молекулах и кристаллах чаще всего носит частично ковалентный характер. Так, согласно квантовомеханич. расчётам, в молекуле Na⁺ Cl^-заряды на атомах Na и Сl равны не заряду эл-на е, а составляют 0,8 е, и определённый вклад в стабилиза­цию этой молекулы вносит и обменное вз-ствие.

Металлическое М. в. характерно для чистых металлов и их соединений между собой и связано с наличием эл-нов проводимости, свободно движу­щихся в решётке металла. Эти эл-ны электростатически взаимодействуют с положительно заряженными атомами металлов, скрепляя их между собой. Металлич. М. в., в отличие от ковалентного и ионного М. в., явл. нело­кализованными и ненаправленными.

Водородная связь возникает в том случае, когда между электроотрицат. атомами (атомами, обладающими боль­шим сродством к эл-ну, напр. О, N, F) находится атом Н. Эл-н в атоме Н слабо связан с протоном, поэтому элек­тронная плотность смещается на более электроотрицат. атом. В результате протон «оголяется» и не препятствует сближению атомов О...О, O...N и т. д., расстояние между к-рыми становится близким к тому, к-рое установилось бы в отсутствие атома Н.

Ван-дер-ваальсово М. в. складыва­ется из отталкивания атомов, обуслов­ленного перекрыванием их электрон­ных оболочек, и дисперсионного при­тяжения. При сближении атомов эл-ны, имеющие противоположно направ­ленные спины, отталкиваются. В ре­зультате межэлектронного отталкива­ния электронная плотность в пр-ве между ядрами двух взаимодействую­щих атомов уменьшается, что приво­дит к увеличению энергии межъядер­ного отталкивания. Т. о., ван-дер-ваальсово отталкивание атомов при их сближении складывается из отталки­вания эл-нов и электростатич. оттал­кивания ядер, дезэкранированных вследствие вз-ствия эл-нов. Диспер­сионное притяжение атомов возникает в результате корреляции в движении эл-нов и явл. чисто квант. эффектом. Ван-дер-ваальсово М. в. ответственно за отклонение св-в реальных газов от св-в идеальных газов, за относит. стабильность разл. конформеров, за структуру и св-ва мол. кристаллов и жидкостей и т. д.

М. в. определяется распределением электронной плотности в системе ато­мов и полностью описывается Шредин­гера уравнением. Для системы двух атомов решение ур-ния Шредингера, учитывающего кулоновское притяжение эл-нов к ядрам, межэлектронное и межъядерное отталкивание, а также кинетич. энергию эл-нов при разл. межъядерных расстояниях, даёт за­висимость потенциальной энергии М. в. от расстояния между атомами. Точное решение получено только для мол. иона H⁺₂. Для систем, состоящих из двух атомов, разработаны разл. приближённые методы решения ур-ния Шредингера. В случае же вз-ствия атомов в многоатомных молекулах или атомов, принадлежащих разным моле­кулам, применяются феноменологич. методы расчёта, базирующиеся на представлениях о точечных атомах. В основе этих методов лежит т. н. приближение Борна — Оппенгеймера, согласно к-рому энергию молекулы (и вообще любой многоатомной систе­мы) можно рассматривать как непре­рывную ф-цию координат ат. ядер.



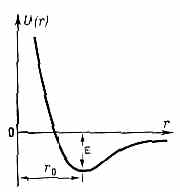
Зависимость потен­циальной энергии межатомного вз-ствия U(r) от межъядерного расстояния r.  — глубина потенциаль­ной ямы, r₀ — равно­весное межатомное расстояние.


Для пары атомов такая ф-ция пред­ставлена на рис. Устойчивое состоя­ние этой пары возникает при сближе­нии атомов на определённое расстоя­ние r₀, отвечающее минимуму потен­циальной энергии М. в. Р а в н о в е с н о е р а с с т о я н и е r₀ и глубина потенциальной ямы  различны для разных типов М. в. Определение потен­циальной энергии U(r) эффективного вз-ствия атомов по существу и есть задача определения М. в. Феноменологич. методы расчёта М. в. основаны на использовании разл. полуэмпирич. ф-л для U(r), в к-рые r₀,  и нек-рые др. величины входят как параметры и подбираются на основании эксперим. данных.

Ковалентное М. в. наиболее часто описывают потенциальной ф-цией Морзе (трёхпараметровым потен­циалом Морзе):

U(r)={1-ехр[-а(r-r₀)]}², (1)

где r₀ примерно равно сумме ковалентных атомных радиусов, а величина а характеризует крутизну потенциаль­ной ямы. Для двухатомной молекулы глубина потенциальной ямы  равна энергии диссоциации, а r₀ — межъ­ядерное расстояние, к-рое наблюда­лось бы в отсутствии внутримол. колебаний и отличалось бы от межъядер­ного расстояния, усреднённого за время колебаний, не более чем на 0,001 нм.

Потенциальную энергию ионного М. в. обычно записывают в виде:

400




где р_A и р_B — дипольные моменты ионов, _а и _B — их поляризуемости, — эмпирич. константа. Первый член (2) учитывает энергию кулоновского притяжения разноимённо заряженных ионов, второй — энергию обменного отталкивания электронных оболочек, третий и четвёртый члены характеризуют энергию вз-ствия свободных зарядов ионов с диполями p_а p_b, образовавшимися в результате поляризации каждого иона в электрич. поле др. иона, пятый — вз-ствие этих диполей друг с другом, шестой и седьмой — энергию деформации диполей квазиупругом приближении). Глу­па потенциальной ямы равна:



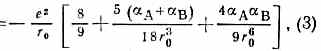
равновесное расстояние r₀ определя­ли ур-нием:



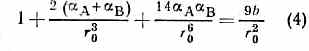
и равно сумме ионных радиусов атомов.

Ионное M. в. определяет структуру энергетику ионных кристаллов.

Для детального описания их структуры используют ф-лу (4), однако для оценки межатомных расстояний с уме­ренной точностью применяют аддитив­ную схему, основанную на системе ионных радиусов.

Металлич. М. в. иногда описывают модифициров. кулоновским потенциа­лом (наз. псевдопотенциалом), эффек­тивно учитывающим вз-ствие эл-нов с оболочкой ионов, с обрезанием на ма­лых расстояниях:



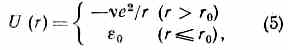
где v — заряд иона, равный числу эл-нов проводимости, приходящихся на один ион металла, ₀ и r₀ — пара­метры обрезания.

Для водородных связей вводят спец. потенциалы, гл. параметрами к-рых явл. r₀ и , напр. используют ф-лу (1). Угловая же зависимость энергии водородной связи управляется ван-дер-ваальсовыми М. в., описываемыми атом-атомными потенциальными ф-циями (см. ниже). Так, угол О — Н...О, напр., не может быть острым, по­скольку в этом случае энергия ван-дер-ваальсова М. в. была бы слишком высокой.

Ван-дер-ваальсово М. в. описывают ф-лой Леннард-Джонса (потенциалом 6—12 Леннард-Джонса):

U (x) = (x^-12 -2x^-6), (6)

где x=r/r₀, или ф-лой Букингема (трёхпараметровым потенциалом Бу­кингема 6-ехр):

U(x)=- Ax^-6 + Bexp(-Cxr₀), (7)

где А, В к С — эмпирич. параметры.

Расстояние r₀ в случае ван-дер-ваальсова М. в. обычно на 0,2—0,3 нм больше, а глубина потенциальной ямы  меньше на 3—4 порядка, чем при валентном М. в. Невалентное М. в. приближённо характеризуется ван-дер-ваальсовыми радиусами, к-рые примерно на 0,1 нм больше ковалентных радиусов. Сумма ван-дер-ваальсовых радиусов соответствует мин. расстоянию, на к-рое атомы могут сблизиться при нормальных условиях. Если r₀ для ковалентного М. в. с хорошей точностью равно сумме ковалентных радиусов атомов, то значение r₀ в ф-лах (6) и (7) больше суммы ван-дер-ваальсовых радиусов (превышение может достигать 0,1 нм).

Система ван-дер-ваальсовых радиу­сов, возникшая на основе многочисл. эксперим. данных, позволяет опреде­лять форму молекулы, если известны длины связей, валентные и двугран­ные углы (см. Молекула). Знание ван-дер-ваальсового «окаймления» молекул очень полезно при изучении структуры мол. кристаллов, а также жидкостей на основе принципа плот­ной упаковки молекул.

Более точное теор. изучение струк­туры мол. кристаллов и жидкостей проводят с помощью метода а т о м-а т о м н ы х п о т е н ц и а л ь н ы х ф-ц и й. В его основе лежит предпо­ложение о том, что энергия кристалла представляет собой сумму энергий вз-ствня пар молекул, а энергия вз-ствия каждой пары молекул скла­дывается из ван-дер-ваальсовых М. в., описываемых потенциальными ф-циями (6) или (7). Такой метод оказыва­ется эффективным для исследования органич. кристаллов, построенных из атомов трёх-четырёх сортов. Так, зная эмпирич. константы  и r₀ в вы­ражении (6) или константы А, В, С в выражении (7), описывающих потен­циальную энергию вз-ствия атомов С...С и Н...Н, можно рассчитать струк­туру и термодинамические свойства многочисл. кристаллов углеводоро­дов.

Метод атом-атомных потенциальных ф-ций применяется и для расчётов конформаций (чаще всего в гибких органич. молекулах, в к-рых враще­ния вокруг хим. связей сравнительно свободны). Минимизируя энергию молекулы по внутр. геом. параметрам (в частности, по углам вращения), находят равновесную конформацию. Применение метода атом-атомных по­тенциальных ф-ций в сочетании с рент­геновским структурным анализом привело к увеличению точности и на­дёжности определения структурных параметров нек-рых белков, полисахаридов, ДНК и транспортных РНК.

Наряду с феноменологич. метода­ми, играющими важную роль в разл. приложениях, в изучении М. в. при­меняются методы решения многоэлектронной задачи для многоатомной молекулы или для двух взаимодейст­вующих молекул (см. Квантовая хи­мия). Подавляющее большинство та­ких методов основано на приближении самосогласованного поля. Неэмпирич. расчёты, проводимые на ЭВМ, поз­воляют получать всё большую инфор­мацию о М. в.

• Torrens I. M., Interatomic potentials, N. Y.— L., 1972; Китайгородский А. И., Молекулярные кристаллы, М., 1971; П о л и н г Л., Общая химия, пер. с англ., М., 1974.

В. Г. Дашевский, А. И. Китайгородский.