Физические теории главного магнитного поля Земли
| Вид материала | Документы |
- Урок на тему «Магнитное поле Земли», 31.68kb.
- Дефицит магнитного поля, 27.98kb.
- Задание 1 Цель: оценить значение сердечника для получения магнитного поля катушки, 33.68kb.
- Домашнее задание по физике на 4 сессию Учебник, 55.57kb.
- Задачи урока: -обучения: продолжить формирование представлений о магнитном поле; рассмотреть, 35.34kb.
- Лабораторная работа № Исследование магнитного поля модели сверхпроводникового индуктора, 75.13kb.
- Разработка урока в 8-м классе "Магнитное поле. Линии магнитного поля", 33.77kb.
- Получил домашнее образование. Основные труды в области электродинамики. Автор первой, 87kb.
- Сборник статей по применению аппарата полимаг-01 Роль импульсного магнитного поля, 158.96kb.
- Магнитное поле. Сила Ампера. Сила Лоренца. Явление электромагнитной индукции, 98.2kb.
Физические теории главного магнитного поля Земли
- Гипотезы о природе магнитного поля Земли (МПЗ)
Все выдвинутые к настоящему времени гипотезы об источниках земного магнетизма можно разделить на 2 группы:
1 – Научные
2 – Фантастические, т.е. предлагающие для Земли как планеты некие особые, свои, новые «законы природы».
- Ядро, как источник магнитного поля Земли
В.Эльзассер (1939 г.) предположил, что внутри ядра вследствие градиентов (тепловых, плотностных и пр.) возникает вихревое движение, первоначально радиальное (т.е. в меридиональных плоскостях). Под влиянием силы Кориолиса вихревые кольца «ложатся» в плоскости, параллельные экваториальной. Различие температур во внешних и внутренних частях этих вихрей (ближе и дальше от оси вращения) обусловливает появление термоЭДС, а железо-никелевый состав ядра (с возможными добавками кремния, окиси магния или серы) с металлической проводимостью (0,09–0,7) 103 Ом–1м–1 – обеспечивает появление токов. При этом сам факт существования вихрей вещества есть источник неоднородностей в ядре, служащих как бы проводником тока в виде контура. Определенная система подобных токов способна создать наблюдаемое на Земле поле центрального диполя.
Аналогичные соображения и в гипотезе Я.И.Френкеля (1947). Ему тоже потребовались вихри в ядре: образование токов связывалось с явлением индукции при вихревом движении металлических масс ядра в магнитном поле. В этом процессе поле должно все время себя самоподдерживать – регенерироваться. И как процесс, подобный ситуации с динамомашиной, он получил название динамоэффекта.
Начальное поле, «запускающее» эффект, Френкелем просто постулировалось, однако это не очень-то и важно: хотя бы космическое магнитное поле или поле гиромагнитного эффекта уже достаточны для запуска и поддерживания динамо. Естественно, что равновесный уровень регенерации в динамо обеспечивается мощностью его энергетического источника, т.е. (например) интенсивностью радиоактивного распада в ядре, обеспечивающего необходимые конвективные движения в ядре.
В настоящее время динамо-теория является основной при решении проблемы природы МПЗ, поэтому остановимся на ней.
Простое, или униполярное динамо
Итак, как Эльзассеру, так и Френкелю необходимо наличие вихря жидкой массы ядра.
Представим вихрь в виде вращающегося твердого проводящего диска; пусть этот диск находится в магнитном поле, параллельном оси его вращения. Радиус диска – а; начальное поле – Во – считаем его однородным; диск вращается со скоростью .
Тогда в точке А диска возникает электрическое поле:
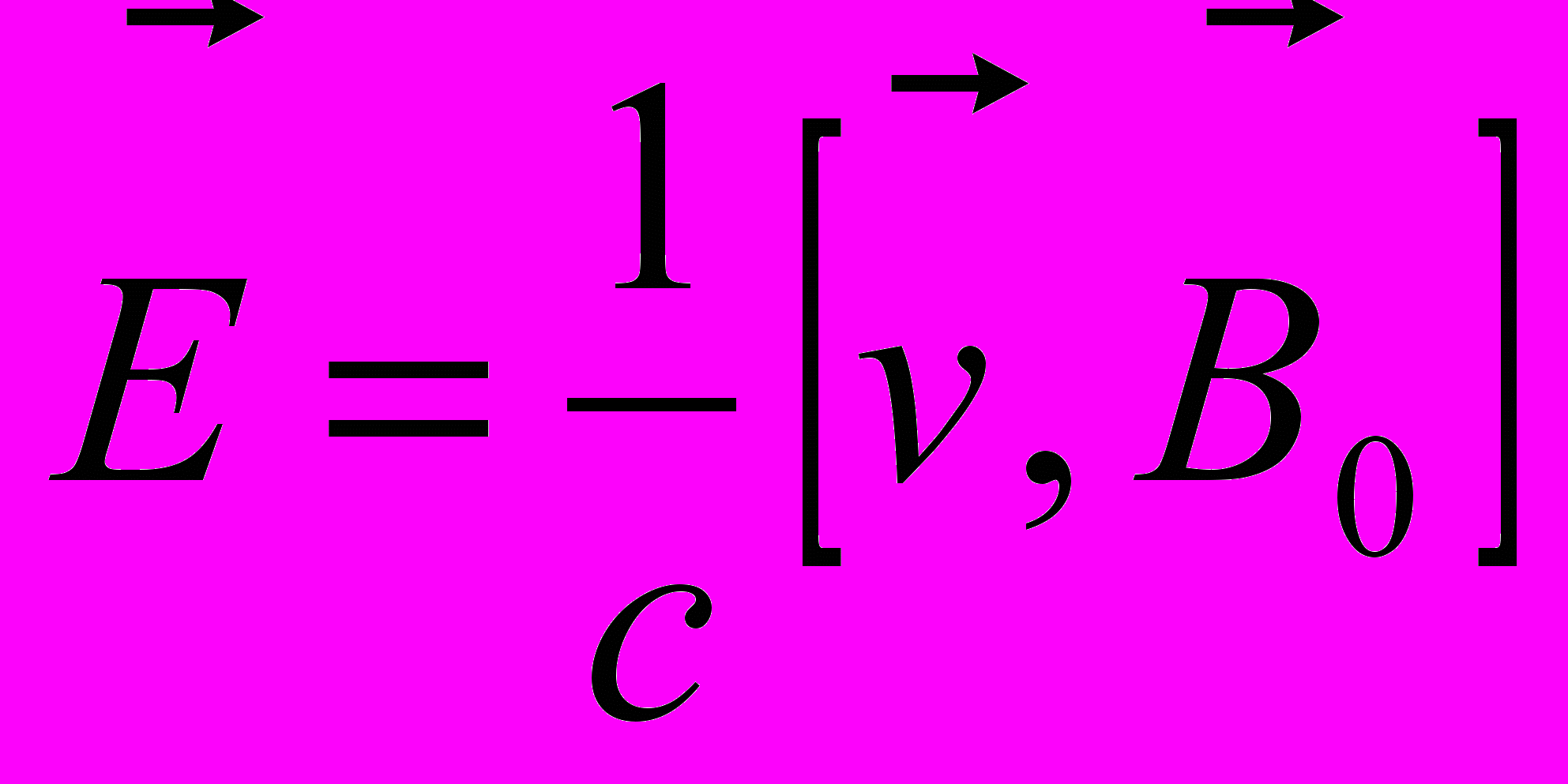 ,
,где
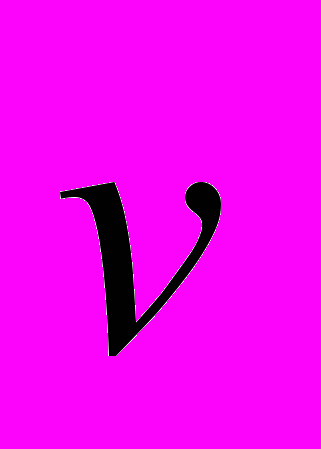 – линейная скорость точки А, равная
– линейная скорость точки А, равная  .
.Полная разность потенциалов между осью вращения диска и его образующей будет
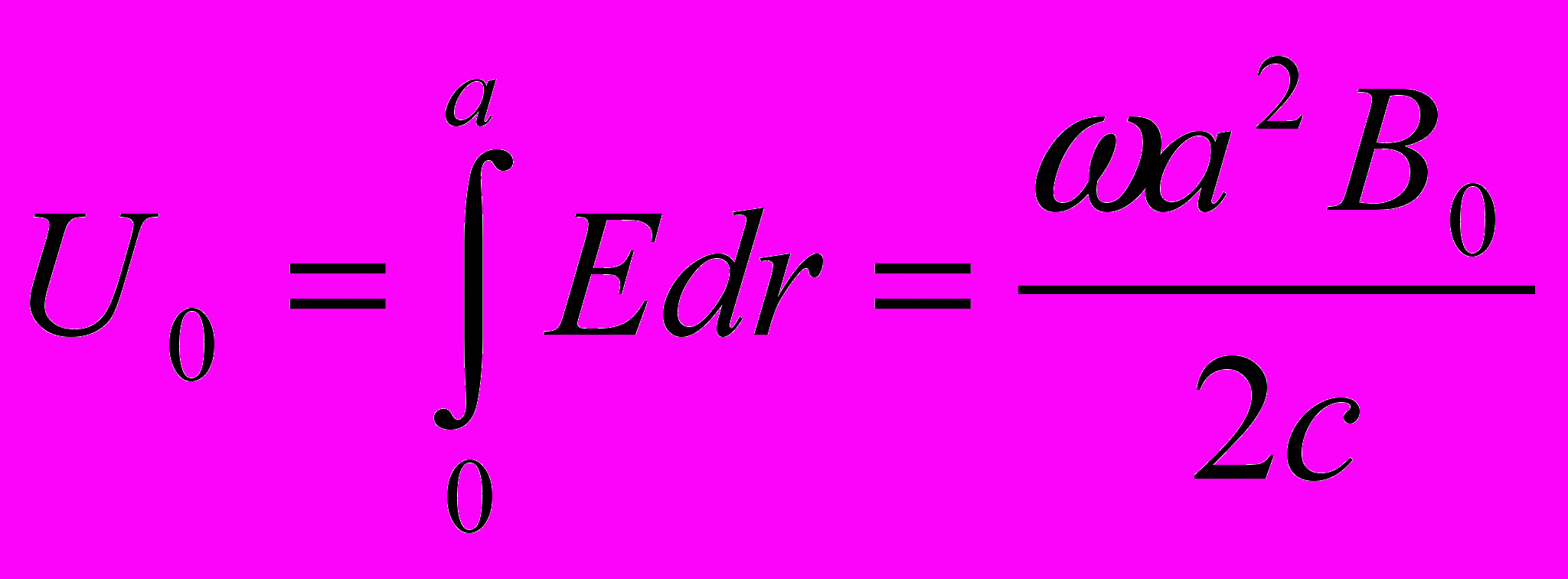 Если теперь каким-то образом суметь снять это напряжение (посредством контактов k и l) и подать его в подходящий проводящий контур и
Если теперь каким-то образом суметь снять это напряжение (посредством контактов k и l) и подать его в подходящий проводящий контур ив
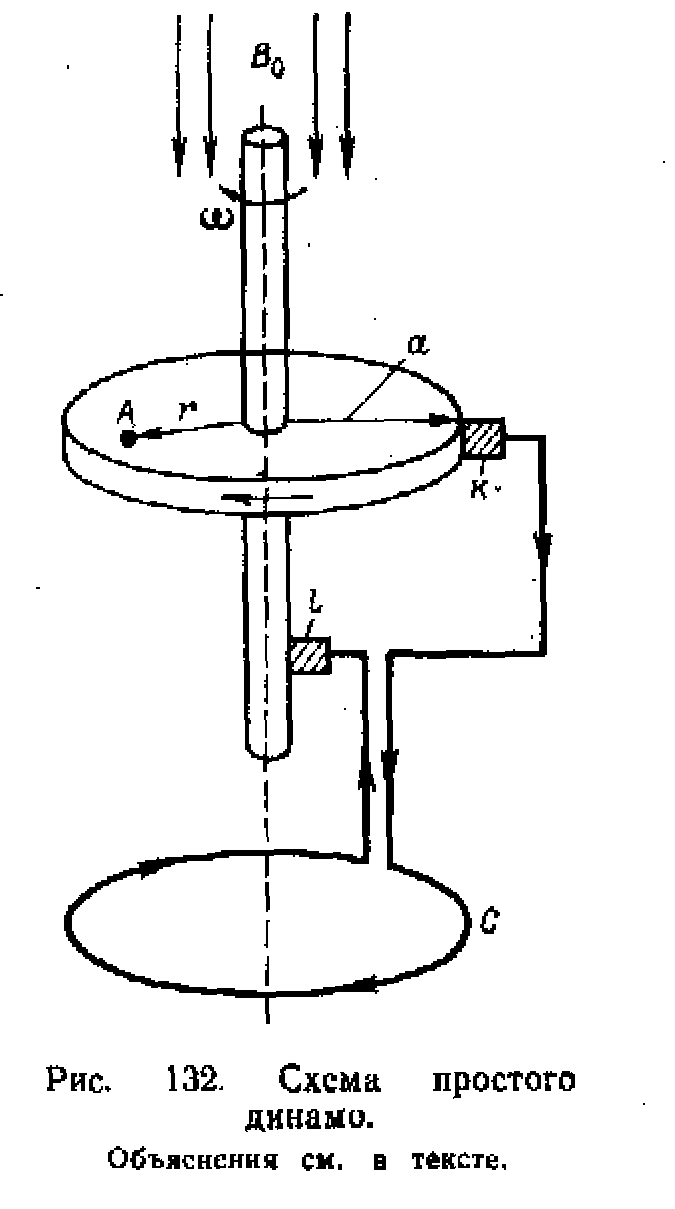
правильном направлении, то и получим собственно то, что называется динамо. Действительно, если проводимость контура равна , то ток в контуре станет:
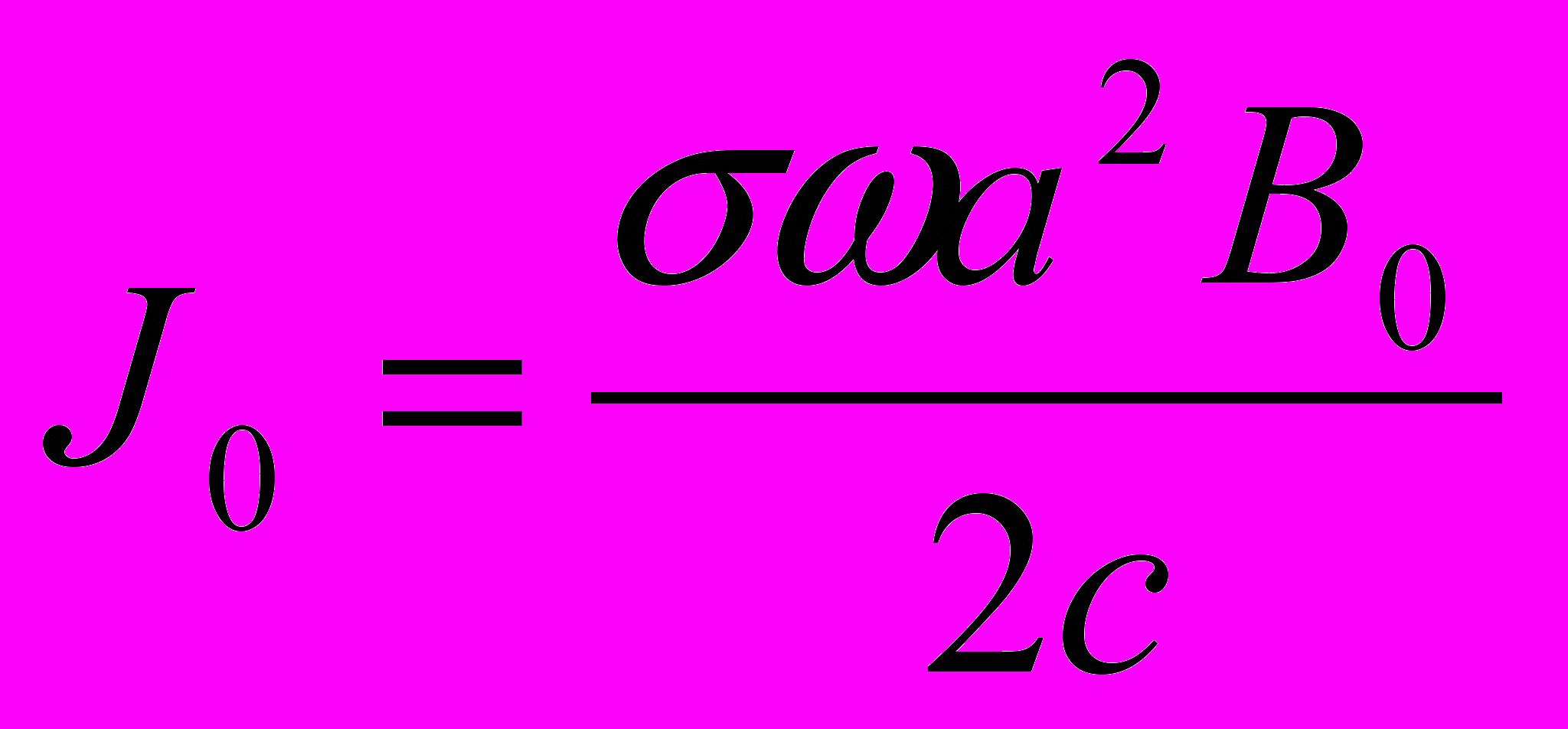 . Это есть начальный ток контура.
. Это есть начальный ток контура.Итак, пусть имеет место ситуация, приведенная на рисунке, тогда появившийся в контуре ток J0 вызовет появление магнитного поля b. Если оно сонаправлено с В0 , то поле, действующее на плоскости диска, возрастет; возрастет на величину Ut и ЭДС:
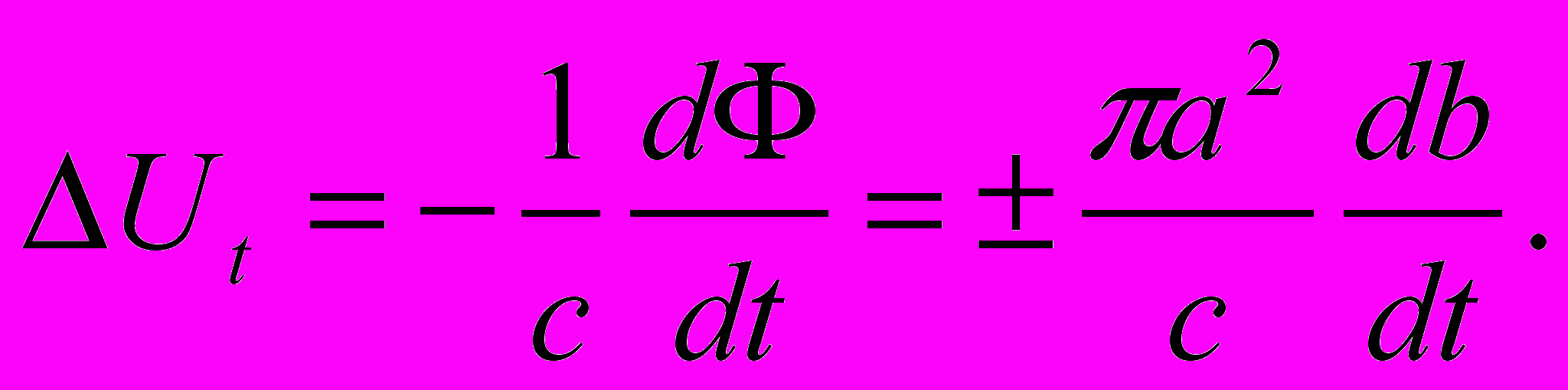
Тогда в каждый момент имеет место:
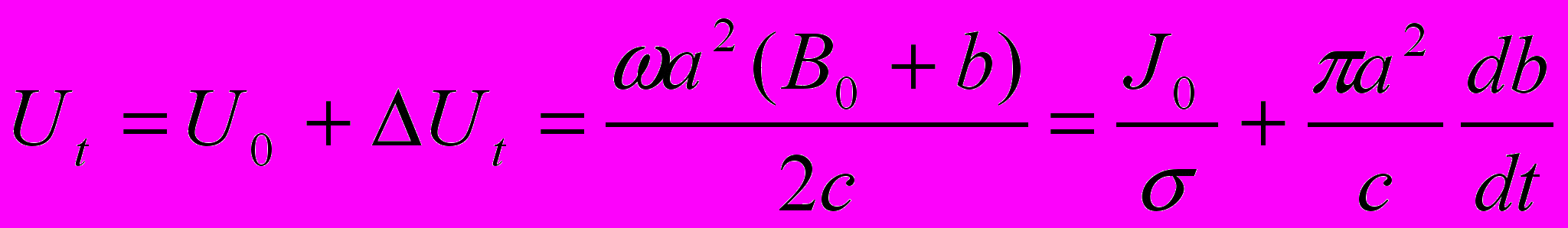 (1)
(1)(Магнитное поле в центре кругового витка радиуса R с током J – в системе СГСМ :
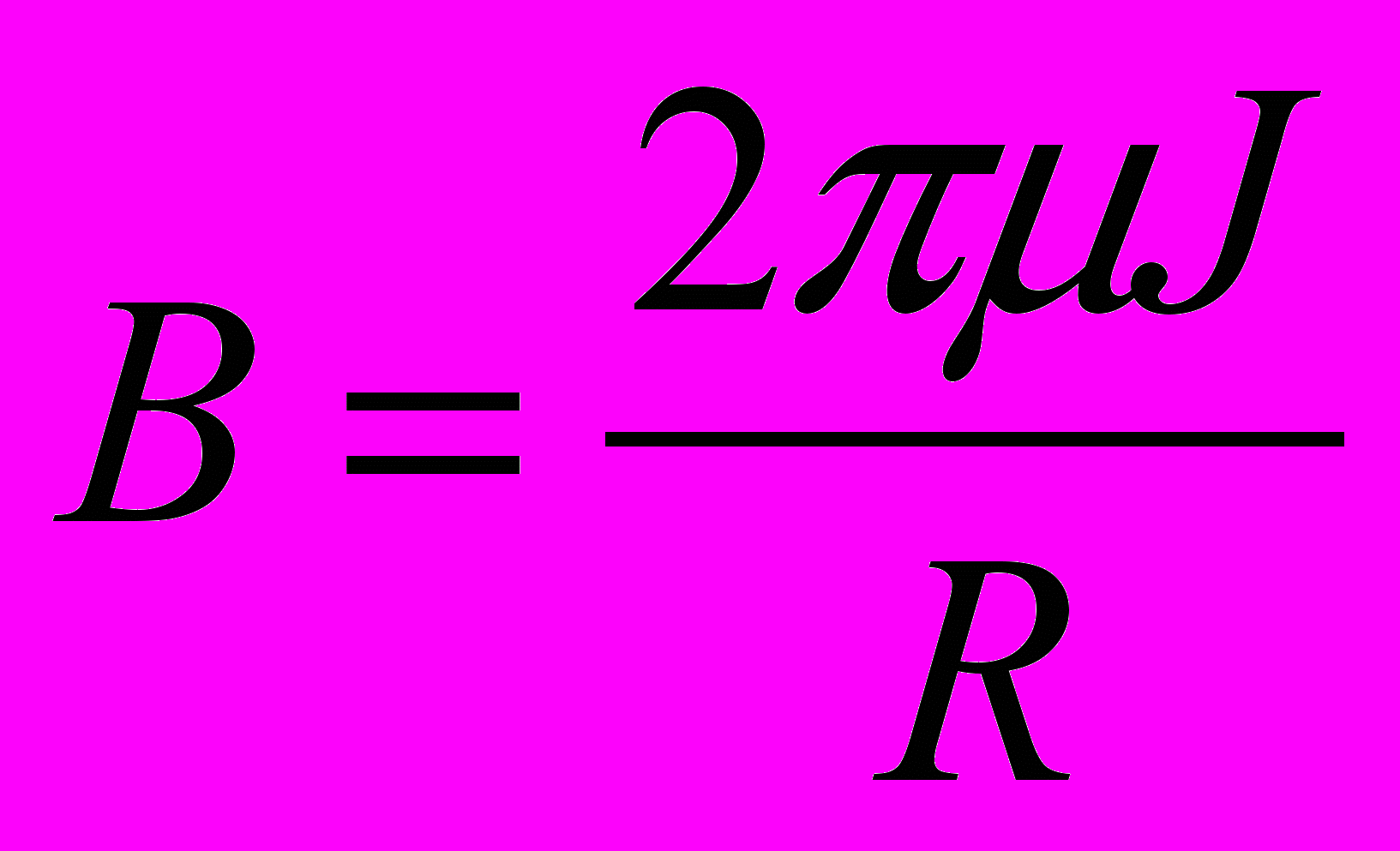 ).
).Тогда, принимая грубо поле b в контуре (его радиус равен а):
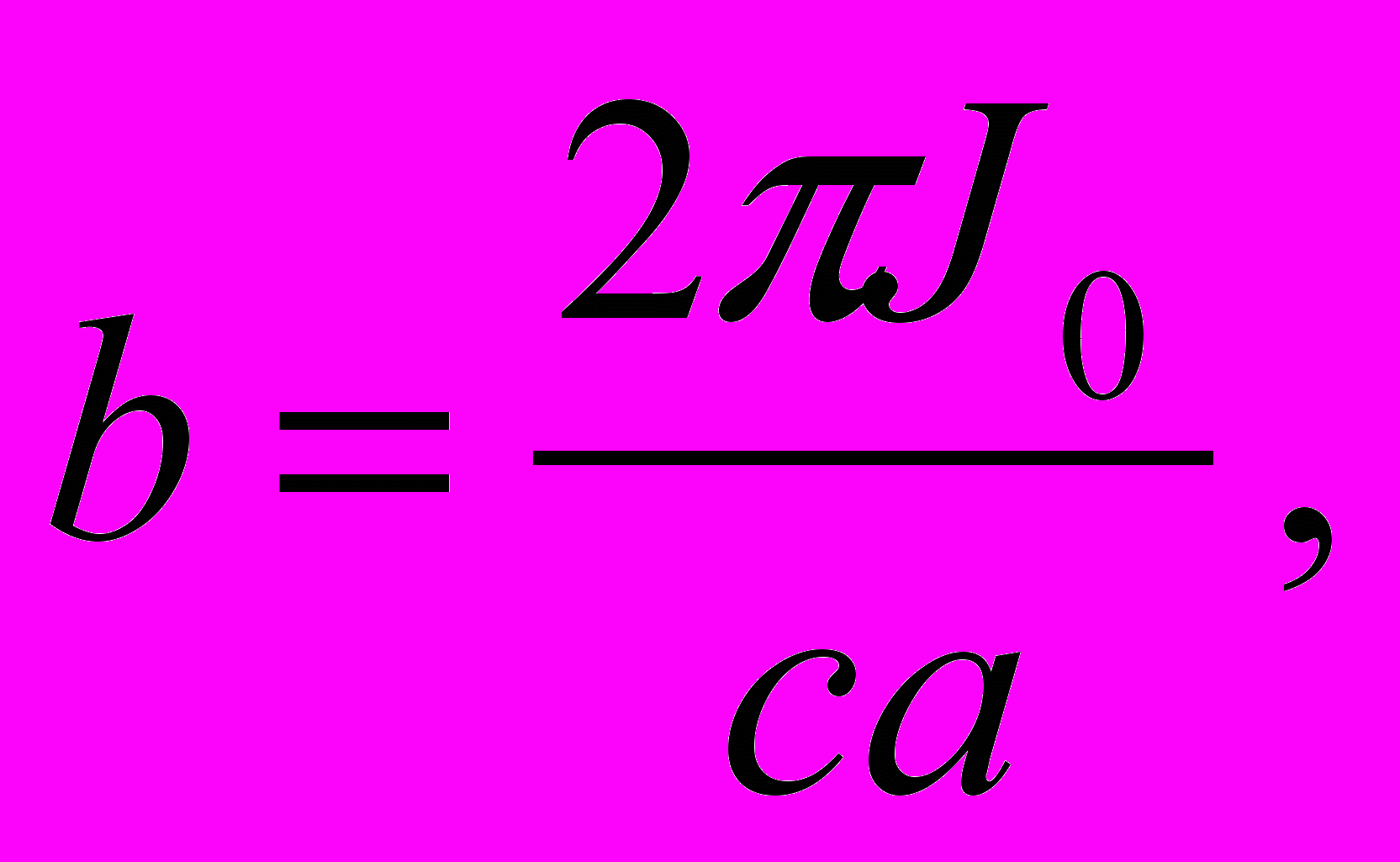
а само поле В0 ничтожно малым, перепишем (1) :
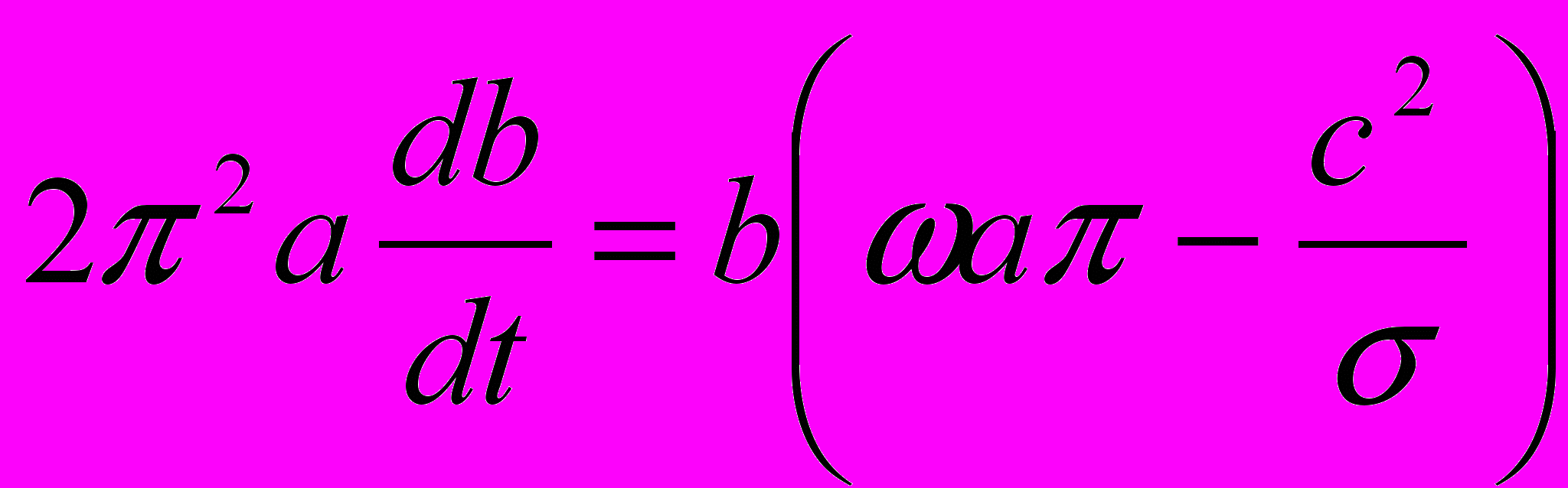 (2) (приняли: = 1).
(2) (приняли: = 1).Из этого уравнения видно, что динамо действительно будет «генерировать» магнитное поле
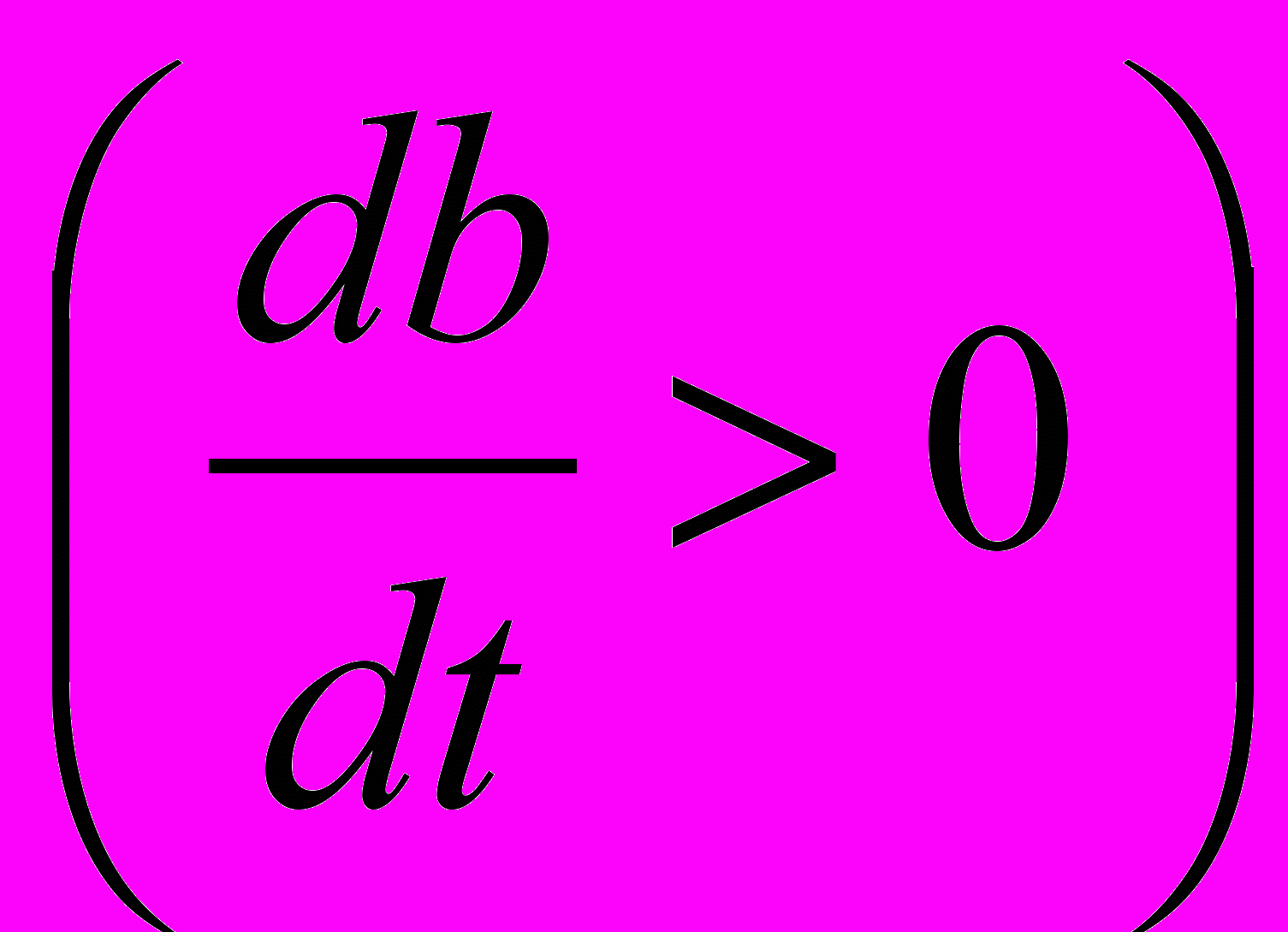 только в том случае, если в (2) скобка справа положительна:
только в том случае, если в (2) скобка справа положительна: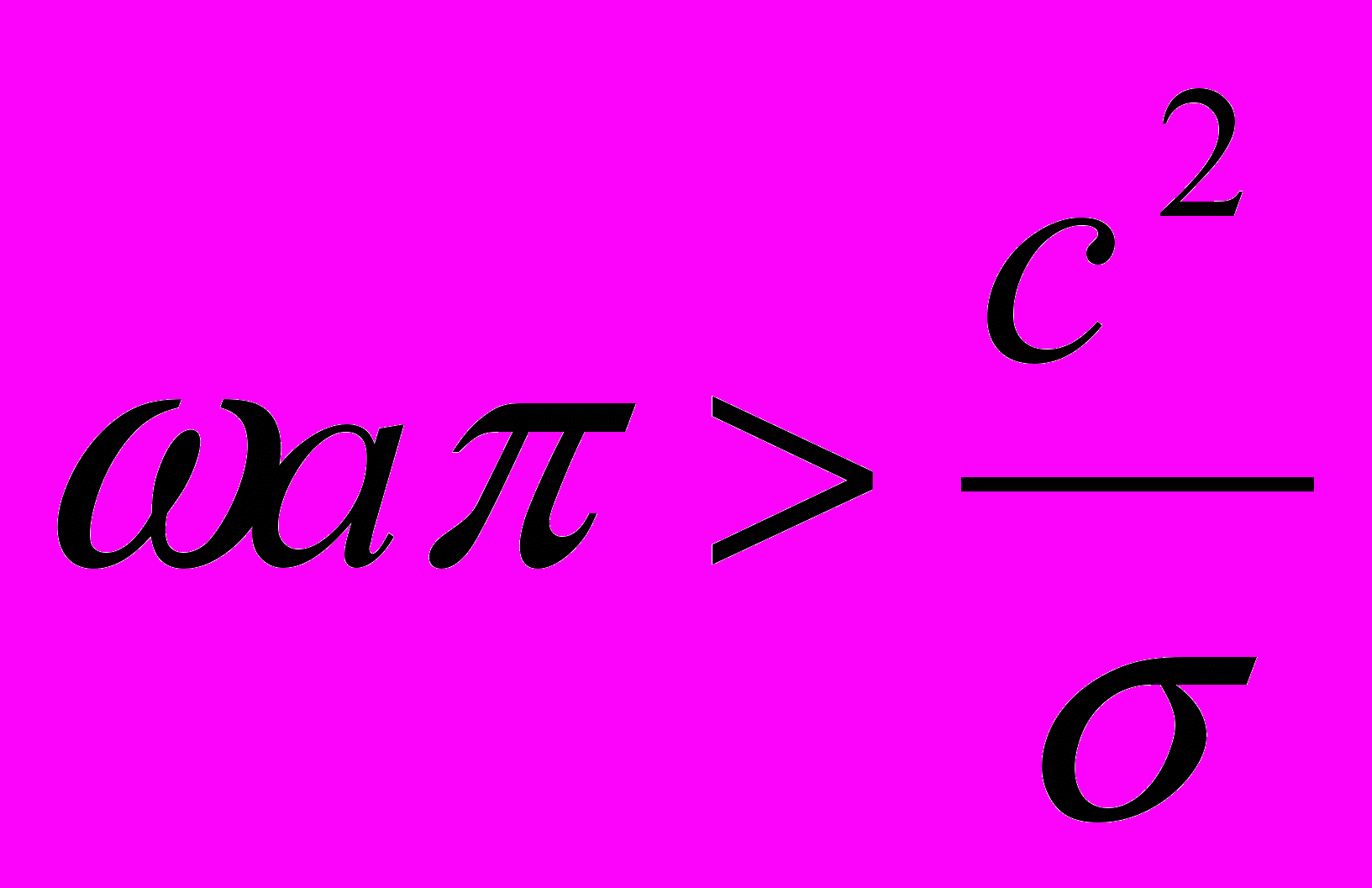 , т.е. регенерация начинается лишь при
, т.е. регенерация начинается лишь при 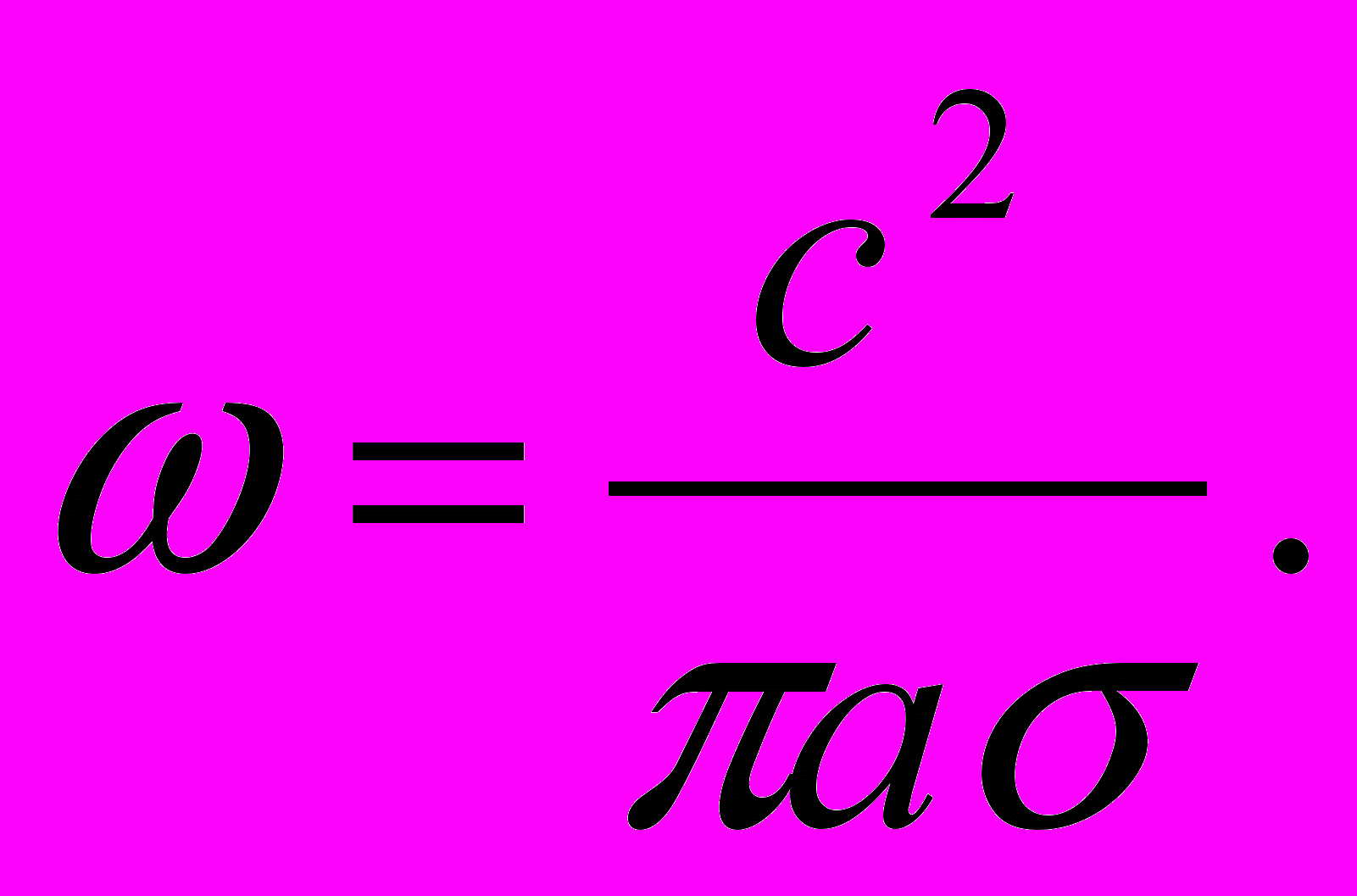
В условиях Земли, принимая: а =1/2 Rядра , получим:
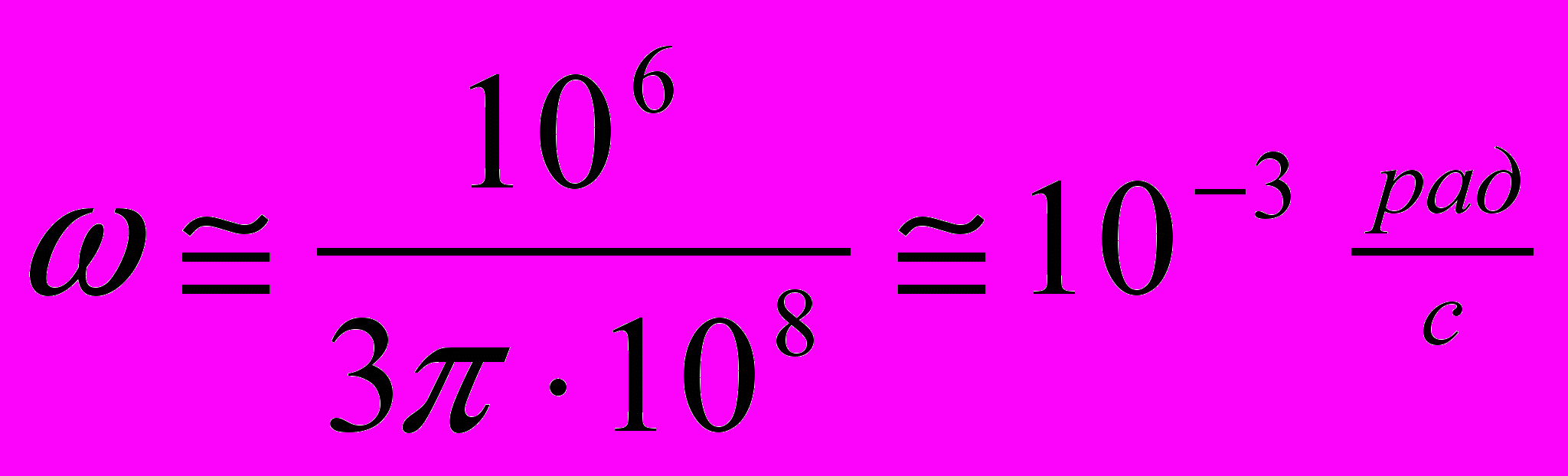 .
.Такая модель, реализуясь, могла бы обеспечить необходимую величину поля b, однако понять, как она в сплошном жидком ядре реализуется – особенно в смысле внешнего по отношению к вихрям, замыкания электрической цепи в виде контура. Кроме того, сама реализация динамо должна действовать разрушительно на вихри, по крайней мере – не давать им располагаться параллельно экваториальной плоскости.
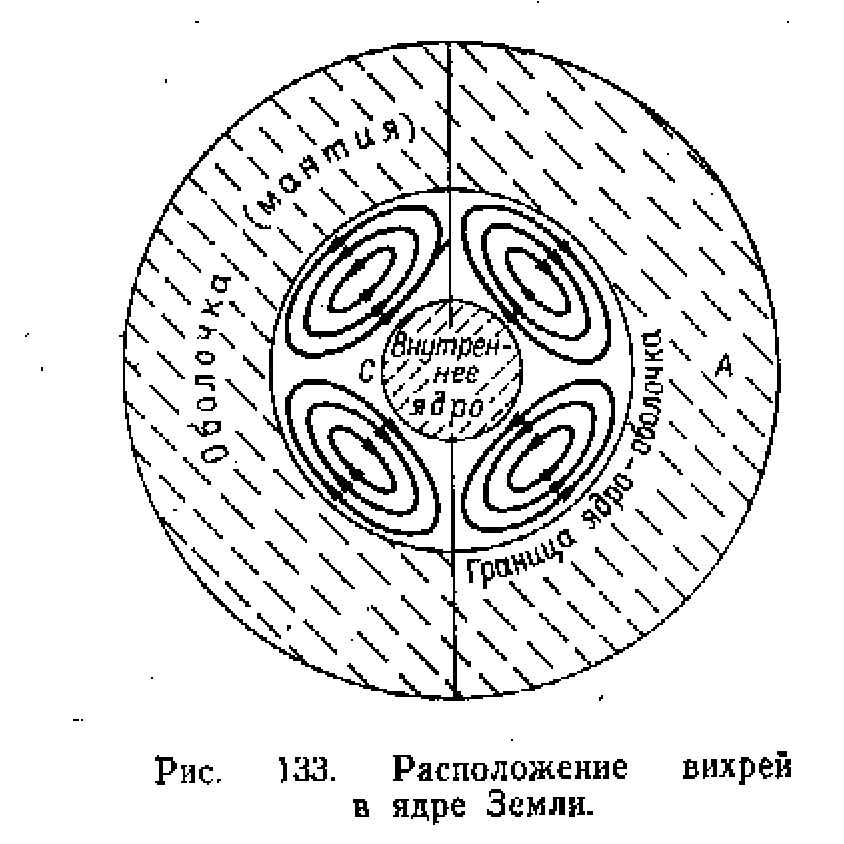
Более строгий учет современных представлений о строении Земли, а именно – учет того, что ядро Земли имеет “ядрышко” – твердую внутренность, – проведен в модели Э.Булларда (1954): он исходит из того, что ядрышко вращается вокруг оси медленней мантии. Разность скоростей проявляется (и «соответствует») скорости западного дрейфа. А вихревые кольца в жидкой части ядра располагаются в меридиональных плоскостях. В принципе, оказалось, что подход Булларда дает удовлетворительное объяснение дипольной части поля, подводит к пониманию векового хода и недипольной части.
Математическое обоснование теории динамо-эффекта
Описание вихрей и токов очень сложно и общего решения не имеет. Объединение гидродинамики и электромагнетизма есть магнитная гидродинамика. Именно на нее опирается теория динамо-эффекта.
Итак, принимая = 1 и отсутствие токов смещения, для ядра можем записать:
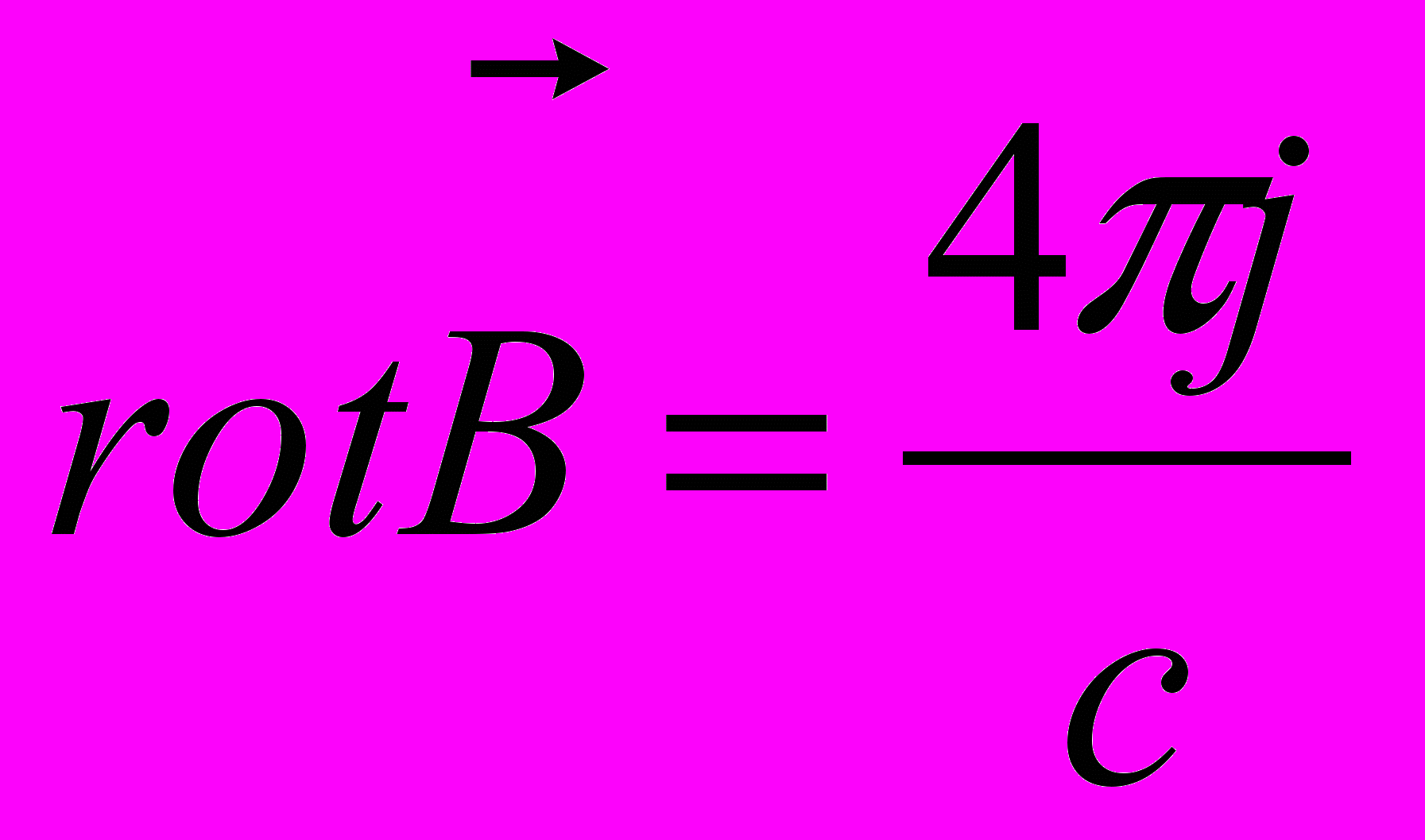 (1)
(1)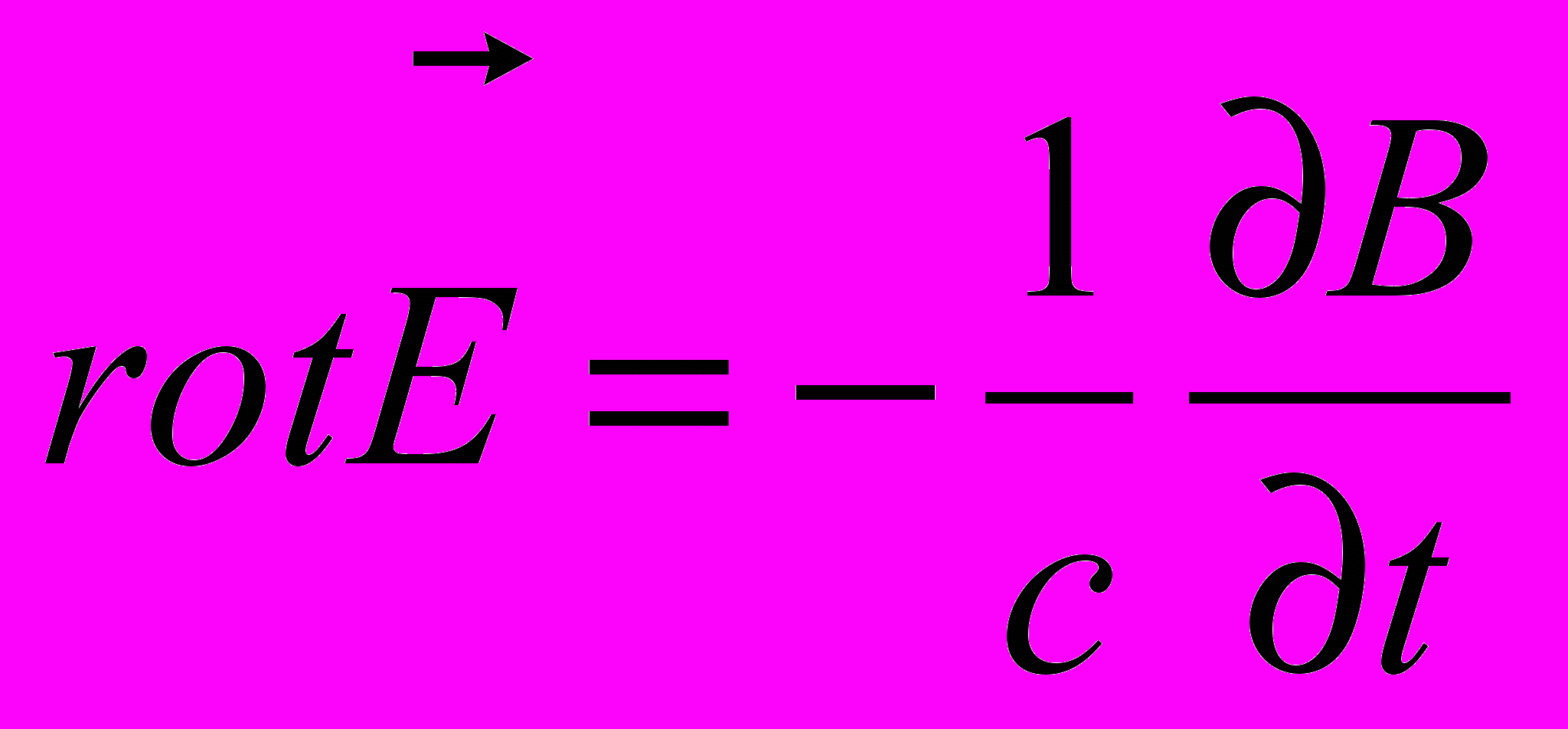 , (2)
, (2)причем:
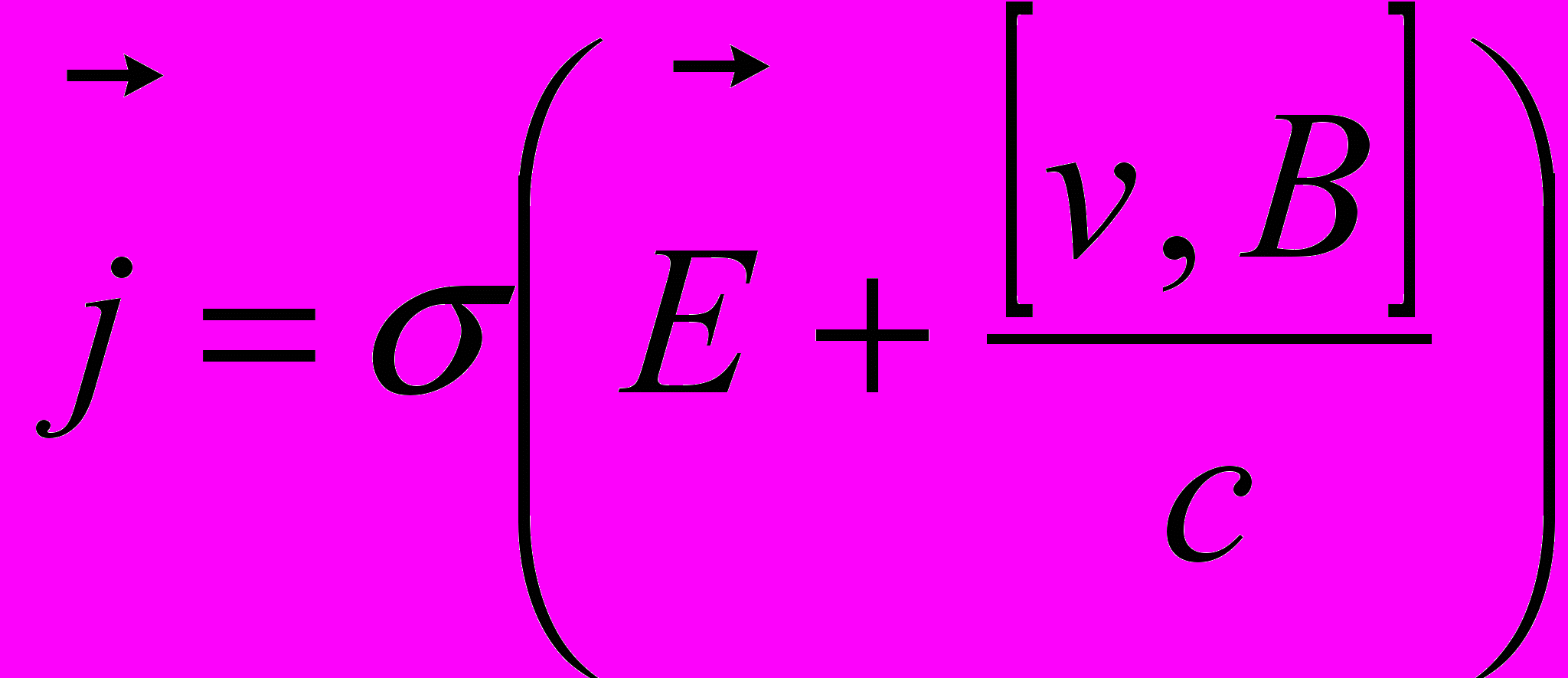 (3)
(3)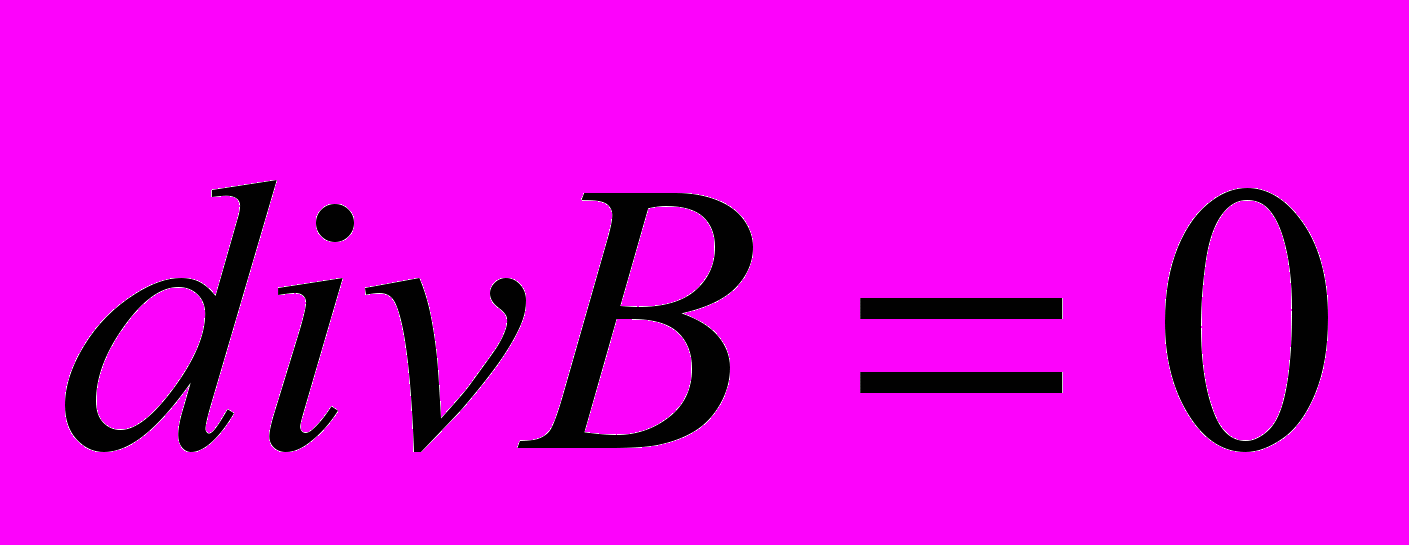 , (4)
, (4)где – проводимость ядра, v – скорость движения жидкой массы ядра.
Подставляя (3) в (1), получаем
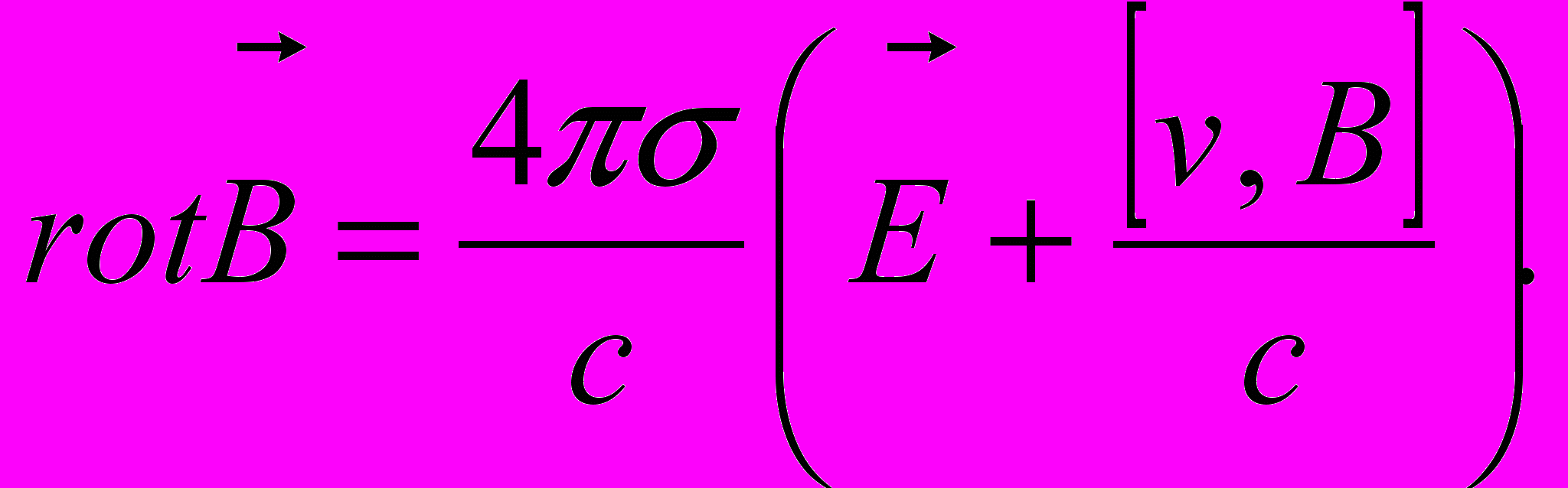
Выполним операцию rot на его обеих частях и учтем (2). Получим:
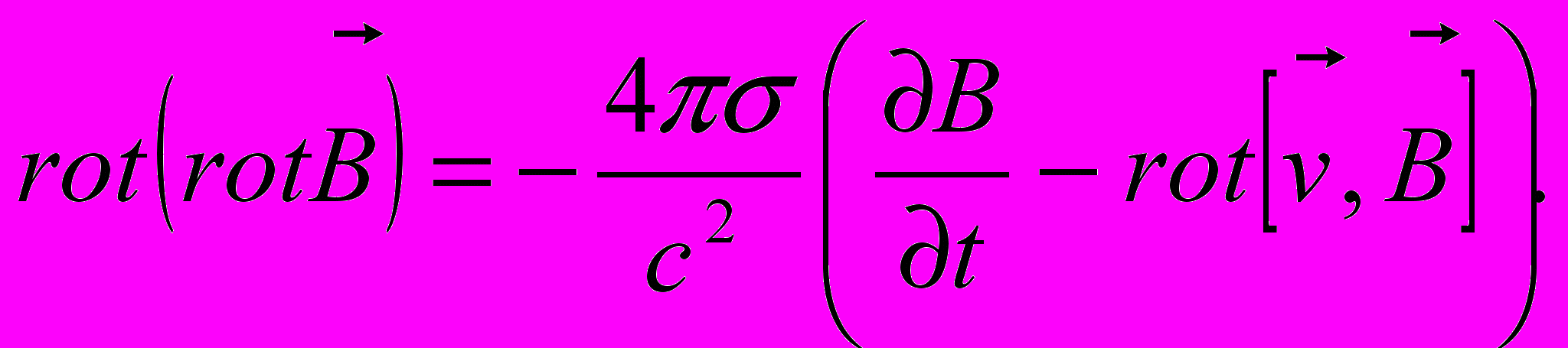
Учитывая теперь равенство из векторного анализа:
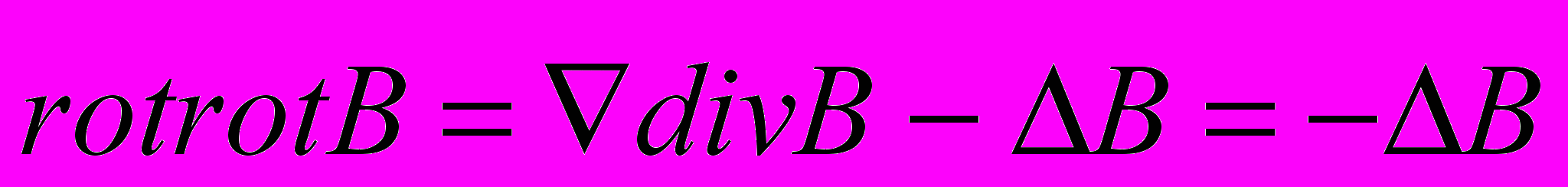 ,
,(согласно (4):
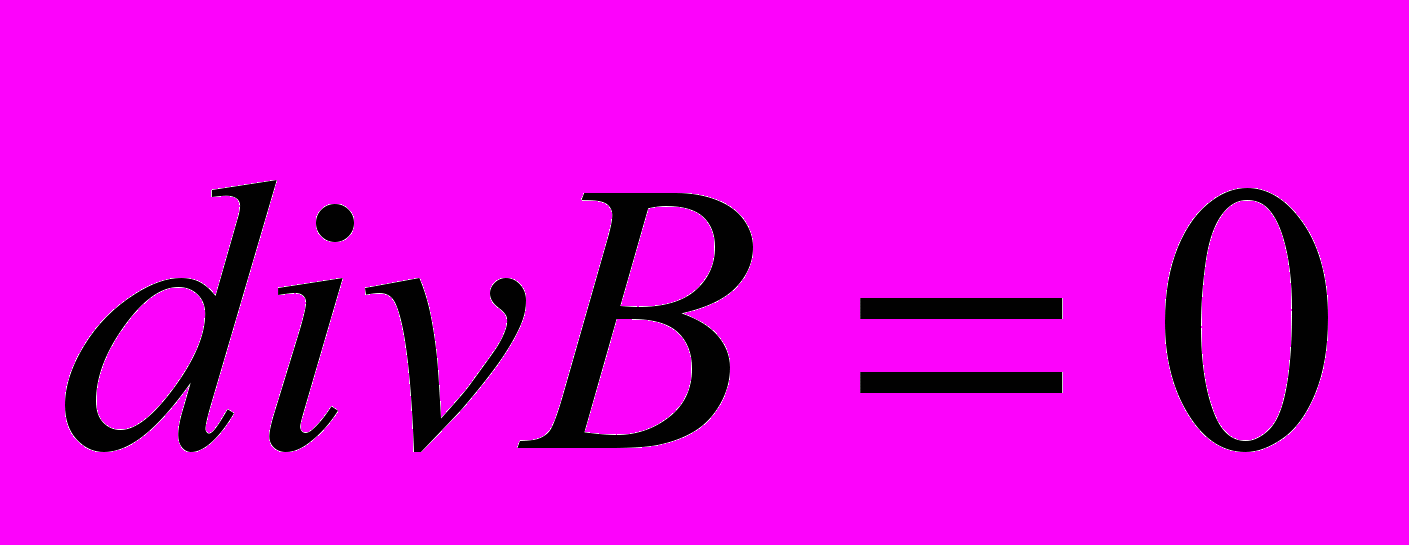 )
)получим:
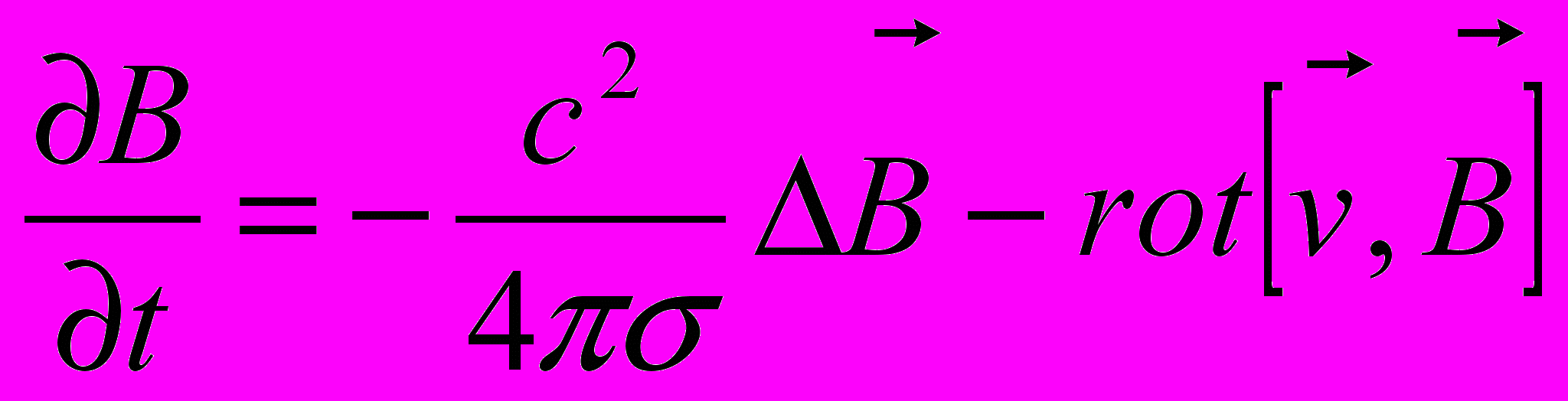 , (5)
, (5)т.е. вместо четырех уравнений (1–4) получили одно – для v и B, главных неизвестных динамо.
В качестве второго уравнения для них прибавим из гидродинамики уравнение Навье-Стокса:
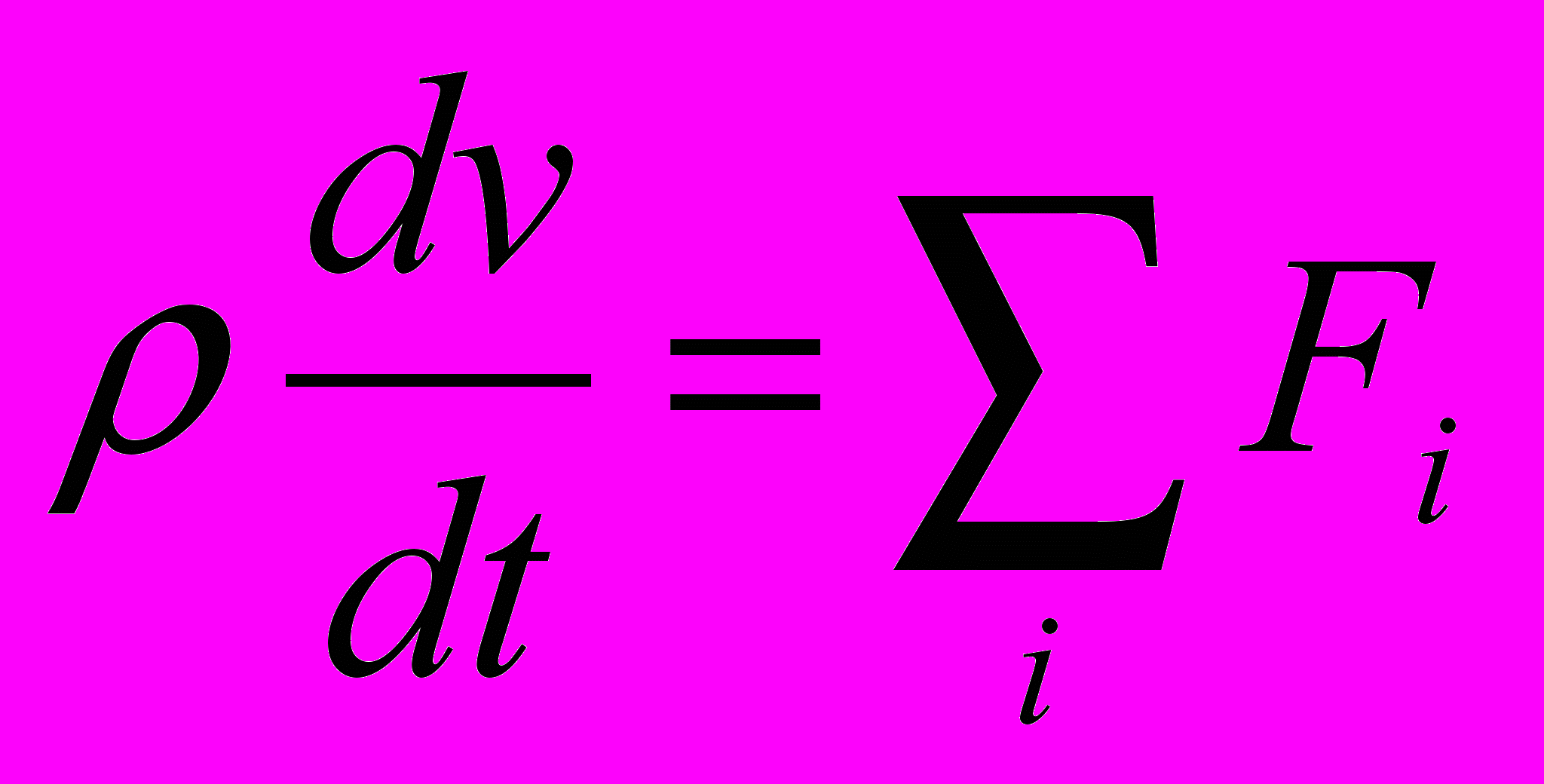 , (6)
, (6)где – плотность жидкости, а
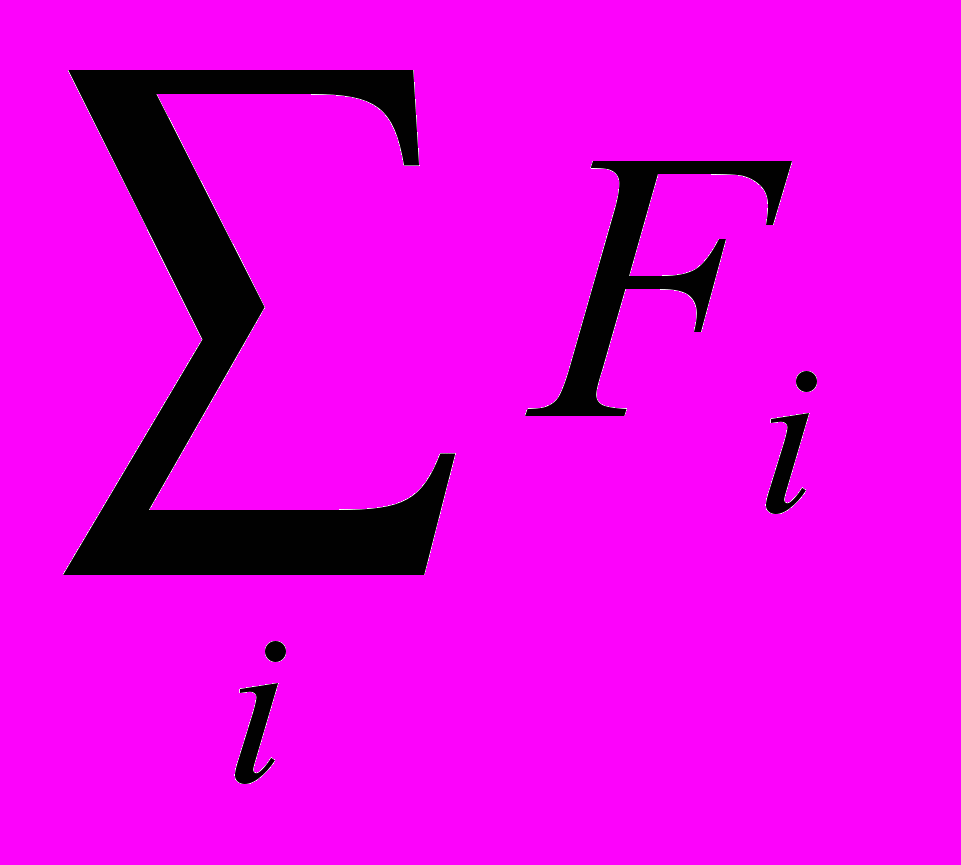 – сумма всех (внутренних и внешних) сил, действующих на единицу объема жидкости. Принимая жидкость несжимаемой, добавим:
– сумма всех (внутренних и внешних) сил, действующих на единицу объема жидкости. Принимая жидкость несжимаемой, добавим: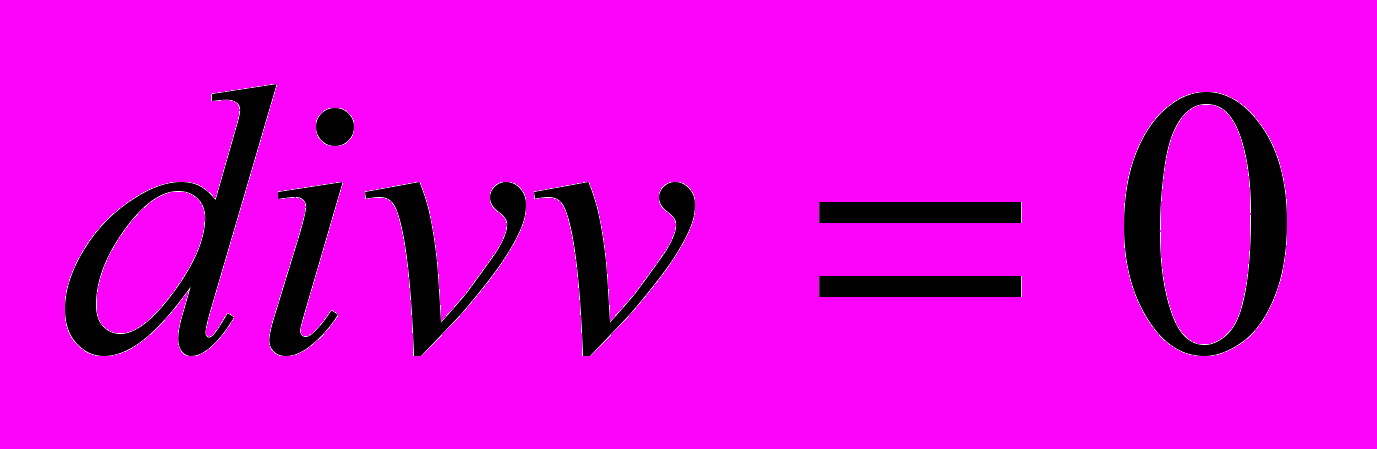 .
.(Кроме того:
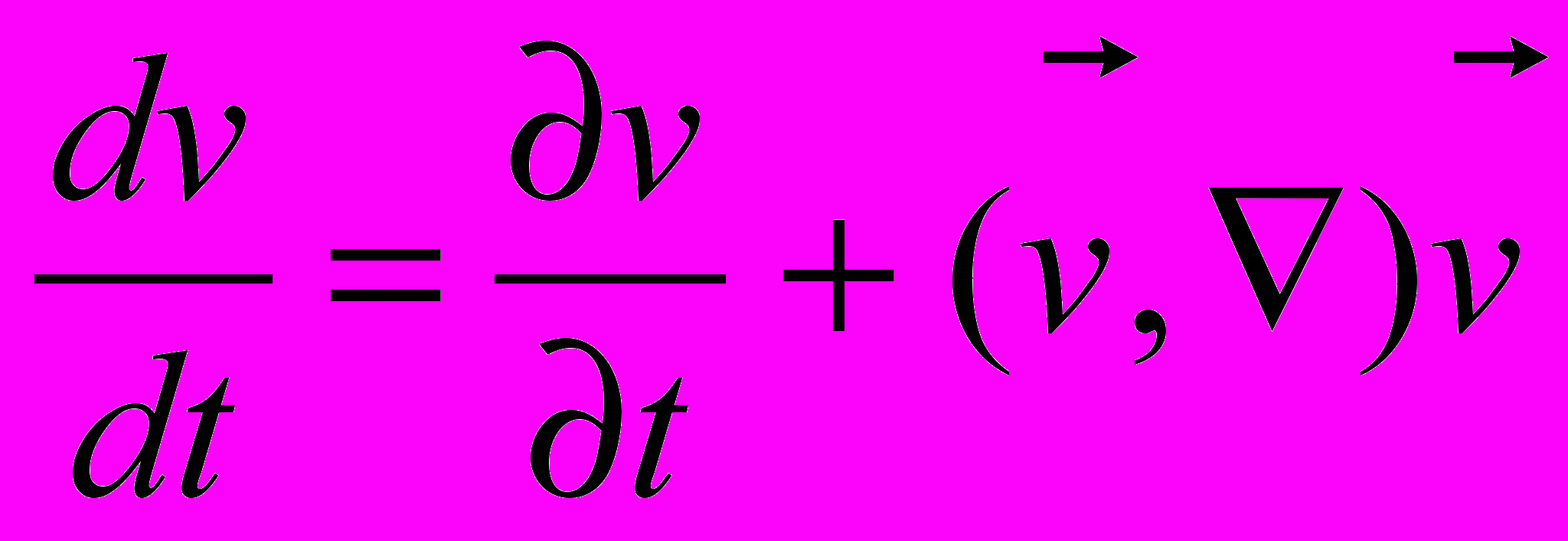 – указывающее, что скорость зависит и от координаты).
– указывающее, что скорость зависит и от координаты).Что это за силы Fi в ядре:
- Вязкое трение в жидкости. Эта сила может быть записана:
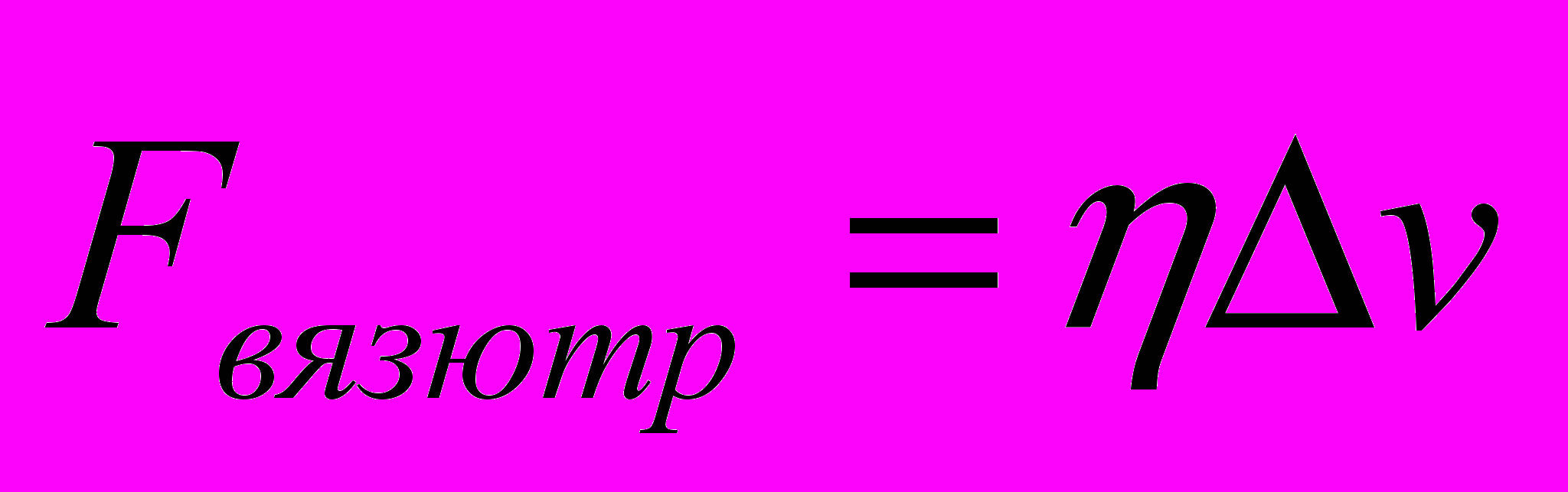 . – Это – внутренняя сила.
. – Это – внутренняя сила.
- Сила инерции: Fин =
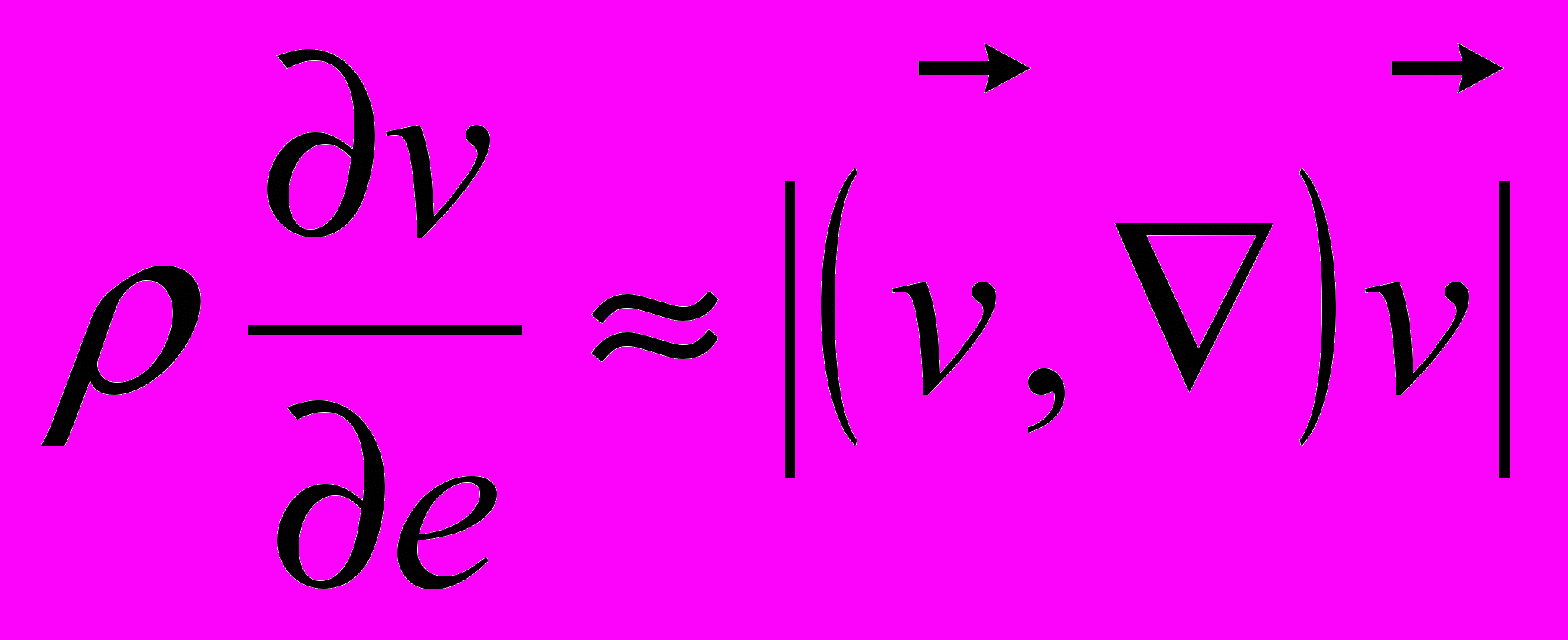 .
.
- Сила тяжести: F2 = g .
- Сила Кориолиса:
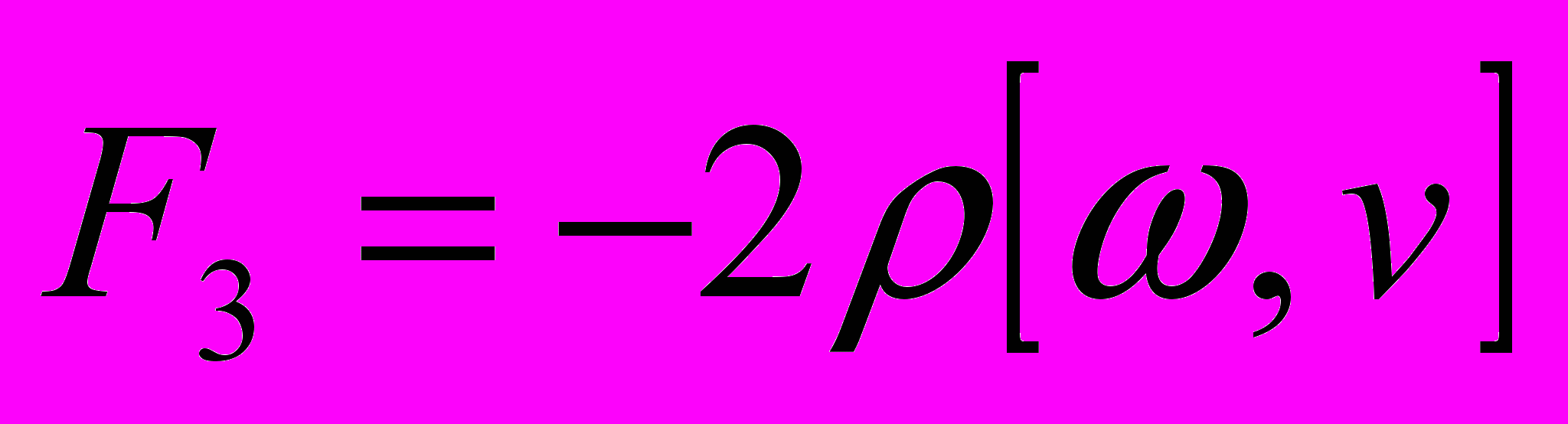 .
.
- Сила типа Архимедовой (за счет разности давлений): F4 = – p.
- При наличии токов – электродинамическая сила; ее можно выразить:
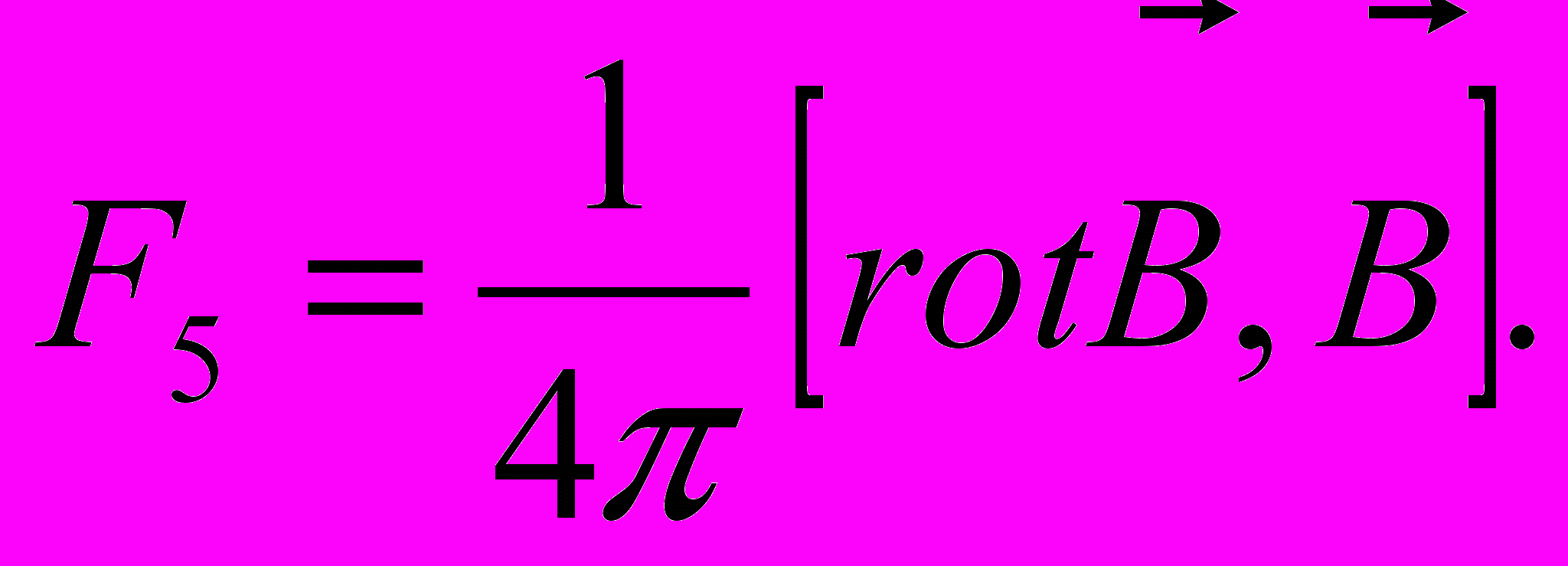 .
.Теперь уравнение Навье-Стокса можно «раскрыть»:

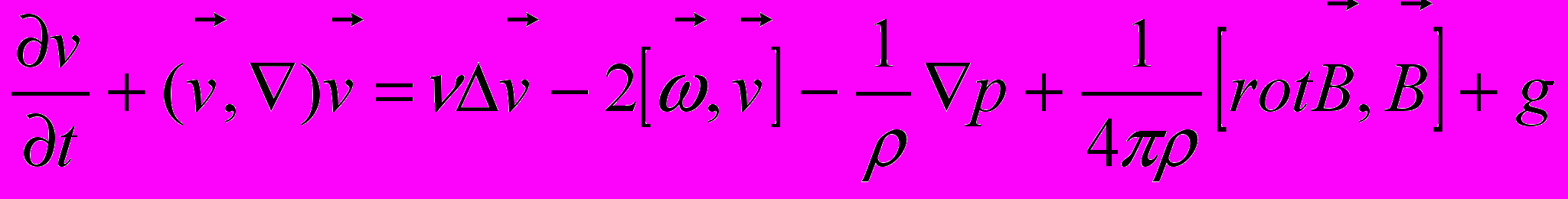 , (7)
, (7)где
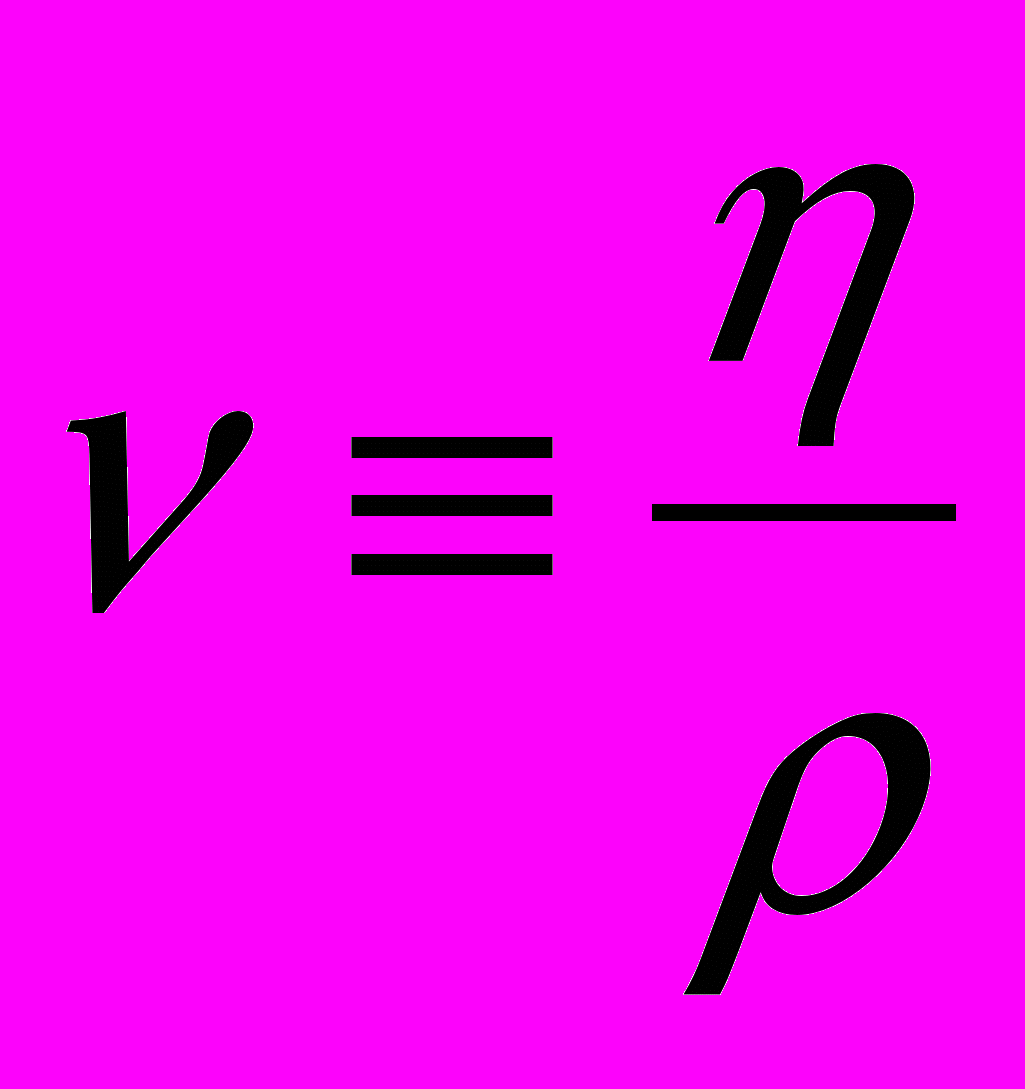 – кинематический коэффициент вязкости. Соответственно, коэффициент
– кинематический коэффициент вязкости. Соответственно, коэффициент 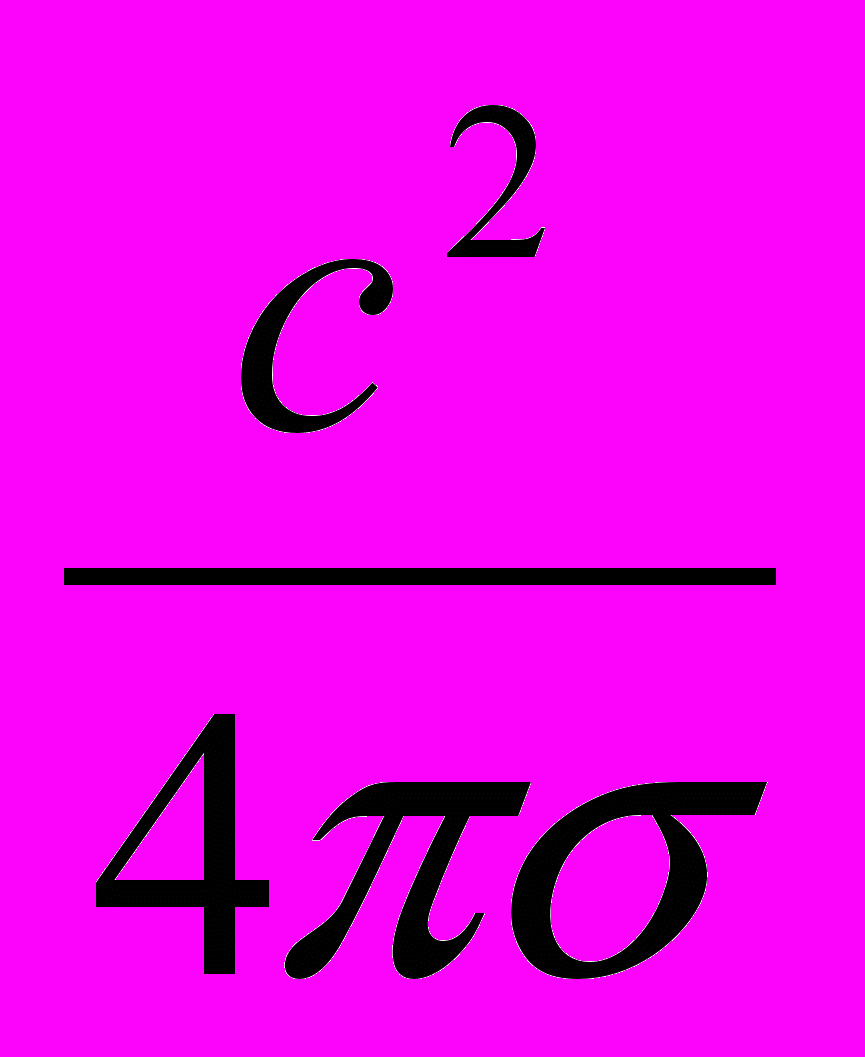 из (5) назван магнитной вязкостью т .
из (5) назван магнитной вязкостью т .В сумме уравнения (5) и (7) составляют систему уравнений магнитной гидродинамики (Не решены в общем виде до сих пор). Их рассмотрение
упрощается если допустить движение жидкости в ядре медленным, а диаметр вихрей – большим. (Пусть это: v0 = 0,1 см/с , L = 3108 см ).
Принимая: = 10 г/см3 ,
10-3 < < 109 ,
B = 50 Э (так принято в модели Булларда),
= 710-5 рад/с (скорость вращения Земли).
Тогда имеем:
Сила инерции:
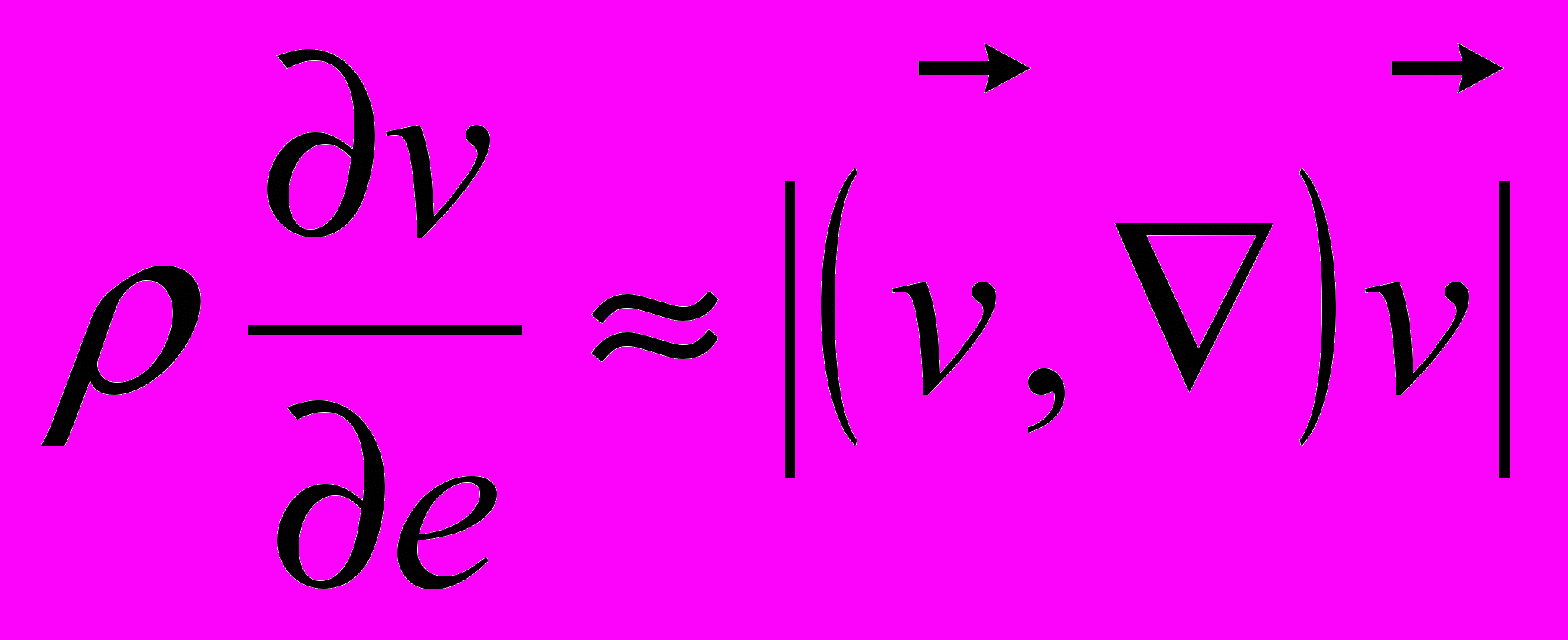 310-10 дин .
310-10 дин .Сила Кориолиса:
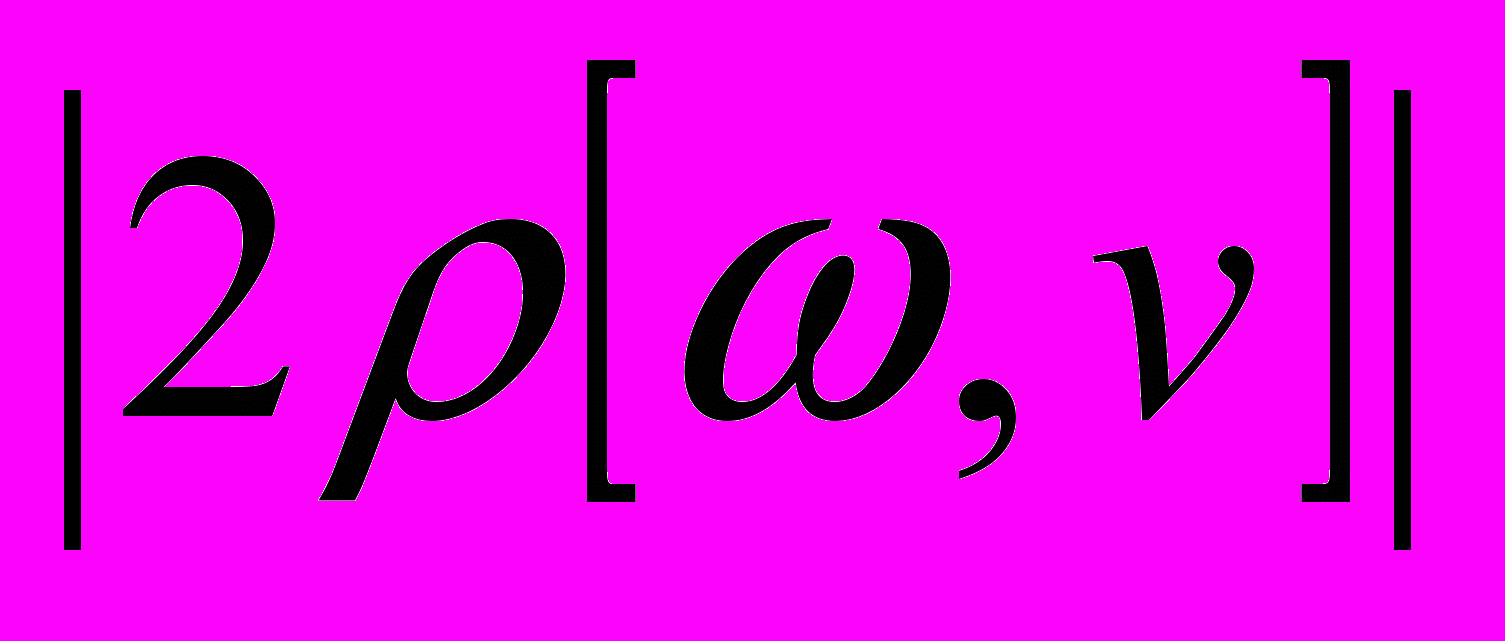 10-4 дин.
10-4 дин. Электродинамическая сила:
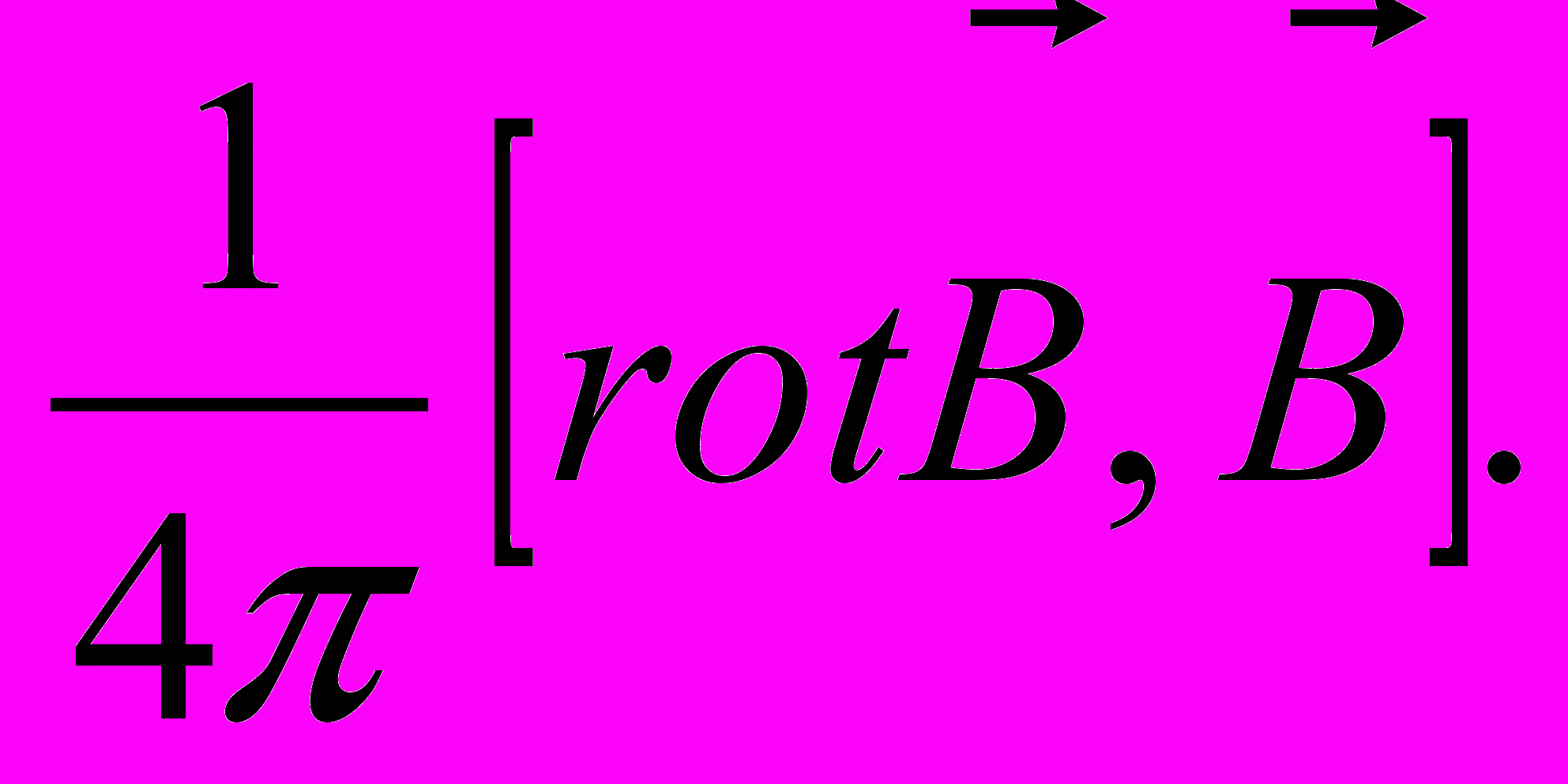 810-6 дин .
810-6 дин .Вязкое трение:
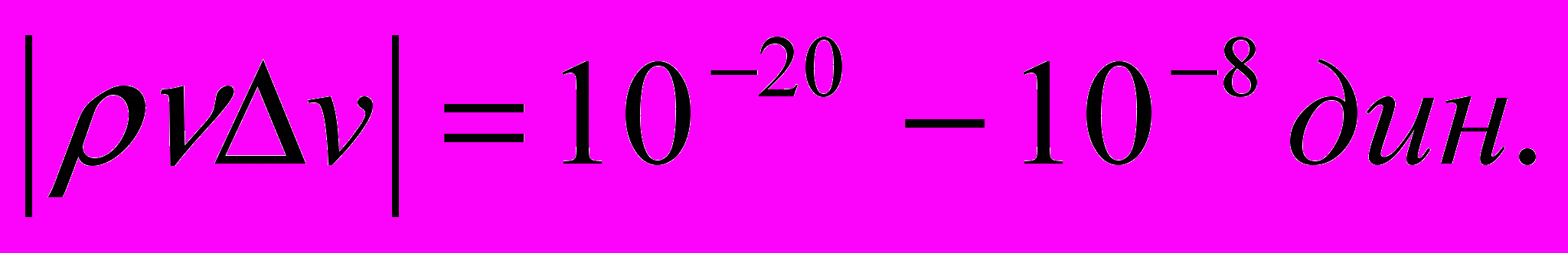
Принимая эти оценки как основу, можно считать существенными лишь часть сил: Кориолиса и электродинамическую. Тогда (7) станет:
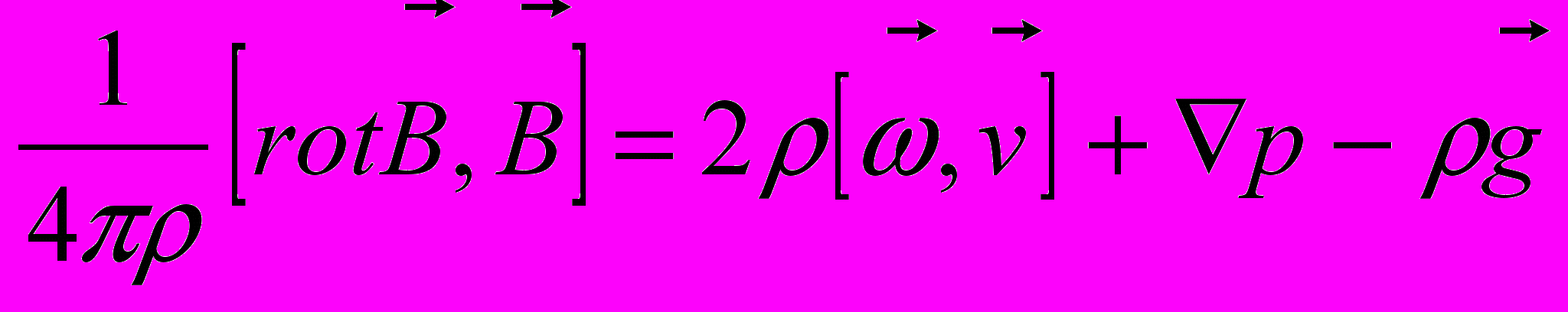 . (8)
. (8)Рассмотрим отдельные частные случаи:
- Движение в жидком ядре в отсутствие магнитного поля
Если движение масс вызвано лишь тепловым различием плотности, то (8) станет:
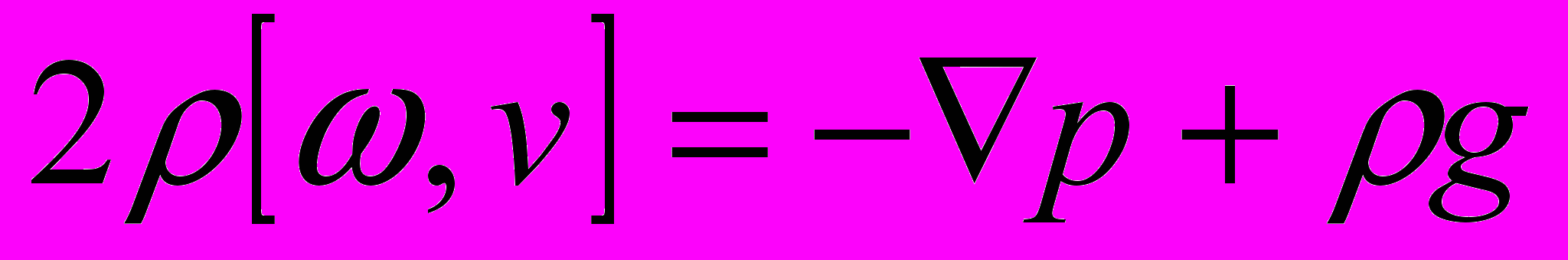 . Это означает: давление в жидкости и тяжесть уравновешиваются силами Кориолиса. Анализ показывает, что здесь движения возможны лишь в плоскостях, перпендикулярных оси вращения Земли. В принципе, это вытекает и из соображений симметрии, но было проверено следующим опытом (опыт Р. Хайда).
. Это означает: давление в жидкости и тяжесть уравновешиваются силами Кориолиса. Анализ показывает, что здесь движения возможны лишь в плоскостях, перпендикулярных оси вращения Земли. В принципе, это вытекает и из соображений симметрии, но было проверено следующим опытом (опыт Р. Хайда).Опыт состоит в следующем (см. рис. 134):
Рассматривается система из трех соосных сосудов.
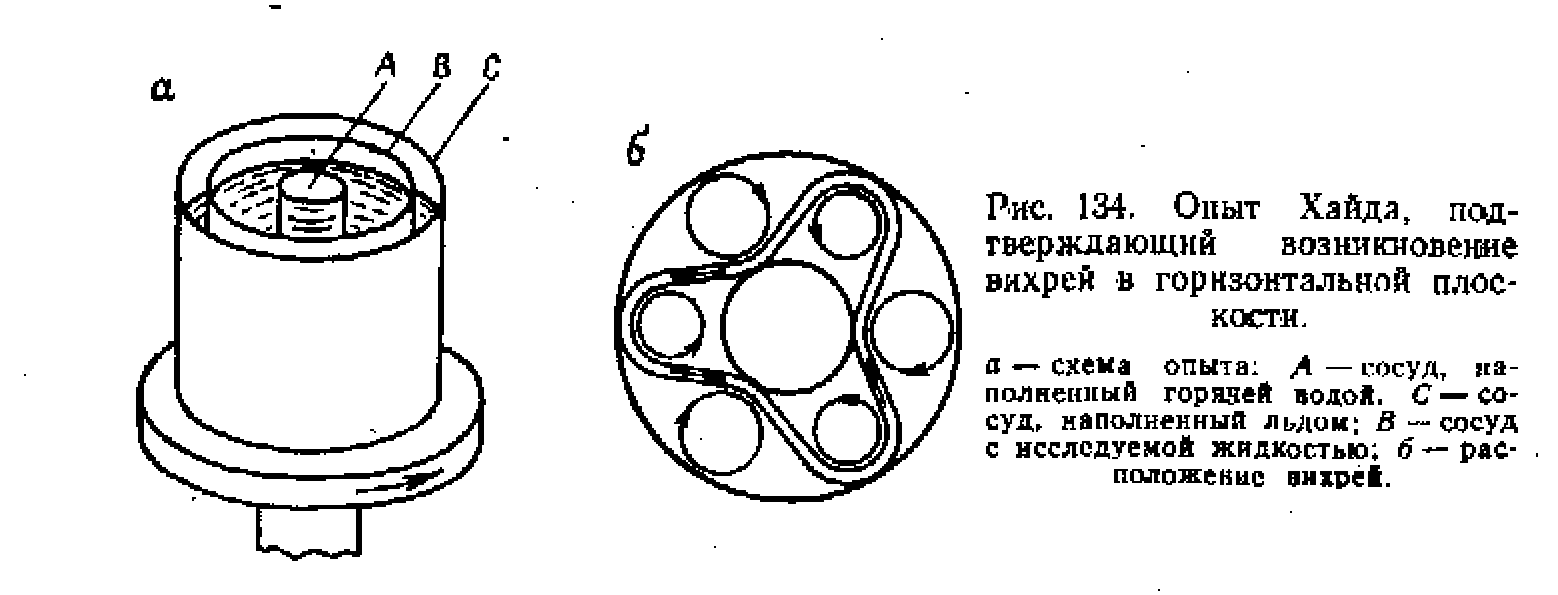
В сосуде В налита вода с примесью замутняющего порошка (порошок позволит наблюдать вихри в сосуде).
В сосуде А – горячая вода. В сосуде С – лед.
С вращением этой системы наблюдалось сначала появление хаотично расположенных вихрей в сосуде В, а затем, с увеличением , все они «укладывались» в горизонтальные плоскости. В итоге, формировалась картина вихрей, подобная той, что приведена на рис 134,б.
(Необходимо, однако, заметить, что в условиях Земли роли Кориолисовых и эелктродинамических сил в выполаживании вихрей противоположны и, будучи равновеликими, эти силы, в итоге, не выводят вихри в экваториальную плоскость).
2. Движение в жидком ядре в присутствии магнитного поля В0 . Ламинарное движение жидкости, перпендикулярное магнитному полю В0.
А. Жидкость – идеальный проводник () и ее вязкость пренебрежима мала, так что:
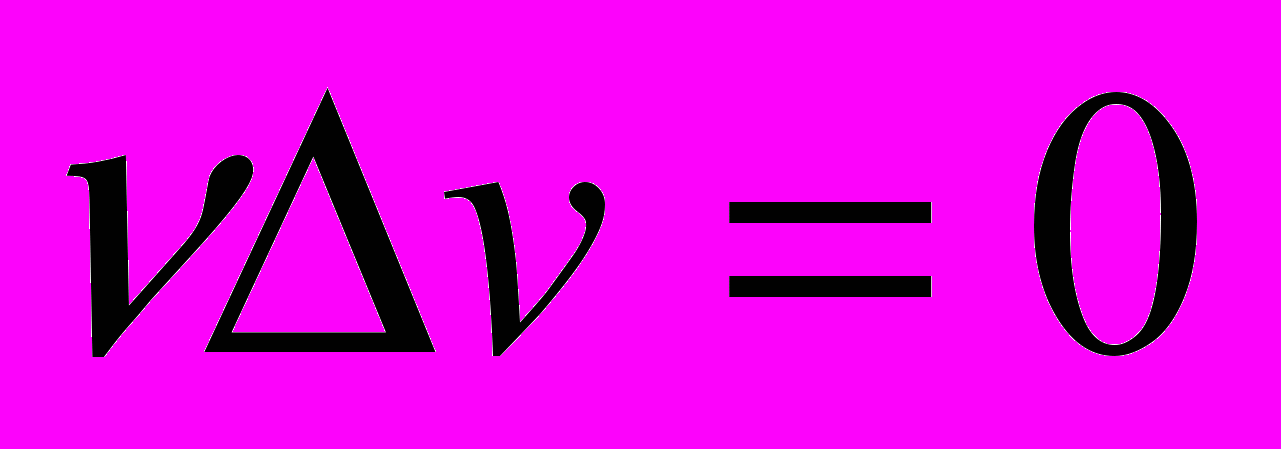 .
.Уравнения (5) и (7) станут:
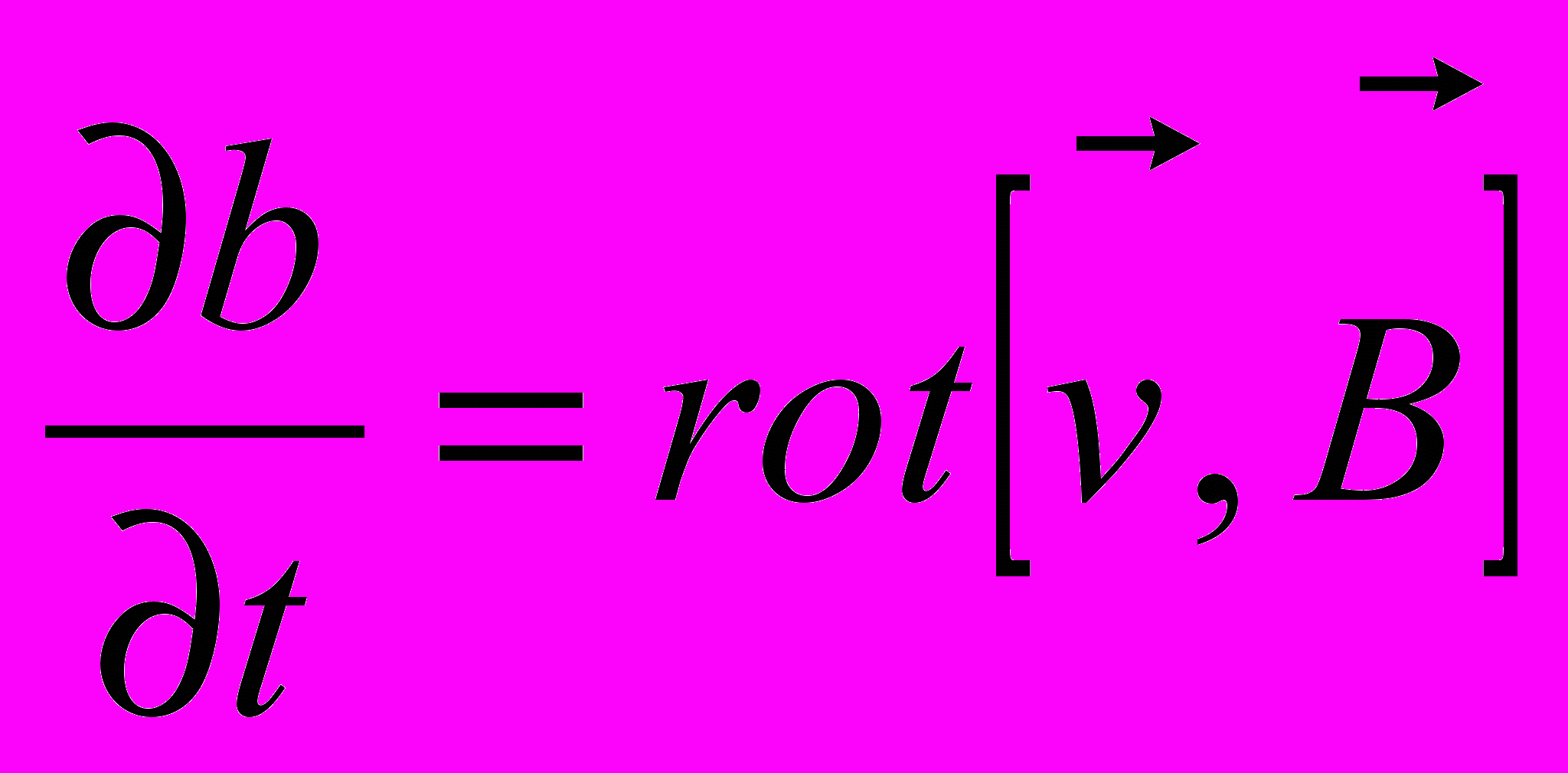 , (5”)
, (5”)
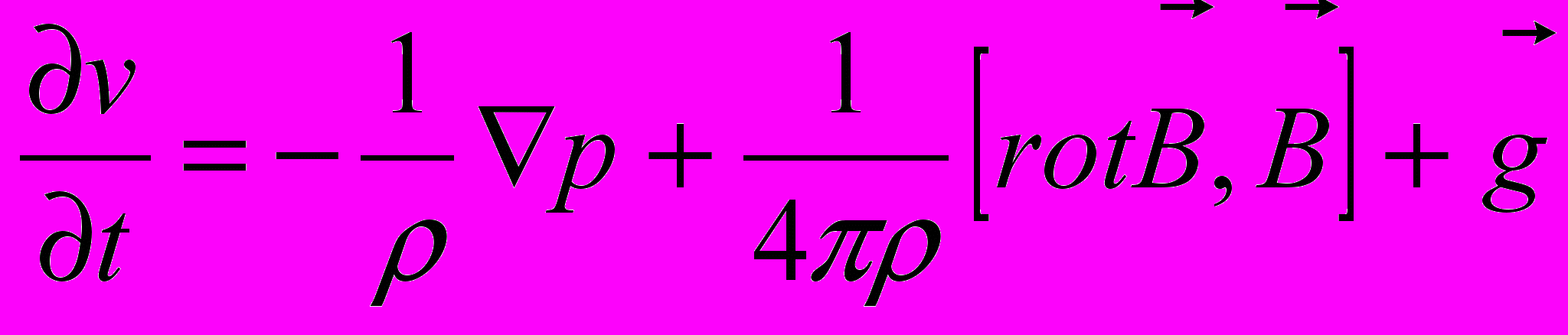 . (7”)
. (7”)Тогда в качестве решений этой системы получаем:
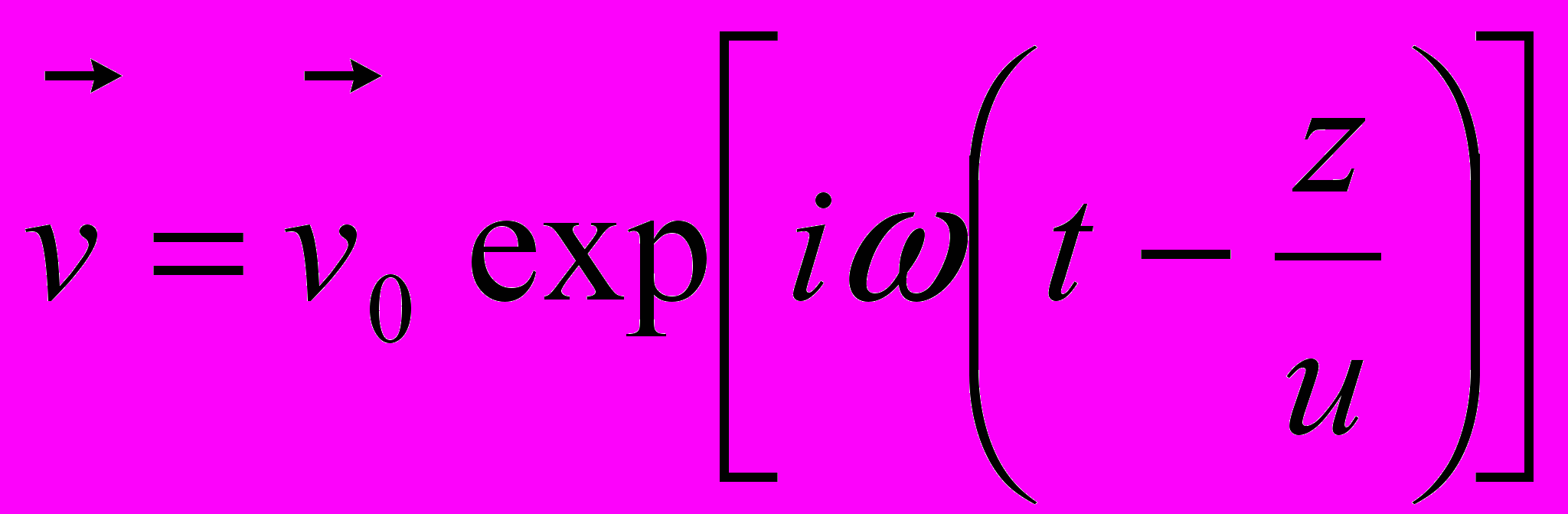 , (9)
, (9)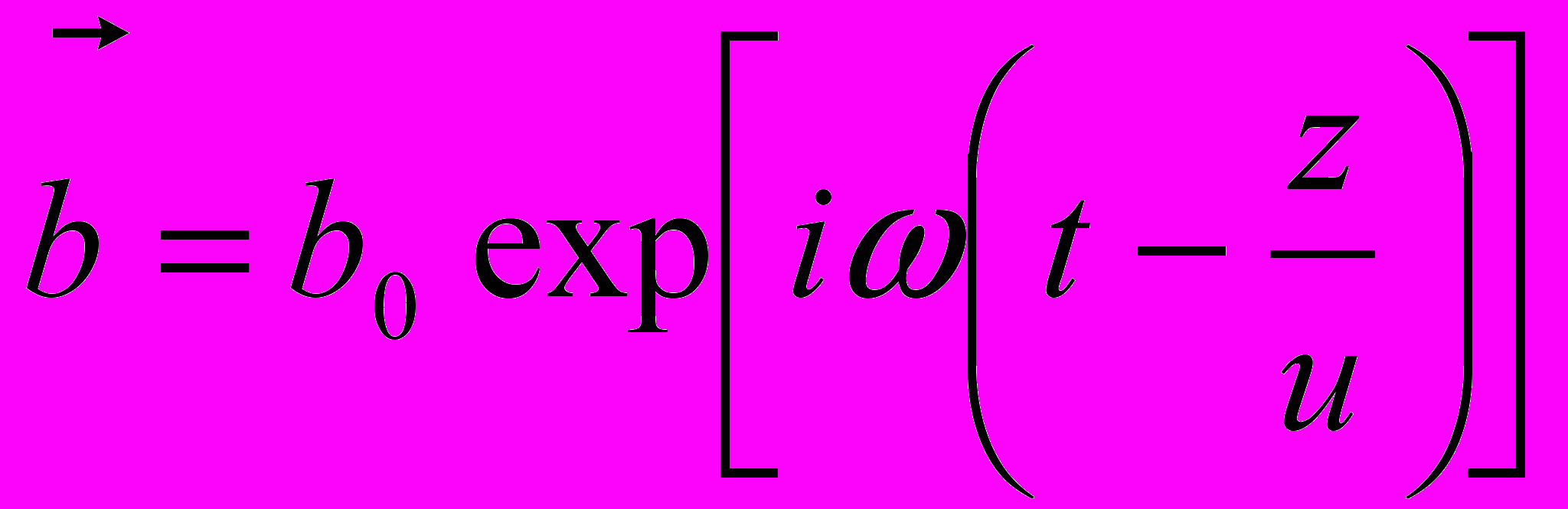 , (10)
, (10)т.е. плоские волны, распространяющиеся в направлении z (z
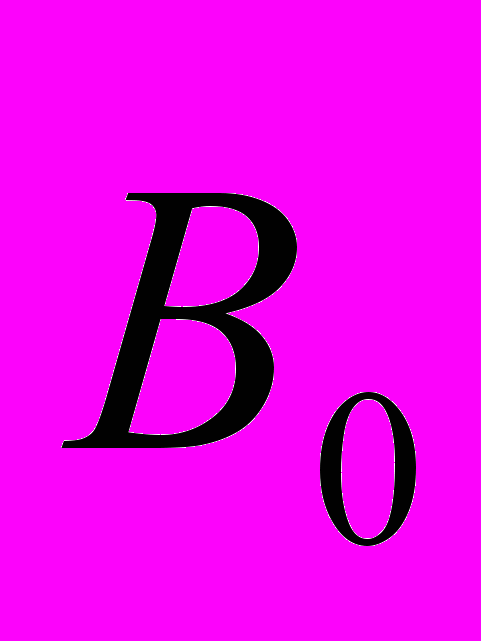 ), или – гидродинамическая и электромагнитная волны. Это – магнитогидродинамические волны (МГД-волны), или волны Альфвена (Альвена). Они, по существу, – поперечные: движение жидкости (базовое) происходит в направлении х, а движение волны – вдоль z. Необходимую для этого упругость жидкости (обязательную для существования именно поперечных волн) обеспечивают электромагнитные силы.
), или – гидродинамическая и электромагнитная волны. Это – магнитогидродинамические волны (МГД-волны), или волны Альфвена (Альвена). Они, по существу, – поперечные: движение жидкости (базовое) происходит в направлении х, а движение волны – вдоль z. Необходимую для этого упругость жидкости (обязательную для существования именно поперечных волн) обеспечивают электромагнитные силы.Уравнение силовой линии для электромагнитной волны при этом окажется1:
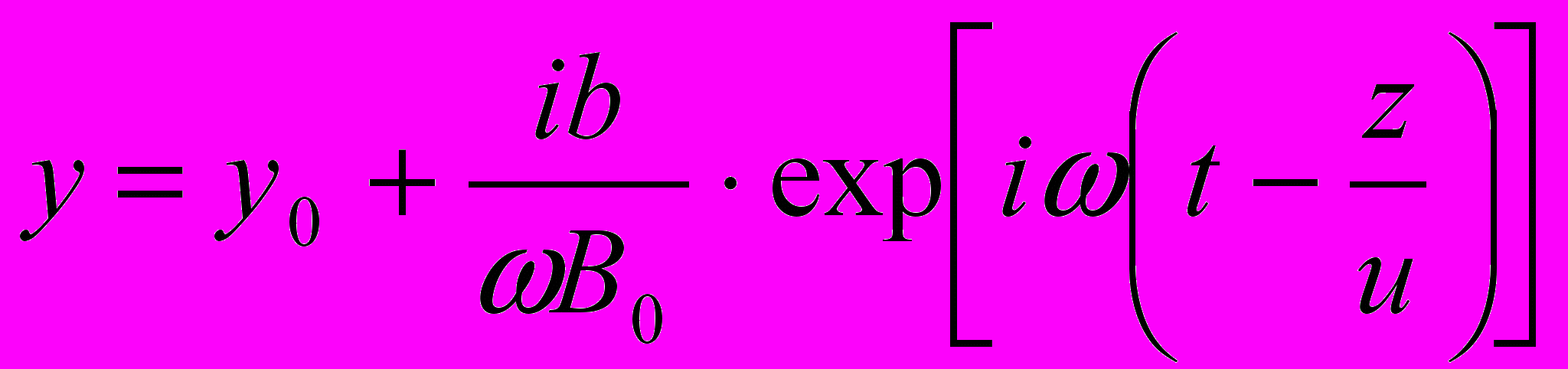 ,
,т.е. силовая линия поля
 , будет совершать волнообразное движение с той же скоростью, что и v и b, но со сдвигом по фазе в 90о. Получается, что силовые линии исходного поля В0 целиком увлекаются потоком жидкости: перемещаются вместе с нею и совершают такие же колебательные движения. Получили случай вмороженных силовых линий; это означает, что силовые линии эл/м. поля как бы “механически” крепко связаны с данной абсолютно проводящей жидкостью.
, будет совершать волнообразное движение с той же скоростью, что и v и b, но со сдвигом по фазе в 90о. Получается, что силовые линии исходного поля В0 целиком увлекаются потоком жидкости: перемещаются вместе с нею и совершают такие же колебательные движения. Получили случай вмороженных силовых линий; это означает, что силовые линии эл/м. поля как бы “механически” крепко связаны с данной абсолютно проводящей жидкостью.Б. Проводимость жидкости – конечная.
Это означает, что магнитной вязкостью
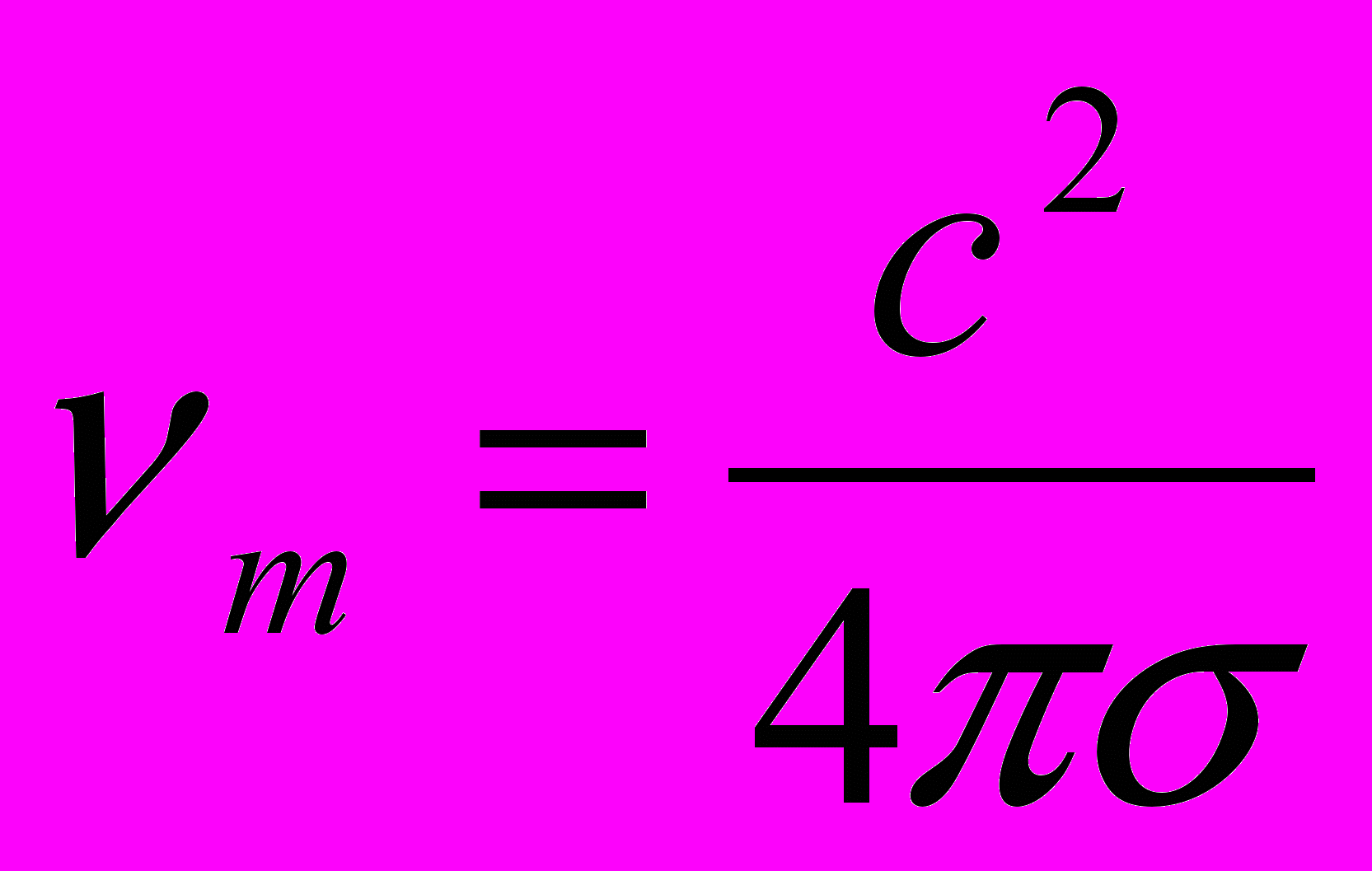 теперь пренебрегать нельзя.
теперь пренебрегать нельзя.В принципе, решения уравнений гидромагнитной динамики здесь подобны тому, что имели в случае А. Имеем:
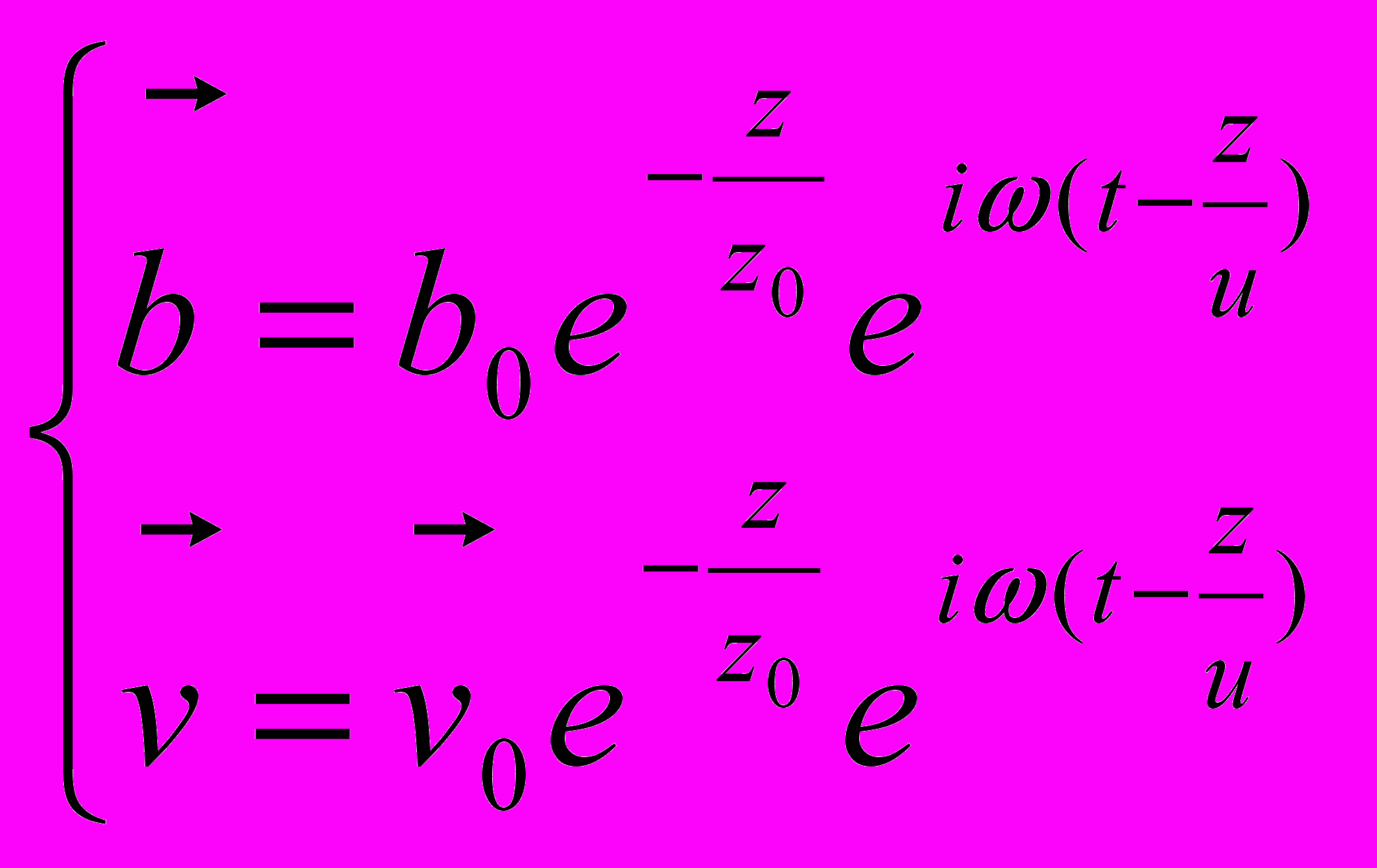 , где
, где 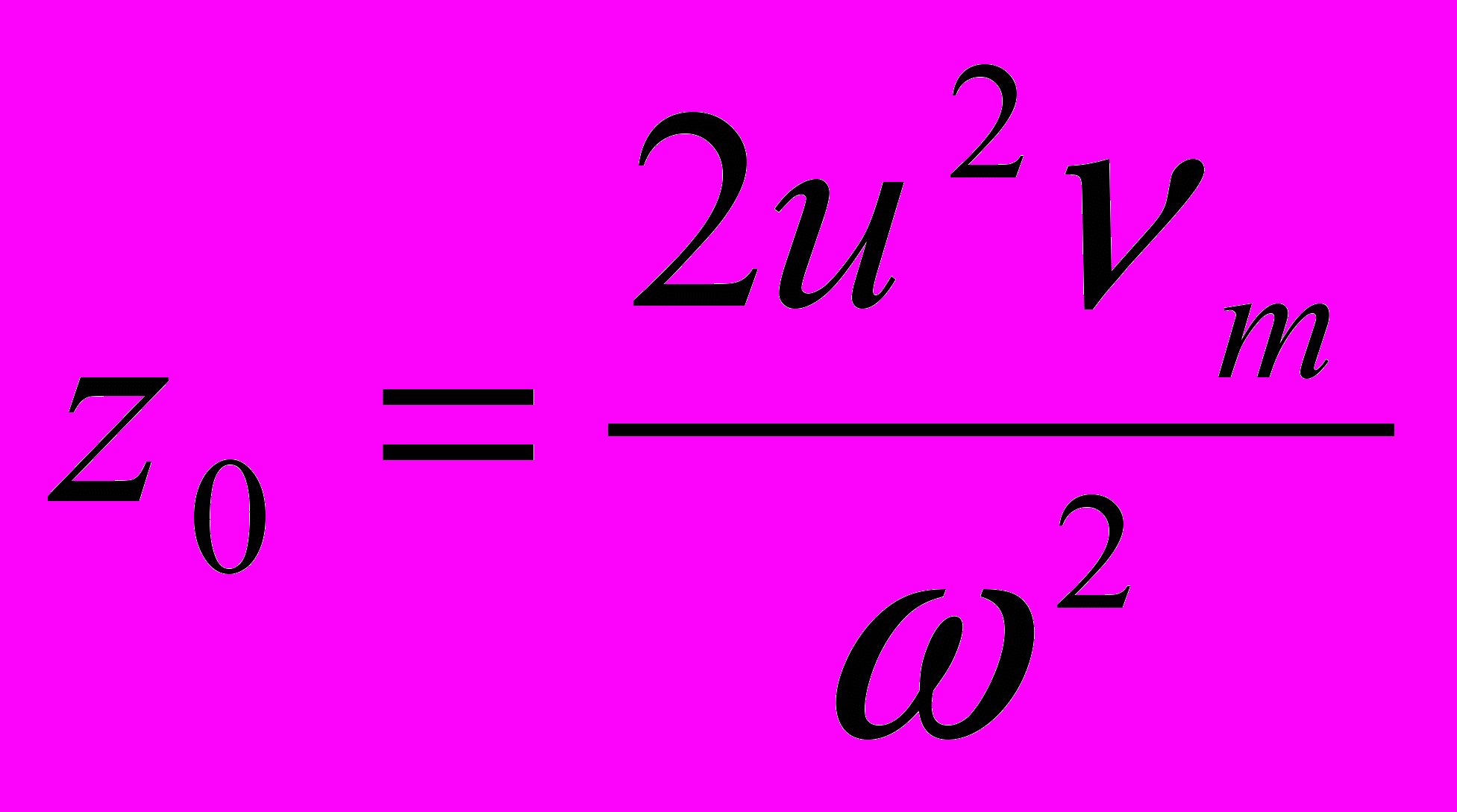 .
.Опять должны существовать МГД-волны, но теперь они уже – затухающие. Очевидно, энергия тратится на выделение джоулева тепла.
В 1949 году С.Ландквист наблюдал волны Альфвена в сосуде со ртутью, помещенном в сильное магнитное (до 10 000 Э) поле.
Вращение проводящей сферы (шара) в постоянном магнитном поле (Ян., 315)
Теория Э.Булларда, объясняющая геомагнитное поле эффектом самовозбуждения, по существу выводит поле решением уравнений магнитной гидродинамики для конкретного случая вращения жидкого проводящего шара радиусом d, в постоянном магнитном поле.
Скорость вращения элемента жидкости:
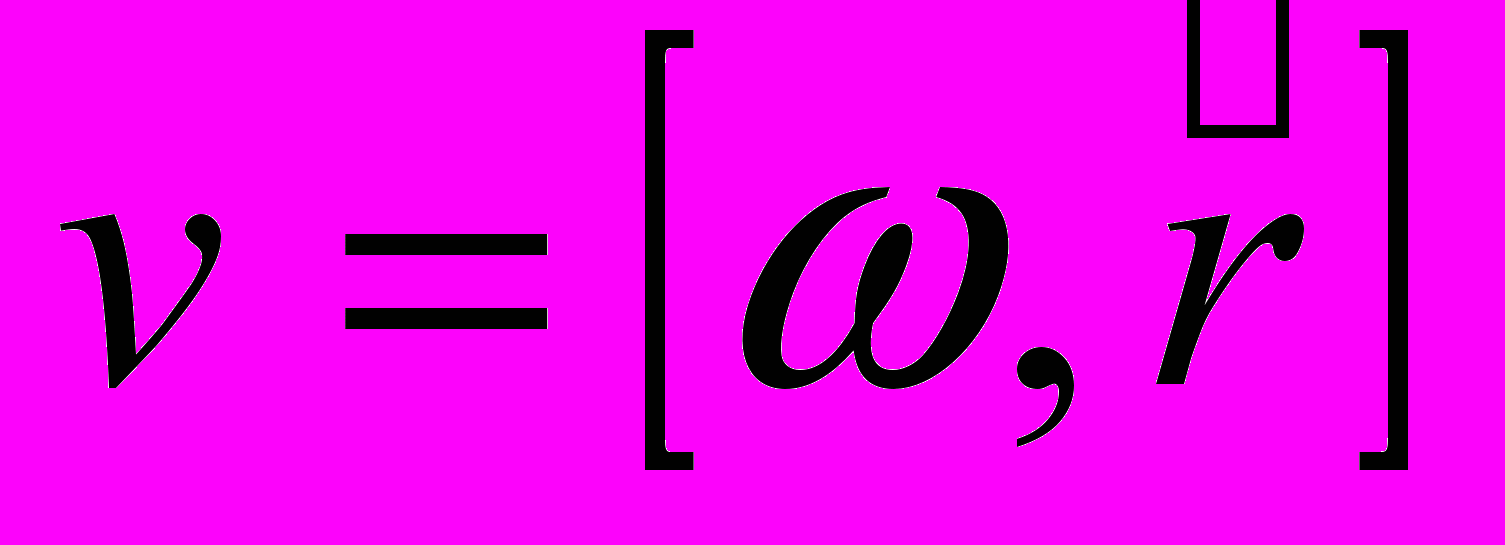 , где = сonst – угловая скорость вращения шара,
, где = сonst – угловая скорость вращения шара, 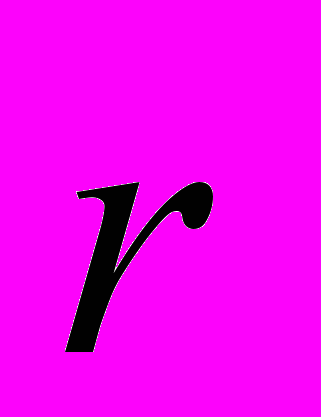 – расстояние элемента от оси вращения.
– расстояние элемента от оси вращения.Задав таким образом способ вращения (движения) жидкости, для пары {(5) + (7)} уравнений магнитной гидродинамики можем оставить только полевую часть (
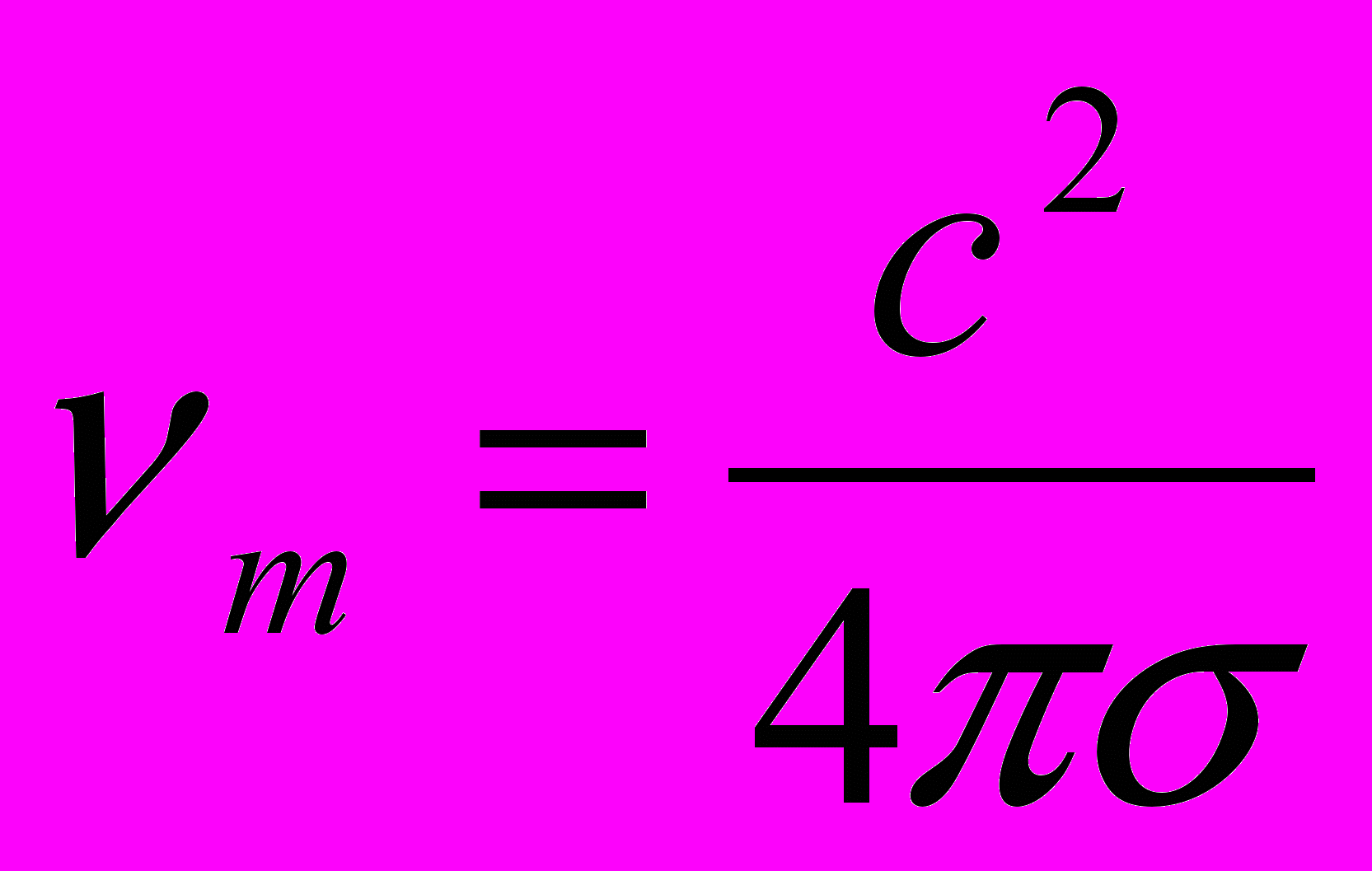 ):
):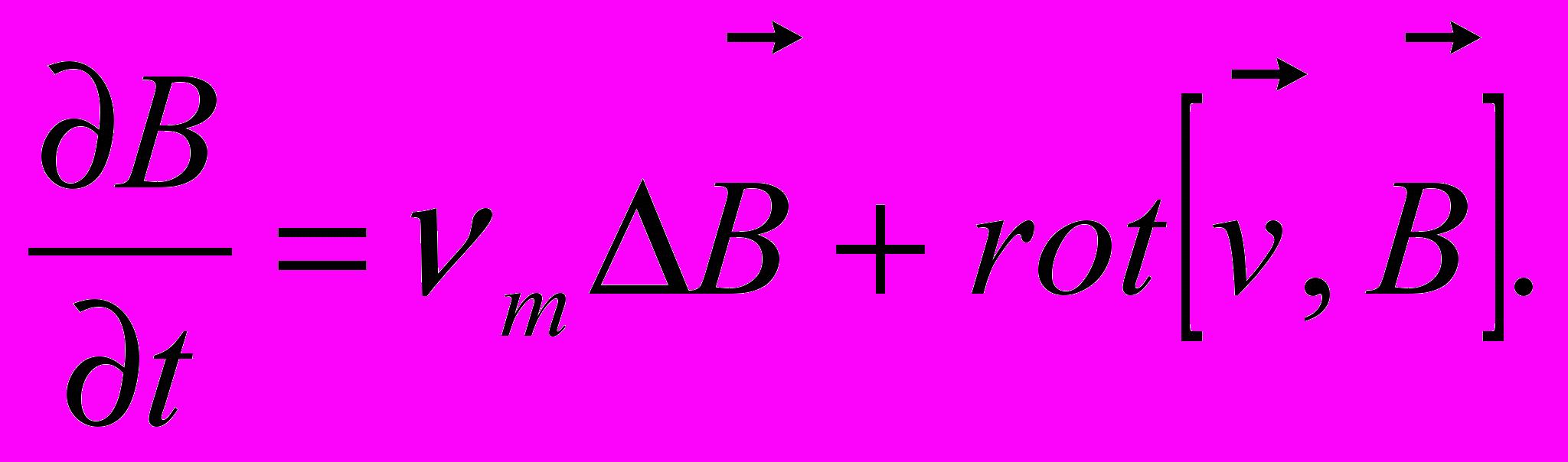 (здесь В – вектор). (1)
(здесь В – вектор). (1)Чтобы решить его, сведем его к линейному. Для этого введем сферическую систему координат. Тогда для v имеем лишь одну координату:
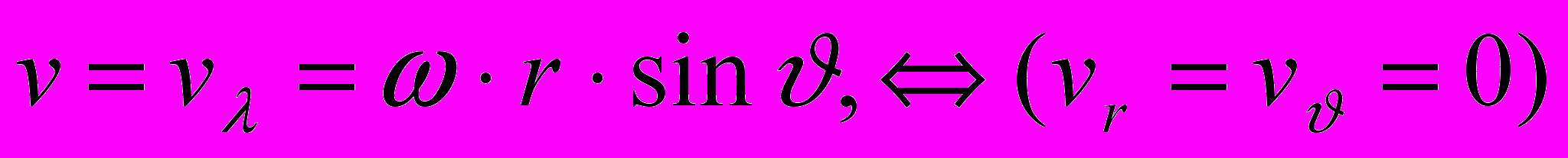 , и для произведения
, и для произведения 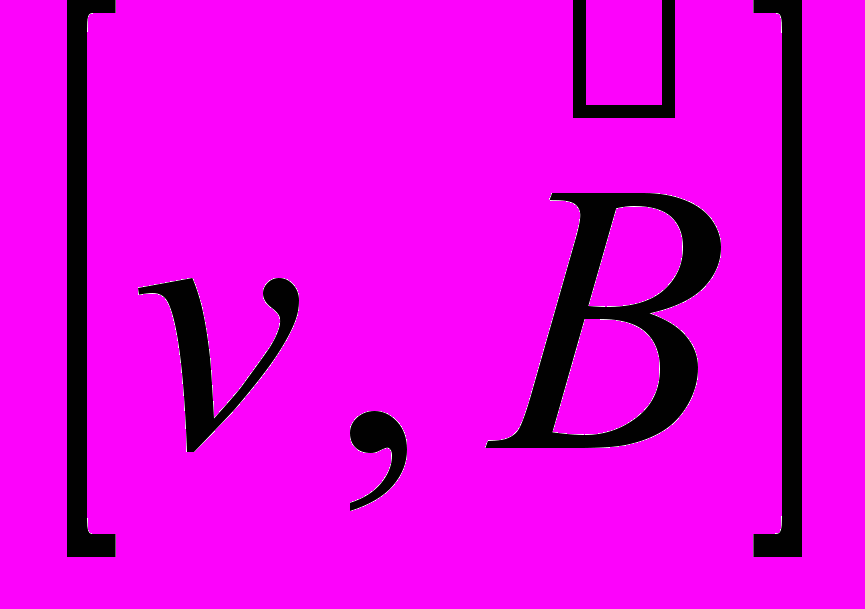 – две:
– две: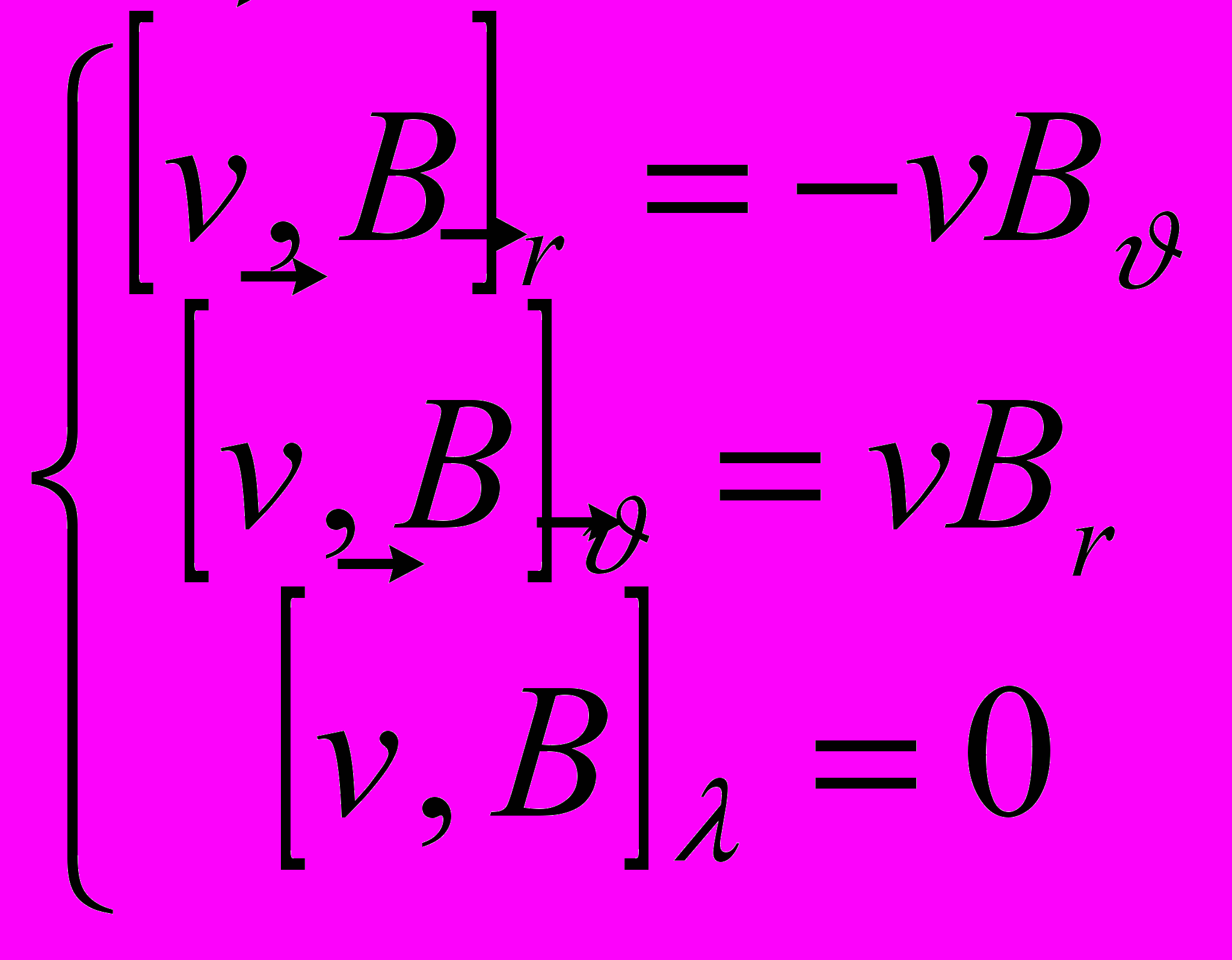 .
.Подставляем все это в (1), преобразуем, получаем:

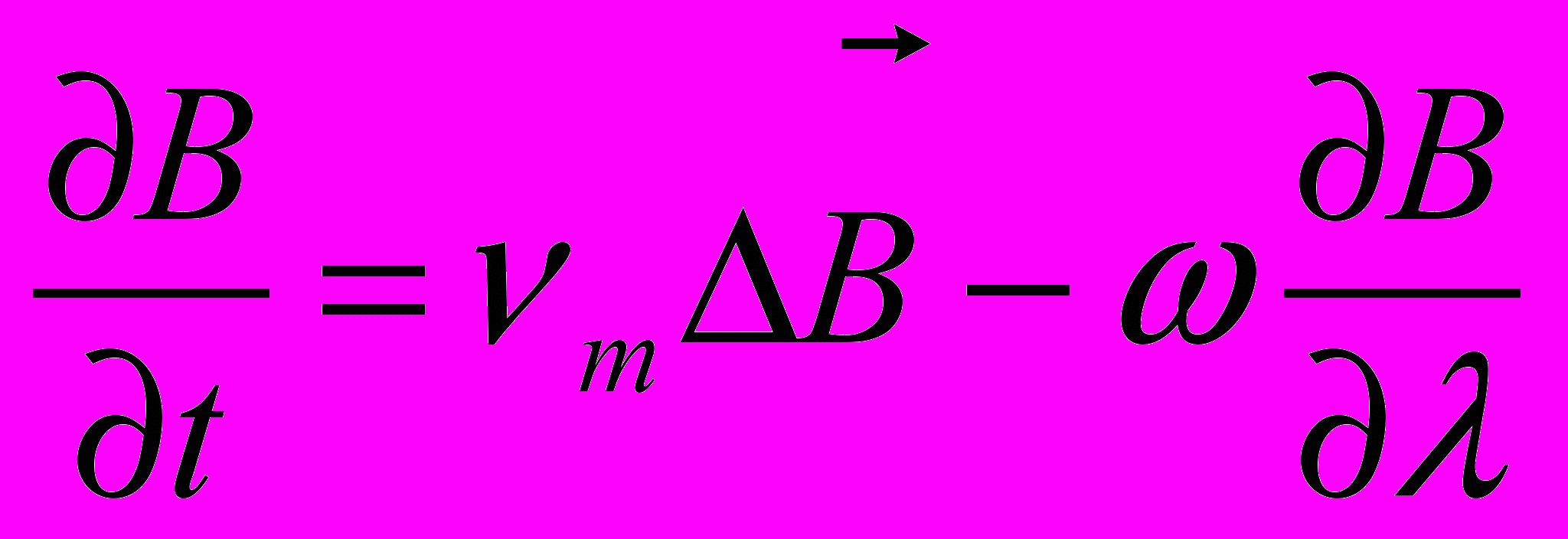 .
. Решение уравнения ищем методом Фурье: полагая В периодической функцией долготы и принимая, что затухание процесса во времени подчиняется “формуле”: B exp(-pt) [ если р – комплексное, то то процесс – колебательный], – запишем для В:
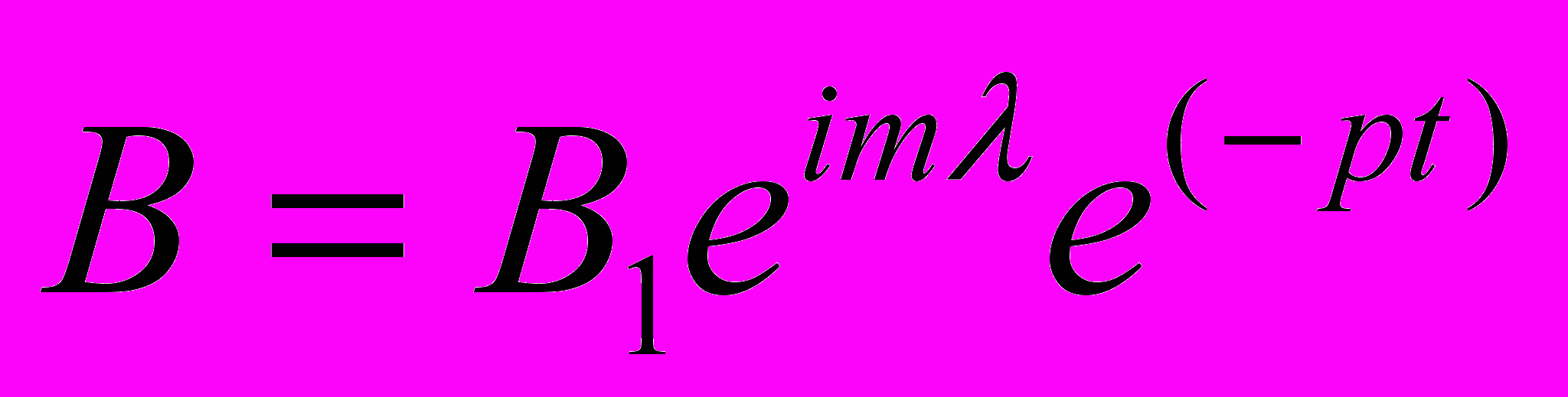 (m – целое число). (2)
(m – целое число). (2)Подставляя (2) в (1), получим:
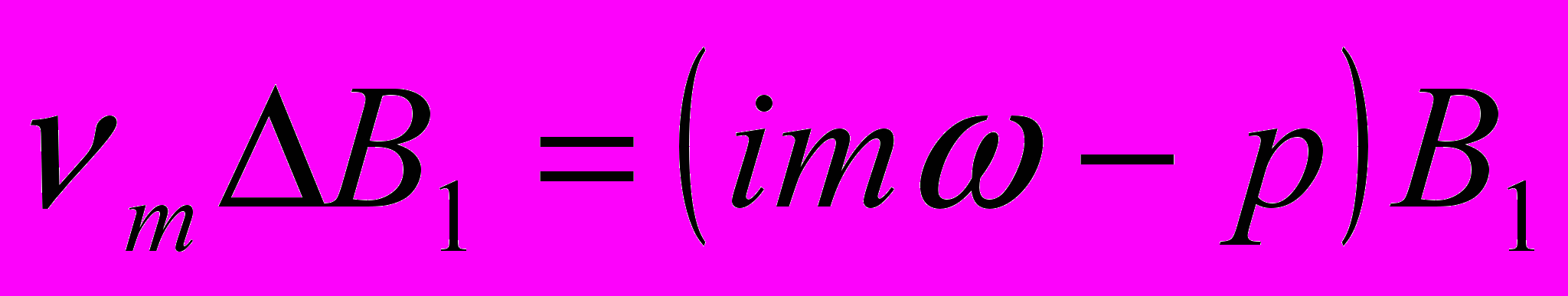 . Обозначив:
. Обозначив: 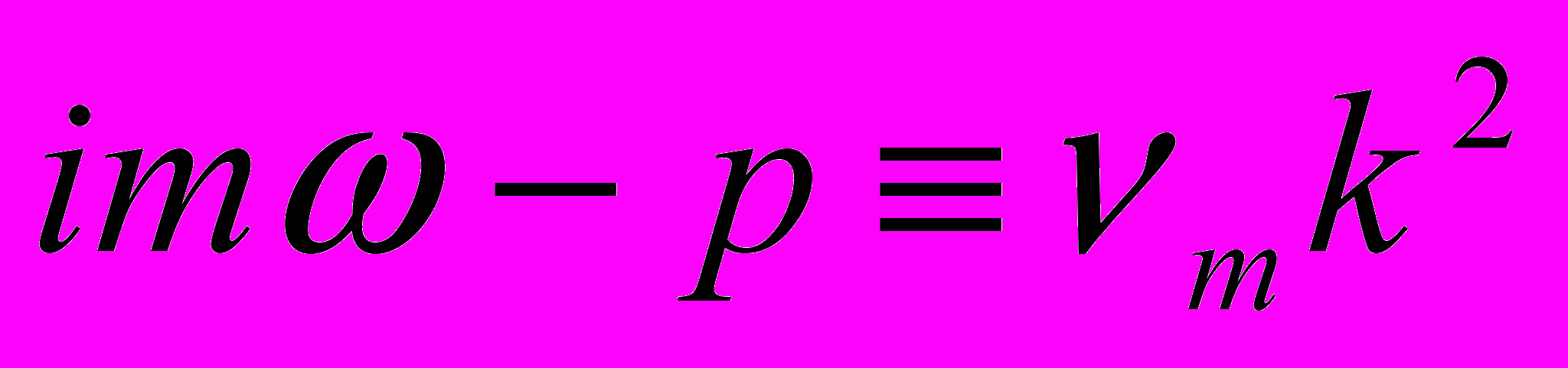 , имеем:
, имеем: 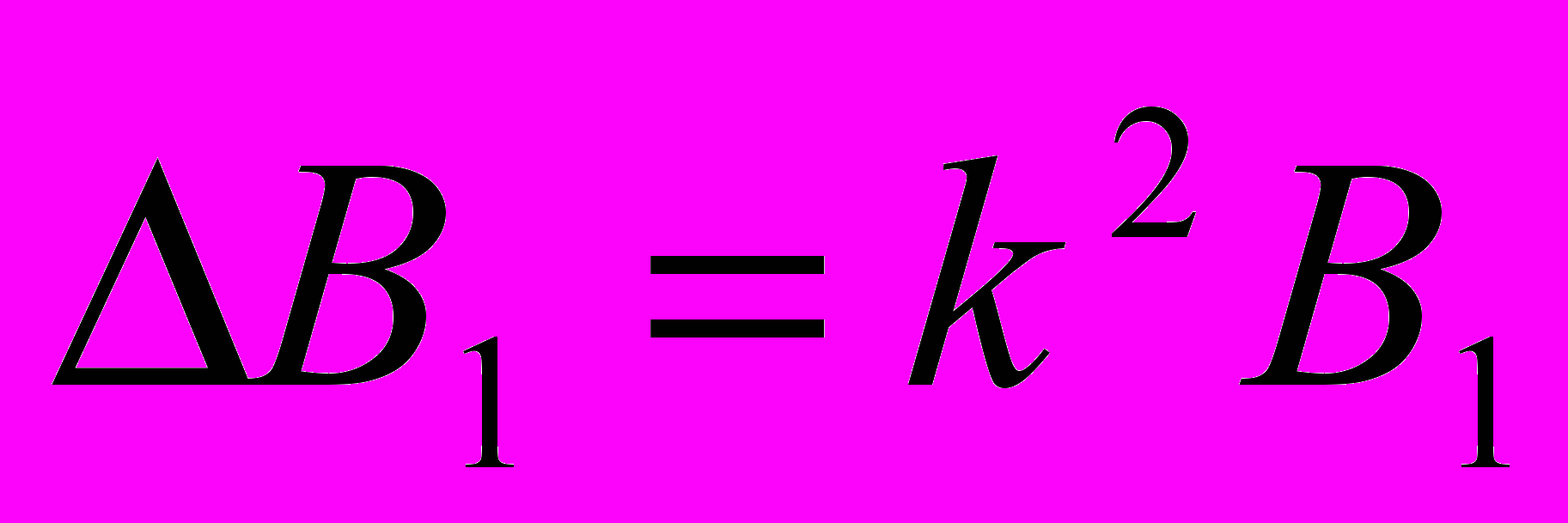 .
.Чтобы решить его, придется представить вектор В1 как сумму двух векторов BT и BS: B1 = BT + BS. При этом BT направлен перпендикулярно вектору r, т.е. всюду идет по касательной к сфере радиуса r. Вектор BS перпендикулярен к BT. Вектор BT назван тороидальным вектором. Вектор BS – полоидальным вектором. Анализ показывает, что эти вектора взаимосвязаны:
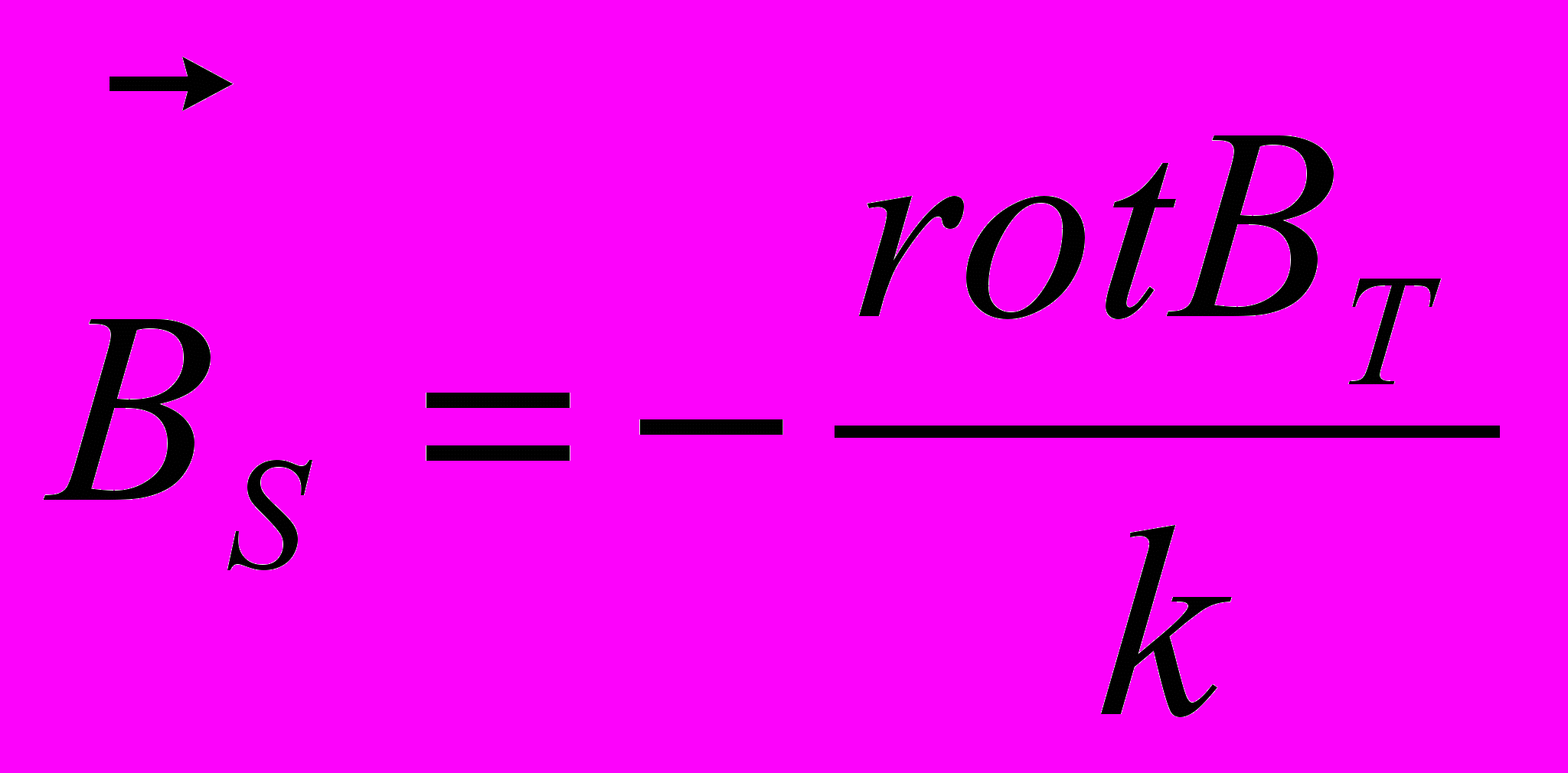 . Практически оказалось, что BT это – поле, “лежащее” на поверхности сферы радиуса r.
. Практически оказалось, что BT это – поле, “лежащее” на поверхности сферы радиуса r.BS – поля, лежащие в главных сечениях шара.
Анализ решения дает многообразные варианты распределения полей BT и BS для проводящего шара (рис.136 и137 на с.318-319 в кн.Яновского).
К теории геомагнитных инверсий
Первая попытка сделана Э.Буллардом. Он показал, что униполярное динамо инверсировать не может. Возможны лишь слабые колебания напряженности поля В.
С Ранкорн, однако, показал, что уравнения магнитной гидродинамики не исключают инверсий МПЗ. Согласно Ранкорну, направление магнитного момента системы токовых контуров определяется исключительно видом (картиной) скоростей жидкости в ядре Земли, оно может изменяться с изменением этой картины на противоположное. В принципе, Ранкорн дал лишь чисто формальный ответ на вопрос о процессе самообращения. – Истинная картина условий в ядре еще неизвестна.
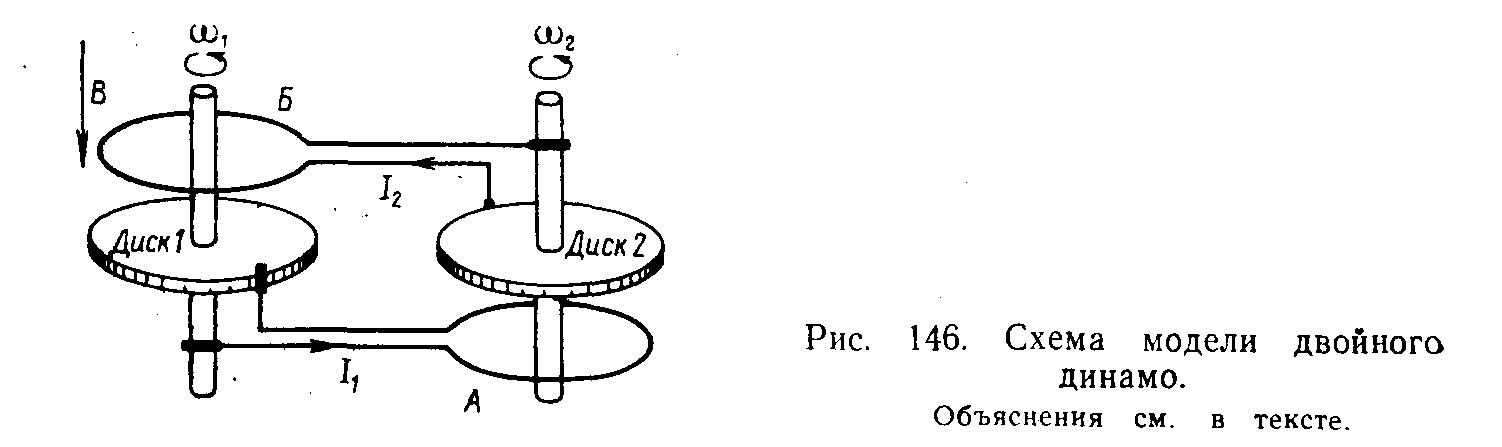
Одно из решений этого вопроса дается моделью двойного (биполярного) динамо, предложенная Т.Рикитаки. Такая модель может самовозбуждаться, но, кроме того, иногда будет находиться в неустойчивом состоянии, вследствие чего будет переходить в состояния с новым (как по величине, так и по направлению) полем В. Вращения дисков 1 и 2 происходят в поле В, параллельном осям дисков.
Теория процесса генерации и регенерации поля в модели, данная Рикитаки, сводится к решению уравнений движения дисков и их электромагнитного состояния. Эти уравнения, в соответствии с законами механики и электродинамики, есть:
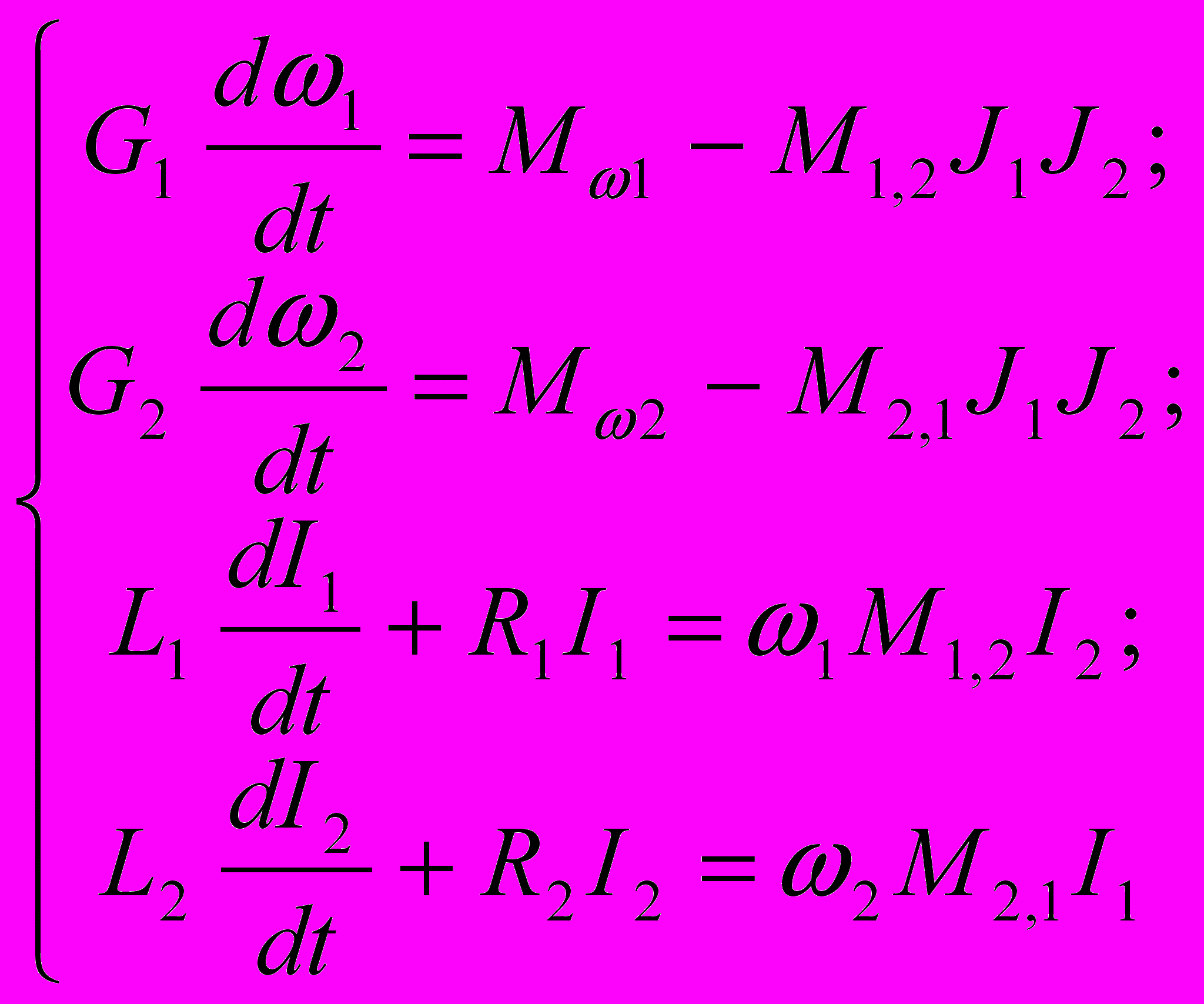 ,
, где L1 и L2 – индуктивности дисков 1 и 2; G1 и G2 – их моменты инерции; M1,2 и M2,1 – взаимные индуктивности контура А с диском 2 и контура Б с диском 1; R1 и R2 – сопротивления контуров А и Б; М1 и М2 – моменты вращения дисков за счет внешних сил.
Решение системы этих уравнений показало, что действительно, если вращение дисков модели поддерживается за счет внешней энергии, то в результирующем поле, кроме общего колебательного процесса, может происходить произвольное число циклов самообращения.
1 Магнитное поле b, складываясь векторно с полем В0, исказит его, и его силовые линии, представляющие собой (без движения жидкости) прямые линии поля В0, параллельные оси z, после возникновения движения будут как-то изменяться по форме (в пределах соотношения величин полей b и B0 ). Дифференциальное уравнение силовой линии в этом случае должно иметь вид:
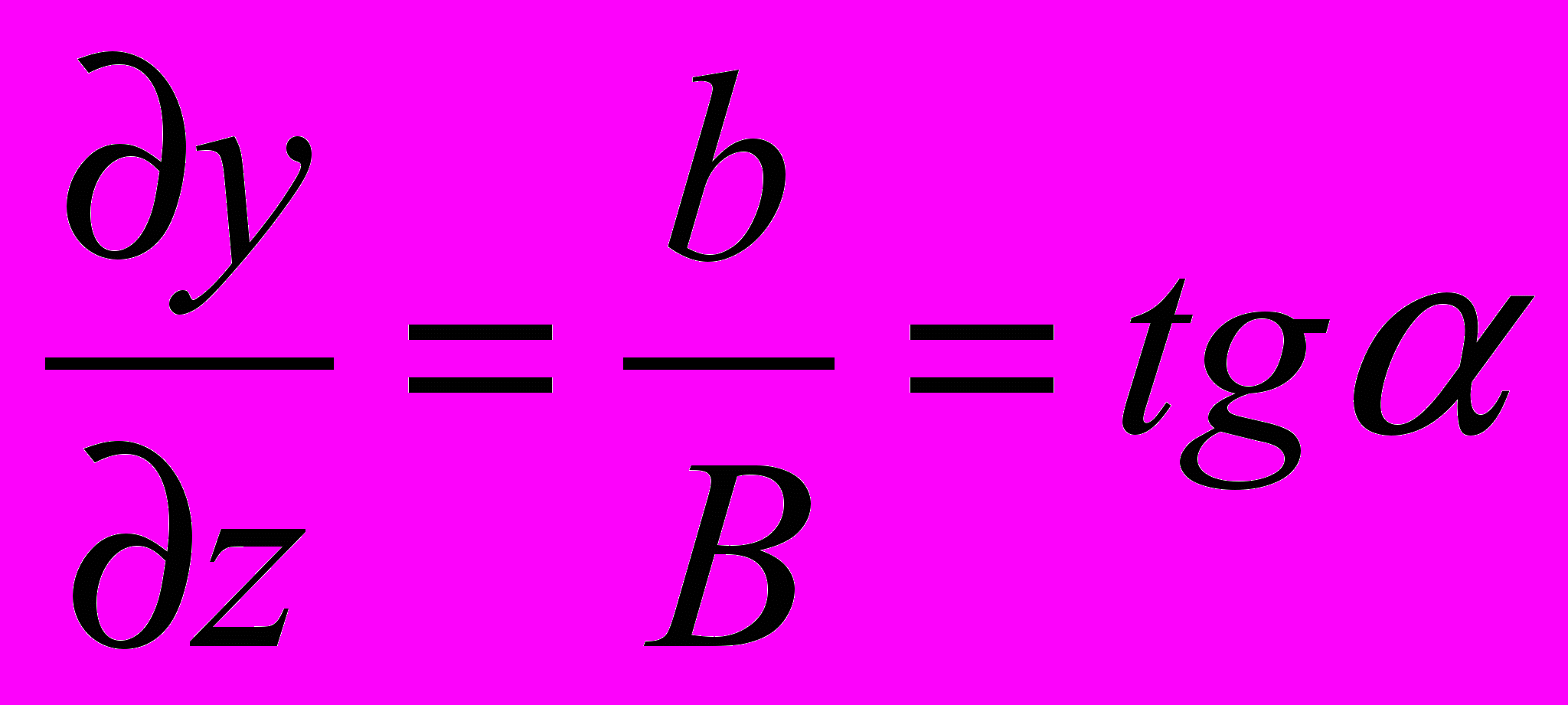 , где – угол, составляемый касательной к силовой линии с осью y (силовая линия, значит, лежит в плоскости yz). Подставляя сюда величину b из (10) и интегрируя, получаем уравнение силовой линии.
, где – угол, составляемый касательной к силовой линии с осью y (силовая линия, значит, лежит в плоскости yz). Подставляя сюда величину b из (10) и интегрируя, получаем уравнение силовой линии.