Geum.ru

Отчет о научно-исследовательской работе разработка модулей для производственных технологий

Вид материалаОтчет

Содержание


Рисунок 2.7 – Обзорный спектр излучения ртутной индукционной лампы
2.3 Расчет ультрафиолетового излучения разряда низкого давления в смеси Hg – Ar
3 Инициирование разряда и источник питания
Подобный материал:
1   2   3   4   5

Рисунок 2.7 – Обзорный спектр излучения ртутной индукционной лампы



На рисунке 2.7 видны основные хорошо известные линии ртутного спектра (365,
404.6, 437.7, 546, желтый дублет: 577–579 нм). Представляет интерес область 250–300 нм, где наблюдается густая сеть ультрафиолетовых линий. Эта часть спектра более подробно представлена на рисунке 2.8. В этой области, согласно справочнику [5], есть большое число линий с высоким потенциалом возбуждения. Детальное исследование распределения заселенностей на высоких уровнях и форма контуров этих линий могут дать много информации о параметрах плазмы. Этот участок спектра подлежит тщательному исследованию в будущем.





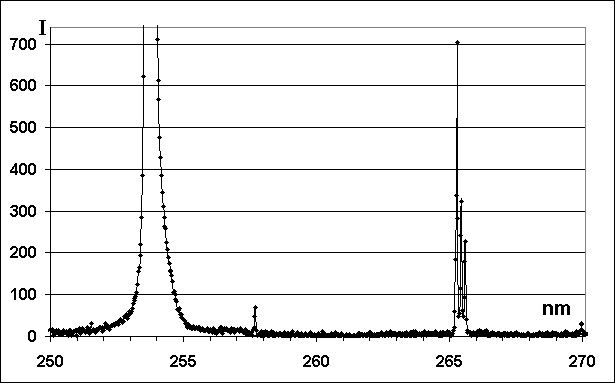
Рисунок 2.8 – Спектр области 250–300 нм


На установке, представленной на рисунке 2.6, была измерена освещенность, создаваемая лампой на расстоянии 1 м в линии 253.652 нм, причем направление наблюдения было перпендикулярно плоскости лампы. Получено значение (49030) мкВт/см2 (погрешность оценена по результатам повторных измерений и может определяться нестабильностью температуры лампы без кожуха). Предполагая индикатрису рассеяния сферической, оценим выход излучения в этой линии в 60 Вт. Оценку не следует считать завышенной, т. к. предварительные эксперименты с лампой в кожухе с малым отверстием показывают, что, располагая датчик в плоскости лампы (но перпендикулярно ее оси), можно получить в два раза большую освещенность. Это компенсирует падение освещенности при расположении приемника под углом к оси лампы.

Анализ спектра излучения лампы показывает, что для данного экземпляра выход излучения в диапазоне 200–300 нм примерно равен выходу излучения в видимом диапазоне спектра. Хотя достигнутый выход в бактерицидном диапазоне вполне позволяет удовлетворить требованиям к модулю для обеззараживания воды, однако перераспределение излучения могло бы дать дополнительную экономию затрат на обеззараживания. Для оптимизации условий в источнике необходимы дополнительные эксперименты и теоретические оценки. Теоретическому выбору условий, обеспечивающих максимальный выход «полезного» излучения посвящен следующий раздел.


2.3 Расчет ультрафиолетового излучения разряда низкого давления в смеси Hg – Ar


Использование безэлектродных индукционных ламп позволяет существенно повысить концентрации атомов ртути и электронов по сравнению с хорошо исследованными люминесцентными лампами, но в тоже время сохранить режим низкого давления по сравнению с дуговыми лампами высокого давления. Типичные параметры люминесцентных ламп: p(Hg)~10–3–10–2 Торр,
ne~1011 см–3. В индукционных лампах эти параметры можно поднять до p(Hg)Торр, ne~1013 см–3, а в импульсно-периодическом режиме – до 1014см–3. Расчет выхода ультрафиолетового излучения в таком широком диапазоне требует учета дополнительных факторов, не учитываемых при расчетах излучения люминесцентных ламп. Достаточно полный обзор имеющихся работ представлен в монографии Миленина и Тимофеева [6]. Качественные зависимости относительной мощности излучения ртутного разряда в широком диапазоне давлений ртути и токов приведены Клярфельдом в работе [7] (рисунок 2.9). Из рисунка 2.9 видно, что переход на большие токи позволяет увеличить выход резонансного излучения и расширить диапазон давления ртути почти до 1 Торр.



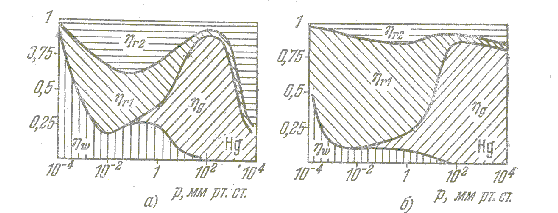
Рисунок 2.9 – Относительный вклад различных механизмов потерь мощности положительного столба в зависимости от давления а) i=1 А, б) i=10 А, w – мощность, теряемая из-за нейтрализации ионов на стенке, r1 – мощность резонансного излучения,
r2 – мощность нерезонансного излучения, g – мощность на нагрев газа (охлаждение теплопроводностью на стенку)


Рассмотрим схему уровней ртути (рисунок 2.10). Основное ультрафиолетовое излучение, способное выходить из трубки в воздух, переносится в линии 254,7 нм. Вторая резонансная линия, 184,9 нм, лежит в области вакуумного ультрафиолета и сильно поглощается в воздухе. Интенсивность излучения из единицы объема в пределах контура линии есть J=NiAэфhi, где Ni – усредненная по объему трубки концентрация на верхнем уровне, Аэф – усредненная эффективная вероятность перехода с учетом поглощения и переизлучения, hi – энергия перехода. Для определения заселенности резонансного уровня 63P1 необходимо учитывать переходы на основной и близко расположенные уровни, а также уход на ионизацию. Большой энергетический разрыв между группой резонансного и двух метастабильных уровней (63Р012) и верхними уровнями позволяет не учитывать переходы с верхних уровней, а уходы наверх учитывать только на основные 7S- и 6D-уровни. Итак, первой задачей является вычисление скоростей элементарных процессов оптических переходов и переходов электронным ударом между указанными уровнями.




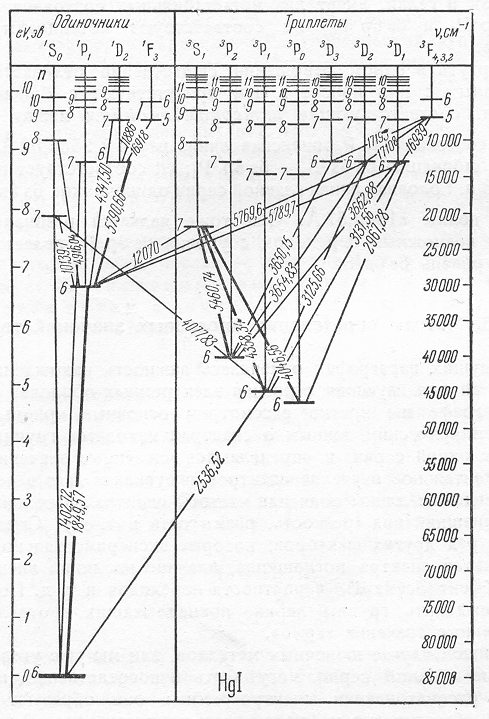
Рисунок 2.10 – Схема уровней атома ртути


2.3.1 Скорости прямых и обратных переходов электронным ударом


Число переходов в единицу времени, осуществляемое одним электроном, равно vN, где
 – сечение процесса, v – относительная скорость электрона, N – концентрация атомов на исходном уровне. Скобки означают усреднение по распределению электронов по скоростям.

На рисунке 2.11 приведены зависимости сечений возбуждения уровней ртути электронным ударом от энергии электронов, рассчитанные Яворским [8]. Данные зависимости характеризуются порогом возбуждения, значением сечения в максимуме и энергией максимума. В таблице 2.2 приведены теоретические и экспериментальные параметры максимума возбуждения, имеющиеся в литературе [8–16]. Для расчета скоростей перехода необходимо аппроксимировать сечение каким-либо аналитическим выражением. Типичные аппроксимации сечений и формулы расчета скоростей для максвелловского распределения электронов по скоростям приведены в [18].

Аппроксимация ступенькой используется при малом пороге возбуждения, сравнимом с температурой электронов. Аппроксимация Фабриканта – при >kTe, а линейная аппроксимация – при больших значениях порога возбуждения >>kTe. Обычно так аппроксимируется сечение ионизации. Скорости обратных переходов (удары второго рода) определяются из принципа детального равновесия:

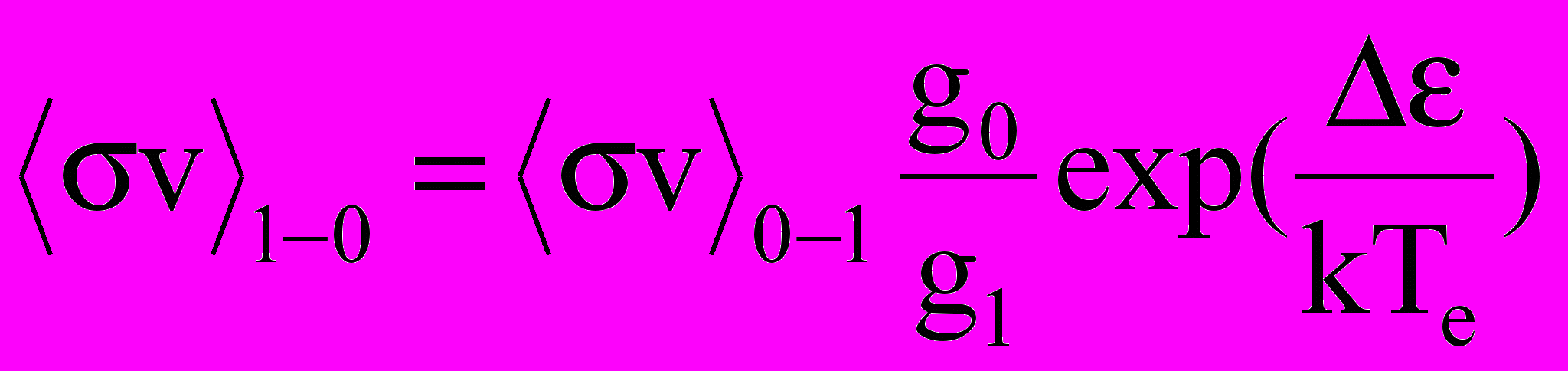, (2.1)


где g0, g1 – статвеса нижнего и верхнего уровней.





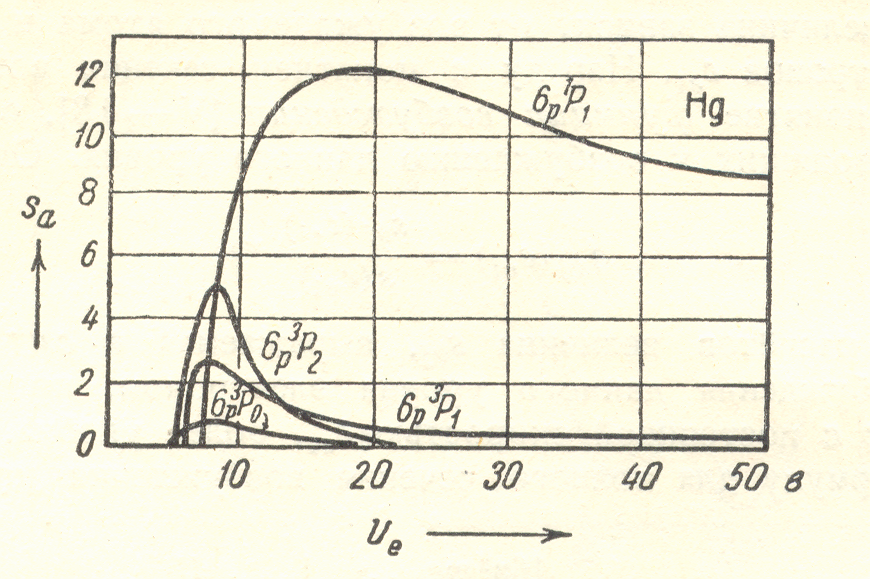
Рисунок 2.11 – Сечение возбуждения уровней 63Р012 и 61Р1 электронным ударом


При отсутствии экспериментальных данных по сечениям или теоретически рассчитанных конкретных переходов необходимо рассчитывать скорости процессов самостоятельно. Обзор теоретических методов определения сечений возбуждения и ионизации приведен в монографии [17].

Таблица 2.2 – Сечение возбуждения в максимуме (макс1016 см2) и энергия максимума (в скобках,
в эВ)

Лит.

переход
[3]
[4]
[5]
[6]
[7]
[8]
[9]
[10]
[11]
средн.

61S0–63P0
0,3(8,0)
0,8(5,4)
0,23(5,3)



0,53(4,8)






0,5(5,5)
0,6(5,5)
0,53(5,2)

61S0–63P1
1,1(9,0)
2,4(5,7)
0,72(5,7)



1,6(5,2)
1,3(5,6)



1,8(5,5)
1,3(5,3)
1,6(5,4)

61S0–63P2
2,3(12)
3,0(6,3)
0,74(6,1)
3,0(5,7)
2,9(5,8)









2,2(6,2)
2,8(6,0)

61S0–61P1
3,8(18)
7,5
5,1(21)


















5(19)

63P0–63P1


















15(0,5)



25(0,14)
20(0,4)

63P1–63P2
19(0,9)















20(1,0)



14(0,4)
18(0,4)

63P2-63D3















0,42(5,6)









0,4(5,6)

63P0-73S1















0,058(4,1)









0,06(4,1)

63P1-73S1















0,17(3,9)









0,17(3,9)

63P2-73S1















0,21(3,4)









0,21(3,4)


Для оптических переходов (L=1, S=0) часто имеются экспериментально измеренные силы осцилляторов f01. В частности, в [5] приведены следующие данные по ртутным переходам:


63P2 – 63D3, =3650,15 f=0,3 E=3,40 эВ

63P1 – 63D2, =3125,62 f=0,15 E=3,96 эВ

63P0 – 63D1, =2967,28 f=0,4 E=4,17 эВ

63P2 – 73S1, =5490,74 f=0,16 E=2,27 эВ

63P0 – 73S1, =4046,56 f=0,16 E=3,06 эВ

63P1 – 73S1, =4358,34 f=0,15 E=2,84 эВ

61P1 – 61D2, =5790,66 f=0,17 E=2,12 эВ

61P1 – 71S0, =10139,79 f=0,287 E=1,23 эВ


Скорости возбуждения вычисляются по формуле


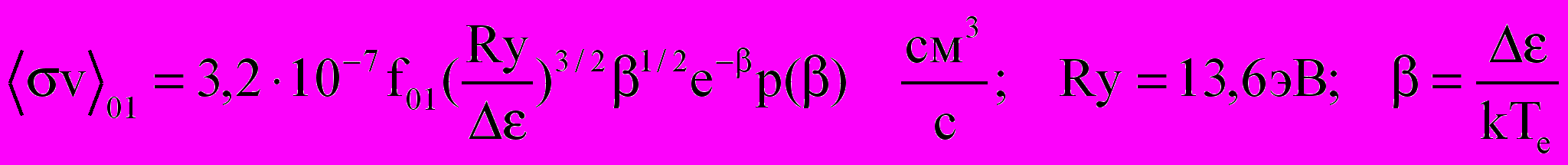(2.2)
0,04
0,1
0,2
0,4
1
2
4
10
>10

P()
0,758
0,493
0,331
0,209
0,10
0,063
0,04
0,023
0,00661/2


Для близких значений энергий уровней <<1


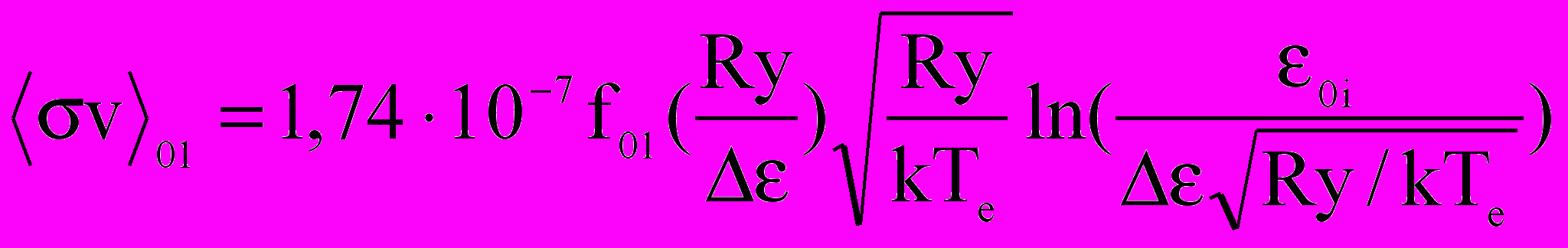. (2.3)


При отсутствии данных f01 и для неоптических переходов можно использовать расчетные формулы:

. (2.4)


При S=0 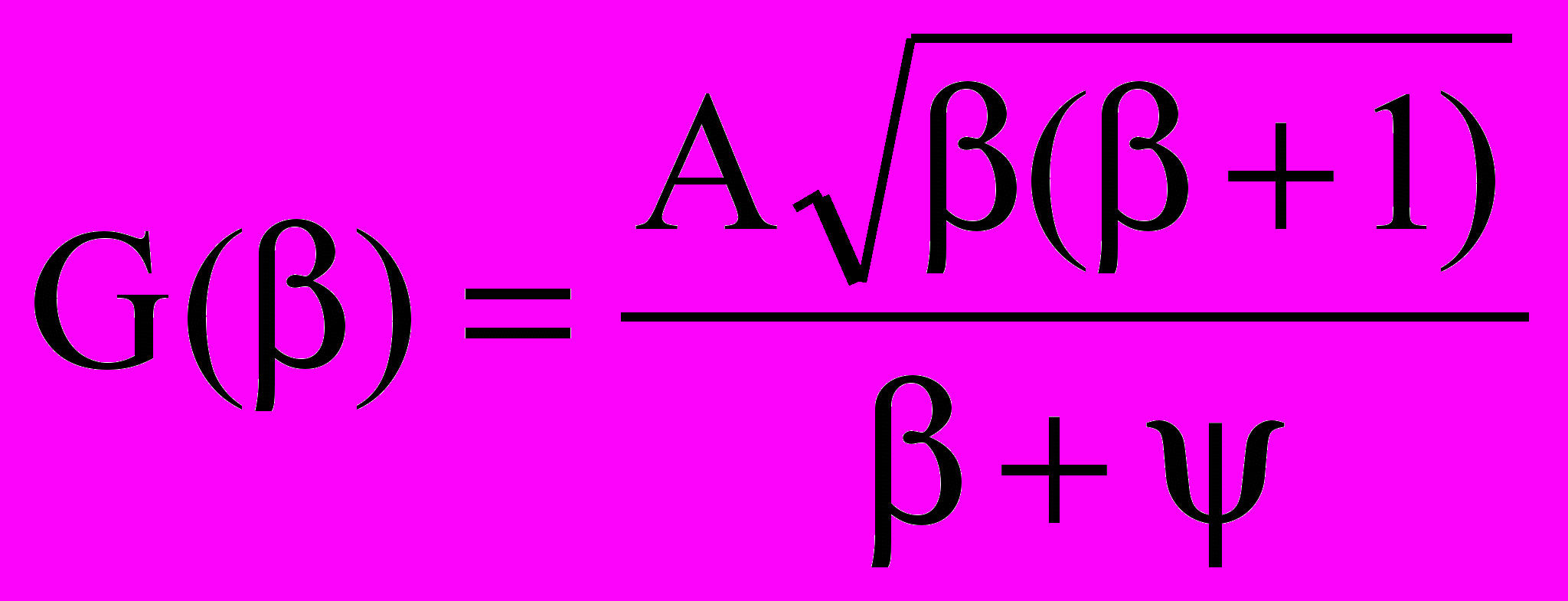; S=1 .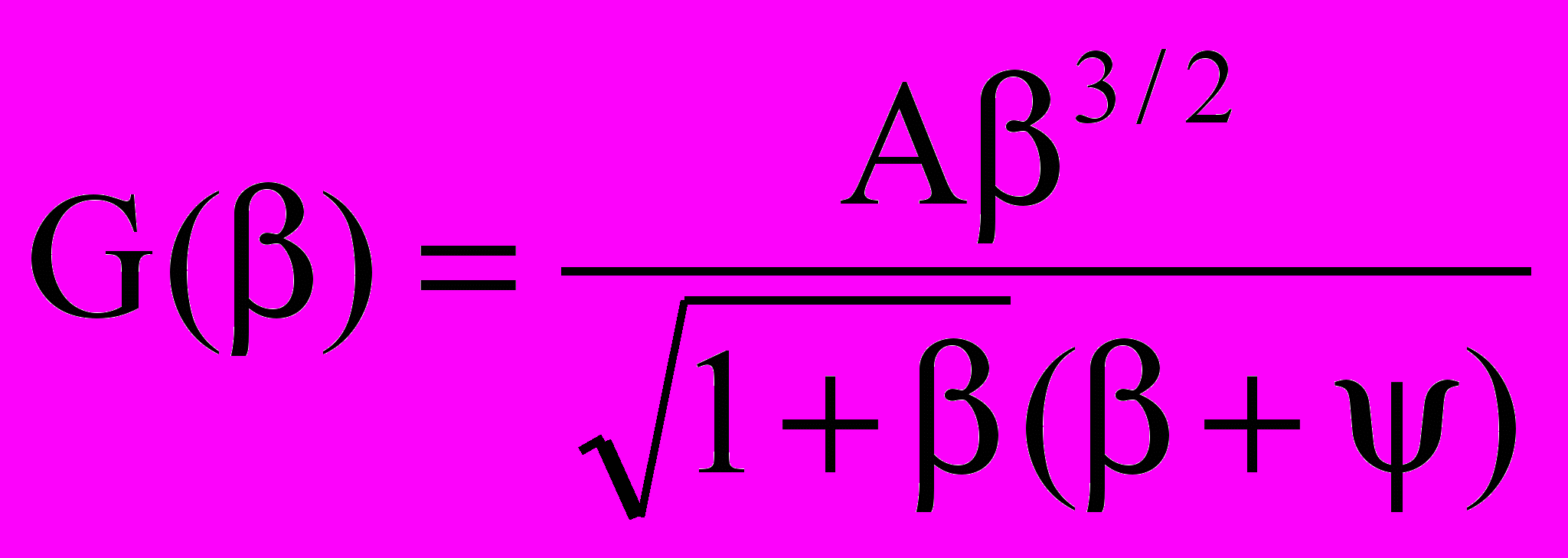


Здесь А и  – табличные значения [17], определяемые по значениям эффективных квантовых чисел верхнего и нижнего уровней, Q – угловой фактор, определяемый по квантовым числам jls верхнего и нижнего уровней. Для скорости ионизации можно использовать формулу Ситона – Лотца [17]:

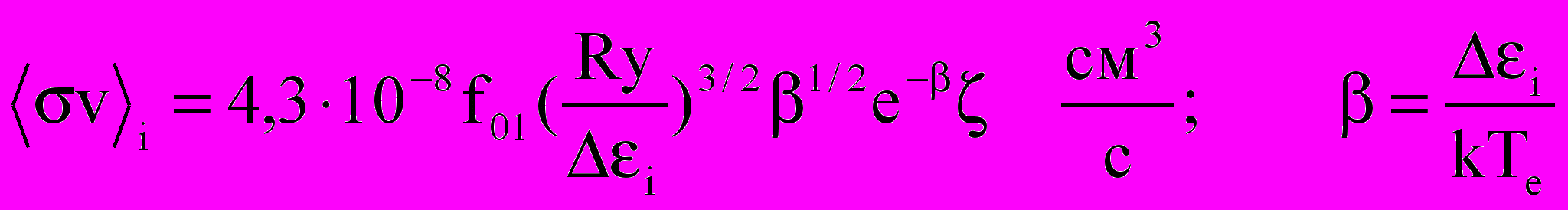. (2.5)


При =1; 4; 8 =0,83; 1,16; 1,26.

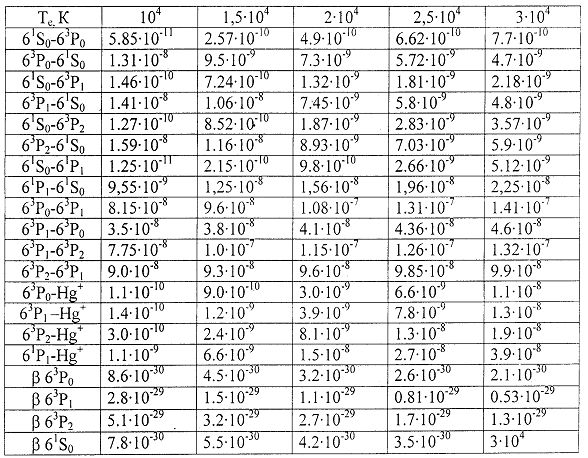
В таблицах 2.3 и 2.4 приведены значения скоростей возбуждения ряда переходов атома ртути для различных значений электронной температуры.


Таблица 2.3 – Скорости возбуждения 73S1 состояния атома ртути <v> см3/с




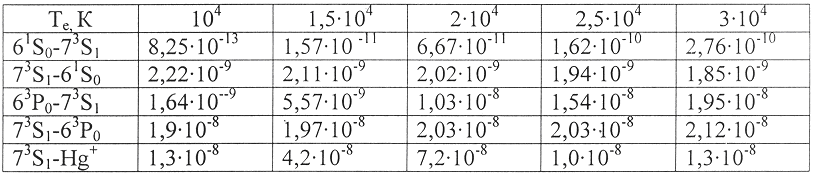
2.3.2 Эффективная вероятность резонансных переходов атома ртути


Вероятности резонансных переходов изолированного атома ртути равны для =184,9 нм А=6,3108 с–1; для =253,7 нм А=9,1106 с–1. В плазме вследствие поглощения и переизлучения эффективная вероятность переходов может существенно снижаться. Теория диффузии резонансного излучения разработана в работах Хольстейна, Бибермана, Векленко [19–24]. Для цилиндрической системы радиусом R получено приближенное выражение усредненной по радиусу эффективной вероятности испускания фотонов:

Аэф=АТ(R); 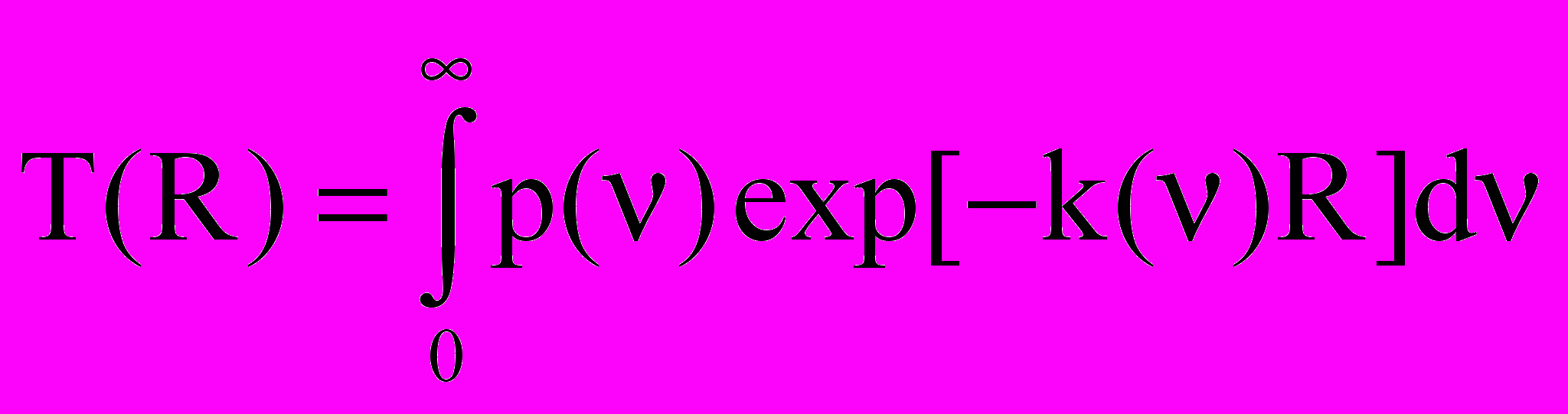. (2.6)


Здесь p() – нормированная на единицу форма линии испускания, k() – коэффициент поглощения,  – коэффициент, равный 1,6 для доплеровского контура, 1,11 – для дисперсионного контура. Для заданных форм контуров вычисление T(R) при k0R>>1 и совпадении форм контуров испускания и поглощения дает:

T(R)(k0R)–1(lnk0R)–1/2 – для доплеровского контура;

T(R)(k0R)–1/2 – для дисперсионного контура.

В работе [25] проведен численный расчет T(R) для смешанной (фойхтовской) формы линии и получена приближенная эмпирическая формула для Аэф:


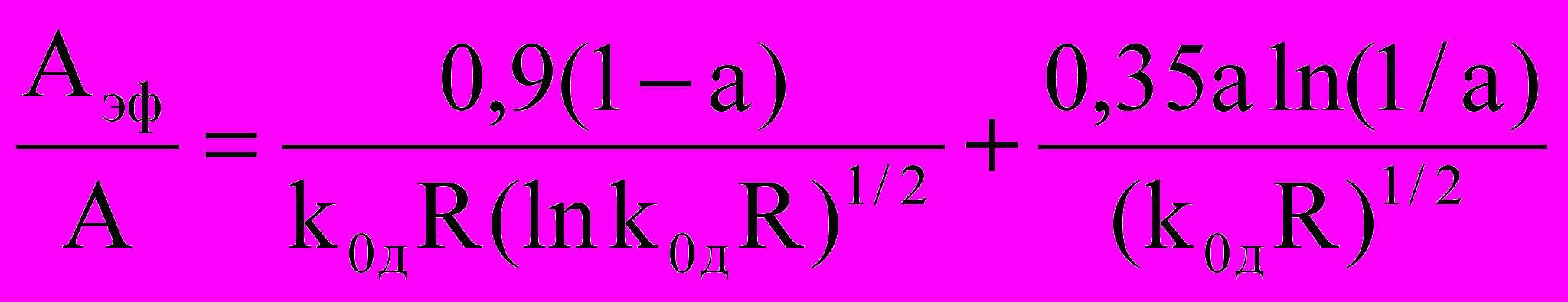, (2.7)


где 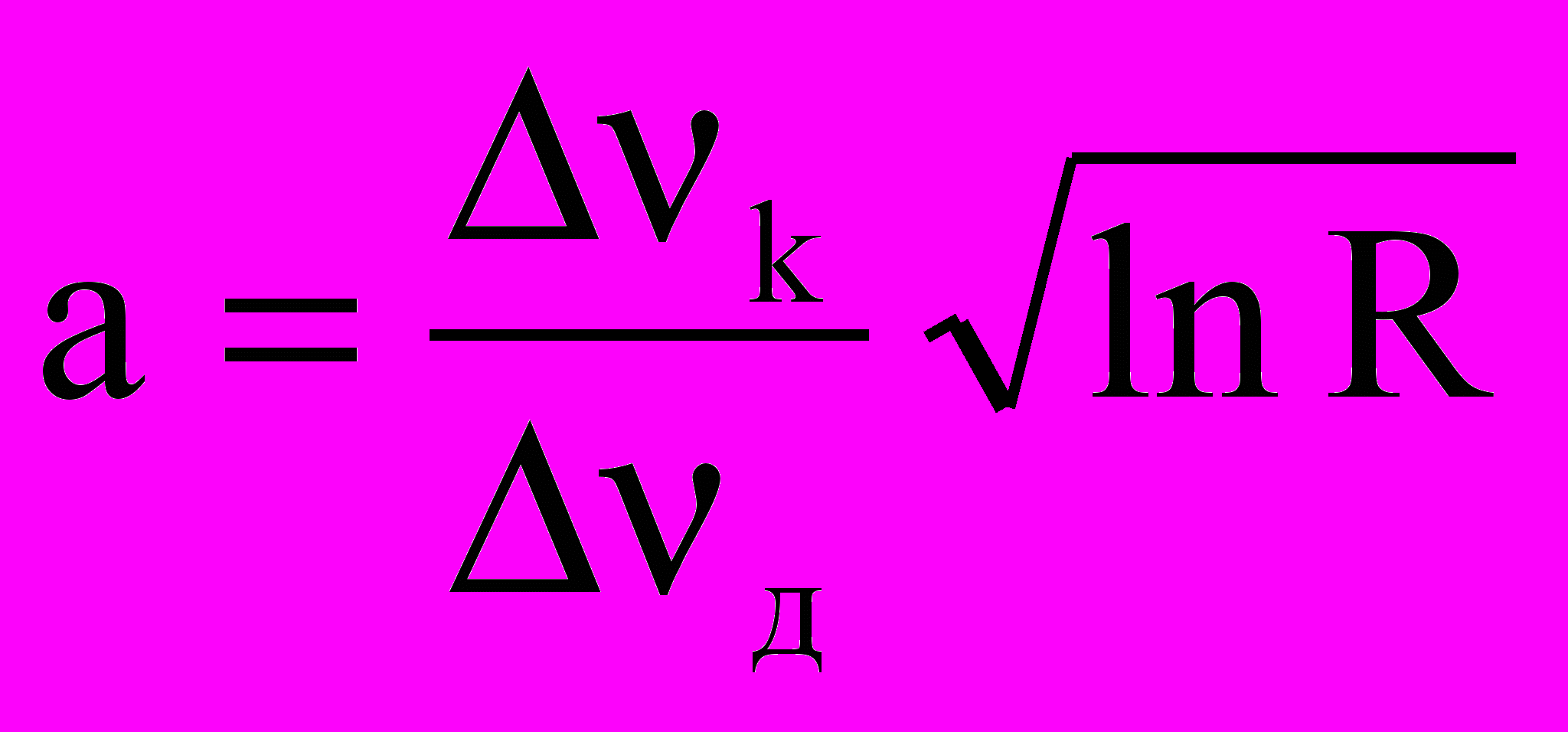– параметр Фойхта, k и д – дисперсионная и доплеровская полуширины контура.


Таблица 2.4 – Скорости возбуждения состояний атома ртути 63P0,1,2; 61P1. <v> см3/с;  см6/с





Коэффициент поглощения линии связан с концентрацией атомов на нижнем уровне [18]


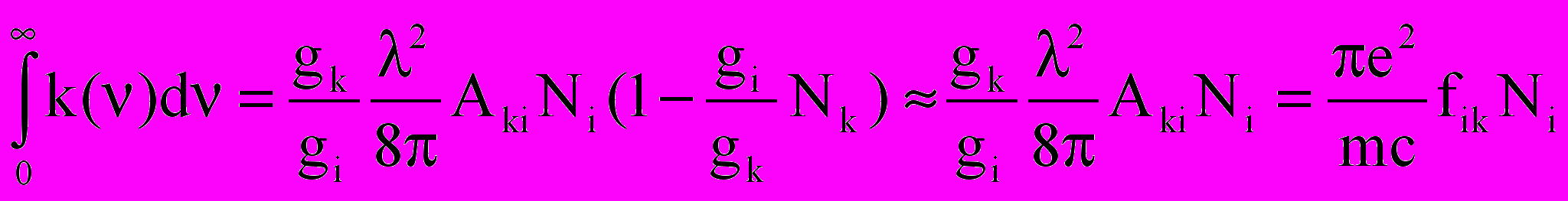. (2.8)


Здесь gk и gi – статвеса верхнего и нижнего уровней. Вероятность перехода связана с силой осциллятора:

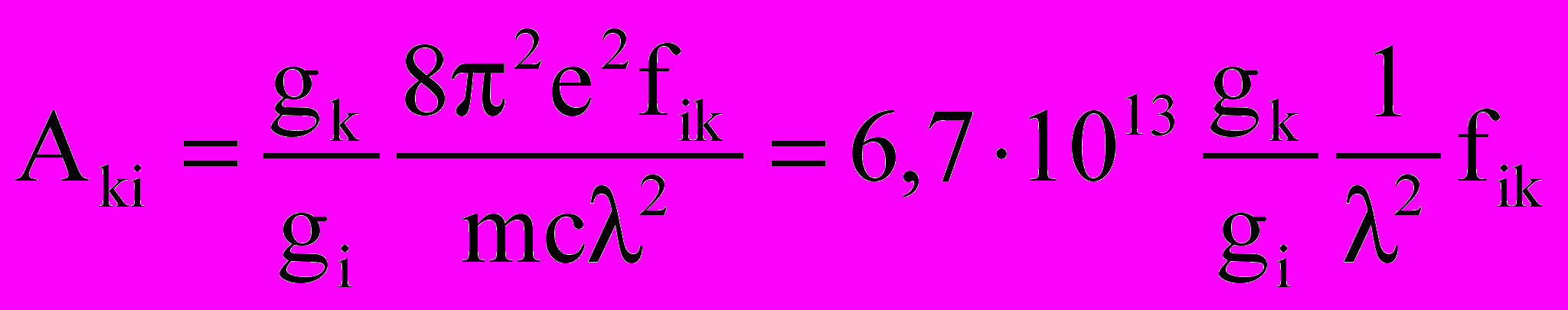, [нм], Аki[с-1]. (2.9)


Выражение для коэффициента поглощения линии можно переписать, заменяя  на :


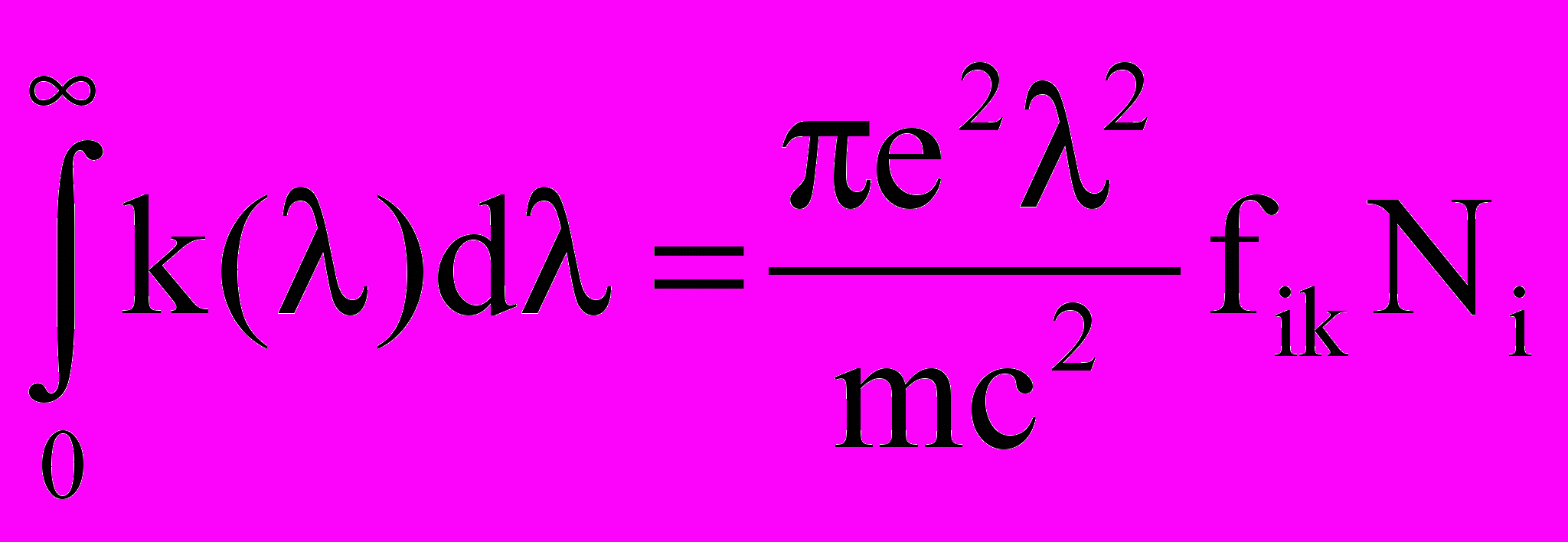. (2.10)


Рассмотрим уширение резонансных линий ртути, определяющее их Аэф, методологически следуя работе [26].

Доплеровское уширение возникает вследствие сдвига частоты излучения при движении излучающего атома. В этом случае коэффициент поглощения на частоте  внутри контура


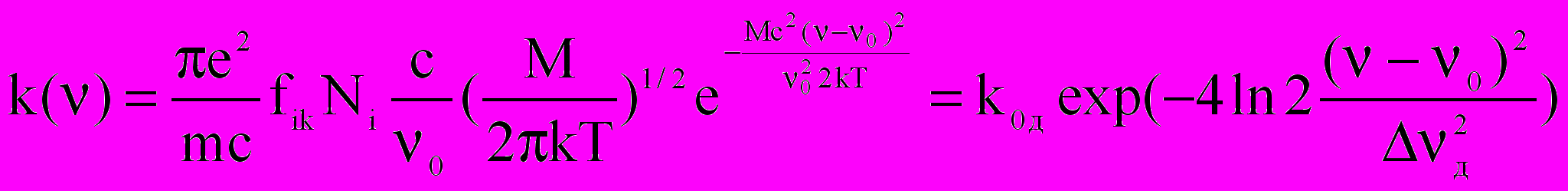, (2.11)


где 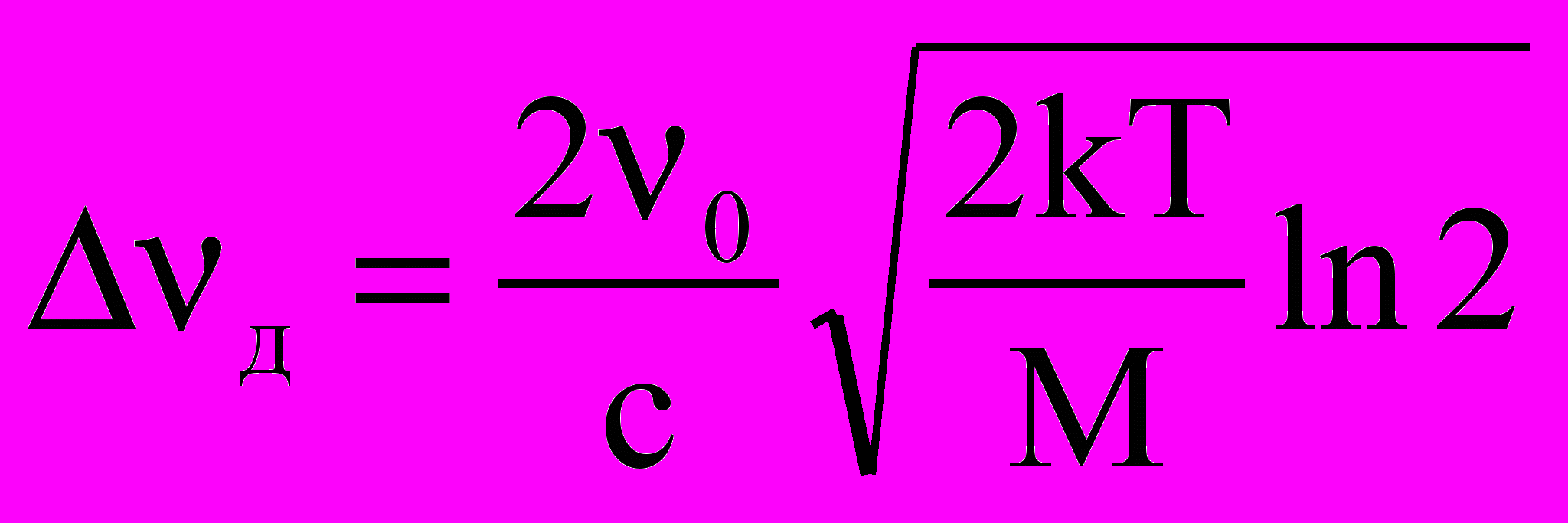, 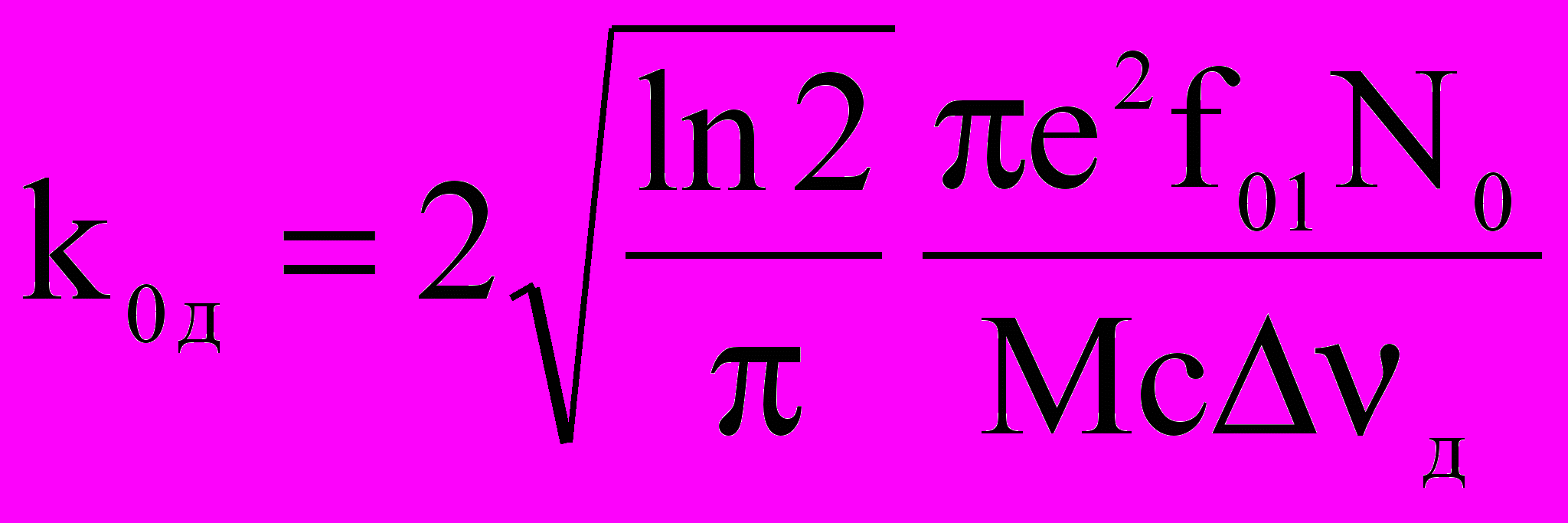. (2.12)


М, Т –масса и температура атомов соответственно.

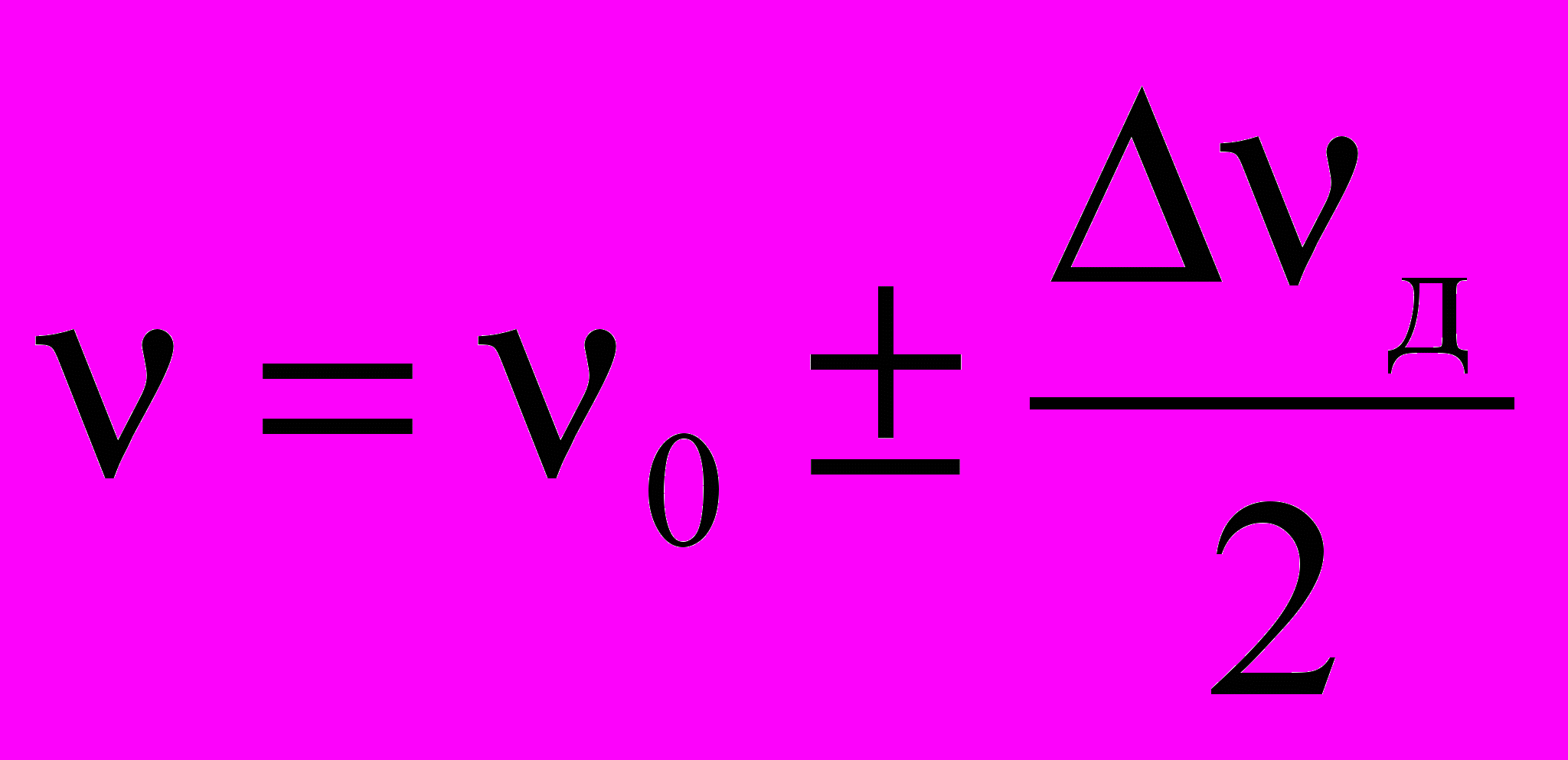
При 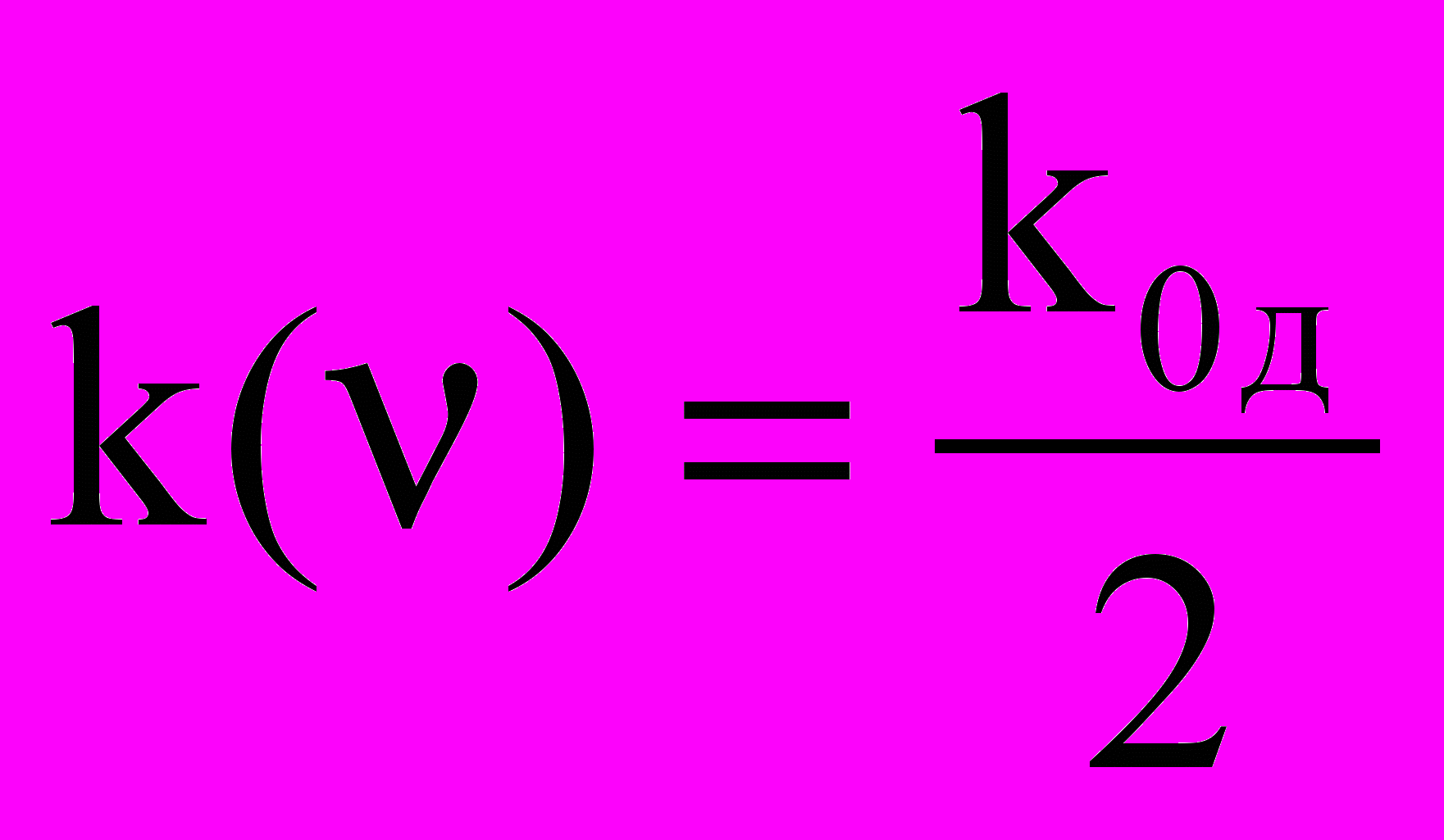. Отметим также, что .

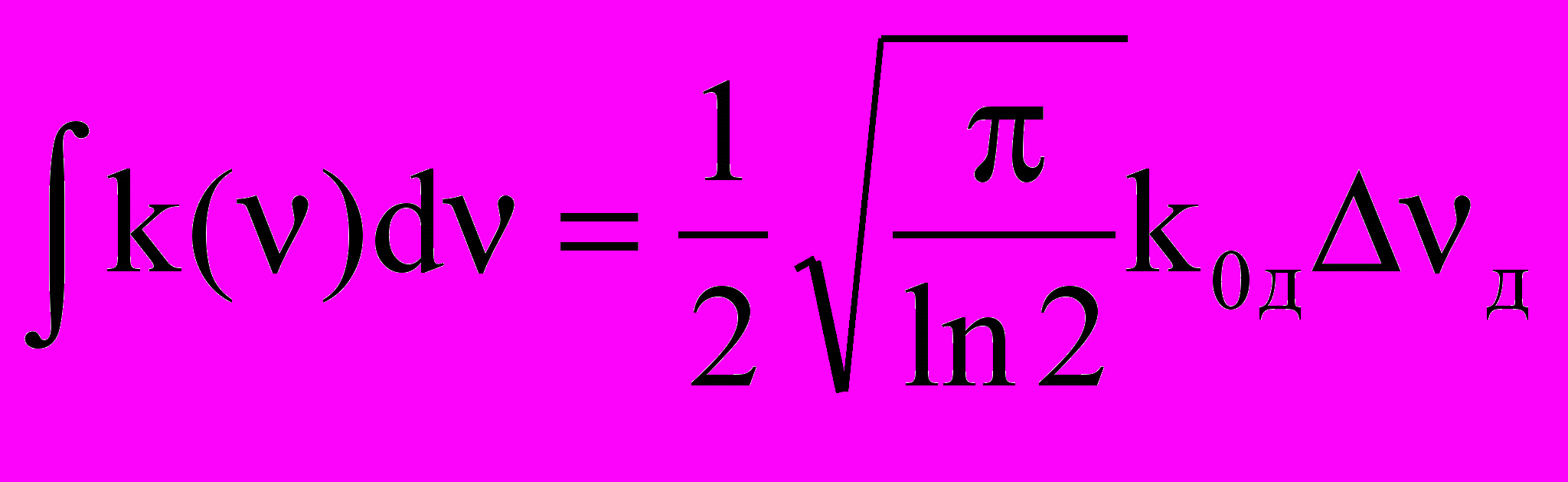Перейдем от частоты к длинам волн. Тогда


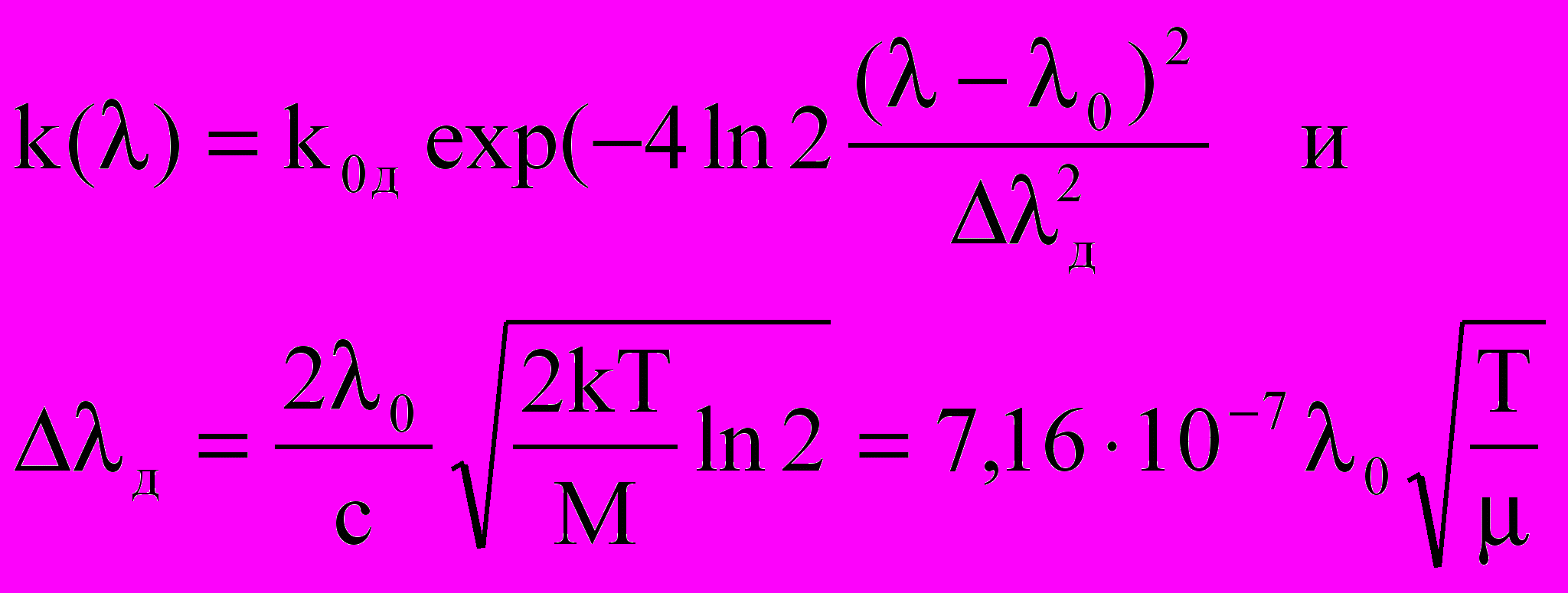, (2.13)


где д,  – в нм, Т – К, =200 – атомный вес ртути. Значение коэффициента поглощения в максимуме можно рассчитать с помощью тождественных выражений:


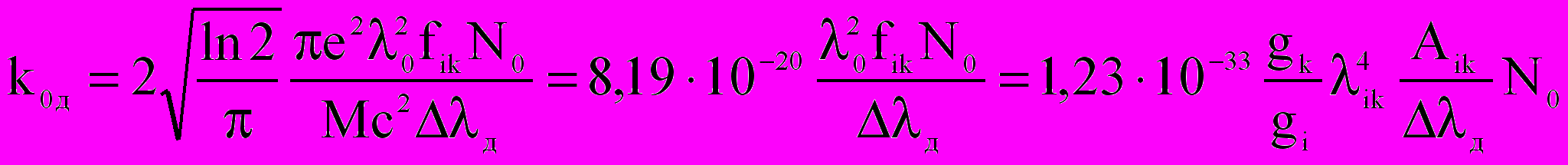, (2.14)


где k0 – в см–1,  и  – в нм, N0 – см–3, А – в с–1.

Для резонансных линий ртути будем иметь:


=184,9 нм f=0,96 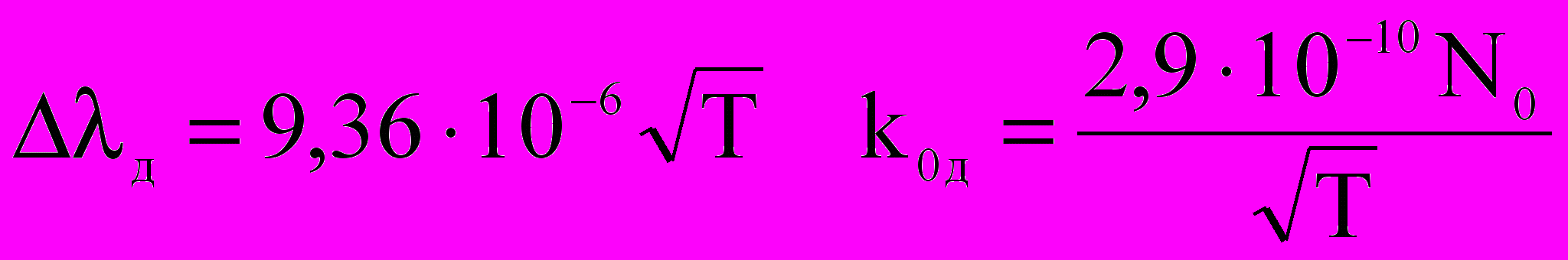; (2.15)


=235,7 нм f=0,026 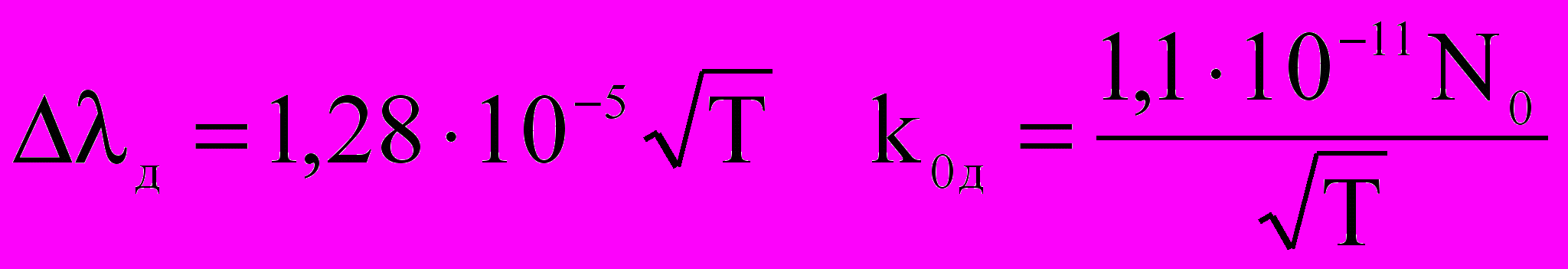. (2.16)

В случае естественного уширения для зависимости k() от частоты получаем так называемую дисперсионную форму

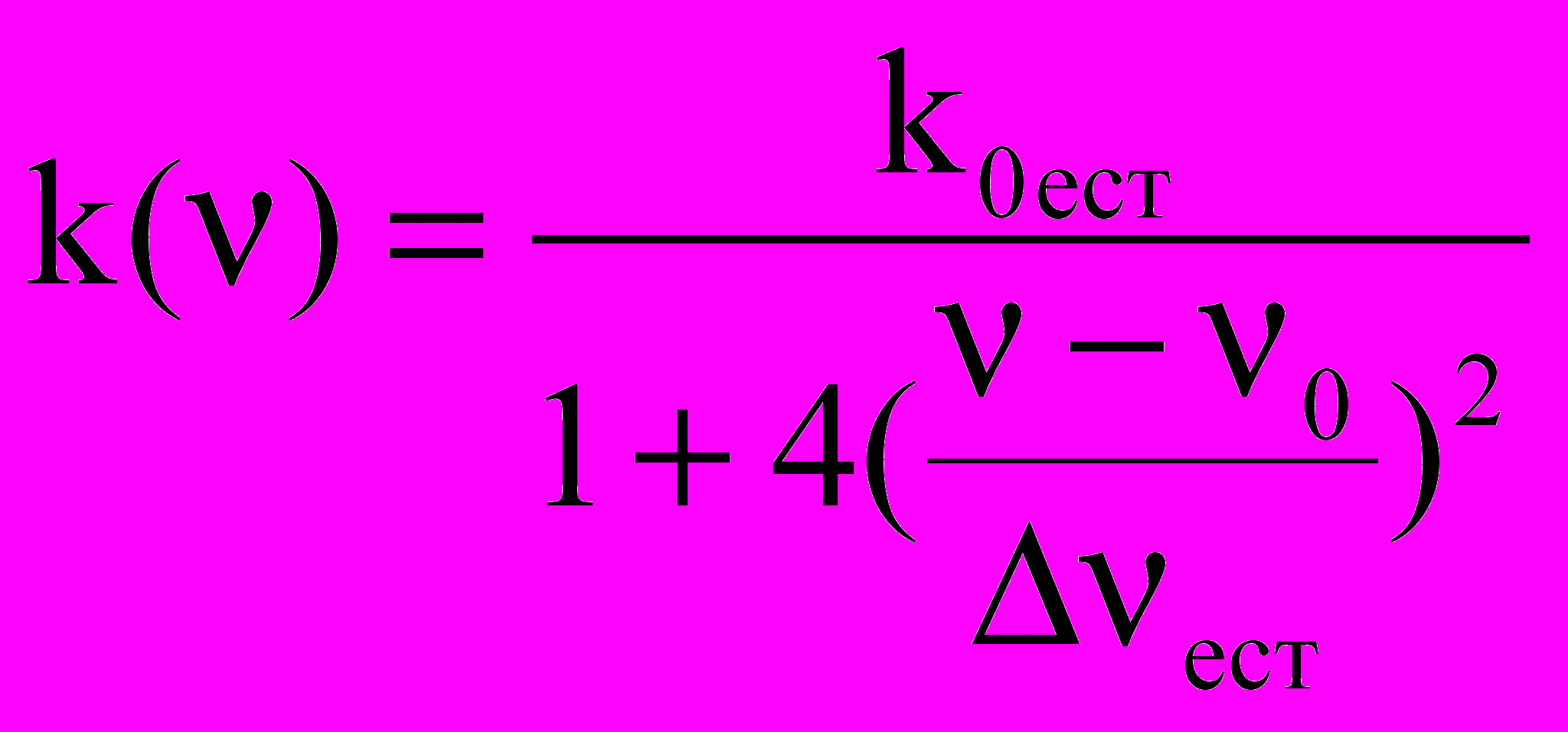, (2. 17)

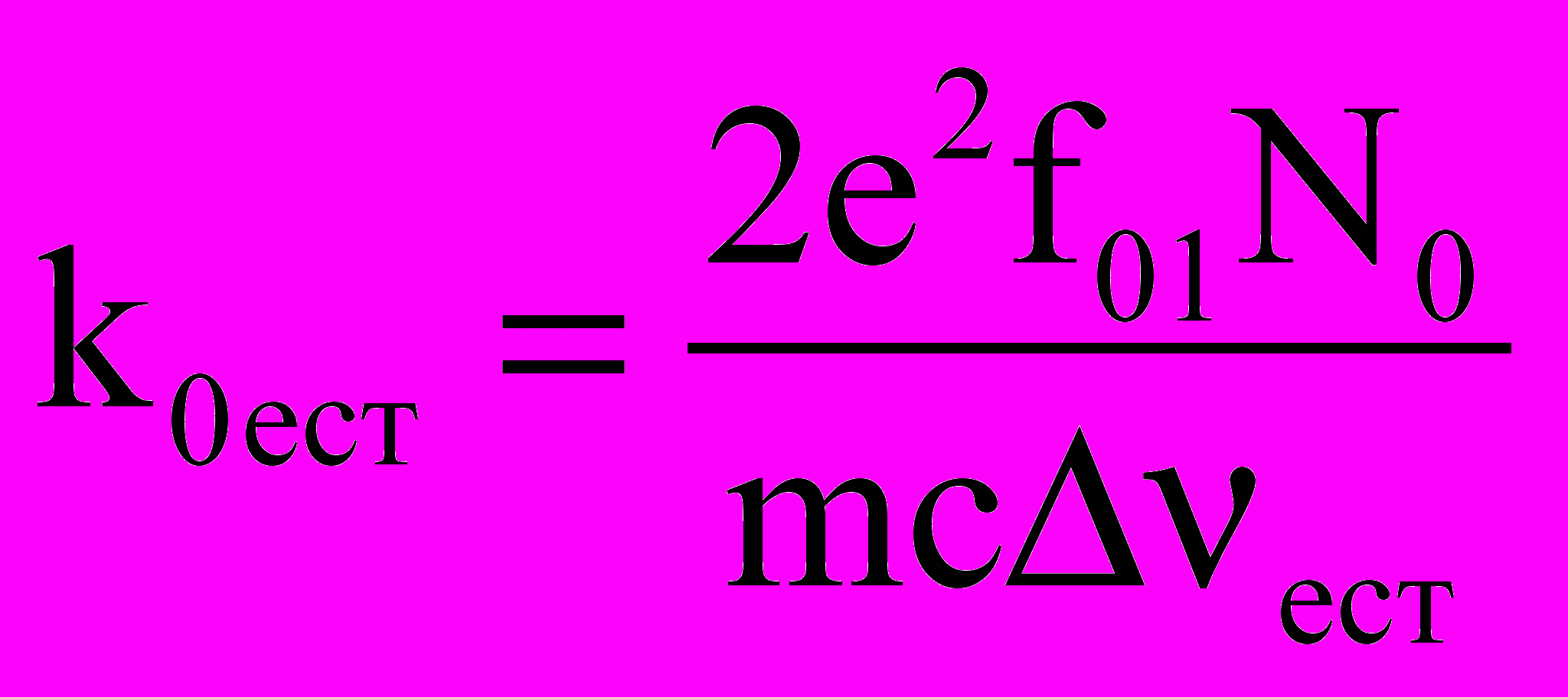, так как 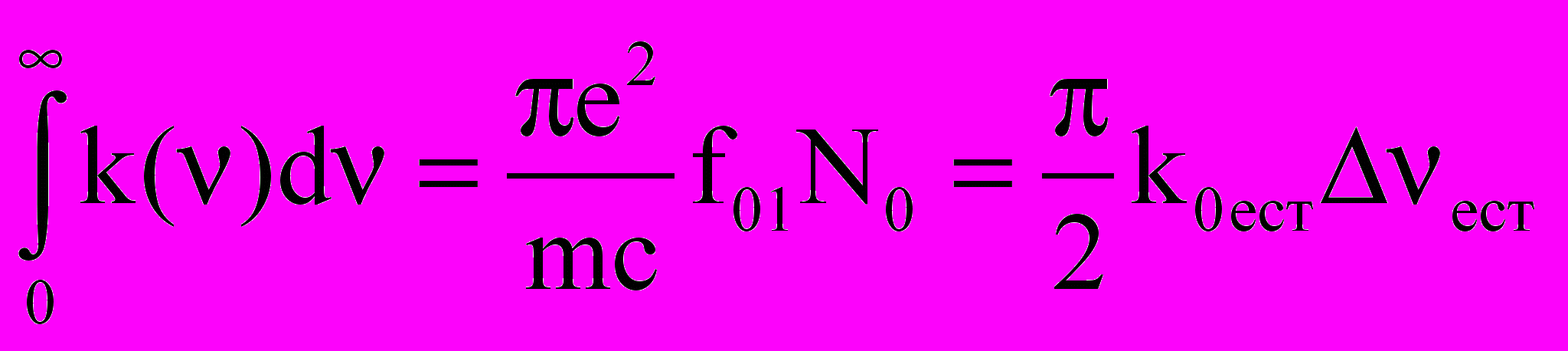. (2.18)


ест=1/(2ik), 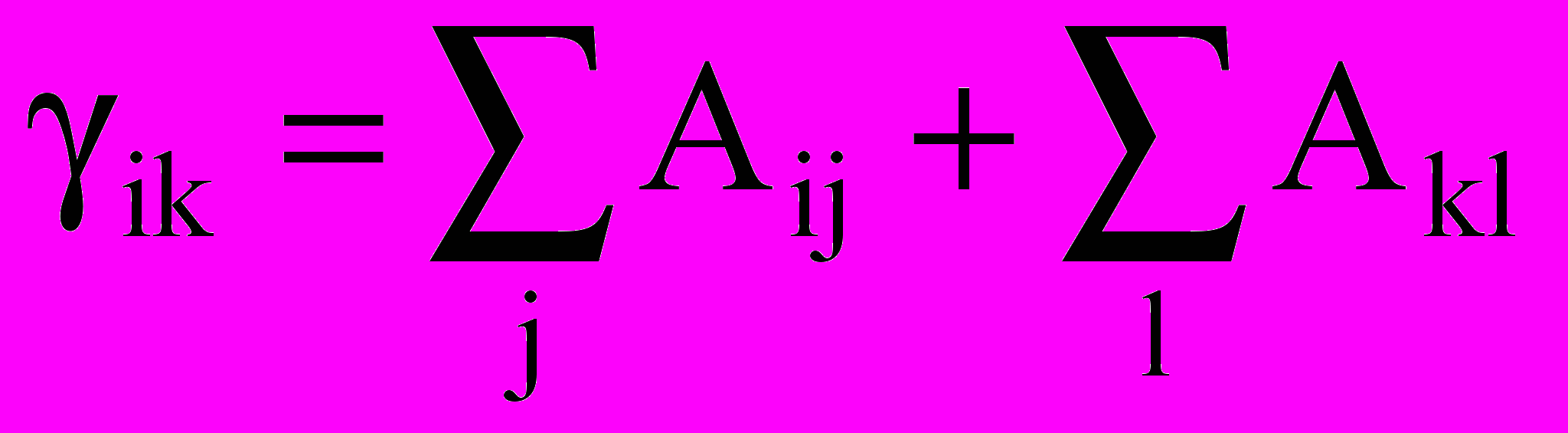(сумма вероятностей спонтанных переходов с верхнего и нижнего уровней данной линии).

Переходя к длинам волн, получим:


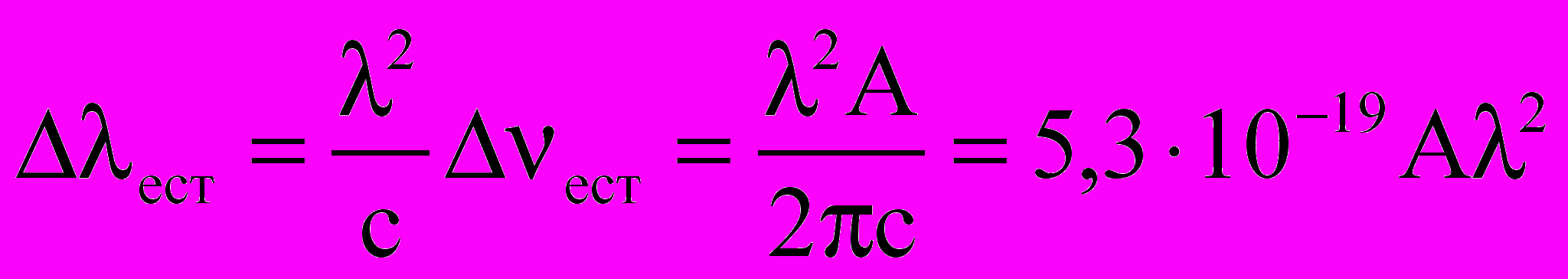,  и  в нм. (2.19)


Оценки естественного уширения для линий ртути дают:


=184,9 нм ест=1,1410–5 нм; =235,7 нм ест=3,110–7 нм.


Уширение линий, вызванное столкновениями с нейтральными атомами при низких давлениях, имеет ударный характер и также приводит к контуру дисперсионной формы с шириной н=1/(0). Согласно кинетической теории газов, где


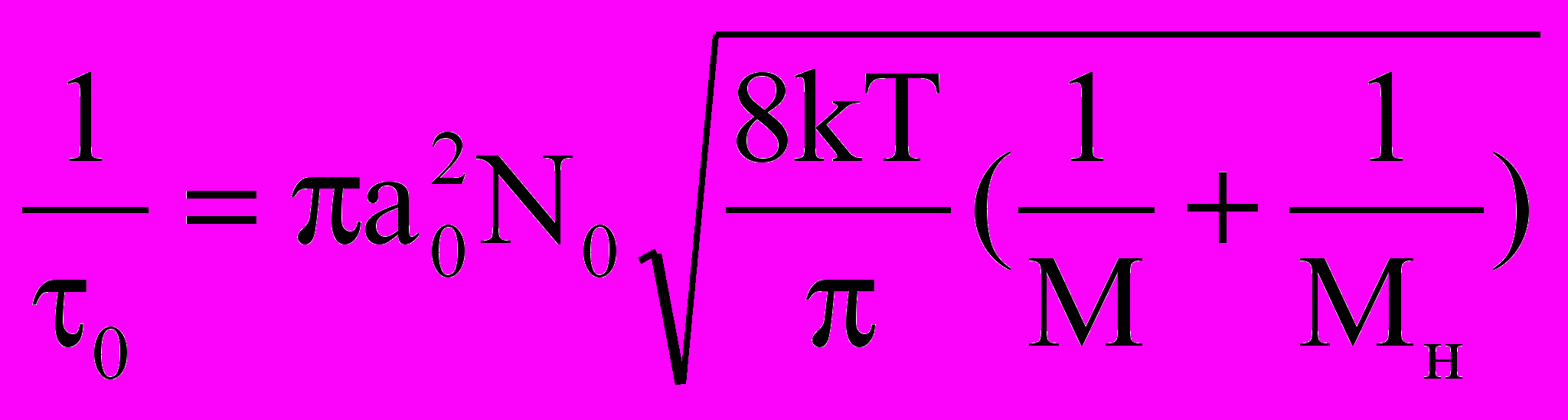, (2.20)


а а02 – эффективное сечение взаимодействия.

Переходя от концентрации к давлению, для ударной ширины можно записать


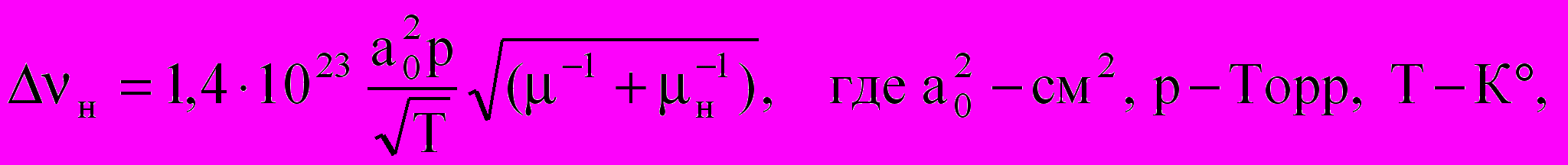(2.21)


 – атомные веса излучающих и уширяющих томов. Преобразуя выражение для длины волны, получаем:

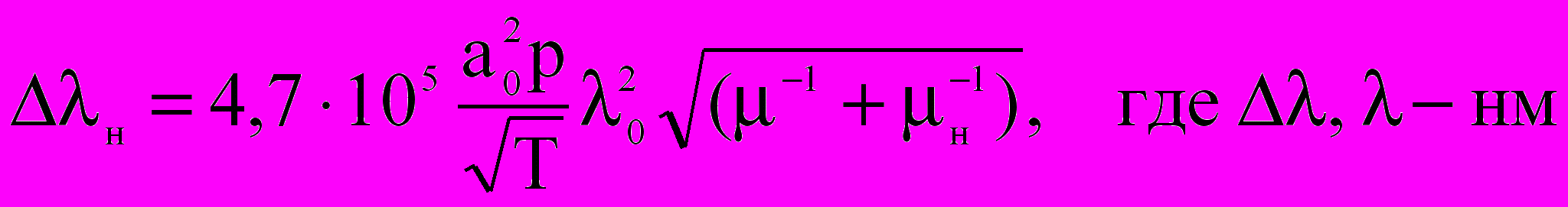. (2.22)


По данным [27, 28] для уширения линии 253,7 нм аргоном a02=7610–16 см2, это дает .

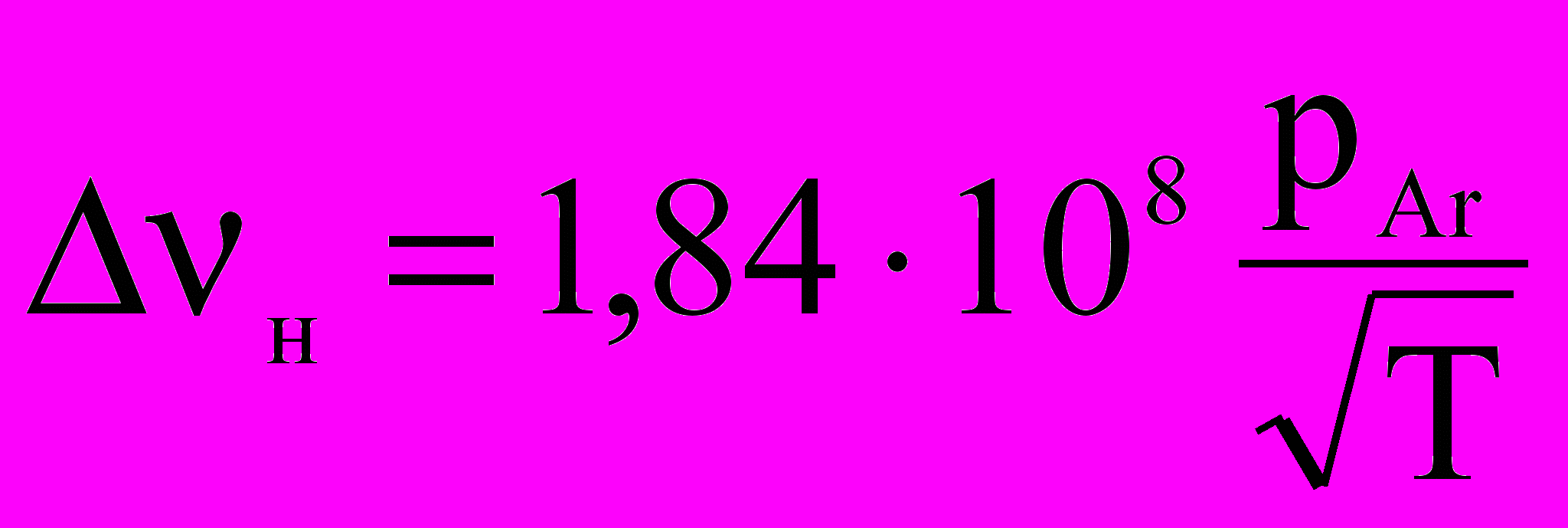По более новым данным [1]:


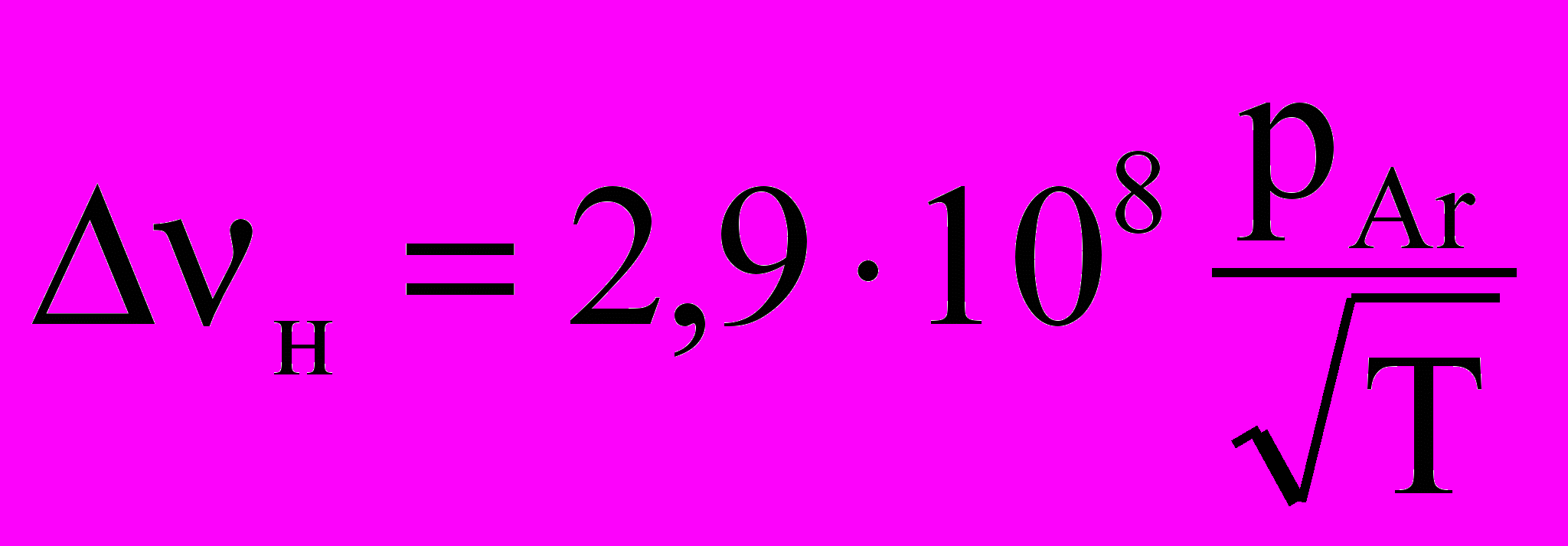– для линии 184,9 нм, 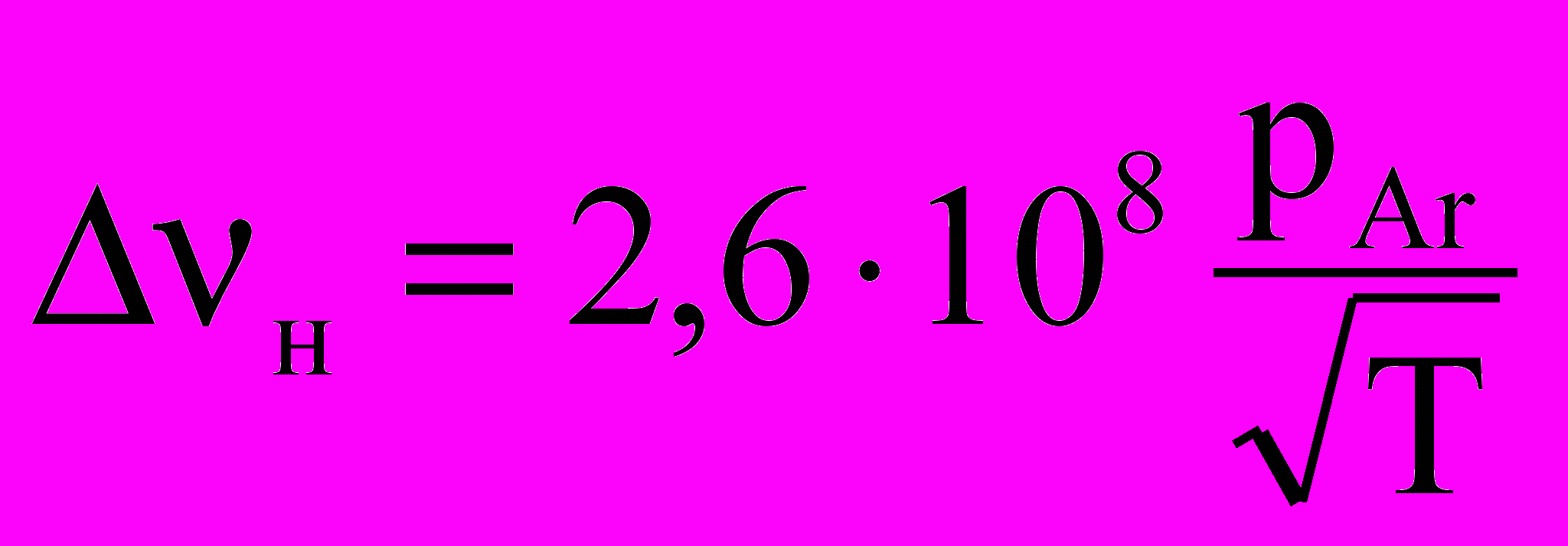– для линии 253,7 нм.


Или в длинах волн:


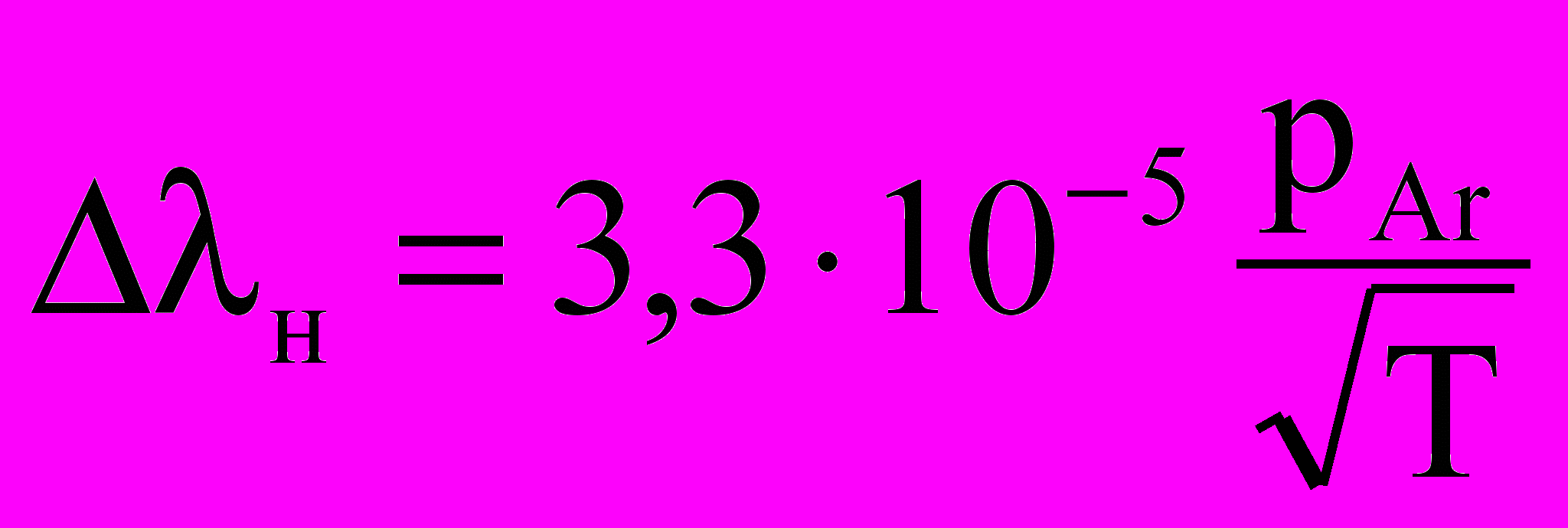– для линии 184,9 нм, 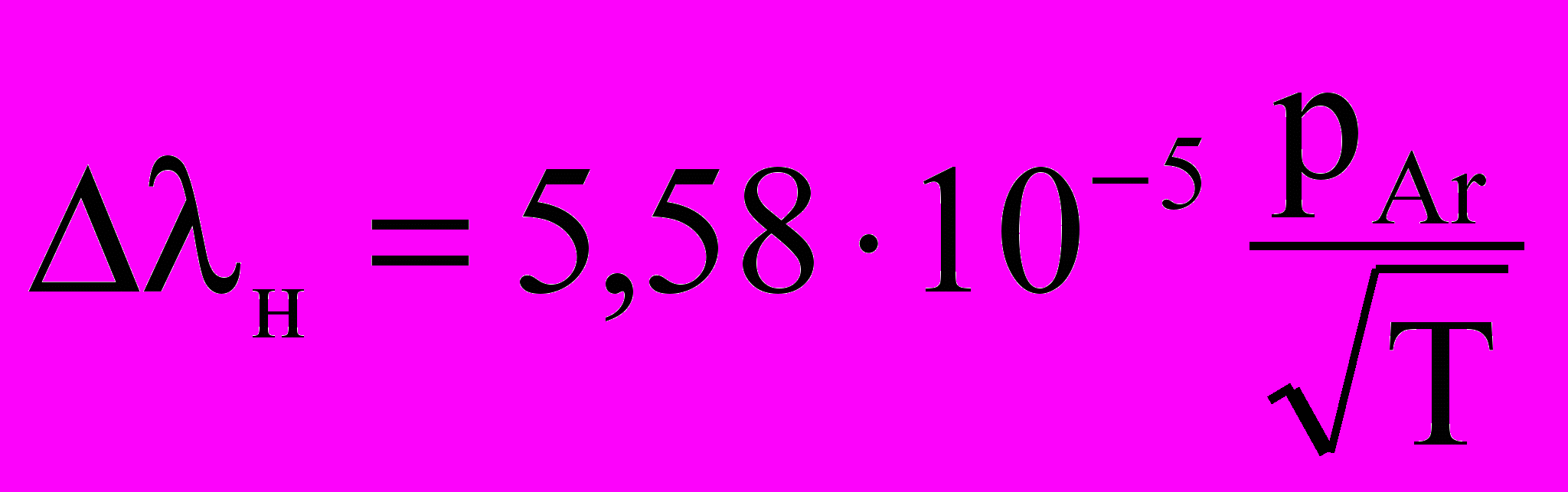– для линии 253,7 нм.


Взаимодействие заряженных частиц с возбужденным атомом существенно сильнее, чем с нейтральными, за счет сильного кулоновского поля заряженных частиц. Однако при малой степени ионизации плазмы оно обычно мало. При низких давлениях наибольший вклад в штарковское уширение вносит ударное уширение электронами. Приближенно его можно учесть аналогично ударному уширению нейтральными атомами, заменив концентрацию и скорость нейтралов соответствующими значениями электронов, а в качестве сечения взаимодействия взять сумму сечений неупругих переходов с данного уровня на все соседние. Тогда


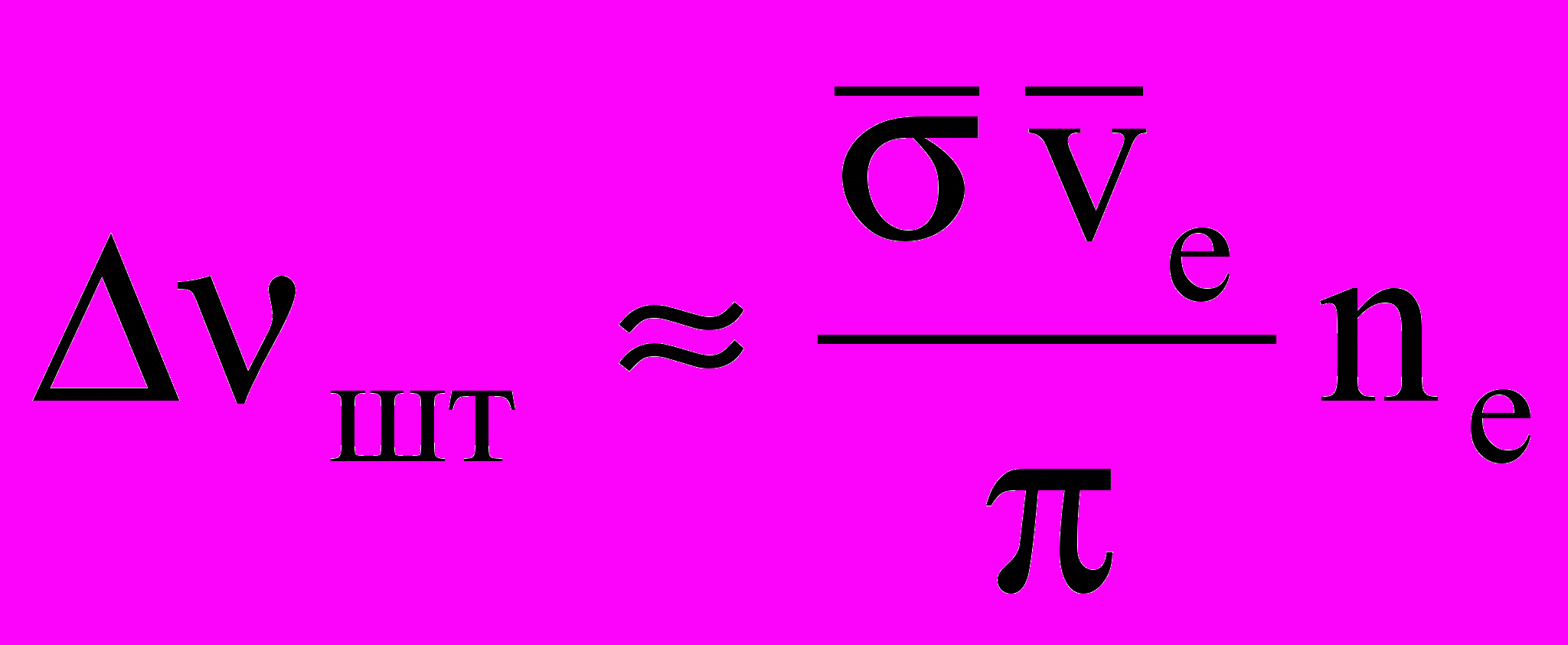. (2.23)

Для уровня 63P1




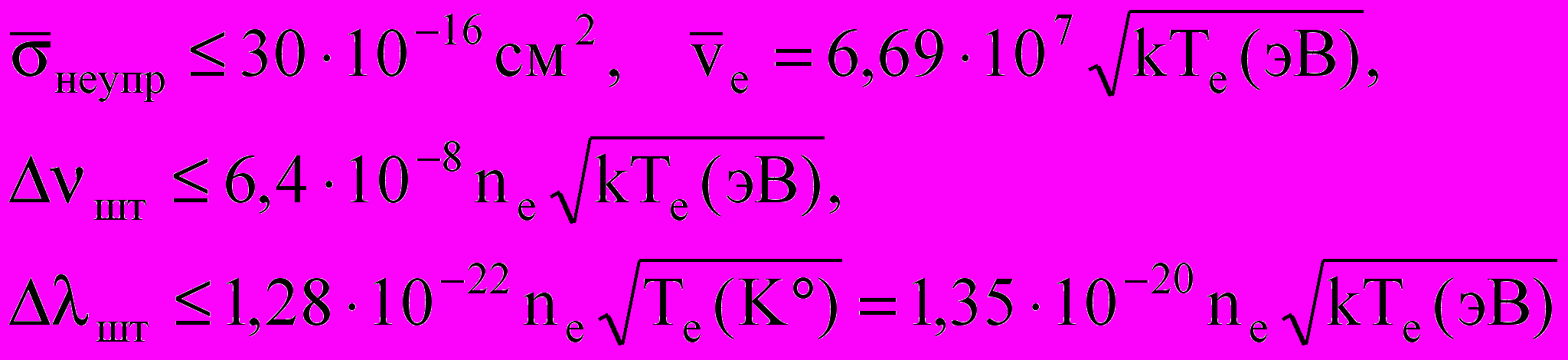
Это сравнимо с уширением атомами аргона при степени ионизации 10–2. Для уровня 61P1 сечение неупругих соударений электронов почти на порядок меньше, чем для уровня 63P1, и штарковским уширением этого уровня тем более можно пренебречь.

Уширение резонансной линии собственным газом значительно сильнее, чем уширение посторонним газом за счет большего сечения взаимодействия. Квантомеханические расчеты [30, 31] дают следующую приближенную формулу для резонансного уширения


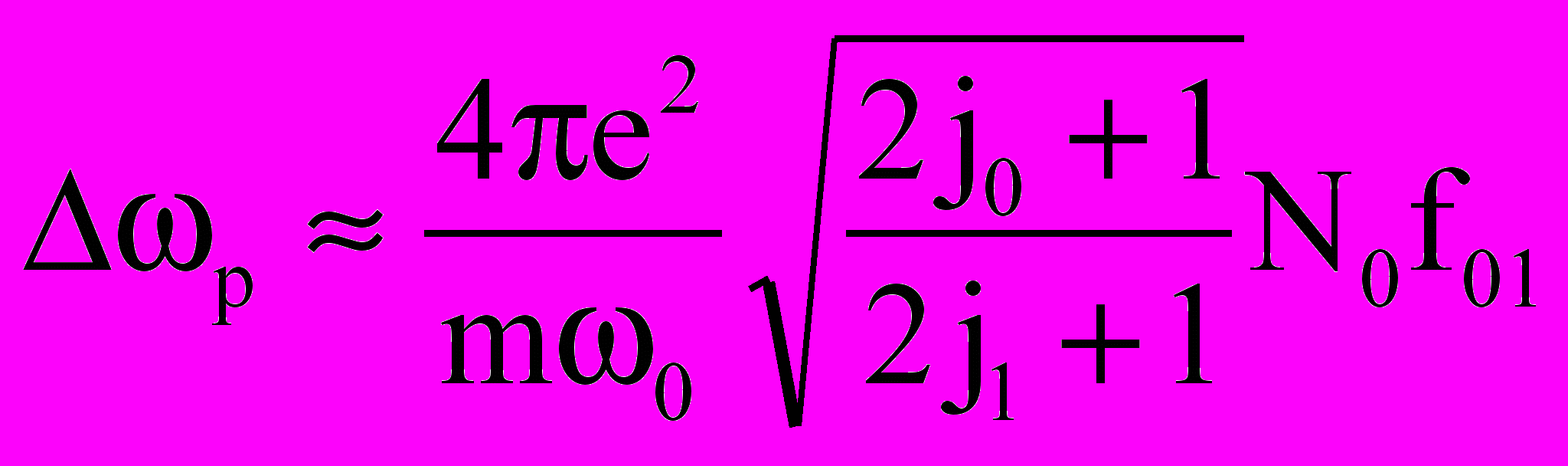. (2.24)


Это дает в длинах волн

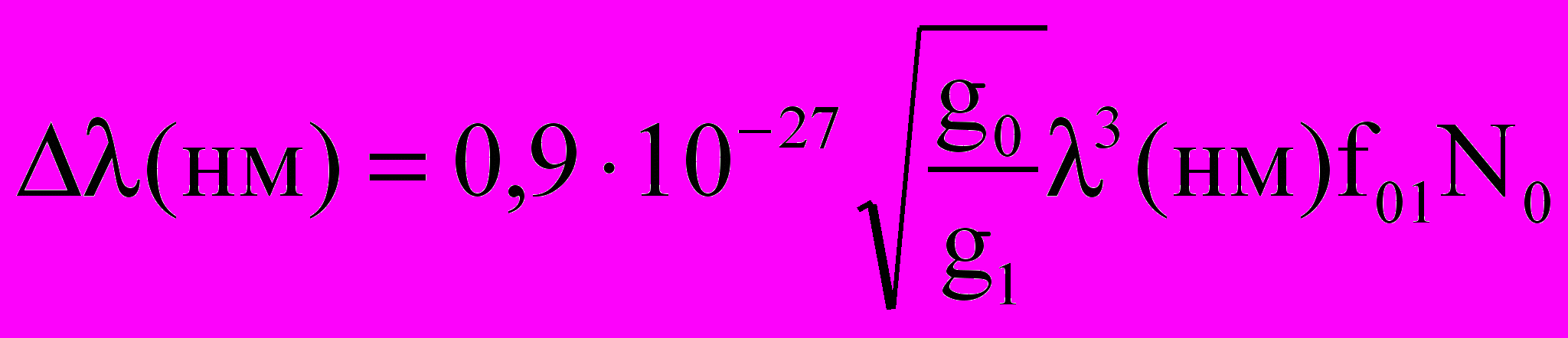
для 253,7 нм р=2,210–22N0 при N0=1,41015см–3 р=ес,

для 184,9 нм р=3,110–21N0 при N0=3,71015см–3 р=ест.

Суммарный контур линии будет состоять из доплеровской части и дисперсионной части, состоящей из естественного, ударного (атомы аргона), резонансного и ударного (штарковского) уширений, кроме линии 184,9 нм, где штарковским уширением можно пренебречь.

=253,7нм

д=1,2810–5 (Т, К)1/2=2,5610–4 нм при Т=400 К;

дисп=3,110–7 + 3,210–6P0Аr + 2,210–22NHg+1,410–20Ne.

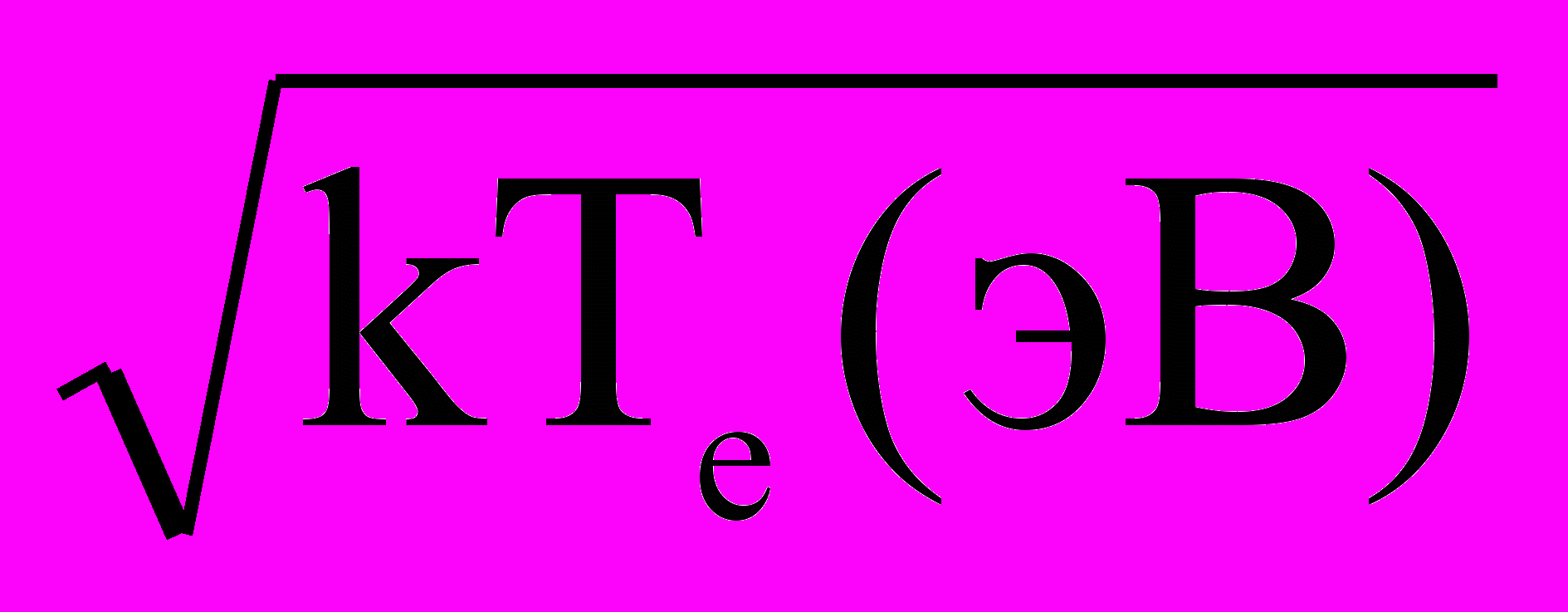=184,9 нм

д=9,410–6(Т,К)1/2=1,910–4 нм при Т=400 К;

дисп=1,1410–5 + 1,710–6P0Аr + 3,110–21NHg.


Давление аргона приведено к температуре Т=300 К (температура заполнения трубки).

При расчете формы контуров линий надо также учесть изотопическое расщепления линий ртути. Естественная ртуть состоит, в основном, из пяти изотопов с долями i, равными: 0,1917; 0,2927; 0,2377; 0,1445; 0,1324. Изотопический сдвиг превышает уширение линий, и поэтому можно рассчитывать поглощение на линиях каждого изотопа независимо с коэффициентом поглощения koд.i, определяемым по концентрации N0i. Вследствие разного поглощения эффективные вероятности Аэф.i для каждого изотопа будут различными, что приведет и к различной заселенности возбужденных состояний по изотопам, не пропорциональной i основного состояния. Обычно это не учитывается, и либо просто считают все изотопы одинаковой концентрации i=0,2 [27, 31], либо расчет заселенности проводят в целом для смеси, усредняя Аэф(Аэф=iАэфi) [6, 32]. Такое приближение занижает общее расчетное поглощение, так как реально для изотопов с большим поглощением доля в заселенности возбужденных состояний возрастает. Наибольшая ошибка будет при малых токах и, соответственно, при малых концентрациях электронов, когда излучение является определяющим для заселенности возбужденного состояния. С увеличением концентрации электронов, когда определяющими становятся электронные удары 1-го и 2-го рода, расчет заселенности уровней в целом для смеси изотопов вполне можно считать допустимым.


2.3.3 Баланс заселенности уровней


При составлении системы уравнений баланса для системы триплетных уровней 63Р012 будем учитывать прямые и обратные переходы между ними и с основным состоянием. Учитывая большой энергетический разрыв до более высоких уровней, переходы наверх будем учитывать только до близлежащих уровней 73S1, 63D123, 61P1 и уровня ионизации. Обратные переходы с этих уровней в общем процессе ступенчатой ионизации должны быть существенно меньшими уходов наверх с них ввиду близкого расположения соседних, еще более высоких уровней. Дополнительно будет учитываться диффузионный уход возбужденных атомов на стенку. Данные по коэффициентам диффузии брались из работ [34–35]. При Т=100 С для уровней

63Р0 коэффициент диффузии равен 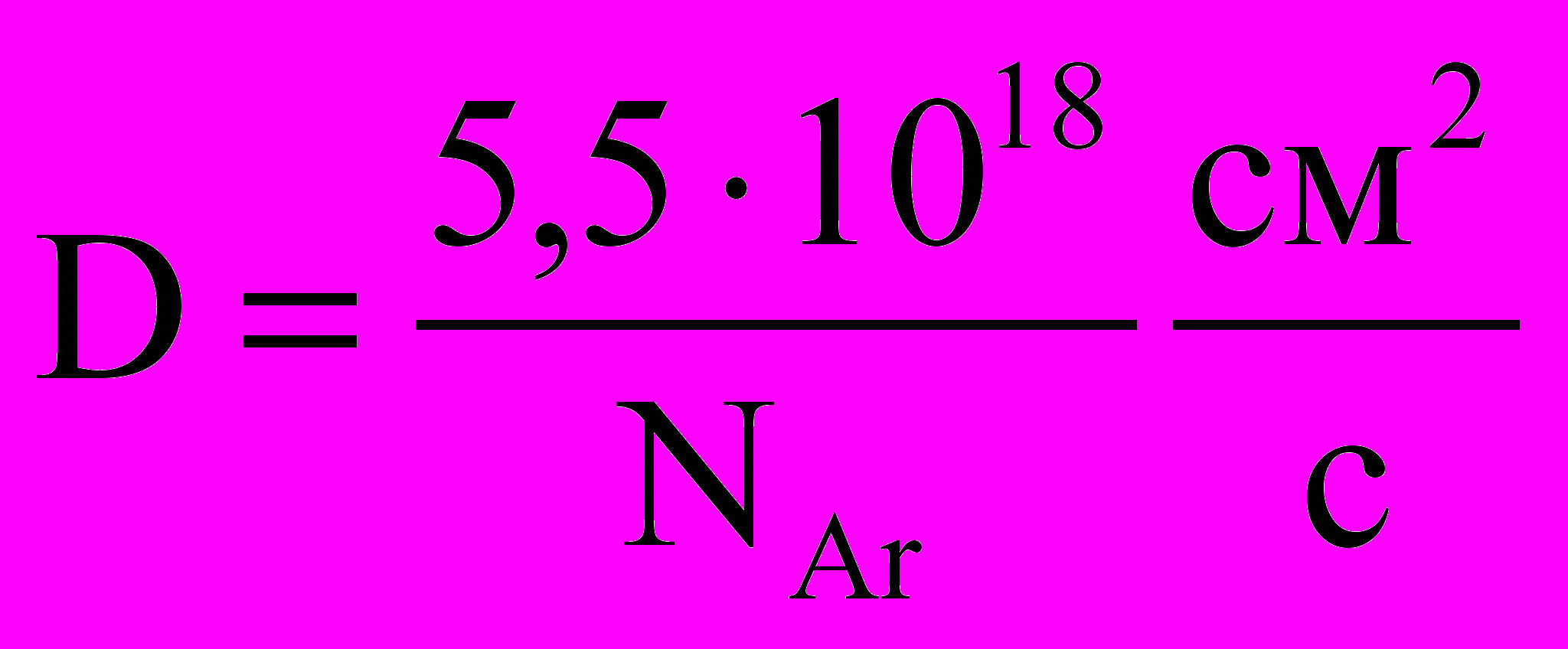; (2.25)

63Р2 коэффициент диффузии равен 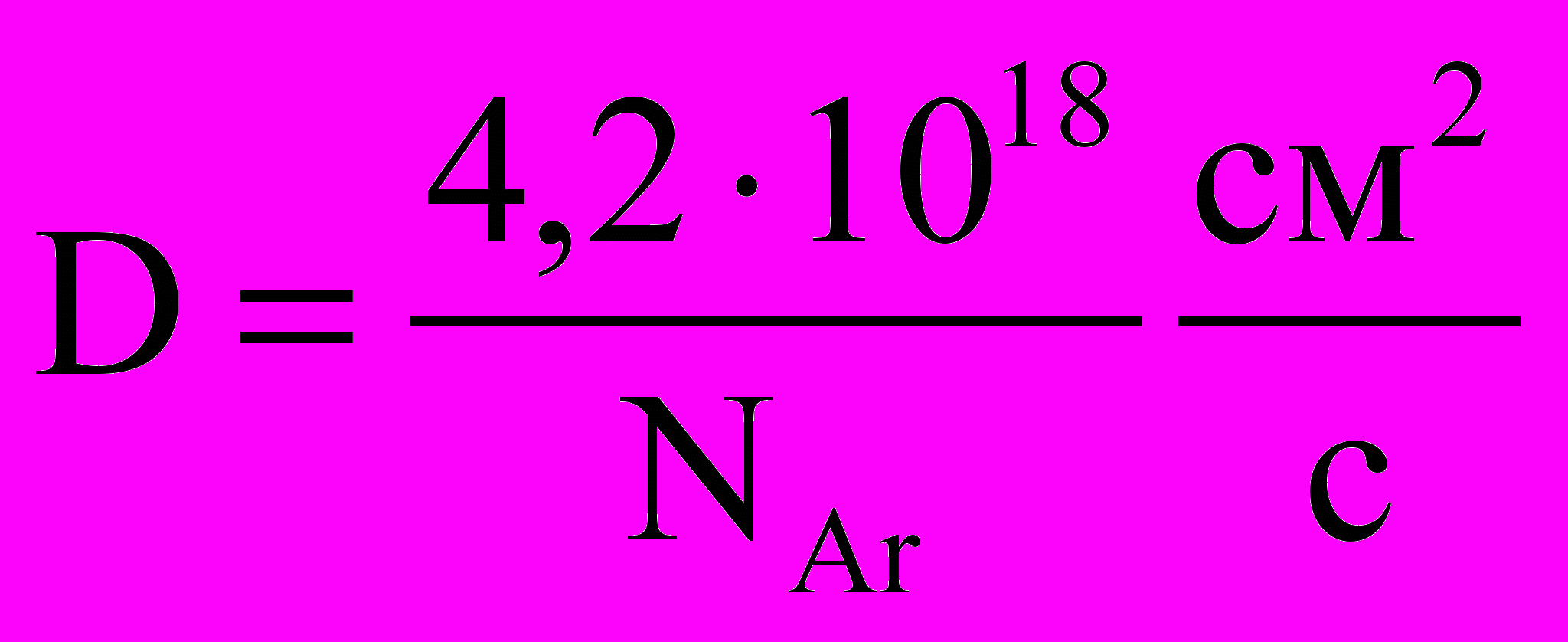. (2.26)

Тогда система уравнений будет:

N0S01+N2S21+N3S31=N1Z1

N0S02+N1S12+N3S32=N2Z2 (2.27)

N0S03+N1S13+N2S23=N3Z3,


где Sij=vij – прямые и Sji=Sij(gi/gj)exp(ij/kTe) – обратные переходы.

Суммированные скорости равны

. (2.28)


Определители матрицы из коэффициентов системы уравнений записываются в виде

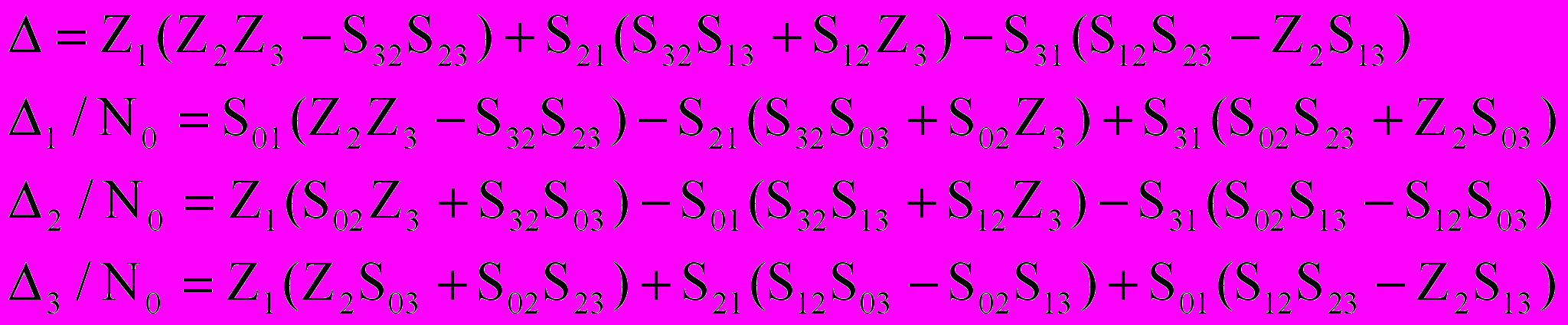. (2.29)


Тогда заселенность по уровням равна

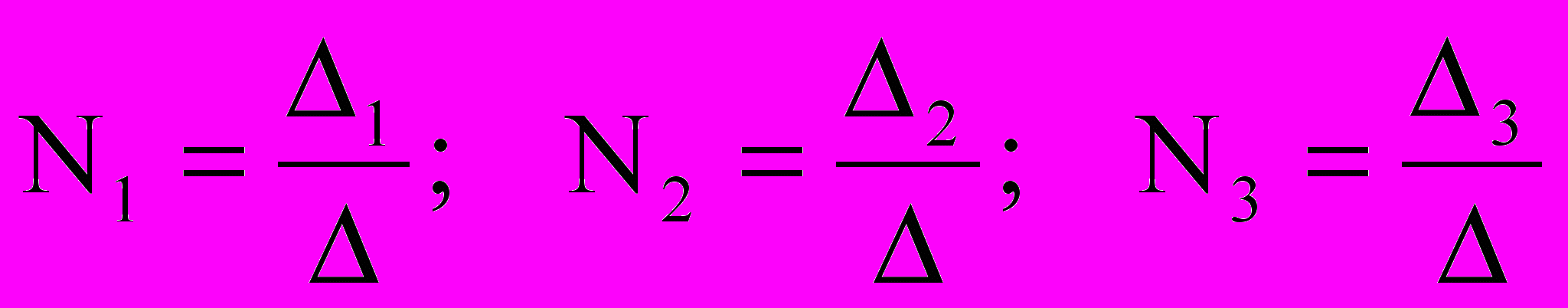. (2.30)


В балансе уровня 61Р1 учитывались заселение с основного и 63Р012-состояний, обратные переходы на эти же уровни, уход наверх на уровни 71S0, 61D2 и ионизация. Ввиду большой вероятности излучения диффузией атомов в состоянии 61Р1 пренебрегалось:


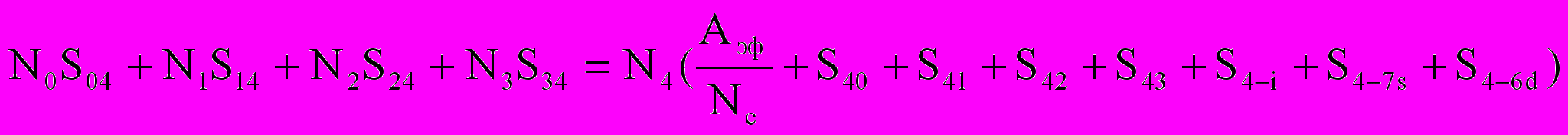.(2.31)

Для уровня 63Р1 коэффициент диффузии принимался равным .

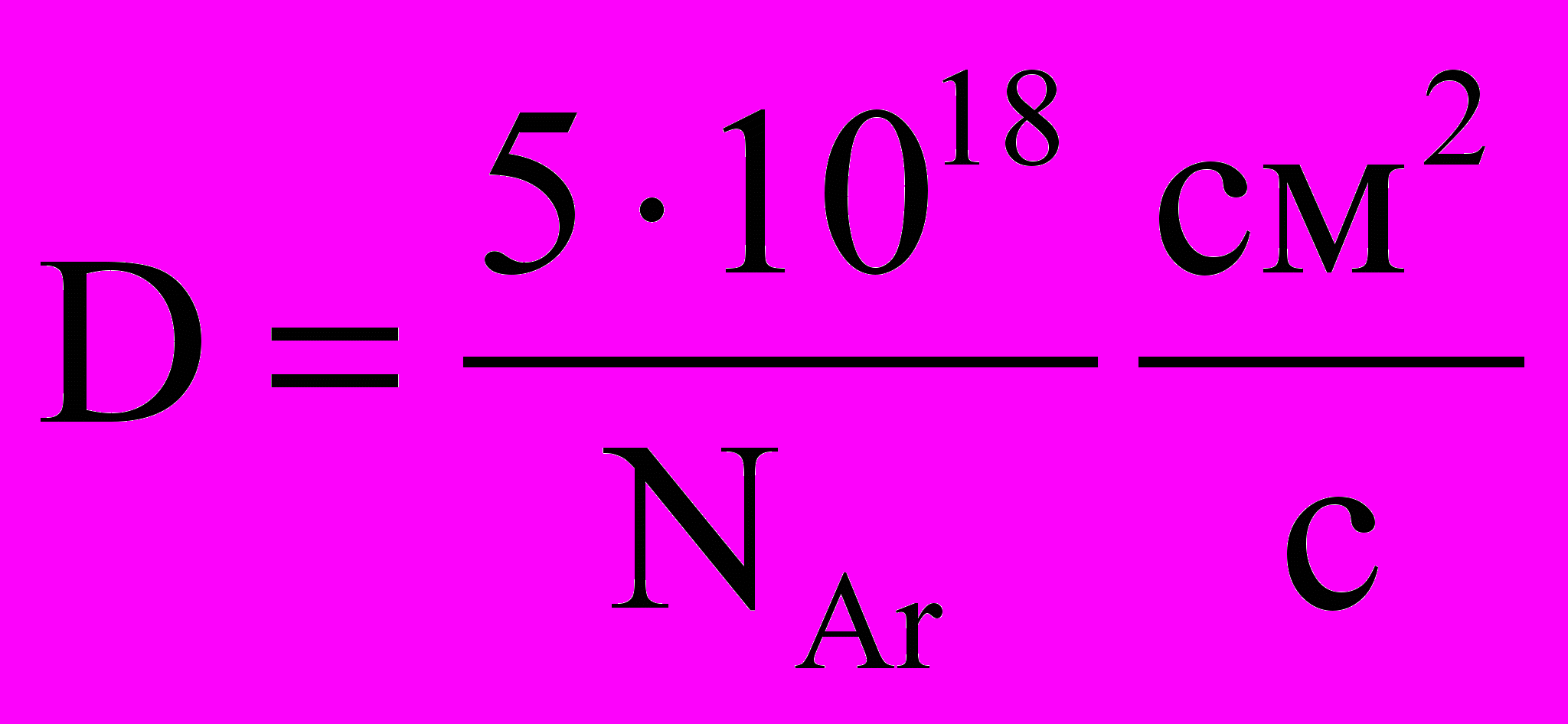Индексы в уравнениях соответствуют: 0 – основной уровень 61S0, 1 – 63P0, 2 – 63P1, 3 – 63P2,
4 – 61P1. Решение системы для 63Р012-уровней при РAr=0 приведено в таблице 2.5 на основании скоростей переходов, приведенных в таблицах 2.3 и 2.4.

Таблица 2.5 – Относительная заселенность (к равновесной в основном состоянии) уровней 63Р012 при толщинах плазмы l=10 см (верхние числа) и l=1 см (нижние числа)


Ne, см–3
1012
1013
1014

Te 104K
1
1,5
2
2,5
1
1,5
2
2,5
1
1,5
2

N0, см–3

1012
63P0
0.14

0.14
0.092

0.092
0.063

0.063
0.041

0.041
0.17

0.17
0.11

0.11
0.080

0.080
0.053

0.053
0.35

0.35
0.28

0.28
0.20

0.20

63P1
0.0032

0.0032
0.0027

0.0027
0.0020

0.0020
0.0016

0.0016
0.031

0.031
0.026

0.026
0.020

0.020
0.016

0.016
0.25

0.25
0.20

0.20
0.15

0.15

63P2
0.13

0.13
0.11

0.11
0.080

0.080
0.060

0.060
0.15

0.15
0.13

0.13
0.096

0.096
0.072

0.072
0.33

0.33
0.27

0.27
0.21

0.21

1013
63P0
0.17

0.14
0.12

0.092
0.082

0.063
0.054

0.041
0.36

0.17
0.30

0.11
0.22

0.080
0.15

0.053
0.79

0.35
0.70

0.28
0.49

0.20

63P1
0.030

0.0032
0.026

0.0027
0.020

0.0020
0.016

0.0016
0.24

0.031
0.20

0.026
0.15

0.020
0.11

0.016
0.70

0.25
0.60

0.20
0.40

0.15

63P2
0.16

0.13
0.13

0.11
0.10

0.080
0.074

0.060
0.34

0.15
0.31

0.13
0.22

0.096
0.17

0.072
0.73

0.33
0.69

0.27
0.48

0.21

1014
63P0
0.47

0.17
0.39

0.12
0.28

0.082
0.19

0.054
0.86

0.36
0.76

0.30
0.53

0.22
0.35

0.15
0.98

0.79
0.86

0.70
0.59

0.49

63P1
0.30

0.030
0.30

0.026
0.21

0.020
0.17

0.016
0.80

0.24
0.70

0.20
0.50

0.15
0.33

0.11
0.90

0.70
0.80

0.60
0.50

0.40

63P2
0.43

0.156
0.40

0.13
0.29

0.10
0.22

0.074
0.79

0.34
0.76

0.31
0.52

0.22
0.37

0.17
0.91

0.73
0.85

0.69
0.57

0.48

1015
63P0












0.86

0.86
0.76

0.76
0.53

0.53
0.35

0.35
0.98

0.98
0.86

0.86
0.59

0.59

63P1












0.82

0.80
0.72

0.70
0.52

0.50
0.37

0.33
0.94

0.90
0.83

0.80
0.54

0.50

63P2












0.79

0.789
0.76

0.76
0.52

0.52
0.37

0.37
0.91

0.91
0.85

0.85
0.57

0.57


2.3.4 Функция распределения электронов по скоростям,

концентрация и температура электронов


Еще Ленгмюр показал, что в разряде в парах ртути низкого давления функция распределения (ФР) электронов по скоростям близка к максвелловской, хотя малые концентрации электронов ne~1010см–3 не должны этого обеспечивать межэлектронными столкновениями. Максвеллизацию Ленгмюр объяснил взаимодействием электронов с плазменными колебаниями. После этого этот вопрос неоднократно анализировался. Крауфорд и Селф [36] максвеллизацию электронов в разряде объяснили характером зависимости упругого рассеяния электронов от энергии. Для ртути она падающая, что снижает потери быстрых электронов, в тоже время как в аргоне – возрастающая, что приводит к существенному уменьшению доли быстрых электронов. В работе [37] экспериментально показано, что в ртутном разряде максвеллизация электронов устанавливается уже через
5 мкс при токе 0,2 А и через 2 мкс при токе 0,8 А.

Таким образом, для проведения расчетов исходными параметрами являются концентрации ртути и аргона, диаметр трубки, а также концентрация и температура электронов. Последние два параметра определяются первыми тремя и разрядным током. Для их оценки можно использовать экспериментальные данные. В [39] исследован чисто ртутный разряд. Результаты приведены на рисунках 2.12, 2.13. С ростом тока концентрация электронов растет практически линейно. С ростом давления паров ртути электронная температура падает, а концентрация растет.





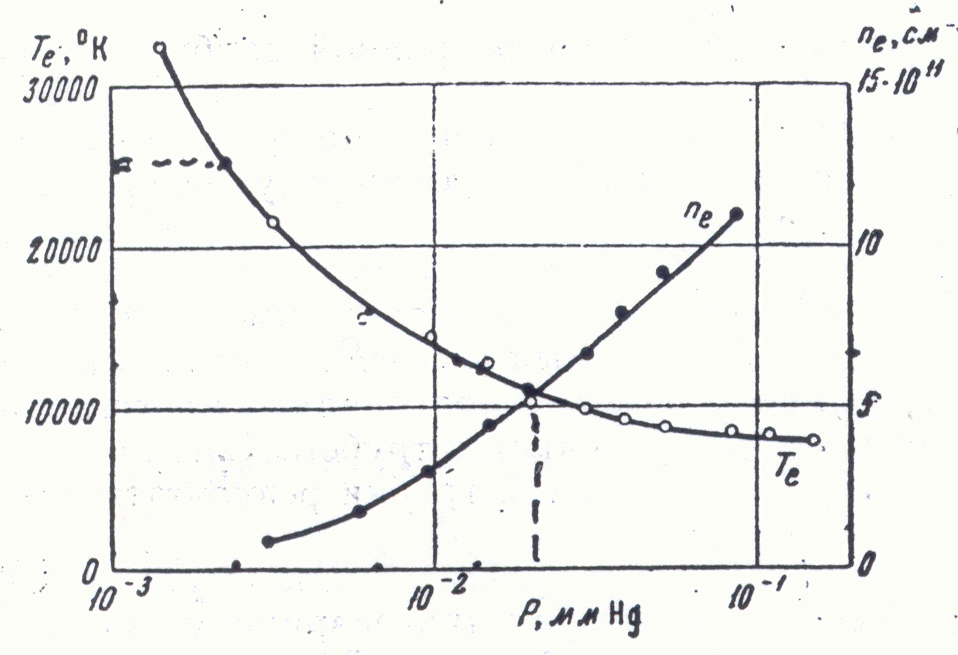
Рисунок 2.12 – Зависимость электронной температуры и концентрации электронов

от давления паров ртути. Ток 2 А, диаметр трубки 26 мм [39]


В [40–42] приводятся параметры плазмы в HgAr разряде.

Для теоретической оценки ne и Te можно использовать следующие положения [7, 38,]:
  1. Концентрация электронов примерно пропорциональна току


, (2.32)

где 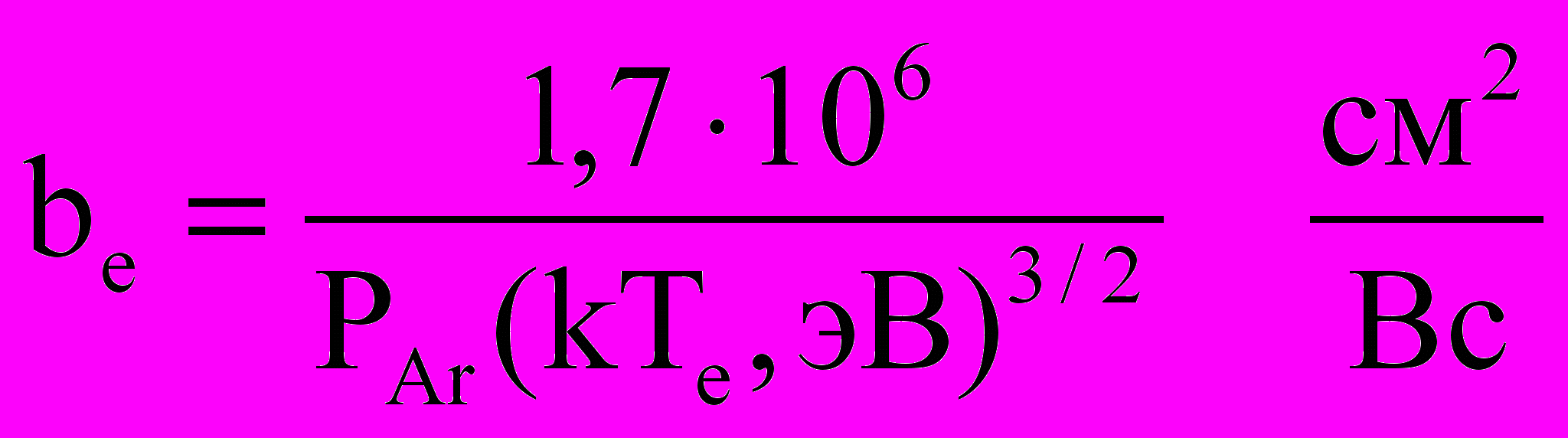– подвижность электронов в аргоне.

2. Температура электронов определяется необходимой ионизацией, обеспечивающей компенсацию ухода электронов на стенку. При прямой ионизации и линейной аппроксимации сечения с наклоном ‘а’

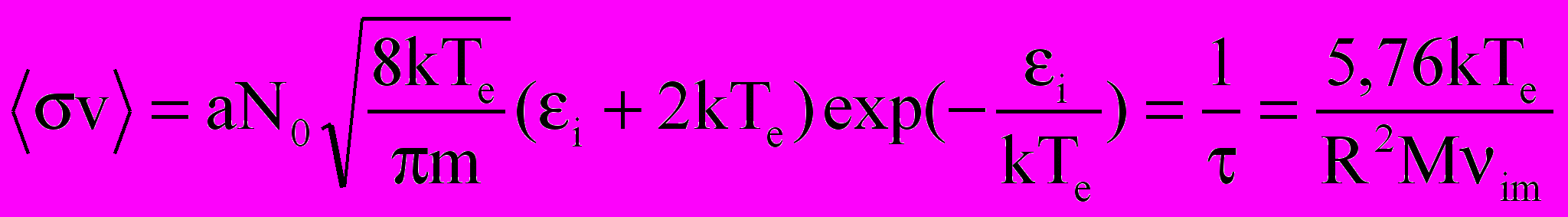, (2.33)


где im – частота ион атомных столкновений,  – время жизни иона до ухода на стенку.




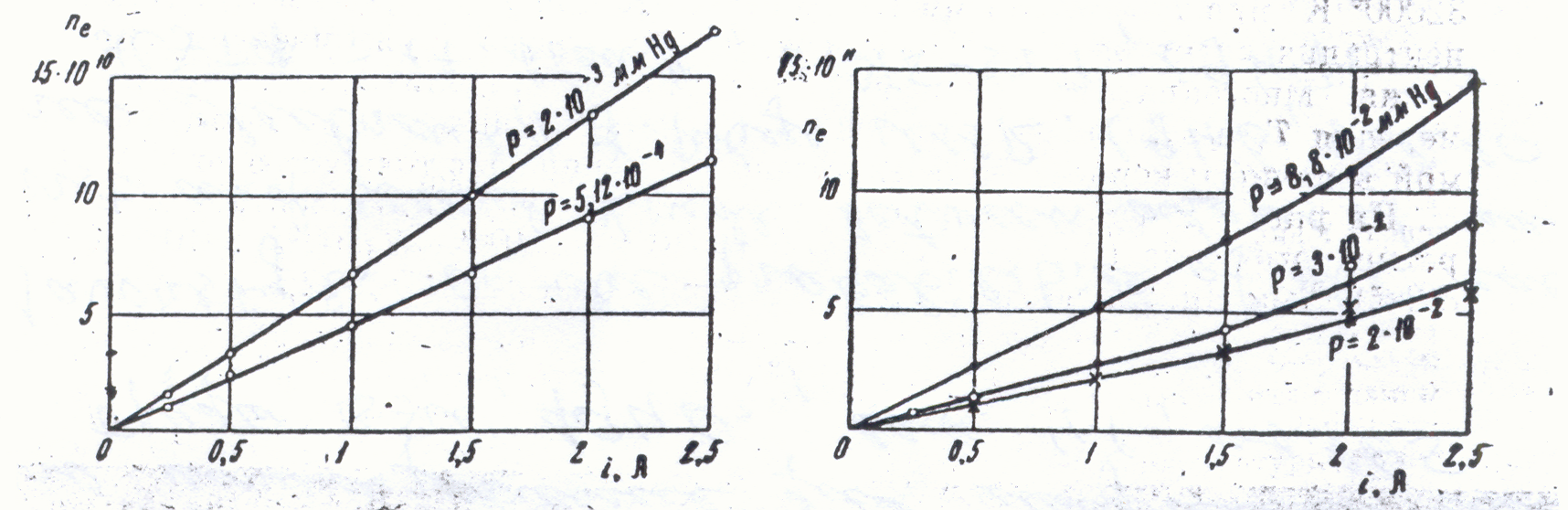
Рисунок 2.13 — Зависимость концентрации электронов от силы разрядного тока

при различных давлениях паров ртути [39]


3. Осевая напряженность электрического поля Ez определяется балансом энергии для обеспечения необходимого Te. IEz=Pст+Pизл+Pгаз, где Pст – мощность, уносимая ионами на стенку, Pизл – мощность излучения, Pгаз – нагрев газа. Te и Ez слабо зависят от тока и давления.





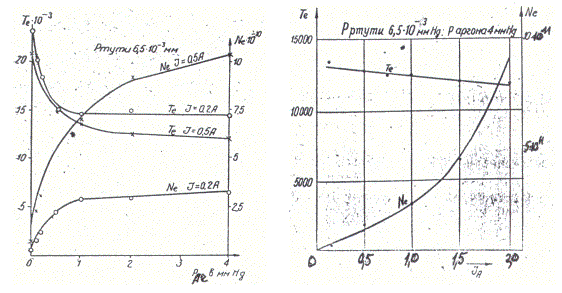
Рисунок 2.14 – Зависимость концентрации и температуры электронов

от давления аргона и силы тока. Диаметр трубки 35 мм [40]


Р
исунок 2.15 –  трубки 26 мм,

PHg=1,210–3 Торр [32]
Рисунок 2.16 –  трубки 26 мм, PHg=1,710–3 Торр [41]



3 ИНИЦИИРОВАНИЕ РАЗРЯДА И ИСТОЧНИК ПИТАНИЯ


3.1 Электротехнические характеристики магнитопроводов


Анализ электротехнических характеристик ферромагнитных материалов является одной из важнейших составляющих при проектировании индукционных газоразрядных устройств трансформаторного типа. Правильный выбор материала позволяет минимизировать потери в магнитопроводе и значительно уменьшить габариты устройства. При этом необходимо учитывать специфику работы сердечника трансформаторного газоразрядного устройства: в отличие от силовых трансформаторов радиоэлектронной аппаратуры, имеющих большое число витков первичной и вторичной обмотки, электротехническим эквивалентом индукционного разряда трансформаторного типа является трансформатор с одним витком вторичной и несколькими витками первичной обмотки. Вторичный виток в данном случае одновременно играет роль нагрузки, характеризуемой напряжением горения разряда U и током в разряде I.