Geum.ru

В. Н. Шивринский проектирование информационных систем учебно-методический комплекс

Вид материалаУчебно-методический комплекс
Подобный материал:
1   2   3   4   5   6   7   8   9   10   11
Глава 6. Расчет погрешностей приборов и систем

Определение погрешностей измерительного звена

по его расчетной характеристике

Оценка погрешностей прибора значительно упрощается, если их расчет разделить на два этапа. На первом этапе определяются погрешности каждого звена в отдельности по его расчетной характеристике. На втором этапе определяются погрешности прибора в целом с учетом его структурной схемы. Такая последовательность расчетов не только упрощает вычисления, но и повышает наглядность полученных результатов, так как выявляется роль каждого звена в формировании общей погрешности прибора. Кроме того, для выполнения расчета на втором этапе не обязательно иметь расчетные данные о погрешностях каждого звена. Могут быть использованы экспериментальные данные или взяты значения погрешностей отдельных звеньев из технических условий (если используются типовые чувствительные или преобразующие элементы).

Вернемся к расчетной (5.2) характеристике прибора:

У = f(X, q1, q2, ..., qn),

где q1, q2, ..., qn - параметры схемы и конструкции.

Первичные ошибки q1, q2,  ..., qn практически малы по сравнению с параметрами q1, q2, ..., qn. Зависимость между приращением выходного сигнала У и первичными ошибками, по аналогии с рассмотренными ранее уравнениями (1.4-1.5), можно представить в виде

У = (dу/dq1)q1 + (dу/dq2)q2, ... + (dу/dqn)qn =

= (dу/dqi)qi. (6.1)

Таким образом, абсолютная погрешность есть взвешенная сумма первичных погрешностей. Коэффициентами веса являются частные производные по параметрам, которые вызывают появление погрешностей. Частные производные вычисляются для расчетных (номинальных) значений q1, q2, ..., qn.

Уравнение (6.1) применимо как к прибору в целом, так и к отдельным его элементам. Параметры q1, q2, ..., qn могут отличаться от номинальных значений как по производственно-технологическим причинам (qi=q'i - основная погрешность), так и из-за отклонения условий эксплуатации (температуры, давления и др.) от нормальных (qi=q''i - дополнительная погрешность).

В качестве примера рассмотрим расчет погрешности маятникового акселерометра (рис.5.1). Статическую характеристику прибора (5.11) можно представить следующим образом

Uвых = 12mlLUob-1h-3E-1o-1a. (6.2)

На основании уравнения (6.1) получим

Uвых = 12lLUob-1h-3E-1o-1am + 12mLUob-1h-3E-1o-1al +

+ 12mlUob-1h-3E-1o-1aL + 12mlLb-1h-3E-1o-1aUo -

- 12mlLUob-2h-3E-1o-1ab - 312mlLUob-1h-4E-1o-1ah -

- 12mlLUob-1h-3E-2o-1aE - 12mlLUob-1h-3E-1o-2ao. (6.3)

Выражение для относительной погрешности получим путем деления уравнения (6.3) на уравнение (6.2):

Uвых = Uвых/Uвых =

= m/m + l/l + L/L + Uo/Uo - b/b - 3h/h - E/E - o/o. (6.4)

Отсюда следует, что относительная погрешность маятникового акселерометра есть взвешенная сумма первичных относительных погрешностей. Коэффициентами веса являются показатели степени параметров.

Выражение (6.1) можно использовать для расчета температурных погрешностей, если считать, что приращения qi параметров qi произошли в результате изменения температуры окружающей среды.

Полагая параметры qi линейно зависящими от температуры

qi = qio(1+i), (6.5)

где i - температурный коэффициент параметра;

qio - значение параметра при нормальной температуре, получим приращения этих параметров в виде

qi = qi - qio= qioi. (6.6)

Подставляя зависимость (6.6) в выражение (6.1), найдем температурную погрешность прибора:

У = (dу/dqi)qioi, (6.7)

откуда условие температурной компенсации будет

(dу/dqi)qioi = 0. (6.8)

Определение погрешностей прибора по структурной схеме

Для расчета погрешности прибора по структурной схеме необходимо знать погрешности всех его преобразующих звеньев, которые могут быть определены различными способами: а) расчетным путем по методике, описанной в предыдущем параграфе; б) по результатам экспериментальных исследований образцов; в) по справочным данным, если используются стандартные звенья.

Допустим, что прибор (или измерительная система) содержит n звеньев, каждое из которых осуществляет определенное функциональное преобразование физических величин. Звенья соединены между собой любым способом (последовательно, параллельно, встречно-параллельно или более сложным образом). Обозначим выходной и входной сигналы системы в целом через У и Х, а выходные сигналы звеньев через У1, У2, ..., Уn. В реальной системе сигналы звеньев У1, У2, ..., Уn, вследствие наличия у них погрешностей, получают независимые приращения У1, У2, ..., Уn, которые в совокупности и дают суммарную погрешность системы У.

Относительная погрешность системы в линейном приближении равна линейной комбинации относительных погрешностей звеньев:

 = 11 + 22 + ... + nn = ii, (6.9)

где  = У/У - относительная погрешность системы;

i = Уi/Уi - относительная погрешность i-го звена;

i - коэффициент влияния i-го звена.

Из уравнения (6.9) следует, что погрешность системы складывается из n составляющих, каждая из которых порождается соответствующим звеном структурной схемы. Коэффициент влияния i представляет собой безразмерный множитель, на который нужно умножить относительную погрешность i-го звена, чтобы определить порождаемую ею составляющую суммарной относительной погрешности системы.

Предположим, что все звенья, кроме i-го, абсолютно точны, а погрешность системы вызвана лишь влиянием i-го звена. Тогда относительная погрешность системы

У/У = iУi/Уi,

откуда

i = (У/У)/(Уi/Уi). (6.10)

Ограничимся случаем, когда все звенья имеют линейные характеристики

Уi = SiXi, (6.11)

где Si - чувствительность i-го звена;

Xi - входной сигнал i-го звена.

При установившемся режиме, когда Xi = const, малое приращение функции (6.11) можно выразить ввиде

Уi = SiXi. (6.12)

Разделив (6.12) на (6.11), получим

Уi/Уi = Si/Si. (6.13)

Аналогично для системы в целом

У/У = S/S, (6.14)

где S - чувствительность системы в целом.

Подставив (6.13) и (6.14) в (6.10), получим

i = (S/Si)(Si/S). (6.15)

Так как рассматривается лишь одна составляющая суммарной погрешности, вызванная влиянием i-го звена, а параметры остальных звеньев принимаются постоянными, то отношение малых приращений чувствительности можно заменить частной производной:

S/Si  dS/dSi. (6.16)

Подставляя (6.16) в (6.15), получим формулу для определения коэффициента влияния i-го звена:

i = (dS/dSi)(Si/S). (6.17)

Если произвести расчет чувствительности прибора по структурной схеме, то можно представить ее как функцию чувствительности звеньев:

S = F(S1, S2, ..., Sn). (6.18)

Частные производные dS/dSi (i = 1, 2, ..., n) могут быть найдены поочередным дифференцированием функции (6.18) по S1, S2, ..., Sn.

Рассмотрим расчет коэффициентов влияния погрешностей звеньев на примере, представленном в работе [13]. Определим безразмерные коэффициенты влияния погрешностей звеньев для структурной схемы, приведенной на рис.6.1,а, если заданы чувствительности звеньев: S1 = 20; S2 = 9; S3 = 1; S4 = 2.



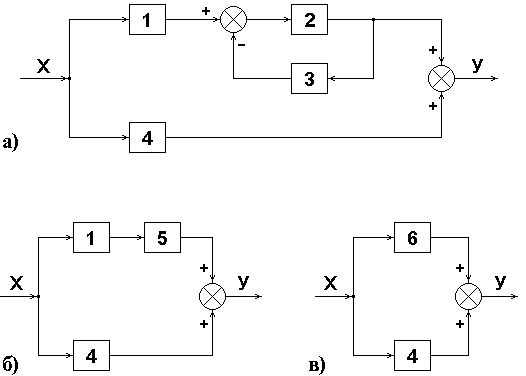
Рис.6.1. К примеру расчета коэффициентов влияния


Заменим встречно-параллельные звенья 2 и 3 с отрицательной обратной связью эквивалентным звеном 5 (рис.6.1,б), чувствительность которого согласно (5.18) равна

S5 = S2/(1 + S2S3).

Затем заменим последовательные звенья 1 и 5 эквивалентным звеном 6 (рис.6.1,в), чувствительность которого в соответствии с (5.7) будет

S6 = S1S5 = S1S2/(1 + S2S3).

Общая чувствительность системы согласно (5.15) определится как

S = S4 + S6 = S4 + S1S2/(1 + S2S3). (6.19)

Дифференцируя выражение (6.19) поочередно по S1, S2, S3, S4 и подставляя полученные частные производные в формулу (6.17), определим безразмерные коэффициенты влияния погрешностей звеньев:

1 = S1S2/(S4 + S2S3S4 + S1S2);

2 = S1S2/[(S4 + S2S3S4 + S1S2)(1 + S2S3)];

3 = - S1S22S3/[(S4 + S2S3S4 + S1S2)(1 + S2S3)];

4 = (S4 + S2S3S4)/(S4 + S2S3S4 + S1S2). (6.20)

Подставляя в (6.20) значения S1, S2, S3 и S4, находим 1 = 0.9; 2 = 0.09; 3 = - 0.81; 4 = 0.1.

Расчет допусков на погрешность прибора

Погрешности возникают в приборах под действием целого ряда внутренних и внешних причин, многие из которых носят случайный характер. Поэтому сами погрешности тоже являются случайными величинами и расчет допусков на погрешность прибора необходимо производить методами теории вероятностей и математической статистики.

Путем статистической обработки случайных погрешностей партии однотипных приборов, полученных в одних и тех же условиях, вычисляют среднее значение погрешности  и среднее квадратическое отклонение  случайной погрешности.

Если известны значения i и i для всех звеньев структурной схемы, то можно вычислить аналогичные показатели для суммарной погрешности прибора. Для этого применяют правила суммирования случайных величин: средние значения суммируются алгебраически, а средние квадратические отклонения - квадратически.

Нижняя н и верхняя в границы допусков на суммарную погрешность прибора связаны с показателями  и  следующей зависимостью:

н =  + t1; в =  + t2, (6.21)

где t1 и t2 - безразмерные параметры, знак которых может быть положительным или отрицательным.

При анализе допусков на суммарную погрешность прибора могут встретиться две задачи:

а) определение вероятности соответствия (или вероятности несоответствия) погрешности прибора допускам при заданных границах поля допуска н и в;

б) определение границ поля допуска н и в при заданной вероятности соответствия (или несоответствия) прибора допускам.

Решение этих задач значительно облегчается, если принять распределение суммарной погрешности прибора по нормальному закону, который наиболее часто встречается на практике [13]. При этом условии вероятность P того, что суммарная погрешность находится в заданных пределах, определяется по уравнению:

P(н <  < в) = Ф(t1) - Ф(t2), (6.22)

где Ф(t) - нормированная функция Лапласа.

Численные значения Ф(t) в зависимости от t приведены в таблице 6.1. Отрицательным значениям t отвечают отрицательные значения Ф(t). Последняя цифра, приведенная в скобках в таблице 6.1, дана для t = 5.0.

Таблица 6.1

Нормированная функция Лапласа Ф(t)

Десятые доли t
t

0
1
2
3
4

0
0.000
0.3413
0.4772
0.4986501
0.4999683

1
0.0398
0.3643
0.4821
0.4990324
0.4999793

2
0.0793
0.3849
0.4860996
0.4993129
0.4999867

3
0.1179
0.4032
0.4892759
0.4995166
0.4999915

4
0.1554
0.4192
0.4918025
0.4996631
0.4999946

5
0.1916
0.4332
0.4937903
0.4997674
0.4999966

6
0.2257
0.4452
0.4953388
0.4998409
0.4999979

7
0.2580
0.4554
0.4965330
0.4998992



8
0.2881
0.4641
0.4974449
0.4999274



9
0.3159
0.4713
0.4981342
0.4999519
(0.4999997)


Вероятность того, что суммарная погрешность  выйдет за пределы допусков (вероятность несоответствия Q допускам), будет

Q = 1 - P(н <  < в) = 1 - [Ф(t1) - Ф(t2)]. (6.23)

Чтобы вероятности соответствия или несоответствия прибора допускам выразить в процентах, нужно их значения, вычисленные по формулам (6.22) или (6.23), умножить на 100%. Вероятность несоответствия прибора допускам, выраженную в процентах, называют также процентом риска.

При определении границ поля допуска по заданной вероятности координату середины поля допуска совмещают со средним значением погрешности , что дает наилучшее использование нормального закона распределения (наибольшую вероятность при одном и том же значении поля допуска). При этом условии t2 = - t1 = t и формулы для определения границ поля допуска принимают вид

н =  - t; в =  + t. (6.24)

Значение параметра t определяют по таблице 6.1, исходя из заданной вероятности: P = 2Ф(t) или Ф(t) = P/2.

На практике часто берут параметр t = 3, что отвечает вероятности соответствия прибора допускам 99.73% или проценту риска 0.27%. При этом условии границы поля допусков

н =  - 3; в =  + 3, (6.25)

а общая ширина поля допусков

в - н = 6.

Следовательно, для обеспечения процента риска, не превышающего 0.27% необходимо: а) совместить середину поля допуска со средним значением погрешности; б) взять общую ширину поля допуска в шесть раз большей, чем среднее квадратическое отклонение погрешности.

Пример [13]. Пусть прибор, структурная схема которого представлена на рис.6.1, имеет звенья с линейными характеристиками. Чувствительность звеньев и их погрешности заданы и сведены в таблицу 6.2. Требуется определить: а) вероятность соответствия прибора допускам и процент риска, если допуск на суммарную погрешность прибора установлен ±1% (н = -1.0%, в = +1.0%); б) границы поля допуска на суммарную погрешность прибора для случая, когда задан процент риска 0.27% (t = 3).

Таблица 6.2

Характеристики звеньев прибора рис.6.1

№ звена
1
2
3
4

Чувствительность
S1 = 20
S2 = 9
S3 = 1
S4 = 2

Среднее значение погрешности звена, %
1 = 0
2 = -5.0
3 = 0.37
4 = 5.5

Среднее квадрати-ческое отклонение погрешности звена, %
1 = 0.2
2 = 1.5
3 = 0.2
4 = 2.0


Решение. Для схемы рис.6.1 в предыдущем параграфе вычислили коэффициенты влияния погрешностей звеньев:

1 = 0.9; 2 = 0.09; 3 = - 0.81; 4 = 0.1.

Определим среднее значение  и среднее квадратическое отклонение  погрешности прибора:

 = ii = 0.90 + 0.09(- 5.0) - 0.810.37 + 0.15.5 = - 0.2;

 = = .

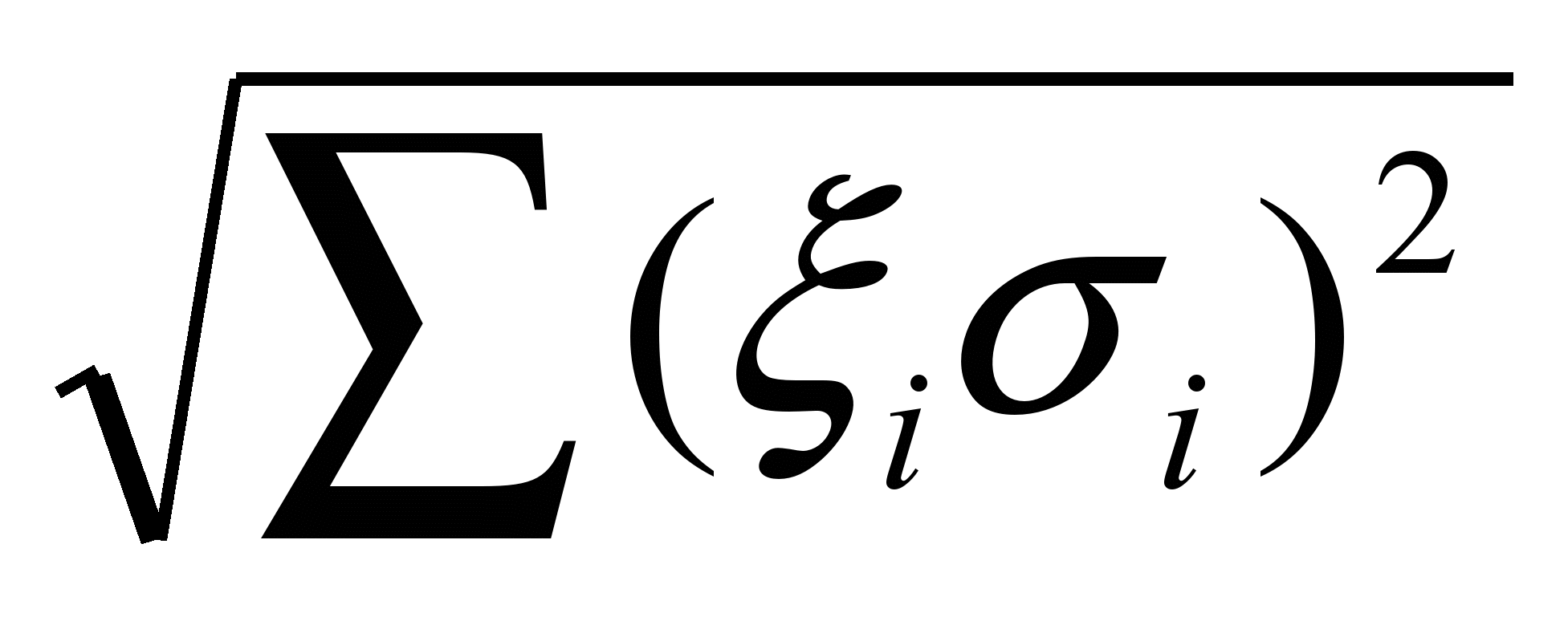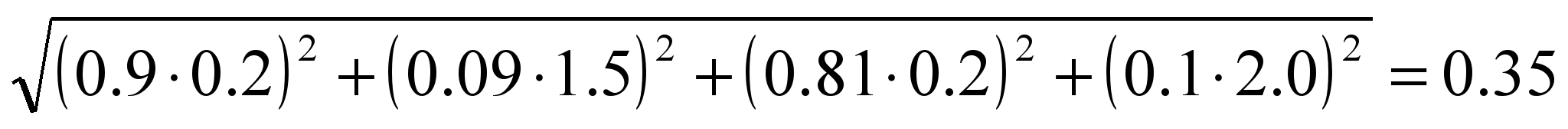По формулам (6.21) определяем параметры t1 и t2 для заданных границ поля допуска (±1.0%):

t1 = (н - )/ = [- 1.0 - (- 0.2)]/0.35 = - 2.28;

t2 = (в - )/ = [1.0 - (- 0.2)]/0.35 = 3.43.

По таблице 6.1 с применением интерполяции находим значения функции Лапласа:

Ф(t1) = - 0.4886; Ф(t2) = 0.4997.

Находим искомую вероятность того, что  будет в пределах ±1.0%:

P = Ф(t2) - Ф(t1) = 0.4997 - (- 0.4886) = 0.9883 или 98.83%.

Процент риска Q = 100 - 98.83 = 1.17%.

По формулам (6.21) получим искомые границы поля допуска на суммарную погрешность, обеспечивающие заданный процент риска 0.27% (t = 3):

н =  - 3 = - 0.2 - 30.35 = - 1.25;

в =  + 3 = - 0.2 + 30.35 = 0.85.