Geum.ru

В. Н. Шивринский проектирование информационных систем учебно-методический комплекс

Вид материалаУчебно-методический комплекс

Содержание


Последовательное соединение
Встречно-параллельное соединение
Подобный материал:
1   2   3   4   5   6   7   8   9   10   11
Глава 5. Расчет характеристик приборов и систем

Общие понятия

Приборы и системы могут работать в статическом и динамическом режимах. В статическом режиме измеряемая величина постоянна и выходной сигнал прибора приобретает установившееся значение. В динамическом режиме измеряемая величина и выходной сигнал прибора изменяются с течением времени. Соответственно расчет характеристик приборов и систем делится на расчет статических и динамических характеристик.

Различают заданную и расчетную статические характеристики. Заданная характеристика - это зависимость между У и Х, требуемая по техническому заданию

Узад = fзад(X). (5.1)

Расчетная характеристика - это зависимость У от Х, полученная в результате расчета конкретной схемы и конструкции прибора

У = f(X, q1, ..., qn), (5.2)

где q1, ..., qn - параметры схемы и конструкции, в число которых входят как геометрические параметры (размеры деталей), так и физические параметры (модуль упругости, электропроводность, магнитная проницаемость и т. п.).

Параметры q1, ..., qn в различных образцах однотипных приборов отличаются от номинальных значений вследствие влияния технологических факторов в процессе изготовления приборов, а также могут изменяться в процессе эксплуатации из-за изменения режимов питания и окружающих условий (температуры, атмосферного давления и др.). Поэтому в уравнении (5.2) величина У является функцией многих переменных, что учитывается при анализе погрешностей.

Если в уравнении (5.2) все параметры приравнять их номинальным расчетным значениям и считать постоянными (q1=q10, q2=q20, ..., qn=qn0), то это уравнение будет выражать номинальную расчетную характеристику

Уном = f(X, q10, ..., qn0). (5.3)

Если при этом учесть, что q10, ..., qn0 - постоянные, то номинальную расчетную характеристику можно записать как функцию одного переменного

Уном = f(X). (5.4)

Методы расчета статических характеристик

Расчет статических характеристик приборов и систем ведется в следующем порядке:

- составляется структурная схема прибора (системы);

- рассчитывают характеристики и чувствительность всех звеньев исходя из принципов их работы, схемы и конструкции;

- производят расчет характеристики и чувствительности прибора (системы) в целом, исходя из вида структурной схемы.

Характеристики звеньев определяются путем анализа физических законов, лежащих в основе их работы. Методы расчета типовых элементов изложены в специальной литературе (например, литература по курсам «Элементы приборных устройств», «Электроника», «Электротехника» и др.).

Иногда характеристики элементов не поддаются точному расчету, но могут быть определены экспериментально. В подобных случаях для получения аналитической зависимости можно применить аппроксимирующую функцию. Например, характеристику термоэлектрического элемента, преобразующего температуру  в электродвижущую силу e, определяют по экспериментально полученным справочным данным, в которых даны в виде таблиц значения e при различных значениях . Задаваясь аналитической зависимостью в виде полинома 2-й степени (e=1+22), можно так подобрать коэффициенты 1 и 2, чтобы вычисленные по этой формуле значения e приближались к табличным данным. Для более точного приближения можно выбрать в качестве аппроксимирующей функции полином 3-й степени.

После того как получены уравнения всех звеньев, входящих в структурную схему, определяется характеристика прибора в целом. С этой целью совместно решаются уравнения звеньев и уравнения дополнительных связей между звеньями, отображающие операции суммирования или вычитания сигналов на структурной схеме.

Для типовых соединений звеньев (рис.4.1) можно вывести стандартные формулы, выражающие статическую характеристику и чувствительность прибора через характеристики и чувствительность звеньев.

Последовательное соединение (рис.4.1,а). Если характеристики звеньев 1, 2, ..., n выражены соответственно уравнениями

У1 = f1(X);

У2 = f2(У1);

. . . . . . . . . .

Уn-1 = fn-1(Уn-2);

У = fn(Уn-1), (5.5)

то результирующая характеристика прибора определяется совместным решением системы уравнений (5.5):

У = fn{fn-1...f2[f1(X)]}. 5.6)

Чувствительность прибора

S = dУ/dX.

Умножим и разделим правую часть данного равенства на dУ1, dУ2, ..., dУn-1, тогда чувствительность прибора определится как

S = (dУ1/dX)(dУ2/dУ1)..(dУ/dУn-1).

Имея в виду, что

dУ1/dX = S1; dУ2/dУ1 = S2; ... dУ/dУn-1 = Sn,

получим окончательно  n 

S = S1S2...Sn = П Si. (5.7)

i=1 

Характеристику прибора можно определить и графическим путем. Для прибора с тремя последовательно соединенными звеньями в четвертях I, П, Ш прямоугольной системы координат строят соответственно характеристики звеньев 1, 2, 3, а затем с помощью построения определяют результирующую характеристику прибора в IV четверти. Если прибор содержит более трех звеньев, то построение ведется в несколько этапов. В начале находят характеристику соединения из первых трех звеньев, затем повторяют построение на другом графике, рассматривая первые три звена как одно звено.

В качестве примера рассмотрим расчет статической характеристики маятникового акселерометра, схема которого приведена на рис.5.1. Здесь m, l - масса и длина маятника; Cпр - жесткость противодействующей пружины; Uo, o - напряжение питания и полный рабочий угол потенциометра; a - измеряемое ускорение; Uвых,  - выходное напряжение и угол поворота движка потенциометра; F - сила, действующая на массу; Mвр - вращающий момент; Mпр - противодействующий момент. Акселерометр работает при малых отклонениях, тогда F ma.



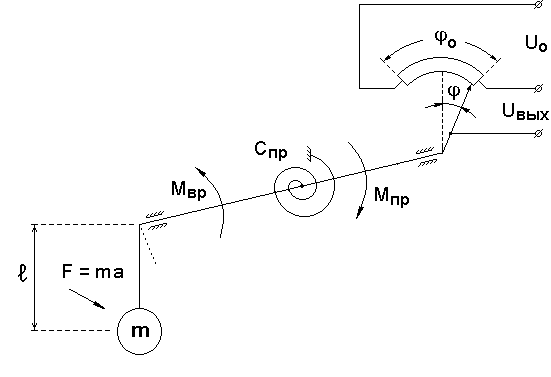
Рис.5.1. Схема маятникового акселерометра

Структурная метрологическая схема маятникового акселерометра приведена на рис.5.2.



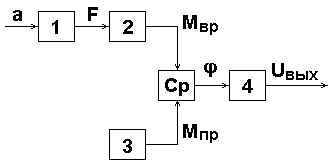
Рис.5.2. Структурная метрологическая схема

маятникового акселерометра


Структурная (динамическая) схема маятникового акселерометра приведена на рис.5.3. Операция сравнения здесь как бы пропадает, хотя и показано, что Mвр = Mпр.



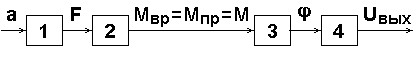
Рис.5.3. Структурная схема маятникового акселерометра


Характеристики звеньев 1, 2, 3, 4 выражены соответственно уравнениями

F = ma;

Mвр = Fl;

Mпр = Cпр;

Uвых = Uo/o. (5.8)

Жесткость спиральной пружины определяется как

Cпр = bh3E/12L, (5.9)

где L - развернутая длина, b - ширина, h - толщина, E - модуль упругости материала спиральной пружины.

В установившемся режиме измерения

Mвр = Mпр. (5.10)

Решая совместно (5.8-5.10), получим

mal = Cпр,

 = mla/Cпр = 12mlLa/(bh3E),

Uвых = 12mlLUoa/(obh3E). (5.11)

Уравнение (5.11) может быть получено непосредственно по структурной схеме прибора (рис.5.3), для этого необходимо определить передаточные коэффициенты звеньев (1-4):

K1 = dF/da = m; K2 = l; K3 = d/dM = 1/Cпр; K4 = dU/d = Uo/o.

Учитывая, что Uвых = Ka, где K = K1K2K3K4, получим статическую характеристику акселерометра в виде (5.11).

Параллельное соединение (рис.4.1,б). Если характеристики n параллельных звеньев имеют вид

У1 = f1(X);

У2 = f2(Х);

. . . . . . . .

Уn = fn(Х), (5.12)

а уравнение связи

У = У1 + У2 + ... + Уn, (5.13)

то статическая характеристика системы получается подстановкой уравнений (5.12) в уравнение связи (5.13):

У = f1(X) + f2(Х) + ... + fn(Х). (5.14)

Для определения чувствительности дифференцируем уравнение (5.14) по входной величине Х:

S = dУ1/dX + dУ2/dХ + ... + dУn/dХ.

Имея в виду, что

dУ1/dX = S1, dУ2/dХ = S2, ..., dУn/dХ = Sn,

получим  n 

S = S1 + S2 + ... + Sn =  Si. (5.15)

i=1

При графическом расчете характеристики всех параллельных звеньев строят в прямоугольной системе координат (в 1-й четверти). Суммируя ординаты всех кривых при фиксированном значении Х, находят координаты точек результирующей характеристики.

Встречно-параллельное соединение (рис.4.1,в). Если характеристики двух встречно-параллельных звеньев имеют вид

У = f1(X1);

Х2 = f2(У), (5.16)

то, решая их совместно с уравнением связи

Х1 = X ± Х2,

получим в неявном виде характеристику системы:

У = f1[X ± f2(У)]. (5.17)

В полученном уравнении знак «плюс» отвечает положительной обратной связи, знак «минус» - отрицательной.

Чувствительность системы при встречно-параллельном соединении звеньев определяется как

S = S1/(1±S1S2). (5.18)

Здесь знак «плюс» отвечает отрицательной обратной связи, знак «минус» - положительной.

При графическом расчете характеристики обоих звеньев строят в прямоугольной системе координат (в 1-й четверти). Суммируя абсциссы этих кривых при фиксированном значении У, находят координаты точек результирующей характеристики.

Методы расчета динамических характеристик

При расчете динамических характеристик приборов могут решаться задачи анализа и синтеза. Анализ динамических характеристик ведется с целью определения характера изменения выходного сигнала прибора во времени У(t) при известном законе изменения входного сигнала Х(t) и при заданных параметрах прибора. Задача синтеза заключается в выборе таких параметров прибора, при которых зависимость У(t) наилучшим образом приближается к желаемой.

Зависимость У(t) называют реакцией прибора на воздействие Х(t). Если бы прибор был идеальным в динамическом отношении (безынерционным), то его выходной сигнал реагировал бы без запаздывания на изменение входного сигнала и воспроизводился бы в соответствии со статической характеристикой У = f(Х), т. е.

У(t) = f[Х(t)]. (5.19)

В реальных приборах (вследствие наличия инерционных масс, демпфирования, тепловой инерции, емкостей и индуктивностей в электрических цепях и т. п.) условие (5.19) не выполняется и возникает динамическая погрешность

Удин = У(t) - f[Х(t)]. (5.20)

В общем случае для расчетного определения У(t) необходимо два уравнения, одно из которых выражает закон изменения Х:

Х = Х(t), (5.21)

а другое отображает физическую схему прибора и дает связь между У, Х и их производными:

f1[У(n), У(n 1), ..., У] = f2[Х(m), Х(m 1), ..., Х], (5.22)

где

У(n) = dnУ/dtn; Х(m) = dmХ/dtm.

Совместное решение и интегрирование уравнений (5.21) и (5.22) позволяет определить реакцию прибора У(t) на воздействие Х(t) при заданных начальных условиях, учитывающих состояние координаты У и ее производных в момент времени t = 0. Число начальных условий равно порядку левой части уравнения (5.22).

Таким образом, реакция прибора У(t) зависит как от внешнего воздействия Х(t), так и от собственных свойств прибора, определяемых уравнением (5.22). Следовательно, один и тот же прибор обладает различной реакцией У(t) на разные воздействия Х(t).

Закон изменения Х(t) в условиях реальной эксплуатации прибора может быть самым различным и содержать как детерминированную, так и случайную составляющие. В целях унификации оценок и возможности сравнения динамических свойств различных приборов при расчетах и экспериментах принято оценивать динамические характеристики приборов при типовых воздействиях - ступенчатом, импульсном, синусоидальном.

Реакцию прибора на ступенчатое воздействие называют переходной функцией, а на импульсное - импульсной переходной функцией. При определении реакции на синусоидальное воздействие обычно рассматривают только вынужденную составляющую колебаний выходного сигнала, которую представляют в виде частотных характеристик. Чаще всего пользуются амплитудно- и фазочастотными характеристиками, показывающими зависимость амплитуды и сдвига фаз выходного сигнала от частоты при постоянной амплитуде входного сигнала.

Дифференциальные уравнения (5.22) многих приборов являются линейными или линеаризуемыми и приводятся к виду

a0У(n)+a1У(n 1)+...+anУ = b0Х(m)+b1Х(m 1)+...+bmХ. (5.23)

Совместное решение и интегрирование уравнений (5.21) и (5.23) позволяет определить У(t). Другой способ нахождения У(t) для приборов, описываемых линейным дифференциальным уравнением (5.23), основан на применении преобразования Лапласа. При этом определяется передаточная функция прибора, равная отношению лапласовских изображений У(p) и Х(p) при нулевых начальных условиях:

W(p) = У(p)/Х(p) =

= (b0pm + b1pm-1 +...+ bm)/(a0pn + a1pn-1 +...+ an). (5.24)

Определяется лапласовское изображение выходного сигнала в виде

У(p) = W(p)Х(p),

где Х(p) - изображение функции Х(t).

Затем находят искомую реакцию

У(t) = L-1{У(p)} = L-1{W(p)Х(p)},

где L-1 - обратное изображение функции.

В качестве примера рассмотрим движение подвижной части магнитоэлектрического измерительного механизма (гальванометра), схема которого приведена на рис.5.4.



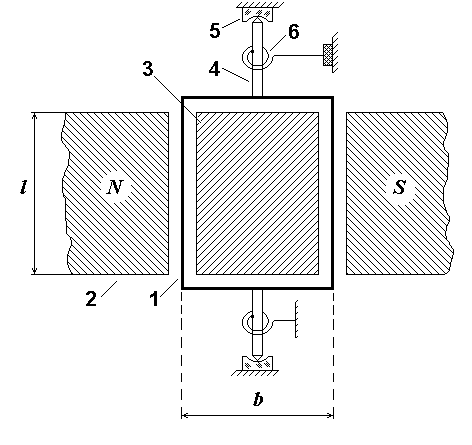
Рис.5.4. Схема магнитоэлектрического механизма

На рис.5.4 приняты следующие обозначения: 1 - рамка, с ней связан указатель (стрелка); 2 - постоянный магнит с полюсными наконечниками; 3 - сердечник; 4 - ось (керн); 5 - подпятник; 6 - противодействующие (токоподводящие) пружины. Для рассматриваемой схемы механизма уравнение моментов сил имеет вид

Mи + Mд + Mп = Mвр, (5.25)

где Mи - момент количества движения (инерционный момент); Mд - демпфирующий момент (момент успокоения); Mп - позиционный момент (противодействующий момент); Mвр - вращающий момент.

Моменты можно выразить через соответствующие коэффициенты:

Mи = J''; Mд = K'; Mп = C; Mвр = BSWI. (5.26)

Здесь  - угол отклонения подвижной части от состояния равновесия; ', '' - первая и вторая производные; J - момент инерции подвижной системы; K - коэффициент демпфирования; C - суммарная жесткость противодействующих пружин; B - магнитная индукция в воздушном зазоре; W - число витков рамки; S - активная площадь рамки (S = bl, b - ширина, l - длина активной стороны рамки); I - ток, протекающий через рамку.

Подставляя (5.26) в (5.25), получим дифференциальное уравнение прибора

J'' + K' + C = BSWI. (5.27)

Характеристическое уравнение

Jp2 + Kp + C = 0

можно записать в виде

p2 + 2p + 2o = 0, (5.28)

где  = K/2J; o = .

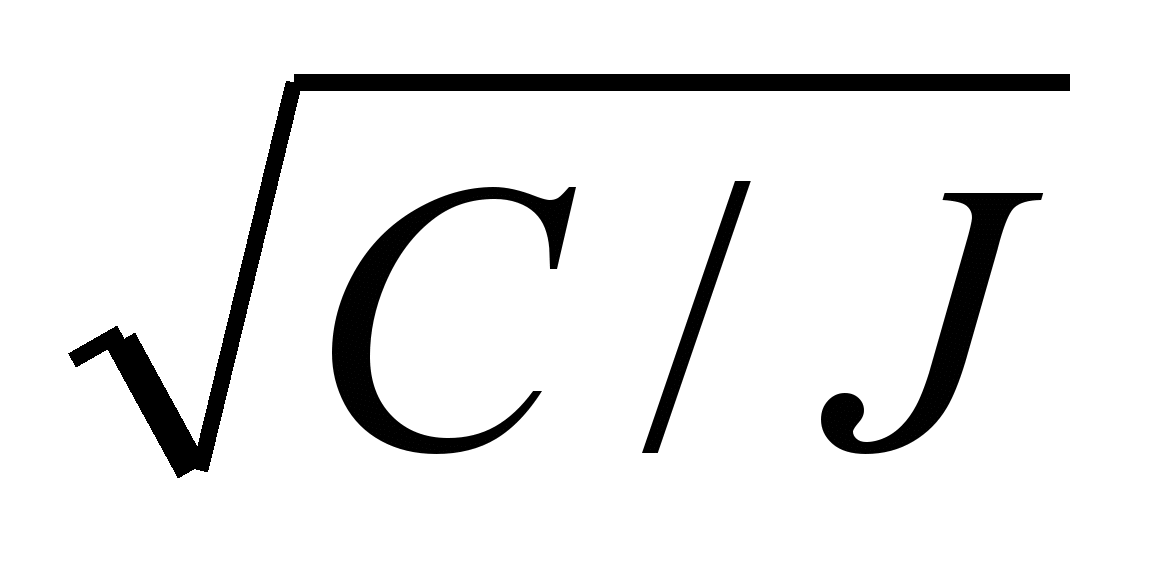Параметр o имеет определенный физический смысл - он определяет круговую частоту собственных недемпфированных колебаний системы.

Для электромагнитного успокоения, при отсутствии металлического корпуса рамки, имеем

K = (BSW)2/(Rиз + Rн), (5.29)

где Rиз - сопротивление рамки измерительного механизма; Rн - сопротивление внешней цепи (наружное).

В установившемся режиме производные '', ' равны нулю, тогда

уст = (BSW/C)I. (5.30)

Введем безразмерный параметр, называемый степенью успокоения подвижной части прибора :

= /o = K/2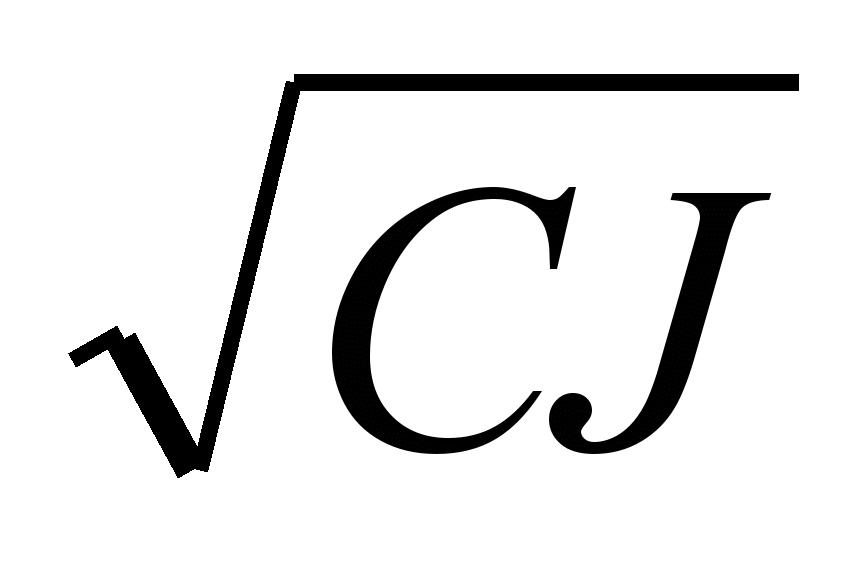. (5.31)

Корни уравнения (5.28) определим из выражения

p1,2 = - o ± o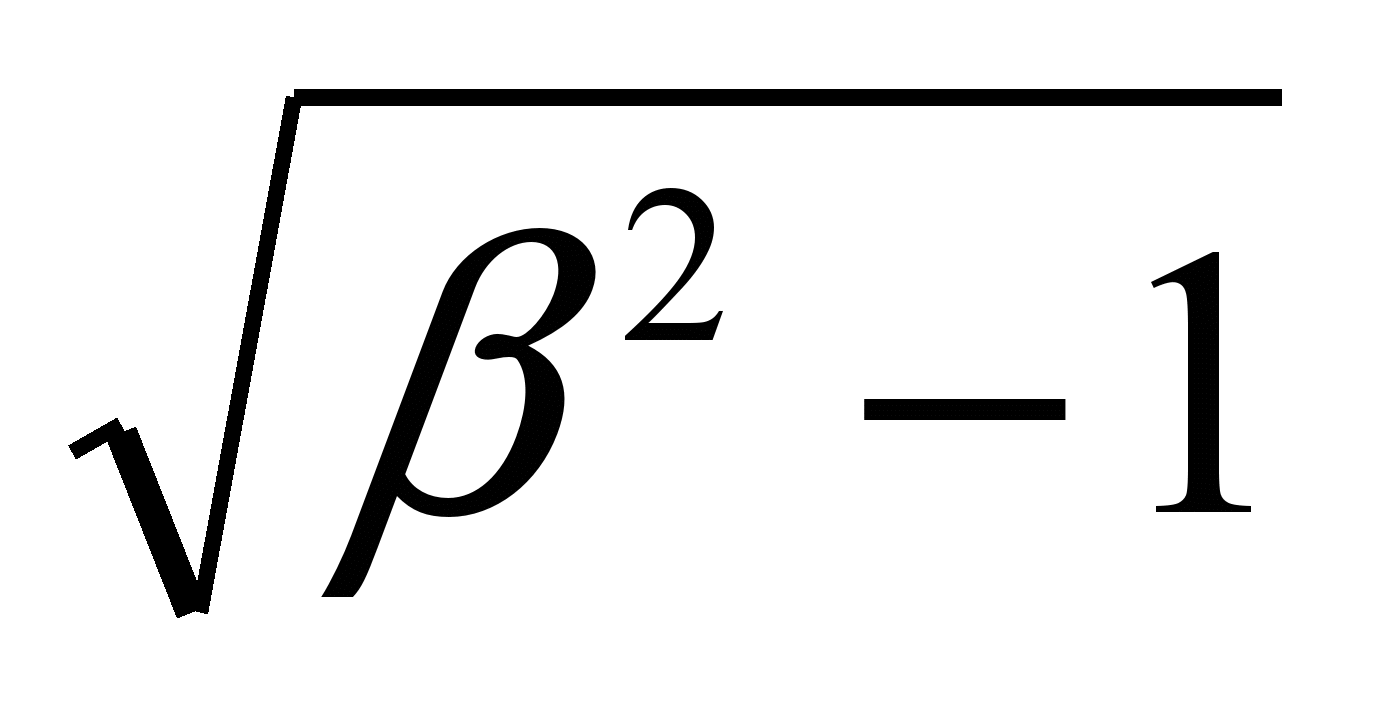. (5.32)

Вид переходного процесса зависит от характера корней p1,2. Здесь могут быть три случая.

Случай 1. Степень успокоения >1, что приводит к неравным действительным корням. Переходный процесс в системе 2-го порядка при >1 и при нулевых начальных условиях имеет апериодический характер (рис.5.5).

Случай 2. Степень успокоения =1, чему отвечают равные корни. Переходный процесс является апериодическим.

Случай 3. Корни неравные и комплексные. Этот случай, отвечающий <1, представляет наибольший интерес, так как в этой области существует некоторое оптимальное значение , при котором длительность переходного процесса получается минимальной. Переходные процессы при <1 имеют колебательный характер. В частном случае, когда отсутствует демпфирование (=0) система совершает незатухающие колебания (при отсутствии сил трения) по закону

(t) = (BSW/C)(1 - cosot). (5.33)

Параметр o представляет собой частоту собственных колебаний недемпфированной системы. В случае 0<<1 система совершает затухающие колебания (рис.5.5). Частота демпфированных колебаний

 = o.

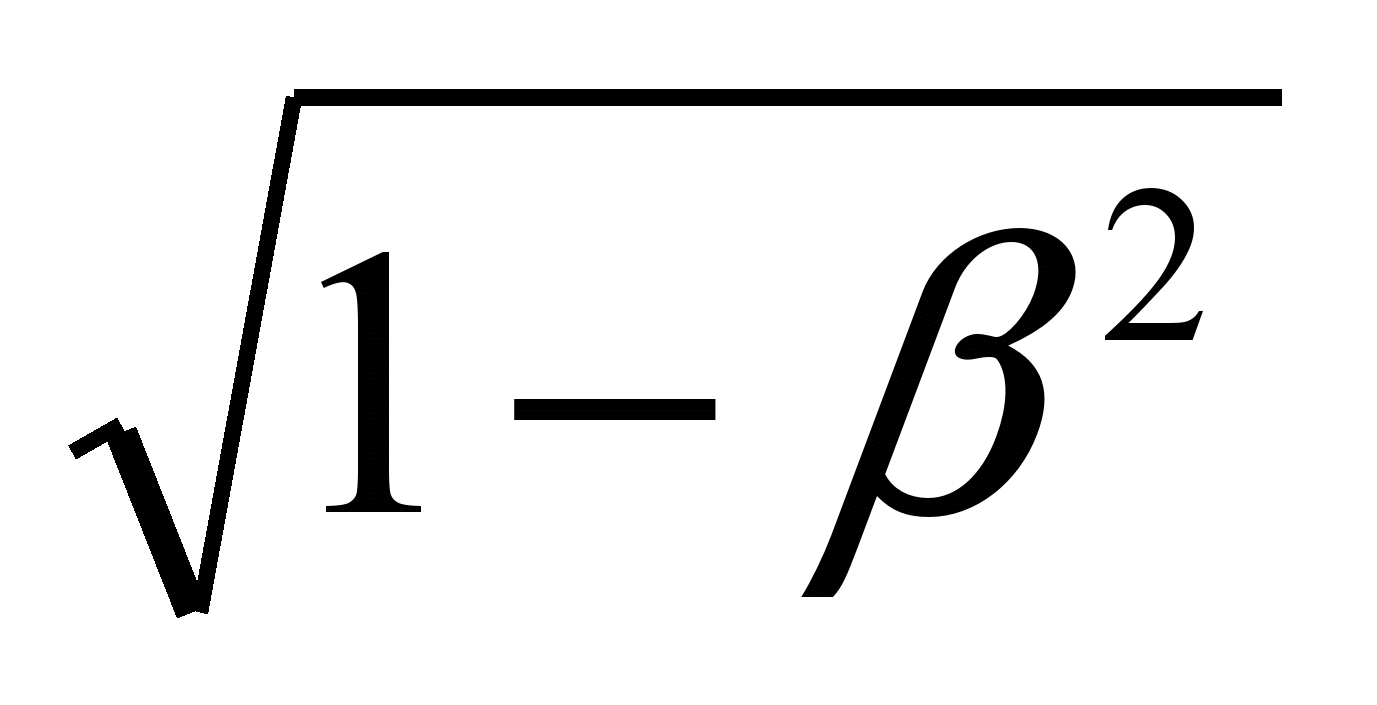Следовательно, с увеличением  от 0 до 1 частота демпфированных колебаний уменьшается от o до 0.

На рис.5.5 представлены графики переходных процессов в системе 2-го порядка при разных значениях степени успокоения : <1 - колебательный режим, >1 - апериодический режим, =1 - критический режим. Изменяя сопротивление цепи прибора (см. уравнение 5.29), можно получить различные режимы его работы.




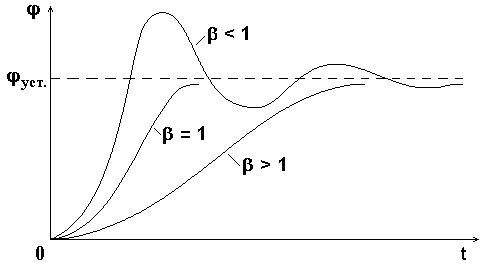
Рис.5.5. График движения подвижной части

гальванометра при разных режимах

Помимо o и , важными показателями колебательного переходного процесса являются декремент затухания и перерегулирование. Декрементом затухания d называют отношение абсолютных значений двух смежных максимальных отклонений выходного сигнала от установившегося значения. Перерегулирование  определяет относительную величину разности между первым максимумом переходного процесса и его установившимся значением.

Опыт показывает, что при степени успокоения =0.9 подвижная часть быстрее всего устанавливается в положение равновесия. Если цепь гальванометра разомкнута, то колебания рамки будут незатухающими (свободными). Период собственных колебаний определяется по формуле (5.34).

TO = 2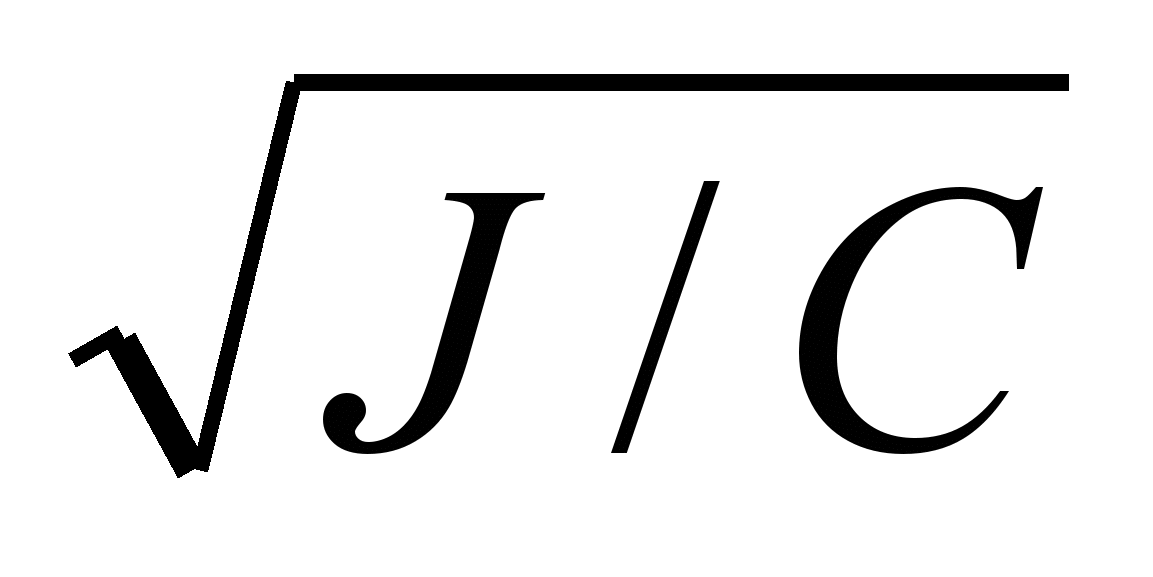. (5.34)

Методы расчета динамических характеристик звеньев и систем достаточно подробно рассматриваются в курсах «Теория автоматического управления и регулирования» и «Системы автоматического управления».


Оптимизация параметров приборов и систем

Задачи синтеза динамических характеристик приборов и систем весьма многообразны. Все они преследуют одинаковую цель, заключающуюся в создании измерительной системы, динамические характеристики которой наилучшим образом приближаются к заданным. Наилучшее приближение достигается обычно путем оптимизации некоторого заранее выбранного показателя динамического качества.

При проектировании оптимальных по быстродействию или по динамической точности измерительных систем могут выбираться различные критерии. Возможно, например, решение следующих задач синтеза: минимизация длительности переходного процесса, максимизация полосы пропускания частот, минимизация фазовых искажений, минимизация дисперсии динамической погрешности при действии случайного полезного сигнала и случайной помехи и т. д. Для повышения быстродействия измерительной системы используют следующие методы, основанные на оптимизации параметров измерительной системы; на введении последовательных корректирующих звеньев; на введении корректирующих обратных связей; на использовании систем с переменной структурой [2].

В качестве примера рассмотрим оптимизацию параметров измерительной системы 2-го порядка из условия минимума длительности переходного процесса. На рис.5.6 представлены графики переходных процессов в системе 2-го порядка для трех близких значений . Минимум длительности переходного процесса будет при таком значении =1, при котором кривая после первого перехода через установившееся значение совпадет с верхней границей допустимой динамической ошибки + (кривая 1). Этой кривой соответствует длительность переходного процесса t1, при которой кривая 1 входит в зону допуска в точке A.



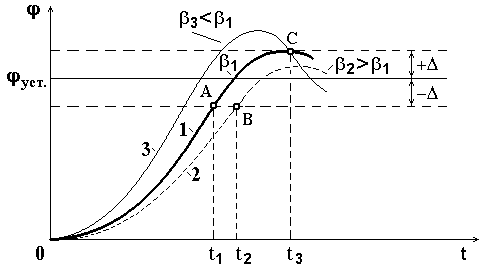
Рис.5.6. К расчету оптимальной степени успокоения по

критерию минимума длительности переходного процесса


Допустим, что 2>1, тогда период колебаний увеличится, и переходный процесс будет описываться кривой 2, расположенной правее кривой 1 и входящей в зону ± в точке B, для которой t2>t1.

Если же 3<1 (кривая 3), то период колебаний уменьшится, но увеличится величина перехода через установившееся значение, из-за чего максимальное отклонение кривой 3 выйдет за пределы верхней границы допуска +. Длительность процесса t3 будет определяться вторым пересечением кривой 3 с верхней границей зоны допусков в точке C, следовательно, t3>t1.

Более подробно вопросы синтеза систем и анализа их динамической точности рассмотрены в работе [14].