Урок з математики в групі ртм-21

Вид материала

Содержание

Тема уроку
Девіз уроку
IV. Застосування набутих знань у практичній діяльності – 28 хв.
V. Підведення підсумків – 5 хв.
1-й учень.
2-й учень.
Запис у зошиті: „Чи може людина втримати корабель?”
4-й учень.
5-й учень.
8-й учень.
А0. За час однієї генерації всі ці А
Методична розробка
Вступ(На сцену виходять Василь та Оксана.) Василь.
Коли народився відомий математик Франсуа Вієт?

Подобный материал:

1 2 3

Тема: Показникова функція.

Тема уроку: Показникова функція у природі, науці, техніці.

Тип уроку: урок закріплення і удосконалення нових знань, умінь і навичок.

Вид уроку: урок-семінар.

Навчальна мета:

навчити учнів застосовувати набуті знання про показникову функцію, зокрема, розглянути приклади застосування показникової функції у банківській справі, фізиці, біології та медицині;
показати дію закону діалектики – єдності і боротьби протилежностей, об’єднати різноманітні процеси в природі і техніці.

Розвиваюча:

розвивати математичну культуру учнів, розширити і поглибити рамки навчальної програми шляхом міжпредметних зв’язків;
привчити учнів користуватися додатковою літературою, робити висновки і узагальнення.

Виховна:

виховувати інтерес до математики, наполегливість, самостійність, відповідальність та вимогливість до себе.

Методична мета: Рівнева диференціація на уроках математики.

Міжпредметні зв’язки:

фізика - тема – „Закони руху в механіці”, „Будова і властивості твердих тіл”, „Реактивний рух”.
біологія - тема – „Будова клітин прокаріот”.

Забезпечення уроку: таблиці оцінювання доповідачів.

Література: М. І. Шкіль Алгебра і початки аналізу, К., „Техніка”, 2000.

Девіз уроку:

„Недостатньо лише мати добрий розум. Головне – раціонально застосовувати його.”

Р. Декарт

Хід уроку

I. Перевірка присутності і готовності учнів до уроку – 2 хв.

II. Актуалізація опорних знань (усне опитування) – 8 хв.

Питання для опитування:

Яку функцію називають показниковою?
Яка область визначення та множина значень показникової функції?
Зобразити графік функції при а >1 і 0
Що означає „експоненціальна” функція?
Назвіть число, яке ставши показником степеня, враз зрівняє всі числа.
Що спільного між графіками всіх показникових функцій?

III. Специфіка семінарського заняття, його мета – 2 хв.

На сьогоднішньому занятті будуть заслухані повідомлення, підготовлені учнями за матеріалами додаткової літератури.

Показникові функції зустрічаються в найрізноманітніших галузях науки – фізиці, хімії, біології, економіці, інформатиці, медицині, лісівництві, картографії, будівництві.Математика — це всеосяжна наука, без знання якої неможливо ні пізнати оточуючий нас світ, ні забезпечити науково-технічний прогрес.

IV. Застосування набутих знань у практичній діяльності – 28 хв.

1. Від складних відсотків до показникової функції (показникова функція в банку) – інформація учня - 4 хв.

2. Показникова функція та інформаційний бум (повідомлення учня) - 4 хв

3. Показникова функція в фізиці – 15 хв.

Виступ учнів по питаннях:

Чи може одна людина втримати корабель?
Падіння з парашутом.
Маса палива для ракети. Закон Ціолковського.

4. Показникова функція в біології та медицині (повідомлення учня) – 5 хв.

V. Підведення підсумків – 5 хв.

1. Висновки:

аналіз діяльності учнів у процесі всього уроку;
повідомлення та обґрунтування оцінок.

2. Домашнє завдання:

Знайти значення функції 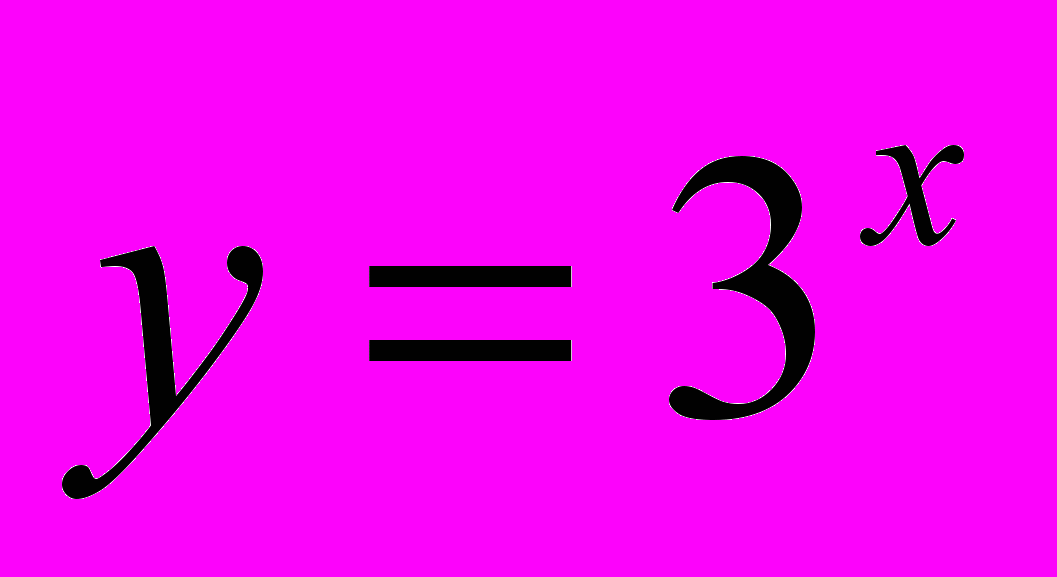, якщо x = 2, x = -2, x = 0.
Знайти область визначення функції .
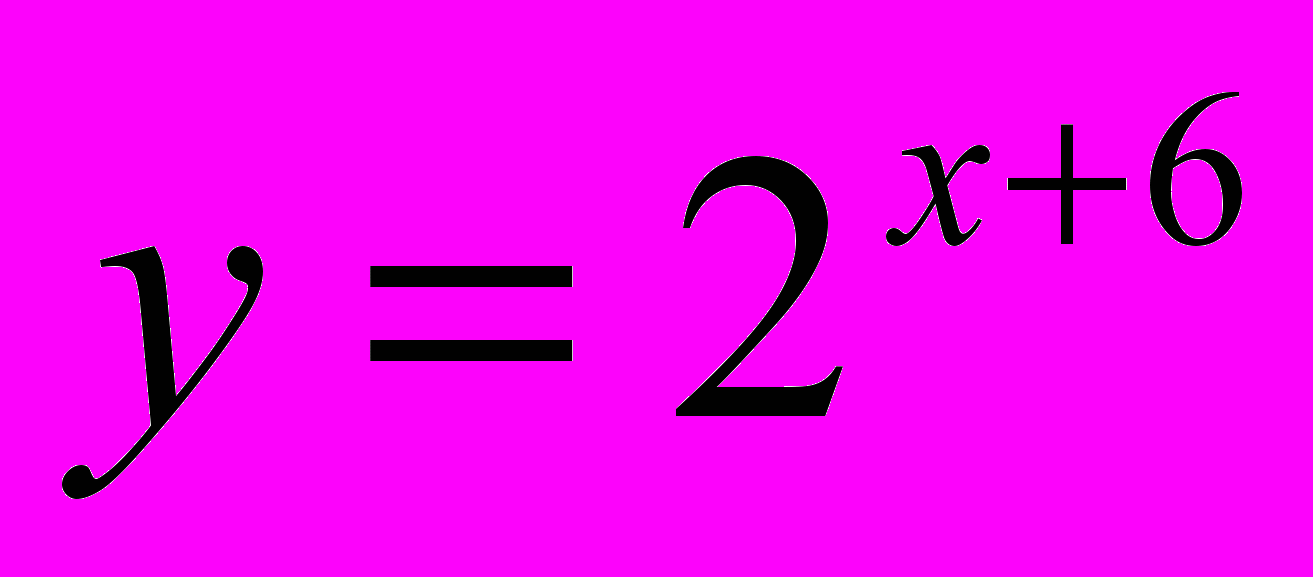Побудувати графік функції .

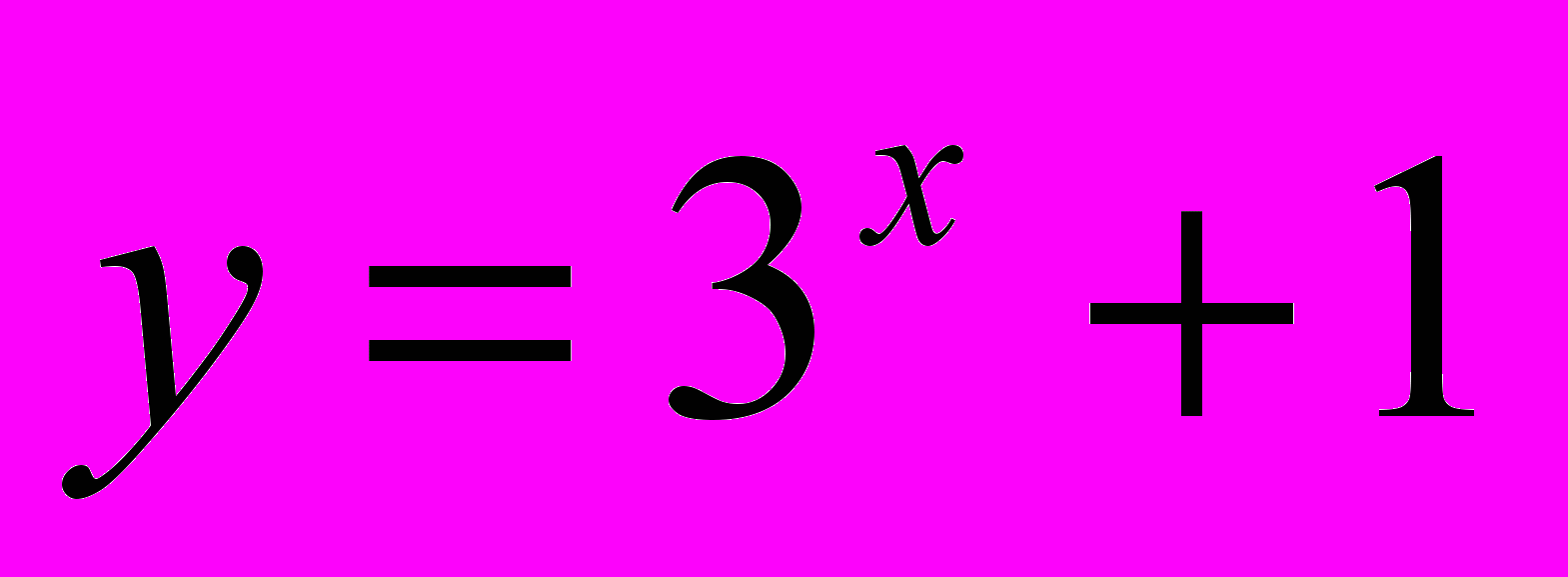Учитель. На сьогоднішньому занятті будуть заслухані повідомлення, підготовлені учнями за матеріалами додаткової літератури.

Запишіть у зошитах тему семінару: „Показникова функція в природі, науці, техніці”.

Показникові функції зустрічаються в найрізноманітніших галузях науки – фізиці, хімії, біології, економіці, інформатиці, медицині, лісівництві, картографії, будівництві.

А почнемо ми з банків, точніше з їх попередників — лихварів. Запишіть: „Показникова функція в банку”.

1-й учень. Ще за стародавніх часів було широко поширене лихварство — віддавання грошей у позику під відсотки. Селянин у разі неврожаю, ремісник, майно якого знищила пожежа, розорений торгівець змушені були йти до лихваря, обіцяючи наступного року повернути суму значно більшу, ніж узята в позику. Наприклад, у Давньому Вавилоні лихварі брали по 20 % лихви на рік. При цьому, якщо боржник не міг повернути борг наступного року, йому треба було платити відсотки не тільки з позиченого капіталу, а й з відсотків, що виросли за рік. Тому через 2 роки слід було заплатити не 40 %, а 44 % лихви, адже 1,2² = 1,44. За 5 років сума боргу збільшувалася в 1,2⁵ разів, тобто майже в 2,5 рази, а за 10 – років більш ніж у 6 разів. Зрозуміло, що більшість боржників були не в змозі повернути борг і, давно виплативши основну суму боргу, були змушені все життя працювати на те, щоб виплатити все зростаючі відсотки. Нарешті зубожілі боржники ставали рабами хижого лихваря.

У XIV—XV ст. у Західній Європі почали з'являтися банки (від фр. banque — лава, контора) — установи, які давали гроші в позику князям та купцям, фінансували за великі відсотки далекі мандрівки та завойовницькі походи. Щоб полегшити розрахунки складних відсотків, склали таблиці, за якими відразу можна було дізнатися, яку суму треба виплатити через п років, якщо була взята сума а під p% річних. Легко підрахувати, що сума, яку треба заплатити, виражається формулою:

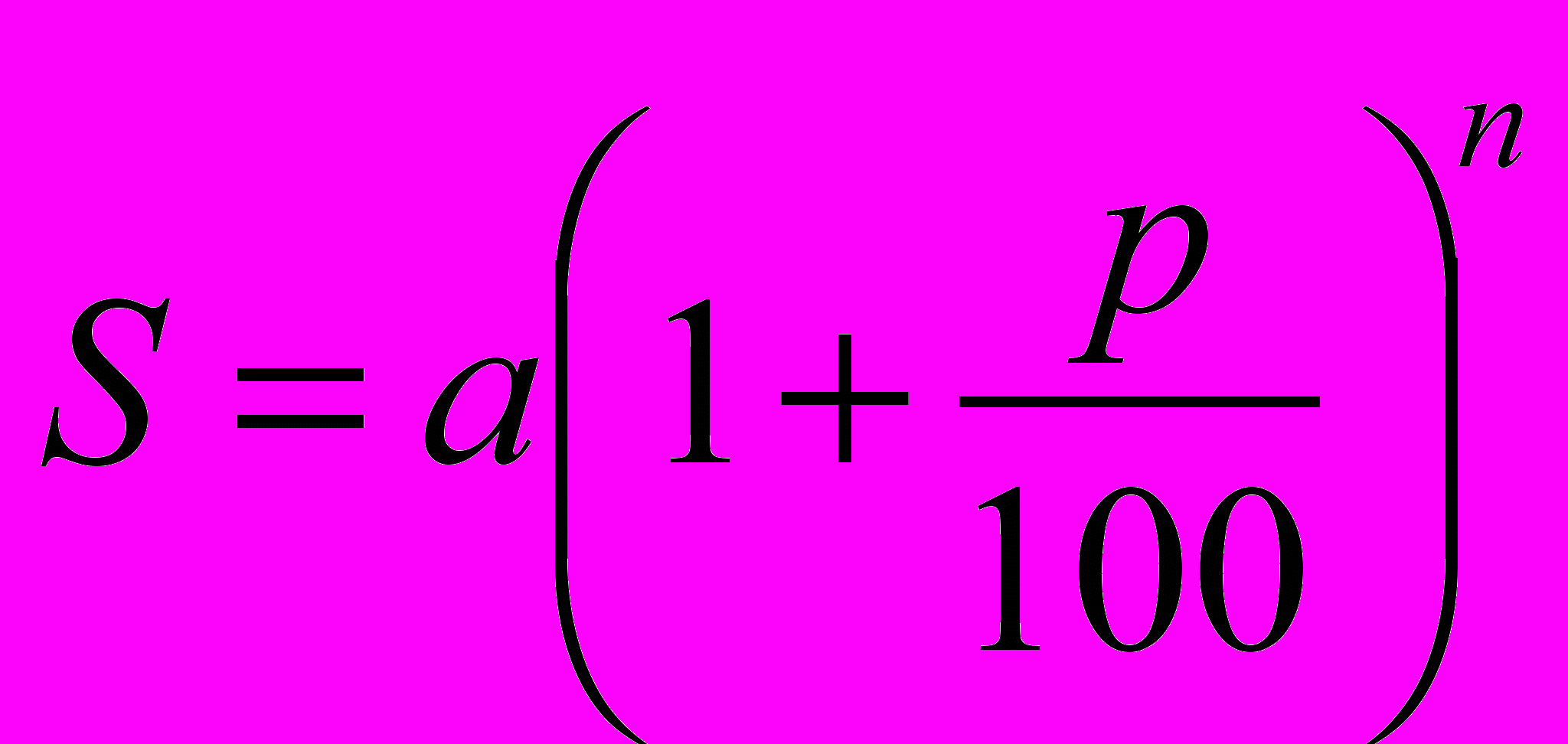
Якщо р — стале, то S є функцією від п. Такі таблиці давали значення показникової функції при різних значеннях основи

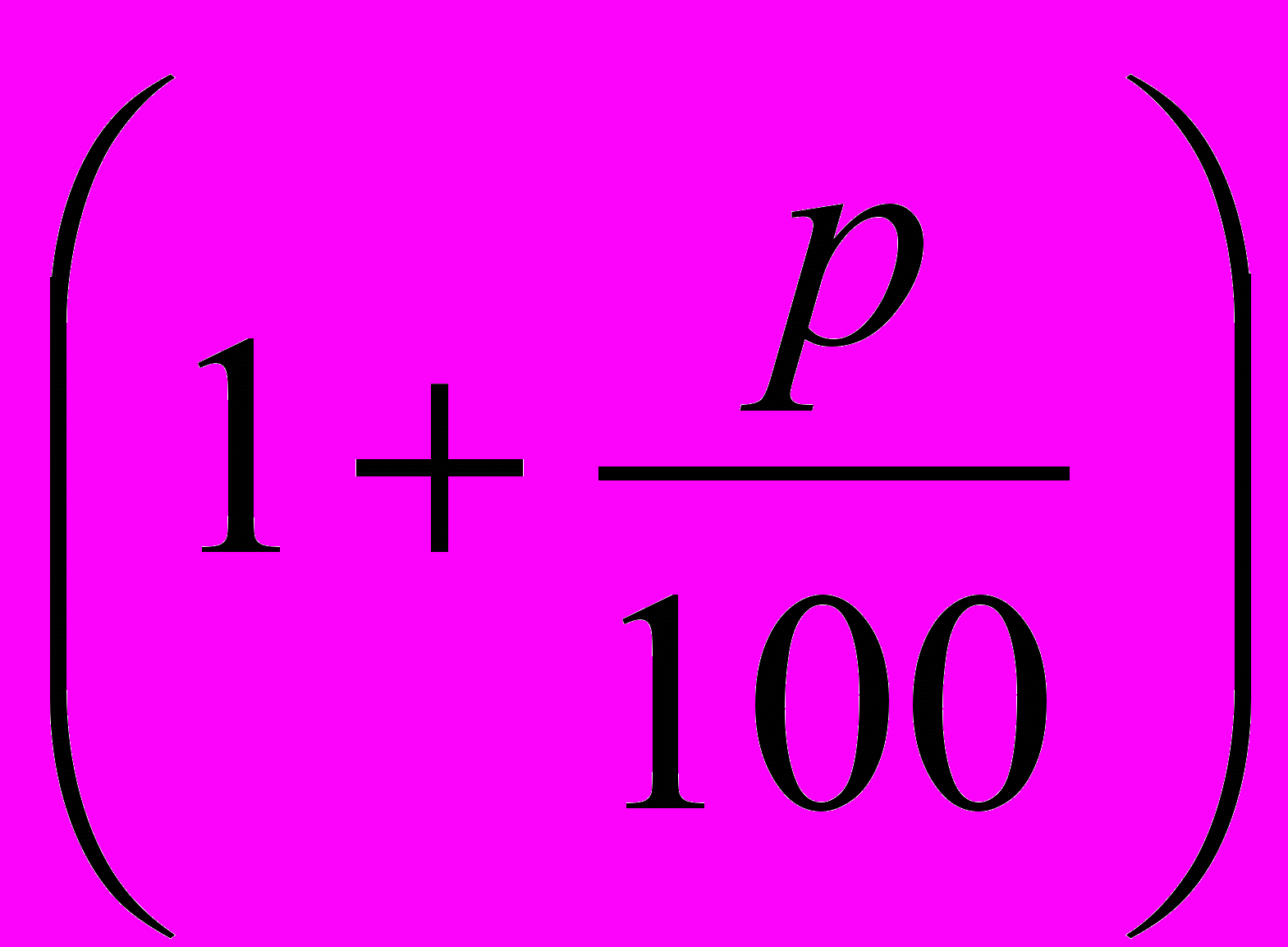і натуральних значеннях п.

Останнє обмеження було не дуже зручним: іноді гроші бралися в борг не на ціле число років, а, наприклад, на 2 чи 6 місяців. Так виникла ідея степеня з дробовим показником. Ця ідея належала ще Архімеду, але вона не була зрозумілою його сучасникам. І лише через 1,5 тисячоліття почали розглядати піднесення чисел до степеня з дробовим показником.

Степінь з ірраціональним показником розглянув Ісаак Ньютон в XVII ст. Після цього Йоганн Бернуллі розглянув степінь зі змінним дійсним показником, тобто ввів показникову функцію.

Учитель: А зараз заслухаємо повідомлення учня про показникову функцію та інформаційний бум. Запишіть: „Показникова функція та інформаційний бум”.

2-й учень. Нині багато говорять про інформаційний бум. Стверджують, що кількість інформації подвоюється кожні десять років. Зобразимо цей процес у вигляді графіка деякої функції.

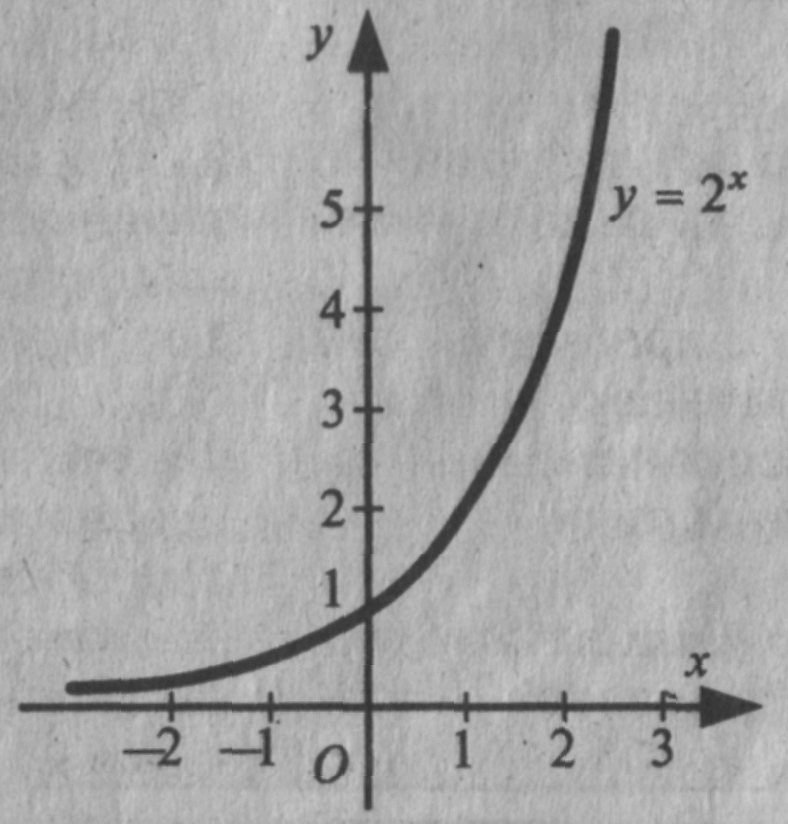
Візьмемо обсяг інформації в деякий початковий рік за 1. Удвічі більший відрізок поставимо над одиничною оцінкою, вважаючи, що оцінка відповідає першому десятку років. Удвічі більший відрізок відповідає другому десятку років, ще вдвічі більший — третьому і т.д. Обрані нами значення аргументу є елементами арифметичної прогресії: 1, 2, З, ... . У той самий час значення функції зростають за законом геометричної професії: 2, 4, 8, ... . Подивимося, який був обсяг інформації до року, прийнятого за початковий. По осі абсцис уліво від початку координат відкладатимемо значення функції в порядку зменшення — у 2 рази менше з кожним кроком. Сполучимо всі побудовані точки плавною лінією. Перед нами графік показникової функції. Головна особливість графіка цієї функції — її крутизна. Показникова функція зустрічається в описі процесів, у яких швидкість зміни величини пропорційна до самої величини.

Учитель. А тепер звернемося до літератури.

3-й учень. У романі Жуля Верна „Матіас Шандор” виведено образ силача Матіфу, який здійснив багато подвигів. Ось один із них.

Готувався спуск на воду корабля. І саме в цей момент до гавані влетіла яхта, яка неминуче врізалася б у корабель, якби з натовпу не вибіг чоловік, який з усієї сили вперся в землю ногами і вчепився в трос, що утримував корабель, щоб затримати спуск. Поблизу стояла гармата. Сміливець швидко накинув на неї трос і з нелюдським зусиллям утримував його 10 секунд, поки трос не лопнув. Але цих 10 секунд було досить, щоб яхта проскочила повз корабель — зіткнення не сталося. Звичайно, ви здогадалися, що сміливий незнайомець — це Матіфу.

Але чи потрібна нелюдська сила, щоб утримати корабель?

Запис у зошиті: „Чи може людина втримати корабель?”

Згадаємо, як відбувається швартування корабля. З нього кидають канат на берег. Людина, що стоїть на пристані, обмотує кілька разів канат навколо стовпа. Сила тертя між канатом і стовпом і утримує судно.

Якщо F₀ — прикладена сила, F— сила, що утримує корабель, то маємо:

1 виток: F= F₀ • k;

2 витки: F= F₀ • к²,

3 витки: F= F₀ • k³,

..................................

x квитків: F= F₀ • k^x;

k залежить від матеріалу, з якого зроблено канат і стовп. Наприклад, коли канат—з конопель, а стовп залізний, то

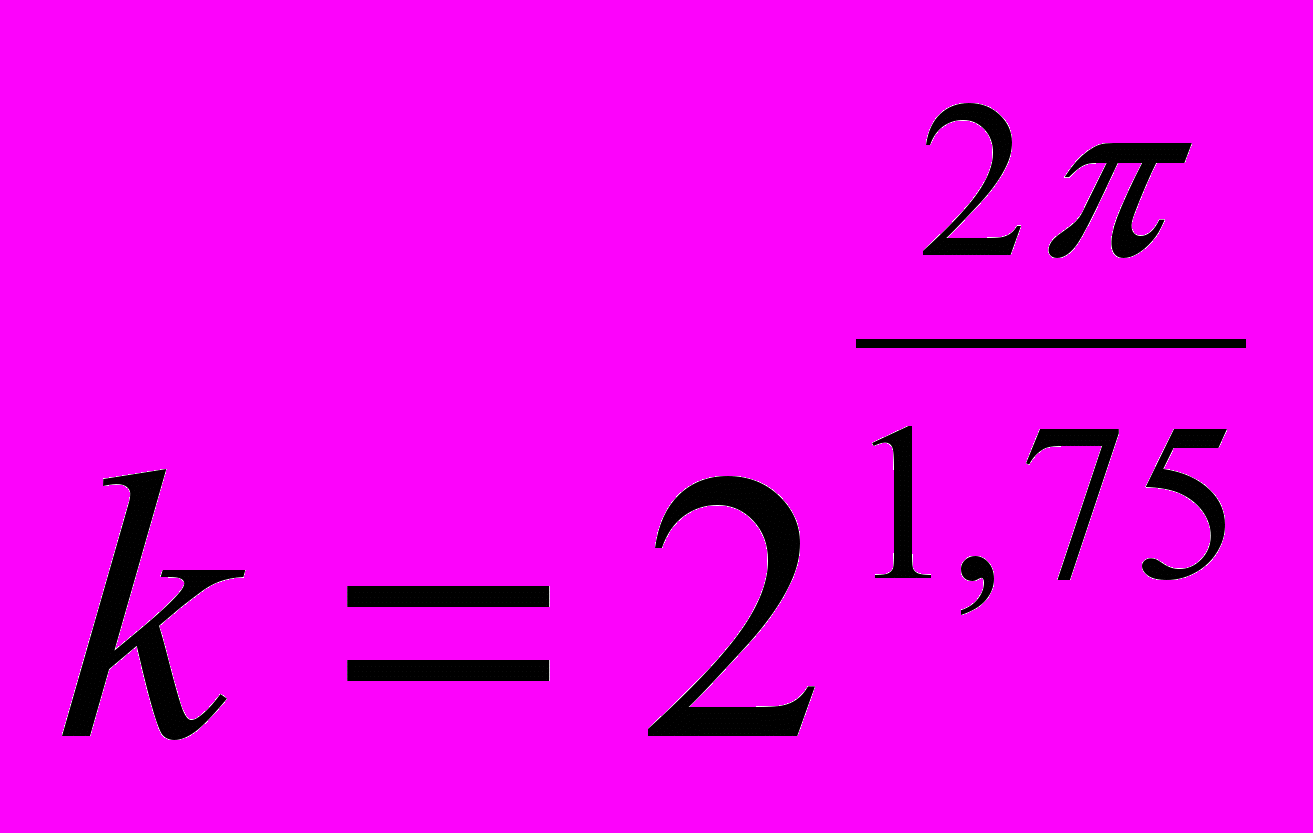. Тобто, обернувши канат 3 рази, силою 22 Н можна утримувати 40 т.

Учитель. До речі, це явище ми використовуємо доволі часто, зав'язуючи шнурки на черевиках, вузлики на мотузку тощо. Оскільки вузол — це мотузок, обвитий навколо іншого мотузка, то він тим міцніший, чим більше разів одна частина мотузка сплітається з другою.

Здавалося б, що спільного між вмиканням і вимиканням струму і падінням з парашутом. Але виявляється, що ці процеси відбуваються за одним законом. Запишіть: „Падіння з парашутом”.

4-й учень. При падінні тіл у безповітряному просторі їх швидкість рівномірно збільшується. Інакше відбувається падіння в повітрі. Вважаємо, що сила опору повітря пропорційна швидкості падіння, тобто 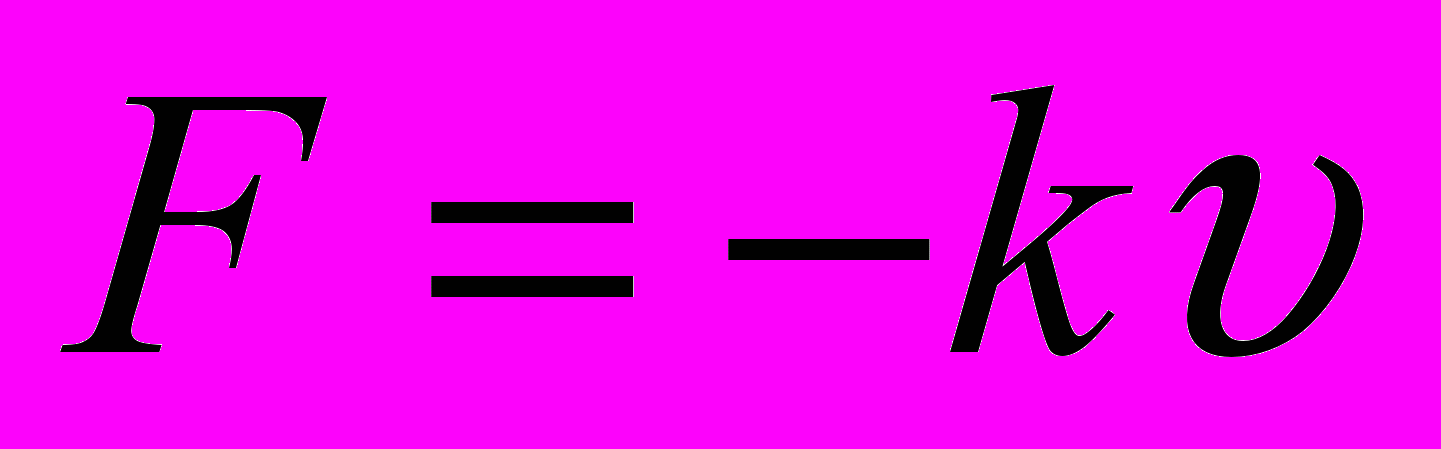(знак „мінус” показує, що напрям сили опору повітря направлений вбік, протилежний напряму падіння). Через t секунд після початку падіння швидкість

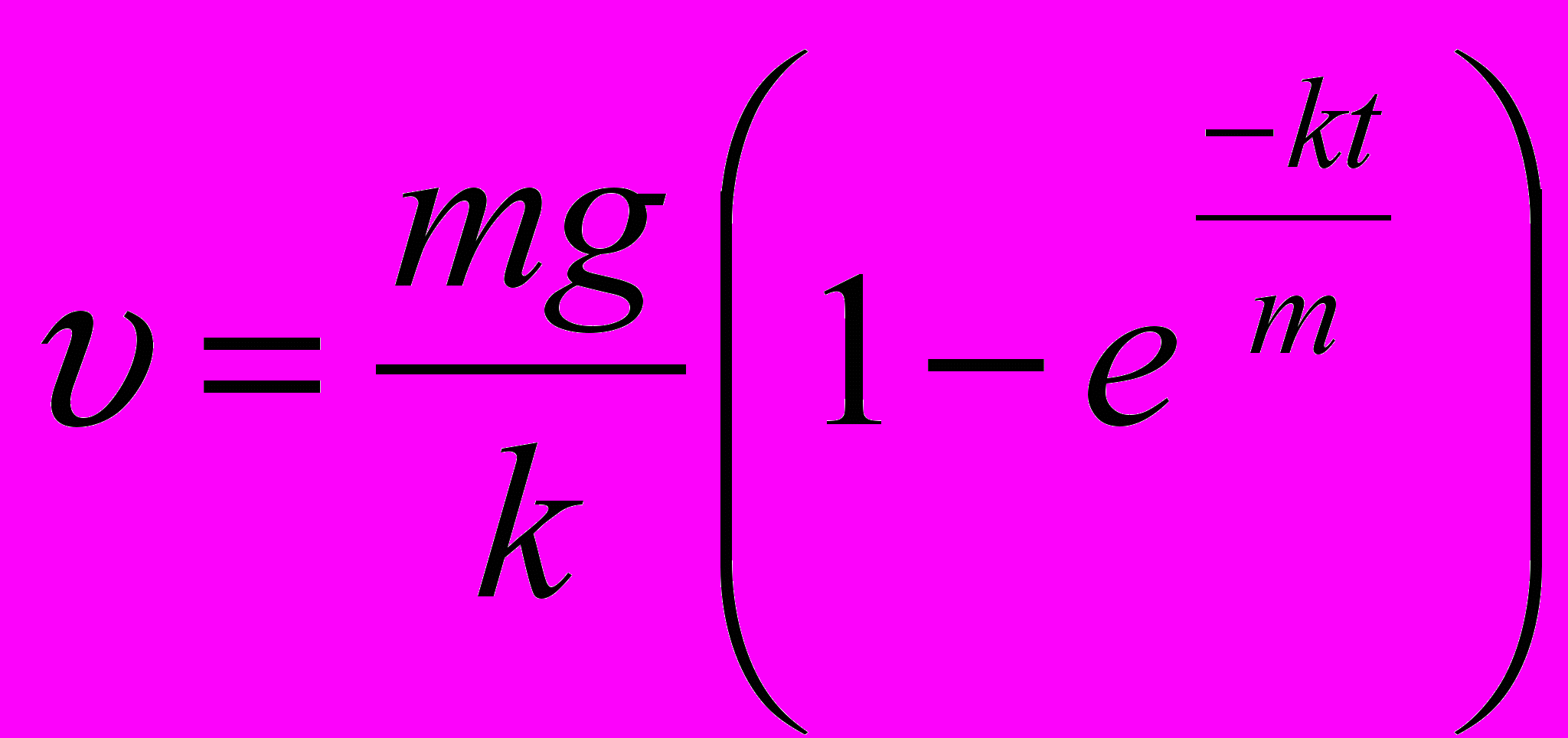, де m – маса парашутиста.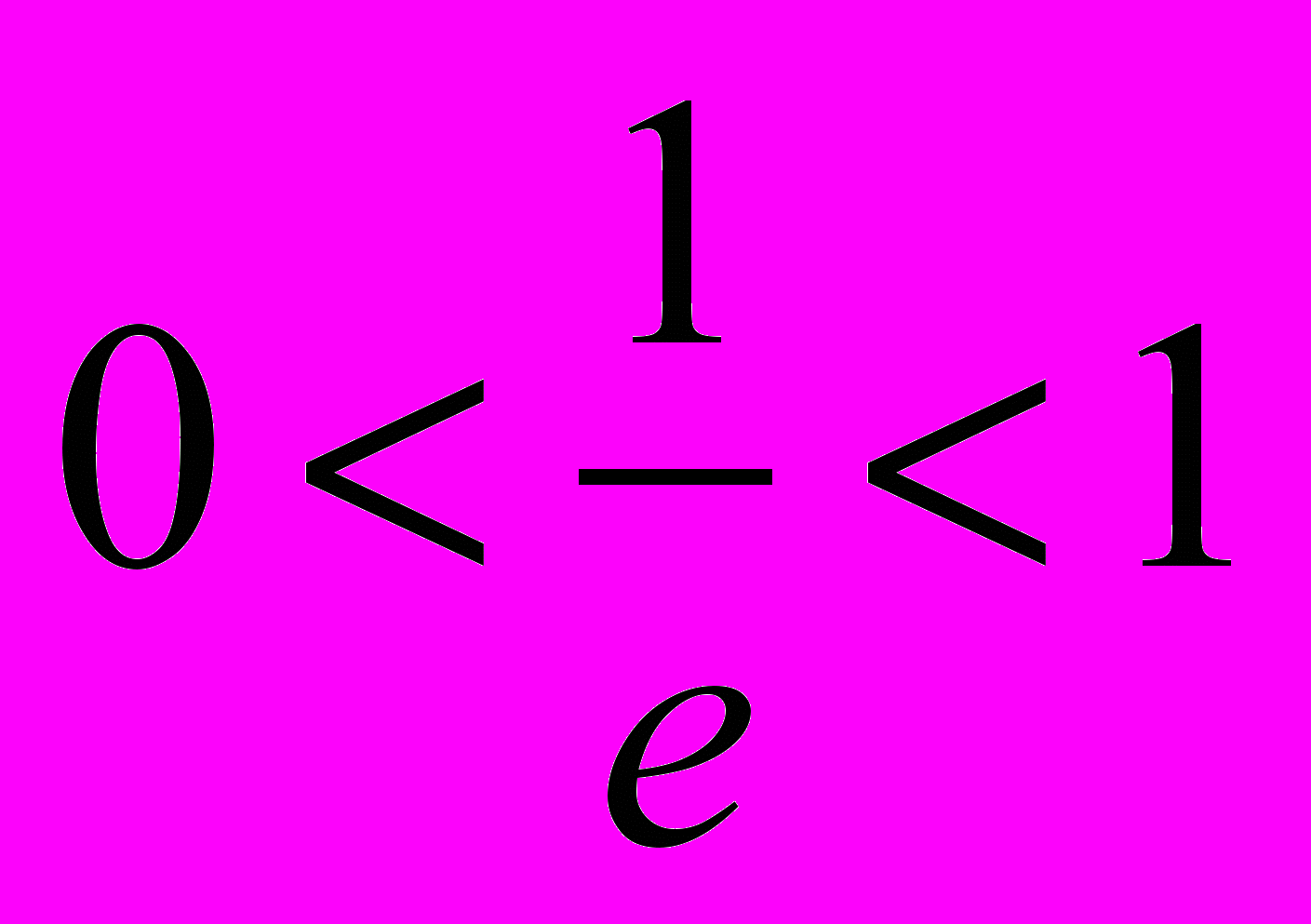

Коли t збільшується, то

зменшується і прямує до 0, вираз у дужках прямує до 1,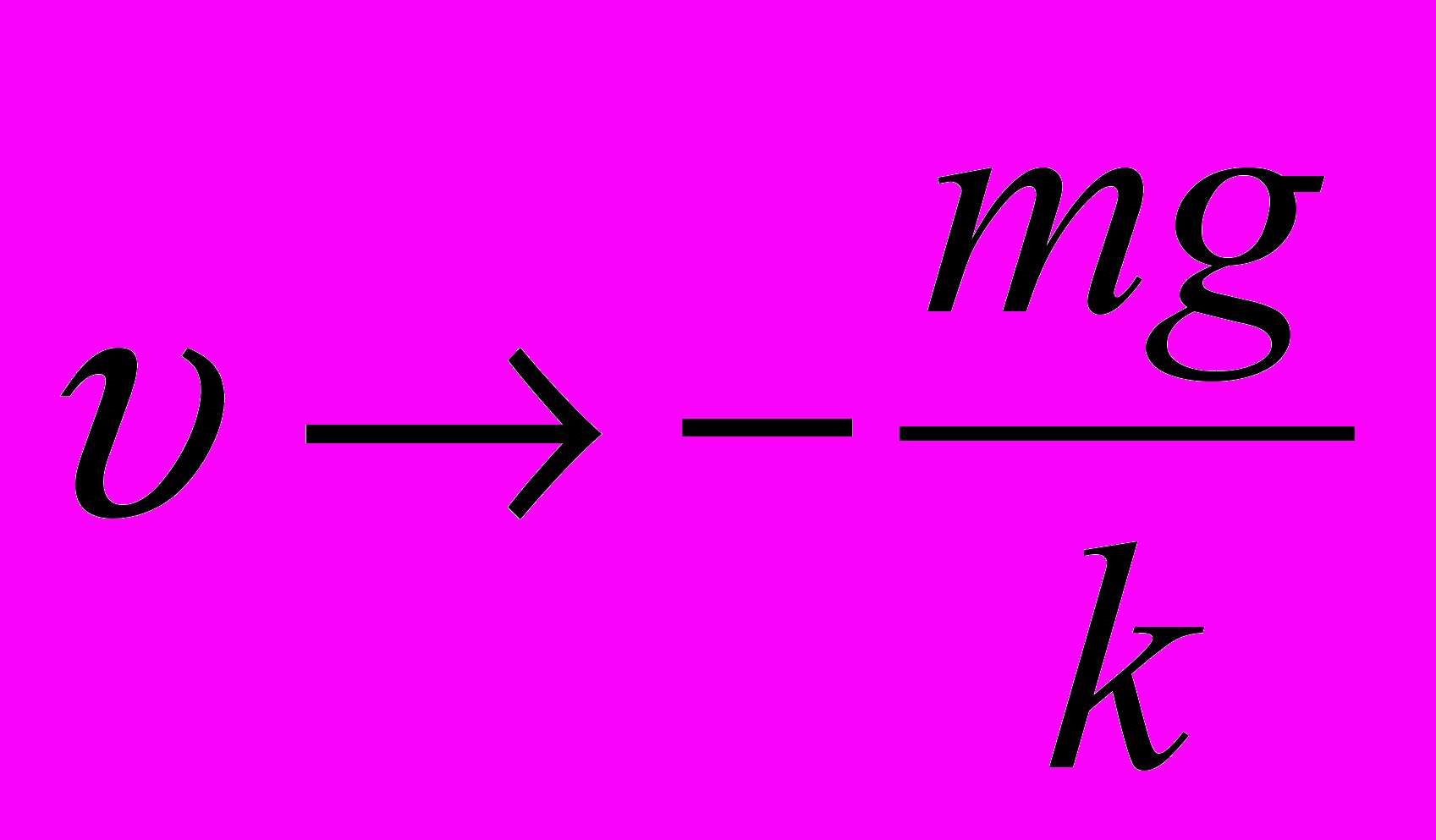

, тобто падіння стане рівномірним;

k залежить від густини повітря, площі поверхні тіла, що падає, тощо.

Наприклад, при падінні з парашутом цей коефіцієнт доволі великий, і тому швидкість приземлення парашутиста порівняно мала — 5 м/с. Ясно, що швидкість падіння пушинки буде меншою, ніж швидкість падіння свинцевої кульки, що має ту саму масу, бо пушинка має більшу площу поверхні і тому більше значення k;. Саме тому пушинка так повільно опускається вниз і так легко підхоплюється потоком повітря. Аристотель у своїх міркуваннях не враховував опору повітря і вважав, що важкі тіла у стільки разів падають швидше за легкі, у скільки разів вони важчі за них. Галілей експериментально заперечив це твердження, кидаючи кулі з похилої Пізанської башти.

Учитель. Останнім часом у засобах масової інформації з'явилося багато повідомлень про цю башту і про проекти запобігання її падіння. Думаю, що всім буде цікаво дізнатися дещо про неї.

5-й учень. Пізанська башта — не окрема споруда, це дзвіниця собору Санта-Марія Маджоре в місті Піза — шедевра світової архітектури, створення його почалося ще в 1063 році. Але нескінченний потік туристів приваблює саме ця «падаюча вежа», її будівництво розпочали в 1174 році майстри з Інсбрука Вільгельм і Баннано. Побудувавши перший поверх висотою 11 метрів і 2 колонадних кільця, Баннано виявив, що дзвіниця відхилилася на 4 см від вертикалі. Майстри припинили роботу і зникли з міста. Лише через 100 років знайшовся сміливець, який наважився продовжити будівництво. Це був архітектор Джованні ді Симоні. Але й він, досягши п'ятого поверху, припинив роботу, бо на той час відхилення від вертикалі становило вже 22 см. Ще через 75 років узявся за роботу архітектор Томазо ді Андре. Він завершив будівництво, піднявши шостий поверх з похилого боку на 11 см і поставивши на восьмому поверсі бронзовий дзвін. І хоч висота башти планувалася 98 м, а остаточна висота була лише 56 м, подолавши 294 сходинки, туристи можуть оглядати всю навколишню місцевість і уявляти, що на цьому місці стояв сам Галілео Галілей і виконував свої досліди, про які ми зараз ведемо з вами мову.

Дослідники вважають, що причиною нахилу башти було використання першими майстрами насосів для відкачування води, які були встановлені в центрі круглої башти, і вода стікала в один бік — у напрямі річки Арно. Останнім часом архітекторів турбує, що кут нахилу Пізанської башти збільшився, тому існує ризик, що вона — не дай Боже! — може завалитися. У 1994 році встановили для підтримки спеціальні свинцеві противаги, в 2001 році провели цілий комплекс профілактичних робіт з укріплення фундаменту, аби зберегти вежу від падіння. Декілька цікавих деталей: у середині 80-х років XX століття відхилення від вертикалі досягло 4,22 м, за останні десятиліття воно збільшується в середньому на 1,2 мм за рік. У 1982 році цей процес практично зупинився, але дзвіниця сама трохи повернулася навколо своєї осі на південний захід. Тому зараз непоодинокі виступи спеціалістів за те, щоб „башту залишити в спокої”, бо будь-яке втручання несе для неї загрозу. „Нехай вона сама себе стабілізує”, — кажуть вони. Пізанська башта важить понад 14 т, і якщо її нахил не буде перевищувати 1 мм на рік, то вона впаде не раніше, ніж через два тисячоліття.

запишіть: 3акон Ціолковського.

6-й учень. Багато складних задач доводиться розв'язувати в теорії міжпланетних подорожей. Однією з них є задача про визначення кількості палива, необхідного для того, щоб надати ракеті швидкість υ₁, потрібну для досягнення Місяця, Венери, Марса або якоїсь іншої планети. Ця кількість залежить від маси m₀ самої ракети (без палива) і від швидкості υ_о, з якою продукти згоряння витікають із сопла ракетного двигуна.

К. Е. Ціолковський розглянув задачу про паливо, нехтуючи опором повітря і притяганням Землі.

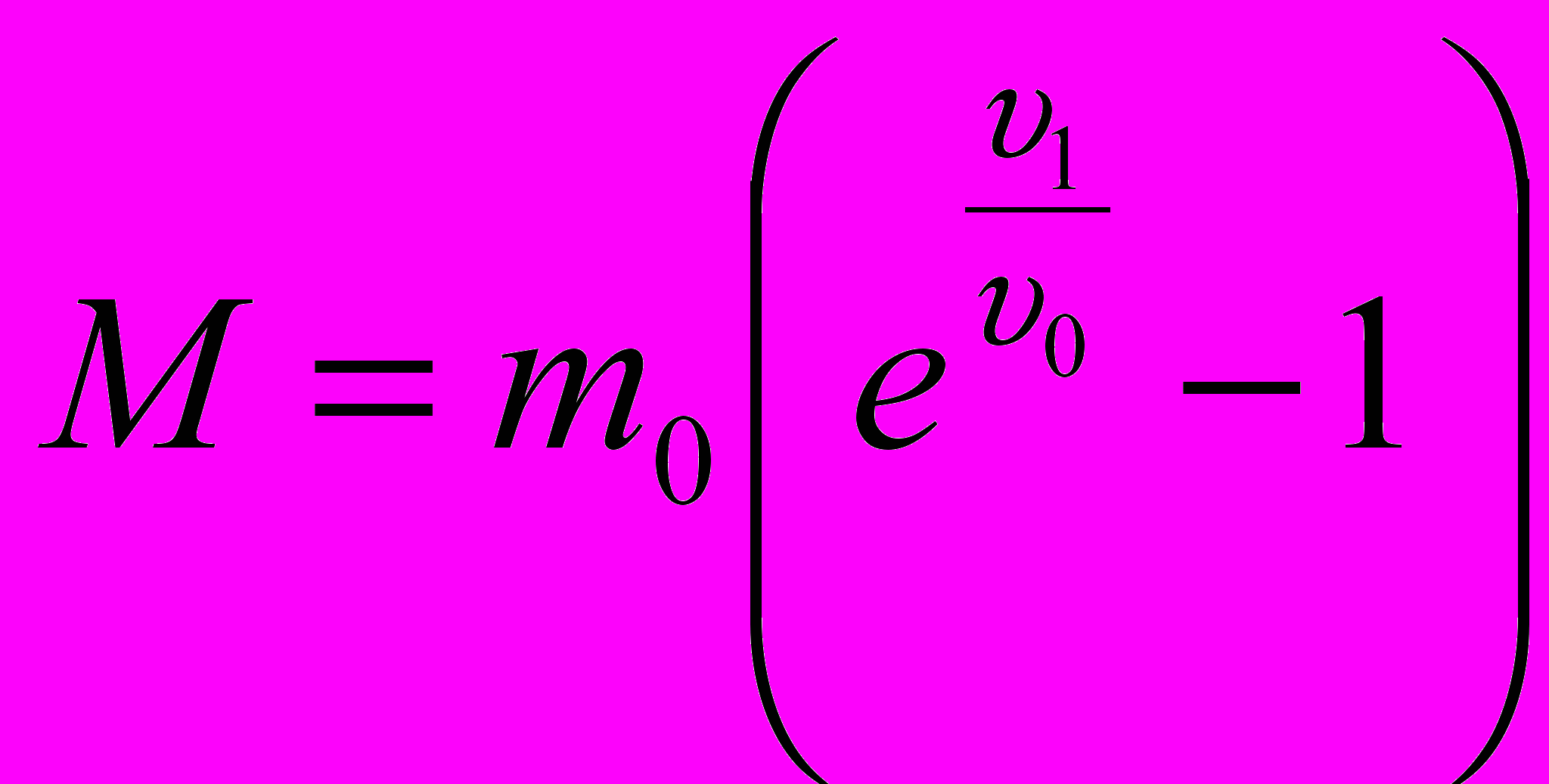
Для ракети масою 1,5 т потрібно за цією формулою 40т пального. Вихід знайшов С. Корольов, запропонувавши багатоступінчасті ракети.

До речі, вам цікаво буде знати, що всі названі четверо генеральних конструкторів ракетно-космічної техніки (С. Корольов, М. Янгель, В. Че-лемей і В. Глушко) — українці, а К. Ціолковський — прямий нащадок Северина Наливайка; його батько, Едуард Ціолковськлй, що мав подвійне прізвище Ціолковський-Наливайко, народився на Рівненщині, у селі Коростятин, мав родичів у Львові.

Учитель. Хотілося б згадати ще про одного видатного українського вченого і винахідника, якого по праву вважають піонером Космосу; за його проектом американці здійснили посадку на Місяць, а траєкторію польоту на Місяць назвали «трасою Кондратюка». Поруч із першою американською ракетою на космодромі на мисі Канаверал споруджено пам'ятник Юрію Кондратюку.

7-учень. Біографія Юрія Васильовича Кондратюка повна трагізму, боротьби і таємниць. Справжнє прізвище вченого — Шаргей. Олександр Гнатович Шаргей народився 21 червня 1897 року. Батьки — земський лікар з Полтави Гнат Бенедиктович і Людмила Львівна Шліпенбах, що веде свою гілку від баронського роду зі Швеції, — померли дуже рано. Дитинство майбутнього вченого пройшло в сім'ї родичів батька в Полтаві, де він закінчив гімназію, потім навчався в Петербурзькому політехнічному інституті. 1917 року його мобілізували в армію і в чині прапорщика відправили на Кавказький фронт. Там Олександра застала революція. Він повертається до Полтави, але рідних не застає. Шаргея мобілізують у білу армію, але він тікає з поїзда. Деякий час працював на станції Бобринськ ремонтником колії, згодом перебирається до Києва, але в серпні 1919 року Київ захопили денікінці і під страхом розстрілу його знову мобілізовують. І знову — втеча з білої армії. Він переховується, працює робітником, пізніше механіком млина і цукрозаводу в Малій Висці на Кіровоградщині, але не припиняє досліджень у галузі космонавтики, пише книгу „Завоювання міжпланетних просторів”.

У ті роки ніхто навіть не міг подумати, що цей обірваний, одягнений в лахміття чоловік — геній, піонер космічної ери. І тільки рідні й близькі, розуміючи всю складність революційного часу, думали над тим, як працівнику млина і кочегарки цукрового заводу відкрити шлях у науку. Вихід був один — змінити біографію.

І коли його мачуха, Олена Петрівна, яка мешкала з дочкою в Києві, на вулиці Саксаганського, дізналася, що в сусідів помер знайомий студент Георгій Васильович Кондратюк, родом з Волині, вона документи покійного передала в Малу Виску. Після довгих роздумів Олександр Гнатович стає на військовий облік як Юрій Васильович Кондратюк, 1900 року народження, син вчителя гімназії з Волині. І з цим прізвищем він входить в історію. У 1925 році рукопис «Про міжпланетні подорожі» автор відправляє до Москви в Головнауку, а в 1929 році виходить книга Ю.В. Кондратюка „Завоювання міжпланетних просторів”.

Він переїжджає до Москви, де працює в галузі промислової вітроенергетики, створює проект вітрової електростанції для Криму на горі Ай-Петрі потужністю 12000 КВт, подібної до якої нема в світі донині. Коли в 1937 році застрелився Серго Орджонікідзе, під егідою якого був цей проект, його закрили. Тоді Кондратюк створює проекти малопотужних вітрових електростанцій. У Підмосков'ї відбулися випробування однієї з них, але все перекреслила війна.

6 липня 1941 року Юрій Кондратюк добровольцем йде в дивізію народного ополчення рядовим роти зв'язку стрілецького полку. Ця дивізія одразу потрапляє на фронт. Довгий час вважалося, що Кондратюк пропав безвісти у першому ж бою 3 жовтня 1941 року, але потім дослідники на основі свідчень очевидців виявили, що він зник наприкінці лютого 1942 року на Орловщині. Ця загадкова загибель породила масу версій. За деякими з них жовтий портфель з рукописами, з якими вчений не розлучався, підібрали німці на полі бою. Його передали німецькому ракетнику Вернеру фон Брауну, творцю ракет „Фау”.

Більше того, писали, що Ю. Кондратюк працював у фон Брауна. Однак ні радянська спец-комісія, ні західні дослідники після війни у вилученій документації німецької ракетної техніки ніяких доказів цих версій не знайшли. Ще є версія, що після війни Кондратюк виїхав у США. Принаймні в Конгресі США, в бібліотеці, зберігаються його рукописи. Як вони туди потрапили, невідомо. Але той самий Вернер фон Браун був, до речі, одним з керівників американської космічної агенції НАСА....

Дехто з дослідників вважає, що Юрій Кондратюк і Вернер фон Браун — одна особа.

Постать Кондратюка продовжує бути загадковою. Він залишив по собі незабутній слід, але від нього на планеті Земля немає бодай могильного горбика...

Його прізвищем названа траса, рухаючись якою ракета з людиною вперше побувала на Місяці, кратер на зворотній стороні Місяця (навіть і тут він у вічній темряві) і вулиця на околиці Києва.

Учитель. Запишіть: „Показникова функція в біології”.

8-й учень. Розглянемо, як зростає популяція бактерій у відповідності з простим життєвим циклом. При цьому час між моментом поділу материнської клітини (народження нової) і моментом, коли вона сама ділиться, називається періодом поділу, або часом генерації.

Нехай число бактерій у культурі становить А₀. За час однієї генерації всі ці А₀ бактерій поділяться навпіл і утвориться 2А₀ бактерій. Через дві генерації їх стане 2 • 2А₀, через три — 2 • 2 • 2А₀ і т.д. Через р генерацій А = 2^Р • А₀.

Нехай час однієї генерації Т, тоді

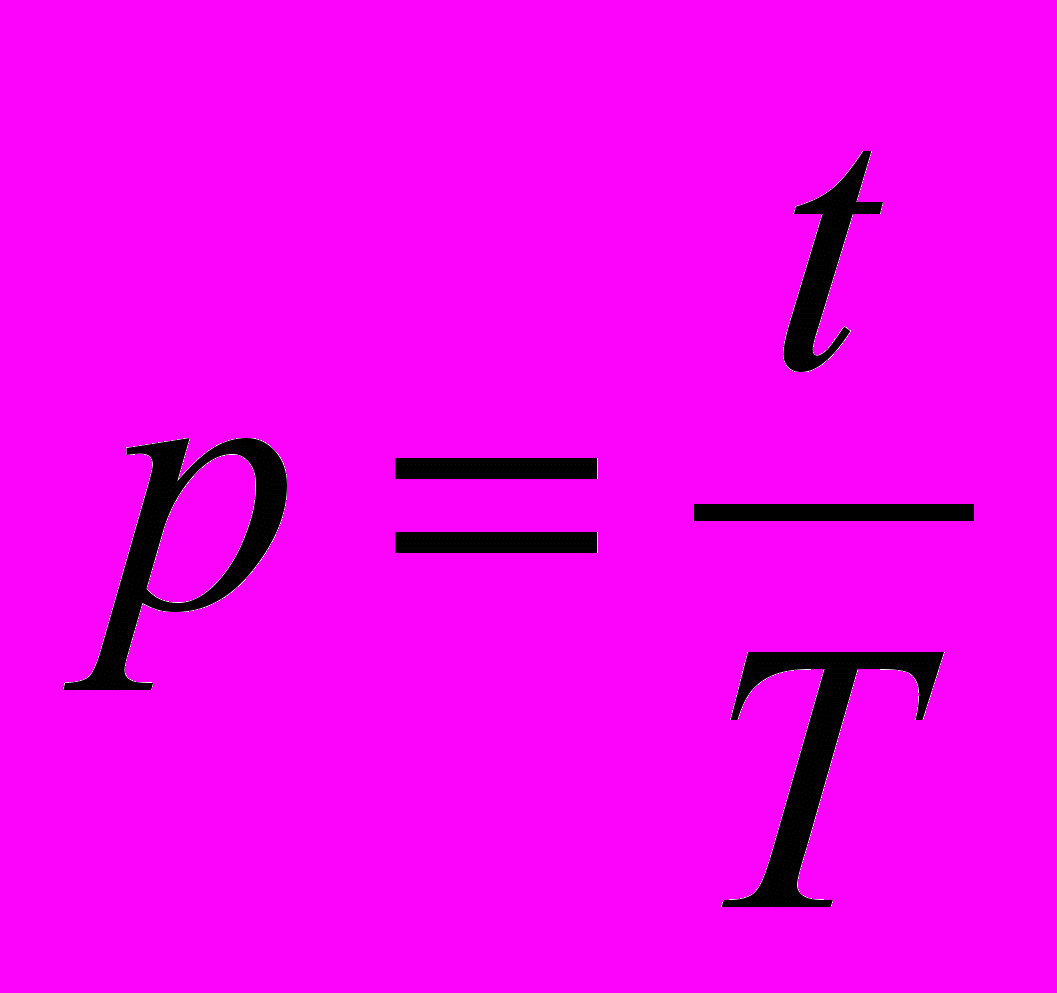, де t час з початку розподілу.

.

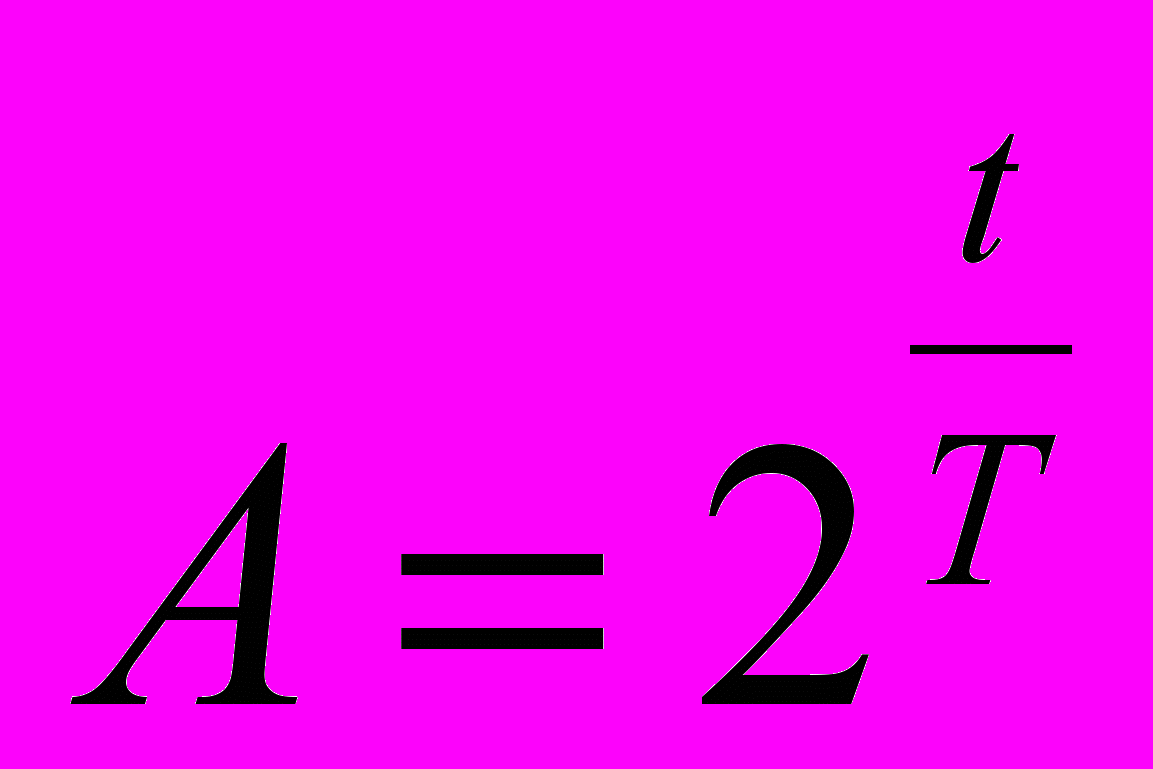Бачимо, що популяція росте за показниковим законом, або, як кажуть, експоненціально (лат. exponense — той, хто показує).

Саме здатність бактерій до швидкого розмноження забезпечує їх кількісну перевагу серед живих форм. Якби не було природних причин, що заважали б вибухам кількості бактерій, сумарна маса яких становила б декілька десятків тисяч тонн, а за дві доби показникового зростання маса однієї бактерії перевищила б у декілька разів масу Земної кулі. Наша планета, проте, не перетворилася на суцільну масу мікробів. І це не тільки тому, що бактерії вичерпують поживні речовини, які підтримують їх зростання, а й тому, що при зростанні вони виділяють велику кількість продуктів, токсичних для них самих.

З відкриттям англійським мікробіологом Флемінгом пеніциліну і народженням нової промисловості знати кількість грибків, утворених у процесі розвитку, стало важливо і можливо при використанні виведеної раніше формули.

Учитель. Розглянемо деякі приклади показникового зростання і спадання в медицині. Запишіть: „Показникова функція в медицині”.

9-учень. Коли людина лякається, в кров виділяється адреналін, який потім руйнується, причому швидкість руйнування пропорційна кількості цієї речовини, що ще залишилася в крові.

При діагностиці хвороб нирок часто визначають здатність нирок виводити з крові радіоактивні ізотопи, причому їх кількість спадає за показниковим законом.

Швидкість зміни кількості ліків у організмі пропорційна їх кількості.

Якщо А(t) — кількість ліків у тілі через час t, R₀ -швидкість надходження ліків до організму (стала — відома величина), k — коефіцієнт пропорційності (стала, що характеризує швидкість виведення ліків з організму), то

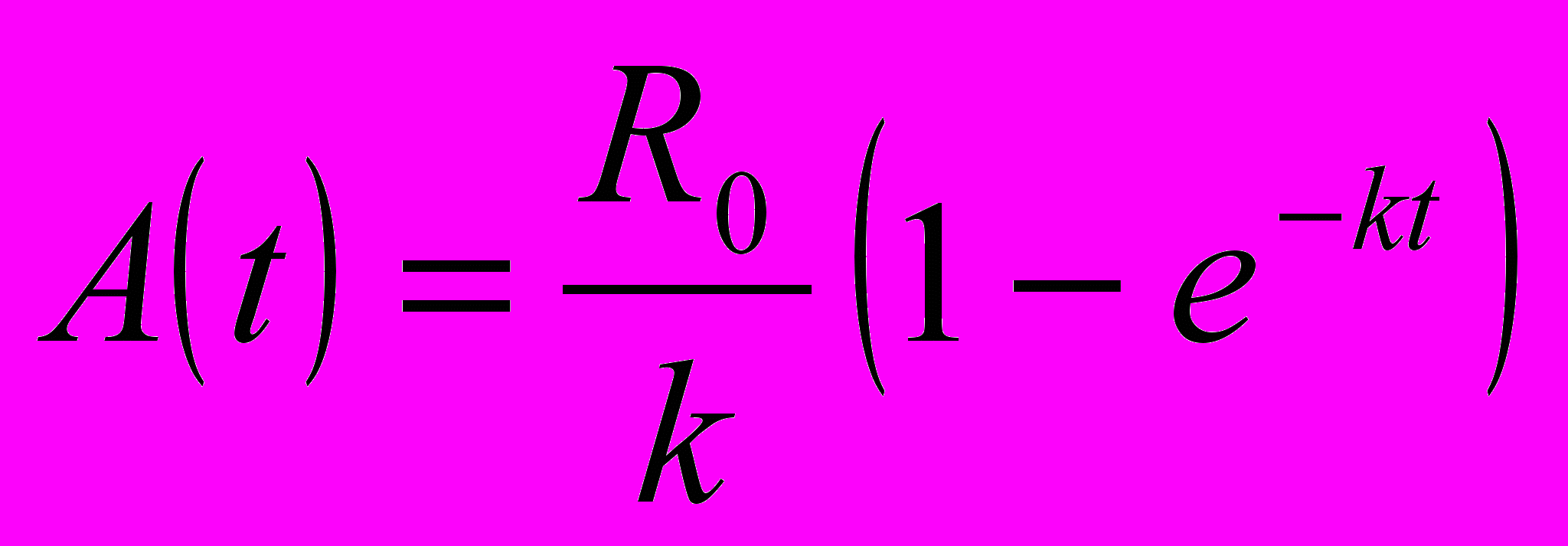
При відновленні концентрації гемоглобіну в крові донора або пораненого за показниковим законом спадає різниця між нормальним вмістом гемоглобіну і наявною кількістю цієї речовини. Як і при радіоактивному розпаді, лікарі розглядають період, за який розпадається або відновлюється половина речовини. Для адреналіну — частки секунди, для ізотопів — хвилини, для гемоглобіну — дні.

Звичайно, показниковий закон виконується дуже приблизно в біологічних системах, бо ми маємо тут справу з дуже складними системами.

Висновки:

На сьогоднішньому семінарі ви ще раз переконалися, що математика — це всеосяжна наука, без знання якої неможливо ні пізнати оточуючий нас світ, ні забезпечити науково-технічний прогрес. Як казав великий Ейнштейн : „Природа – це реалізація найпростіших математичних ідей”.

Література:

1. Виленкин Н. Я. „Функции в природе и технике”, М., „Просвещение”,М.,1978.

2. Детская знциклопедия, т. ІІІ, АПН РСФСР, 1959.

3. Клейнер Г. М., Клейнер Л. М. Математическая и научная картина мира. — К..: Рад. шк., 1984.

4. Петрик М., Баб’юк М. Основи математичного моделювання та застосування математичних методів у наукових дослідженнях. —Тернопіль: Підручники і посібники, 1998.

Література про Ю.В. Кондратюка:

1. Газета „Київснерго” № 4 (56) — 27.02.2003, стаття Володимира Циганенка „Історія. Наш земляк — винахідник вітроенергетики”.

2. Карацуба С. Американські „Аполони” на місячних трасах Ю. В. Кондратюка // Хроніка - 2000 — С. 543—548.

3. Сорока М. Земна ідея Юрія Кондратюка // Урядовий кур'єр — 2002 — 26 січня.

4. Малишевський І. Під чужим ім'ям // Дзеркало тижня — 2002 — 23 лютого — 1 березня.

5. Онишкевич Л. Микола Кибальчич, Юрій Кондратюк і Сергій Корольов — три українських піонери космічних досліджень//Сучасність — 1987 — С. 66.

МЕТОДИЧНА РОЗРОБКА

позакласного заходу

з предмета „Математика”

Вступ

(На сцену виходять Василь та Оксана.)

Василь. Оксанко, а чого це народу стільки зібралося?

Оксана. Сьогодні ж у нас свято знавців математики!

Василь. І що? Усі присутні — знавці?

Оксана.

Не знаю як ти, а я знавець.

Як берусь я до задачі,

То не стогну і не плачу,

І для мене не проблема

Найскладніша теорема!

Василь. А у мене все навпаки.

Як берусь я до задачі,

То над нею зразу плачу.

Як вивчаю аксіому,

То в спині у мене ломить.

Оксана. Так, так!... І коли ж це ти встиг так з математикою «посваритися»?

Василь. (Чухає потилицю.) Навіть не пригадаю... І взагалі, математика — це така нудна наука.

Оксана. Нудна наука? Що ти верзеш, телепню!? Мовою математики говорить весь світ!

Василь. Що? І про кохання теж?

Оксана. А до чого тут кохання?

Василь. А до того... Спробуй освідчитись у коханні мовою х та у...

Оксана. А навіщо мені освідчуватись? Я лише можу сказати, що кохання — це х, тобто невідоме, тому що ніхто достеменно ще не відповів, що це таке.

Василь. Кохання — це первісне поняття! Зрозуміла?

Оксана. Ти хочеш сказати, що це поняття, яке не означають?

Василь. Авжеж! Хіба не зрозуміло?

Оксана. Якщо ти такий розумний, я згодна з тобою подискутувати на цю тему, тільки іншим разом, а зараз нам час припинити балачки, адже всі вже зачекалися.

Ведучий 1

Доброго дня, шановні виступаючі та гості. Щороку у стінах нашого училища проводиться тиждень науки, яку, за словами Ломоносова, «уже для того вчити потрібно,що вона розум у порядок приводить». Геніальний французький учений Блез Паскаль, який у молоді роки пізнавши найвищі моменти натхнення, писав: «Предмет математики настільки серйозний, що не можна втрачати нагоди зробити його трішки цікавішим.»

Ведучий 2

Легендою і джерелом дискусій Піфагор став ще в стародавні часи. У 306р. до н.е. йому, як найрозумнішому з греків, поставили пам'ятник у римському форумі. З тих часів мало що прояснилося в біографії Піфагора, в історичній ролі організованого ним союзу, клубу чи ордену піфагорійців. І досі висуваються нові гіпотези, тлумачення щодо діяльності стародавнього мудреця. Його біографія поповнюється все більшою кількістю деталей, що дає підставу піддавати сумніву їх вірогідність. Різні перекази скоріше ознайомлюють нас з легендами про Піфагора, ніж з його біографією і вченням, але ж і легенди зберігають зерна істини.

Ведучий 3

Отже, давньогрецький математик народився на острові Самос, що біля Іонійського узбережжя Середземного моря, у багатій купецькій сім'ї. Здобув добру освіту, навчався музики, займався гімнастикою, був навіть переможцем на Олімпійських іграх.

За переказами, Піфагор, щоб ознайомитися з мудрістю східних учених, виїхав до Єгипту і нібито прожив там 22 роки. Добре оволодівши всіма науками єгиптян, у тому числі й , математикою, він опинився у Вавилоні, де прожив 12 років і ознайомився з науковими знаннями вавилонських жерців. Перекази при- , писують Піфагору й відвідання Індії. Це ймовірно, бо Іонія та Індія тоді мали торговельні зв'язки.

Повернувшись на батьківщину близько 530 р. до н. е., Піфагор спробував організувати свою філософську школу. Проте з невідомих причин він незабаром залишив Самос і оселився в місті Кротоні грецької колонії на півночі Італії. Тут Піфагору вдалося організувати свою школу, яка діяла майже 30 років і здобула велику популярність, головним чином досягненнями в галузі математики та астрономії. Школа Піфагора, або, як її ще називають, піфагорійський союз, була одночасно і філософською школою, і політичною партією, і релігійним братством. Статут піфагорійського союзу був дуже суворим. Кожний, хто вступав до нього, відмовлявся від особистої власності на користь союзу, зобов'язувався не проливати крові, не вживати м'ясної їжі, берегти таємницю вчення свого вчителя. Членам школи заборонялося навчати інших за винагороду.

Емблемою союзу і розпізнавальним знаком піфагорійців була пентаграма - правильний п'ятикутник. Піфагор вважав пентаграму незвичайною фігурою і дарував її зображення тільки друзям як символ дружби. Діагоналі п'ятикутника утворюють зірку, яку піфагорійці вважали символом здоров'я. Користуючись цією фігурою, вони впізнавали один одного. За переказами, один піфагорієць тяжко захворів на чужині і не зміг перед смертю розрахуватися з чоловіком, який його доглядав. Він запропонував господареві на стіні будинку намалювати зірчастий п'ятикутник. Через кілька років інший піфагорієць, який подорожував цією місцевістю, побачив п'ятикутник, дізнався у господаря про те, що трапилося, і щедро йому віддячив.

Ведучий 4

Піфагор був і маестро формул, і людинознавець. Вчений довгий час жив у племені Гіагонів. Знання, які він отримав там, і досі викликають подив. Таблиці Піфагора містять цікаві відомості про людей. Виявляється, сутність людини проглядається у даті народження, від нас залежить лише, чи зуміємо реалізувати те, чим обдаровані природою, чи зуміємо перебороти обставини.

Ведучий 1

Піфагор був не лише великим математиком, а й філософом. Його вислови актуальні і в наш час.

Роби лише те, що в результаті не засмутить тебе і не примусить каятися.
Не роби ніколи того, чого ти не знаєш. Але навчися усього, що варто знати, і тоді будеш вести спокійне життя.
Не зневажай здоров'ям свого тіла. Доставляй йому вчасно їжу і питво, і вправи, без яких воно бідує.
Привчайся жити просто, без розкоші.
Не закривай очей, коли хочеться спати, не проаналізувавши успіх своїх вчинків за минулий день.
Не порушуй справедливість.
Не сідай на подушку (тобто не зупиняйся на досягнутому).
Не гризи свого серця (тобто не піддавайся меланхолії).
Не поправляй вогонь мечем (тобто не дратуй тих, хто і без того в гніві).
Не приймай під свій дах балакунів і легковажних людей.
Усе впорядковується відповідно до чисел.
Лише не благородна людина здатна в очі хвалити, а поза очі злословити.
Тимчасова невдача краще тимчасової удачі.
Твори велике, не обіцяючи великого.
Живи з людьми так, щоб твої друзі не стали недругами, а недруги стали друзями.

Ведучий 2

За філософськими поглядами Піфагор був ідеалістом, захисником інтересів рабовласницької аристократії. Можливо, в цьому і полягала причина від'їзду його із Самосу. Адже в Іонії дуже великий вплив мали прихильники демократичних поглядів.

За вченням Піфагора, числа становлять містичну суть речей, математичні абстракції таємниче керують світом, встановлюючи у ньому певний порядок. Спроби осмислити світ у числах та числових відношеннях вели до визнання закономірності буття і були пов'язані з вивченням властивостей чисел та геометричних фігур. Числа визнавались не просто виразами закономірного порядку, а й основою матеріального світу. У суспільних питаннях під порядком піфагорійці вбачали панування аристократії. Давньогрецьку демократію вони засуджували як порушення існуючого порядку. Отже, піфагорійська філософія була примітивною спробою обґрунтувати панування рабовласницької аристократії.

Ведучий 3

На перший погляд математика і музика нічого спільного не мають. Але варто лише на мить замислитися і зв'язок відразу відшукається. Музика невідривна від нот, кожна з яких має свою тривалість. Рахуючи тривалість нот «раз — і — два — і — три — і...», відділяємо такти, стежимо за ритмом. А такі назви тривалостей нот, як «половинна», «четвертна», «восьма», «шістнадцята» та інші схиляють до думки про безпосередній зв'язок музики і математики. І це лише найпростіші приклади.

Розглядаючи цей зв'язок глибше, можна помітити, що музика просто

немислима без математики.

Проте найяскравішим прикладом поєднання математики і музики є дослідження Піфагора. Але те, що він був ще й прекрасним музикантом, відомо не всім. Математичний талант і музичне обдарування дали можливість Піфагору першим здогадатися про існування природного звукоряду. Для того щоб це довести, Піфагор побудував напівінструмент — монохорд (дослівно перекладаться, як «однострунний»). Він накреслив шкалу для того, щоб зручно було ділити струну на частини. У результаті досліджень і експериментів з монохордом він отримав математичне пояснення звучання струни, що коливається: струна по-різному звучить залежно від своєї довжини та товщини. Досліди Піфагора лягли в основу науки, яку зараз називають акустикою. Але звукоряд Піфагора не був досконалим. Вдосконалив його Андреас Веркмейстр — знаменитий органіст і теоретик музики. Клавіатура фортепіано поділена на сім частин (октав), у кожній з яких сім білих і п'ять чорних клавіш. Це зараз нам так здається, що інакше і бути не може, але свого часу відкриття Веркмейстра було революцією у музиці. Пізніше Г. Гендель запропонував ускладнення звукового ряду і розрахував звукоряд так, щоб з'явились допоміжні клавіші.

Ще один цікавий факт. Доведено, що діти, які займаються музикою, краще засвоюють математику, зокрема геометрію. Це тому, що навчання музики пов'язане з розумінням, запам'ятовуванням, читанням нотних текстів, які складаються переважно з символів. Навички, сформовані в такий спосіб, полегшують засвоєння математичної символіки. Крім цього, у дітей дуже добре розвинута творча і просторова інтуїція. Під час занять на музичному інструменті кожна рука грає свою партію, а тому працюють обидві півкулі головного мозку одночасно (під час розумових операцій задіяна лише одна півкуля). Тому гра на музичному інструменті безпосередньо перед виконанням домашніх завдань є своєрідним «гімнастичним тренажером» для мозку, підготовкою його до продуктивної праці, а можливо — і для геніальних відкриттів.

Німецький філософ, математик і фізик Г. Лейбніц одного разу влучно сказав, що «музика — несвідома вправа душі в арифметиці».

Давайте ж поринемо у чарівний світ музики.

Звучить пісня про «Піфагорові штани» (на мелодію пісні «Рибка», яку виконує група «Фабрика»),

Хто ж про штани ті не чув,

Що в математиці існують.

Сам Піфагор їх змайстрував,

І досі всіх вони хвилюють.

Приспів

Штанці мої, штанці,
Штанці дуже дивні,
Штанці мої, штанці,
Штанці ексклюзивні!

Штани ті зовсім не прості:
Дизайн в квадратах заховався,

Сума квадратів двох штанин
З квадратом третім порівнявся.

Приспів

Штани ті справді чарівні
Бо ж не старіють і не рвуться.
Ви штаненята одягніть,
У суті їхній розберіться.

Приспів

Сам Піфагор про них сказав,
Що модні завжди вони будуть.
І вік який би не настав,
Штани ці люди не забудуть.

Приспів.

Ведучий 4

З ім'ям Піфагора насамперед асоціюється відома теорема. Німецький поет Г. Вебер у своєму творі писав:
Ввів інший поет вже цю тему

В свій вірш, - але як мені буть?

Прадавню одну теорему

Не можу ніяк я забуть.

Стояв там трикутник, як ментор,

Й один кут прямий в ньому був,

І саме ось цим елементом

Він славу й визнання здобув.

Вродливиці гіпотенузі,

Що стрімко здіймалася ввись,

Два катети, вірнії друзі,

В любові до смерті клялись.

Та їхні обійми їй тісні.

То ж пісню співає вона,

Й геометрам всім у цій пісні

Втіх більше, аніж від вина.

Хто зовсім ще глузду не втратив.

Не може забути про це.

Що сума для а й в квадратів

Квадратові рівна для с!

Ця пісня й холодній медузі

Тепла і жаги додала.

Вже лиш за це гіпотенузі

Й двом катетам честь і хвала!

Ведучий 1

Мабуть, найпопулярнішою з усіх теорем є теорема Піфагора. Причинами такої популярності є простота, краса, значення. Справді, теорема Піфагора проста, але не очевидна. Це поєднання двох суперечностей і надає їй особливої привабливості. Теорема Піфагора має велике значення: вона використовується дуже часто, той факт, що існує близько 500 різних доведень цієї теореми, свідчить про велику кількість її реальних реалізацій.

Відкриття теореми Піфагора оточено ореолом красивих легенд. Переказують, що на честь такого відкриття Піфагор приніс у жертву бика, навіть гекатомбу - жертву із ста биків. А втім, якщо вчений справді був у Вавілонії, він міг довідатися про те, що шумеро-вавілонські математики знали і використовували під час розв'язування задач теорему, названу пізніше його ім'ям, за багато років до народження Піфагора. А щодо жертви богам, то Піфагор був вегетаріанцем і непримиренним противником пролиття крові тварин. Присвоєння цій знаменитій теоремі імені Піфагора свідчить про те, якого значення надавали в той час доведенню математичних тверджень, як високо цінували Піфагора як вченого.

Ведучий 2

Німецький поет XIX століття Адельберт фон Шаміссо теоремі присвятив сонет.

Як істину відкрив - сіять їй вічно.

Вона нам - найнадійніша опора.

Так в древній теоремі Піфагора

Й донині бездоганно все й логічно.

Богам дарунок щедрий був й незвичний

За те, що осяйнуло його вчора:

Чекало сто биків розправа скора,

В віках луна їх рев жертовний звично.

З тих пір бики жахаються й тремтять.

Як істину нову являє прогрес.

Безсилі їй на перешкоді стать,a

Й зливається їх рев в жалобний хор,

Знов древній страх той в генах їх воскрес.

Що в них колись вселив ще Піфагор.

Ведучий 3

Теорема Піфагора має народні назви. У Франції та деяких областях Німеччини в середні віки її називали «ослиним мостом», оскільки доведення теореми було величезною перешкодою, так званим мостом, перейти який могли тільки розумні учні. У математиків арабського Сходу вона одержала назву «теореми нареченої». Річ у тім, що в деяких списках «Начал» Евкліда ця теорема називалася «теоремою німфи» за подібність креслення з метеликом, що грецькою звався німфою. Але цим слоном греки називали деяких богинь, а також наречених. При перекладі арабський перекладач, не звернувши уваги на креслення, переклав слово «німфа» як «наречена», а не «метелик».

І знову у нас музична перерва.

Частівка Гіпотенузи і Братів катетів

Я, весела Гіпотенуза,

А ми, Брати-катети,

Заспіваємо частівки

Вам_у про математику.

Вирішили ми завзято

Геометрію вивчать.

Зараз скажемо відверто:

Не будем байдикувати.

Теорема Піфагора -

Всюди вона з нами:

Чи будинок ми будуєм.

Чи пливем морями.

Любі числа, теореми.

Формули чудові!

Ви професій гарних й різних

Друзі та основа.

Піфагоре - грецький вчений!

Ти довів нам теорему.

Тепер мусимо її

Ми доводити самі.

Теорема, теорема.

Ти звучим, немов поема.

Ну а я. Гіпотенуза,

Є для Катетів, як муза.

Ведучий 4

В часи найдавніші і в нашій вже ері

Творцями була відома

Прекрасна теорема.

Теорема Піфагора - універсальна,

її застосування багатогранне

Теорему Піфагора використовують всюди:

В науці, в мистецтві і в архітектурі.

Землеміри Стародавнього Єгипту для побудови прямого кута чинили так. Мотузок ділили вузлами на 12 рівних частин і в кінці зв'язували. Потім мотузок натягували на землі так, щоб утворився трикутник зі сторонами 3, 4 і 5 поділок. Кут трикутника, протилежний стороні, яка має 5 поділок був прямий . Тому прямокутний трикутник із сторонами 3, 4 і 5 одиниць називають Єгипетським або Піфагоровим.

Цікаво, що саме такі пропорції археологи знаходять у розмірах тесаних плит піраміди Хефрена у Єгипті.

Стародавній спосіб побудови прямих кутів з використанням відношення сторін у єгипетському трикутнику іноді застосовують на будівництві і тепер.

Слово катет грецького походження. Грецьке «катетос» — це висок, перпендикуляр. Цей термін поширився лише у XVIII ст. Термін гіпотенуза походить від грецького слова, яке означає «та, що тйгнеться під чимось», «та, що стягує». Прямокутний трикутник, як і рівно- сторонній, з давніх часів привертав до себе увагу геометрів. І в наш час властивостями прямокутного трикутника дуже часто користуються для знаходження невідомих відстаней, для розв'язування задач теоретичного характеру тощо.

Ведучий 1

Один професор скористався теоремою Піфагора на практиці. Йому запропонували ліжко, що виявилося закоротким для нього. Професор виміряв довжину ліжка а, його ширину в і обчислив з точністю до міліметрів, що його довжина менша а² + в²

Тоді він ліг на ліжко по діагоналі, остаточно впевнений у великій практичній користі теореми Піфагора.

Ведучий 2

Найдавніше наукове відкриття,

Що має назву теореми Піфагора,

Ввійшло у математику й життя,

Як геніальна і міцна опора.

Та стародавні греки й єгиптяни

При виконанні на місцевості робіт,

Не знаючи ще теореми Піфагора,

Робили й будували все як слід.

Уже багато в світі нововведень,

Та теорему Піфагор довів.

Тепер відомо понад 500 доведень,

А він з Самоси вперше це зумів.

Ведучий 3

Важливість теореми Піфагора ілюструє такий цікавий факт.

Наприкінці XIX ст. було відкрито на Марсі «канали», які тривалий час вважалися штучними. Для налагодження зв'язку з марсіянами запропонували на величезному просторі Західносибірської низини побудувати гігантську геометричну фігуру, яка б світилася, — рисунок теореми Піфагора, бо вважали, що ця теорема справедлива скрізь і що жителі будь-якої планети повинні зрозуміти такий сигнал. Передбачали, що, побачивши це зображення, марсіяни зроблять висновок, що на Землі живуть розумні істоти, і дадуть відповідь також мовою математики. Адже математику вважають універсальною мовою Всесвіту!

У 1955 р. в Греції було випущено поштову марку, що ілюструє теорему Піфагора. Дивлячись на неї, можна наочно пересвідчитися в тому, що в прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів.

Ведучий 4

А на завершення─ знову звучить музика.

музичний антракт з «Піснею про кохання та математику» (на мелодію «Біля млина калина»).

Біля школи дівчина, що чекає вона?

Може, вийде хлопчина — і не буде одна.

Він розв'яже задачі, ті задачі складні.

І стоїть, ледь не плаче — і вдень і вночі.

Приспів

І тепер я через нього

Математику вивчаю.

Хай завжди його вона

Та й до мене повертає!

Щоб йому догодити і сподобатись, знов

Теорему йду вчити — от що робить любов!

І тепер всі задачі я розв'язую вмить,

Щоб йому показати, як потрібно любить.

Приспів

Я у долі попрошу, може, милість пошле

І мій милий хлопчина все ж обнімить мене.

Поцілує, пригорне.Прошепочуть уста:

«Ти моя аксіома, неймовірна й проста!»

Приспів

(співають Оксана і Василь)

Ведучий 1

Дякуємо всім за увагу і нехай з нами вічно живе неповторна, довершена краса і сила математики.

Мета: розвивати логічне мислення, в нестандартних ситуаціях, розвивати інтерес до математики, її історії, навчити правильно говорити, відстоювати свою точку зору, а також виховувати цілеспрямованість.

Прилади: карточки з цифрами від 1 до 5, кома

Підготовка: За тиждень до конкурса, вибрати команди, командам дати завдання: підготовитися до конкурсу привітання, до конкурсу капітанів підготувати по три запитання.

На дошці: ”В математиці живе художник, архітектор і навіть поет. ”

Ведучий. Як говорив М. В. Ломоносов „Математику вже тому вчити треба, що вона розум до порядку приводить.»

Доброго дня всім нашим глядачам, учасникам, а також шановним гостям. Геніальний французький учений Блез Паскаль, який в молоді роки пізнав найвищий політ музи, писав: «Предмет математики настільки серйозний, що не можна втрачати момент, зробити його трохи цікавішим».

Конкурси:

1. Привітання.

2. Роздуми.

3. Брейн-ринг.

4. Конкурс капітанів.

5. Конкурс глядачів.

6. Усний рахунок.

7. Хто швидше?

Перш за все познайомимося з нашими командами. Кожна команда повинна була продумати, як вона представить своїх гравців, свою емблему та девіз. Це буде перший конкурс, який називається „Привітання” і вас будуть оцінювати ваші ж однокласники. Та команда, яка отримає більшу кількість оплесків отримає 3 бали.

Ведучий. Ми познайомилися з командами, і зараз проведемо невеличку розминку. Для цього кожній команді необхідно відповісти на запитання, та команда, яка дасть правильну або близьку до правильної відповідь одержує право грати першою. Отже, уважно слухайте запитання:

Коли народився відомий математик Франсуа Вієт?

(У 1540 р.)

Розминка

Ведучий. Кожне питання оцінюється в один бал.

1 команда

1. Які числа називаються простими?

2. Як називаються прямі, що не перетинаються?

3. Кут менший 90º…

4. Як називається чотирикутник, в якого всі сторони паралельні?

5. Число при додаванні до якого сума не змінюється?

6. Як називається частина прямої, що має початок і немає кінця?

7. Як називається відрізок, що сполучає вершину трикутника з серединою протилежної його сторони?

8. Як називається кут, що дорівнює 90º?

9. Як називається трикутник, який має кут 90º?

2 команда

1. Які числа називаються „складеними”?

2. Як називається кут більший за 90º?

3. Як називається чотирикутник, в якого тільки дві сторони

паралельні?

4. Число при множенні на яке добуток не змінюється?

5. Як називаються прямі, що перетинаються під прямим кутом?

6. Як називається частина прямої, яка складається з усіх точок площини і знаходиться між двома іншими?

7. Як називається перпендикуляр, проведений з вершини трикутника до протилежної його сторони?

8. Як називається кут, що дорівнює 180º?

9. Як називається трикутник, в якого дві сторони рівні?

Ведучий. Натупний конкурс „Роздуми”.

Ви уважно слухаєте роздуми немовлят про якийсь математичний об’єкт. Якщо з першого роздуму зрозуміло про який предмет іде мова, відповідаєте і отримуєте 3 бали. Якщо ви незрозуміли або відповіли неправильно, слухаєте другий роздум. Кажете відповідь і отримуєте 2 бали. А якщо ви відповіли на роздум номер три,то отримуєте 1 бал.

1 команда

1. Вони такі незамітні, але дуже потрібні, важливі, в геометрії без них неможливо.

2. Вони зустрічаються не тільки в геометрії, Але і у всіх книжках.

3. Іноді, коли учень не вивчив урок і погано відповідає, вчитель ставить її в журнал і каже: «Підготовишся краще на другий раз, будеш відповідати».

(Крапка)

2 команда

1. Вони бувають великі і маленькі, різного об’єму і одинакової форми, вони оточують нас всюди.

2. Вони… як сік Джафа , як пачка печива, морозиво таке також буває.

3. Майже всі приміщення мають таку форму. І зараз ми знаходимося всередині такого приміщення.

(Паралелепіпед)

Ведучий. Підводимо підсумки за два конкурси і переходимо до третього конкурсу „Брейн-ринг”. Як же оцінюється даний конкурс: кожне запитання оцінюється в один бал.

1. Яка теорема в середині століття називалася „магістр математики”?

(Теорема Піфагора)

2. Якщо квадрат і ромб мають однакові сторони, то площа якої фігури більша?

(Площа квадрата більша, оскільки висота ромба менша за його сторону)

3. Вітрина, актриса, тритон. Яке число об’єднує всі ці слова?

(Три)

4. Що більше cos 40º чи sin 50º?

(cos 40º = sin (90º – 40º) = sin 50º)

5. „Математику вже тому вчити треба, що вона розум до порядку приводить.»

(М. В. Ломоносов)

6. Як знайти центр кола, користуючись тільки косинцем?

(Покласти вершину прямого кута в точку кола так, щоб його сторони перетинали коло. Відмітити ці точки перетину, потім з’єднати їх – дістанемо діаметр кола. Таким самим методом побудувати другий діаметр. Їх точка перетину і буде центром кола)

7. Поясніть переклад і походженння слова «геметрія».

(«Гео» - земля, «метрейн» - виміряти)

8. Кому належать слова «Математика – це політ»?

(В. Чкалов)

9. Яке велике творіння давньогрецької математики лежить в основі підручника геометрії для середньої школи в усіх країнах світу? Хто її автор?

(Лежить відоме «Начало» Евкліда, написані в IV столітті до н. е.)

10. Для перевірки того, що вирізаний кусок має форму квадрата, кравчиня перегинає його по кожній з діагоналей і переконується, що краї обох частинспівпадають. Чи достатня така перевірка?

(Ні, оскільки вказані дії задовільняють також і ромб)

Ведучий. Четвертий конкурс – це „Конкурс капітанів”. Капітан кожної команди почергово задає свої три запитання іншому капітану. Кожне запитання оцінюється в три бали.

Ведучий. П’ятий конкурс – „Конкурс глядачів”. Потрібно скласти „Математичний алфавіт”. Необхідно для кожної букви алфавіта придумати математичний термін. Наприклад: А – алгоритм, Б – бісектриса і т. д. Поки наші глядачі і вболівальники думають над математичним алфавітом, ми проведемо наступний конкурс „Усний рахунок”.

Командам роздаються карточки з цифрами від 1 до 5, кома. Гравцям потрібно стати в тій послідовності, в якій будуть розташовані цифри в результатах даних обчислень.

1 команда

1. 15,15 + 19,1 = … (34,25);

2. 73,8 : 6 = … (12,3);

3. 2,5 * 4 + 135,23 = … (145,23).

2 команда

1. 9,16 + 6,15 = … (25,3);

2. 92,4 : 7 = … (13,2);

3. 124,43 + 0,25 * 4 = … (125,43).

Ведучий. Давайте послухаємо нові алфавіти і підрахуємо бали наших команд.

Останній конкурс – це конкурс „Хто швидше?”. Команди відповідають почергово на запитання. За кожну правильну відповідь 1 бал. Якщо одна команда дала неправильну відповідь хід переходить до суперника. Якщо жодна з команд дала неправильну відповідь наступне запитання оцінюється в 2 бали.

1. Чому дорівнює 2^-2?

(1/4.)

2. Чому дорівнює (-18)⁰?

(1.)

3. Чому дорівнює (-1)³²?

(1.)

4. Якщо x² = 1, то x = …

(-1 або 1.)

5. Графіком функції y = x² є …

(Парабола.)

6. Графік функції y = x² симетричний відносно …

(Осі ординат.)

7. cos(π/2 - α)=…

(sinα.)

8. sin(π/2 + α) =…

(cosα.)

9. Чому дорівнює sin2α?

(2sinαcosα.)

10. Чому дорівнює arcsin1/2?

(π/6.)

11. Чому дорівнює sin(α+β)?

(sinαcosβ+cosαsinβ.)

12. Чиї це слова: «Математику вже тому вчити треба, що вона Розум до порядку приводить.»?

(М. Ломоносов.)

13. Хто з учених-математиків у дуже молодому віці (20 років) загинув на дуелі?

(Е. Галуа.)

14. Хто з великих математиків брав участь у кулачному бою на 58-ій олімпіаді, яка проходила у 548 році до н. е.?

(Піфагор.)

15. Які лінії перетинаються в центрі вписаного кола?

(Бісектриси.)

16. Чому дорівнює сума кутів рівнобедреного трикутника?

(180º.)

17. Тригонометрія – це вчення про…

(Тригонометричні функції.)

18. Що означає розв’зати рівняння?

(Знайти всі його корені або показати, що таких немає.)

19. Які рівняння мають однакові розв’язки?

(Рівносильні.)

20. Основні фігури стереометрії?

(Точка, пряма, площина.)

Ведучий. Підрахуємо бали і визначимо переможця.

Великий російський письменник Л. Толстой сказав, що людину можна оцінювати дробом, знаменник якого – це все те добре , що він думає про себе сам, а чисельник – це все те добре, що про цю людину думають інші. Чим більший чисельник, тим більший самий дріб. Бажаємо всім, щоб щастя додавалося, горе віднімалося, щоб достаток примножувався, а кохання ділилося.

Blog

Урок з математики в групі ртм-21

Содержание