Делаховой Светланы Дмитриевны, учителя математики с. Намцы, 2010 год. Оглавление Оглавление 2 Раздел Эссе 3 Раздел образовательная программа

Вид материала

Образовательная программа

Содержание Раздел 3. Основные результаты деятельности педагога 3.1. Уроки Топологические опыты. Лист Мебиуса. Историческая справка. Таблица учета знаний

Подобный материал:

• Неустроева Николая Ильича п. Чокурдах 2010 г. Оглавление Общие сведения об учителе, 330.97kb.
• Октябрьской Революции Краснознаменной академии (ввиа) имени профессора Н. Е. Жуковского, 1685.68kb.
• Васильевой Василисы Ивановны 2010 г. Оглавление Резюме Эссе образовательная программа, 553.36kb.
• Учебное пособие Оглавление Введение Раздел Социальная психология как наука Раздел Изучение, 933.46kb.
• Шишигина Егора Антоновича директора моу сатагайская средняя общеобразовательная школа, 783.43kb.
• С изменениями от 31 декабря 2002 г Приказом гугпс, 1150.26kb.
• Эмоциональное и познавательное развитие ребенка на музыкальных занятиях, 456.98kb.
• Вахренева Наталия Николаевна, педагог дополнительного образования Г. Кировск 2007 год, 349.5kb.
• Кожич Павел Павлович Минск 2010 г Оглавление Оглавление 2 Применение информационных, 302.47kb.
• Одобрен Советом Республики 22 декабря 2010 года оглавление общая часть раздел I. Основы, 5453.98kb.

Раздел 3. Основные результаты деятельности педагога

3.1. Уроки

Элементы творчества на уроках наглядной геометрии.

Задача учителя – организовать процесс обучения таким образом, чтобы каждое усилие по овладению знаниями протекало в условиях развития познавательных способностей учащихся, формированию у них таких основных приемов умственной деятельности, как анализ, синтез, абстрагирование, обобщение, сравнение. Школьников необходимо учить самостоятельно работать, высказывать и проверять предложения, догадки; уметь делать обобщения изучаемых факторов.

Творческая деятельность учащихся не ограничивается лишь приобретением нового. Работа будет творческой, когда в ней проявляется собственный замысел учащихся, ставятся новые задачи и самостоятельно решаются при помощи приобретаемых знаний.

В развитии творческих способностей учащихся играет предмет наглядной геометрии. Геометрия – это не только раздел математики, школьный предмет – это прежде всего феномен общечеловеческой культуры. Геометрическое мышление в своей основе является разновидностью образного мышления, что функционально присуще правому полушарию головного мозга; по мере развития геометрического мышления возрастает роль левого полушария. Отсюда важность геометрии для детей 8-12 лет с доминирующим развитием правого полушария.

Геометрия располагает огромными возможностями для эмоционального, эстетического, творческого и духовного развития человека.

Важнейшей педагогической проблемой является разрешение противоречия между первичностью пространственных форм с точки зрения процесса познания мира их физическим реализмом и традиционной логикой построения геометрических курсов, развивающихся от плоской к пространственной геометрии.

Одна из задач математики – заинтересовать внимание всех школьников, а для этого необходимо показать математику во всей ее многогранности, акцентируя внимание на интересных занимательных задачах. На мой взгляд, учебник И.Ф. Шаригина, Л.Н. Ерганжиевой «Наглядная геометрия 5-6класс» успешно осуществляет эти задачи. Впервые этот учебник, я взяла в руки в 1995 году после получения премии Сороса и с тех пор не расстаюсь. Методической линией этого курса является организация разнообразной геометрической деятельности: наблюдение, экспериментирование, конструирование, в результате которой учащиеся самостоятельно «добывают» знания и развивают такие качества и умения, как интуиция, воображение, творчество, изобразительные знания. Программа курса соответствует интересам ребенка этого возраста, темы и задания носят игровой характер. Детям очень нравятся игра «Танграм», «Пентамино», задачи со спичками, геометрические головоломки. Они с удовольствием занимаются «Оригами».

Урок наглядной геометрии проводится один раз в неделю. По данному учебнику можно работать в классе с любым уровнем математической подготовки. Учебник способствует развитию творческих способностей, интереса к математике, к выбору технических специальностей учащихся.

Ниже приводится описание открытого урока наглядной геометрии в 6 «а» классе.

Топологические опыты. Лист Мебиуса.


Цель: 1. развитие познавательной и творческой деятельности учащихся.

2. Прививать навыки самостоятельного поиска новых закономерностей, побуждать их любознательность.

3. Развитие культуры коллективного умственного труда.

4. Формирование и развитие интереса учащихся к занятиям математикой, расширять кругозор.

Форма занятия: Дидактическая игра.

Пособия: таблица, карточки, цветные мелки.

Наборы: бумажные ленты, клей, ножницы.

1. Организационный момент.
   

Сегодня мы на уроке познакомимся сравнительно молодой областью геометрии «топологией» и решим топологические задачи.

Для этого мы посетим кафе, название которого узнаем, отгадав этот ребус.

«Топология» (по другому – «геометрия положения») изучает идею непрерывности свойства фигур и тел, которые не меняются при непрерывных ситуациях. Но в кафе действует пропускная система. Пропуск это наше домашнее задание.

№ 10,11,12- заранее подготовить и комментировать решение.

№ 9

2. Знакомство с меню. Занимаем места.
   

Меню.

Салат.

Китайский салат «чи-чао-тю» (хитроумный узор из 7 частей или танграм).

Эксперимент вместе с классом Л.М.

Историческая справка.

Таинственный и знаменитый лист Мебиуса («лента Мебиуса») придумал в 1858 году немецкий геометр Август Фердинанд Мебиус (1790-1860), ученик «короля математиков» Гаусса. Мебиус был первоначально астрономом, как Гаусс и многие другие из тех, кому математика была обязана своим развитием.

В те времена занятия математикой не встречали поддержки, а астрономия довала достаточно денег, чтобы не думать о них, и оставляла время для собственных размышлений. И Мебиус стал одним из крупнейших геометров 19 века. В возрасте 68 лет ему удалось сделать открытие поразительной красоты. Это открытие односторонних поверхностей, одна из которых – лист Мебиуса.

1. берем бумажную ленту и заклеим.
   

А С

АС

ВД

В Д

Получается обыкновенное кольцо

2. 
   

А С

АД

ВС

В Д

Получается лист Мебиуса.


Первом посадим во внутреннюю сторону паука, а на наружную сторону паука и разрешить им показать как угодно, запретив лишь перелезать через края кольца, то паук не сможет поймать мухи. А если их обоих посадить на лист Мебиуса, то муха будет съедена, если, конечно, паук ползает быстрее.


Первые блюда Мебиуса (эксперименты).

1. Суп харчо
   
2. Борщ
   
3. Рассольник
   
   1. Суп харчо: Склейте лист Мебиуса шириной 5 см. Что получится, если разрезать его вдоль, отступив от края сначала на 1 см. затем на 2 см., на 3 см., на 4 см.
      
   2. Борщ: Приготовьте два кольца: одно простое и одно перекрученное. Склейте их так: А затем разрежьте вдоль. Каков результат разрезания?
      
   3. Рассольник: На обеих сторонах листа на равном расстоянии от краев провести по 2 пунктирные линии.
      

Склеить лист Мебиуса. Разрезать по пунктирным линиям. Описать полученный результат. Если лента не перекручена?

Ответы:

3) (Получается 2 кольца. 1 вдвое длиннее первоначальной ленты и вдвое перекручено. Оно получилось из краев ленты. Другое – лист Мебиуса – состоит из центральной части исходного листа Мебиуса.)

1. 3 кольца.
   

1. кольцо – лист Мебиуса – 1 перекрут, ширина 1 см., длина = длине исходного кольца.

2,3 – кольцо с двумя перекрутами, ширина 1 см., длина в 2 раза больше исходного.

2 и 3 кольца сцеплены с 1 кольцами между собой.

Графы.

Вторые блюда:

Котлеты «Дом»

1. Шницель «Конверт»
   
2. Тефтели «Круг»
   

1. 2)
   

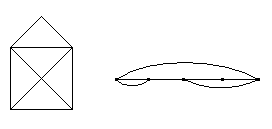
1. Задание: Можно ли вычертить одним росчерком. Графы – это связанные схемы, которые состоят из точек – вершин графа и отрезков (кривых) соединяющих эти точки – ребер. (Подсчитать сколько)
   

Вершины называются четными, если выходит четное число ребер, нечетными, если выходит нечетное число ребер.

Задание: Подсчитать сколько нечетных вершин и предположить какое?

Вывод: Если на графе больше двух нечетных узлов, то ее нельзя нарисовать одним росчерком.


IV. Напиток:

Анаграмма.

Мапрея, чул, резоток, рипетрем, оглу. (прямая, луч, отрезок, угол)

Десерт: Оцумизна (Оценка умений и знаний)

Выставление оценок. Д/з.

Вывод

1. группа: Е. Боря, А. Дуня
   
2. группа: А. Лена, К. Люба
   
3. группа: Д. Дима, В. Женя
   

Литература:

1. Наглядная геометрия 5-6 кл. Шарыгин, Ерганжиева.
   
2. Графы в математике и в жизни. В-6 Заесенок В.П.
   
3. Разрезание квадрата, одним росчерком и другие геометрические задачи. В-8. Сост: Рослова Л.О.
   
4. Необычные задачи математики. Касаткин В.Н.
   
5. Ленинградские математические кружки. С.А. Генкин, И. В. Итенберг, Д. В. Фомин.
   

Результаты опытов

Кол-во перекручиваний		После	разреза		Является ли Мебиусом
	Кол-во колец	Длина колец	Число перекручиваний	Ширина колец

Таблица учета знаний

№ п/п	Фамилия и имя	дом. задание					Кафе «Топология»
		9	10	11	12	Салат	1 блюдо	2 блюдо	Напиток	Десерт оценка

Учитель математики НУГ Делахова С.Д.