Комплекс учебно-методических материалов нижний Новгород 2010 Печатается по решению редакционно-издательского совета гоу впо нглу специальность: Менеджмент организации

Вид материала

Содержание

Формы организации логистических систем
3. Описание практических занятий
Оптимизация распределения грузопотоков
Случай «вырожденный»

Подобный материал:

1 2 3 4 5 6 7 8 9

Рисунок 2.14. Пример конфликтных затрат

Обеспечение уровня сервиса потребителей

Выходом логистической системы является ее эффективность или результативность. Под эффективностью логистической системы понимается степень обеспечения уровня сервиса при обслуживании потребительского рынка производственно-сбытовой системой.

Существует два варианта цепочки взаимодействия "поставщик-потребитель" в ПСС: во-первых, это поставка производственной системой готовой продукции конечному потребителю, и, во-вторых, это поставка сырья, материалов и комплектующих изделий с места их возникновение до предприятия-потребителя. В том и другом случае понятие сервиса поставки должно определяться однозначно.

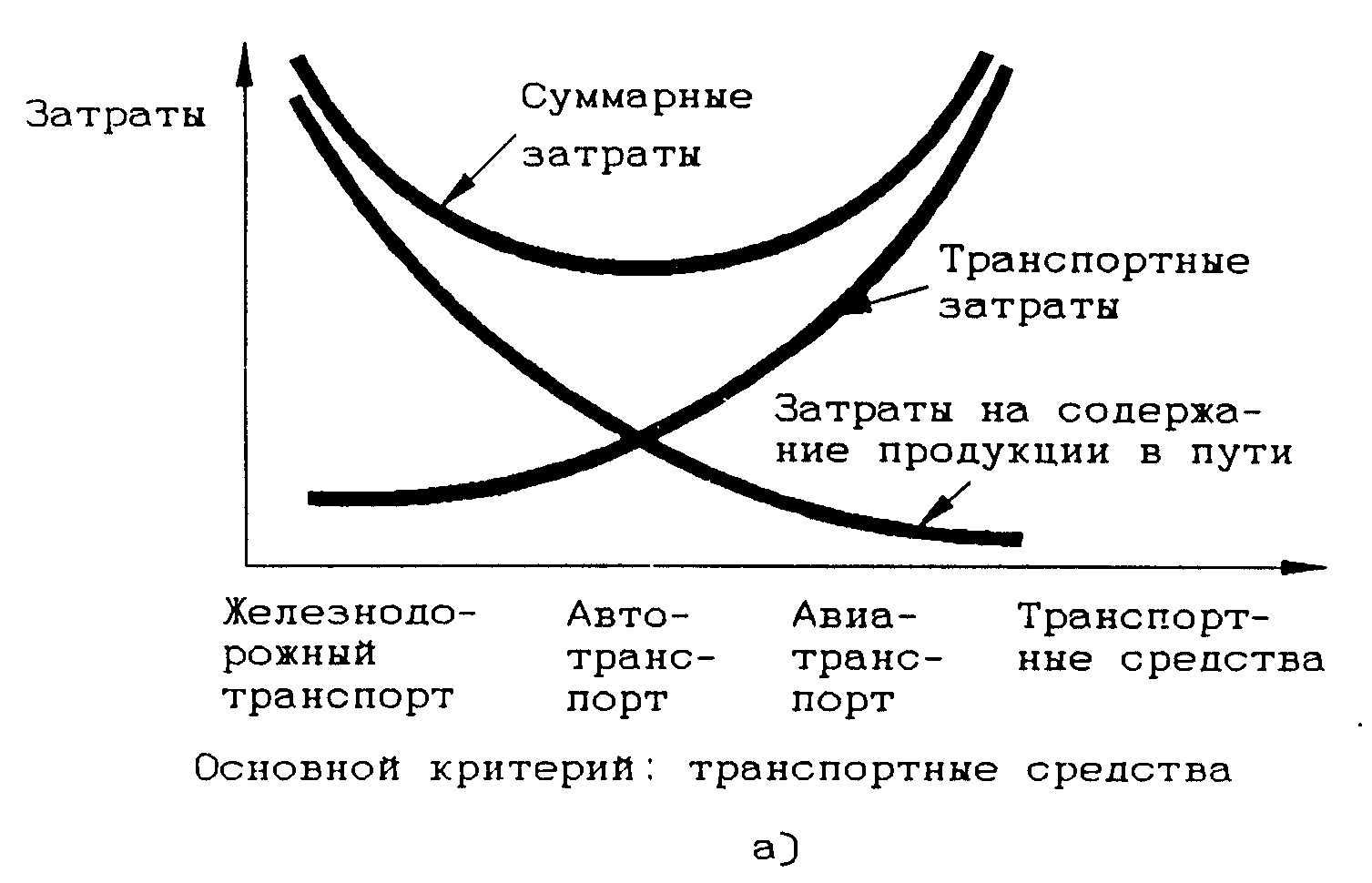
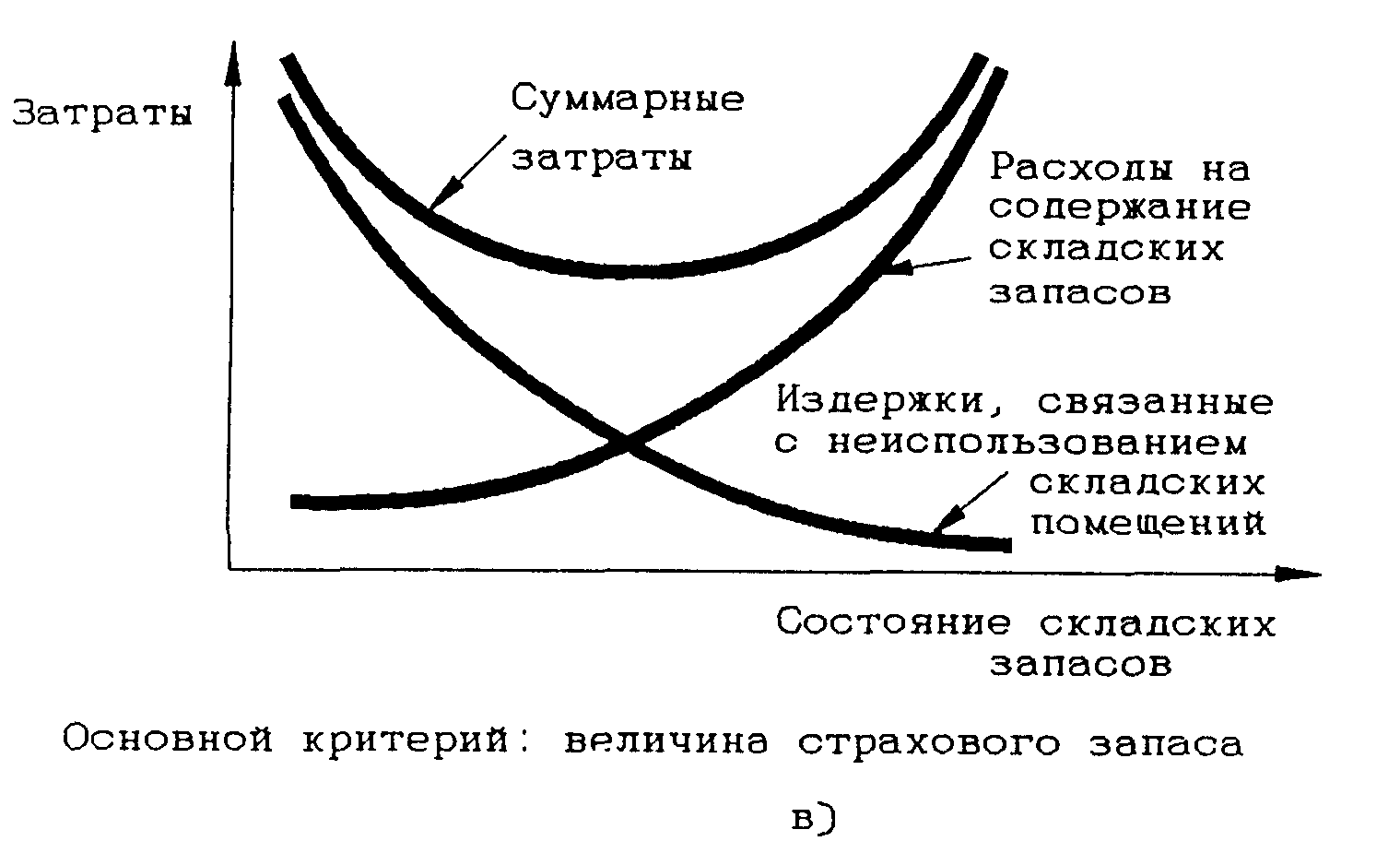
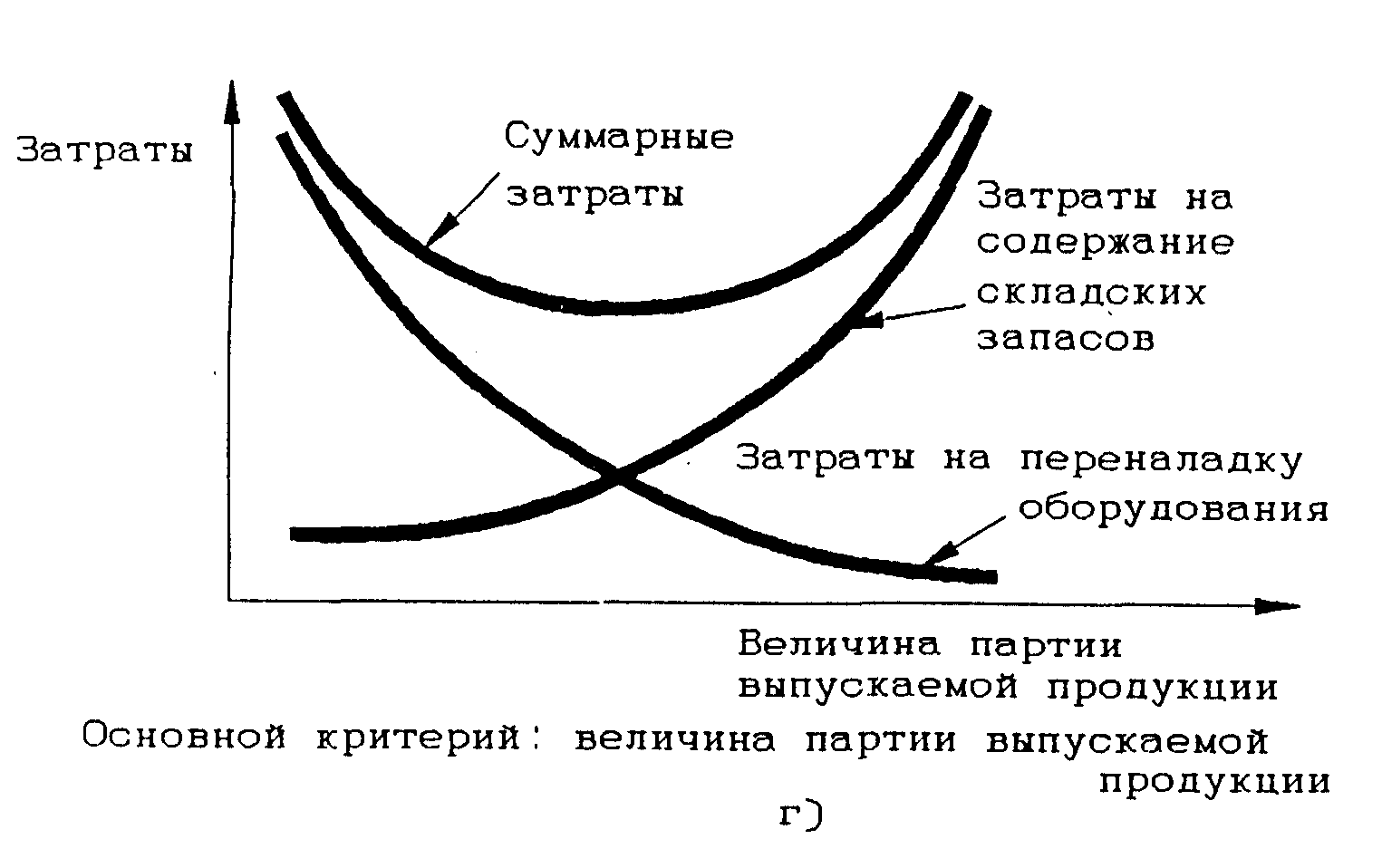
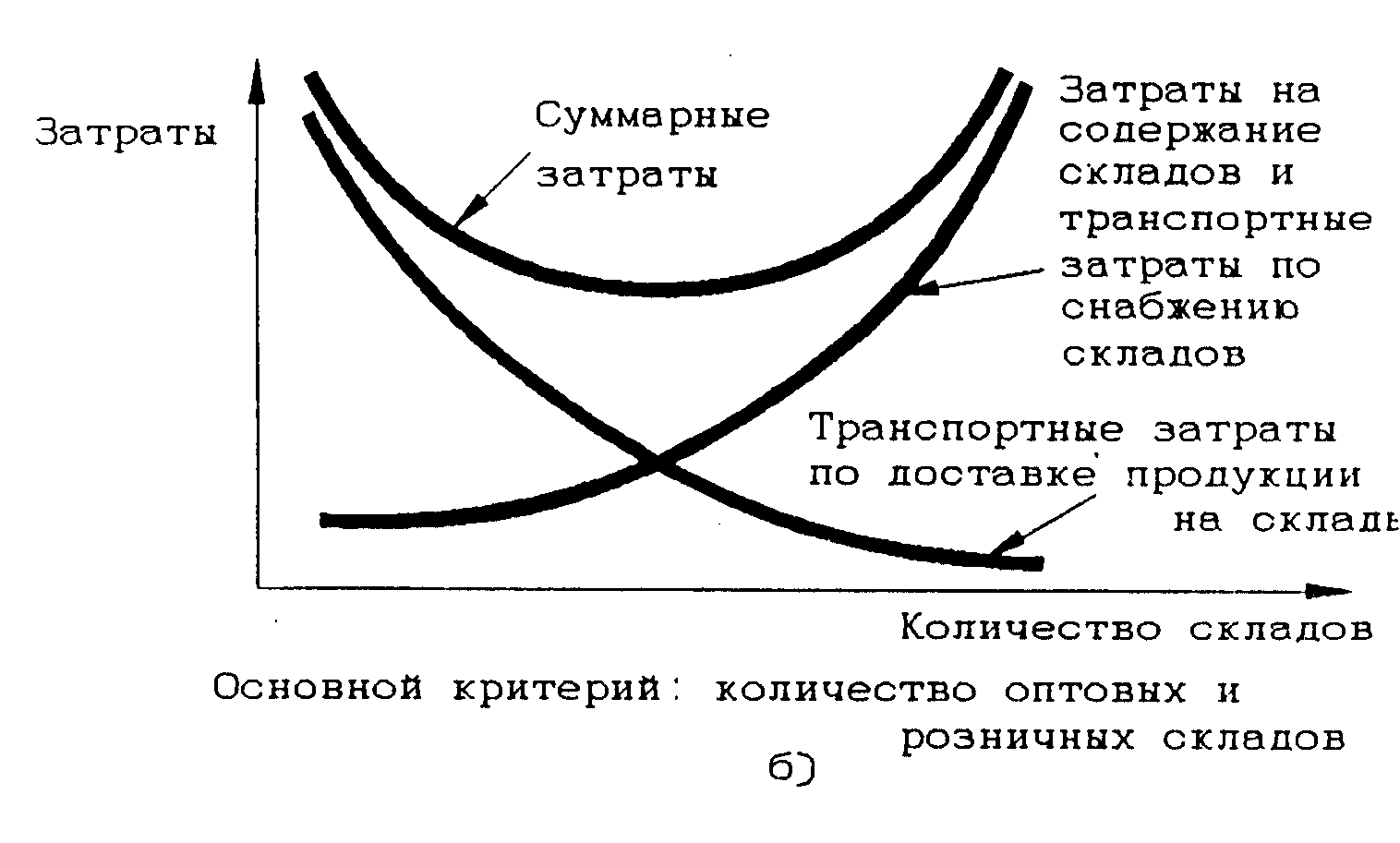
Рисунок 2.15. Примеры стыковки конфликтующих затрат в логистической подсистеме

Если рассмотреть логистический процесс с точки зрения изменения логистических объектов, то можно определить выходные характеристики, которые должна обеспечить логистическая система:

точность времени поставки;
точность места поставки;
точность номенклатуры и ассортимента поставляемого груза;
точность количественных и качественных показателей поставляемого груза.

Таким образом, сервис поставок включает четыре основных компонента:

время поставок;
надежность поставок;
надежность закупок товаров у поставщиков;
гибкость поставок.

Под временем поставок понимается выполнение требуемых периодов поставки продукции с момента получения ПСС заявки на поставку продукции до момента получения потребителем заказа. В случае, если заявка превышает производственные мощности предприятия при его нормальном режиме работы, то для выполнения потребительского спроса используется как запас готовой продукции, так и резервы мощностей для дополнительного выпуска продукции.

Большую важность для потребителей имеет надежность поставок. Этим понятием определяется вероятность точности исполнения заказа, что оказывает влияние на объемы хранимой продукции на складах потребителей: чем вероятность точности выполнения заказа меньше, тем потребитель должен держать на складах большие объемы продукции, что сказывается на эффективности работы их логистической системы.

В свою очередь, надежность поставок зависит от стабильности и четкости производственного процесса, а также от готовности поставщиков к поставкам. Готовность поставщиков к поставкам может определяться следующими показателями:

1. Показатели, связанные с количеством заказов:

1.1. Показатели степени готовности поставки (относительная готовность поставок)

СГП_{1 =} ^{количество выполненных заказов}_*100% (2.2)

^{количество полученных заказов}

СГП₂₌ ^{количество выполненных заказов за счет складских запасов}_*100% (2.3)

^{количество выполненных заказов}

СГП₃₌ ^{количество выполненных заказов за счет складских запасов}_*100% (2.4)

^{количество полученных заказов}

1.2. Показатель абсолютной готовности поставок.

АГП ₌ ^{количество не выполненных заказов}_*100% (2.5)

^{количество полученных заказов}

1.3. Количество невыполненных заказов за определенный период времени.

1.4. Количество отложенных заказов за определенный период времени.

1.5. Количество невыполненных и отложенных заказов за определенный период времени.

2. Показатели, связанные с величиной спроса.

2.1. Показатель степени готовности поставки.

СГП₌ ^{поставленное количество продукции}_*100% (2.6)

^{требуемое количество продукции}

Показатели 2.2 - 2.5 по смыслу аналогичны показателям 1.2 - 1.5.

3. Показатели, связанные с временным периодом.

3.1. Показатели готовности поставок.

ГП₁₌ ^{период времени без невыполненных и отложенных заказов}_*100% (2.7)

^{весь период времени}

ГП₂₌ ^{период времени обеспечения поставок за счет запасов на складе}_*100% (2.8)

^{весь период времени}

4. Показатели, связанные с просроченными поставками.

П₁₌ ^{период запаздывания поставок}_*100% (2.9)

^{количество полученных заказов}

П₂₌ ⁽^^{периодов запаздывания по всей продукции)*(заказанное кол-во продукции)}_*100% ^{количество поставленной продукции}

(2.10)

Следующий показатель: надежность закупок товаров у поставщиков охватывает два фактора:

точность поставок;
состояние поставок.

Под понятием точность поставок понимается поставка продукции требуемого ассортимента в определенном количестве. В случае, если поставщик не в состоянии обеспечить поставку требуемого ассортимента продукции, он должен предложить замену отсутствующей продукции, и лишь в случае отсутствия заменителя предложить другую продукцию. В противном случае у поставщика есть большая вероятность потери потребителя. Для удобства работы с потребителем на предприятиях используются экспертные системы, являющиеся частью логистической системы.

Фактор состояния поставок определяет качество и сохранность поставляемой продукции. В большей степени он зависит от упаковки и транспортных средств.

Показатель гибкости поставок определяет логистическую систему поставщиков с точки зрения удовлетворения особых запасов со стороны потребителя или возможности стыковки логистических подсистем потребителей и поставщиков. Гибкость поставок в значительной степени зависит от следующих трех факторов:

метод получения заказа;

метод поставок;
информация, поступающая от потребителей.

Метод получения заказа определяет регламент работы поставщиков по приему заказов на поставку продукции, а также время реагирования на полученный заказ о возможности его выполнения в заданные сроки. Этот показатель имеет прямую зависимость от уровня и качества информационно-логистической системы.

Таким образом, уровень качества обеспечения сервиса потребителей стоит в прямой зависимости от затрат на создание и функционирование логистической системы. Следует отметить, что в любой логистической системе существует стратегический потенциал, который может улучшить функционирование системы.

Во-первых, это мероприятия по уменьшению затрат. К ним относятся:

1) рационализация инвестиций:

автоматизация материальных потоков;
автоматизация обработки информации и системы управления;

2) мероприятия по сокращению затрат:

уменьшение запасов,-
избежание избыточности;
оптимизация использования ресурсов.

Во-вторых, это мероприятия по улучшению работы логистической системы:

1) инвестиции:

в производственные подразделения;

- в информационно-логистические системы для увеличения четкости в управлении;

2) оптимизация структуры:

увеличение уровня сервиса;
повешение гибкости системы;
улучшение параметров поставок.

Эффективность логистической системы.

В задачу проектирования логистической системы входит, помимо разработки оптимального технологического маршрута, разработка оптимальной сети снабжения, размещение предприятий, пропускник и производственных мощностей, центров распределения, рыночных регионов, а также транспортных моделей, размеров партий и ожидаемых объемов запасов.

Логистическая система должна обеспечить оптимальный баланс между затратами и уровнем обслуживания заказчика. Если в качестве входных данных при разработке и функционировании логистической системы принимаются затраты на систему в целом, то выходным показателем является тот уровень сервиса, который обеспечивается в процессе функционирования системы. Показатель обеспечения уровня сервиса является одним из параметров, влияющих на доход предприятия. Причем, учитывая составляющие, которые определяют понятие сервиса, можно утверждать, что чем меньше рассогласование между требуемым и фактическим уровнем сервиса, тем эффективнее работа логистической системы. При атом не следует забывать, что естественное состояние любой системы -- это минимизация затрат. Таким образом, получается задача по определению фактического уровня U_ф сервиса в постановке нелинейного программирования.

Необходимо определить фактический уровень сервиса, обеспечивающий затраты логистической системы

S_лс= f (U_ф)  min (2.11)

с одной стороны, и, с другой стороны, максимальным образом приближенный к требуемому уровню сервиса U_м, т.е. относительный показатель уровня сервиса должен стремиться к нулю:

U_м / U_ф –1  0 (2.12)

При атом существует система ограничений по затратам на логистическую систему по каждому подразделению:

f₁ (U_ф)  F₁l=1, L (2.13)

где f₁ - функция затрат на логистическую систему в подразделении 1, участвующем в производственно-распределительном процессе ;

L - количество подразделений, участвующих в производственно-распределительном процессе;

F₁ - максимально возможный лимит затрат на логистическую систему в подразделении 1.

Таким образом, с точки зрения математики необходимо решить следующую задачу: минимизировать функцию (2.11) при условии (2.12) и системе ограничений (2.13).

При таком подходе к функционированию логистической системы можно определить оптимальный уровень сервиса. Поскольку уровень сервиса влияет на доход предприятия, а естественным состоянием любого предприятия является увеличение прибыли, то в качестве критерия вффективности функционирования логистической системы принимается минимум потерь от необеспечения требуемого уровня сервиса:

Ф=Д (U_т) – S (U_т)  - Д (U_ф) – S (U_ф)  (2.14)

где Д (U_т) и S (U_т) - соответственно доход и затраты предприятия при обеспечении системой требуемого уровня сервиса, а также при снятии ограничений (13), т.е. затраты на логистическую систему не лимитированы, тогда Д (U_т) – S (U_т) представляют собой максимум возможной прибыли Д (U_ф) и S (U_ф) - соответственно доход и затраты предприятия при фактическом (или оптимальном) обеспечении уровня сервиса.

Для решения данной задачи необходимо определить каждую составляющую, что представляет собой отдельное исследование. Следует лишь отметить, что функции дохода Д (U) и затрат S (U) в общем случае являются нелинейными относительно уровня сервиса, что значительно усложняет решение данной задачи.

В

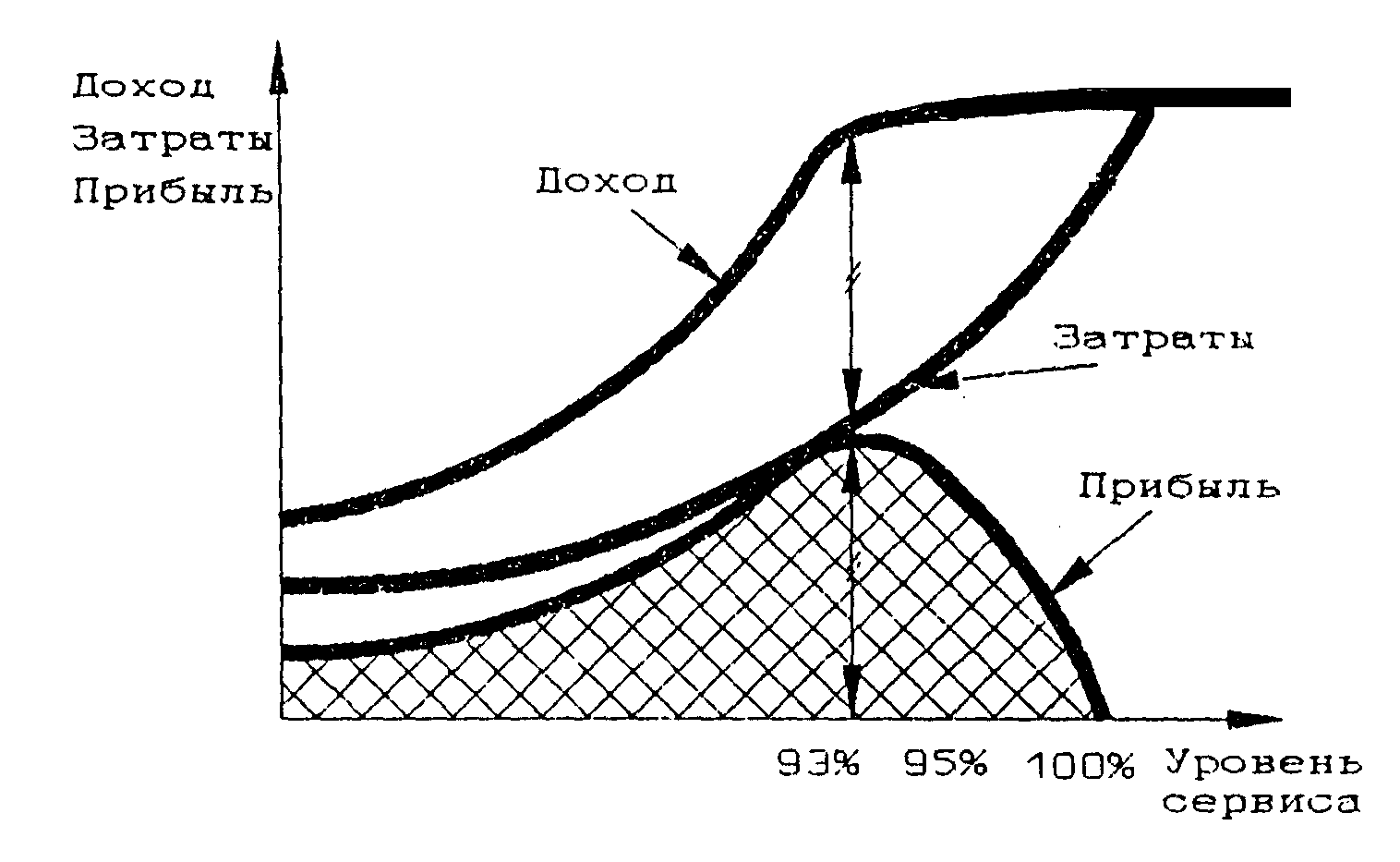
качестве примера на рисунке 2.16 представлено типовое влияние уровня сервиса на прибыль предприятия.

Рисунок 2.16. Типовое влияние уровня сервиса на прибыль предприятия

ФОРМЫ ОРГАНИЗАЦИИ ЛОГИСТИЧЕСКИХ СИСТЕМ

Построение организационной структуры логистической системы, как правило основывается на тех задачах, которые определены для решения в рамках логистической системы. Подобный подход является достаточно традиционным и простым, поскольку в каждом функциональном подразделении существует определенный круг логистических задач, которые могут решаться как локальные задачи логистической системы.

Примерная организационная структура логистической системы, основанная на логистических задачах функциональных подразделений, представлена на рисунке 2.17.

Недостатки настоящей организационной структуры очевидны и заключаются в следующем.

Существует конфликт целей между функциональными подразделениями . На рисунке 2.18 приведен пример возможных конфликтов целей в функциональных подразделениях.
Конфликты внутренних целей в одном подразделении, т.е. между выполнением основных задач функционального подразделения и возникающих при этом логистических задач.
Проблемы связи между подразделениями. Эти проблемы основаны на существовании административных и территориальных ограничений функциональных подразделений.

Тем не менее, построение организационной структуры в зависимости от возникающих функциональных задач является достаточно удобной с точки зрения их конкретизации и для некоторых предприятий является оправданной. Небольшие предприятия, выпускающие ограниченный круг номенклатуры, которая имеет сбыт на достаточно локальном рынке сбыта, могут воспользоваться такой организационной структуры логистической системы.

Состав логистической системы в данном случае зависит от состава функциональных подразделений и полностью им соответствует.

На предприятиях, где организационная структура управления является функциональной, предлагается структура управления логистической системы, представленная на рисунке 2.19. Наравне с традиционными подразделениями логистической системы здесь выделяются два новых подразделения: подразделение "стратегического планирования", которое участвует в руководстве логистической системой с точки зрения соблюдения сроков при выполнении стратегических задач, и подразделение "контроллинга", функциями которого являются планирование и контроль затрат во всей логистической системе. Планирование и координация всех логистических процессов осуществляется через подразделение логистики, занимающееся распределением ресурсов, в котором также устанавливается и взаимозависимость отдельных составляющих логистической системы.

На предприятиях, имеющих штабную организационную структуру, существуют три варианта организации структуры логистической системы: централизованная организация логистической системы, децентрализованная организация логистической системы и централизованная организация с элементами децентрализации (Рис.2.20 а,б,в).

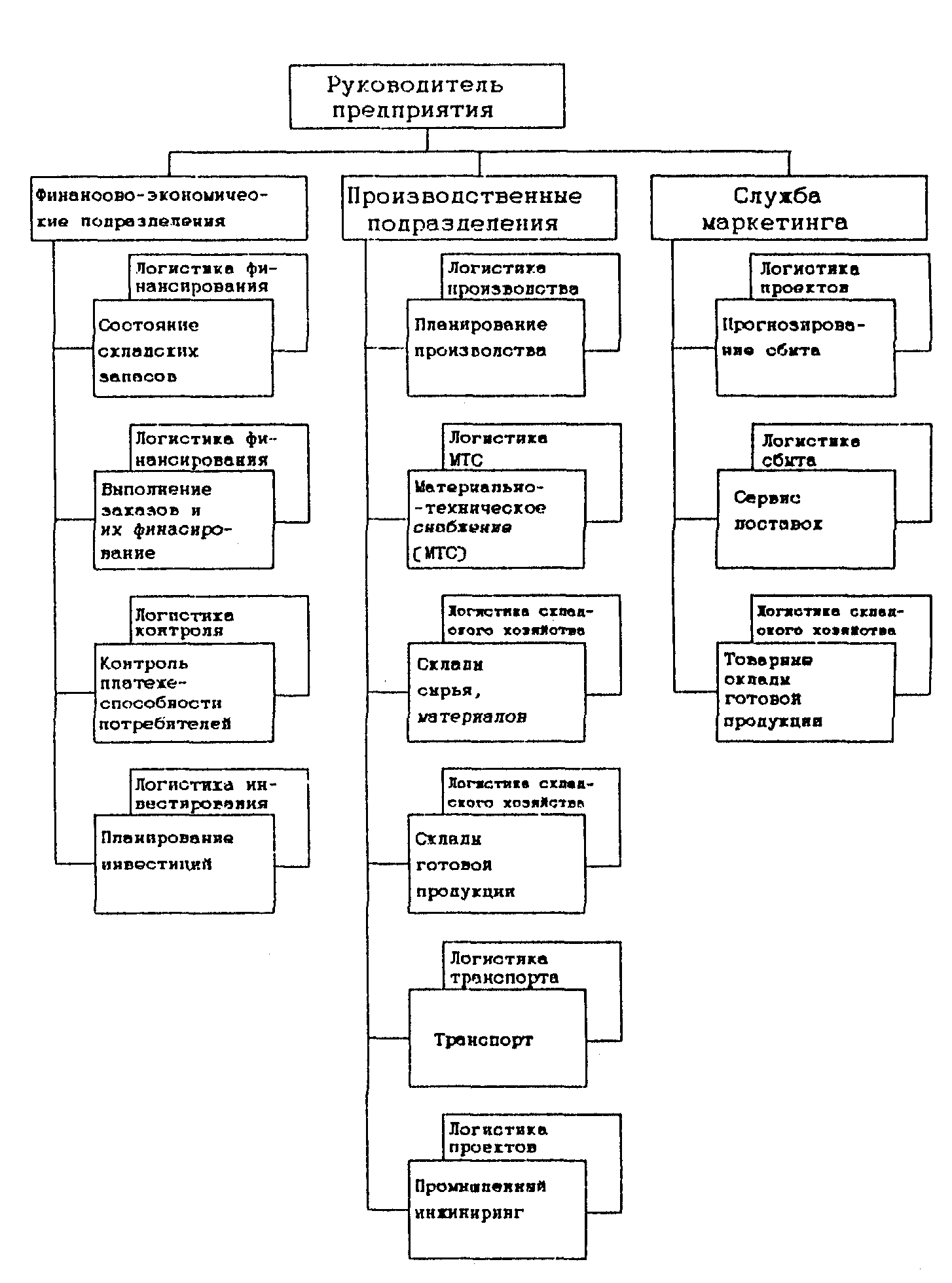
Рисунок 2.17. Организационная структура логистичсеской системы, основанная на логистических задачах функционального подразделения

Маркетинг		Финансирование	Производство
сеть поставок		выполнение заказов		взаимосвязь со складами
сервис поставок		состояние складских запасов		транспорт
увеличение складских запасов		уменьшение складских запасов
сокращение срока выполнения заказов		сокращение стоимости выпоянения заказов
сокращение сроков поставки готовой продукции потребителям	-------------------------------------------			использовакие наиболее дешевого способа поставок
использование сети внешних складов		уменьшение финансирования на внешнее складирование		размещение складов около произволственных подразделений

Рисунок 2.18. Пример возможных конфликтов целей в функциональных подразделениях

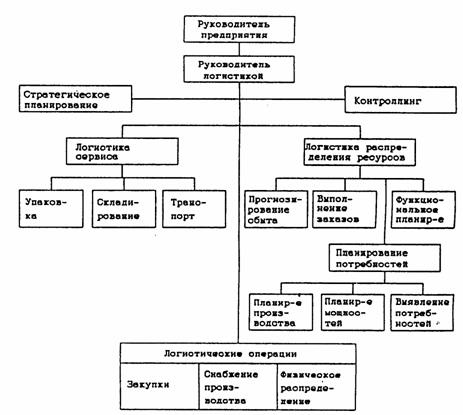
Рисунок 2.19. Организационная структура управления логистикой на предприятиях с функциональной системой управления

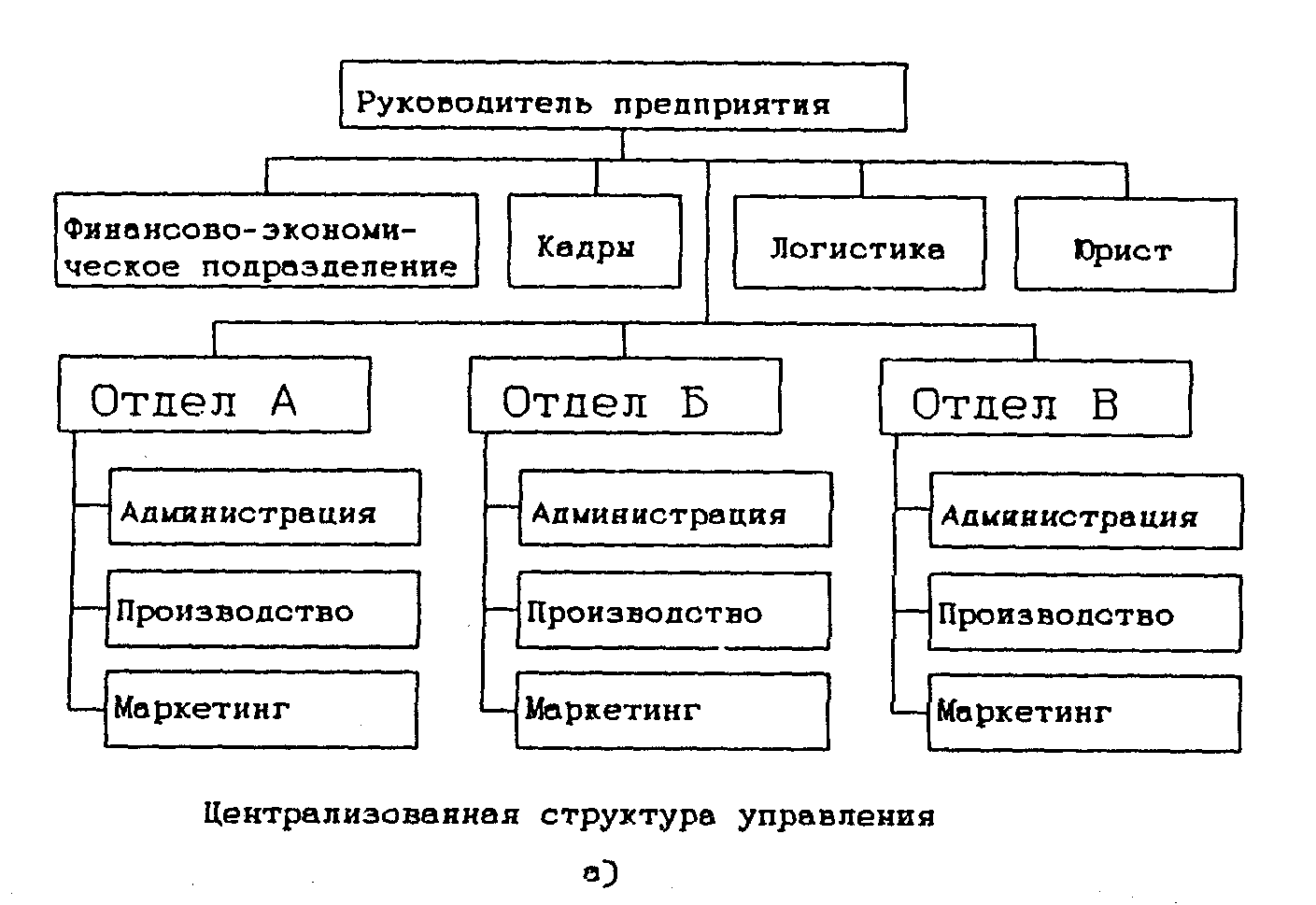
Рисунок 2.20 а. Организационные структуры логистической системы на предприятиях со штабной организационной структурой управления

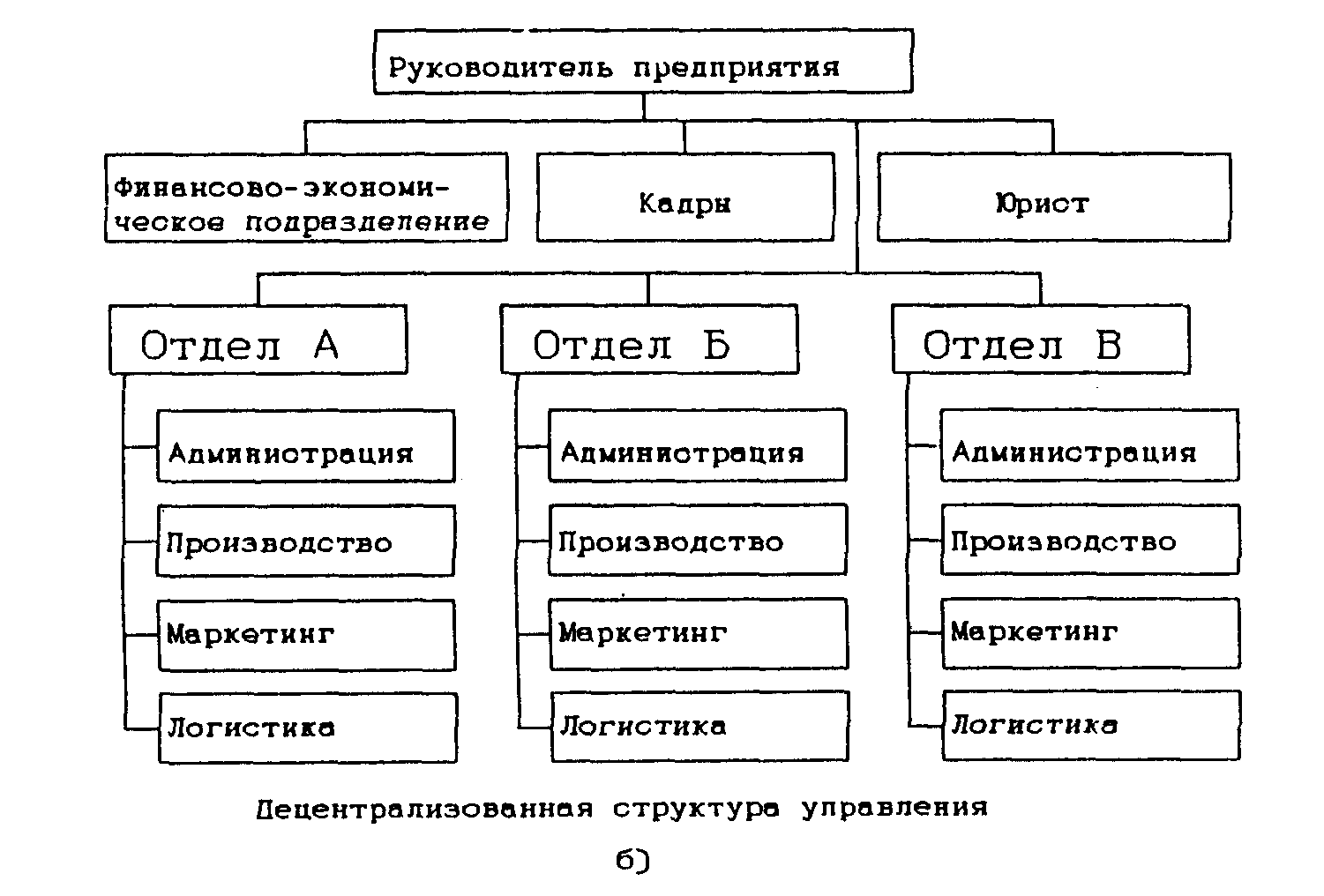
Рисунок 2.20 б. Организационные структуры логистической системы на предприятиях со штабной организационной структурой управления

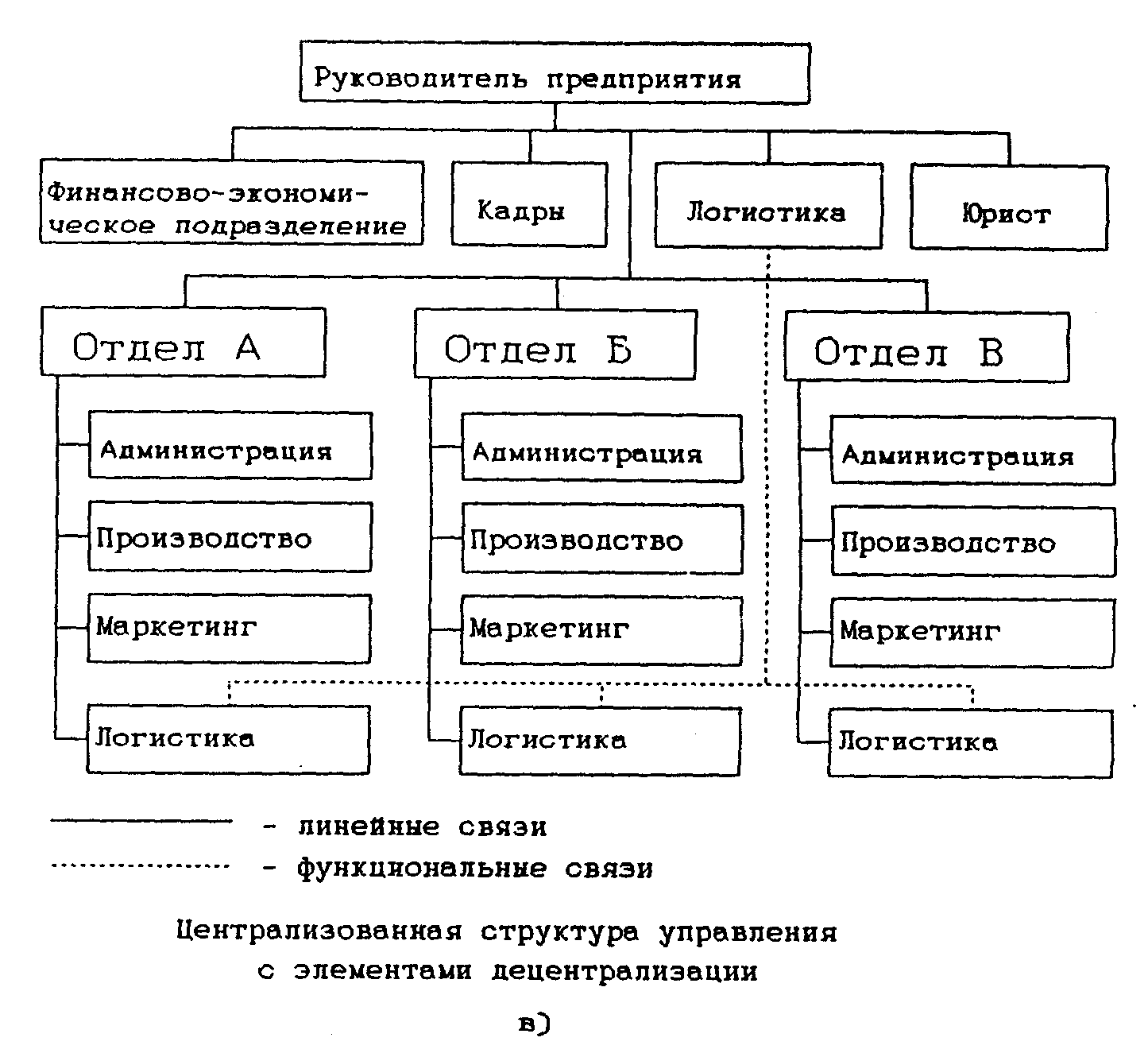
Рисунок 2.20 в. Организационные структуры логистической системы на предприятиях со штабной организационной структурой управления

3. ОПИСАНИЕ ПРАКТИЧЕСКИХ ЗАНЯТИЙ

Цель практических занятий состоит в прочном усвоении знаний, полученных в ходе освоения дисциплины путем решения практических задач, в овладении умением анализировать полученные результаты и делать соответствующие выводы. Студенты при решении поставленных задач используют лекционный материал, а так же источники и справочную литературу.

Оптимизация распределения грузопотоков

в промышленном районе

(

Транспортная задача)

Транспортная задача линейного программирования является основной математической моделью, используемой для составления оптимальных поставок и грузовых перевозок.

Сформулируем транспортную задачу. Для m станций отправления и n станций назначения заданы размеры отправления и прибытия однородного или взаимозаменяемого груза, выраженные в тоннах, вагонах или других единицах. Известная стоимость перевозки единицы груза от каждой станции отправления до каждой станции назначения . Требуется составить такой план перевозок, в котором общая величина транспортных расходов была бы минимальной.

Поставленные нами условия можно сокращенно записать так:

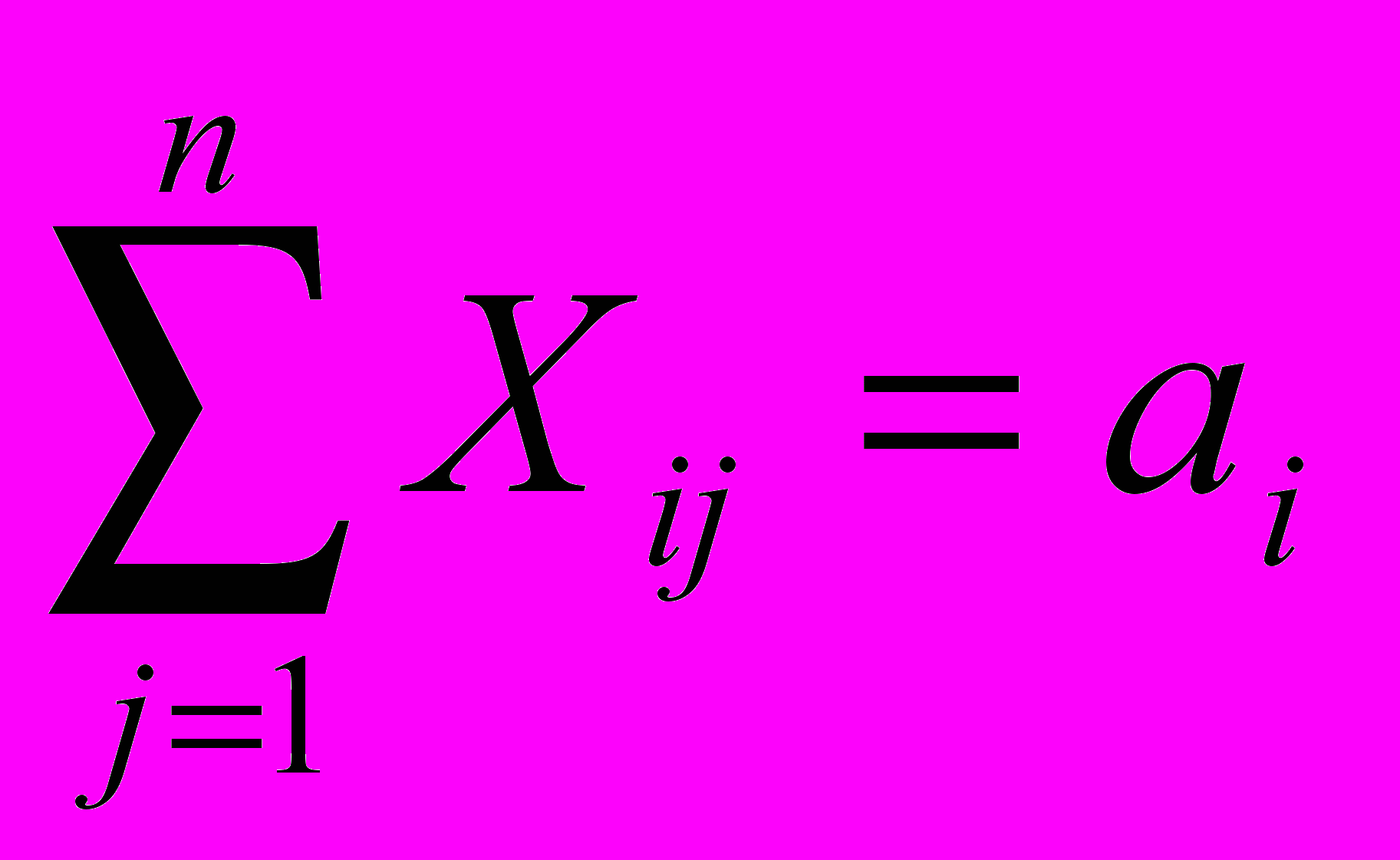, (3.1)

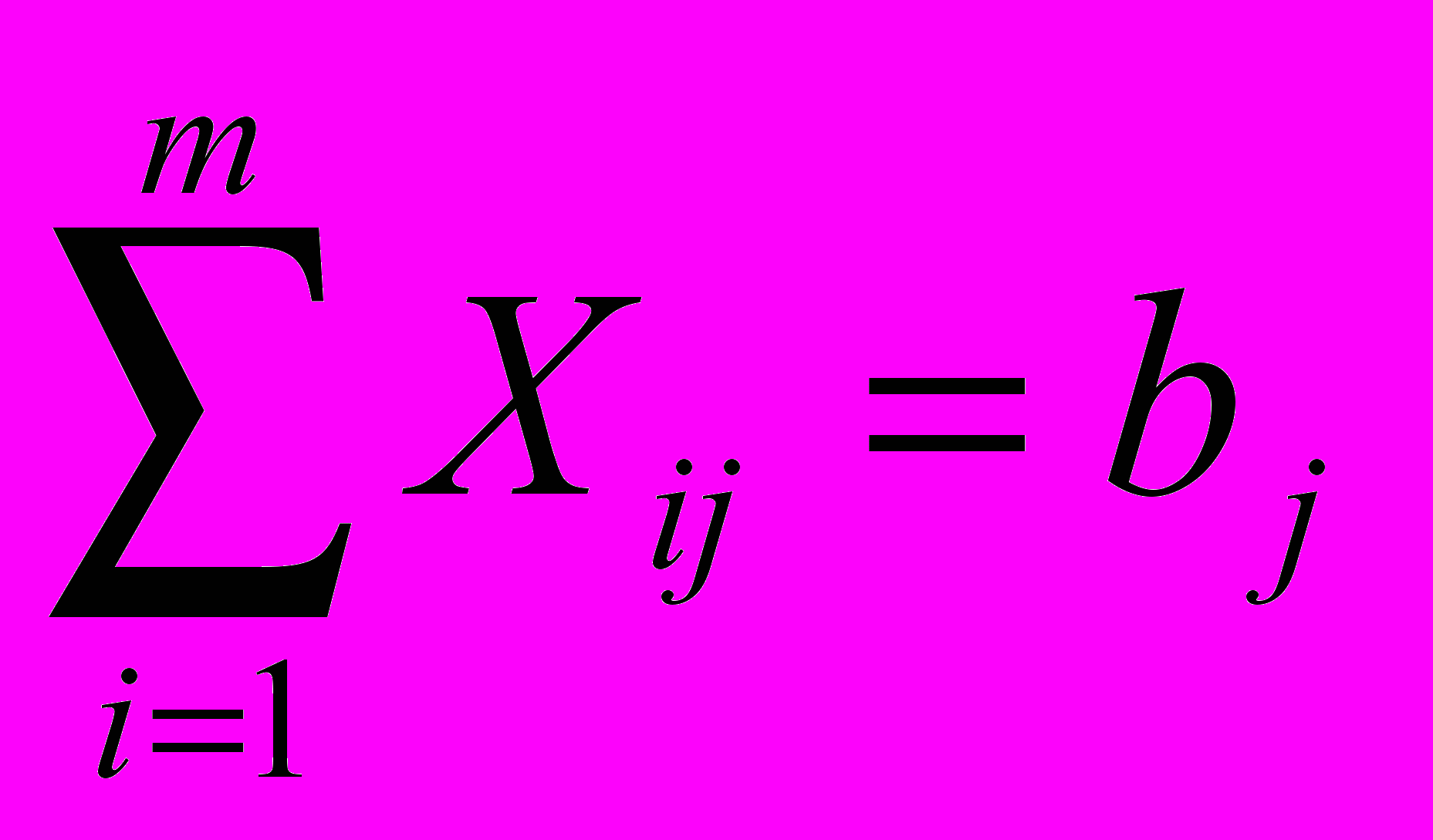, (3.2)

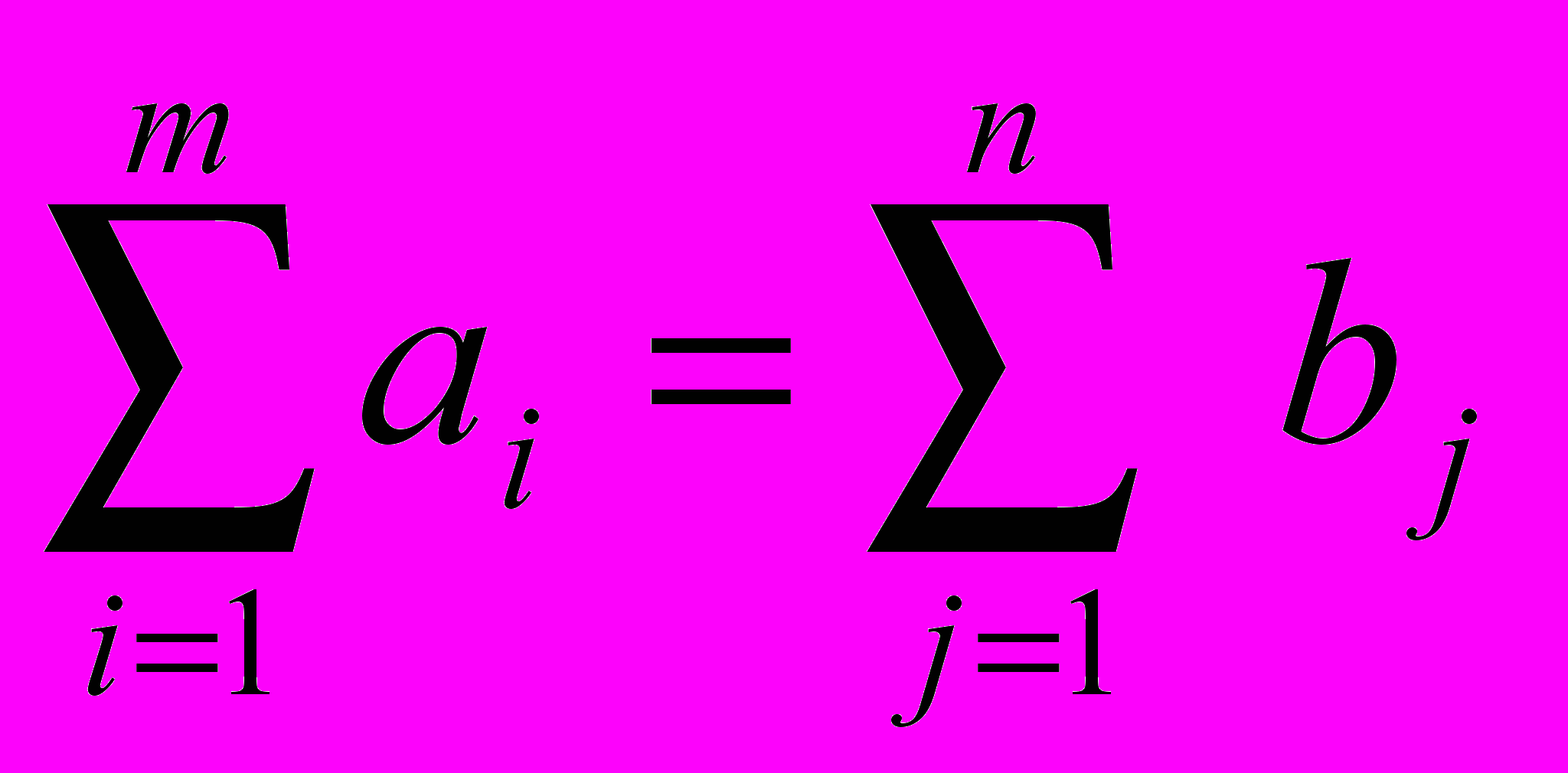, (3.3)

На рисунке 3.1 приведен пример решения транспортной задачи

Для решения задачи задано:

Значения потребностей и возможностей;

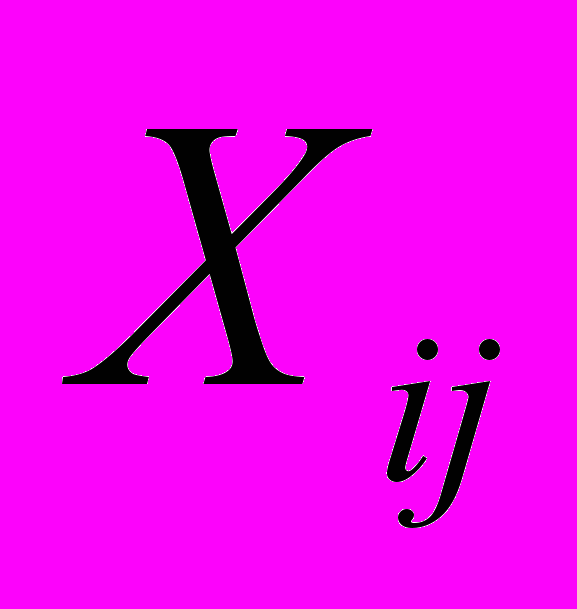-численные значения корреспонденции (значения находятся в левом нижнем углу ячеек);

N-общее число корреспонденций;

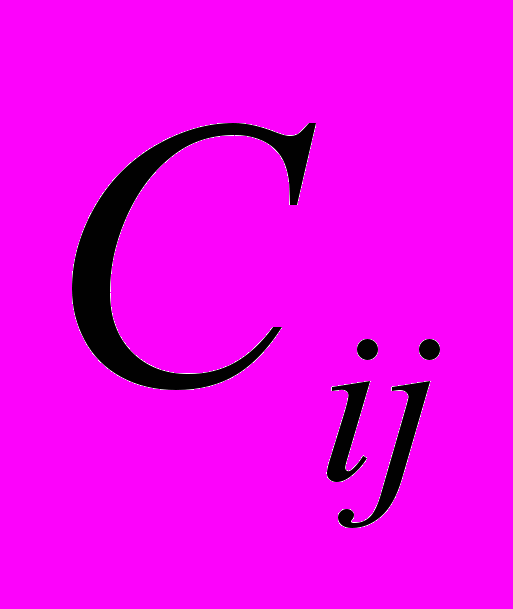-стоимость перевозок от j-го источника i-му потребителю (значение находится в правом верхнем углу ячеек);

n- количество столбцов ;

m- количество строк .

1

1

0

3

2

5 -2	+1 4	70 3	60 2	130 +2 1
20 1 1 2	50 2 31	3	4	70 Потребности 5
100 2 0	3	4	5	150 1 50
+3 1 -2 1	40 5 4	10 3	4	50 +1 2

50

60

80

90

120

Источники (возможности)

Рисунок 3.1.- Пример решения транспортной задачи

Сформулируем математически глобальную цель нашей задачи: необходимо найти такой план перевозок, для которого справедливо следующее выражение:

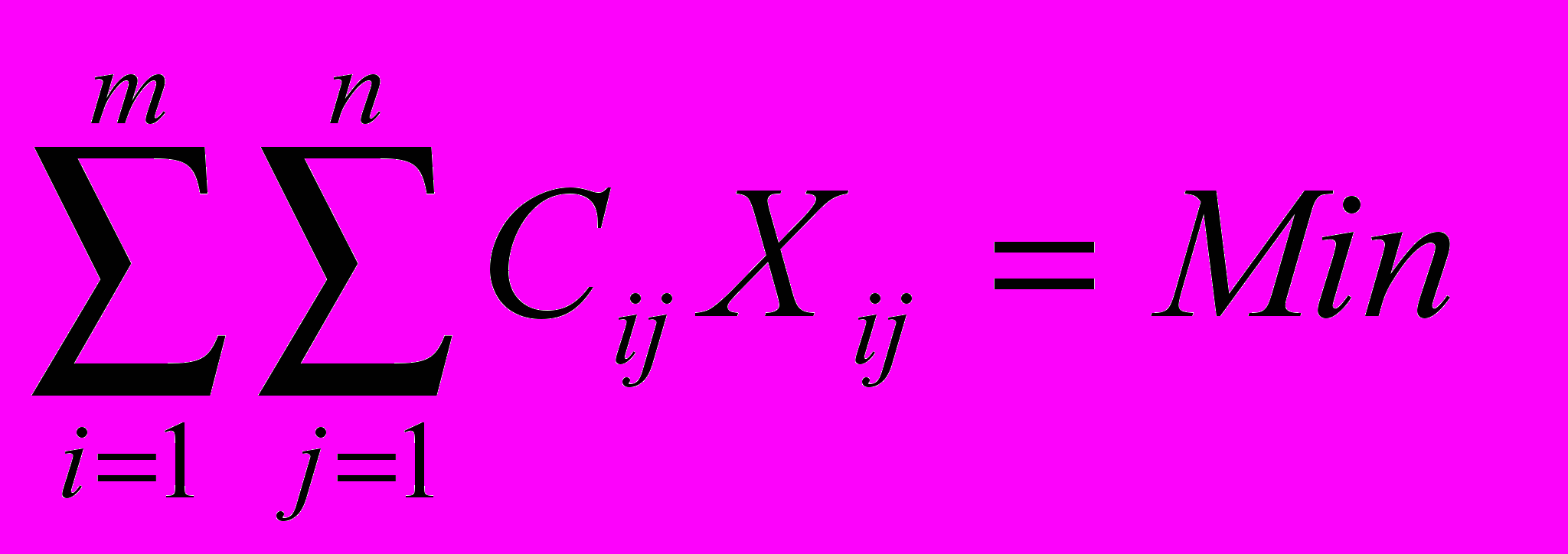, (3.4)

Этапы решения задачи:

Построение базисного плана:

При построении базисного плана будем руководствоваться теоремой №1.

Теорема № 1

Всегда можно построить такой базисный план, для которого будет справедливо следующее соотношение:

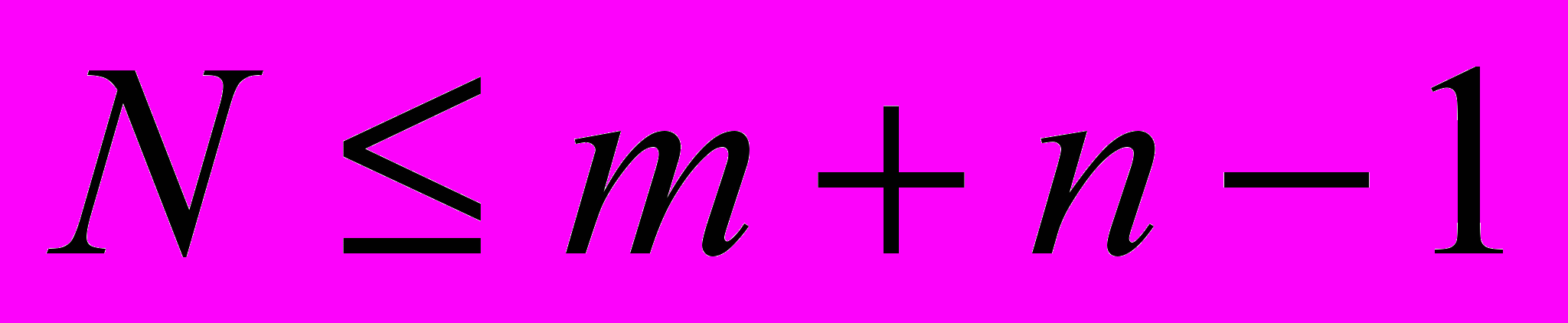, (3.5)

От качества построения начального плана зависит число итераций, или последовательных приближений, хотя к оптимальному плану можно прийти при любом его построении. В данном случае приводится один из лучших.

Базисный план будем строить по принципу наименьшей стоимости доставки грузов. Для этой цели выбирается строка с максимальной потребностью (столбец с максимальной возможностью) и начинается удовлетворение данной потребности с ячейки с минимальной стоимостью доставки и далее по степени увеличения данной стоимости. Затем анализируются оставшиеся строки (столбцы) в порядке убывания потребностей (возможностей).

В нашем случае первой просматривается 3-я строка.

Минимальная стоимость доставки 1, туда помещается максимально возможная поставка 50, однако этого недостаточно 3-ему потребителю, поэтому следующей заполняем ячейку со стоимостью доставки 2. Помещаем туда поставку 100. Таким образом, 3-его потребителя удовлетворили полностью.

Далее аналогично заполняем строки соответственно 1,2 и 4. Последнюю строку заполняем по остаточному принципу.

2) Доказательство оптимального плана:

Для этого используем метод потенциалов.

Потенциалы транспортной задачи аналогичны потенциалам в электротехнике, механике или гидравлике, так что можно построить электрическую, механическую или гидравлическую модель, которая будет полностью соответствовать транспортной задаче. С экономической точки зрения потенциалы представляют собой систему условных цен (оценок), соответствующих пунктам производства и потребления.

Сделаем следующие обозначения : Vj-потенциал столбца, Ui-потенциал строки. Для доказательства оптимальности плана будем использовать теорему №2.

Теорема №2

План перевозок (поставок) будет оптимальным, если одновременно будут выполняться следующие условия:

Для

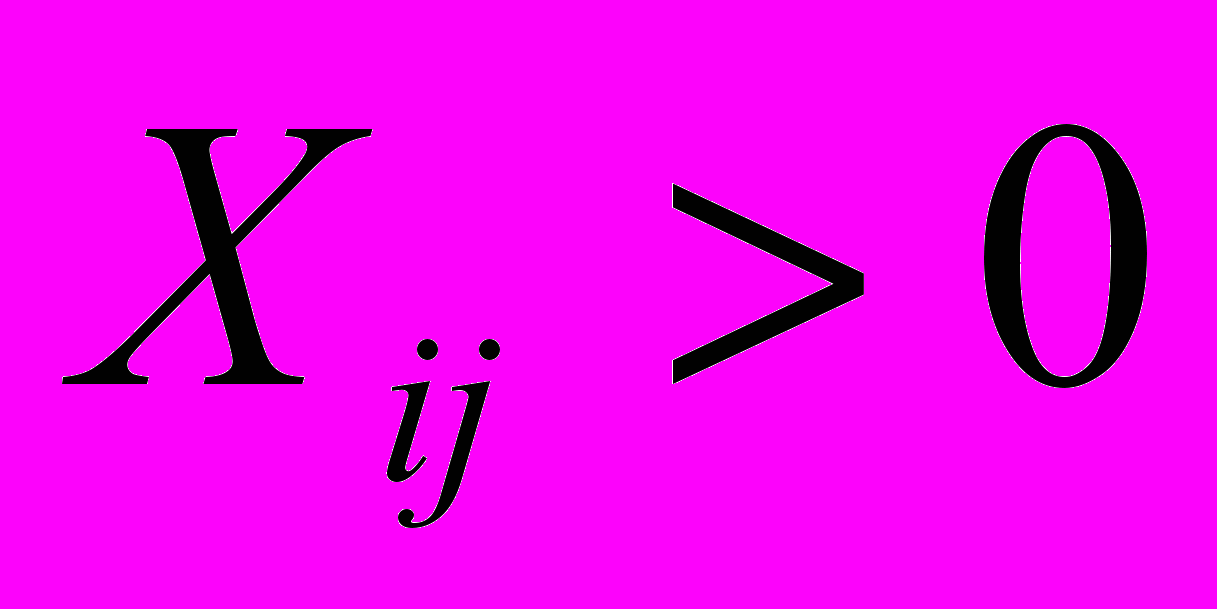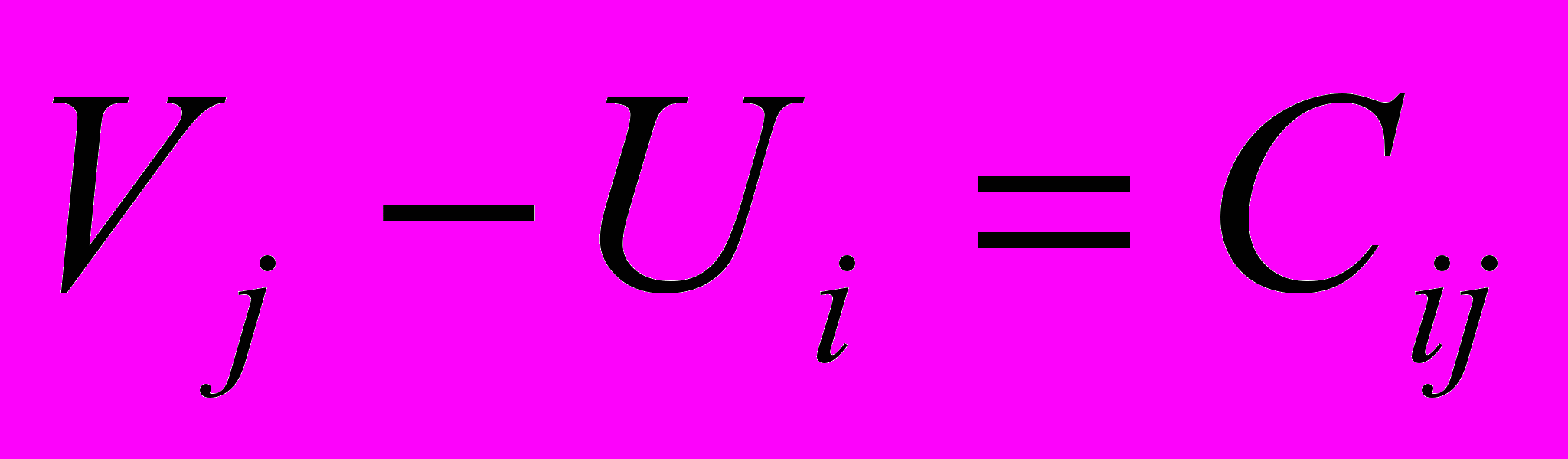, (3.6)

Для

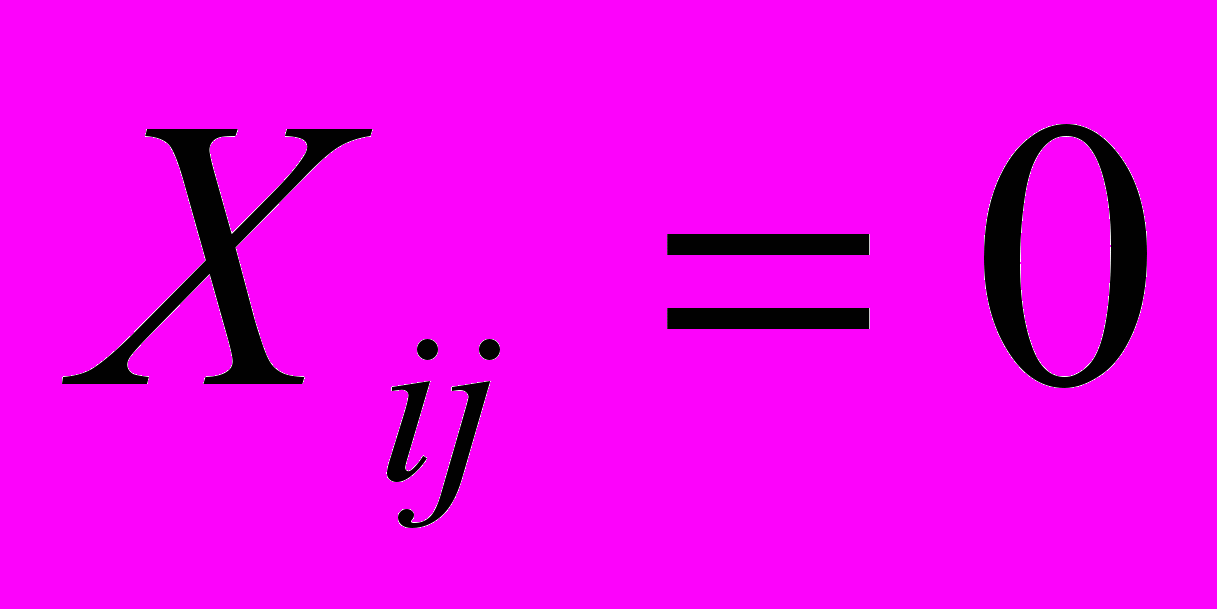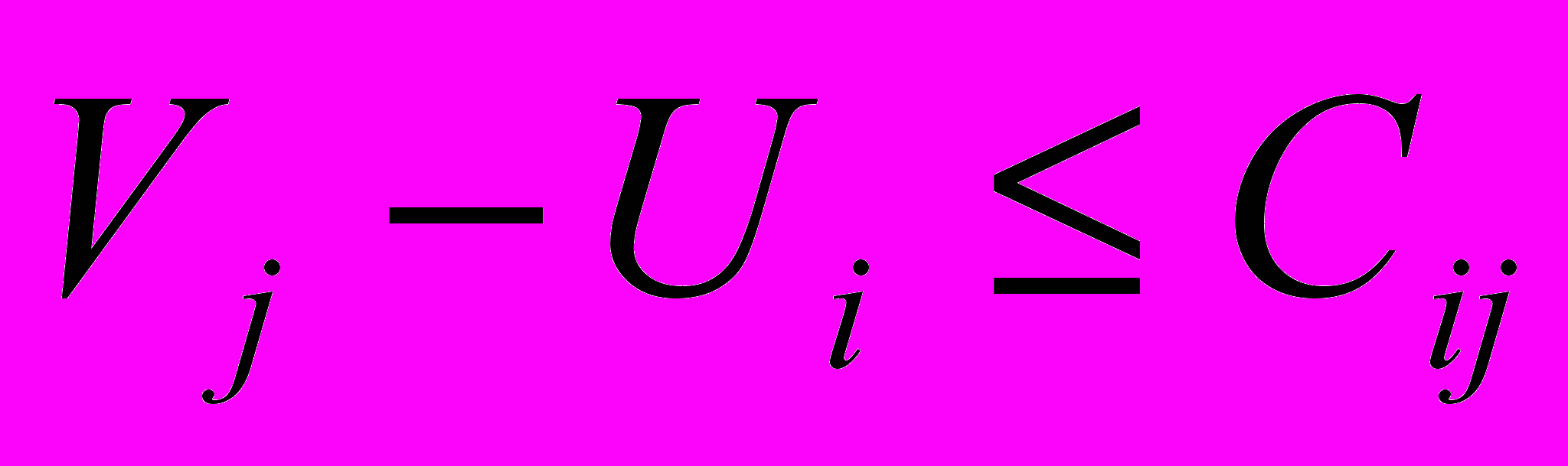, (3.7)

Находим потенциалы строк и столбцов. Строке с максимальной потребностью (столбцу с максимальной возможностью) присвоим потенциал равный нулю и на основании выражения (3.6) найдем все остальные потенциалы. В рассматриваемой задаче максимальное потребление 150 (3-я строка). Этой строке присваиваем потенциал 0. Потенциалы строк на рис.3.1 проставлены слева, а потенциалы столбцов вверху.

Потенциалы всех строк и столбцов определяются однозначно только в том случае, если N=m+n-1.

Если же N< m+n-1, то такой случай называется «вырожденный»и для его решения применяется специальный прием.

Если же по какой-то причине окажется, что

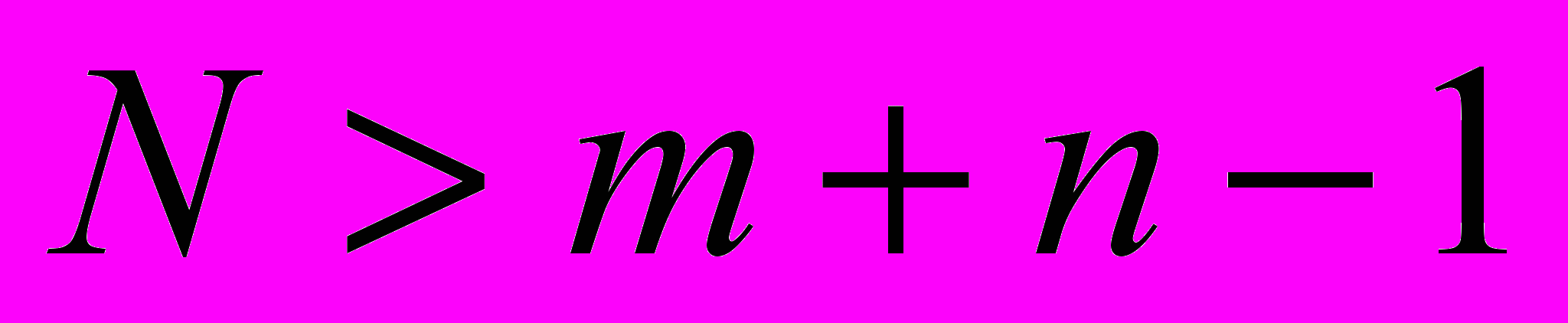, то это противоречит теореме №1 (условие (3.5) и задача данным методом не решается. В данной задаче потенциалы всех строк и столбцов определяются однозначно.

На основании выражения (3.7) определяем оптимальный и не оптимальный план. Условие (3.7) записано для пустых клеток. В тех ячейках, где это условие не выполняется необходимо записать величину небаланса

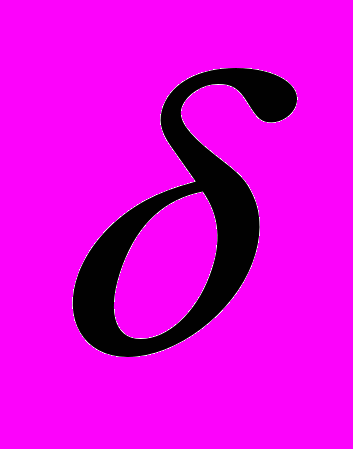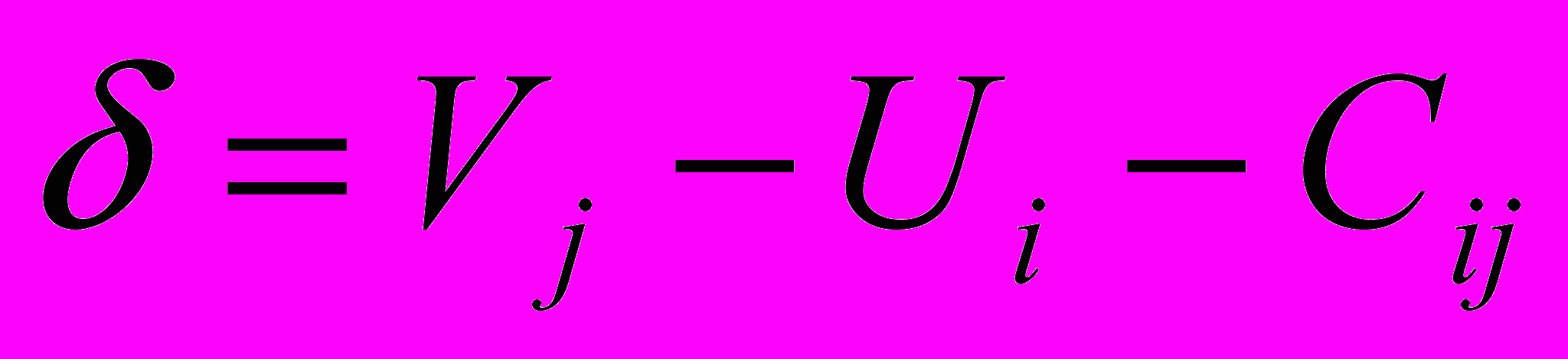, (3.8)

В нашей задаче, как видно из рис.3.1, условие (3.7) для всех ячеек не выполняется. Небалансы записываются в ячейках со знаком +, чтобы не перепутать с численным значением корреспонденций. Таким образом, базисный план не оптимальный, следовательно, необходимо выполнить передвижку.

Передвижка выполняется следующим образом.

Выбирается ячейка с максимальным небалансом (если их несколько, то любая из них), этой ячейке присваивается №1 ( в данном примере это ячейка с небалансом +3) и далее выполняется обход по матрице по замкнутому контуру ходом шахматной ладьи, таким образом, чтобы во всех остальных угловых клетках были корреспонденции. Угловые клетки контура на рис.3.1 обозначены в ячейках в левом верхнем углу. Для наглядности их лучше обозначить другим цветом или обвести кружком.

В четных клетках выбирается минимальная корреспонденция и выполняется передвижка из четных клеток в нечетные на величину данной корреспонденции (в данном примере минимальная корреспонденция 20, контур передвижки выделен на рисунке).

Переходим к следующей итерации. После передвижки матрица имеет вид, показанный на рис.3.2.

Получившийся план снова проверяем на оптимальность. Рассчитываем потенциалы строк и столбцов и проверяем выполнение условия (3.7). Так как для второго плана условие (3.7) для всех клеток так же не выполняется, то данный план не оптимальный.

Снова находим клетку с максимальным небалансом - это клетка с небалансом +3. Находим замкнутый контур и выполняем аналогично передвижку. Переходим к третьей итерации (рис.3.3)

Для третьей матрицы условие (3.7) для всех клеток выполняется, поэтому данный план является оптимальным, т.е. выражение (3.4) будет минимальным.

Переход от первого плана ко второму позволил сделать улучшение плана, которое можно рассчитать следующим образом:

4

3

6

2

5 1	+1 4	70 3	60 2	130 1
1 4	70 2	3	4	70 5 1
100 2 0 4	3 +3 1	4	5	150 1 50
20 1 1 2	20 5 2	10 3	4	50 2

50

60

80

90

120

Рисунок 3.2. –Матрица для второй итерации

4

1

3

3

2

5 1	4	70 3	60 2	130 1
1 1	70 2	3	4	70 5
80 2 0	3 20	4	5	150 1 50
40 1 1	5	10 3	4	50 2

50

60

80

90

120

Рисунок 3.3. –Матрица для третьей итерации

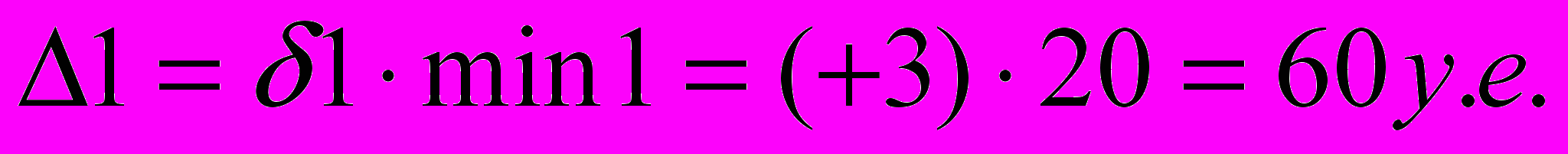
Переход от второго к третьему:

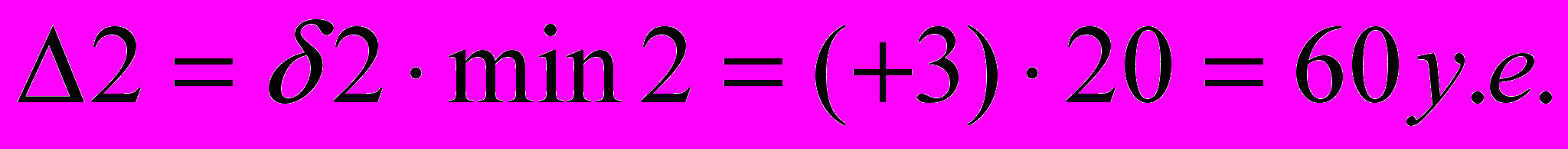
Общее улучшение:

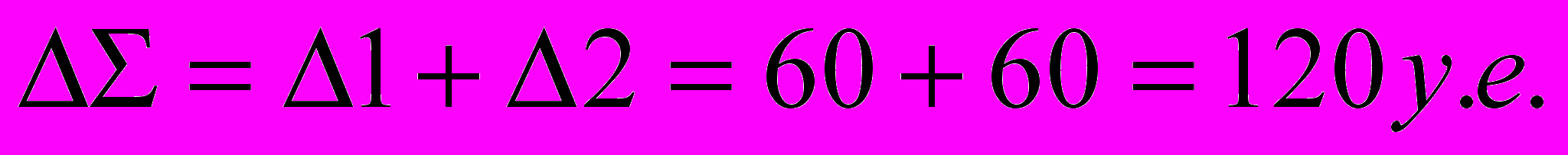
Случай «вырожденный»

(если N
Рассмотрим следующую задачу.

3

1

2

2

1

150 1 0	2	3 0	4	150 5
2 -1	20 3	4	5	50 Потребности 1
3 -2 30	70 4 4	5	2 +2 1	100 1 +2
4 0	5 3	100 3	40 2 2	200 60 1

60

40

100

120

180

Источники (возможности)

Рисунок 3.4. - Вырожденный случай. Первая итерация

Решение задачи начинаем, как и в предыдущем примере. Строим базисный план и выясняем, что число корреспонденций равно 7. Условие (3.5) выполняется, значит, план базисный. Присваиваем потенциал, равный 0 четвертой строке и находим потенциалы 3,4 и 5 столбцов. Далее нет возможности найти очередной потенциал.

В тех случаях, когда нет возможности найти очередной потенциал в какой-нибудь из ячеек необходимо проставить нулевую корреспонденцию. Баланс она не испортит, но число корреспонденций увеличится. В случае необходимости проставить 2, 3 и т.д. нулевых корреспонденций, т.е. довести их число до m+n-1.

Затем находим все остальные потенциалы и на основании условия (3.7) проверяем оптимальность данного плана.

Т.к. условие (3.7) во всех ячейках не выполняется, то, следовательно, оптимальность данного плана не доказана. Присваиваем №1 ячейке с максимальным небалансом (+2) и выполняем обход по матрице по замкнутому контуру, как показано на рис.3.4. Передвигаем минимальную корреспонденцию 40 из четных клеток в нечетные. Получаем следующий план (рис.3.5)

3

3

5

4

150 1 3	2	3	4	150 5
30 2 2	50 3	4	5	50 1
3 1 30	30 4 3	5	2 40 4	100 1
40 4 0	5 2	100 3	2 1 +1	200 60 1

60

40

100

120

180

Рисунок 3.5.- Вырожденный случай. Вторая итерация.

Проверка плана на оптимальность показала, что в одной ячейке имеется небаланс +1, значит, план не оптимальный. Снова ищем контур обхода, как показано на рис.3.5 и выполняем передвижку минимальной корреспонденции 40.

Получаем план, показанный на рис.3.6. Число корреспонденций равно 7 и план аналогичен базисному, однако при нахождении потенциалов нулевую корреспонденцию ставим в ячейке, где после передвижки появляется расчетный 0. Проверяем выполнение условия (3.7) и доказываем, что данный план является оптимальный.

3

1

2

4

3

150 1 2	2	3	4	150 5
2 1	50 3	4	5	50 1
3 0 30	70 4	5	2 0	100 1
4 0	5	100 3	40 2	200 60 1

60

40

100

120

180

Рисунок 3.7.- Вырожденный случай. Третья итерация

Что же произошло? В первом случае мы неудачно выбрали место расположения нулевой корреспонденции и ушли от оптимального плана, и вполне вероятно могли прийти к другому оптимальному плану, потому что их может быть в общем случае несколько. В данном случае этого не произошло и мы доказали, что базисный план оптимальный.

Blog

Содержание