Решение Ученого совета ргсу от «26»

Вид материала

Решение

Содержание Функциональное и логическое программирование. «физико-математическое образование» Теоретические основы информатики. «прикладная математика и информатика» 2. Математический анализ 3. Обыкновенные дифференциальные уравнения 5. Численные методы 6. Элементы функционального анализа 7. Теория вероятностей и математическая статистика. 8. Дискретная математика. 9. Оптимизация и оптимальное управление. 10. Информатика, языки программирования, программное обеспечение. «экология и природопользование»

Подобный материал:

• Решение Ученого совета ргсу от «13», 4667.32kb.
• Заседание ученого совета бгарф от 26 апреля 2011, 38.35kb.
• Проект Решение Ученого совета гоу впо «Нижневартовский государственный гуманитарный, 58.07kb.
• Решение Ученого Совета, 752.27kb.
• Л. Л. Абрамова 2011 г решение, 36.89kb.
• Решение Ученого совета, 74.32kb.
• Заседание Ученого совета мгимо, 74.57kb.
• Уважаемый председатель ученого совета! Уважаемый президент, 520.56kb.
• Решение ученого совета ргтэу от 21 февраля 2011 года, 93.32kb.
• Решение ученого совета ниу итмо от 27. 12. 2011 по вопросу, 45.91kb.

Функциональное и логическое программирование. Основные отличия декларативных и процедурных языков программирования. Области применения языков Лисп, Пролог. Лямбда-исчисление А. Чёрча и теория рекурсивных функций. Символьные выражения: атомы и списки, функции. Предикаты и предложения. Списки: работа со списками, внутреннее представление списков.Рекурсия: рекурсия по значению, рекурсия по аргументу, параллельная и взаимная рекурсия. Простые и составные объекты данных. Динамические базы данных: объявление и использование, загрузка и сохранение фактов, добавление и удаление фактов.

Рекомендуемая литература:

1. Метакидес Г., Нероуд А. Принципы логики и логического программирования. – М.: Факториал, 1998.
   
2. Хендерсон П. Функциональное программирование: применение и реализация. - М.: Мир, 1983. – 349 С.
   
3. Братко И. Программирование на языке Пролог для искусственного интеллекта. – М.: Мир, 1990. – 560 С.
   

Направление подготовки «ФИЗИКО-МАТЕМАТИЧЕСКОЕ ОБРАЗОВАНИЕ»


ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ В ФИЗИКО-МАТЕМАТИЧЕСКОМ ОБРАЗОВАНИИ


Экзаменующийся должен показать знания фундаментальных положений основных дисциплин, являющихся базовыми для информатики и образования в современной информационной среде (теоретические основы информатики, компьютерные сети, интернет и мультимедиа технологии, педагогика, психология, языки и методы программирования, технологии и методики обучения информатике и др.).


Теоретические основы информатики. Понятие информации. Информационные процессы. Непрерывная и дискретная формы представления информации. Количество и единицы измерения информации. ЭВМ как универсальное средство обработки информации. Измерение количества информации. Информационные сообщения и сигналы. Принципы преобразований сигналов различного типа. Теория кодирования.

Литература:

1. Акулов О.А., Медведев Н.В. Информатика: базовый курс: Учеб. пособие для студентов вузов - М., 2005.
   
2. Могилев А.В., Пак Н.И., Хённер Е.К. Информатика. – М., 2008.
   

Информационные системы и сети. Информационно-поисковые и справочные системы, базы и банки данных. Управление базами данных. Архитектура систем баз данных. Введение в реляционные базы данных. Реляционные объекты данных: домены и отношения. Целостность реляционных данных. Реляционные операторы: реляционная алгебра, реляционное исчисление. Язык SQL. Основы компьютерных сетей. Обзор вычислительных сетей. Разделение ресурсов компьютера. Построение сети. Сетевое программное обеспечение. Глобальные вычислительные сети.

Литература:

1. 
   Избачков Ю.С., Петров В.Н. Информационные системы: Учебник для вузов. 2-е изд. – СПб., 2006.
   
2. Могилев А.В., Пак Н.И., Хеннер Е.К. Информатика: Учебное пособие для студентов педагогических вузов. – М., 2005.
   

Компьютерные сети, интернет и мультимедиа технологии. Интернет как технология и информационный ресурс (сеть). Технология электронной почты. Технология обмена файлами (FTP). Технология WWW. Поиск информации в сети Интернет. Язык HTML как средство создания информационных ресурсов Интернет. Язык " onclick="return false">
Литература:

1. Митин А.И., Василенко Л.А. Глобальная компьютерная сеть INTERNET (история, организация, доступ, перспективы). - М., 1996.
   
2. Калиногорский Н.А., Галевский Г.В. Эффективные технологии работы в сети Интернет. - М., 2004.
   
3. Информатика: Учебник для вузов / под ред. Н.В.Макаровой. – М., 2008.
   

Педагогика. Педагогическая профессия.  Понятия: образование, воспитание, обучение, самовоспитание, социализация. Закономерности и принципы обучения. Единство образовательной, воспитательной и развивающей функций. Государственный образовательный стандарт. Современные методы, модели и средства обучения. Сущность воспитания и его место в образовательном процессе. Тенденции развития мирового образовательного процесса. Социальное воспитание и социализация личности. Понятие педагогических технологий, их обусловленность характером педагогических задач. Виды педагогических задач. Педагогические технологии. Понятие управления и педагогического менеджмента. Государственно-общественная система управления образованием.

Литература:

1. Байкова Л.А., Гребёнкина Л.К. Педагогические мастерство и педагогические технологии. – М., 2000.
   
2. Коджаспирова Г.М. Педагогика. – М., 2009.
   

Психология. Психология как наука; предмет психологии. Понятие о человеке: антропологический и эволюционный подходы к его изучению. Формы взаимодействия человека с миром. Субъект; индивид, личность, индивидуальность. Познание, общение, деятельность; поведение. Сознание и самосознание. Функциональная и структурная организация психики; процессы, состояния, свойства. Психологическая компетентность и психологическая культура. Влияние образования на развитие. Здоровьесберегающая среда как фактор развития человека. Психическое развитие в разные возрастные периоды. Социализация, социальное поведение, социальное познание, социальные качества личности; социальная психология личности. Виды и феномены взаимодействия, человек как субъект взаимодействия; общение и взаимодействие.

Литература:

1. Соколова Е.Е. Введение в психологию. Изд.3. В 6 т. Т.1. – М., 2008.
   
2. Введение в социальную психологию: Учеб. пособ. / В.Г. Крысько. – М., 2000.
   

Технологии и методики обучения информатике. Методическая система обучения информатике в школе, общая характеристика ее основных компонентов. Цели и задачи обучения информатике в школе. Структура обучения информатике в средней общеобразовательной школе. Стандарт школьного образования по информатике. Пропедевтика основ информатики в начальной школе. Базовый курс школьной информатики. Дифференцированное обучение информатике на старшей ступени школы. Программное обеспечение по курсу информатики. Планирование учебного процесса по курсу информатики. Формы обучения, проверки и оценки его результатов. Методика изучения основных разделов курса информатики.

Литература:

1. Бешенков С.А., Е.А.Ракитина Е.А., Матвеева Н.В., Милохина Л.В. Непрерывный курс информатики – М., 2008.
   
2. Лапчик М.П., Семакин И.Г., Хеннер Е.К. Теория и методика обучения информатике. Учебник. – М., 2008.
   

Информационные и коммуникационные технологии в физико-математическом образовании. Использование информационных и коммуникационных технологий (ИКТ) для построения открытой системы образования. Информационные образовательные ресурсы учебного назначения: их классификация и дидактические функции. Проектирование, разработка и использование в школьном образовательном процессе информационных ресурсов учебного назначения. Образовательные информационные технологии и среда их реализации. Использование мультимедиа и коммуникационных технологий для реализации активных методов обучения. Дистанционные технологии в образовании. ИКТ в обучении информатике.

Литература:

1. Роберт И.В., Панюкова С. В., Кузнецов А.А., Кравцова А.Ю. Информационные и коммуникационные технологии в образовании/ Учебно-методическое пособие. – М., 2006.
   
2. Полат Е.С., Моисеева М.В., Нежурина М. И. Педагогические технологии дистанционного обучения. – М., 2006.
   

Дискретная математика. Множества и отношения. Операции над множествами. Функции. Основы математической логики. Математический язык. Булева алгебра. Элементы комбинаторики. Основные задачи комбинаторики и методы комбинаторных рассуждений. Элементы теории графов.

Литература:

1. Яблонский С.В. Введение в дискретную математику. - М., 1986.
   
2. Бочаров В.А., Маркин В.И. Основы логики: Учебник для вузов - М., 2001.
   

Теория алгоритмов. Понятие вычислимой функции. Разрешимые и перечислимые множества. График вычислимой функции. Формальная теория вычислимости. Тезис Чёрча. Конечные и бесконечные машины. Понятие программы. Теорема о параметризации. Существование универсальной программы. Компьютер фон Неймана. Диагональный метод. Проблема останова. Примеры неразрешимых и неперечислимых множеств. Алгоритмическая сводимость проблем. Эффективные операции над вычислимыми функциями. Теорема о неподвижной точке. Общее понятие исчисления. Грамматики. Языки и машины. Меры сложности вычисления. Приложения теории алгоритмов в информатике.

Литература:

1. Гуц А.К. Математическая логика и теория алгоритмов: Учеб. пособие. – М., 2009
   
2. Карпов Ю.Г. Теория автоматов. – СПб., 2003.
   

Численные методы. Теория погрешностей. Решение системы линейных уравнений, нелинейного уравнения. Методы наилучшего приближения. Дискретный вариант среднеквадратических приближений. Понятие об определении параметров функциональной зависимости. Численное дифференцирование. Общий случай вычисления производной произвольного порядка. Численные методы решения дифференциальных уравнений.

Литература:

1. Бахвалов Н.С. Численные методы. – М., 2004.
   
2. Поршнев С.В. Численные методы. Курс лекций. – СПб., 2004.
   

Теория вероятностей и математическая статистика. Статистические закономерности. Статистическая устойчивость и статистическое определение вероятности. Пространство элементарных событий, события. Свойства вероятности. Условная вероятность и ее свойства. Независимость двух и n событий. Определение случайной величины, ее свойства. Дискретные случайные величины, закон распределения. Непрерывные случайные величины. Геометрические вероятности. Независимость испытаний. Практическое использование приближенных формул. Математическое ожидание, дисперсия случайной величины, их свойства. Среднее квадратичное отклонение. Понятие о центральной предельной теореме. Задачи математической статистики.

Литература:

1. Жукова Г.С. Математика для студентов экономических специальностей. Ч.I,2.  М., 2004.
   
2. Гмурман В.Е. Теория вероятностей и математическая статистика.  М., 1998.
   

Основы искусственного интеллекта. Теоретические подходы и проблемы построения систем искусственного интеллекта, перспективы их развития. Основные подходы и модели представления знаний. Методы и средства обработки знаний для нахождения рациональных решений. Базы знаний. Основные классы систем искусственного интеллекта.

Литература:

1. Андрейчиков А.В., Андрейчикова О.Н. Интеллектуальные информационные системы. Учебник для вузов.– М., 2006.
   
2. Ясницкий Л.Н. Введение в искусственный интеллект. Учеб. пособие для вузов. – М., 2005.
   

Языки и методы программирования. Характеристики классов языков программирования. Трансляция и трансляторы. Язык Паскаль. Предметная область языка. Алфавит, лексика, пунктуация, ключевые слова. Структура программы. Заголовок, описания данных, тело программы. Форматы структуры. Величины в программе. Простые и сложные типы данных. Управляющие структуры: серии, ветвления, циклы. Присваивания. Операторы ввода и вывода, форматы вывода. Подпрограммы: процедуры и функции, их роль в программах. Формальные и фактические параметры. Локальные и глобальные переменные. Способы обмена параметрами между программой и подпрограммами.

Литература:

1. Аляев Ю.А., Козлов О.А. Алгоритмизация и языки программирования Pascal, C++, Visual Basic. – М., 2002.
   
2. Биллиг В.А. Основы программирования на С#. – М., 2006.
   

Архитектура вычислительных систем. Архитектура компьютера. Принципы работы микропроцессора и микроЭВМ. Вычислительная система. Архитектура вычислительной системы. Аппаратное и программное обеспечение. Особенности ЭВМ различных поколений. Структура ЭВМ. Структура памяти. Взаимодействие процессора и памяти. Основной алгоритм работы процессора. Понятие архитектуры микропроцессора. Арифметико-логическое устройство. Регистры и счетчики. Программно-доступные регистры. Понятие о машинном языке. Язык ассемблера и язык макроассемблера.

Литература:

1. Бройдо В.Л., Ильина О.П. Архитектура ЭВМ и систем: Учебник для вузов. – СПб., 2009.
   
2. Могилев А.В., Пак Н.И., Хённер Е.К. Информатика. – М., 2008.
   
3. Степанов А.Н. Архитектура вычислительных систем и компьютерных сетей. – СПб., 2007.
   

Направление подготовки «ПРИКЛАДНАЯ МАТЕМАТИКА И ИНФОРМАТИКА»


МАТЕМАТИЧЕСКОЕ И ИНФОРМАЦИОННОЕ ОБЕСПЕЧЕНИЕ ЭКОНОМИЧЕСКОЙ ДЕЯТЕЛЬНОСТИ


1. Линейная алгебра и аналитическая геометрия

1. Определители и их свойства.
   
2. Ранг матрицы. Теорема о базисном миноре. Теорема о ранге матрицы.
   
3. Исследование разрешимости систем линейных алгебраических уравнений. Общее решение системы линейных алгебраических уравнений.
   
4. Линейные пространства. Базис и размерность. Преобразование координат вектора при переходе к новому базису. Линейные подпространства.
   
5. Линейные операторы. Матрица оператора. Образ и ядро линейного оператора. Обратный оператор.
   
6. Евклидовы и унитарные пространства. Неравенство треугольника. Неравенство Коши-Буняковского.
   
7. Собственные значения и собственные векторы линейного оператора. Характеристический многочлен. Собственное подпространство.
   

Литература

1. Ильин В.А., Ким Г.Д. Линейная алгебр и аналитическая геометрия. М.: Изд-во МГУ. 2002 (и последующие издания).
   
2. Воеводин В.В. Линейная алгебра. М.: Наука. 1986 (и последующие издания).
   

2. Математический анализ.

1. Предел числовой последовательности. Cвойства сходящихся последовательностей. Частичные пределы. Критерий Коши.
   
2. Непрерывные функции и их свойства. Свойства функций, непрерывных на отрезке.
   
3. Производная и ее свойства. Правила вычисления производной. Уравнение касательной к кривой.
   
4. Производные и дифференциалы высших порядков. Формула Тейлора.
   
5. Определенный интеграл Римана. Основные свойства. Критерий интегрируемости.
   
6. Интеграл с переменным верхним пределом и его свойства. Формула Ньютона-Лейбница.
   
7. Числовые ряды. Сходимость ряда, сумма ряда. Критерий Коши сходимости ряда. Признаки сходимости числовых рядов.
   
8. Функциональные ряды. Равномерная сходимость. Признак Вейерштрасса равномерной сходимости. Непрерывность суммы функционального ряда.
   
9. Степенные ряды и их свойства. Радиус сходимости. Ряд Тейлора.
   
10. Ряды Фурье. Достаточные условия равномерной сходимости рядов Фурье.
    
11. Экстремумы функции многих переменных. Необходимые и достаточные условия экстремума.
    

Литература

1. Кудрявцев Л.Д. Математический анализ. Т. 1, 2. М.: Высшая школа. 1973 (и последу-ющие издания).

2. Лаврентьев М.А., Шабат Б.В. Методы теории функций комплексного переменного. М.: Наука. 1978 (и последующие издания).


3. Обыкновенные дифференциальные уравнения

1. Обыкновенные дифференциальные уравнения. Основные понятия. Уравнения первого порядка, интегрируемые в квадратурах.
   
2. Задача Коши. Теоремы существования и единственности решения задачи Коши.
   
3. Системы линейных дифференциальных уравнений первого порядка. Общее решение.
   
4. Устойчивость по Ляпунову и асимптотическая устойчивость решений систем дифференциальных уравнений. Случай систем с постоянными коэффициентами. Простейшие типы точек покоя.
   

Литература

1. Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление. М.: Наука. 1969 (и последующие издания).
   
2. Тихонов А.Н., Васильева А.Б., Свешников А.Г. Дифференциальные уравнения. М.: Наука. 1985 (и последующие издания).
   

Литература

1. Тихонов А.Н., Самарский А.А. Уравнения математической физики. М.: Наука. 1980 (и последующие издания).
   
2. Олейник О.А. Лекции об уравнениях с частными производными. М.: Бином. 2005 (и другие издания).
   

5. Численные методы

1. Задача интерполирования функций. Интерполяционный многочлен в формах Лагранжа и Ньютона.
   
2. Численное интегрирование
   
3. Численное дифференцирование.
   
4. Методы решения нелинейных уравнений.
   
5. Прямые методы решения систем линейных алгебраических уравнений.
   
6. Итерационные методы решения систем линейных алгебраических уравнений.
   
7. Численные методы решения задачи Коши для обыкновенных дифференциальных уравнений. Метод Рунге-Кутта.
   

Литература

1. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. М.: Наука. 1987 (и последующие издания).
   
2. Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы для инженеров. М.: Высшая школа. 1994 (и последующие издания).
   

6. Элементы функционального анализа

1. Метрические пространства. Открытые и замкнутые множества. Полнота. Принцип сжимающих отображений и его приложения.
   
2. Нормированные и банаховы пространства. Линейные операторы, их ограниченность и непрерывность, норма. Пространство 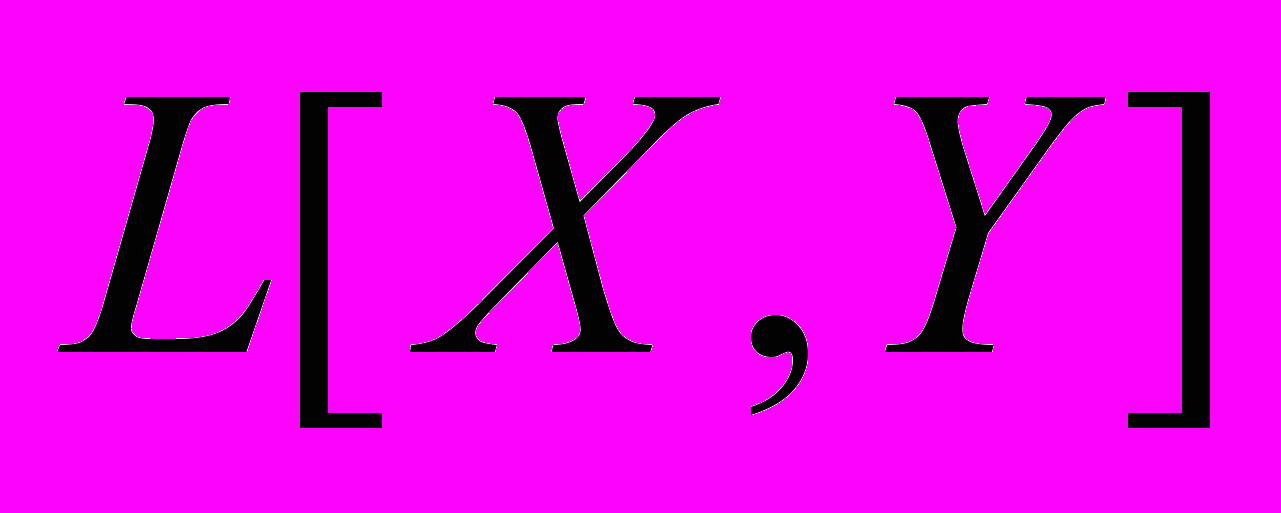и его полнота.
   
3. Гильбертовы пространства. Ортонормированные системы. Ряды Фурье.
   

Литература

1. Треногин В.А. Функциональный анализ. М. Наука. 1986 (и последующие издания).
   
2. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа М.: Наука. 1976 (и последующие издания).
   

7. Теория вероятностей и математическая статистика.

1. Классическое определение вероятности. Геометрическое определение вероятности.
   
2. Алгебра событий.
   
3. Основные теоремы теории вероятности: сложения и умножения вероятностей,
   
4. формула полной вероятности, формула Байеса.
   
5. Случайные величины. Дискретные и непрерывные случайные величины. Функция
   
6. распределения, плотность вероятности. Математическое ожидание, дисперсия.
   
7. Свойства математического ожидания, дисперсии случайной величины. Нормальное
   
8. распределение.
   
9. Основные понятия математической статистики. Выборка из генеральной совокупности. Оценки параметров случайной величины. Свойства несмещенности, состоятельности, эффективности.
   

Литература

1. Жукова Г.С. Математика для студентов экономических специальностей. Часть II.-М.: Изд-во РГСУ, 2004. – 362 с.

2. Гмурман В.Е. Теория вероятностей и математическая статистика. - М.: Высшая школа, 1998.


8. Дискретная математика.

1. Понятие множества. Наивная и аксиоматическая теория множеств. Операции над множествами: объединение, пересечение, дополнение, разность, декартово произведение. Диаграммы Венна. Мощность множества (общее представление).
   
2. Графы и их элементы. Способы представления графов в ЭВМ.
   
3. Связность. Циклы. Деревья. Сети.
   

Литература

1.Яблонский С.В. Введение в дискретную математику. М.: Высшая школа, 2004. 384 с.

2.Новиков Ф. А. Дискретная математика для программистов. СПб: Питер, 2005. 301 с.


9. Оптимизация и оптимальное управление.

1. Программное управление, обратная связь. Задачи оптимального управления Майера, Лагранжа, Майера-Больца. Принцип максимума Понтрягина.
   
2. Управляемость и наблюдаемость. Критерии управляемости. Принцип оптимальности Беллмана. Линейно-квадратичная задача оптимального управления.
   
3. Выпуклые множества и их свойства. Выпуклые функции и их свойства. Критерии выпуклости гладких функций.
   
4. Правило множителей Лагранжа. Теорема Куна-Таккера.
   
5. Метод градиентного спуска.
   

Литература

1.Александров В.В. и др. Оптимальное управление движением. М.: Физматлит, 2005.-376 с.

2.Афанасьев В.Н., Колмановский В.Б., Носов В.Р. Математическая теория конструирования систем управления. М.: Высшая школа, 1998. 574 с.


10. Информатика, языки программирования, программное обеспечение.

1. Структура ЭВМ и программный принцип управления Дж. фон. Неймана. Основные виды архитектуры ЭВМ. Программное и аппаратное обеспечение ЭВМ.
   
2. Основные понятие о языках программирования: синтаксис, семантика, формальные способы описания языков программирования. Языки Turbo Pascal, C.
   
3. Типы данных, способы и механизмы управления данными.
   
4. Процедурно-ориентированный и объектно-ориентированный подходы в программировании. Понятие класса. Свойства, методы и события класса.
   
5. Текстовые файлы и их особенности. Структура текстового файла. Работа с текстовыми файлами. Примеры программ обработки текстовых файлов.
   
6. Организация баз данных. Модели данных. Основные функции поддержки баз данных. Язык запросов SQL.
   

Направление подготовки

«ЭКОЛОГИЯ И ПРИРОДОПОЛЬЗОВАНИЕ»


ЭКОЛОГИЯ


Предмет и объекты изучения экологии. Место экологии в системе научных знаний. Аутэкология, демэкология, синэкология. История развития науки и ее задачи. Экология – теоретическая основа охраны окружающей среды и рационального использования природных ресурсов.