Логико-лингвистические модели предикации и предикативности

Вид материала

Реферат

Содержание Нормальные формы в логике первого порядка Описание ситуаций в предикатной форме P3(№8, “Беломорск“)&P P1(“Свирь”, №1)&P P13(“Беломорск”, капремонт, s

Подобный материал:

• Лингвистические основы информатики, 16.8kb.
• Отдел образования Несвижского райисполкома Учреждение образования, 228.72kb.
• Iv-я Всероссийская научная конференция «Нечеткие системы, мягкие вычисления и интеллектуальные, 92.67kb.
• Исследование бытия и распада жанровой системы русской поэзии xviii-начала XIX века, 4010.98kb.
• С. 277 III. Некоторые специально-лингвистические вопросы перевода художественной литературы, 562kb.
• Лекция 7 Моделирование процессов, 67.29kb.
• Логико-математические модели мышления и основополагающие принципы системного развития, 132.9kb.
• [25/01/2010] Лингвистические права стали предметом спора в ряде европейских стран,, 84.53kb.
• Дискурс как лингвистическая реальность и лингвистические реалии в пространстве языка, 33.46kb.
• Сборник статей Xмеждународной научно-практической конференции «Лингвистические и культурологические, 109.57kb.

Нормальные формы в логике первого порядка

В этом параграфе введем специальные формы аналитических представлений в логике предикатов первого порядка. Эти представления аналогичны каноническим формам представления в логике высказывания: дизъюнктивной и конъюнктивной нормальным формам. Напомним, что высказывание представлено в дизъюнктивной нормальной форме (ДНФ), если оно записано в следующем виде:

F = F₁  F₂  ...  F_m.

При этом высказывания F_i имеют вид:

F_i1  F_i2  ...  F_ir,

причем каждое F_ij есть или буква (базовый элемент), или буква с отрицанием. Примером ДНФ может служить:

F = abh 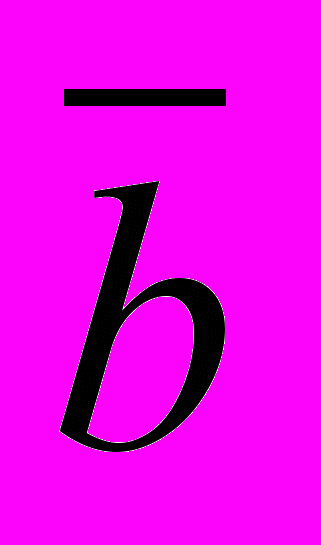 c.

Высказывание представлено в конъюнктивной нормальной форме (КНФ), если оно записано в следующем виде:

F = F₁  F₂ & ... & F_l.

При этом высказывания F_i имеют вид:

F_i1  F_i2  ...  F_is,

причем каждое F_ij есть или буква, или буква с отрицанием.

Примером КНФ может служить:

F = (a 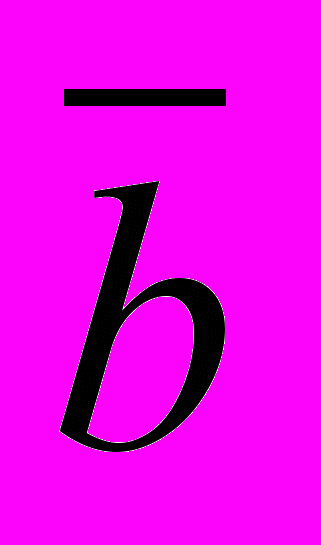  h) & (b  ).

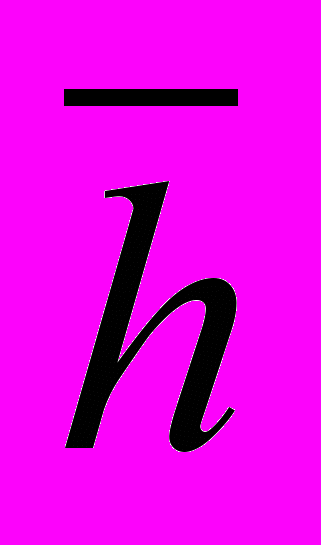Аналоги этих представлений есть и в логике предикатов первого порядка. Будем говорить, что формула Ф представлена в предваренной нормальной форме (ПНФ), если она представлена в следующем виде:

Ф = ʞ₁x₁ʞ₂x₂...ʞ_nx_nM,

где каждый ʞ_ix_i – квантор общности x_i или квантор существования x_i, а M – формула, не содержащая кванторов. Например,

Ф = xz(R(x) & Q(z)).

Часть записи в ПНФ, предшествующая M, называется префиксом. Формула M, не содержащая кванторов, называется матрицей.

Для преобразования формулы к ПНФ используются эквивалентные преобразования, указанные в примере 3-8, а также специальные правила вынесения кванторов в префиксную часть (вынесение кванторов за скобки). Эти правила имеют следующий вид (пусть F есть формула, не содержащая x):

1. ʞxR(x) F = ʞx(R(x) F);
   
2. ʞxR(x) F = ʞx(R(x) F);
   

если G и Q – формулы, содержащие переменную x, то

3. xG(x) & (xQ(x)) = x(G(x) & Q(x));
   
4. xG(x)  (xQ(x)) = x(G(x)  Q(x));
   

Правило 3 отражает тот факт, что при наличии связанных переменных квантор общности может быть вынесен за скобки (т. е. формула может быть преобразована в ПНФ), если в этой формуле кванторы соединены операцией конъюнкции. Такая же возможность есть и для кванторов существования, если они соединены в формуле операцией дизъюнкции (правило 4).

Существенно, что квантор  не может быть выражен через дизъюнкцию, а квантор  – через конъюнкцию, т. е. формулы

A₁: xG(x)  xQ(x)

и

A₂: x(G(x)  Q(x))

не эквивалентны, как не эквивалентны формулы

A₁: xG(x)  xQ(x)

и

A₂: x(G(x)  Q(x))

Тем не менее, есть возможность преобразования двух последних формул в ПНФ, если прибегнуть к искусственному приему, суть которого заключается в том, что некоторая связанная переменная x одного квантора меняется переменной y, но такой, которая не входит в область значений переменной другого квантора, т. е. не встречается в G(x).

Такой прием будем называть стандартизацией связанных переменных. При этом одна переменная в области действия квантора заменяется другой без изменения истинности формулы.

Пусть имеется формула  = xG(x)xQ(x). Преобразуем  путем переименования всех вхождений x в формулу, являющуюся второй частью в дизъюнкции. Тогда получим  = xG(x)yQ(y). Используем первое из перечисленных выше правил эквивалентных преобразований:

 = xy(G(x)Q(y)).

Стандартизируем формулу, описывающую афоризм К. Пруткова:

 = xyP(x, y)&xzQ(x, z).

Вынесем за скобки x:

 = x(yP(x, y)&(zQ(x, z))).

Здесь кванторы существования y и z связаны знаком конъюнкции, что на первый взгляд препятствует выносу этих кванторов за скобки. Но на самом деле в формуле yP(x, y) только y – связанная переменная, а в формуле zQ(x, z) связанной переменной является z. Поэтому вполне можно и здесь вынести кванторы y и z за скобки, приведя к предваренной нормальной форме:

 = xyz(P(x, y)&Q(x, z)).

Описание ситуаций в предикатной форме

Рассмотренный предикатный язык, подобно языку реляционного типа, может служить для описания ситуаций, складывающихся на объекте управления и среде, в которой этот объект функционирует. Приведем несколько примеров, описывающих следующую ситуацию:

К причалу №1 подходит судно “Свирь”, пришедшее с грузом леса. Портальный кран №8 занят на разгрузке судна “Беломорск” на причале №2. Этой же операцией занят портальный кран №5. Портальный кран №6 свободен, но не может быть перемещен на причал №1 из-за крана №5.

Будем последовательно вводить необходимые предикаты, и описывать наблюдаемую ситуацию. Введем предикаты P₁(x, y) и P₂(x, z). Первый предикат будет истинным, если судно x приближается к причалу y. Областью определения переменной x будет служить множество, состоящее из всех названий судов, а областью определения y – множество всех номеров причалов. Второй предикат будет истинным, если судно x имеет груз z. Областью значений переменной z будут всевозможные значения грузов. При этих предположениях первой фразе описания наблюдаемой ситуации “К причалу №1 подходит судно ‘Свирь’, груженое лесом”, будет соответствовать следующая предикатная запись:

P₁(“Свирь”, №1)& P₂(“Свирь”, лес).

Введем предикат P₁(u, x), который является истинным, если портальный кран u занят на операции разгрузки судна x. Областью значений u является все множество названий для портальных кранов. Введем также предикат P₄(u, y), который является истинным, если портальный кран u находится на причале y. Тогда вторая фраза описания наблюдаемой ситуации: “Портальный кран №8 занят на разгрузке судна ‘Беломорск’ на причале №2” на предикатном языке выглядеть так:

P₃(№8, “Беломорск“)&P₄(№8, №2).

Третьей фразе “Этой же операцией занят портальный кран №5” соответствует описание:

P₃(№5, “Беломорск“).

Введем предикат P₅(u), который истинен, если портальный кран u свободен. Кроме того, введем предикат P₆(u, y), который принимает истинное значение, когда портальный кран u можно передвигать на причал y. Наконец, введем предикат P₇(u₁, u₂) определены на том же множестве значений, что и u. Этот предикат является истинным, если портальный кран u₁ является препятствием для портального крана u₂. С учетом введенных предикатов последняя фраза описания ситуации “Портальный кран №6 свободен, но не может быть перемещен на причал №1 из-за крана №5” может быть представлен как

P₅(№6)& P₆(№6, №1)&P₇(№5, №6).

Конъюнкция записей для всех фраз описания приводит к полной записи наблюдаемой ситуации:

P₁(“Свирь”, №1)&P₂(“Свирь”, лес)&P₃(№8, “Беломорск“)&P₄(№8, №2)& P₃(№5, “Беломорск“)&P₅(№6)&P₆(№6, №1)&P₇(№5, №6).

Таким образом, получилось описание наблюдаемой ситуации с некоторым нарушением условия логики предикатов. Как уже известно, истинность или ложность предиката P целиком определяется теми конкретными значениями, которые принимают его переменные из области своего определения, и принятой интерпретацией самого предиката. В данном случае интерпретация предиката уже задана. Например, предикат P₅(№6) будет всегда истинным или всегда ложным, так как он зависит лишь от одной переменной, и эта переменная приняла определенное значение. Другими словами, утверждение: “Портальный кран №6 свободен” будет тождественно истинным или тождественно ложным. Ясно, что это не соответствует действительности. Истинность и ложность высказывания, полученных из предикатов при замене переменных их значениями, зависит от той конкретной наблюдаемой ситуации, которая в данный момент описывается. Значит, на самом деле, все предикаты, входящие в описание ситуации, кроме указанных в приведенном ранее примере про агрегаты, зависят еще от некоторой общей для всех предикатов переменной s, значения которой берутся из множества наблюдаемых ситуаций. Такие предикаты будет называть ситуативными. Заметим, что при реляционных описаниях элементарные синтагмы (xry) также могут быть ситуативными. Актуализация того или иного отношения между x и y зависит, конечно, от наблюдаемой ситуации. В иной ситуации этого отношения между x и y может и не быть. Те предикаты и элементарные синтагмы, которые не зависят с точки зрения интерпретации от текущей ситуации, называются неситуативными. Они в свою очередь делятся на динамические и статические. Примером динамического предиката может служить предикат P₈(v, t*), в котором переменная t принимает значения из множества T, элементами которого являются некоторые отметки времени. Смысл этого предиката следующий: “В момент времени t* включить насос v”. Истинность этого предиката определяется значением переменной t. Если t>=t*, то этот предикат считается истинным, в противном случае – ложным. Отметим, что истинность или ложность этого предиката связана не с фактическим состоянием насоса v (включен или выключен), а с фактором выдачи на объект управления соответствующего императива: “Включить насос v”. Статический предикат в условиях данной системы управления и данного объекта управления интерпретируется лишь в зависимости от значений своих обычных переменных. Например, статическим будет предикат P₄(u , y), если портальные краны в порту, которыми управляют, не могут передвигаться от причала к причалу.

Статические предикаты или элементарные синтагмы отражают в модели знаний некоторые постоянные сведения об объекте управления, а динамические и ситуативные – текущие наблюдаемые состояния этого объекта и окружающей среды.

Рассмотрим описание следующей ситуации: “Судно ‘Свирь’ быстро приближается к причалу, где уже стоят суда”. Введем предикат P₉(x, y, s). Смысл этого предиката таков, что он является истинным, если ситуация s такова, что судно x быстро приближается к причалу y. Вместо такого ситуативного предиката можно было бы ввести предикат P₁₀(x, w), в котором переменная w принимает значения из множества скоростей для судов. Для этого предиката можно задать интерпретацию, не зависящую от текущей ситуации (в том смысле, что таблица определения истинности для предиката P₁₀ не содержит в качестве переменной s). Но такой предикат можно использовать для описания данной ситуации в виде конъюнкции P₁₀(x, w)& P₁(x, y) только в том случае, если имеется информация о наблюдаемой скорости судна “Свирь”. Если ввести предикат P₁₁(x, y , s), принимающий значение И, когда судно x находится в ε-окрестности причала y, то описание данной ситуации на предикатном языке будет иметь следующий вид:

P₉(“Свирь”, y*, s*)&x(P₁₁(x, y*s*)).

Здесь y* означает некоторый фиксированный причал, точное значение которого не указано. Повторение его в обеих формулах, входящих в конъюнкцию, свидетельствует о том, что y в этих двух формулах принимает одинаковое значение. Значение s* фиксирует определенную ситуацию.

Обратимся к тексту описания такой ситуации: “У причала находятся три судна. На причале находится груз – лес в количестве 1000 тонн”. Рассмотрим конъюнкцию трех ситуативных предикатов:

P₁₁(x¹, y*, s*)& P₁₁(x², y*, s*)& P₁₁(x³, y*, s*).

В этой записи y* есть некоторый фиксированный причал, одинаковый для всех трех предикатов. Аналогично s* соответствует тому, что истинность всех трех предикатов оценивается в одной и той же фиксированной ситуации. Наконец, x¹, x², x³ показывают, что в различных предикатах берутся не совпадающие между собой значения переменной x. Рассмотрим ситуативный предикат P₁₂(y, q, s), в котором переменная q принимает значения, совпадающие с тем или иным количеством леса, находящегося в ситуации s на причале y. Окончательная запись ситуации этого примера выглядит так:

P₁₁(x¹, y*, s*)& P₁₁(x², y*, s*)& P₁₁(x³, y*, s*)& P₁₂(y*, 1000, s*).

Посмотрим, как строятся предикатные записи, когда в описании ситуации присутствует модификатор.

Используем такую ситуацию: “Судно ‘Беломорск’, прошедшее капитальный ремонт, не находится у причала №8”. Введем ситуативный предикат P₁₃(x, h, s), переменная h которого принимает значения из множества следующего вида: H={не проходило ремонта, проходило мелкий ремонт, проходило профилактический ремонт, проходило средний ремонт, проходило капитальный ремонт}. Тогда исходная ситуация этого примера может быть передана с помощью следующего предикатного описания:

P₁₃(“Беломорск”, капремонт, s*)&(P₁₁(“Беломорск”, №8, s*)).

Из сравнения приведенных описаний ситуаций с реляционными описаниями тех же ситуаций видно, что оба типа языка вполне пригодны для использования в моделях знаний. Для предикатных языков трудности вызывают модальности, оценки и квантификаторы типа: “почти для всех”, ”в 25% случаев”, ”только для x*” и т.п. Таким образом, реляционные описания предпочтительнее предикатных при описании ситуаций, но у последних есть одно неоспоримое преимущество – наличие эффективных процедур вывода, чего лишены реляционные описания.

Литература

1. Демьянков В. З. Семантические роли и образы языка. (Найдено в Internet).
   
2. Заде Л.А. Понятие лингвистической переменной и его применение к принятию приближенных решений. - М.:Мир, 1976.-165 с.
   
3. Зензеров В.Н. Предикативность и/или предикатность синтаксических структур? // Сб.: Предикативность и полипредикативность. Конструктивный аспект. — Киров: КГПИ, 1990. – С. 66–78.
   
4. Кастанеда Гектор-Нери. Художественный вымысел и действительность: их фундаментальные связи (очерк онтологии совокупного опыта).
   
5. Качанов Ю. Л. “Россия” как предмет социологии. Социологические исследования, №10, 2001.
   
6. Курдюмов В.А. Идея и форма. Основы предикационной концепции языка. - М., 1999. - 194 с. (монография).
   
7. Мельников Г.П. Системология и языковыe аспекты кибернетики М.: Сов. радио, 1978.
   
8. Поспелов Д.А. Логико- лингвистические модели в системах управления. - М.: Энергоиздат, 1981. - 231с.
   
9. Романов А.Ф., Шемакин Ю.И. Индуктивно-дедуктивный логический вывод в нечетких условиях // Изв. АН: серия техническая кибернетика, № 5, 1992.
   
10. Ронина E.A. Косвенно-предикативные конструкции с неличными формами глагола в латинском и испанском языках, Омск, 1996.
    
11. Сорокин Б. Ф. Философия филологии (найдено в Interner).
    
12. Соссюр Ф. Заметки по общей лингвистике. - Прогресс, М., 1990.
    
13. Стеблин-Каменский М.И. Спорное в языкознании. - Л., 1974. - С. 34-47.
    
14. Сусов И.П. Введение в теоретическое языкознание. Модуль 5. Основы общего синтаксиса (найдено в Internet).
    
15. @mail.infostar.ru. Сологубов А.П. Логическая модель чувственной сферы сознания.
    
16. ссылка скрыта Подгорная Ю. Аспекты художественного перевода: название текста.