Логико-лингвистические модели предикации и предикативности
| Вид материала | Реферат |
СодержаниеОбщезначимость и противоречивость |
- Лингвистические основы информатики, 16.8kb.
- Отдел образования Несвижского райисполкома Учреждение образования, 228.72kb.
- Iv-я Всероссийская научная конференция «Нечеткие системы, мягкие вычисления и интеллектуальные, 92.67kb.
- Исследование бытия и распада жанровой системы русской поэзии xviii-начала XIX века, 4010.98kb.
- С. 277 III. Некоторые специально-лингвистические вопросы перевода художественной литературы, 562kb.
- Лекция 7 Моделирование процессов, 67.29kb.
- Логико-математические модели мышления и основополагающие принципы системного развития, 132.9kb.
- [25/01/2010] Лингвистические права стали предметом спора в ряде европейских стран,, 84.53kb.
- Дискурс как лингвистическая реальность и лингвистические реалии в пространстве языка, 33.46kb.
- Сборник статей Xмеждународной научно-практической конференции «Лингвистические и культурологические, 109.57kb.
Общезначимость и противоречивость
В пропозициональной логике формула называется общезначимой, если она интерпретируется как истинная при любой интерпретации входящих в нее переменных. Примером общезначимой формулы исчисления высказываний может служить формула (a & b) ( (a b)). Это легко проверить, задав все четыре возможных комбинации, интерпретирующие а и b, и, убедившись, что во всех случаях формула интерпретируется как истинная. Аналогично определяется общезначимость формул в исчислении предикатов. Формула является общезначимой, если она интерпретируется как истинная при любой возможной интерпретации входящих в нее термов и функциональных переменных.
В пропозициональной логике формула называется противоречивой, если она интерпретируется как ложная при любой интерпретации входящих в нее переменных. Примером такой формулы исчисления высказываний является формула (a & a). Аналогично определяется противоречивость формул в исчислении предикатов. Предикатная формула является противоречивой, если для всех интерпретаций входящих в нее термов и функциональных переменных она является ложной.
Между общезначимостью и противоречивостью формул имеют место следующие связи:
- формула общезначима тогда и только тогда, когда ее отрицание противоречиво;
- если формула общезначима, то она непротиворечива (но не наоборот);
- если формула противоречива, то она не общезначима (но не наоборот).
Для компактности последующих записей условимся опускать знак конъюнкции, скобки при операции отрицания и внешние скобки у формул там, где это не приводит к неоднозначному пониманию. Кроме того, как и ранее, вместо знака отрицания будем использовать черту над соответствующим выражением.
Так, легко убедиться, что следующие 18 формул являются общезначимыми:
- (AB) (A B);
- (A B) (B A);
- (AB)(BA);
- (A (B C)) ((A B) C);
- (A(BC))((AB)C);
- (A (BC)) ((A B)( A C));
- (A (BC)) ((A B) ( A C));
- (AИ) И;
- (AЛ) A;
- (AИ) A;
- (AЛ) Л;
- (A
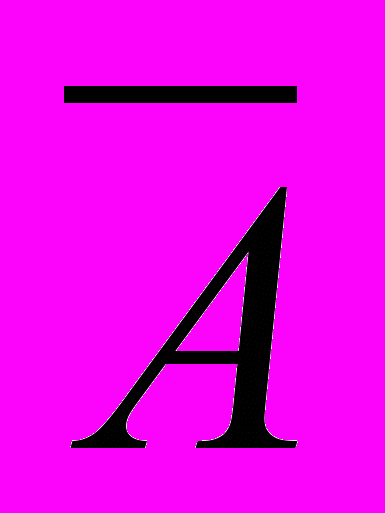 ) И;
) И;
- (A
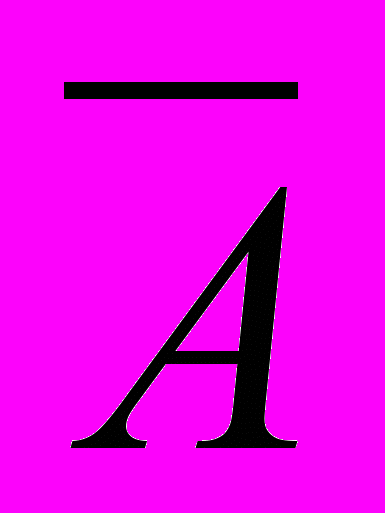 ) Л;
) Л;
-
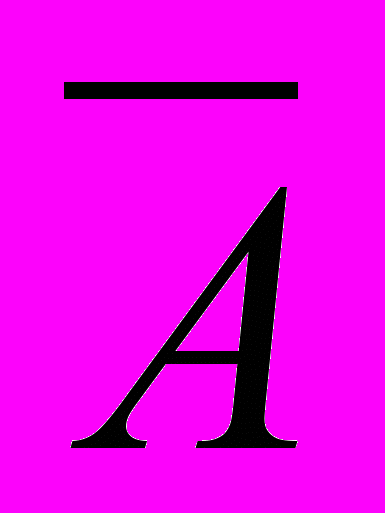 )А;
)А;
-
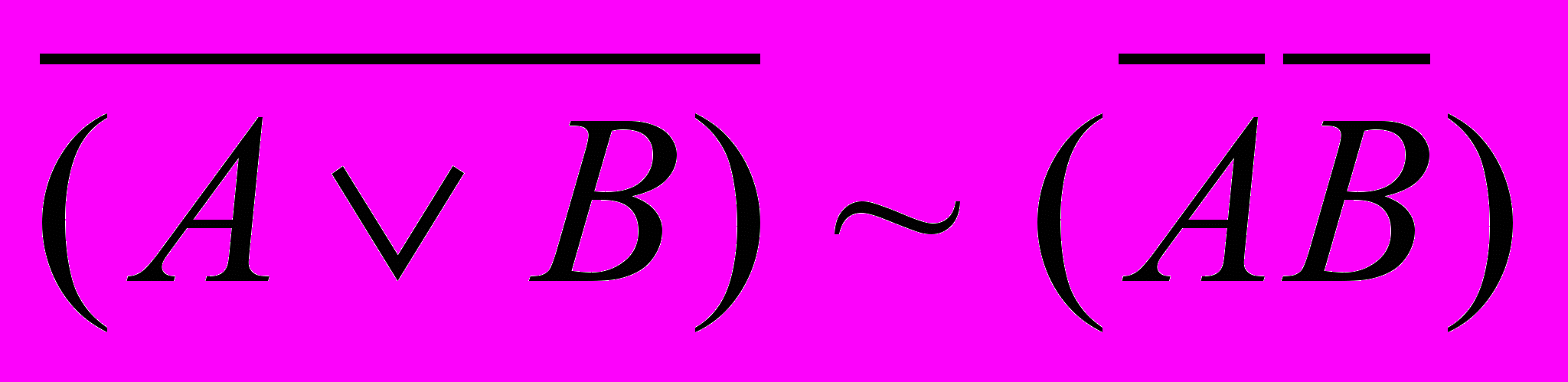 ;
;
-
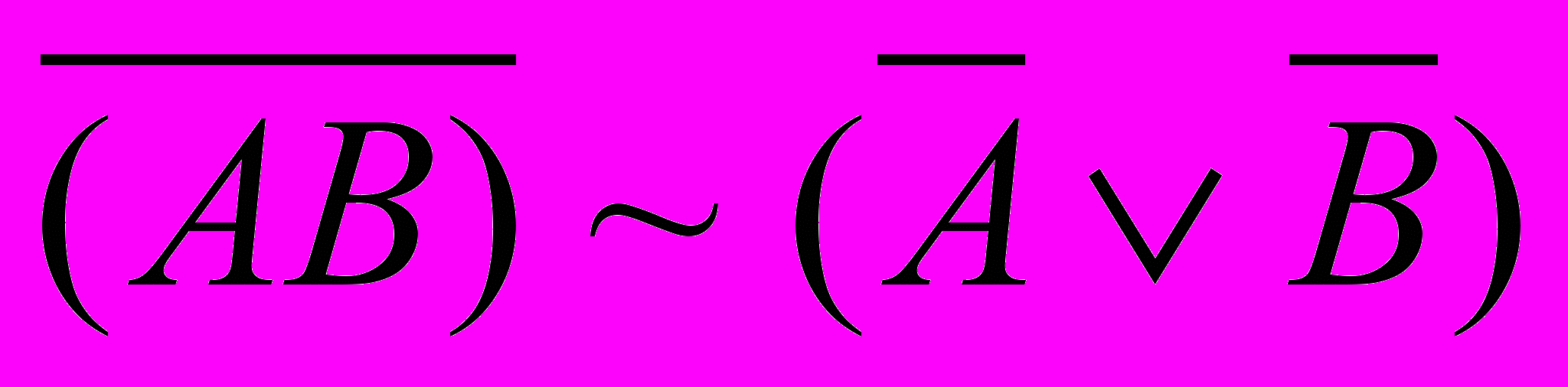 ;
;
-
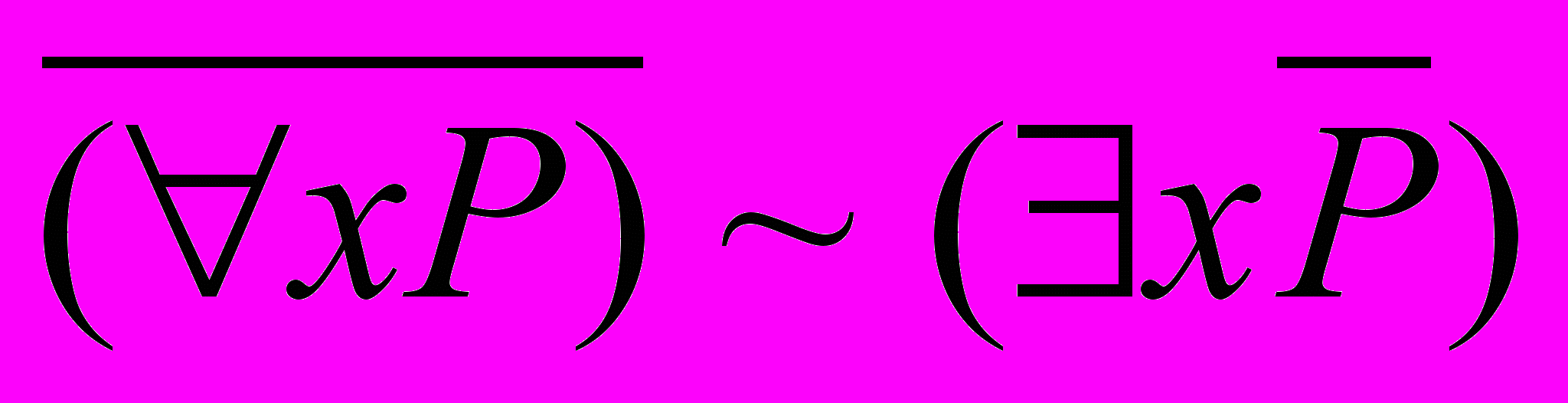
-
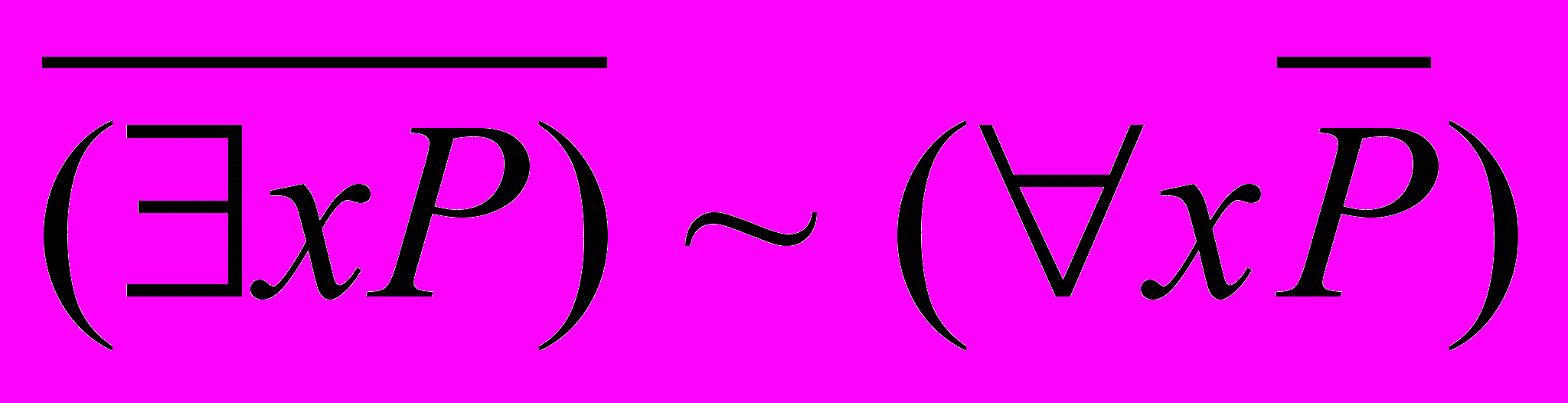
В качестве примера покажем, что формула
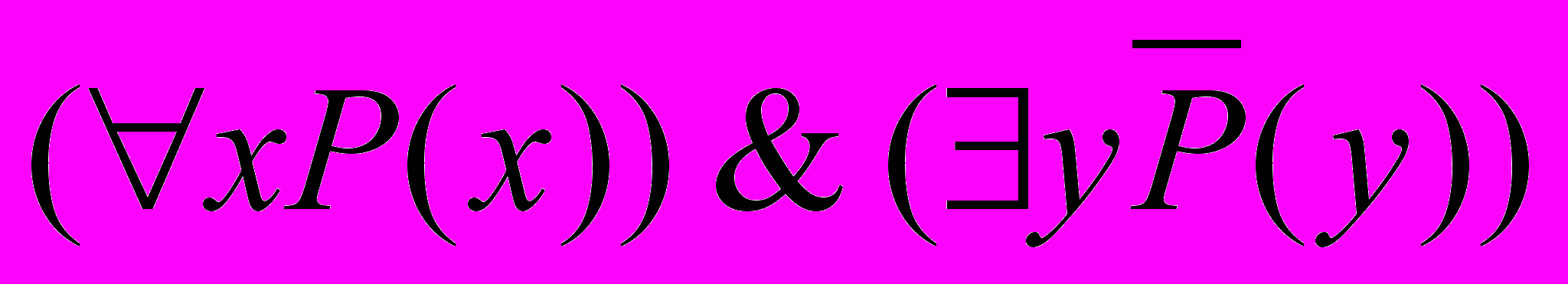 непротиворечива при условии, что x и y определены на некоторой области D.
непротиворечива при условии, что x и y определены на некоторой области D.Введем обозначения:
1=
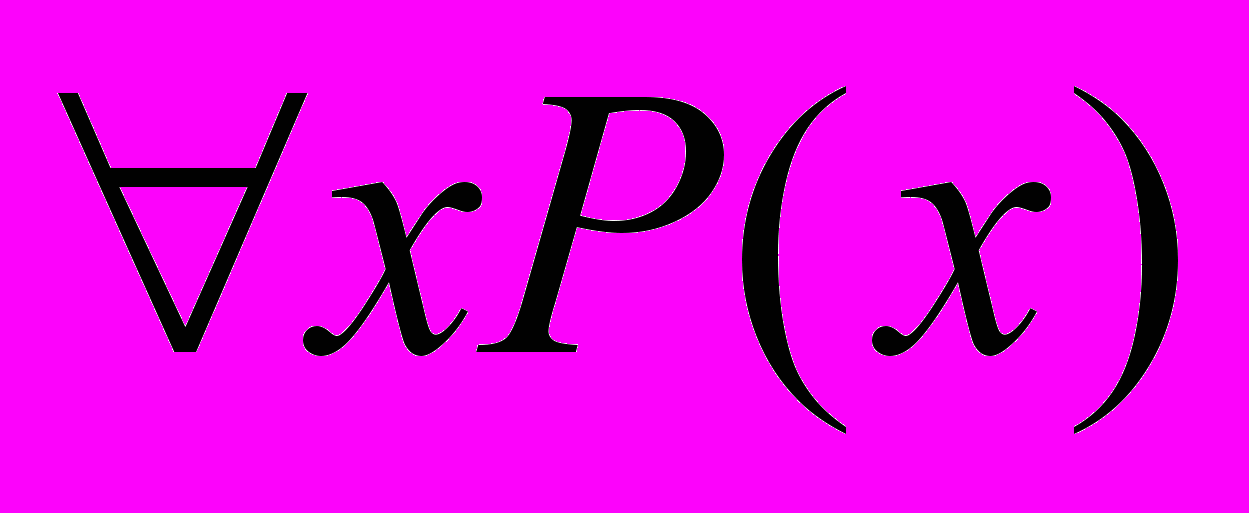 ; 2=
; 2=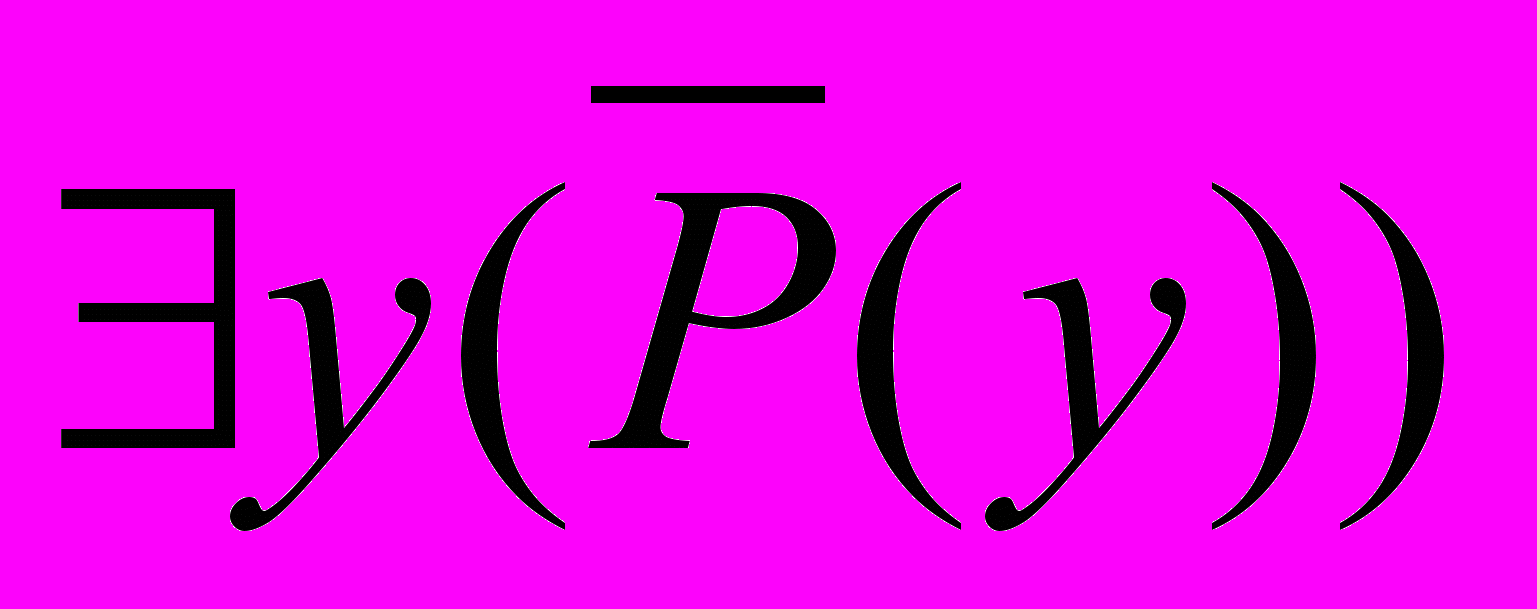 ; =12.
; =12.Преобразуем вторую формулу, выведя знак отрицания из под знака квантора и заменив его квантором общности:
2=(yP(y)).
Если в некоторой области значения переменных x и y совпадают, то, очевидно, что формула всегда ложна. Действительно, если x=y, то формула xP(x)& (xP(x))) ложна, так как это равносильно выражению A&(A)=Л. Рассмотрим случай, когда x и y в заданной области принимают разные значения.
Пусть y приняло такое значение, что
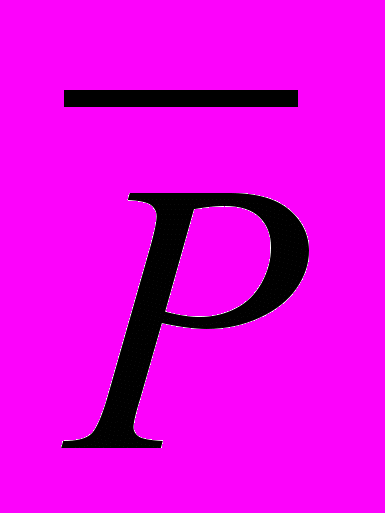 (y) оказался истинным. Это означает, что при таком значении y предикат P(y) ложен. Так как x принимает значения из того же самого множества D, что и y, следовательно, ложно утверждение xP(x) (оно не выполняется для рассматриваемого значения y).
(y) оказался истинным. Это означает, что при таком значении y предикат P(y) ложен. Так как x принимает значения из того же самого множества D, что и y, следовательно, ложно утверждение xP(x) (оно не выполняется для рассматриваемого значения y).Если же 2 никогда не принимает истинного значения, то формула всегда интерпретируется как ложная, так как A&Л=Л.
Таким образом, при любых значениях x и y формула является ложной, следовательно, она противоречива.
В качестве очередного примера покажем, что формула =
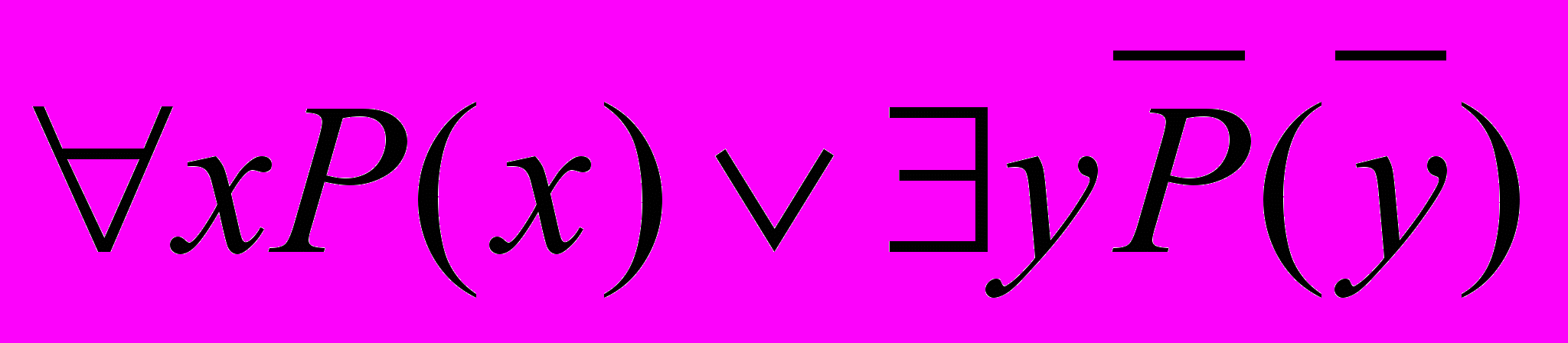 является общезначимой. Так как =12, где 1=xP(x); 2=
является общезначимой. Так как =12, где 1=xP(x); 2=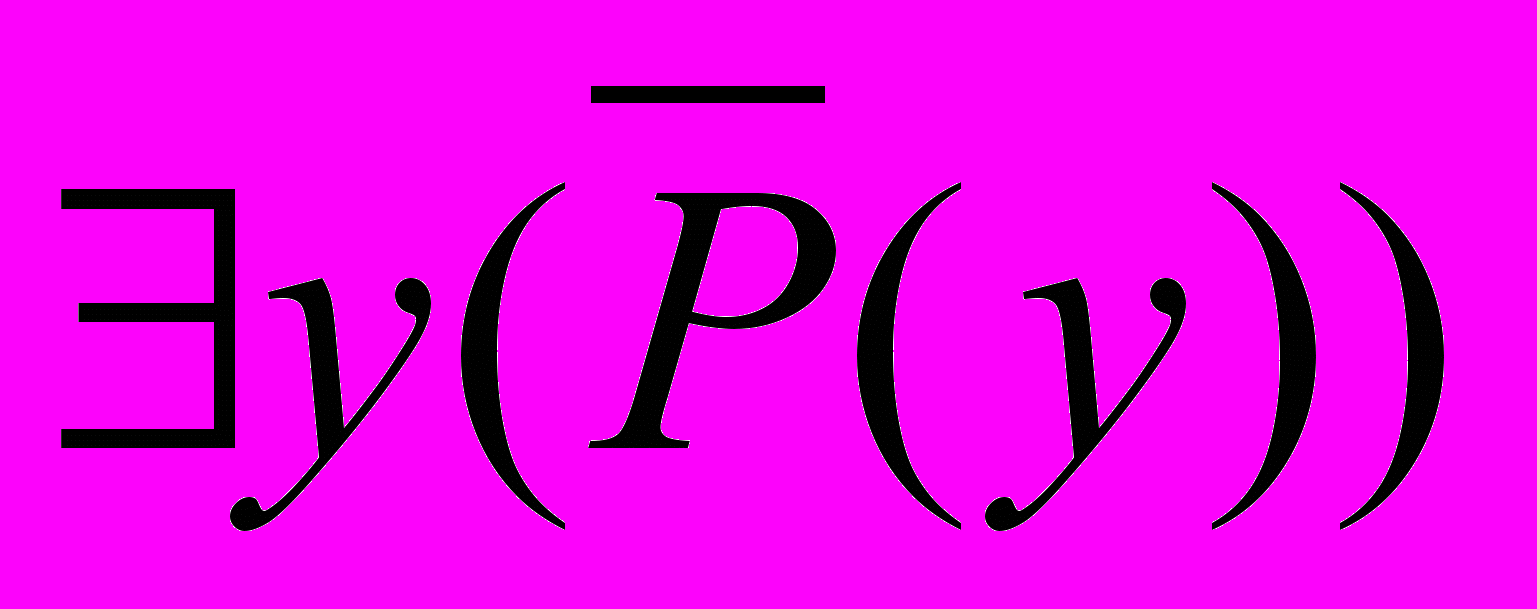 , то для истинности достаточно найти такую интерпретацию, при которой была бы истинна любая из формул 1 или 2 (или обе вместе). Но 1 и 2 связаны между собой следующим образом:
, то для истинности достаточно найти такую интерпретацию, при которой была бы истинна любая из формул 1 или 2 (или обе вместе). Но 1 и 2 связаны между собой следующим образом: 2=
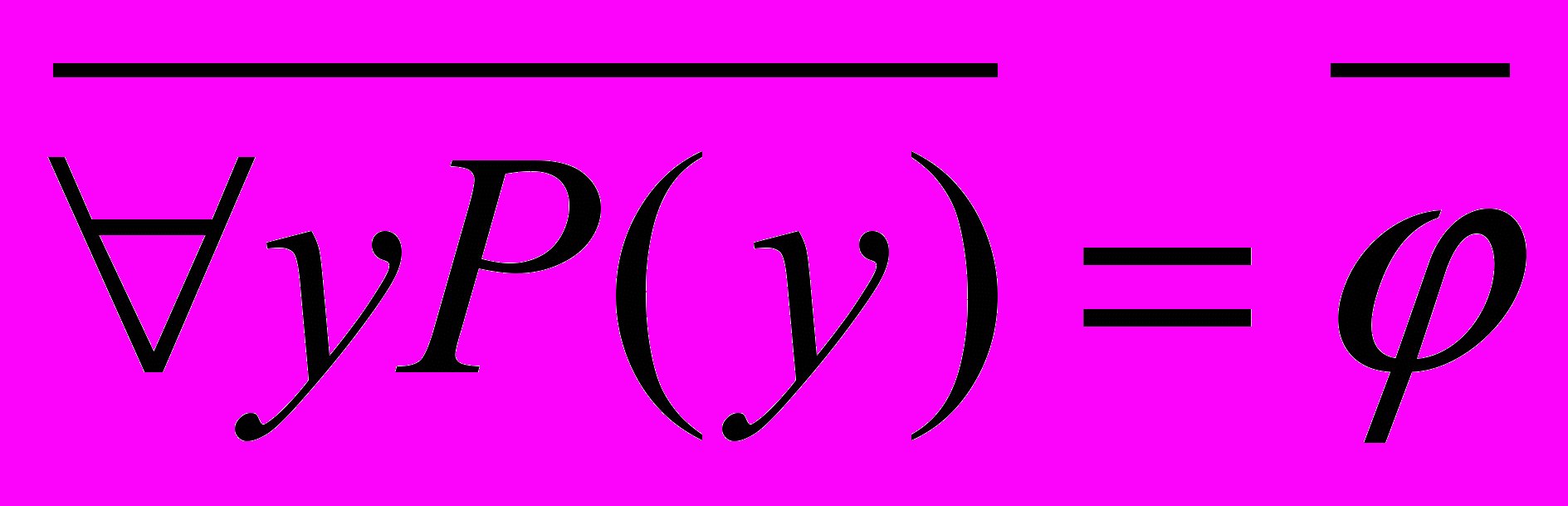 1.
1.Отсюда на основании соотношения 12 (из 18 соотношений) можно получить: =12=1
 1=И.
1=И.Приведенные примеры проверки общезначимости и противоречивости чрезвычайно просты. Для общего случая эти процедуры проводить весьма нелегко, так как число различных предикатов бесконечно, а, следовательно, бесконечно и число возможных их интерпретаций. А никаких других общих приемов для решения подобных задач нет. Положение несколько упрощается при использовании предикатных описаний в реальных управленческих задачах. В этих случаях всегда имеется фиксированное множество различных предикатных символов и конечное число интерпретаций (так как множества Xi в конкретных приложениях всегда конечны и заданы). Поэтому для практических случаев перебор всегда конечен (хотя и может быть весьма большим по объему). Это позволяет использовать при доказательстве общезначимости и противоречивости формул (это оказывается нужным при поиске управленческих решений) обычные процедуры сокращения, характерные для алгоритмов решения переборных задач.
Например, требуется определить, является ли общезначимой формула xP(x), совпадающая по смыслу с утверждением: “Все агрегаты отремонтированы”.
Если речь идет о реальном производстве, для которого множество агрегатов задано (например, D={агрегат №1, агрегат №2, ..., агрегат №805}), то нужно проверить истинность исходной формулы путем определения истинности 805 высказываний вида “Агрегат №i отремонтирован”. Если все эти высказывания истинны, то исходная формула “общезначима“. Конечно, такое определение общезначимости не совпадает с тем, о котором говорилось выше, поэтому это слово взято в кавычки. Но на практике об этом можно не помнить.
