Логико-лингвистические модели предикации и предикативности

Вид материала

Реферат

Содержание Логическое следование и теорема дедукции P часто называют посылкой Формула Q является логическим следствием формул P

Подобный материал:

• Лингвистические основы информатики, 16.8kb.
• Отдел образования Несвижского райисполкома Учреждение образования, 228.72kb.
• Iv-я Всероссийская научная конференция «Нечеткие системы, мягкие вычисления и интеллектуальные, 92.67kb.
• Исследование бытия и распада жанровой системы русской поэзии xviii-начала XIX века, 4010.98kb.
• С. 277 III. Некоторые специально-лингвистические вопросы перевода художественной литературы, 562kb.
• Лекция 7 Моделирование процессов, 67.29kb.
• Логико-математические модели мышления и основополагающие принципы системного развития, 132.9kb.
• [25/01/2010] Лингвистические права стали предметом спора в ряде европейских стран,, 84.53kb.
• Дискурс как лингвистическая реальность и лингвистические реалии в пространстве языка, 33.46kb.
• Сборник статей Xмеждународной научно-практической конференции «Лингвистические и культурологические, 109.57kb.

Логическое следование и теорема дедукции

Итак, был введен синтаксис языка L. Теперь построим процедуры, связанные с правилами вывода этого исчисления. Будем говорить, что формула Q логически следует из формулы P, если для всех интерпретаций, в которых P истинна, формула Q также истинна. Факт логического следования будем обозначать так: P|Q. Логическое следование по существу, описывает некоторый элементарный шаг процедуры вывода новых формул.

Формулу P часто называют посылкой или основанием, а формулу Q – следствием или заключением.

В более общей форме логическое следствие может иметь такой вид: P₁ , P₂ ,..., P_k |Q. Эта запись означает, что при всех интерпретациях, при которых истинны одновременно все P_i , где i=1, 2, ..., k, истинна и формула Q. Если система аксиом состоит только из общезначимых формул, то при наличии правил вывода типа логического следования из этих общезначимых формул будут выводиться также лишь общезначимые формулы.

Между общезначимостью и логическим следованием существует тесная связь, выражаемая в виде теоремы дедукции, доказательство которой можно найти в любом учебнике по математической логике.

Теорема дедукции. Формула Q является логическим следствием формул P₁ , P₂ ,..., P_k тогда и только тогда, когда формула (P₁&P₂& ... &P_k)Q является общезначимой.

Следствием этой теоремы является тривиально следующее из нее утверждение: формула Q является логическим следствием формул P₁ , P₂ ,..., P_k тогда и только тогда, когда формула P₁&P₂& ... &P_k&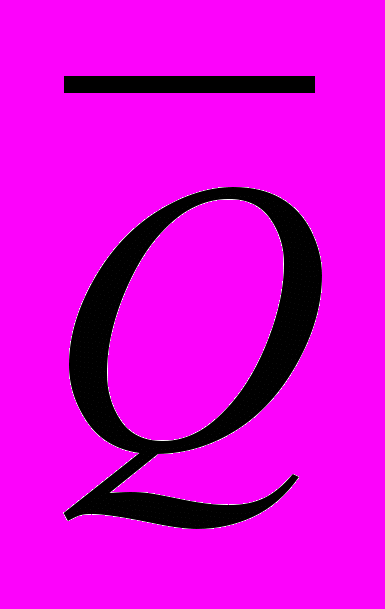 является противоречивой.

Рассмотрим пример. Даны три формулы: ₁ = x(A(x)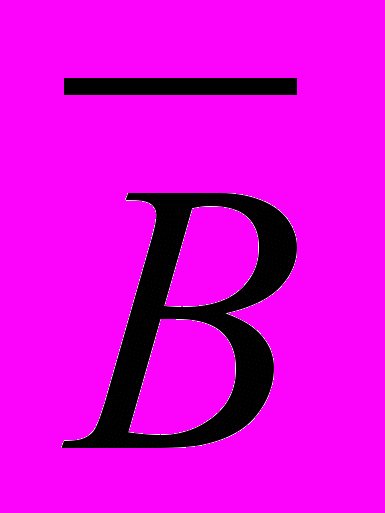(x)); ₂ = x(B(x) & D(x)); ₃ = x(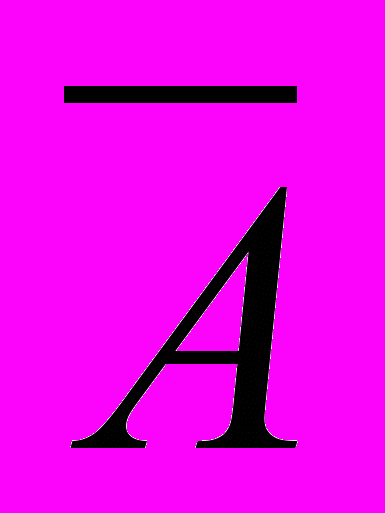(x) & D(x)).

Докажем, что ₃ есть логическое следствие формул ₁ и ₂. Пусть найдена такая интерпретация, что ₁ и ₂ истинны в ней. Это означает, что найдется x=a такой, что B(a) & D(a) является истинной. При этом 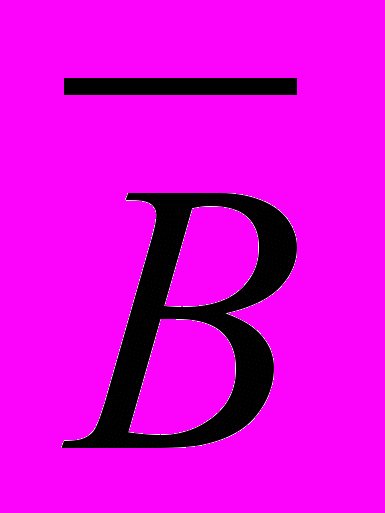(а) ложно. Перепишем ₁, заменив импликацию дизъюнкцией в соответствии с соотношениями из 18 приведенных ранее:

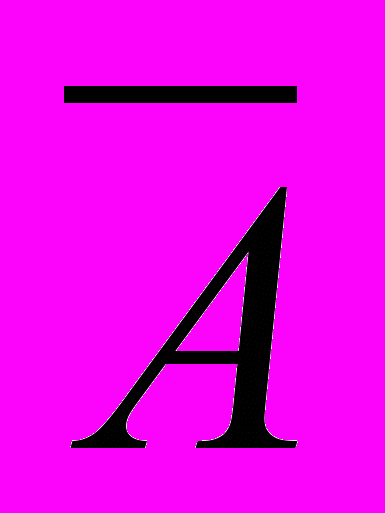₁ = x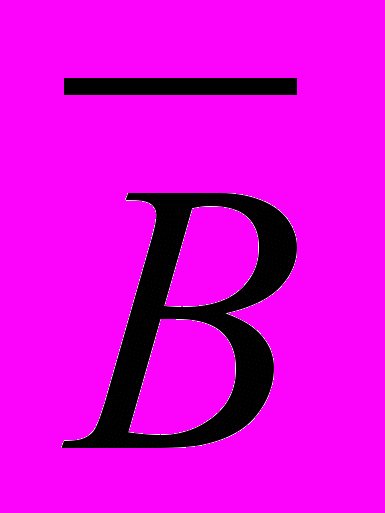((x) (x)).

При x=a ₁ истинна, а 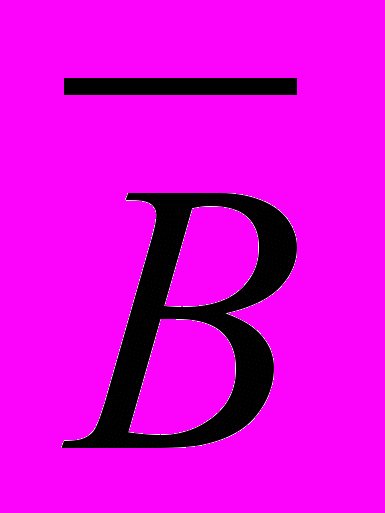(a) ложно. Отсюда следует, что 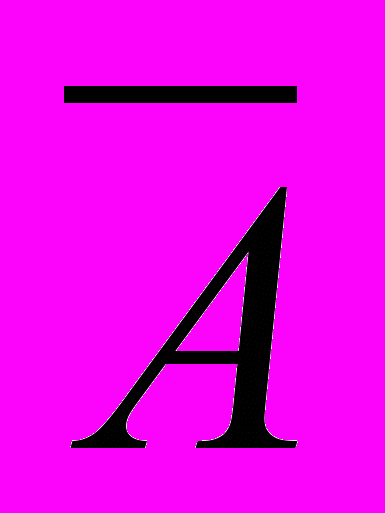(a) является истинным. Из истинности же ₂ при x=a вытекает, что D(x) является истинным. Таким образом, при x=a формула ₃ является истинной. А поскольку интерпретация, при которой ₁ и ₂ истинны, была произвольной, то доказано, что ₃ логически следует из ₁ и ₂.

Пример. Докажем тот же факт, что и в предыдущем примере, использовав теорему дедукции. Для этого покажем, что формула (₁&₂)  ₃ является общезначимой. Последовательно получаем:

₁ & ₂ = (x(A(x) 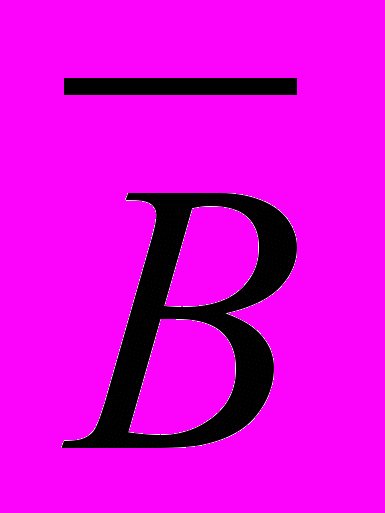 (x))) & (x(B(x) & D(x))).

Если ₁&₂ ложна, то по свойству импликации (₁&₂)₃является истинной. Поэтому рассмотрим лишь тот случай, когда ₁&₂ является истинной. Надо показать, что в этом случае ₃ также является истинной, ибо это обеспечивает истинность импликации. Но это установлено в предыдущем примере. Поэтому (₁&₂)₃ является общезначимой, и ₃ есть логическое следствие ₁ и ₂.

Пример. Дана формула ₁ = 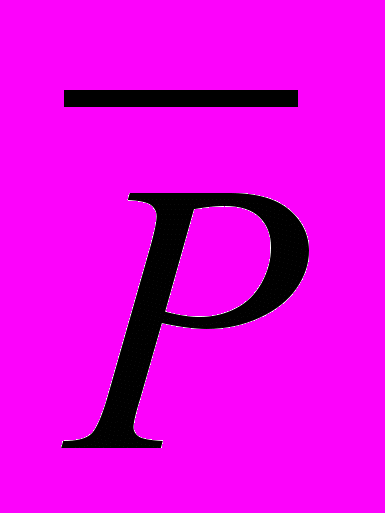(x). Требуется показать, что из нее не следует формула ₂ 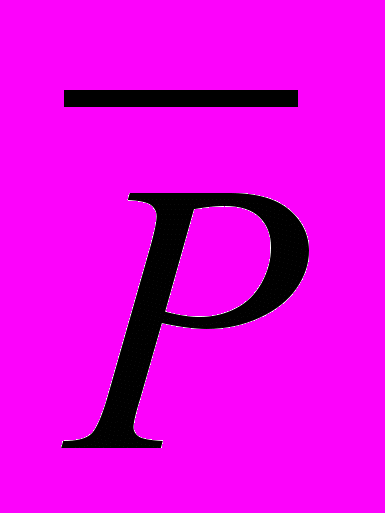= x((x)).

Зададим некоторую область значений для переменной x, например D={1, 2}. Покажем, что нужное утверждение следует уже из анализа этой простейшей области значений переменной. Рассмотрим четыре возможные интерпретации предикат P(x), которые сведем в таблице 5.

Таблица 5

I	X	P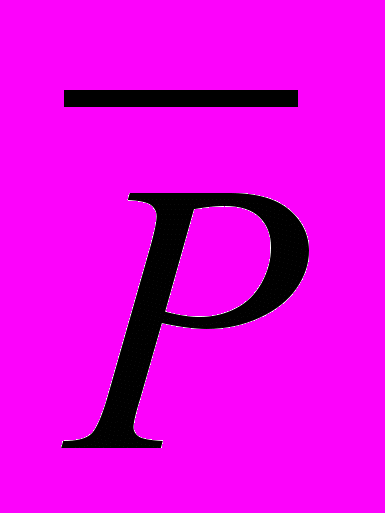(x)	(x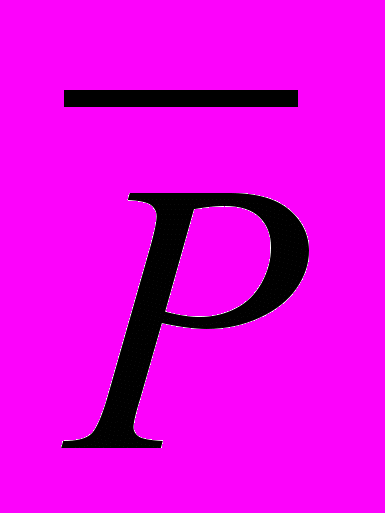)	x((x))
I1	1 2	Л Л	И И	И 	И И
I2	1 2	Л И	И Л	Л 	И Л
I3	1 2	И Л	Л И	Л 	Л И
I4	1 2	И И	Л Л	Л 	Л Л

Из этой таблицы видно, что только при интерпретации I₁ не нарушаются условия логического следования. Поэтому ₂ не следует из ₁.

Пусть даны формулы ₁ = x(P(x)  Q(x)); ₂ = P(a); ₃ = Q(a).

Покажем, что ₃ логически следует из ₁ и ₂. Пусть I есть интерпретация, при которой ₁&₂ является истинной. Тогда в этой интерпретации ₁ и ₂ по отдельности также истинны. Преобразуем ₁ к виду ₁ = x(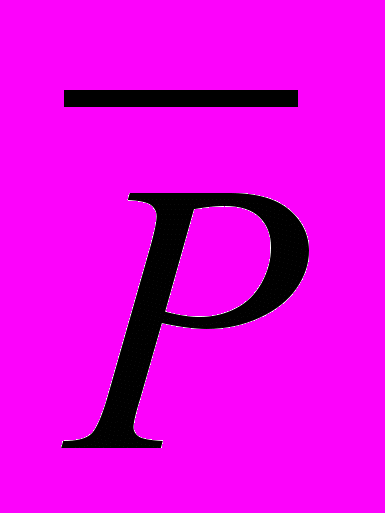(x)  Q(x)).

Пусть в интерпретации I формула ₃ оказалась ложной. Это означает, что при x=a должна быть ложной ₁, так как 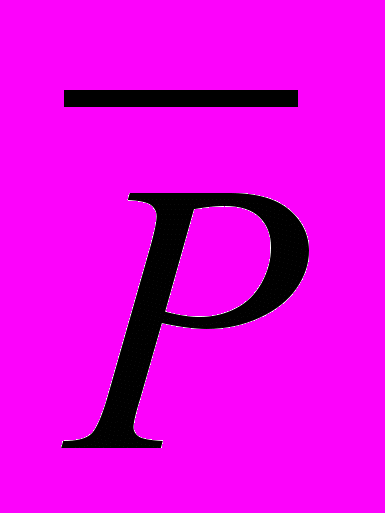(a) является ложным (по предложению ₂, а, следовательно, P(a), являются истинными). Полученное противоречие подтверждает вывод об истинности ₃ при истинности ₁ и ₂. Это значит, что ₃ логически следует из ₁ и ₂.