Geum.ru

Лекция 7 Моделирование процессов

Вид материалаЛекция

Содержание


Системы массового обслуживания
Абстрактные автоматы
Сети Петри.
Марковские цепи
Подобный материал:

Лекция 7

Моделирование процессов.

Системы массового обслуживания. Абстрактные автоматы. Сети Петри. Марковские цепи


Для моделирования производственных процессов широко применяют имитационные модели. Имитационные модели применяют, когда необходимо обеспечить наблюдение за ходом процесса в течение определенного временного периода (или когда невозможно применить аналитические модели математического программирования к решению задач управления). При построении имитационных моделей выбирают некоторые базовые единицы модели – объекты, или сущности. Это могу различные физические объекты, например, производственный участок, единица оборудования, деталь, узел и т.д. Объектам присваивают атрибуты. Фиксированные атрибуты описывают природу и характеристики объекта, переменные – состояние объекта. Состояние моделируемой системы описывается состояниями всех характеризующих ее объектов. Связи между объектами задаются атрибутами. Фиксированные атрибуты описывают статические, переменные – динамические связи. В зависимости от характера изменения атрибутов различают непрерывные и дискретные модели. В моделях дискретных событий выделяют набор работ. Такими работами, например, могут быть технологические операции по обработке деталей. Построение модели в этом случае состоит в логико-математическом описании соответствующих работ, событий и процессов.

Системы массового обслуживания


Системы массового обслуживания (СМО) представляют собой системы специального вида, реализующие многократное выполнение однотипных задач. Модели СМО применяются во многих областях экономики, финансов, производства и быта, для изучения режимов функциони­рования обслуживающих систем, и исследование явлений, возникающих в процессе обслуживания.

Системы массового обслуживания это системы, которые определяются наличием потока клиентов и обслуживающих устройств. На входе модели - набор параметры системы (характер потока заявок, число каналов и их производительности и правила работы СМО). Выход - показатели качества обслуживания (время ожидания, вероятность отказа, длина очереди и др.). Модели СМО позволяют оптимизировать эти процессы обслуживания, т.е. достигать оп­ределенного уровня обслуживания (максимального сокращения очереди или потерь требований) при минимальных затратах, связанных с просто­ем обслуживающих устройств.

Методами теории массового обслуживания могут быть решены многие задачи из области маркетинга. В организации торговли эти методы позволяют определить оптимальное количество торговых точек данного профиля, численность продавцов, частоту завоза товаров и другие параметры. Другим характерным примером систем массового обслуживания могу служить склады или базы снабженческо-сбытовых организаций. Для таких организационных систем задача сводится к тому, чтобы установить оптимальное соотношение между числом поступающих на базу требований на обслуживание и числом обслуживающих устройств, при котором суммарные расходы на обслуживание и убытки от простоя транспорта были бы минимальными. Теория массового обслуживания может найти применение при расчете площади складских помещений, при этом складская площадь рассматривается как обслуживающее устройство, а прибытие транспортных средств под выгрузку – как требование.

Абстрактные автоматы


Абстрактные автоматы используют для описания объектов АСУ, для которых характерно наличие дискретных состояний и дискретный характер работы во времени. К числу таких объектов относятся элементы и узлы ЭВМ, устройства контроля и регулирования, системы коммутации, программы и операционные системы.

Абстрактный автомат можно представить видом:

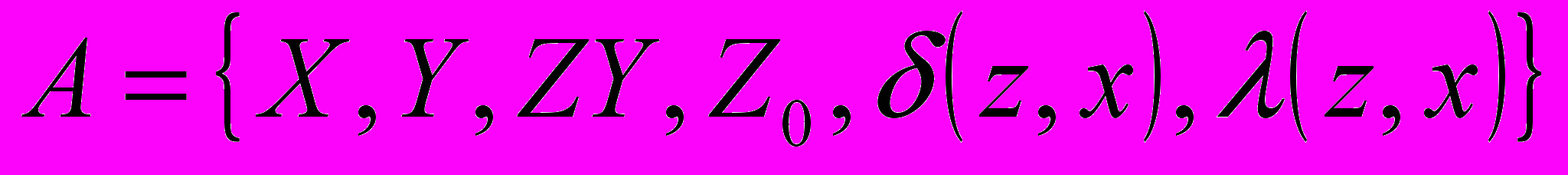, где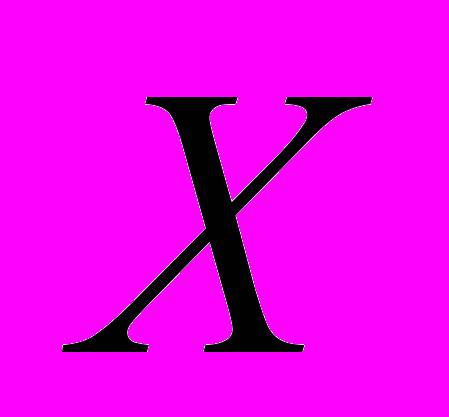

- конечное множество входных сигналов (входной алфавит автомата);

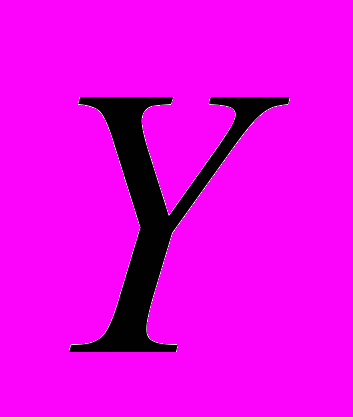- конечное множество выходных сигналов (выходной алфавит автомата);

- выходное множество состояний автомата;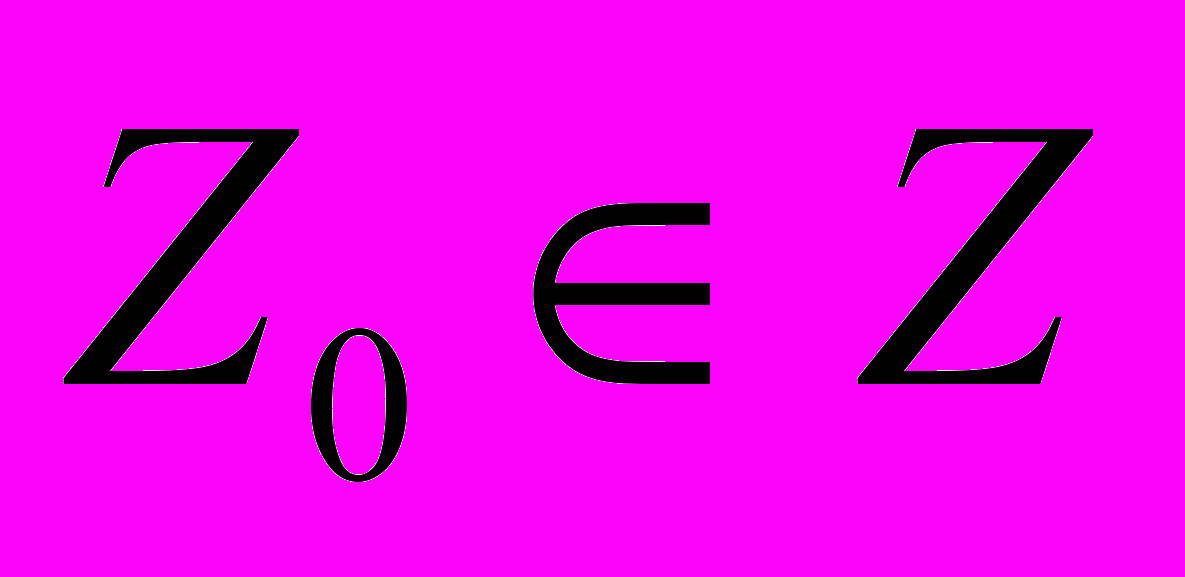

- начальное состояние автомата;

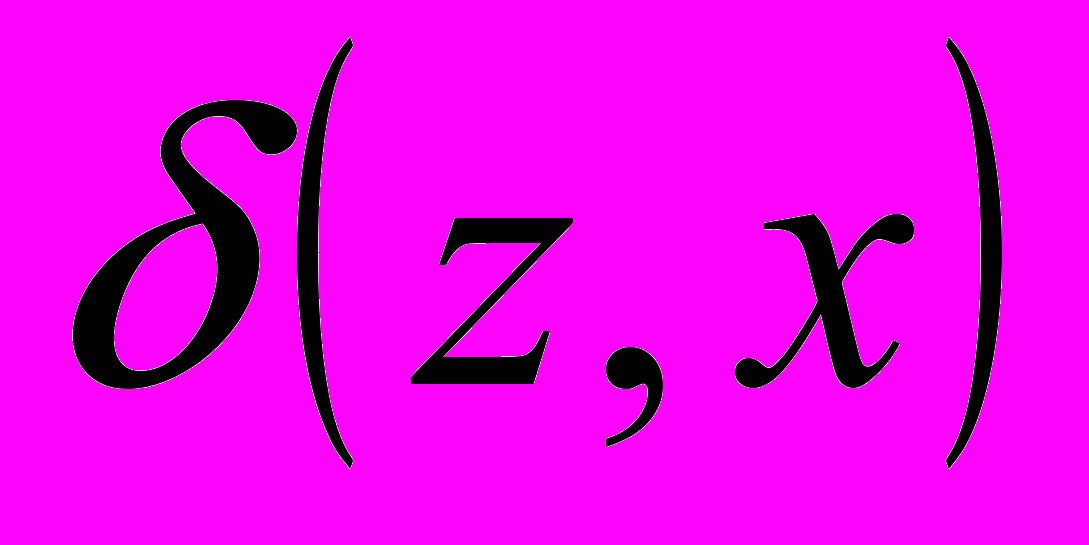- функция переходов автомата,

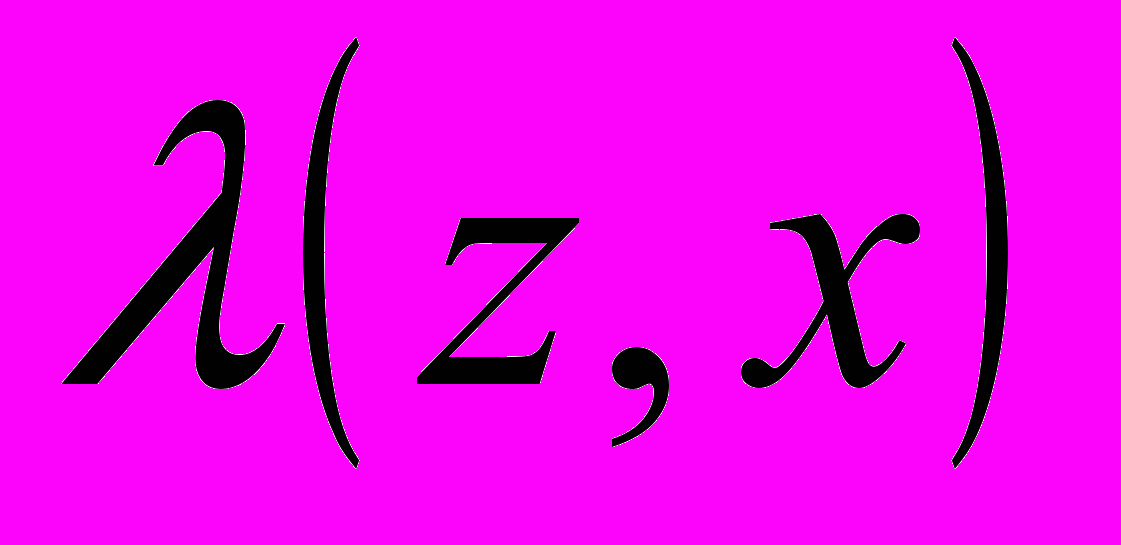- функция выходов или сдвинутая функция выходов.

Функци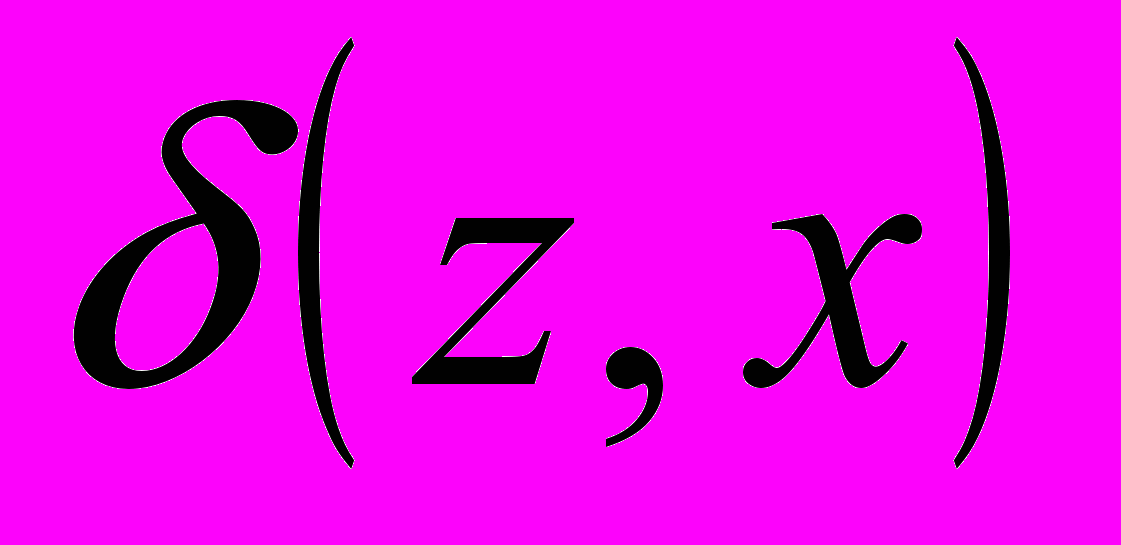и и 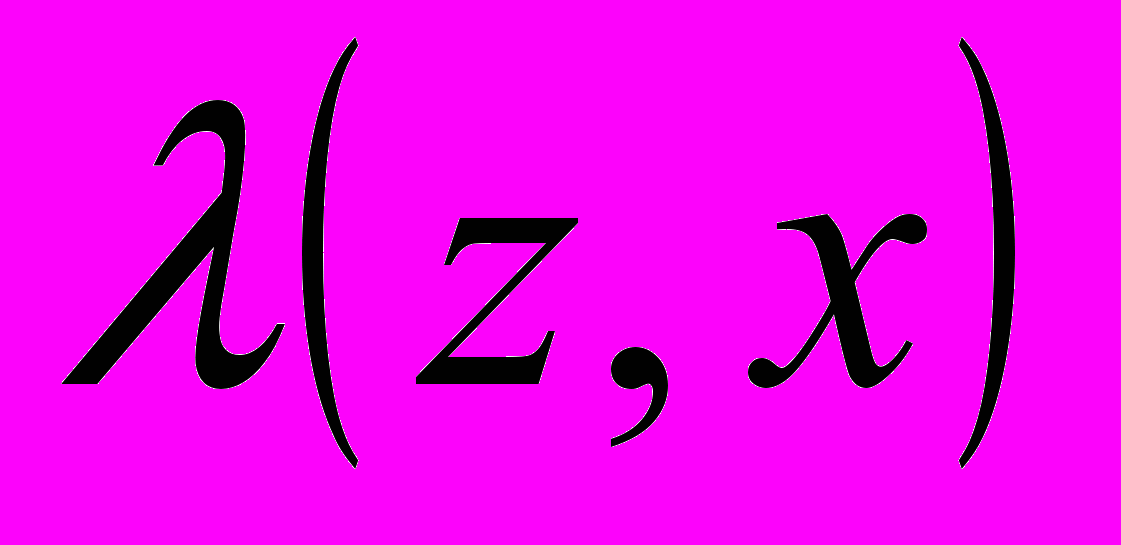задают однозначное отображение множества 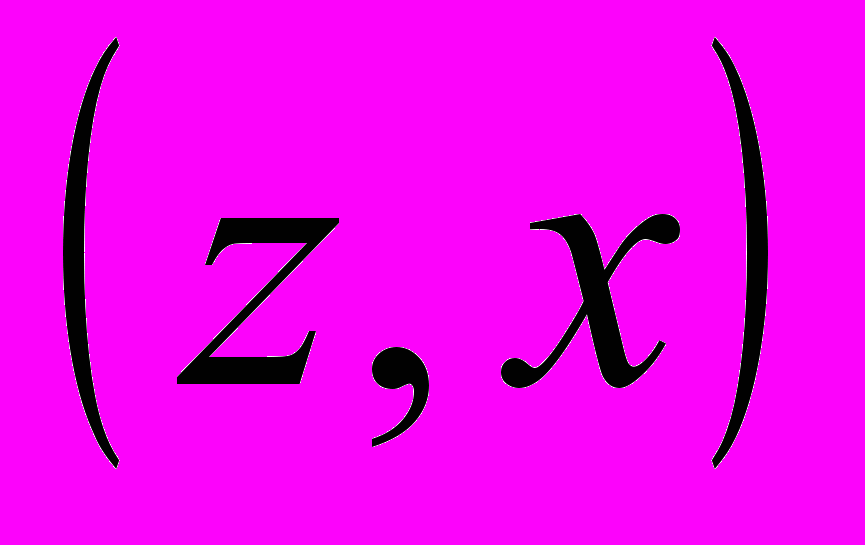, где и 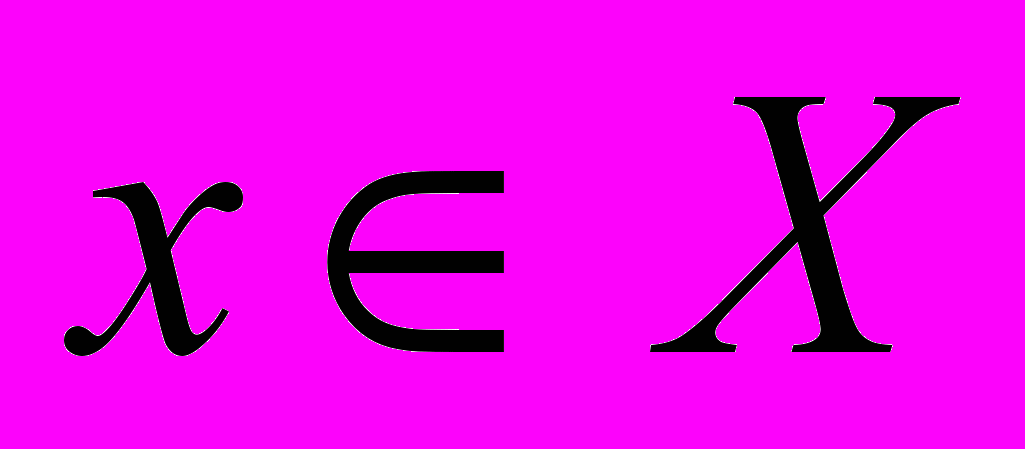в множества X и Y. Автомат, заданный функцией выходов, называется автоматом первого рода, автомат, заданный сдвинутой функцией выходов, - автоматом второго рода.

Абстрактный автомат функционирует в дискретном времени, принимающем целые неотрицательные значения В каждый момент времени автомат имеет определенное состояние 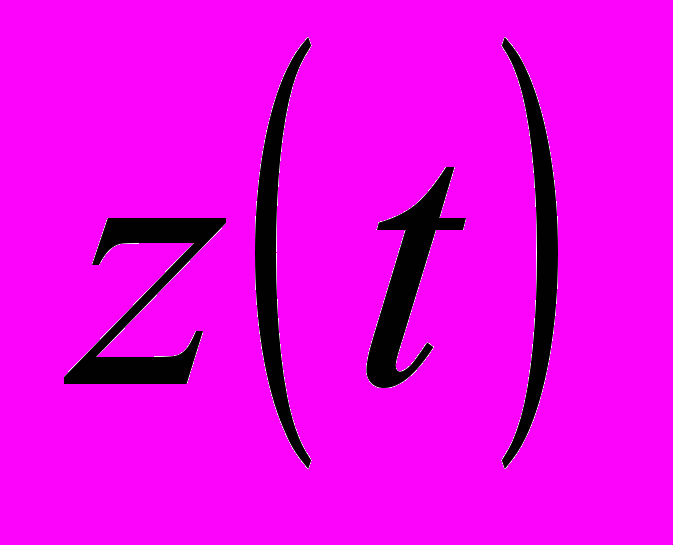из множества Z состояний автомата, причём в начальный момент времени 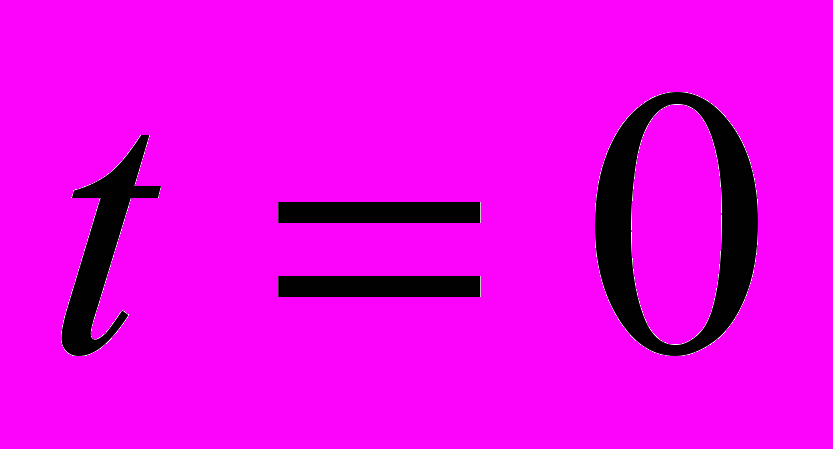автомат всегда находится в начальном состоянии 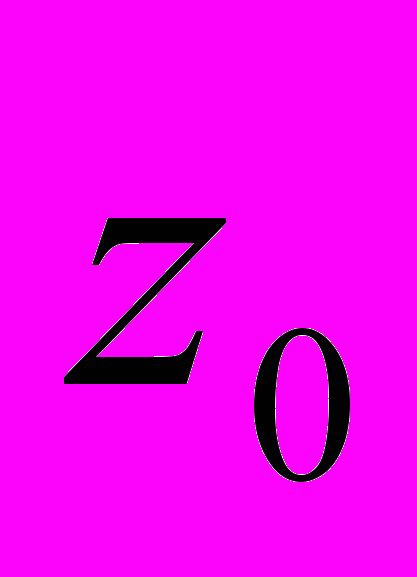, т.е. 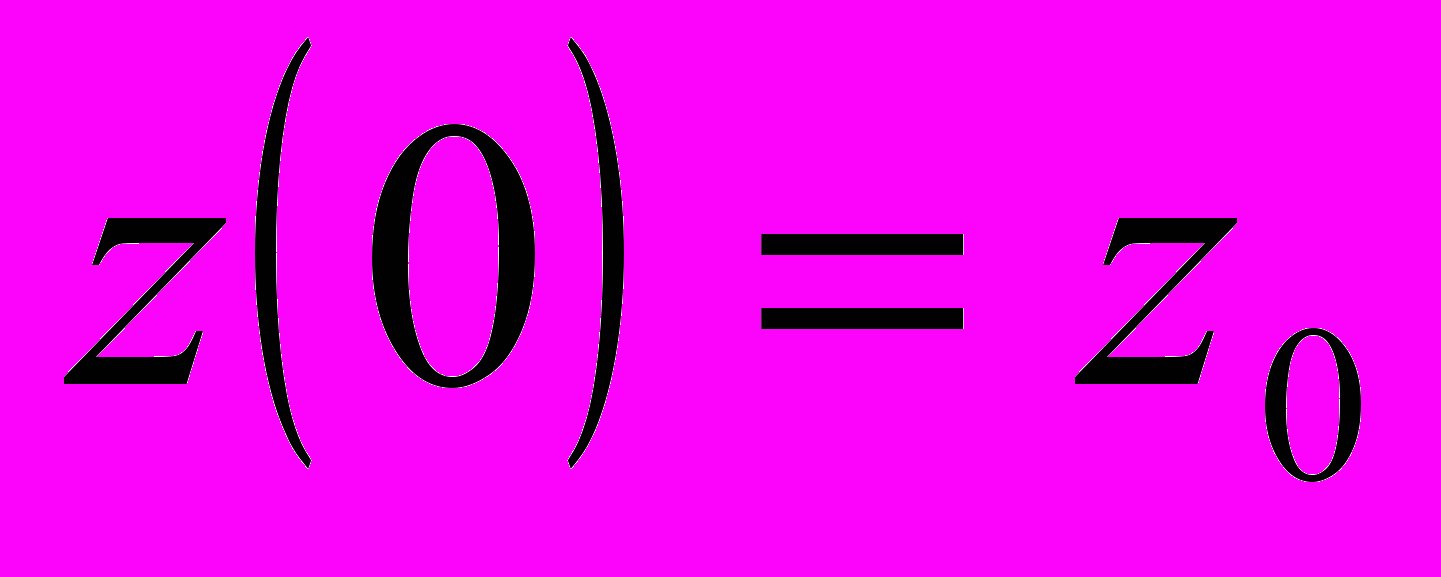. В каждый момент времени , отличный от начального, автомат способен воспринимать входной сигнал 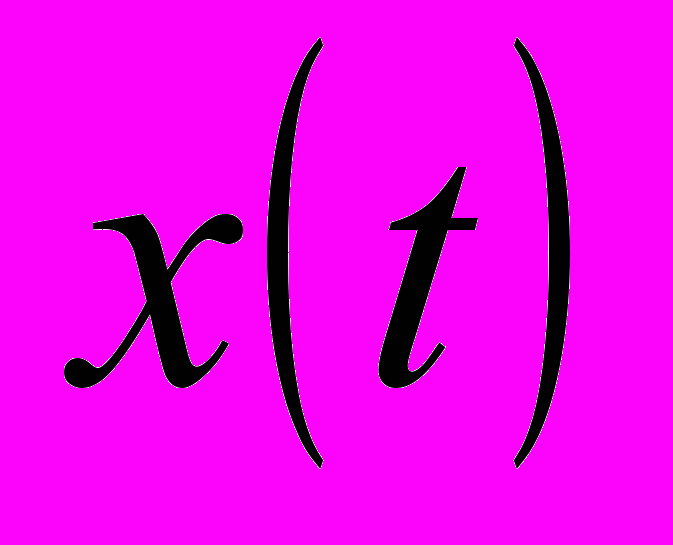- и выдавать соответствующий выходной сигнал. Закон функционирования абстрактного автомата первого рода задаётся уравнениями ;

,

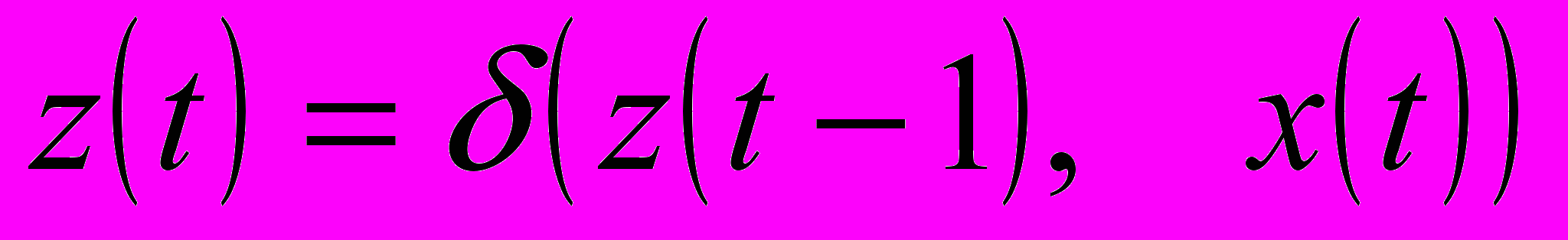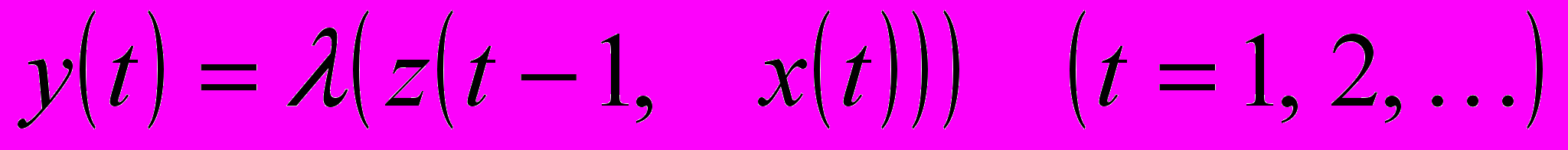для автомата второго рода – уравнениями

,

.

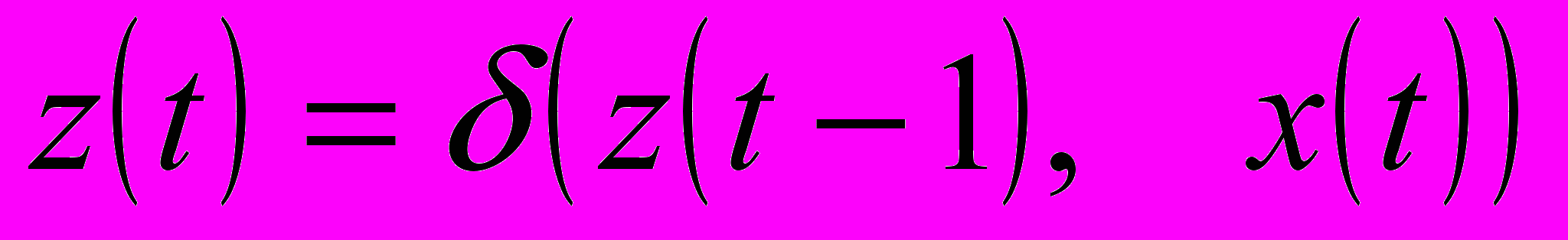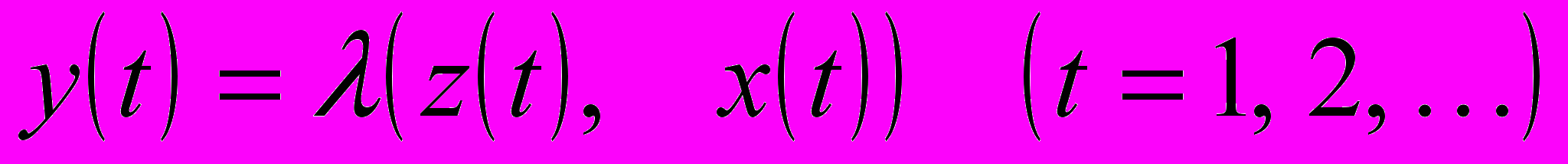Сети Петри.


В абстрактном автомате рассматриваются последовательные переходы состояния. Поэтому такая модель неприменима для объектов, способных выполнять свои функции параллельно. Для моделирования таких объектов используют сети Петри. Сети Петри – это инструмент описания и исследования мультипрограммных, асинхронных, распределенных, параллельных, недетерминированных и/или стохастических систем обработки информации.

В качестве графического средства сети Петри могут использоваться для наглядного представления моделируемой системы, подобно блок-схемам, структурным схемам и сетевым графикам. Вводимое в этих сетях понятие фишек позволяет моделировать динамику функционирования систем и параллельные процессы. В качестве математического средства аналитическое представление сети Петри позволяет составлять уравнения состояния, алгебраические уравнения и другие математические соотношения, описывающие динамику систем.

Моделирование в сетях Петри осуществляется на событийном уровне. Определяются, какие действия происходят в системе, какие состояние предшествовали этим действиям и какие состояния примет система после выполнения действия. Выполнения событийной модели в сетях Петри описывает поведение системы. Анализ результатов выполнения может сказать о том, в каких состояниях пребывала или не пребывала система, какие состояния в принципе не достижимы. Однако такой анализ не дает числовых характеристик, определяющих состояние системы.

Простая Сеть Петри из трех элементов: множество мест, множество переходов и отношение инцидентности. Сети Петри имеют удобную графическую форму представления в виде графа, в котором места изображаются кружками, а переходы прямоугольниками. Места и переходы соединяются направленными дугами, каждой дуге сопоставляется некоторое натуральное число. Это число называется кратностью дуги, которое графически изображается рядом с дугой. Дуги, имеющие единичную кратность, обозначаются без приписывания единицы.

Само по себе понятие сети имеет статическую природу. Для задания динамических характеристик используется понятие маркировки сети. Графически маркировка изображается в виде точек, называемых метками (tokens), и располагающихся в кружках, соответствующих местам сети. Отсутствие меток в некотором месте говорит о нулевой маркировке этого места.




Рис. 7.1 – маркированная сеть Петри

Сети Петри могут применяться:

1) Для моделирования бизнес-процессов. Функциональные диаграммы в нотации IDEF3 могут быть преобразованы в сеть Петри. Каждой работе на диаграмме соответствует переход сети Петри. Позиции соответствуют стрелкам, соединяющим работы напрямую и перекресткам. Метки соответствуют продукции, документов и т.д. Причем в зависимости от перехода интерпретация метки может отличаться.

2) Для моделирования параллельных вычислений и устройств. Если представить себе переход как процедуру, то она корректно выполняется при наличии значений всех своих аргументов и вырабатывает значения всех выходных переменных. В таком случае входные позиции перехода соответствуют аргументам, выходные – возвращаемым значениям. В другой интерпретации переход может представлять некоторое устройство. Устройство может (но не должно) сработать, если выполнились все входные условия.

3) Для моделирования процесса обучения. Тогда позиция соответствует некоторому состоянию процесса обучения, метка сопоставляется обучаемому, переход ассоциируется с изучением какой-либо темы обучаемым.

Марковские цепи


Метод моделирования на основе Марковских цепей широко применяют в таких областях, как автоматизация проектирования и организации в автоматизированных системах научных исследований, в системах исследования и проектирования, в системах массового обслуживания, при анализе различных сторон деятельности человека, в автоматизированном управлении производственными и другими процессами. Модели на основе Марковских цепей используется на этапах проектирования, создания, внедрения, эксплуатации систем, а также на различных уровнях их изучения, начиная от анализа работы элементов и кончая исследованием системы в целом при их взаимодействии с окружающей средой.

Цепи Маркова предназначены, главным образом, для полного описания как долговременного, так и локального поведения процесса. Марковские процессы (процессы без последействия) играют огромную роль в моделировании систем массового обслуживания (СМО), а также в моделировании и выборе стратегии управления социально-экономическими процессами, происходящими в обществе, в частности, применяются управляемые цепи Маркова.

Марковские процессы являются частным видом случайных процессов.

Различают следующие виды Марковских случайных процессов:
  • с дискретными состояниями и дискретным временем (цепь Маркова);
  • с непрерывными состояниями и дискретным временем (Марковские последовательности);
  • с дискретными состояниями и непрерывным временем (непрерывная цепь Маркова);
  • с непрерывным состоянием и непрерывным временем.

Марковские процессы с дискретными состояниями представляют в графа состояний, где кружками обозначены состояния 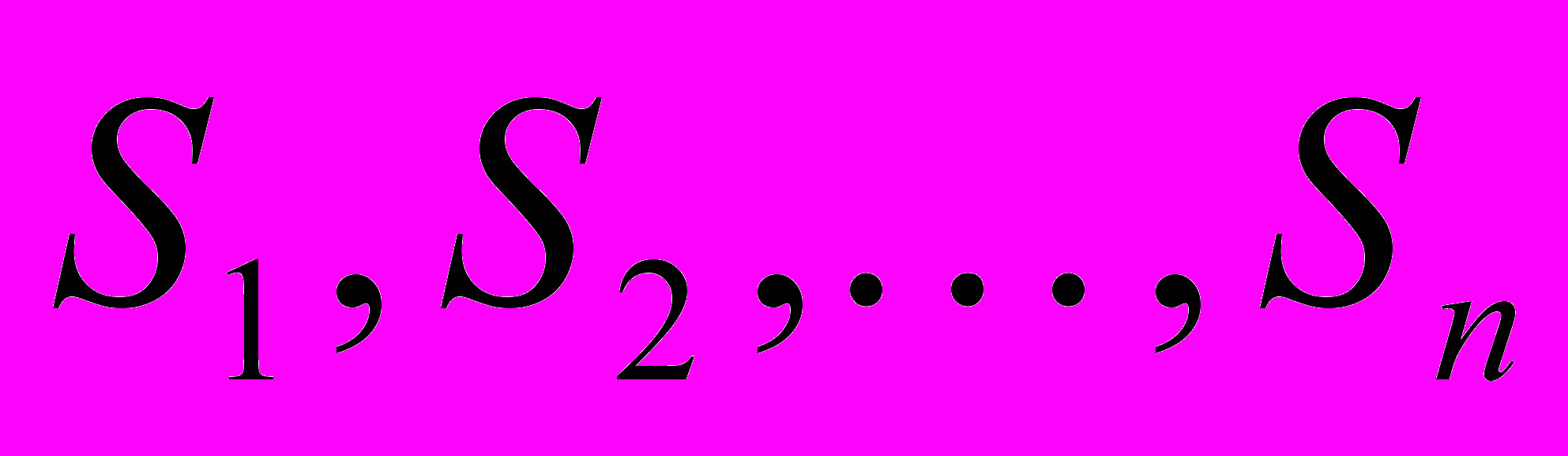системы , а стрелками – возможные переходы из состояния в состояние. Возможные задержки в прежнем состоянии изображают «петлей». Число состояний системы может быть как конечным, так и бесконечным (но счетным).

Под управляемыми Марковскими цепями понимают такие цепи, в которых имеется возможность управлять значениями переходных вероятностей.




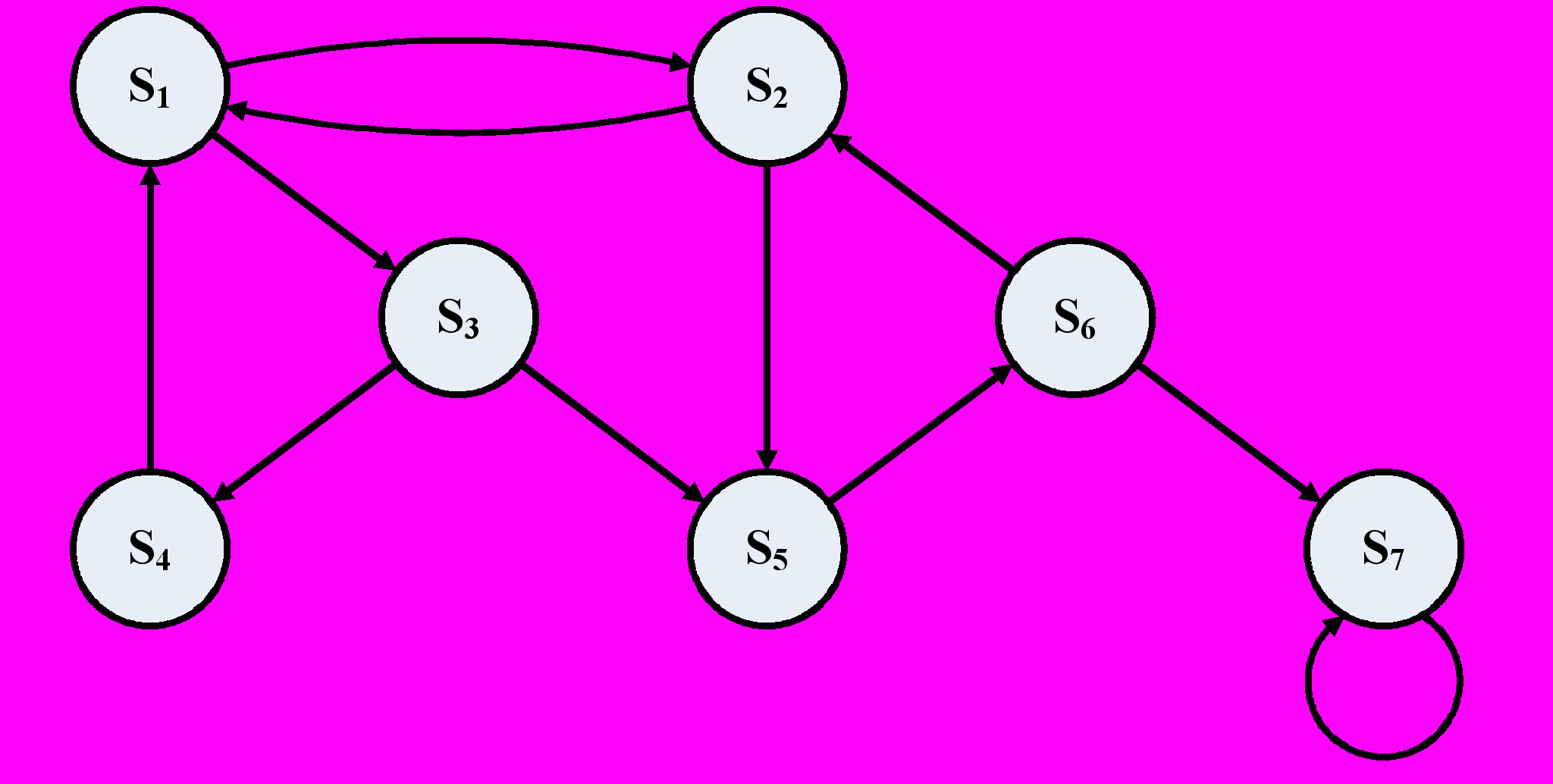
Рис. 7.2 – Граф состояний системы .