Теоретический курс: Что означает термин «логика» Каковы объект и предмет логики

Вид материала

Документы

Содержание Разновидности определений через род и видовое отличие По объему Важнейшие функции деления Структура деления Правила деления и возможные ошибки в делении Виды деления понятий и сходные с ним процедуры

Подобный материал:

• Попов Владлен Александрович  литература, 7.67kb.
• Вопросы по курсу: Математическая логика и теория алгоритмов (2 курс), 30.21kb.
• Настоящий курс «Логика» читается как курс общей формальной логики гуманитарных специальностей., 571.6kb.
• 1. Основы теории коррозии Термин коррозия происходит от латинского "corrosio", что, 205.52kb.
• Объект и предмет социологии. Методы социологии, 1392.07kb.
• Л. В. Логика Предмет и цель логики Предметом формальной (традиционной) логики являются, 427.46kb.
• Лекция №11 (2 часа) Коллектив как объект и субъект воспитания Термин «коллектив», 154.46kb.
• Социология как наука. Объект и предмет социологии. Место социологии в системе, 67.7kb.
• Математическая логика, 1012.22kb.
• Классическая логика предикатов, 30.55kb.

Разновидности определений через род и видовое отличие

1. генетическое – раскрывает происхождение предмета. Широко применяется в геометрии (при определении, например, круга, шара, конуса и др.), химии и других науках. Грамматическим признаком таких определений является присутствие выражения «который образуется путем…» и подобных по смыслу. Например, «цилиндр – это геометрическая фигура» (родовое понятие), «которая образуется при вращении прямоугольника вокруг одной из сторон» (заданы видовые признаки, отличающие цилиндр от других геометрических фигур).
   

2) сущностное – раскрывает сущностные качества, важнейшую природу определяемого предмета. Наиболее часто используемое и востребованное в мышлении определение. Большая часть определений, которые можно встретить в учебниках – определения такого рода. Используемое нами определение логики – сущностное. Сущностное определение философии – «учение о наиболее общих законах развития природы, общества и мышления».


3) функциональное – раскрывает назначение предмета, его функции, роль. Широко применяется, например, в технических науках. Нередко используется и в гуманитарном знании, особенно в исторических науках. Из числа часто используемых в обыденном мышлении: «Фен – бытовой электроприбор» (родовое понятие), «предназначенный для сушки и укладки волос» (видовые признаки, отличающие фен от прочих электроприборов).


4) структурное – раскрывает строение предмета, характеризует составляющие элементы системы. Его грамматические признаки - наличие в языке конструкций типа «состоящее из…» Часто используется в технических науках и естествознании.


Виды неявных определений

1. определение через отношение к своей противоположности. (Широко используется при определении философских категорий: «бытие», «материя», «причина», «необходимость» и др.)
   
2. контекстуальные (от слова «контекст»). Противоположно явному сущностному определению. Содержание понятий раскрывается всем содержанием письменной или устной речи. (Широко используется как прием в художественной литературе и философии, например).
   
3. остенсивное (от лат. слова ostendo – «показываю»). Устанавливает значение термина путем непосредственной демонстрации предмета.
   

Остенсивные определения чаще всего дополняют явные (дано определение через род и видовое отличие, оно, кстати, не всегда просто и понятно для восприятия, и к нему прилагается также некая иллюстрация, наглядный пример, рисунок, картинка, фото и т.д.). В этом случае они оказываются чаще всего весьма эффективными.

При использовании исключительно остенсивных определений, без указания на сущностные признаки обобщаемых в понятии предметов, появляется опасность подмены существенных признаков несущественными. Скажем, перед нами познавательная задача, определить, содержание понятия «ноу-хау в автомобилестроении». Специалист в соответствующей области, разумеется, в первую очередь позаботится о формулировании словесного, сущностно-функционального и структурного определения, а затем продемонстрирует соответствующие примеры. Однако если просто указать соответствующие примеры путем т.н. «простого тыканья пальцем: вот этот, этот и тот…», мы можем принять в данном случае несущественное, цвет, форму кузова, отделку салона автомобиля за важнейшие, образующие содержание этого понятия.

Характерно, что аппеляция к примерам и наглядным изображениям, иллюстрирующим общетеоретические определения и правила – это не прихоть примитивного, неразвитого разума, а необходимое требование любого познания, где в принципе возможно обращение к уровню примеров.


Отношения между понятиями


В формальной логике принято разделять понятия на сравнимые и несравнимые.

Несравнимыми считаются понятия, которые принадлежат к разным универсальным классам. (Напоминаем, что универсальный класс – это предельно широкая предметная область; понятие, являющееся пределом обобщения для данного. Например, универсальным классом для понятия «юрист» является понятие «человек») Несравнимые понятия для формальной логики, например, «врач» и «больничный лист». У них разные универсальные классы – «человек» и «документ». Соответственно сравнимые понятия имеют общие признаки в своем содержании и принадлежат к одному и тому же универсальному классу.

Дальнейший анализ несравнимых понятий в формальной логике не осуществляется.

Отношения между сравнимыми понятиями иллюстрируются следующей схемой:





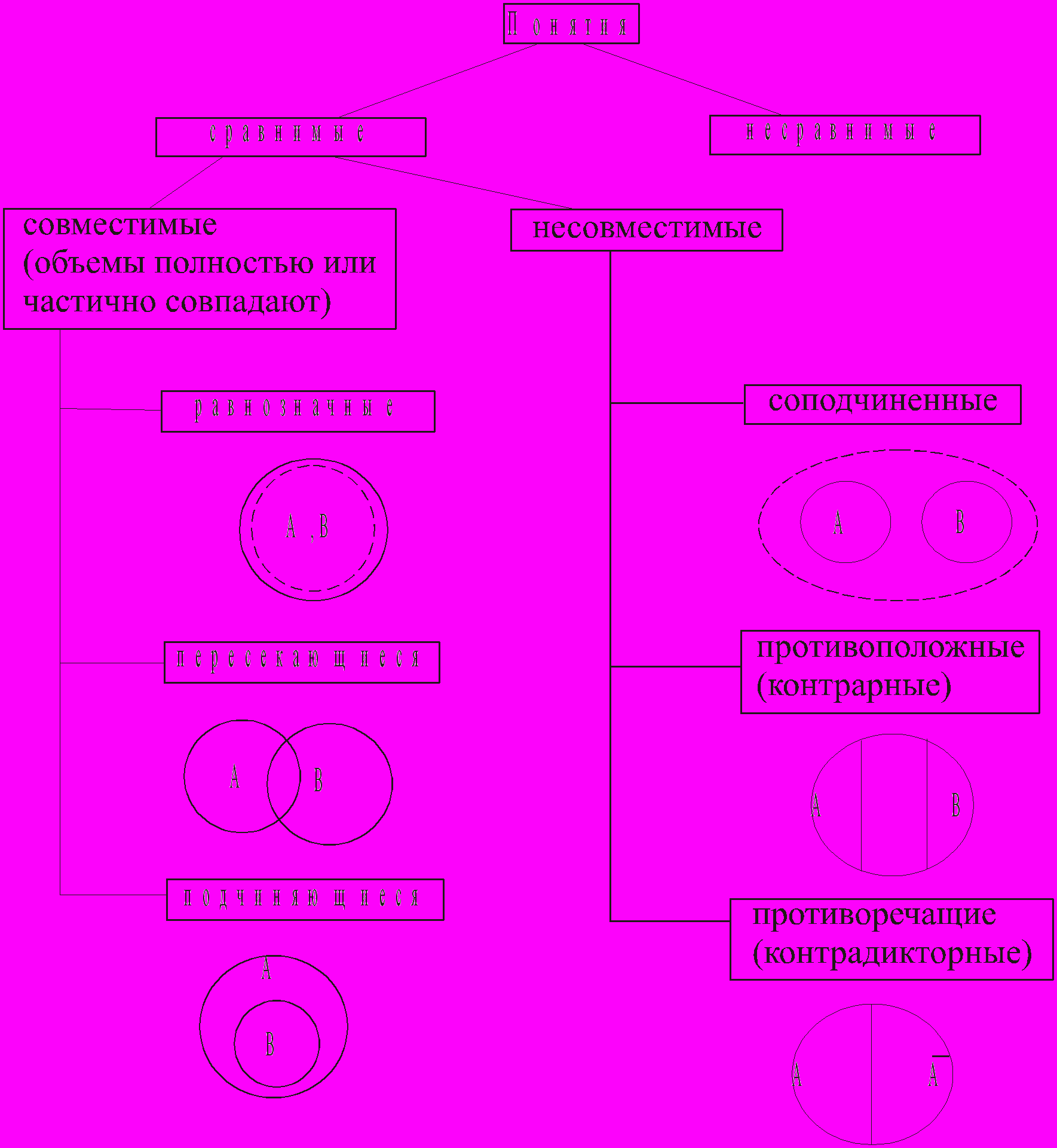
Совместимыми называются понятия, которые имеют общие элементы объема (совместимы, например, понятия А - «студент» и В - «автолюбитель» или понятия А - «автомобиль» и В - «средство передвижения»).

Несовместимые понятия общих элементов объема не имеют. Несовместимы, к примеру, понятия А - «тайга» и В - «пустыня». Одни и те же элементы не могут входить одновременно в оба множества. Они при этом сравнимы, так как принадлежат к одному и тому же универсальному классу - «географический объект».

Рассмотрим далее более подробно отношение совместимости. Равнозначные понятия именуются еще иначе эквивалентными или равнообъемными. Пожалуй, последний из синонимов наиболее точно отражает суть дела. Важно именно то, что подобного рода отношение свидетельствует о полном совпадении объемов понятий, а не признаков, заданных в их содержании. То есть понятия эти совсем необязательно являются синонимами в привычном лингвистическом смысле.

Равнообъемны, например, понятия А - «сын» и В - «внук». Любое лицо мужского пола войдет в качестве элемента в объем обоих понятий, ибо каждый из них является чьим-то сыном, внуком, правнуком и т.д., ныне живущих или ныне покойных, но именно сыном, внуком, правнуком и т.д. Аналогично равнообъемны понятия А – «дочь» и В - «внучка».

Логически эквивалентными с точки зрения совпадения объемов могут быть и единичные понятия: А – «автор романа «Война и мир»» и В – «автор романа «Анна Каренина»». Объемы понятий совпадают – Л.Н.Толстой.

Немало в языке равнообъемных понятий, полностью или почти полностью эквивалентных по смыслу, и соответственно по объему, но имеющих разноязычное происхождение. Эквивалентными, например, признаются философами понятия: А – «мораль», оно латиноязычного происхождения, и В – «нравственность», русскоязычный термин.

Или ситуация подобного рода, еще более распространенная: логически эквиваленты понятия А – стол, В – Tisch (нем.), С – table (англ.), Д – tavolo (итал.), Е – mesa (испан.).

Пересекающиеся понятия (по другой терминологии «перекрещивающиеся») имеют общие элементы объема, вместе с тем, каждый из объемов имеет собственные элементы, не входящие в объем другого понятия. В отношении пересечения находятся, например, понятия А – «студент» и В – «москвич». Есть общие элементы объема: студенты, являющиеся москвичами = москвичи, являющиеся студентами. И существуют в объеме каждого из понятий части, не входящие в объем другого понятия: студенты (А) - немосквичи и среди москвичей (В) - люди, которые не являются студентами.

Перейдем к отношению несовместимости. Напоминаем, что у таких понятий нет общих элементов, но они при этом сравнимы, то есть принадлежат к одному и тому же универсальному классу.

В отношении соподчинения находятся понятия, которые не имеют общих элементов объема, при этом в сумме не исчерпывают объема родового понятия и не отражают в своем содержании противоположных признаков. Например, понятие А – «гражданское право» и понятие В – «уголовное право». Или другой пример. Понятие А – «юрист» и понятие В – «врач».

Обратите внимание на то, что термины «противоположность» (по латиноязычной терминологии – «контрарность») и «противоречие» (по-латински «контрадикторность») не совпадают.

В отношении противоположности находятся, например, такие понятия: «большой» - «малый», «высокий» - «низкий», «красивый» - «уродливый» и т.д. В сумме, в каждой паре, они не исчерпывают объем родового понятия. Однако существует еще и часть объема, подразумевающая наличие средних, не диаметрально противоположных свойств (в наших примерах - не большой, но и не малый; не высокий, но и не низкий; не красивый, но и не уродливый).

Отношение противоречия подразумевает, не только то, что в их содержании обобщаются полярные, противоречащие друг другу признаки, но и то, что такие понятия в сумме, попарно, исчерпывают объем родового понятия: «большой» - «небольшой», «высокий» - «невысокий», «красивый» - «тот, кто не красив» и т.д.


В логике существуют задачки, в которых предлагается выявить отношение не между двумя понятиями, что было нами рассмотрено выше, а между большим числом понятий. Обратите внимание на то, что прежде чем работать с понятиями, в том числе и в таком несколько искусственно смоделированном контексте, требуется обязательно однозначно, а значит логически правильно, определить все используемые понятия.


Виды понятий


Основные виды понятий можно проиллюстрировать следующей схемой:




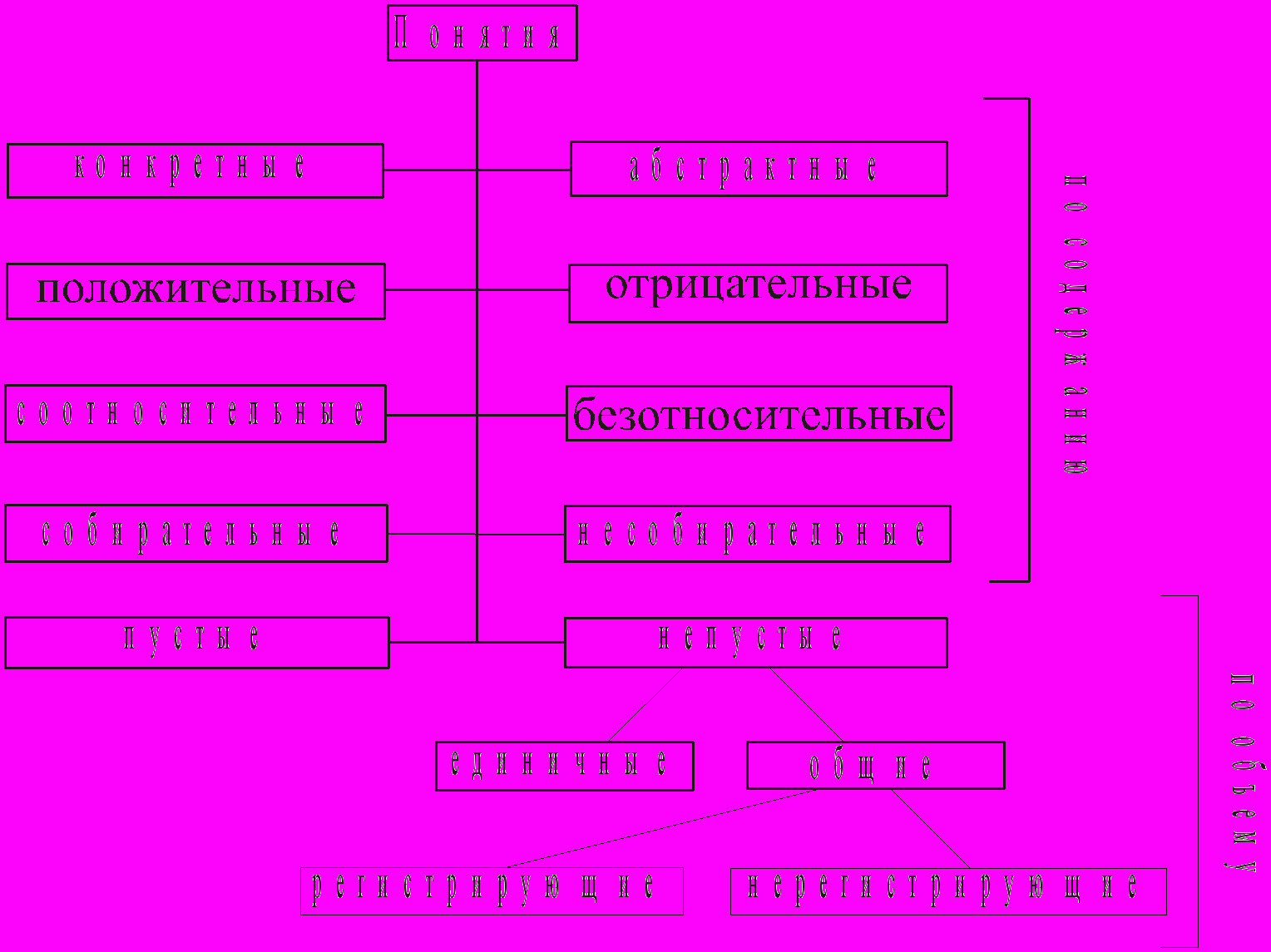
Конкретными называются понятия, которые обозначают целостные предметы и явления, например, «книга», «стул», «город». К числу конкретных принадлежат также понятия «конфликт», «революция», «преступление» и др. Ведь они обозначают именно целостные явления, а не отдельные свойства и признаки. Термин «конкретное понятие» совсем не всегда связан по смыслу со школярским выражением «то, что можно потрогать руками…», то есть с понятием предмета в узком смысле слова. Также речь не идет о том, что в содержании конкретных понятий обобщаются отчетливые, хорошо измеряемые признаки.

Абстрактные понятия в свою очередь обозначают свойства, признаки, отношения, которые сами по себе, как нечто целостное, не существуют. Например, «красота», «доброта», «продолжительность», «платежеспособность», «конфликтность», «революционность» и др.

Не следует путать эти относительно четкие, принятые в формальной логике, определения понятий «конкретный» и «абстрактный» с расхожим житейским словоупотреблением, когда под термином «абстрактное понятие» подразумевается понятие с расплывчатым содержанием, с трудом поддающееся окончательной и четкой рационализации и алгоритмизации. К примеру, нередко можно услышать: «Красота – это абстрактное понятие, оно у каждого свое». Подобная оценка (быть абстрактным понятием) нередко применяется и к другим понятиям высокого уровня обобщения, в основном философского порядка: морального и эстетического сознания.


Деление понятий на положительные и отрицательные мы уже рассматривали выше, в связи с правилами определения понятий. Напомним, что положительным в логике считается понятие, которое образовано в мышлении на основе наличия признаков, свойств, отношений. Большая часть понятий в мышлении являются положительными. Это важное в философском смысле свойство отражает приоритет позитивной, созидающей направленности человеческой деятельности и мышления. Отрицательные понятия образованы в мышлении соответственно на основании отсутствия признаков, свойств, отношений: «недееспособность», «неплатежеспособность», «антифашист», «агностицизм» и др.


Деление понятий на соотносительные и безотносительные является наиболее условным среди всех прочих. Соотносительным считается понятие, которое имеет смысл только в контексте непосредственного отношения с другими понятиями. Например, классическим примером соотносительного понятия является понятие «мать». Нельзя быть матерью, не имея детей. Вероятно, соотносительными будут понятия «врач» («пациент»), «учитель» («ученик»).

Некоторая проблема заключается только в том, что все понятия в мышлении взаимосвязаны с другими прямо или опосредованно. Поэтому когда речь заходит о делении понятий на соотносительные и безотносительные подразумевается степень непосредственной связи с другими понятиями в мышлении. Безотносительные понятия имеют относительно самостоятельный смысл, вне непосредственной, прямой связи с другими понятиями.


Достаточно условным является деление понятий и на собирательные и несобирательные. Собирательным в логике считается понятие, в котором мыслится целостная совокупность предметов и явлений. Например, собирательными в большинстве возможных контекстов мышления будут понятия: «семья», «коллектив», «студенческая группа», «флот», «армия», «лес».

Несобирательные понятия обозначают отдельно существующие явления и предметы: «человек», «собака», «философ», «груз», «юбилей» и др.

Обратите внимание на то, что одно и то же понятие может быть и собирательным и несобирательным в зависимости от контекста. Скажем, в суждениях «Человек – мыслящее существо» и «Человек произошел от обезьяны» подразумевается, скорее всего, несобирательное значение этих терминов. Вместе с тем, контекст мышления врача или анатома в большинстве случаев будет подразумевать собирательное значение термина.

Многие понятия, которые по своей основной природе являются, казалось бы, собирательными, могут выступать в качестве несобирательных. «В лесу много грибов этим летом» - подразумевается собирательный смысл понятия «лес». «Он пошел в лес» - контекст несобирательный, направленный на то, чтобы подчеркнуть, что он именно в лесу, а не в поле, огороде, в доме или клубе. Здесь термин употреблен в разделительном значении. Задача - отличить одно от другого.

«Весь город в этот день вышел на улицу» - собирательное значение, город как совокупность людей. «Он поехал в город» - несобирательный смысл, одно (город) нужно отличить от другого (другой деревни, соседнего села, собственного дома и проч.). Стоит, однако, впрочем, дополнить предыдущее суждение другими, ну, например, «В городе он будет ходить по магазинам», как перед нами собирательный смысл понятия «город», город как определенная совокупность возможных объектов, входящих в его структуру, в том числе и магазинов.


По объему понятия делятся, во-первых, на пустые (они же еще могут называться нулевыми) и непустые. Пустым считается понятие, если в мышлении оно существует, а в реальной действительности предметов, явлений, свойств, которое это понятие обозначает, нет. Классический пример такого рода понятий – «вечный двигатель». К числу нулевых понятий можно отнести понятия «идеально красивый человек», «идеальный газ» и др. Всевозможные вымышленные литературные персонажи по объему представляют собой для формальной логики также пустые понятия. Соответственно непустые понятия обозначают явления, предметы, свойства, существующие в реальной действительности.

В свою очередь непустые понятия делятся на единичные (существует только один, единственный элемент в объеме) и общие (количество элементов – больше единицы). Примеры единичных понятий – город Киев, улица Автозаводская г. Москвы, автор романа «Война и мир» и др.

Общие понятия в свою очередь делятся на регистрирующие и нерегистрирующие. Регистрирующим считается понятие в том случае, когда количество элементов его объема можно подсчитать и указать некое определенное n-значение. К числу регистрирующих можно отнести, например, такие понятия: «ветеран Великой Отечественной войны», «житель Юго-Восточного округа г. Москвы», «студент юридического факультета МГИУ», «профессор, работающий в МГИУ» и др.


Деление понятий

Деление – это логическая операция, заключающаяся в систематическом перечислении всех непересекающихся частей объема понятия по какому-то одному основанию.

Термин, наиболее близкий понятию деление - классификация. Однако, в строгом, формально-логическом смысле слова классификация является только одной из разновидностей деления.

Пожалуй, именно для логической операции деления подходит в первую очередь характеристика «разложить все по полочкам», ибо именно благодаря логической процедуре деления, если она выполнена правильно, каждый элемент объема занимает свое, строго определенное место, на основании опять же четко определенного признака.

Деление является незаменимой, часто выполняемой процедурой в научном и деловом мышлении.


Важнейшие функции деления:

1. упорядочить многообразную информацию, систематизиров ее по какому-либо признаку, обеспечить тем самым более легкий и эффективный доступ к каждому отдельному элементу объема. Эта функция несет в себе в большей степени практическую, прагматическую составляющую;
   
2. систематизация элементов объема на основе определенных признаков помогает, в конечном счете, более глубоко изучить сущность, природу соответствующих явлений. Через изучение возможного многообразия достигается лучшее понимание соответствующего явления в целом. Это функция познавательная, направленная главным образом на теоретическое постижение мира.
   

СТРУКТУРА ДЕЛЕНИЯ


1. Делимое понятие – исходное понятие, объем которого изменяется посредством деления.

2. Члены деления – подклассы, понятия, на которые распределяется объем делимого понятия.

3. Основание деления – признак, по которому производится деление.


Структуру деления можно проиллюстрировать следующей схемой:



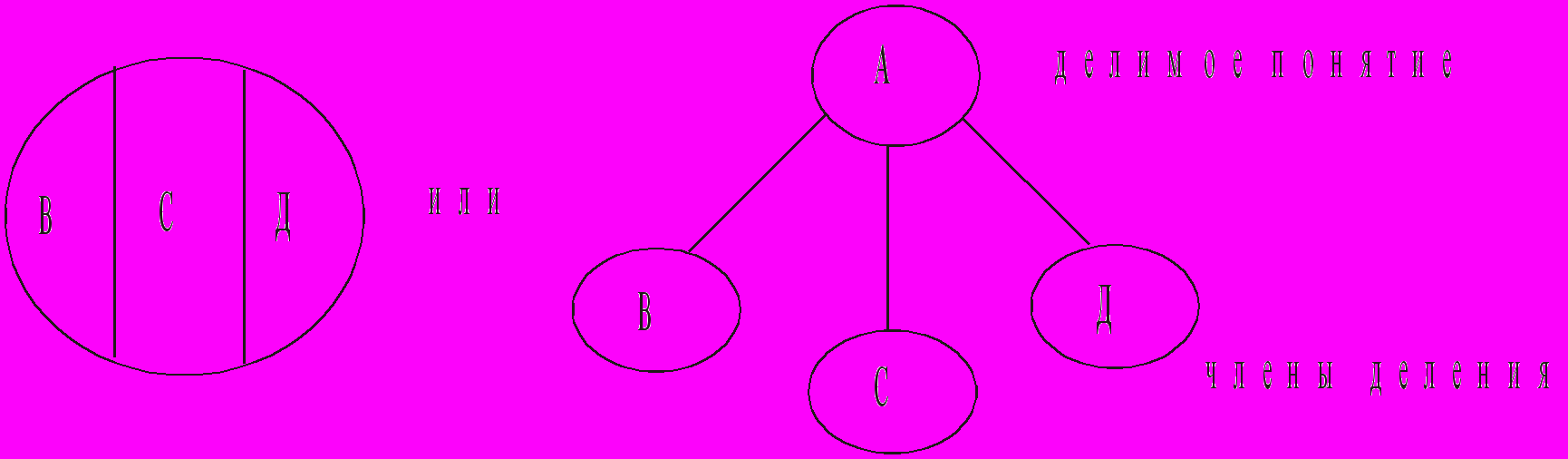
Нередко признак, по которому производится деление, содержится в его структуре в скрытом виде. Основание деления должно быть выявлено и четко оговорено во-избежании возможных ошибок в процедуре деления.


ПРАВИЛА ДЕЛЕНИЯ И ВОЗМОЖНЫЕ ОШИБКИ В ДЕЛЕНИИ


Деление понятий связано с рядом возможных нарушений соответствующих правил. Наиболее частая ошибка при выполнении логической операции деления – подмена деления членением целого на части.

По сути дела, это даже и не ошибка в делении, а отсутствие самой процедуры деления, связанное с непониманием самой его логической природы. Когда осуществляется логическая операция деления, мы пытаемся ответить на вопрос: «Каким бывает предмет?» или, иначе говоря, «Какие разновидности этого явления или предмета существуют?». В случае же членения целого на части мы имеем дело с вопросом– «Из чего, из каких частей состоит предмет?». Например, если предстоит деление понятия «институт» нельзя сказать, что итогом этой логической процедуры будет – факультеты, деканаты, кафедры, лаборатории и прочее.

Справедливости ради, надо сказать, что нередко деление и членение целого на части совпадают между собой, особенно когда мы имеем дело с понятиями высокого уровня обобщения. Например, если мы ведем речь об отраслях права (гражданское, уголовное и др.) перед нами одновременно и виды права, и его составные части. Примерно ту же картину мы бы имели перед собой, если бы вели речь о структуре морали: концептуальная, должная, сущая мораль одновременно образуют ее структуру и являются ее разновидностями.

Правила деления	Возможные ошибки
1. Деление должно производиться строго по одному основанию. Недопустимо производить подмену признака в процессе деления. К тому же признак, по которому производится деление, должен быть четким, хорошо измеряемым. Иначе мы будем иметь дело с типологией, допускающей наличие одних и тех же элементов объема сразу в нескольких подклассах. Логически нормальная процедура деления ориентирована на то, что каждый элемент объема займет строго определенное, фиксированное положение в системе. Условием этого и является четкость, устойчивость, измеримость признака деления.	При нарушении этого условия происходит перекрещивание объ­емов понятий, которые являются членами деления. Логически правильное деление проводит четкие границы между различными подклассами.
2. Деление должно быть соразмерным. (А=В+С+Д – объем делимого понятия должен быть в точности равен сумме объемов членов деления).	а) Неполное деление – перечисляются не все члены деления, что-то не названо, «забыто». Если природа соответствующего явления достаточно хорошо известна, то подобного рода логическая ошибка может быть списана на небрежность и обоснована самоочевидностью и определенной трудоемкостью процедуры. Если же сущность соответствующего явления, напротив, не изучена достаточно, она малоизвестна, то возникает опасность сведения объема исходного, делимого понятия только к тем членам (подклассам) деления, которые были названы. Все прочее в объем делимого понятия как бы и не входит. б) Избыточное деление с лишними членами. Является, как правило, следствием нарушения единственности и измеримости критерия деления.
3. Члены деления должны быть соподчиненными понятиями (не должны пересекаться и входить один в другой).	Пример ошибки такого рода: деление студентов на отличников, успевающих и неуспевающих. – Члены деления находятся в отношении частичного совпадения.
4. Деление должно быть непрерывным (переходить к ближайшим видам, не пропуская их).	Скачок в делении. Пример: право делится на трудовое, уголовное, наследственное и др.

Важнейших, основополагающих правил деления два: единственного, четко обозначенного критерия и соразмерности. Все прочие являются производными от них. Главным образом, от правила, согласно которому следует делить объем понятие в соответствии с одним, хорошо измеряемым критерием.


ВИДЫ ДЕЛЕНИЯ ПОНЯТИЙ И СХОДНЫЕ С НИМ ПРОЦЕДУРЫ