Тарасенко В. Фрактальная логика
| Вид материала | Книга |
- Программа курса и темы практических занятий; Логика в таблицах и схемах. Логика как, 1722.34kb.
- Логика в образовании, 153.37kb.
- Математическая логика, 1012.22kb.
- Логика богочеловечества, 213.06kb.
- Н. В. Папуловская Математическая логика Методическое пособие, 786.38kb.
- Основы логики. Логика, 20.66kb.
- А. А. Ивин логика учебное пособие, 3160.22kb.
- Вопросы к экзамену по дисциплине «Логика», 15.87kb.
- А. А. Ивин логика учебное пособие, 3123.01kb.
- Вматематике понятие фрактал появилось в конце семидесятых годов после выхода в свет, 308.55kb.
2.2 Процедуры генерации логических рядов с помощью обратных связей. Прямая и обратная задача генерации логического ряда.
Уточним и формализуем данные в разделе 1.7 определения.
Постоянное атомарное высказывание - символы a, b, c…
Значения постоянных высказываний в случае классической логики высказываний - И или Л. В общем случае высказывание может иметь k значений. Значения постоянных высказываний не меняются при изменении итерации.
Переменное атомарное высказывание - символы ai, bi, ci …
Сложное высказывание - высказывание, составленное из атомарных высказываний, тех или иных логических символов (например - , , \/, &, , в классической логике) и технических знаков (скобки, запятые) по правилам определеной логики высказываний (например - классической или рейхенбаховской).
Обратная связь - формула, описывающая способ присвоения нового значения высказыванию ai+1, при известных старых значениях ai по правилам определенной логики высказываний.
Записывается с помощью символа двоеточия ":". Формула содержит левую и правую часть. Слева от двоеточия записывается переменное атомарное высказывание, справа - сложное высказывание, значение которого будет присвоено переменному атомарному высказыванию в следующей итерации.
Пример.
Запись "ai+1: ai&b" означает: присвоить переменному атомарному высказыванию ai+1 значение сложного высказывания ai&b.
Система обратных связей - несколько обратных связей, меняющих свои значения одновременно на одной итерации. Система записывается путем записи в строчку всех обратных связей через точку с запятой.
Пример записи системы обратных связей:
ai+1: ai&b i; bi+1: ai&b i&c
Вероятность перехода – числовое значение от 0 до 1 изменения значения переменного атомарного высказывания на новое. Вероятность определяется с помощью генератора случайных чисел с равномерным распределением вероятности.
Пример.
Запись "0.8ai+1: ai&b" означает: присвоить переменному атомарному высказыванию bi+1 значение сложного высказывания ai&b с вероятностью 0.8. Ясно, что с вероятностью 0.2 обратная связь сохранит свое старое значение.
Если в обратной связи вероятность не указана, то она по умолчанию, равна 1.
Бифуркация – расщепление возможных значений атомарных высказываний с некоторой вероятностью.
Пример:
0.8ai+1: ai&b; 0.2ai+1: ai&c
Это означает следующее: в обратной связи высказывание ai+1 принимает значение ai&b с вероятностью 0.8, а значение ai&c с вероятностью 0.2.
Начальные условия - значения переменных атомарных высказываний при i=0. Запись a0 = И означает: «Присвоить начальному условию высказывания ai значение И.
Мир (множество) начальных условий – совокупность всех комбинаций значений начальных условий.
Возможность - значения переменных атомарных высказываний при i0.
Мир (множество) возможностей - совокупность всех комбинаций значений возможностей в обратной связи или системе обратных связей.
Граничные условия - значения постоянных атомарных высказываний в формуле.
Мир (множество) начальных и граничных условий - совокупность всех комбинаций значений начальных условий и значений граничных условий.
Прямая задача генерации логического ряда – построить логический ряд при заданных обратных связях, граничных и начальных условиях, проанализировать все аттракторы рядов в мире начальных и граничных условий.
Обратная задача генерации логического ряда – по логическому ряду реконструировать тип логики и систему обратных связей, которая сгенерировала этот ряд истинности.
Пример решения прямой задачи генерации.
Дана система высказываний, построенная с помощью классической логики высказываний:
ai+1: (ai&bi) c; bi+1: (c\/ai) bi
Граничные условия: c есть Л.
Исследуем поведение системы при разных начальных условиях.
Рассмотрим мир начальных условий с фиксированными граничными условиями, и мир возможностей, обозначив одинаковыми цифрами одинаковые возможности и комбинации начальных условий:
Таблица 2.2.1 Исследование логического ряда
в мире начальных условий
| Вариант начальных условий | A0 | b0 | c | a1 | b1 | Возможность по варианту н.у. при i=1 |
| 1 | И | И | Л | Л | И | 3 |
| 2 | И | Л | Л | И | И | 1 |
| 3 | Л | И | Л | И | И | 1 |
| 4 | Л | Л | Л | И | Л | 2 |
Видно, что мир возможностей уже при первой итерации беднее мира начальных условий – в нем нет варианта 4.
Исследуем каждую комбинацию начальных условий.
Пусть a0 есть И, b0 есть И (комбинация 1), тогда по таблице, a1 есть Л, b1 есть И и реализуется вариант 3 (такой же как a0 есть Л, b0 есть И), который опять переходит в вариант 1. Обозначим знаком “>” переход от одной возможности к другой. Схема переходов: 1>3>1>3>…
Ряд для ai есть ИРЛ. Значение bi будет истинным всегда.
Для начальных условий по набору 2 переходы будут: 2>1>3>1… Аналогично и для 3: 3>1>3>1…
Для начальных условий при варианте 4: 4>2>1>3>1…
Вывод: при всех значениях начальных условий в случае граничных условий с есть Л, наша система приходит к предельному циклу, при котором bi есть И, а аi колеблет свое значение.
Теорема 1 прямой задачи генерации.
Рассмотрим систему из n переменных высказываний k-значной логики, с вероятностью перехода 1. Такая система может иметь только два аттрактора – аттрактор первого рода или аттрактор второго рода с максимально возможным периодом длиной в kn значений.
Доказательство. Выпишем все возможные варианты переходов из мира начальных условий в возможности, используя обозначения предыдущего примера. Их всего kn. Запишем их в kn строчки:
1>1, 1>2, 1>3, …, 1> kn ,
2>1, 2>2, 2>3, …, 2 > kn ,
3>1, 3>2, 3>3, …, 3> kn,
…
kn >1, kn >2, kn >3, …, kn > kn .
Наличие какой-либо системы высказываний означает, что в мире возможностей одновременно не может быть двух разных переходов - из всех комбинаций переходов одновременно может реализоваться только по одной комбинации высказываний из каждой строчки.
Действительно, любое высказывание ai не может при одном и том же i иметь одновременно два значения.
Например, если у нас – в результате системы высказываний реализовался переход 1>1, то в этой системе высказываний переход из возможности 1 в возможность 2 невозможен.
Пусть Х – какое либо начальное условие из мира начальных условий (1, 2, 3…, kn), переходящее в возможность.
Назовем возможность новой, если она еще не реализовывалась в переходе, и старой, если она уже где-то встречалась.
При i=0 есть kn–1 новых возможностей, при i=1 есть kn-2 и т.д. Цикл образуется тогда, когда у нас встречается на i-q итерации старая возможность – повтор возможности. Если возможности на i и i+1 итерациях одинаковы, то образуется на цикл, а фиксированное значение. Таким образом, получается аттрактор ряда истинности первого рода.
С каждой новой итерацией количество новых возможностей уменьшается. Допустим, что у нас не встречаются старые возможности – циклы и фиксированные значения не образуются. Но тогда на на i+1 итерации число новых возможностей станет равным нулю, и мы неизбежно перейдем к старой возможности, которая образует цикл.
Таким образом, самый длинный цикл будет длину kn.
Теорема доказана.
2.3 Операции с логическими рядами
Рассмотрим множество всех логических рядов, обозначив отдельный ряд буквами А, В, С…
Назовем операцией над логическим рядом правило образования нового логического ряда, через преобразование каждого значения старого логического ряда.
Операции могут быть унарными – над одним рядом и бинарные – с двумя рядами.
Рассмотрим множество классических рядов и зададим на нем логику классических рядов (ЛКР) в виде набора унарных и бинарных операций.
Зададим бинарные операции по аналогии с классической логикой высказываний – конъюнкцию &, дизъюнкцию \/, импликацию , тождество .
Например, А&B означает, что результатом этой операции является логический ряд, образованный конъюнкцией логических значений рядов А и В с одинаковыми номерами итераций. То есть, начальным условием этого ряда будет конъюнкция начальных условий А и В, значением при i=1 будет конъюнкция значений А и В при i=1 - и так далее до бесконечности.
Зададим три унарные операции – отрицание, обозначаемое знаком , левый сдвиг на n значений – ln, правый сдвиг на n значений – rn.
Левый сдвиг на n значений – ln, операция, в результате которой получается новый ряд, образованный сдвигом всех значений старого ряда на n значений влево.
То есть i-тое значение преобразуется в i-1 значение. Если значение i-n определить невозможно (i-n – отрицательное число), то оно отбрасывается, и ряд пишется с i-n значения.
Правый сдвиг на n значений – rn, операция, в результате которой получается новый ряд, образованный сдвигом всех значений старого ряда на n значений влево.
То есть i-тое значение преобразуется в i-1 значение.
Законом ЛКР будем называть ряд с аттрактором первого рода – И.
То есть, множество детерминированных аттракторов ЛКР состоит из одного аттрактора – значения И.
Частным случаем закона является получившийся в результате некоторой операции И-вырожденный ряд (ИВ).
Формализм ЛКР:
А, В, С… – классические логические ряды, ИВ, ЛВ, ЛРЛ, ИРЛ – их частные случаи.
Операции: &, \/, , , , ln, rn, где n меняется от 0 до бесконечности.
Технические символы: ), (,
Если А, В – классические логические ряды, то А&В, А\/В, АВ, АВ, А, lnА, rnА - тоже классические логические ряды, где n константа – целое число, которое может меняться от 1 до бесконечности.
Теорема 1 ЛКР:
Законы классической логики высказываний имеют аналоги (так же записанные ряды и операции) в ЛКР.
Доказательство следует из того, что все высказывания ЛКР, составляющие ряды - ai "подчиняются" законам классической логики – по определению ЛКР.
Вот некоторые аналоги законов.
АА – закон тождества,
А А – двойного отрицания.
В ЛКР есть специфические законы. Например:
ЛВ – закон отрицания Л-вырожденного ряда,
ЛРЛ\/ИРЛ – закон "аннигиляции" двух разных рядов лжеца.
А\/ИВ – закон дизъюнкции с истинно-вырожденным рядом.
(A&ЛВ) – закон отрицания конъюнкции ЛВ ряда,
l1ЛРЛИРЛ – закон сдвига ряда лжеца,
или в общем случае: lnЛРЛИРЛ где n – нечетное число.
Введем обозначения для различных логик. Модификации ЛКР, связанные с изменением числа операций будем обозначать ЛКР1, ЛКР2 и так далее.
Логику рейхенбаховских рядов зададим по аналогии с операциями, введенными на высказываниях с тремя значениями Рейхенбахом и обозначить ее модификации соответственно ЛРР1, ЛРР2 и так далее.
Логики, состоящие из k значений, где k – целое число от 4 до бесконечности обозначим как ЛkР1, ЛkP2 и так далее.
Например, для четырехзначных логических рядов можно задать логики Л4Р1, Л4Р2, Л4Р3 и так далее.
2.4 Кортежи, масштабы и инварианты логических рядов. Самоподобие. Определение регулярного логического фрактала.
Введем следующие понятия:
Кортеж – конечная последовательность, упорядоченный набор компонентов – элементов кортежа.
Логический кортеж – кортеж, составленный из логических значений, принятых в данной k-значной логике.
Далее, употребляя термин "кортеж" мы будем иметь ввиду логический кортеж.
Длина кортежа – число компонентов кортежа.
Кортежи бывают:
Унарные – состоящие из одного значения – с единичной длиной,
Бинарные – состоящие из двух значений,
n-ки (тройки, четверки и так далее) – состоящие из трех, четырех и более значений.
Рассмотрим примеры кортежей в ЛКР:
Унарные – <И>, <Л>
Бинарные – <ИИ>, <ИЛ>, <ЛИ>, <ЛЛ>
Тройки – <ИИИ>, <ЛИИ>, <ЛЛИ>, <ЛЛЛ>, <ИЛЛ>, <ИИЛ>, <ИЛИ>, <ЛИЛ>.
Так как число кортежей при фиксированной длине кортежа конечно, то каждый логический ряд можно представить как бесконечную последовательность кортежей.
Рассмотрим в качестве примера ИРЛ, отделяя кортежи пробелом:
ИРЛ как последовательность унарных кортежей: И Л И Л И Л И Л …
ИРЛ как последовательность бинарных кортежей: ИЛ ИЛ ИЛ ИЛ ИЛ …
ИРЛ как последовательность троек: ИЛИ ЛИЛ ИЛИ ЛИЛ ИЛИ ЛИЛ …
ИРЛ как последовательность четверок: ИЛИЛ ИЛИЛ ИЛИЛ ИЛИЛ…
ИРЛ как последовательность пятерок: ИЛИЛИ ЛИЛИЛ ИЛИЛИ ЛИЛИЛ ИЛИЛИ …
Введем понятие масштаба и инварианта.
Масштаб с разрешением n (n-й масштаб) – бесконечный буквенный ряд, получающийся при последовательном обозначении составляющих ряд разных кортежей, длиной n разными буквами.
При этом, для обозначения кортежей надо придерживаться следующего правила: начинать обозначение надо каждый раз с одной и той же буквы греческого алфавита при рассмотрении ряда на новом количестве значений в кортеже, а новый кортеж, встречающийся на исследуемом масштабе, обозначать следующей буквой алфавита.
Для ИРЛ масштаб с разрешением 1 будет следующим:
…
масштаб ИРЛ с разрешением 2:
…
масштаб ИРЛ с разрешением 3:
…
масштаб ИРЛ с разрешением 4:
…
масштаб ИРЛ с разрешением 5:
…
Видна интересная закономерность – четные масштабы тождественны между собой и нечетные масштабы тоже тождественны между собой.
Для описания масштабных характеристик рядов введем следующие определения:
Самоподобным рядом или инвариантом (инвариантным относительно определенных масштабов) будем называть ряд, у которого есть минимум два тождественных масштаба.
Универсальным инвариантом (универсально инвариантным) будем называть такой ряд, все масштабы которого тождественны.
ИРЛ не является универсально инвариантным, так как он имеет не тождественные масштабы.
ИРЛ является самоподобным или инвариантным относительно четных масштабов – четные масштабы имеют одинаковую структуру и ИРЛ является инвариантным относительно нечетных масштабов – нечетные масштабы тоже имеют одинаковую структуру. Примерами универсально инвариантного ряда являются ИВ и ЛВ.
Тривиально инвариантным на выделенных масштабах рядом будем называть с тождественными обозначениями кортежей на описанных нами масштабах. ИРЛ на четных масштабах, а так же ИВ и ЛВ на всех масштабах являются тривиально инвариантными и самоподобными рядами.
Регулярным логическим фракталом будем называть самоподобный ряд, у которого есть хотя бы два масштаба, внутри которых обозначения кортежей не тождественны. Или, другими словами, регулярный логический фрактал это самоподобный ряд, минимум два масштаба которого не являются тривиально инвариантными.
ИВ и ЛВ не являются логическими фракталами, а ИРЛ и ЛРЛ являются регулярными логическими фракталами.
2.5 Формализм масштабного преобразования. Преобразованный логический фрактал.
n-мерное масштабное преобразование – унарная операция - преобразование данного логического ряда (затравки) в новый логический ряд путем последовательной замены кортежей длиной n затравки на новые кортежи.
Масштабное преобразование должно быть задано на всем наборе возможных значений кортежей длиной n для данной k-значной логики. Полученный новый логический ряд так же может подвергаться масштабному преобразованию либо конечное число раз, либо до бесконечности.
Заметим, что масштабное преобразование можно интерпретировать в терминах обратной связи, рассмотренной в 1.4 – преобразование последовательно применяется к уже преобразованному этим преобразованием логическому ряду. Ясно, что эта обратная связь отличается от обратной связи – генератора логического ряда через итерации начальных условий.
Обозначим две задачи масштабного преобразования. Прямая задача масштабного преобразования – по заданной затравке и масштабному преобразованию описать результат преобразований через заданное конечное число преобразований или бесконечное число преобразований.
Обратная задача масштабного преобразования – по заданному ряду реконструировать множество затравок и соответствующие им масштабные преобразования.
Будем обозначать преобразование кортеж затравки в кортеж нового ряда знаком решетки – “#”. Назовем это преобразование на отдельном кортеже решеткой. Количество решеток R в преобразовании рассчитывается по формуле: R=kn, где k – количество значений в логике (для ЛКР это 2, для ЛРР это 3 и т.п.), n – длина кортежа.
Пример масштабного преобразования затравки иллюстрирован рисунком 2.5.1.
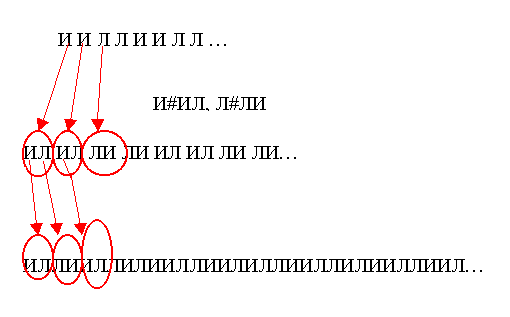
Рисунок 2.5.1 Схема масштабного преобразования затравки.
Масштабное преобразование чем-то напоминает сокращения в языке. Хофштадтер19 (в блестящем переводе Марины Эскиной) рассмотрел следующее суждение: «БОГ, одолевающий гения», где слово «БОГ» – сокращение слов «БОГ», «Одолевающий», «Гения». При последовательной расшифровке сокращений получаем бесконечно разворачивающуюся последовательность суждений, в которых слово «БОГ» оказывается бесконечным сокращением самого себя. Интересно, что в этом случае обозначает слово БОГ?
Рассмотрим одномерное масштабное преобразование кортежей затравки в ЛКР. Набор значений унарных кортежей: И, Л. Поэтому для осуществления преобразования необходимы две решетки. В качестве примера можно взять следующий вариант преобразования:
И#ИЛ, Л#ЛЛ (2.4.1)
Это одномерное масштабное преобразование – преобразование унарных кортежей в бинарные кортежи.
Возможны и другие преобразования. Например:
И#ИЛЛЛЛИИ, Л#ЛИ (2.4.2)
Рассмотрим двухмерное масштабное преобразование. Весь набор бинарных кортежей следующий: <ИИ>, <ИЛ>, <ЛИ>, <ЛЛ>. Для осуществления преобразования необходимы четыре решетки. В качестве примера можно взять следующий вариант преобразования:
ИИ#Л, ИЛ#ЛЛЛИИИ, ЛИ#ИИ, ЛЛ#ИИИИИИИИИИЛ (2.4.3)
Вот еще один вариант:
ИИ#Л, ИЛ#Л ЛИ#И, ЛЛ#И (2.4.4)
Это – двухмерное масштабное преобразование – преобразование бинарных кортежей унарными кортежами.
Рассмотрим отдельную решетку в n-мерном масштабном преобразовании. Пусть минимальное количество значений в преобразовании справа от всех решеток – f, максимальное – s.
Если во всех решетках преобразования n
Масштабные преобразования (2.4.1) и (2.4.2) являются расширениями унарных кортежей. Масштабное преобразование (2.4.4) – сжатием бинарных кортежей. Масштабное преобразование (2.4.3) – не является расширением или сжатием.
Пример 2.4.1.
Возьмем ИРЛ в качестве затравки, и зададим для нее расширение унарных кортежей: И#ИЛИ, Л#ИИЛ.
Выпишем получившиеся ряды, последовательно их нумеруя:
Затравка: И Л И Л …
1: ИЛИ ИИЛ ИЛИ ИИЛ …
2: ИЛИ ИИЛ ИЛИ ИЛИ ИЛИ ИИЛ ИЛИ ИИЛ ИЛИ ИЛИ ИЛИ ИИЛ …
3: ИЛИ ИИЛ ИЛИ ИЛИ ИЛИ ИИЛ ИЛИ ИИЛ ИЛИ ИЛИ ИИЛ ИЛИ ИЛИ ИИЛ ИЛИ ИЛИ ИЛИ ИИЛ…
Пример 2.4.2
Зададим для ряда 3 из предыдущего примера сжатие бинарных кортежей:
ИИ#Л, ИЛ#И, ЛИ#И, ЛЛ#И.
Выпишем получившиеся логические ряды:
Затравка: ИЛ ИИ ИЛ ИЛ ИИ ЛИ ИЛ ИИ ИЛ ИЛ ИИ ИЛ ИЛ ИИ ЛИ ИИ ЛИ ЛИ ИЛ ИИ ИЛ ИЛ ИИ ЛИ ИЛ …
1: ИЛ ИИ ЛИ ИЛ ИИ ЛИ ИЛ ИЛ ИИ ИЛ ИИ ЛИ…
2: ИЛ ИИ ЛИ ЛЛ ЛИ ЛИ…
3. ИЛ ИИ ИИ…
Введем обозначение n-мерных масштабных преобразований по следующему принципу:
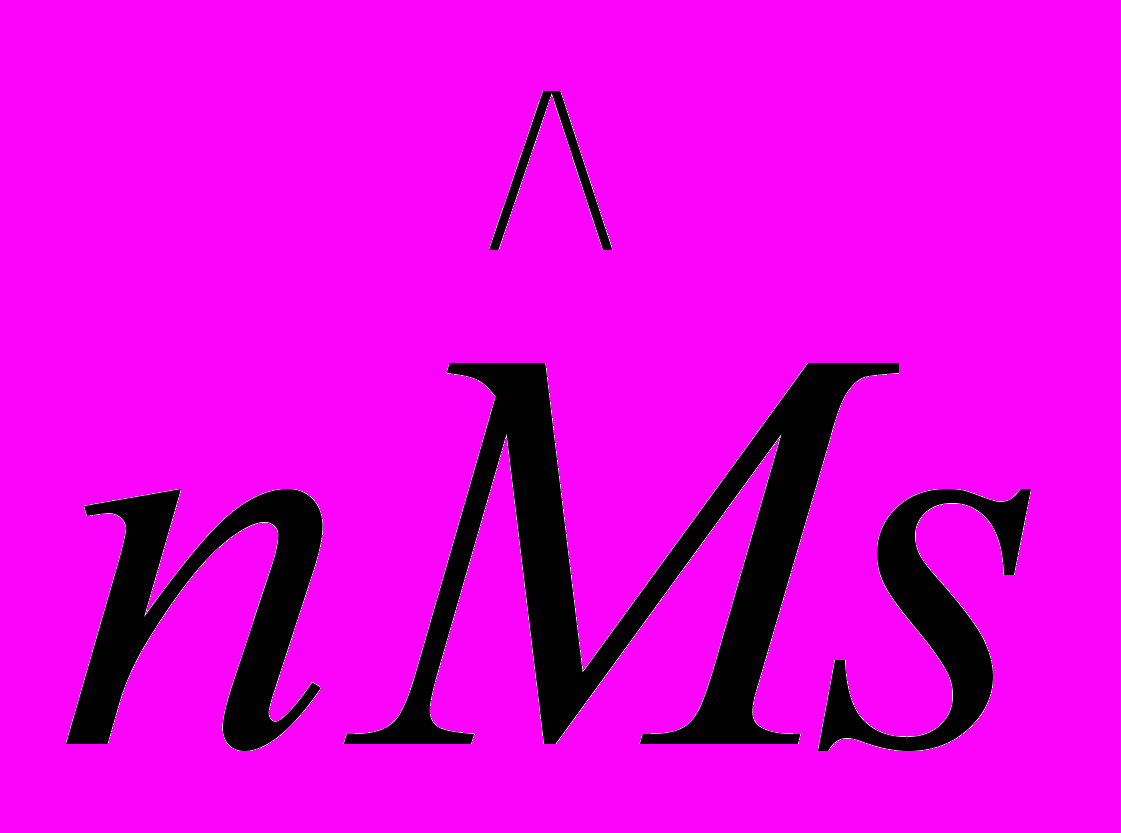, где s – порядковый номер масштабного преобразования. Ясно, что для любой n количество масштабных преобразований бесконечно.Преобразованным логическим фракталом мы будем называть ряд, полученный в результате масштабного преобразования кортежей затравки неединичными кортежами, содержащими разные логические значения. Масштабное преобразование может осуществляться конечное или бесконечное число раз.
Соответственно если такой ряд является результатом бесконечного числа преобразований, то это бесконечно преобразованный логический фрактал. Если ряд является результатом s преобразований кортежей затравки, то это s-преобразованный логический фрактал.
Ясно, что если преобразование будут содержаться одинаковые логические значения, то в результате мы получим ЛВР или ИВР.
Теорема масштабного преобразования.
Если в n-мерном преобразовании справа от решеток стоят кортежи с одинаковой длиной не равной n и нетождественными логическими значениями внутри кортежа, то получившийся в результате хотя бы одного такого преобразования ряд является регулярным логическим фракталом.
Доказательство.
Пусть справа от решеток в преобразовании стоит q кортежей. Рассмотрим затравку – ряд А и результат преобразования – ряд В.
У ряда В есть два тождественных масштаба – с разрешением n и с разрешением s.
Так как логические значения внутри кортежей разные, то ряд В не является тривиальным. Поэтому, по определению, ряд В является логическим фракталам.
Теорема доказана.
Пример.
Рассмотрим затравку – ИВ.
Зададим преобразование:
И#ИЛ, Л#ИЛ
В результате получим последовательность рядов:
ИИИИИИИИ…
ИЛИЛИЛИЛ…
ИЛИЛИЛИЛ…
…
В результате бесконечного числа преобразований мы получаем ИРЛ, который является регулярным фракталом, бесконечно преобразованным фракталом из затравки ИВ и s-преобразованным логическим фракталом из затравки ИВ где s – целое положительное число.
2.6 Фрактальная монадология.
Монадой мы будем называть кортеж с заданным масштабными преобразованиями.
Этот кортеж будем называть затравкой монады.
Будем обозначать монады в честь автора "Монадологии" буквой L.
Пример.
Запись И L И#ИИИЛЛ, Л#ЛЛИИ означает монаду с затравкой в виде кортежа <И> и заданными масштабными преобразованиями для двух кортежей И#ИИИЛЛ, Л#ЛЛИИ.
2.6.1 Готфрид Вильгельм Лейбниц (1646 - 1716)
Кортеж-затравку будем называть реальным кортежем. Оставшиеся кортежи, на которых нам надо задавать преобразования, будем называть виртуальными.
Например, если кортеж-затравка в ЛКР <ИЛ>, то виртуальными кортежами будут кортежи <ЛИ>, <ИИ>, <ЛЛ>. Масштабное преобразование монады надо задавать для всей совокупности реальных и виртуальных кортежей, общее количество которых равно R=kn (см.2.5).
Монада, при устремлении преобразований в бесконечность, преобразуется в логический ряд - частный случай логического фрактала, с которым можно проделывать все операции, описанные выше. Таким образом, монада, наряду с обратной связью, может быть генератором логического ряда.
Пример.
Рассмотрим монаду И L И#ИЛ, Л#ИЛ.
Получаем последовательность кортежей:
И
ИЛ
ИЛИЛ
ИЛИЛИЛИЛ
ИЛИЛИЛИЛИЛИЛИЛИЛ
ИЛИЛИЛИЛИЛИЛИЛИЛИЛИЛИЛИЛИЛИЛИЛИЛ
В результате устремления этой процедуры к бесконечности, получим ИРЛ.
Монадология – решение прямой и обратной задачи – задачи по конструкции (реконструкции) монады.
Прямая задача – описать получившийся логический ряд с заданной затравкой-кортежем и масштабным преобразованием. Рассмотреть миры затравок и миры масштабных преобразований по определенным параметрам и описать получившиеся ряды. Исследовать их на тривиальность и самоподобие – по аналогии с логическими рядами.
Обратная задача – по заданному ряду или кортежу установить затравку-кортеж и масштабное преобразование.
2.7 Тезис о построении логического фрактала через два типа обратных связей
Вернемся опять к машине обратной связи, рассмотренной в разделе 1.6.
Проводя аналогии между этой моделью и описанными процедурами построения логических фракталов, можно увидеть то, что для построения логического ряда необходимо различать по крайней мере два типа обратных связей.
Первый тип обратной связи, описанный в 1.6, применяется для начальных условий и служит механизмом генерации логического ряда. Назовем эту связь итерационной обратной связью. Согласно доказанной нами теореме, эта обратная связь всегда сходится либо к аттрактору первого рода, либо к аттрактору второго рода.
Таким образом, можно сказать, что для этой обратно связи всегда найдется масштаб, на котором сгенерированный обратной связью ряд преобразуется с некоторым правым сдвигом в вырожденный ряд. Говоря иначе, итерационная обратная связь с единичной вероятностью всегда образует ряд с повторяющимся на бесконечности кортежем.
Значит, итерационная обратная связь является отрицательной – она всегда сходится к какому-то кортежу.
Второй тип обратной связи применяется для затравки – логического ряда, к которому применяются масштабные преобразования. То есть, масштабные преобразования тоже могут быть интерпретированы в терминах обратной связи. Назовем эту связь масштабной обратной связью.
Эта обратная связь может быть положительной и генерировать логический фрактал. В связи с этим мы можем сформулировать тезис о построении логического фрактала:
Любой логический фрактал может быть построен как совокупность итерационной и масштабной обратной связи.
Этот тезис можно использовать в качестве общего определения логического фрактала.
2.8 Количественные характеристики логического фрактала
2.8.1 Энтропия и кортежная размерность
Для оценки сложности и скорости устремления количества масштабных кортежей ряда к бесконечности введем соответственно понятия энтропии и кортежной размерности логического ряда.
Мы уже знаем, что на масштабе с разрешением n в k-значной логике возможно К= kn различных кортежей.
Количество различных кортежей – это сложность ряда. Так как степенная зависимость велика для количественной оценки, введем, по аналогии с термодинамической энтропией, определение возможной энтропии логического ряда на заданном масштабе (W):
W = logk K, (2.8.1.1)
Подставляя значение К, получаем: W = n logk k = n.
При увеличении разрешения масштаба, возможная энтропия логического ряда линейно увеличивается.
Однако логические фракталы демонстрируют гораздо меньшее разнообразие кортежей. Мало того, количество различных кортежей часто оказывается независимым от масштаба.
В качестве примера можно привести ЛРЛ и ИРЛ которые демонстрируют либо один, либо два различных кортежа на всех масштабах.
Ситуация удивительно напоминает ситуацию с природными структурами – вместо комбинирования новых и новых возможных структур-кортежей, природа "ленится" создавать новые структуры на новых масштабах. Например, вихревые структуры встречаются как на микро-масштабах (атомные и молекулярные структуры) мезо-масштабах (турбулентность воды или облаков) так и на мега-масштабах (спиральные галактики). Возможно, эта природная "лень" по производству новых форм лежит в основе самоподобия природных фракталов.
Такая "лень" присуща и знаковым системам – системам из слов конечной длины. Из-за того, что в системах реализуются не все возможные, а только ограниченные слова, в них образуется информация, в противовес энтропии всех возможных состояний.
Илья Пригожин и Грегуар Николис20 сравнили марковский процесс и хаотический процесс типа аттрактора Рёсслера с точки зрения вероятности наличия тех или иных последовательностей состояний. Их результаты можно интерпретировать как исследование логического ряда на предмет наличия тех или иных кортежей.
Напомним, что марковским называется процесс с дискретным временем у которого есть марковское свойство – свойство отсутствия последствий: состояние системы в настоящий момент премени t0 однозначно определяет распределение вероятностей будущего развития при t>t0 и информация о прошлом поведении процесса до момента t0 не влияет на это распределение.
Логический ряд можно представить как марковский процесс, если марковским свойством будет обладать вероятность появления логического значения на некоторой итерации.
Николис и Пригожин рассмотрели марковский процесс, удовлетворяющий закону больших чисел и оценили число кортежей, превышающих некоторую заданную вероятность.
На примере создания биополимера, авторы рассмотрели случай, когда все кортежи аминокислот равновероятны. Они к выводу о том, что описание возникновения структуры биополимера неадекватно с точки зрения гипотезы равновероятности возникновения последовательностей аминокислот с фиксированной длиной. Всегда существуют выделенные последовательности аминокислот, формирующих биополимер.
Этот пример является дополнительной иллюстрацией "лени" природы, отбирающей из всех возможных комбинаций только ограниченное количество возможностей.
Рис 2.8.1 Илья Романович Пригожин (род. 1917) – бельгийский химик русского происхождения, лауреат Нобелевской премии по химии (1977 г.) за исследование диссипативных структур, образующихся в открытых системах.
Николис и Пригожин рассмотрели аттрактор Рёсслера как хаотическую последовательность нахождения системы в трех состояниях X,Y, Z:
ZYXZXYXZXYXZYXZXYXZYXZYXZXZYXZYXZXYXZYX…
Далее они переписали эту последовательность c помощью гиперсимоволов (кортежей) - = ZYX, = ZXYX, =ZX:
…
Далее авторы посчитали условные вероятности возникновения последовательностей (кортежей) с различной длиной на различных масштабах и показали, что появление кортежей не равновероятно. Это позволяет говорить о неслучайности процедуры, генерирующей рассматриваемый процесс.
Только на масштабе с разрешением пять аттрактор Рёсслера можно схематизировать марковским процессом.
Анализируя последовательность, генерируемую странным аттрактором, Николис и Пригожин замечают:
"При ближайшем рассмотрении статистических характеристик таких последовательностей выясняются некоторые удивительные особенности. Например, из всех возможных 37 последовательностей семисимвольной длины, которые можно построить на X, Y, Z, в динамике реализуются только 21. Более того, примерно для половины из них условная вероятность некоторого символа при условии, что заданы пять предыдущих символов, оказывается равной единице. Следовательно, всё выглядит так, как если бы в систему были встроены "грамматические правила", автоматически выполняемые в результате динамики."21
Для оценки только тех кортежей, которые реализовались в данном ряде на данном масштабе j, введем представление о масштабных кортежах (МCj). Для ЛРЛ и ИРЛ MCj=2 при нечетных j и МCj=1 на четных масштабах.
Реализованные кортежи являются информационной характеристикой логического ряда, описывая возникшую структуру.
Можно представить информацию через вероятность появления кортежа в ряде. Если в ряде присутствуют все возможные на масштабе кортежи, то информация в таком ряде равна нулю, а энтропия максимальна.
Введем определение масштабной информации IМj:
IМj = Р (МCj) logk Р(МCj) (2.8.1.2)
Р (МCj) – вероятность возникновения масштабных кортежей, которую можно оценить через отношение числа реализовавшихся масштабных кортежей за s итераций к числу всех возможных кортежей на этом масштабе. Ясно, что s должно быть достаточно большим.
Информация может меняться в зависимости от масштаба рассмотрения – например, у ИРЛ на масштабе 1 информация равна 0, а на других масштабах – нет.
Дадим определение накопленной на f масштабах информации IS:
IS=
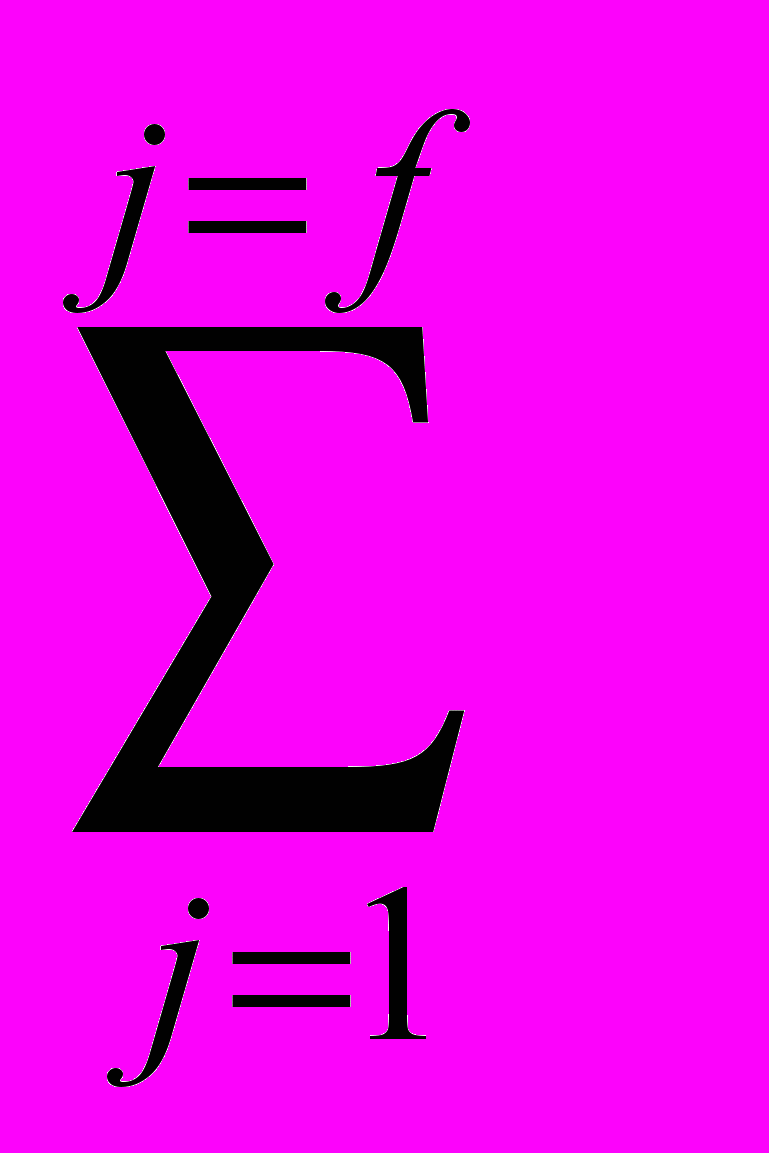IМj (2.8.1.3)Дадим определение накопленного на разных масштабах числа кортежей М:
М =
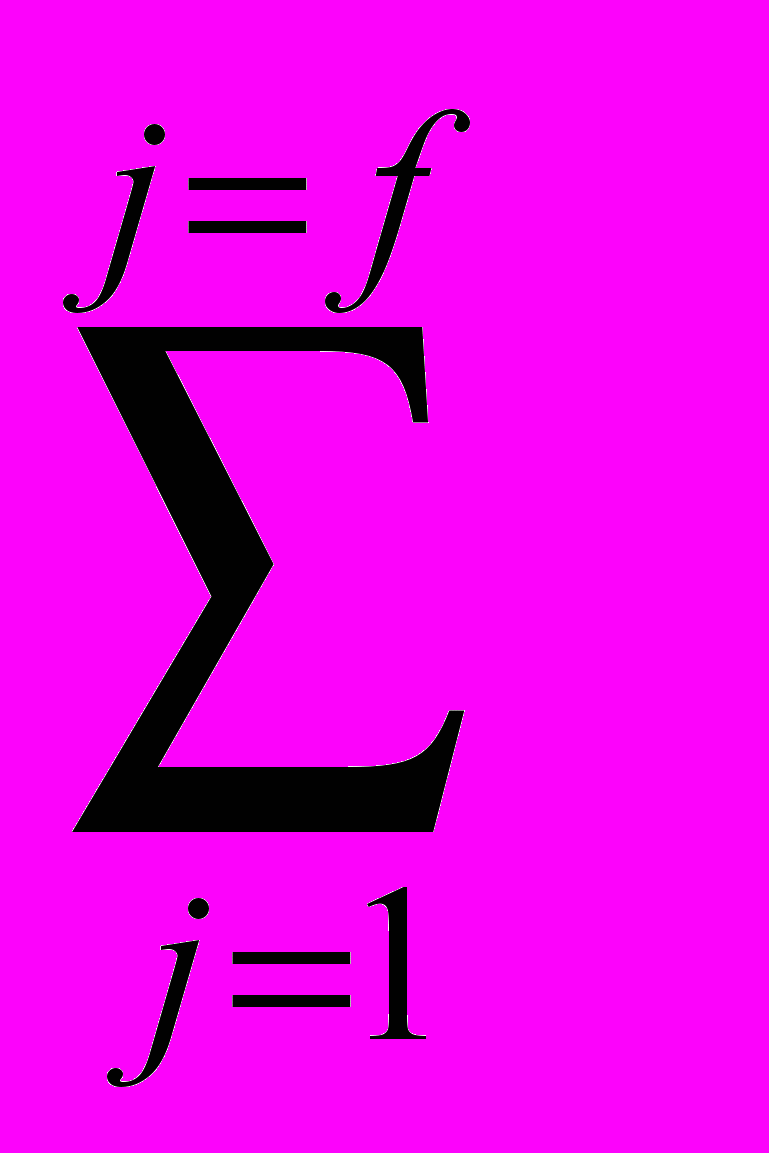МСj (2.8.1.4)Ясно, что при наличии самоподобия ряда М и IS стремятся к бесконечности при устремлении к бесконечности f. Однако скорости устремления к бесконечности накопленной информации и накопленной энтропии разные.
Если рассматриваемый нами ряд обладает фрактальной структурой, то стремление М к бесконечности можно аппроксимировать степенным законом:
М(n) nD (2.8.1.5)
Разрешение масштаб
а n – характерная длина кортежа на которой мы "рассматриваем" масштаб выступает в данном случае аналогом покрытия бесконечного множества значений логического ряда, образующего меру.
Представим логический ряд как ряд кортежей длиной n. Кортежу с номером i сопоставим вероятность Pi, того, что этот кортеж будет принадлежать некоторому ранее заданному и конечному множеству кортежей или иметь какое-либо свойство (например, свойство принадлежать множеству реализовавшихся на данном масштабе кортежей). Далее можно ввести набор величин Dq, вычисляемых для разных значений q:
Dq =
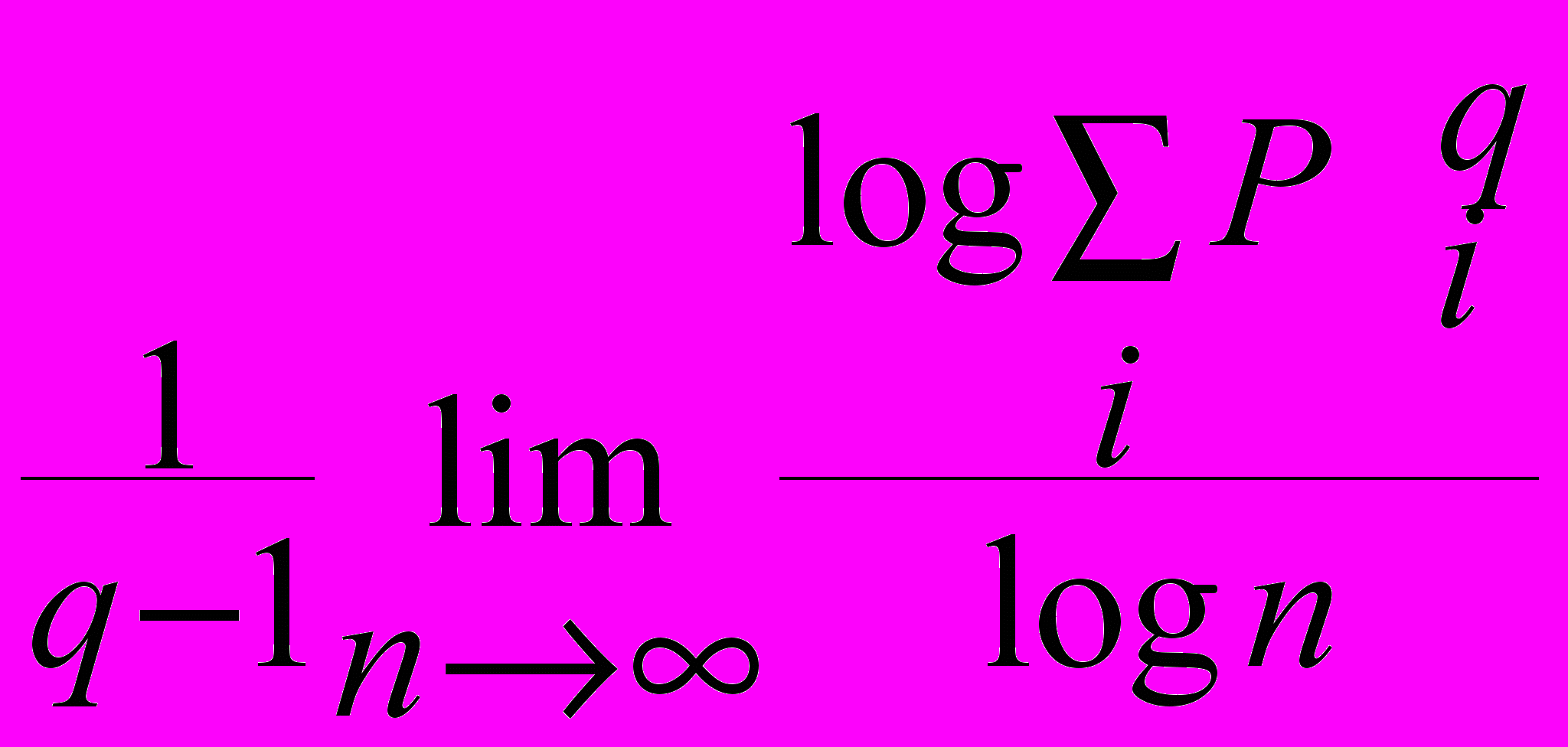,где суммирование ведется по всем кортежам.
Dq будет аналогом обобщенных размерностей.
В следующем подразделе постараемся формализовать интуиции размерности логического ряда более точно.
2.8.2 Аналог Хаусдорфовой размерности для логического ряда
Предположим, что рассматриваемый логический ряд есть результат бесконечного последовательного масштабного преобразования
кортежа A0:А1 =
А0, Аj = A j-1 = … = j A0 (2.8.2.1)Рассмотрим изменение масштаба при увеличении разрешения масштаба n в a раз:
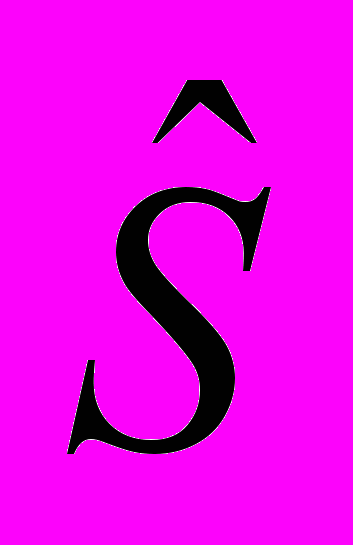Ai (n) = Ai (n/a) (2.8.2.2)Рассмотрим внутреннюю характеристику кортежа L – например, количество значений И на масштабе А:
L (
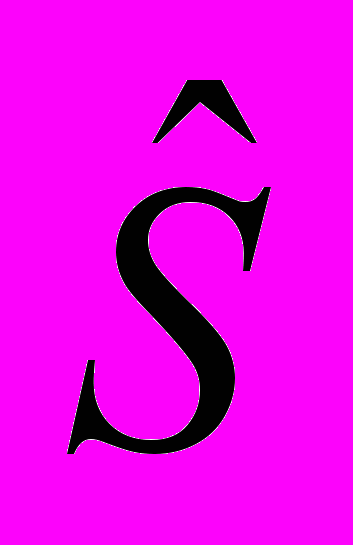Aj+1) = L (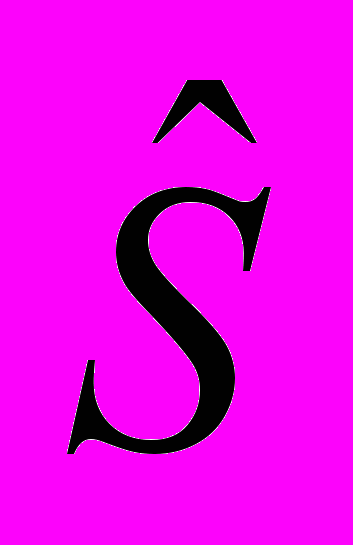Aj) (2.8.2.3)В зависимости от вида внутренней характеристики можно типологизировать различные размерности.
Если у логического ряда существует подобие:
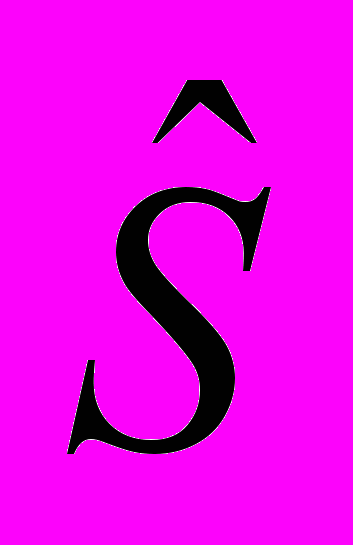
= , (2.8.2.4)то можно записать между L (Aj) и L (
Aj) в виде:L (
Aj) = ad L (Aj), (2.8.2.5)где d – некоторая степень – аналог размерности Хаусдорфа-Безиховича, определяемая в пределе:
d =
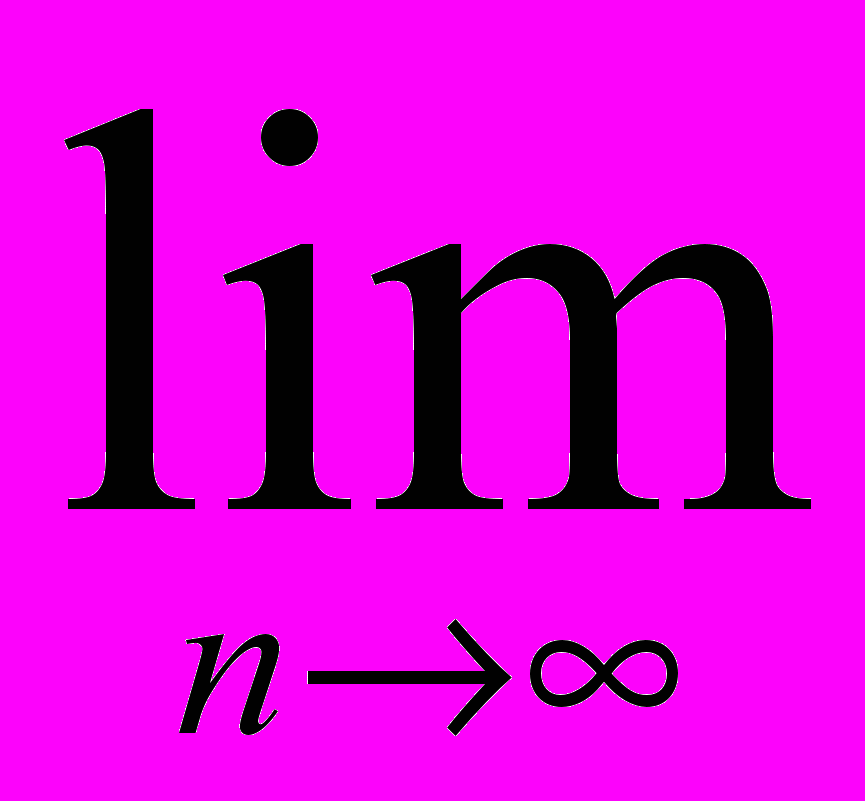
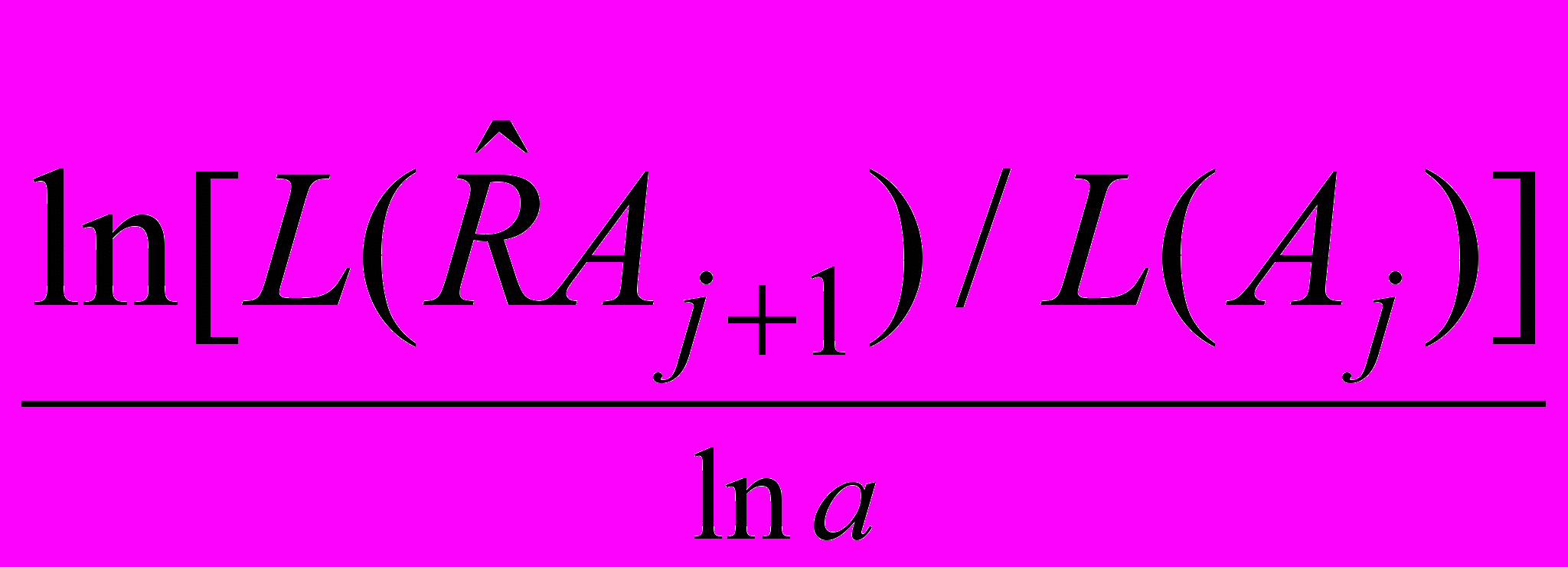(2.8.2.6)2.8.3 Аналогия с броуновским движением
Рассмотрим обратную связь a=И, 0.5ai+1: ai. Процесс эквивалентен бросанию монеты и генерирует логический ряд со случайным распределением значений.
Представим этот ряд как движение броуновской частицы, в котором перемещение частицы на расстояние + можно интерпретировать как И, а перемещение на - как Л.
При случайном процессе, перемещение броуновской частицы задается гауссовым или нормальным распределением вероятностей:
р(,) =
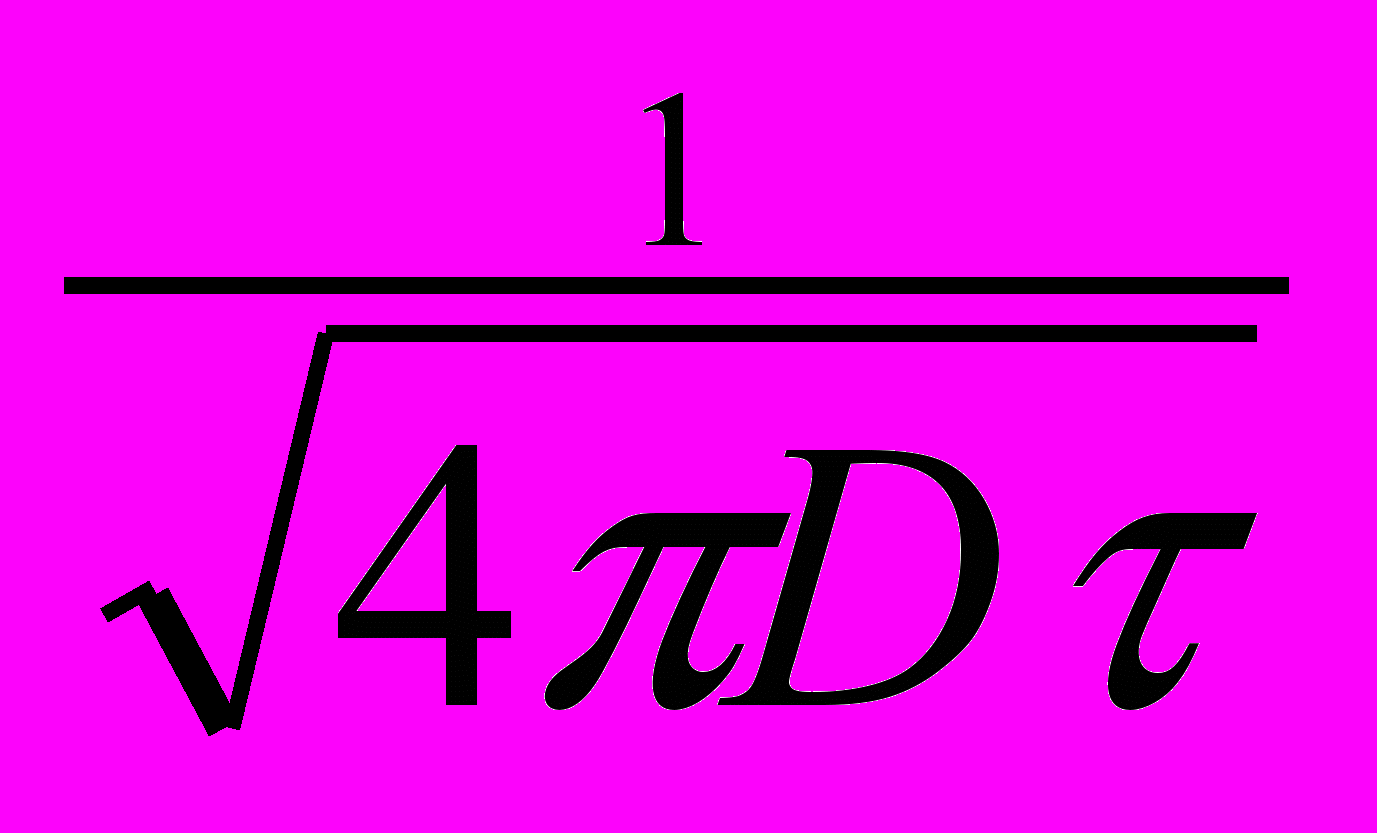exp (-
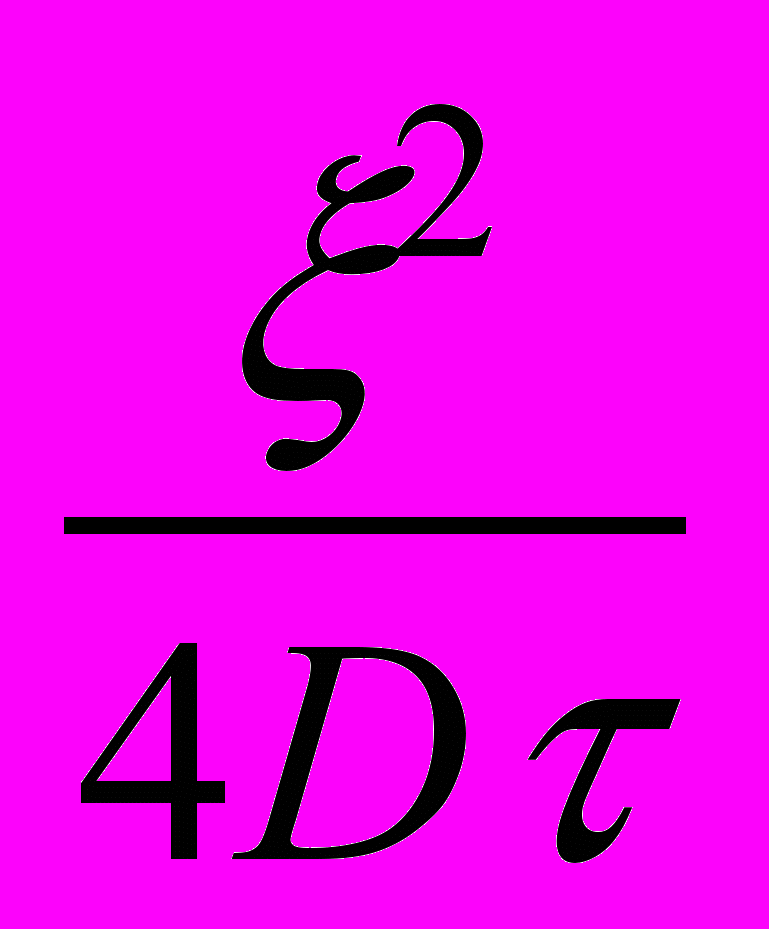) (2.8.3.1)Это означает, что на каждом интервале длительностью изменение параметра моделируется случайным образом, и вероятность того, что заключено между и +d, равна p(,)d. Последовательность значений {i} есть набор независимых гауссовых случайных чисел с дисперсией
2 =
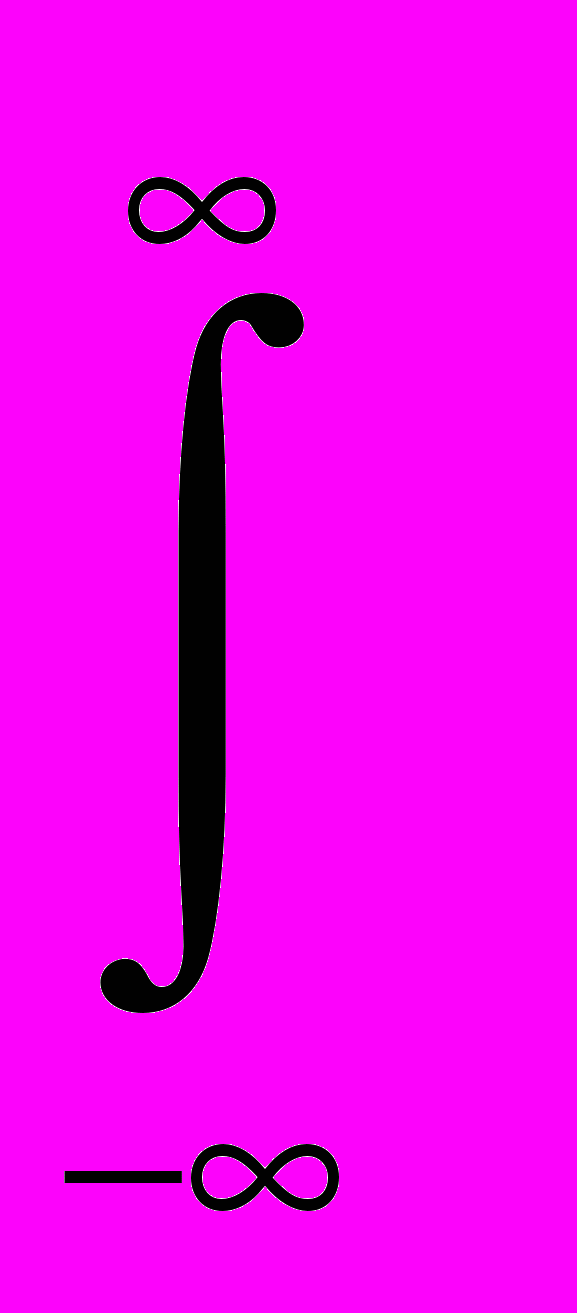2 р(,)d = 2D, (2.8.3.2)где коэффициент D подчиняется соотношению Эйнштейна, которое носит достаточно общий характер:
D =
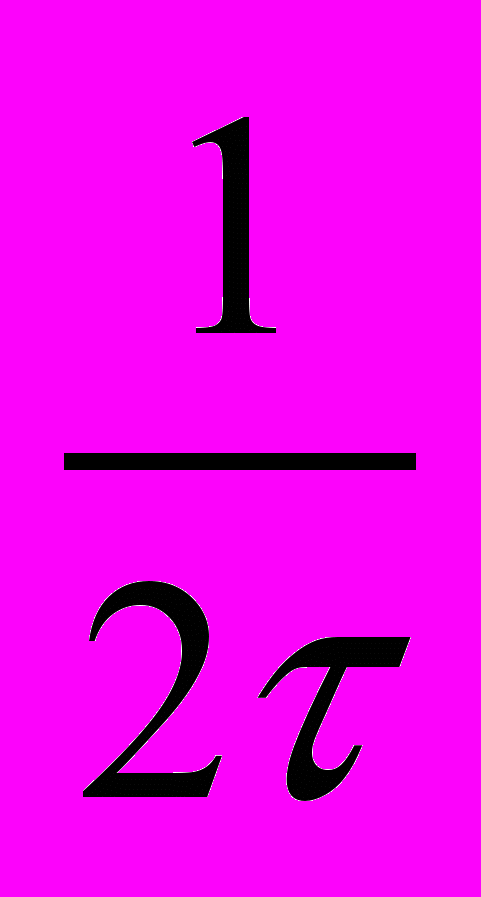2. (2.8.3.3)Данное, хорошо известное в статистике, соотношение справедливо для всевозможных стохастических процессов с разными видами распределения вероятностей.
Если заново определить , заменив /
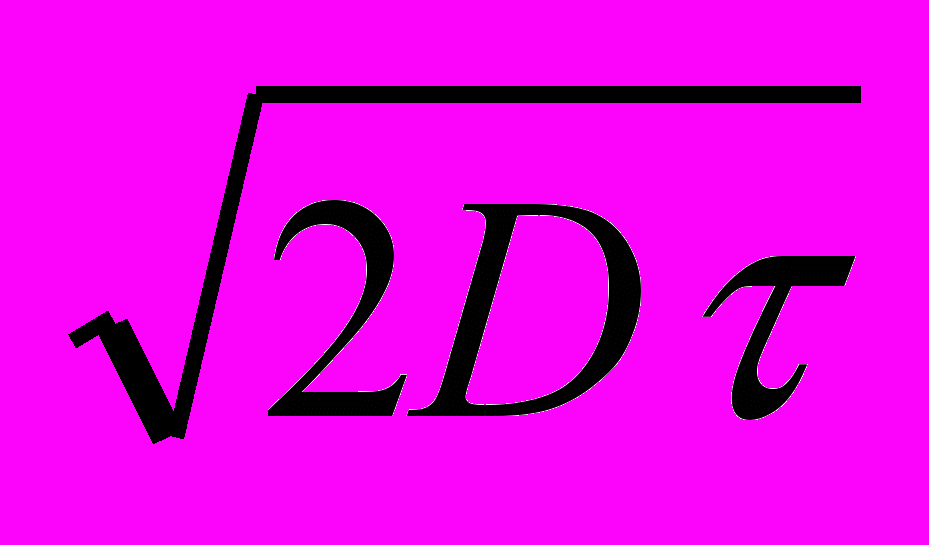на , новая дисперсия станет единичной и гауссовский процесс станет стандартным. Тогда, установив, что начальное значение равно нулю, текущее значение в момент времени t будет определяться какХ(t=n) =
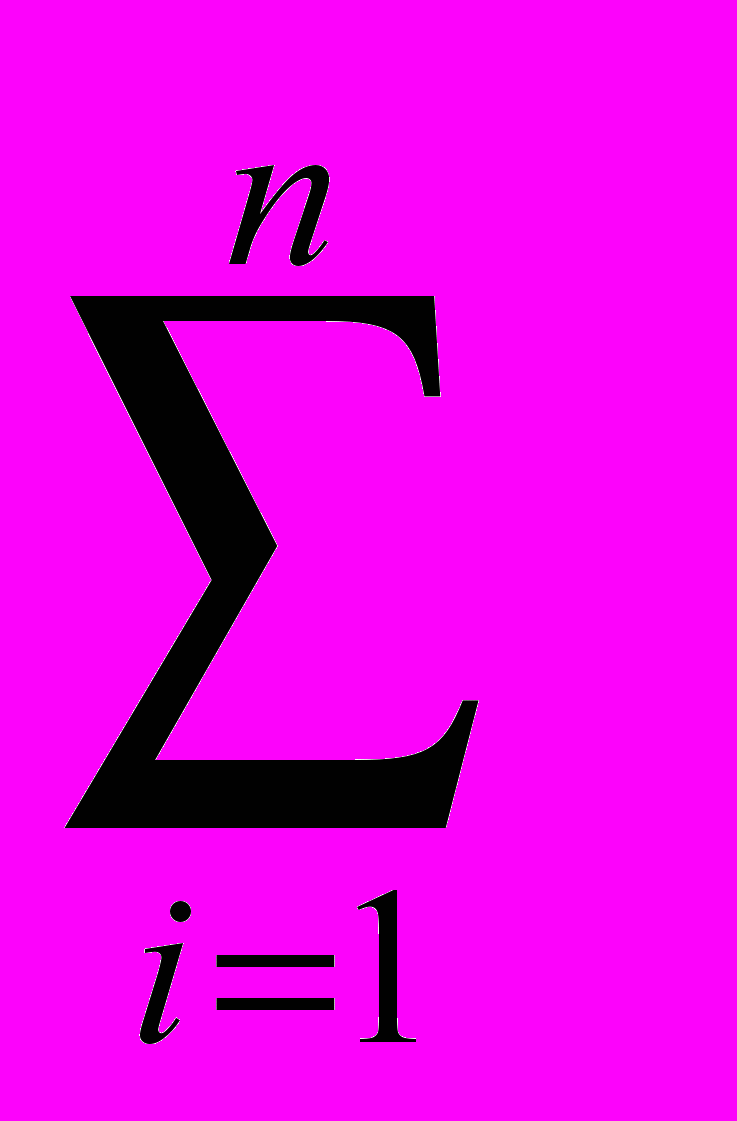i. (2.8.3.4)В книге Енса Федера "Фракталы"22 суммировано рассмотрение хорошо известного гауссовского процесса с точки зрения его масштабной инвариантности (в некоторых книгах используется термин автомодельность).
В этом случае процесс рассматривается в разных масштабах времени - с разным временным разрешением. То есть, регистрации параметра процесса производятся через каждый промежуток времени b, где b - некоторое произвольное число. Показано, что какое бы число b временных шагов ни разделяло моменты наблюдений, приращение всегда составляют гауссов случайный процесс с независимыми значениями с =0 и дисперсией
2 = 2Dt при t=b. (2.8.3.5)
То есть, с увеличением временного интервала фиксации параметра процесса в b раз, дисперсия процесса тоже увеличивается в b раз, а распределение вероятности, в зависимости от масштабного преобразования, будет иметь следующий вид:
р(,b) =
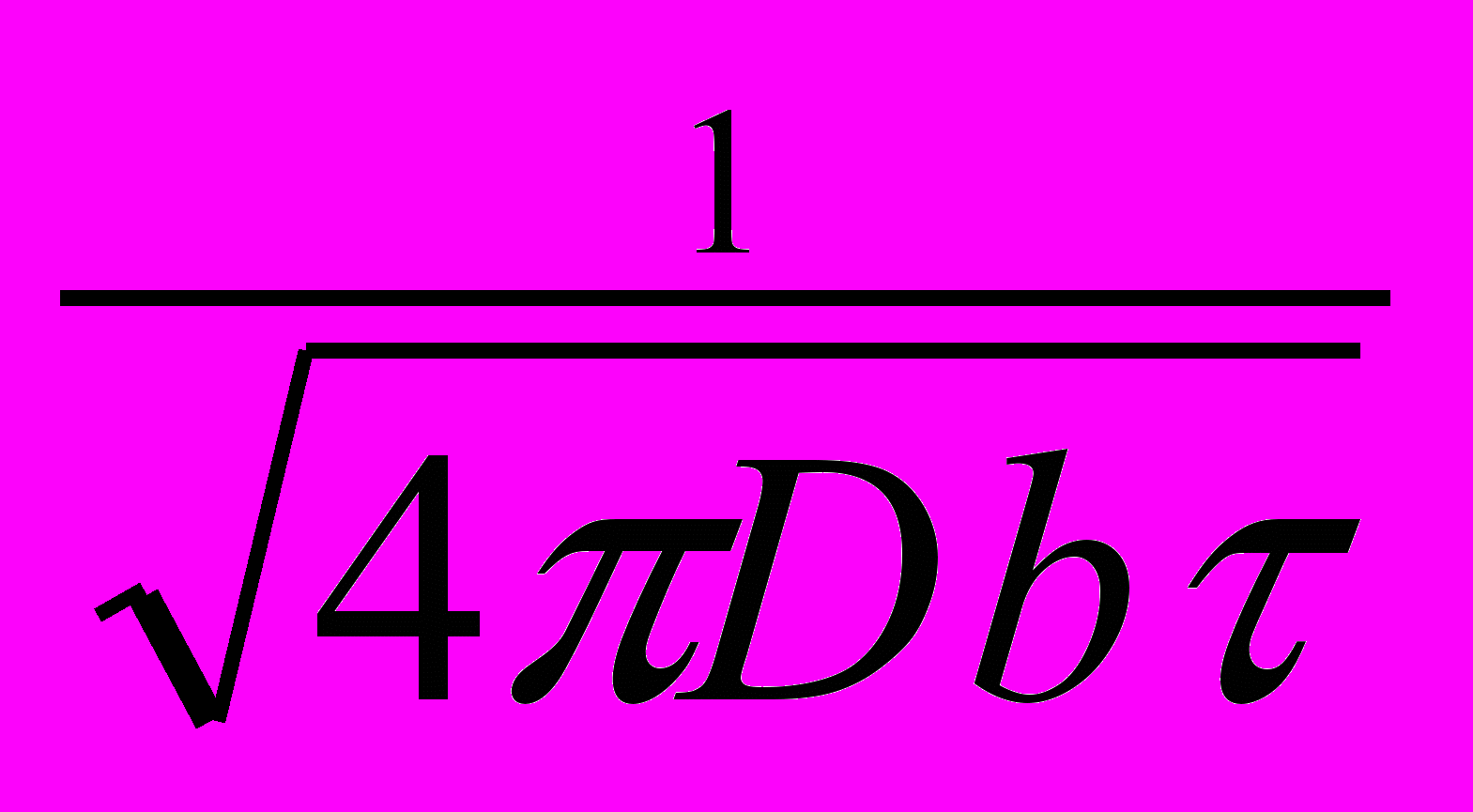exp (-
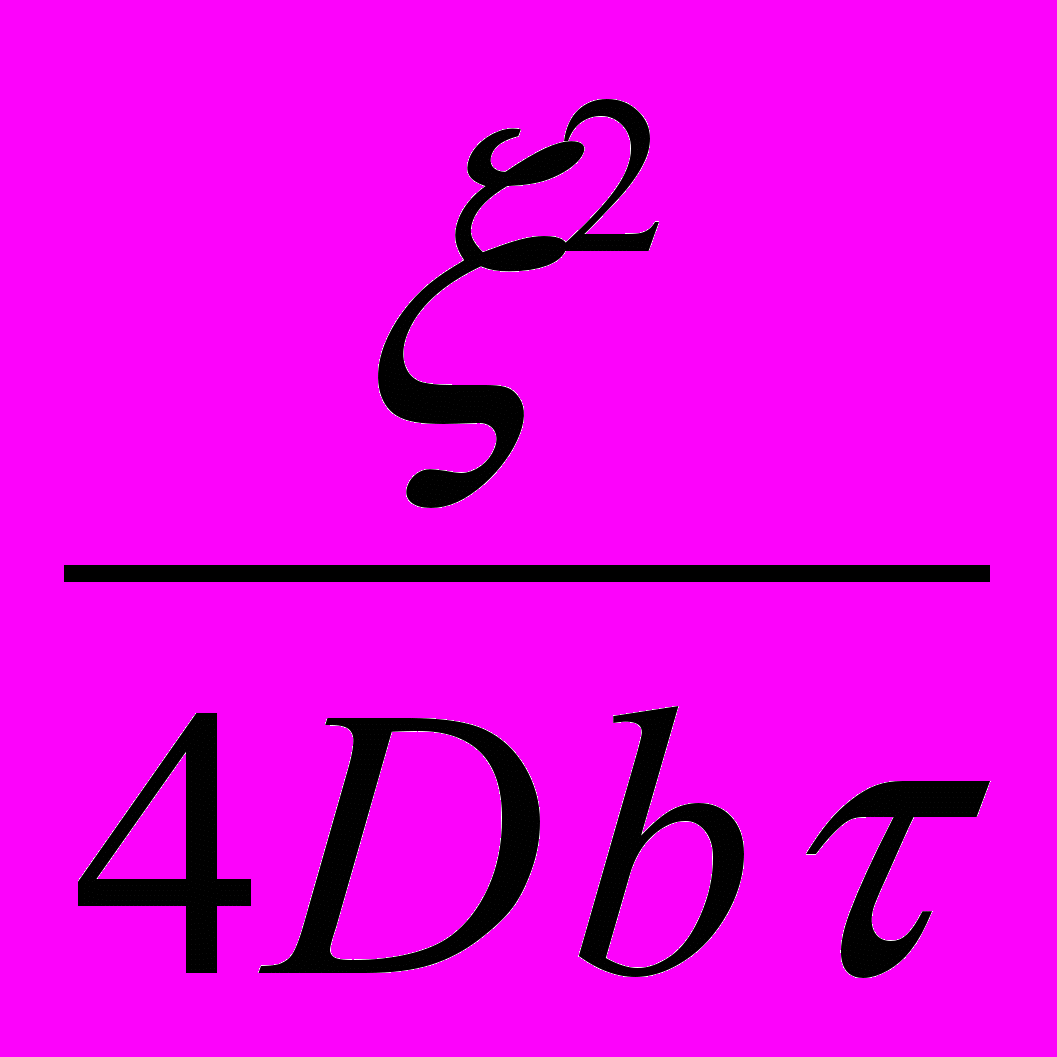). (2.8.3.6)Исходя из этого, можно сделать вывод о том, что гауссовский процесс обладает свойством подобия (скейлинга).
Он инвариантен в смысле распределения, то есть не меняет вида при преобразовании, которое меняет масштаб времени в b раз, а масштаб Х в b1/2 раз. Или можно сказать, что при изменении масштаба временного рассмотрения гауссовского процесса в b раз, текущее значение параметра процесса меняется в b1/2 раз.
Видно, что у этого процесса масштабы времени и значений меняются в разных пропорциях.
Преобразования, которые меняют масштабные характеристики процесса в разных пропорциях, называются аффинными, а процессы, не меняющие своего вида, характера протекания, при аффинном преобразовании, называются самоаффинными.
Н. Винер постулировал случайную функцию Х(t) гауссовского процесса с независимыми значениями {} через приращение, для любой пары моментов времени t и t0:
Х(t) - Х(t0) t - t0Н, где Н=1/2 и t t0. (2.8.3.7)
Мандельброт ввел понятие обобщенного броуновского движения, заменив в последней формуле значение Н равное 1/2 на любое действительное число из интервала 0