Тарасенко В. Фрактальная логика

Вид материала

Книга

Содержание В латинском языке есть поговорка: “назвать (именовать) значит узнать” 1.6 Парадоксы как фракталы. Фрактальная логика: обратная связь как модель "монстров" и парадоксов. 1.7 Парадокс лжеца: логический формализм через понятие обратной связи Илилилилилилилил… (1.7.2) 2.1 Определение логического ряда. Виды рядов. Аттрактор логического ряда Ряд лжеца Илилилилил… (2.1.2)

Подобный материал:

• Программа курса и темы практических занятий; Логика в таблицах и схемах. Логика как, 1722.34kb.
• Логика в образовании, 153.37kb.
• Математическая логика, 1012.22kb.
• Логика богочеловечества, 213.06kb.
• Н. В. Папуловская Математическая логика Методическое пособие, 786.38kb.
• Основы логики. Логика, 20.66kb.
• А. А. Ивин логика учебное пособие, 3160.22kb.
• Вопросы к экзамену по дисциплине «Логика», 15.87kb.
• А. А. Ивин логика учебное пособие, 3123.01kb.
• Вматематике понятие фрактал появилось в конце семидесятых годов после выхода в свет, 308.55kb.

Таблица 1.5.3

А	В	А\/ В	А  В
И	И	И	И
И	Н	И	Л
И	Л	И	Л
Н	И	И	И
Н	Н	Н	И
Н	Л	Л	И
Л	И	И	И
Л	Н	Н	И
Л	Л	Л	И

Введение в предмет рассмотрения фрактальных размерностей или характеристик, связанных с гладкими моделями, зависит от наблюдателя – специфического познавательного субъекта с "загруженными" теоретическими и социокультурными установками.

Изучение когнитивного статуса наблюдателя – любимая тема исследований автопоэзиса. В этом можно найти еще одно концептуальное пересечение теории автопоэзиса и фрактальной геометрии.

Наиболее ярко зависимость от наблюдателя видна на примере введения понятия размерности. Вот, что пишут по этому поводу в уже упоминавшейся статье Ю.А.Данилов и Б.Б.Кадомцев:

“Мандельброт обратил внимание на то, что довольно широко распространенное мнение о том, будто размерность является внутренней характеристикой тела, поверхности или кривой неверно (в действительности, размерность объекта зависит от наблюдателя, точнее от связи объекта с внешним миром).

Суть дела нетрудно уяснить из следующего наглядного примера. Представим себе, что мы рассматриваем клубок ниток. Если расстояние, отделяющее нас от клубка, достаточно велико, то клубок мы видим как точку, лишенную какой бы то ни было внутренней структуры, т. е. геометрический объект с евклидовой (интуитивно воспринимаемой) размерностью 0. Приблизив клубок на некоторое расстояние, мы будем видеть его как плоский диск, т. е. как геометрический объект размерности 2. Приблизившись к клубку еще на несколько шагов, мы увидим его в виде шарика, но не сможем различить отдельные нити - клубок станет геометрическим объектом размерности 3. При дальнейшем приближении к клубку мы увидим, что он состоит из нитей, т. е. евклидова размерность клубка станет равной 1. Наконец, если бы разрешающая способность наших глаз позволяла нам различать отдельные атомы, то, проникнув внутрь нити, мы увидели бы отдельные точки - клубок рассыпался бы на атомы, стал геометрическим объектом размерности 0.”

Возьмем на заметку тот факт, что говоря о зависимости размерности от наблюдателя, авторы подчеркивают прагматику введения размерности, которая носит комплиментарный характер:

“Но если размерность зависит от конкретных условий, то ее можно выбирать по-разному. Математики накопили довольно большой запас различных определений размерности. Наиболее рациональный выбор определения размерности зависит от того, для чего мы хотим использовать это определение. (Ситуация с выбором размерности вполне аналогична ситуации с вопросом: «Сколько пальцев у меня на руках: 3 + 7 или 2 + 8?» До тех пор, пока мы не вздумали надеть перчатки, любой ответ можно считать одинаково правильным. Но стоит лишь натянуть перчатки, как ответ на вопрос становится однозначным: «5 + 5».)

Подчеркнем, что размерность сильно зависит от того как ее измерять. Это означает, что кроме формул для подсчета размерности необходимо точно задать и некий операциональный набор способа измерения размерности.

В одном из первых в отечественной литературе обзоров по фракталам¹⁴ (или фракталям - если сохранять род слова Fractal при переводе), Я.Б. Зельдович и Д.Д. Соколов приводят такой пример. Положение точки области плоскости, ограниченной квадратом можно задать двумя измерениями, и тогда ее размерность будет равна двум, а можно исхитриться, и представить себе эту область в виде ломаной с очень сильно прижатыми друг к другу звеньями, сложенными наподобие столярного метра. Тогда, для задания положения точки хватит и одного измерения, и размерность будет равна единице.

"Монстр" - кривая Пеано (1.3.10) напоминает подобный столярный метр – при уменьшении длины ее звеньев, она начинает заполнять всю плоскость.

Точно таким же свойством обладает траектория броуновской частицы – чем больше время наблюдения, тем плотнее частица заполняет плоскость. Размерность определяет степень сложности траектории частицы в фазовом пространстве, степень негладкости этой траектории.



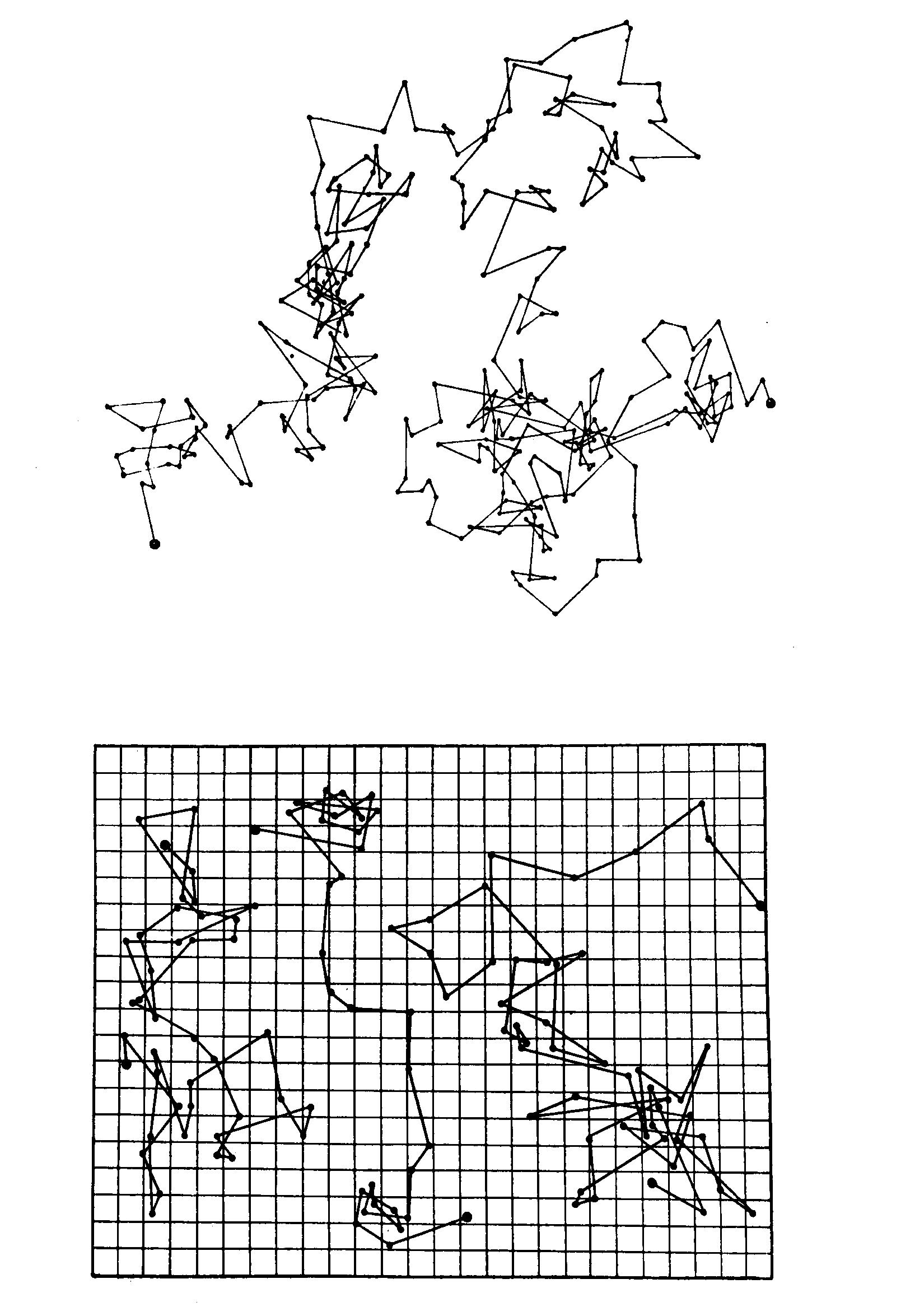
Рис. 1.5.4 Фрактальная траектория броуновской частицы. Рисунок из книги: Mandelbrot B. The Fractal Geometry of Nature. Freeman, San-Francisco.1977


Именно изломанность, пилообразность, негладкость "монстров" вызвала ассоциации при создании термина "фрактал" у Мандельброта¹⁵:

“ В латинском языке есть поговорка: “назвать (именовать) значит узнать”: Nomen est numen. До тех пор, пока я не принялся за своё изучение, упоминаемые в предыдущих разделах множества не нуждались в убедительном термине для их обозначения. Однако, когда классические монстры начали включаться в мои труды, и начали возникать многочисленные новые “монстры”, потребность в термине стала чрезвычайно необходимой. Это стало особенно острым, когда нужно было дать имя первому предшественнику этого эссе."

Термин "фрактал" закрепил и развил новый познавательный статус "монстров". С появлением имени у "монстров" появилось лицо, они перешли из области негативных примеров в область позитивных определений.


1.6 Парадоксы как фракталы. Фрактальная логика: обратная связь как модель "монстров" и парадоксов.


Мандельброт проанализировал "монстров" с точки зрения представлений фрактальной геометрии, показав общность между монстрами, природными объектами и множествами Жюлиа и Мандельброта.

Так же как и эти объекты, "монстры" обладают фрактальной размерностью и демонстрируют самоподобие.

Наиболее ярко понятие самоподобия иллюстрируется с помощью рассмотренной нами ранее фигуры Коха. Действительно, при увеличении ее фрагмента с помощью геометрического преобразования подобия можно получить фигуру тождественную той, чей фрагмент мы увеличивали.

Так же, как и для береговой линии, для кривой Коха или треугольника Серпинского можно вводить разного рода размерности.

В частности, “степень убегания” (1-D) длины (L) фигуры Коха в зависимости от единичной длины звена () оценивается по следующей формуле:

L ()  ^1-D,

где D = ln4/ln3  1.2628... - предложенная Мандельбротом степенная характеристика “убегания длины” или фрактальная размерность (по определению) триадной кривой Коха - мера изрезанности этой кривой”.

Итак, Мандельброт превратил "монстров" из "пугал", за которыми надо было охотиться с целями исключения из "нормальных" геометрических рассуждений в концептуально оформленные геометрией предметы измерения и построения.

Этот же мыслительный ход можно осуществить и по отношению к парадоксам.

Действуя по аналогии, можно предположить, что парадоксы есть частные случаи логических фракталов, которыми должна оперировать фрактальная логика.

Мы сознательно не будем жестко определять термины "логический фрактал" и "фрактальная логика", постепенно вводя представления о частных случаях логических фракталов и соответствующих логик. Пока ограничимся представлением о том, что фрактальная логика – это набор понятий и представлений, основанных на принципах фрактальной геометрии, применяемых к логическим объектам с бесконечным количеством значений.

Фрактальная геометрия оперирует парадоксальными геометрическими предметами, результаты измерения которых (длина, площадь, объем) устремляются к бесконечности. В качестве начальной (а потому неточной) метафоры можно сказать, что фрактальная логика оперирует парадоксальными логическими объектами, число логических значений которых также стремится к бесконечности.

Фрактальная логика превращает бесконечный парадокс из «монстра» и «пугала» в концептуальный предмет формального, инструментального и социокультурного рассмотрения.

Для того, чтобы сделать термины "логический фрактал" и "фрактальная логика" не только метафорами, но и понятиями оформленной и формализованной логической концепции, рассмотрим понятие обратной связи.

Интерпретация построения “монстров” – фракталов через обратную связь содержится в книге Пайтгена, Юргенса и Заупе “Хаос и фракталы: новые горизонты науки”¹⁶.

Российский математик Александр Зенкин¹⁷ интерпретировал парадокс лжеца как процесс с обратной связью.

В свое время Алан Тьюринг предложил свой знаменитый мысленный эксперимент – машину Тьюринга, и выдвинул тезис о том, что любая вычислимая (частично рекурсивная – имеющая завершение) функция может быть запрограммирована (вычислена с помощью конечного алгоритма) на машине Тьюринга. Интеллект человека, по мнению Тьюринга, устроен похожим образом, поэтому машина в принципе может мыслить.

Машину Тьюринга можно интерпретировать в терминах отрицательной обратной связи – вычислительные процедуры за конечное число шагов сходятся к нужному значению функции.



Рис. 1.6.1 Алан Матисон Тьюринг (1912-1954)

Автор оригинальных трудов по математической логике, вычислительной математике, искусственному интеллекту. В годы второй мировой войны, будучи в Англии, успешно работал над дешифровкой сообщений нацистского командования.


Для систематизации и сравнения процедур генерации “монстров” и парадоксов, мы рассмотрим нечто подобное: мысленный эксперимент - машину логической обратной связи, схема которой представлена ниже.



блок

управления










входной блок блок обработки выходной блок




линия обратной связи




Рис 1.6.2 Машина обратной связи.


Машина состоит из трех блоков памяти: входного блока (ВХБ), выходного блока (ВБ), блока управления (БУ) и одного процессорного блока обработки (БО), связанных между собой связями. Блок управления нужен для “запуска” машины.

Общая схема работы состоит из двух циклов – цикла запуска машины и рабочего цикла:

Цикл запуска:

1. Ввод информации в блок управления
   
2. Ввод информации во входной блок
   
3. Пересылка информации из блока управления в блок обработки
   

Рабочий цикл:

1. Пересылка информации из входного блока и ввод ее в блок обработки
   
2. Работа блока обработки
   
3. Пересылка информации из блока обработки в выходной блок
   
4. Пересылка информации из выходного блока во входной блок.
   

В качестве примера работы логической машины с обратной связью, приведем рассмотренный выше пример генерации кривой Коха:

1. Цикл запуска – в блок управления вводится “затравка” – единичный отрезок. Это нулевая итерация нашей фигуры – i=0.
   
2. Запускается рабочий цикл: затравка преобразуется в блоке обработки в первое поколение фигуры - отрезок делится на три равные части, средняя часть отбрасывается, а на ее месте строится ломаная, являющаяся фрагментом равностороннего треугольника со стороной, равной, одной третьей длины отрезка. Это первая итерация нашей фигуры – i=1.
   
3. Полученное первое поколение “отправляется” на выходной блок,
   
4. Обратная связь переносит первое поколение на вход.
   

После этого по тому же алгоритму, примененному для отдельному отрезку звеньев ломаной, первое поколение преобразуется во второе поколение в рабочем блоке: i=2.

Получающийся “монстр” – результат бесконечного числа циклов работы машины при i.

В устремлении процедуры на бесконечность состоит главное отличие нашей машины от машины Тьюринга. Построение фракталов всегда осуществляется не на конечном, а на бесконечном числе итераций.

Теперь интерпретируем с помощью обратной связи парадокс лжеца.

Рассмотрим высказывание А, соответствующее суждению “Я лгу”.

Пусть оно будет истинным. С точки зрения обратной связи это означает, что на нулевой итерации при i=0, значение А равно И.

Далее, нам надо интерпретировать парадоксальное умозаключение “Значение А истинно, значит, А ложно” как обратную связь – процедуру, присваивающую новое значение высказыванию А при изменении счетчика итераций.

Обратная связь меняет значение А при i=1 на Л. Таким же образом, при i=2 значение А равно И, при i=3, опять Л – и так далее.

Таким образом, цикл запуска будет следующим:

Ввод информации в блок управления – установление i=0,.

Ввод информации во входной блок - значение А есть И

Пересылка информации из блока управления в блок обработки

Рабочий цикл:

Пересылка информации из входного блока и ввод ее в блок обработки

Работа блока обработки – смена значения А на противоположное (с И на Л или с Л на И), увеличение значения счетчика итераций на единицу,

Пересылка информации из блока обработки в выходной блок.

Пересылка информации из выходного блока во входной блок.

Построим таблицу истинности высказывания А в зависимости от итераций - различных i:

i = 0	i = 1	i = 2	i = 3	i = 4	I = 5	i = 6	i = 7	i = 8	…
И	Л	И	Л	И	Л	И	Л	И	…

Таблица 1.6.1 Таблица истинности парадокса лжеца

Парадокс – это результат бесконечного изменения логического значения машиной обратной связи.

Таким образом, математический “монстр” и логический парадокс лжеца могут быть представлены как результат бесконечного числа итераций машины обратной связи.

На основании этой общности мы будем постепенно вводить представление о логических фракталах.


1.7 Парадокс лжеца: логический формализм через понятие обратной связи


Предположим, что значение высказывания “Я лгу” зависит от итерации i. Назовем это высказывание переменным высказыванием.

Назовем начальным условием значение переменного высказывания при i=0.

Если высказывание имеет только одно значение, то такое высказывание мы будем называть постоянным.

Рассмотрим феноменологию парадокса лжеца – то есть, не будем интерпретировать то, как обратная связь преобразует высказывание, а лишь зафиксируем, что на выходе из обратной связи появляется высказывание с противоположным логическим значением. Это может зафиксировать операция отрицания.


Введем следующие обозначения:

ai – обозначение высказывания “Я лгу” на i-той итерации. Его значение может быть И или Л. Ясно, что переменное высказывание может быть представлено как ряд постоянных высказываний классической логики высказываний.

= – обозначение операции ввода начальных данных – присвоения значения высказыванию при i=0. Запись a0=И означает, то, что мы задаем на нулевой итерации значение И. Это интерпретация нашего предположения о том, что высказывание “Я лгу” истинно.

: - обозначение обратной связи, переводящей значение высказывания с i итерации на i+1 итерацию бесконечное число раз. Слева будем записывать обозначение значение на i+1итерации, справа – на i итерации, в результате которой формируется значение на i+1 итерации.

 - обозначение операции отрицания, преобразующей значение обратной связи на противоположное – Л преобразуется в И, И преобразуется в Л.


Тогда обратную связь парадокса лжеца можно формализовать следующим образом:


a0=И, ai+1:  ai


В результате действия обратной связи образуется переменное высказывание или ряд постоянных высказываний:


а0 a1 a2 a3 a4… (1.7.1)


Далее, пользуясь рядом (1.7.1) последовательно запишем значения переменного высказывания, рассчитанные по этому формализму. Таблица истинности из прошлого раздела будет представима в виде ряда значений переменного высказывания или ряда значений атомарных высказываний:

ИЛИЛИЛИЛИЛИЛИЛИЛ… (1.7.2)

Таким образом, в этой интерпретации логическое значение парадокса лжеца – бесконечное чередование значений, генерируемых обратной связью.

Заметим, что указанное представление можно распространить и на теоретико-множественные парадоксы. Суждение “Множество всех множеств, не содержащих себя в качестве элемента, принадлежит самому себе” может быть представлено как бесконечная последовательность значений такого рода высказываний.

Структура парадокса в нашей интерпретации – бесконечная последовательность чередующихся логических значений.

Глава 2 Логические ряды и логические фракталы


2.1 Определение логического ряда. Виды рядов.


Введем точное представление о логическом ряде.

Логический ряд – одномерная упорядоченная последовательность логических значений k-значной логики, пронумерованных от 0 до бесконечности.

Ряды бывают сходящиеся, в этом случае значение ряда постоянно при i, периодические – значение устойчиво повторяется, и апериодические – значения, появляющиеся в произвольном порядке.

Аттрактор логического ряда – устойчивая на бесконечность структура значений логического ряда. Может быть: неизменное значение (аттрактор первого рода – унарный кортеж¹⁸), комбинация значений (аттрактор второго рода – бинарный кортеж, n-ka), апериодичность (аттрактор третьего рода).

Пусть мы задали для данной k-значной логики конечное множество аттракторов. Назовем их детерминированными аттракторами.

Законом будем называть ряд, для которого доказано наличие аттрактора из множества детерминированных аттракторов. Пример закона классической логики дан в разделе 2.3.

Значение высказывания, в случае двухзначной логики, может быть И или Л. В общем случае может быть любое конечное число вариантов значений. В качестве примера логического ряда двузначной логики можно привести ряд, представленный в таблице 1.5.1. Каждый член этого ряда упорядочивается номером. Номер значения фиксируется итерацией логического ряда i. Итерация i меняется от 0 до бесконечности.

Назовем классическим рядом ряд составленный из высказываний классической логики высказываний двухзначной логики.

Назовем рейхенбаховским рядом ряд с тремя возможными значениями – И, Л, Н и составленный из высказываний рейхенбаховской логики высказываний, описанной выше.

Назовем начальным условием значение логического ряда при i=0.

Обозначим специальными терминами частные случаи логических рядов:

Вырожденный ряд – логический ряд, с одинаковыми значениями.

Например:


ИИИИИИИИИИ…. (2.1.1)


Соответственно, в частных случаях, И - вырожденный ряд (ИВ) – ряд с истинными значениями, Л-вырожденный ряд (ЛВ) – ряд с ложными значениями. Вырожденный ряд – пример ряда с аттрактором первого рода.

Вырожденный ряд – пример закона на множестве детерминированных аттракторов с одним элементом – И.

Ряд лжеца – классический логический ряд с регулярно чередующимися друг за другом значениями истинности и ложности. В зависимости от начальных условий, существует два ряда лжеца:

ИЛИЛИЛИЛИЛ… (2.1.2)

ЛИЛИЛИЛИЛИ… (2.1.3)

Мы будем различать И-ряд лжеца (ИРЛ) – ряд при начальном условии И – случай (2.1.2), и Л-ряд лжеца (ЛРЛ) – ряд при начальном условии Л – (2.1.3).

В нашей терминологии ряд лжеца имеет аттрактор второго рода.