Geum.ru

Вматематике понятие фрактал появилось в конце семидесятых годов после выхода в свет в 1977 году книги Б. Мандельброта «Фрактальная геометрия природы»

Вид материалаДокументы

Содержание


Arbor vegetalis
Подобный материал:
Т.Бонч-Осмоловская

Фракталы в литературе


В математике понятие фрактал появилось в конце семидесятых годов после выхода в свет в 1977 году книги Б.Мандельброта «Фрактальная геометрия природы».

Слово фрактал имеет латинский корень fractus – состоящий из частей, фрагментов. Мандельброт определил фрактал как «структуру, состоящую из частей, которые в каком-то смысле подобны целому» (Федер Е. Фракталы. Пер. с англ.-М.: Мир, 1991). Фракталы быстро стали популярны, не в последнюю очередь благодаря красочным компьютерным иллюстрациям, рис.1 (Мандельброт был сотрудником корпорации IBM).




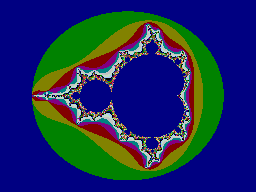
рис.1. Фрактал Мандельброта.


Внимательное изучение фракталов привело к пониманию, что они существовали и были известны ученым (Пуанкаре, Фату, Жюлиа, Кантор, Хаусдорф) и до Мандельброта, и заслуга последнего состояла скорее в привлечении внимания к этим структурам и указании на чрезвычайно широкое распространение фрактальных объектов в нашем мире.

И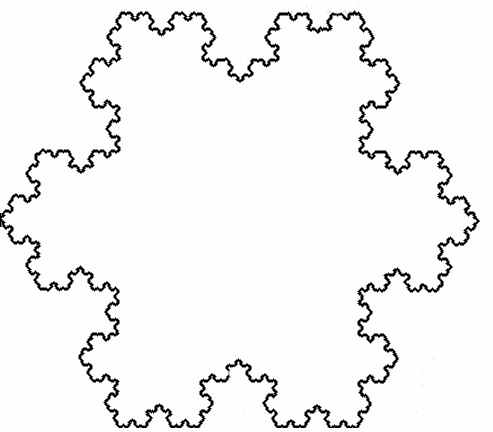з рукотворных, математических кварталов известны кривая или снежинка Гельги фон Кох (рис.2, 3), треугольник Серпинского (рис.4), и другие, строящиеся с помощью некоторого алгоритма, примененного к кривой или поверхности.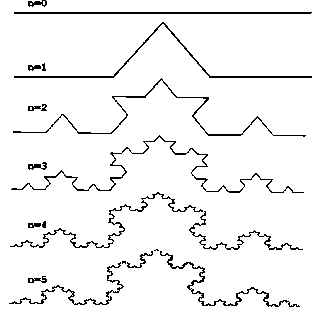





Рис.2. Снежинка Кох. Рис.3. Построение кривой Кох.

Для таких кривых (рис.2,3,4) часть рисунка n-ной итерации будет в точности тождественна части (n-1)-ой итерации большего размера.

Рисунки, подобные рис.1, изображают области притяжения к различным точкам, аттракторам, в пространстве системы нелинейных уравнений. Различные области отражаются на картинке разными цветами. Система нелинейных уравнений могут характеризоваться чрезвычайной чувствительностью к малейшим изменениям параметров системы, в результате чего сколь угодно близкие на фазовом пространстве точки могут в конечном итоге стремиться к различным аттракторам. Что означает, что увеличение масштаба изображения не приведет к упрощенной его версии, а только к появлению картинки, подобной исходной. В этих случаях речь идет именно о подобии, а не о точном тождественном воспроизведении.

Именно фракталы этого типа являются визитной карточкой Мандельброта. Причем свойство фрактальности, то есть схожести структур целого фазового пространства и его части, повторяется бесконечное количество увеличений масштаба – маленький кусочек исходной картинки при увеличении выглядит аналогично всей картинке, вырезанный кусочек из этой маленькой картинки при увеличении выглядит аналогично его предшественнику, и так далее.


Р

ис.4. Треугольник Серпинского.


И эти сложные математические объекты, создание которых невозможно без помощи компьютера, привлекают неизменный интерес как математиков, так и людей, чрезвычайно от нее далеких, привлекают своей завораживающей и повторяющейся красотой, подобной очарованию сменяющих друг друга картинок в детском калейдоскопе. Сходные последовательные изображения погружают зрителя в волшебный ирреальный мир, кружит голову идеей бесконечного повторения, подобия и перерождения.

Быстро было обнаружено множество природных объектов, строение которых сходно с фракталами – это и ветки деревьев, повторяющие более крупные ветви, повторяющие ствол, и снежинки, и кровеносные пути и нервы, разветвляющиеся на более мелкие пути, которые ветвятся на еще более мелкие, и карта мозговых полушарий, да и любая карта, при увеличении масштаба превращающаяся в иную карту, фрагмент которой при следующем увеличении есть еще одна схожая карта, и т.д.

Р
ис. 5. Фрактальный лес (из книги Michael Barnsley. Fractals everywhere. Boston: Academic Press, 1988)


Похоже, что весь окружающий мир, за редкими бессмысленными исключениями, представляет собой фракталы.

Однако, несмотря на их вездесущесть, нам неизвестны исследования литературных фракталов, что, конечно, является огромной лакуной в общей картине мироздания. И мы поставили задачей изучить литературные произведения с целью обнаружить среди них фракталы, скрытые или явные.

Представление о фракталах, и мечта о литературных фрактальных произведениях характерны для человеческой мысли с незапамятных времен: вспомним хотя бы мечту о книге книг – книге, состоящей из книг, или книге, включающей в себя иные книги – если это и не фрактал, то первая к нему итерация.

Тот факт, что писатели прошлого никогда не слышали и не могли слышать о фракталах, ровно ничего не означает: «когда писатель (и вообще художник) говорит, что, работал, не думал о правилах, это означает только, что он не знал, что знает правила», (У.Эко. Заметки на полях «Имени розы». Рассказывание процесса. // У.Эко. Имя Розы. СП-б, Симпозиум, 1997. С.602).

Попытаемся сформулировать, что представляют собой фракталы как произведения-сплав визуального искусства и математики, чтобы можно было соотносить с ними произведения литературы.

В целом мы будем считать фрактал произведением искусства, которое характеризуется двумя основными характеристиками: 1) часть его неким образом подобна целому (в идеале, эта последовательность подобий распространяется на бесконечность, хотя никто никогда не видел действительно бесконечной последовательности итераций, строящих снежинку Кох); 2) фракталы обладают особым шармом, завораживающей красотой, погружение в воронку которой может завести чрезвычайно далеко.

Пытаясь определить литературные фракталы, мы встречаемся с некоторыми принципиальными трудностями: во-первых, литературный текст, по сравнению с произведением визуального искусства, обладает одной существенной особенностью – он линеен, существует направление его прочтения от начала до конца. Впрочем, с этой особенностью текста успешно справляются как создатели палиндромов, закручивающих текст в двустороннее обращаемое кольцо, так и создатели интерактивной литературы, предлагающие читателю произвольно или по некоторому закону изменять порядок прочтения фрагментов текста.

Еще одной особенностью текста является его конечность. Эта особенность свойственна и визуальным работам, и именно фракталы вывели визуальные произведения за рамки формальной конечности.

Как же можно создать бесконечный текст? Этим вопросом задавался герой рассказа Х.-Л.Борхеса «Сад расходящихся тропок»: «…я спрашивал себя, как может книга быль бесконечной. В голову не приходит ничего, кроме цикличного, идущего по кругу тома, тома, в котором последняя страница повторяет первую, что и позволяет ему продолжаться сколько угодно» (Х.-Л.Борхес. Соч. в 3-х т. т.1. С.326).

Посмотрим, какие еще решения могут существовать.


Самыми простым бесконечным текстом будет текст из бесконечного количества дублирующихся элементов, или куплетов, повторяющейся частью которого является его «хвост» – тот же текст с любым количеством отброшенных начальных куплетов. Мы постарались максимально упростить примеры, подобрав короткие и, по возможности, забавные стишки.

Схематически такой текст можно изобразить в виде неразветвляющегося дерева или периодической последовательности повторяющихся и повторяющихся куплетов. Единица текста – фраза, строфа или рассказ, начинается, развивается и заканчивается, возвращаясь в исходную точку, точку перехода к следующей единице текста, повторяющей исходную. Такой текст можно уподобить бесконечной периодической дроби: 0,33333…, ее еще можно записать как 0,(3). Видно, что отсечение «головы» – любого количества начальных единиц, ничего не изменит, и «хвост» будет в точности совпадать с целым текстом.

… …













Рис.6. Неразветвляющееся бесконечное дерево тождественно самому себе с любого куплета.


Среди таких бесконечных произведений – стихи для детей или народные песенки, как, например, стишок о попе и его собаке из русской народной поэзии:

У попа была собака, он ее любил.

Она съела кусок мяса, он ее убил.

В землю закопал,

Надпись написал,

Что

У попа была собака…


Или стихотворение М.Яснова «Чучело-мяучело»:

Чучело-мяучело

На трубе сидело.

Чучело-мяучело

Песенку запело.

Чучело-мяучело

С пастью красной-красной –

Всех оно замучило

Песенкой ужасной.

Всем кругом от чучела

Горестно и тошно,

Потому что песенка

У него про то, что:

Чучело-мяучело

На трубе сидело…


Схематично эти тексты могут быть записаны как «А говорит, что А говорит, что А…».

Другие стихотворения этого класса обладают схемой типа «А становится В, становится А, становится В…», например:


Еду я и вижу мост, под мостом ворона мокнет,

Взял ворону я за хвост, положил ее на мост, пусть ворона сохнет.

Еду я и вижу мост, на мосту ворона сохнет,

Взял ворону я за хвост, положил ее под мост, пусть ворона мокнет…


К последним текстам можно отнести знаменитую притчу о бабочке Чжуан Цзы, если перефразировать ее следующим образом: «Притча о философе, которому снится, что он бабочка, которой снится, что она философ, которому снится, что он бабочка, которой снится, что она философ, которому снится…».

Заметим, что тема сна и сновидений еще встретится нам в других произведениях фрактальной литературы.

Подвариант схемы – «А, который В, который А, который В, который…»: «Игры, в которые играют люди, которые играют в игры, в которые играют люди, которые…».

К подобным текстам относится и знаменитый парадокс с изречениями на двух сторонах карточки, первое из которых гласит: «Утверждение на обратной стороне карточки ложно», и другое: «Утверждение на обратной стороне карточки истинно». Перефразируя их в единый бесконечный лексически фрактальный текст, получаем: «ложным является утверждение, что истинным является утверждение, что ложным является утверждение, что истинным…».

Здесь же представлено и двойное отражение, производящее уходящую в бесконечность последовательность отражений, и характерная для фрактальных текстов парадоксальность, завораживающая энигматичность, выводящая читателя из рамки привычных представлений к горизонтам неведомого.

Бесконечные стихотворения фрактальны лексически – бесконечно повторяется тождественный элемент текста, и фрактальный рисунок возникает из самой записи текста. Структура таких произведений очень проста. Ее можно изобразить или в виде замкнутой кривой (первый случай) или двух замыкающих друг друга кривых (второй случай).




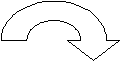
Рис.7. Змея, кусающаяся себя за хвост. Рис 8. Две змеи, пожирающие друг друга.

В кольце может быть и большее число звеньев, как, например, в случае замкнутой логической схемы из трех элементов, описывающей строение стихотворения для детей Р.Сефа «Бесконечные стихи»:

Кто вечно хнычет и скучает –

Тот ничего не замечает,

Кто ничего не замечает –

Тот ничего не изучает,

Кто ничего не изучает,

Тот вечно хнычет и скучает.

Если скучно стало – почитай сначала.

Видно, что увеличение числа звеньев в кольце, хотя и обладает глубоким философским значением, мало отражается на общей фрактальности этих текстов.

Простота этих стишков не должна служить основанием для отказа им во фрактальной сущности, вспомним, что и фракталы Мандельброта, и кривые с дробной размерностью задаются достаточно простыми алгебраическими формулами или алгоритмами, и это также одна из особенностей фракталов – простая задача имеет необычайно сложные решения.

А первое основное свойство фракталов, свойство гомоморфности частного целому, нашим детским стихотворениям присуще.

В результате возникает в точности повторяющиеся «куплеты», которые производят бесконечную последовательность повторений, никогда и ничем не исчерпывающуюся. Эти повторы точны и математически строги. Попробовав повторять их действительно долго, мы легко увидим, что через несколько циклов повторений они потеряют и забавность, и очарование, и превратятся в скучную, нудную, ужасную тавтологию.

(Или в некую мантру, хотя это уже крайний случай.)

В отличии от бесконечных куплетов, фрагменты фракталов Мандельброта все же не тождественны, а подобны друг другу, и это качество и придает им завораживающее очарование.

Чтобы избежать точного повторения куплетов бесконечных стихотворений, поэты приходят к стихам с вариациями и конечным последовательностям куплетов.

Стихи с вариациями это, например, запущенная в оборот С.Никитиным и ставшая народной песенка «У Пегги жил веселый гусь», в которой варьируются Пеггины приживалы и их привычки: «У Пегги стройный жил жираф, он элегантен был, как шкаф»,  «У Пэгги жил веселый глюк, он самый лучший Пэггин друг», «У Пегги жил смешной пингвин, он различал все марки вин», и т.д.

Сочинено уже если не бесконечное, то довольно большое число куплетов: утверждают, что кассета «Песни нашего века» вышла с двухстами вариациями песенки, и, вероятно, число это продолжает расти.

Стихотворения с вариациями можно уподобить первым мутациям строгого структурного кода, пробующего различные варианты записи в потенциальном поле бесчисленных возможностей, и радующего комбинаторике соответствий и несоответствий: «У Пегги жил веселый слон, он скушал синхрофазотрон, спляшем, Пегги, спляшем!».

Дурная бесконечность здесь преодолевается за счет со-творчества, наивного, забавного и радующего самого автора – ребенка или барда.


Конечные куплеты – это те стихотворения, в которых уже в исходном тексте объявлено, что число их строф конечно и с каждой прочитанной строфой неуклонно уменьшается. К таким произведениям относятся: песенка про десять зеленых бутылок («Ten green bottles hanging on the wall…»), в которой куплеты различаются только числом висящих на стене бутылок, в каждом следующем 0 на единицу меньшем, чем в предыдущем, песенка про пять сосисок («Five fat sausages sizzling in a pan…»), которые постепенно исчезали со сковородки, песенка про десять негритят («Ten little nigger boys went out to dine…»), в которой различия уже событийные, аналогичная песенка про одиннадцать солдат Ю.Кима, и другие.

Изначально заданная конечность последовательности куплетов сразу же вносит интонации черного юмора в эти стихотворения. Недаром такие куплеты предназначены скорее для многочисленной взрослой аудитории, находящейся в состоянии эйфории – в баре, на слете КСП и др. Убывающие герои стихотворений шагают в небытие с улыбкой на лице, под одобрительный хохот аудитории – «ах, ах, ах, еще один упавший вниз…». Впрочем, это уже совсем другая песня.

Возвращаясь к фрактальным произведениям, заметим, что и куплеты с вариациями, и конечные куплеты так и не выходят за пределы схемы неветвящегося дерева.

Посмотрим, возможны ли литературные фракталы с вариациями, которые могут вывести читателя от кристаллической решетки неживой природы и от примитивной цепочки разовых мутаций к сложным и самоорганизующимся, изобретательным и страстным живым структурам.


Обратимся к структуре ветвящегося дерева: из земли вырастает ствол, от ствола отходят крупные ветви, от крупных ветвей отходят ветви поменьше, от них – совсем маленькие веточки, на которых растут листья, цветы и плоды.





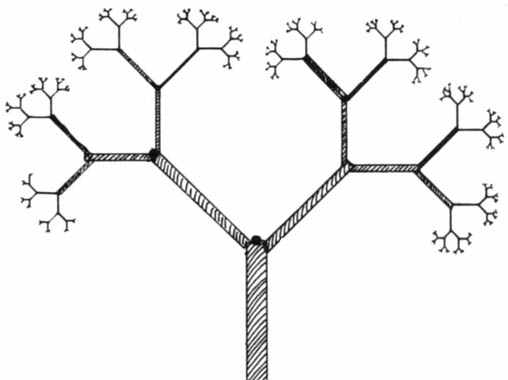
Рис.8. Структура ветвящегося дерева.


Заметив, что ближайшее рассмотрение листа или цветка может привести нас к обнаружению той же фрактальной природы, остановимся на этой ступени. Кстати, поразмыслим немного, а сколько же на самом деле развилок требуется, чтобы фигура воспринималась как фрактальная. Вероятно, ответ лежит где-то между психологическими константами три и семь.

Как мы видели, одинаковых куплетов можно спеть три-пять, куплетов с заданным пределом – около десяти, куплетов с вариациями – достаточно много, но за одно исполнение вряд ли больше тех же десяти.

Замечено, что рассматривание последовательности увеличивающихся масштабов фракталов Мандельброта на компьютере, требующее от наблюдателя только нажатия кнопки мыши, обычно не идет дальше трех-семи приближений, после чего внимание переключается на другую картинку. На рисунке 2 снежинка Кох представлена пятью приближениями, на рисунка 8 – можно обнаружить семь развилок у дерева.

Стремящийся к большим и бесконечно большим числам человеческий разум, в реальности вполне удовлетворяется тремя, пятью, семью или девятью итерациями к этой самой бесконечности. Большие усложнения могут вызвать, видимо, только скуку, головную боль или, у самых настойчивых исследователей, психические проблемы.

А что же подлинная бесконечность, подлинное и совершенное знание? Видимо, она лежит за пределами человеческого восприятия, и принадлежит высшему. Как утверждает писатель семнадцатого века Марин Мерсенн в «Quaestiones super Genesim», «наличие у человека чувства бесконечности уже является доказательством бытия Бога» (цит. по Eco, Umberto. The Search for the Perfect Language. Blackwell Publishers Inc. 1995. Р.142).

Но стремление человека к бесконечному, принципиально недостижимому, и есть доказательство его человечности.


Однако вернемся к нашим деревьям. Именно дерево выбрал для общего названия своего учения испанский мистик, мыслитель и миссионер Рамон Лулль. Ему принадлежат книга «Древо науки», в которой на 1300 листах ин-фолио, более чем 400 000 словами живописуется общее древо знаний, состоящее из шестнадцати меньших деревьев отдельных наук и искусств.

В этой книге суммируется все написанное Луллием, а это более двухсот томов, посвященных устройству, взаимосоотношению и взаимоподобию сущностей и предметов мира.

Корнями Древа Науки Луллия являются девять основных принципов, или универсальных категорий. Из них Древо вырастало в шестнадцать ветвей, каждое из которых представляло собой отдельное древо. Каждое из этих шестнадцати деревьев, которому посвящалось отдельное описание, делилось на семь частей – корни, ствол, основные ветви, меньшие ветви, листья, фрукты и цветы. Восемь из деревьев представляли собой предметы главной таблицы Лулля, tabula generalis: это древо Arbor elementalis, которое описывало объекты подлунного мира или элементы, elementata; Arbor vegetalis; Arbor sensualis; Arbor imaginalis, которое показывало воображаемые образы, которые отражают в сознании явления и предметы, представленные на других деревьях; Arbor humanalis et moralis, (память, ум и желание); Arbor coelestialis, (астрономия и астрология); Arbor angelicalis; Arbor divinalis, которые описывало божественные категории. К этим восьми деревьям Лулль добавлял еще восемь: Arbor mortalis, (добродетели и пороки); Arbor eviternalis, (жизнь и смерть); Arbor maternalis, (Богоматерь); Arbor Chrisanalis, (Христос); Arbor imperialis, (правительство); Arbor apostolicalis, (церковь); Arbor exemplificalis, (знание); Arbor quaestionalis, которое содержало четыре тысячи вопросов ко всем темам книги.


Рис.9. Фрактал-папоротник.


Эти шестнадцать деревьев не стоят сами по себе, отдельно друг от друга. В действительности, они являются частью друг друга, чтобы вместе образовать

мета-дерево, архитектурно схожее с японской пагодой, чья крыша состоит из нарастающих друг над другом крыш. Так, ^ Arbor vegetalis является частью Arbor elementalis, Arbor sensualis включает в себя оба эти древа, Arbor imaginalis построено на них трех, и на всем этом, вырастает древо человечества (Llinares, Armand. Raymond Lulle, philosophe de l’action. Paris: RUF, 1963. P.211-212).

К
нига Луллия является структурно-фрактальной, структура нескольких ее уровней, различных деревьев, подобна другим уровням и всему Древу целиком, как тождественны друг другу «ветви папоротника» с рис.9.

Таким образом, Луллий создавал монументальные литературные фракталы за 700 лет до их открытия. И все же труд Луллия сложен и трудно доступен, и чтобы по достоинству оценить его красоту, нужно на долгие годы погрузиться в изучение древних языков и великого Искусства каталонского мистика.


Рассмотрим более простые деревья. К ним, очевидно, относятся любые родословные, и прежде всего описанные в Книге Бытия, главе 4, где говорится о детях Адама, Каине и Авеле, и о потомках Каина, а также о сыне Адама, Сифе, главе 5, где рассказывается о рождении у Сифа Еноса, у Еноса Каинана, у Каинана Малелеила, у Малелеила Иареда, у Иареда Еноха, у Еноха Мафусаила, у Мафусаила Ламеха, и у Ламеха Ноя, глава 10, о Ное, который породил Сима, Хама и Иафета, и их потомках, а также глава 11, о потомках Сима.


Ной


Ламех


Мафусаил


Енох


Иаред


Малеил

Каинан


Енос




Каин Авель Сиф




Адам

Рис.10. Древо потомков Адамовых.


Ветхозаветные родословные до Ноя практически линейны, обозначая только имена первенцев, после появления которых на свет родитель «жил еще восемьсот лет, и родил сынов и дочерей». Эти анонимные сыны и дочери не представляют интереса для авторов Библии, ибо все они были уничтожены во время потопа, и родословная человека начинается сызнова ветвящимся деревом сынов Иафета, Хама и Сима, заселивших землю после потопа и породивших двенадцать колен Израилевых. Потомок Сима в девятом колене – Авраам, заключает завет с Господом, и дальше родословные отчисляются уже от него, и Иисус будет Иисусов Христом, Сыном Давидовым, Сыном Авраамовым (Мф:1,1). Всего же прародителей Иисуса насчитывается семьдесят шесть поколений (Лук.: 3,23-38).

Летописи, хроники, романы-эпопеи, повествующие о жизни нескольких поколений одной семьи, воспроизводят эту же структуру, как семья человека является частью всего человечества, и генеалогическое древо его, будь он король или свободный гражданин, подобно генеалогическому древу человечества от самых его корней.

В этом проявляются и фрактальные свойства – часть родословной человечества, реальная или вымышленная, подобна всей его родословной, и костяк текста, опирающегося на структуру реального или вымышленного родословного дерева, подобен текстам Книги Бытия, хочет того его автор или нет. Несомненно, это накладывают на автора определенные обязательства.

Другие литературные фракталы, видимо, не налагают такой ответственности на писателя.


Изобразим литературное произведение следующего фрактального типа кривой, сходной с кривой Кох. В отличие от ломаной Кох, где две конечные точки соединяются прямой линией, мы будем изначально считать процесс прохождения от начала до конца текста нелинейным. Простое повествование, или первую итерацию, мы будем изображать округлой кривой, соединяющей две конечные точки, вторая итерация будет изображаться кривой меньшего радиуса на середине первой, третья – еще одной меньшей кривой, наложенной на предыдущую, и т.д. Количество кривых второго уровня сложности может быть равно как одному, так и некоторому числу, больше одного. Число усложнений, говоря теоретически, неограниченно.





Рис.11. Фрактал «рассказ в рассказе».

Если кривую без изломов рассматривать как некоторое простое литературное произведение – рассказ, то кривая внутри нее представляет собой «рассказ в рассказе», явление в литературе знакомое, нередкое и достаточно древнее. Вспомним хотя бы хрестоматийный рассказ Л.Н.Толстого «После бала», где авторский текст открывает и замыкает рассказ, внутри которого находится история, рассказанная ее героем, Иваном Васильевичем.

Но «рассказы в рассказах» появлялись и много раньше – так, в «Метаморфозах» Овидия внутри истории об обращении Ио в корову, находится рассказ о Пане и Сиринге. Этим повествованием посланец Зевса пытается усыпить стоокого Аргуса, стража несчастной Ио. А внутри «Золотого осла» Апулея мы встречаем изложение истории об Амуре и Психее.

Это случай одной итерации, что уже интересно, но, вероятно, не является полноценным фрактальным литературным произведением. Если «сверху» количество повторов ограничивалось, как мы видели, числом около семи, то ограничением «снизу» будет, вероятно, число три – нужно хотя бы три повторения или структурные итерации, чтобы литературное произведение воспринималось как фрактальное, потенциально допускающее усложнение до бесконечности.

Уникальную коллекцию «рассказов в рассказах» можно найти в сборнике арабских «Сказок тысячи и одной ночи», повествующем о царе Шахрияре, который, убедившись в неверности всех женщин, еженощно берет себе невинную девушку, чтобы наутро казнить ее. И так продолжается до тех пор, пока не появляется Шахразада, образованная дочь визиря, со своей младшей сестрой Дунязадой. Младшая сестра просит Шахразаду рассказывать ей сказку на ночь, разумеется, после того, как царь «удовлетворит свою нужду в супруге». (Заметим, что здесь литературные фракталы снова стоят рядом со снами или с колыбельными сказками, как и в истории Ио).

Уже первая сказка Шахразады включает в себя рассказы в рассказе – внутрь истории о злом духе и купце, осужденном демоном на смерть, заключены три истории старцев, которыми они выкупают каждый по трети крови купца. Первый рассказ длится две ночи с маленьким хвостиком, а на протяжении следующих семи ночей Шахразада рассказывает царю историю о рыбаке, которая устроена еще сложнее.

Сначала рыбак достает из моря кувшин с замурованным там джинном и случайно высвобождает истомившегося в неволе духа. Джинн кратко пересказывает ему историю собственных злоключений (первая фрактальная итерация первого порядка), заключая рассказ новостью: он так озверел в этом сосуде, что поклялся убить своего освободителя, так что ничего не попишешь, рыбак, готовься к смерти. Рыбак после положенных мольб и стенаний умудряется обмануть джинна и вновь упрятать его в кувшин. Теперь они поменялись ролями, и уже злой дух умоляет рыбака пощадить его. Но рыбак твердо отказывает джинну, аргументируя свой отказ сходством их истории с историей везиря царя Юнана и врача Дубана. Если предыдущее вложение, рассказ джинна, было простым и кратким, то история царя и его врача (которая есть вторая фрактальная итерация первого порядка) сама является рассказом со вложенным в него рассказом. Итак, некий искусный врач излечил тяжело больного царя, и тот его чрезвычайно возлюбил и день за днем одаривал подарками. Но визирь царя, разумеется, из самых добрых побуждений, уговаривает царя жестоко наказать врача, и даже убить его – ведь если он настолько сведущ в медицине, то легко убьет царя, так что тот и не заметит. Царь не хочет быть неблагодарным и рассказывает визирю историю (заключенная внутрь итерации первого порядка итерация второго порядка) о царе ас-Синдбаде, убившем сокола, который хотел спасти его от яда, капавшего в чашу царя. Параллельно истории сокола звучит история (итерация второго порядка-бис) о прекрасной газели, перепрыгнувшей через голову царя после того, как он успел пообещать убить всякого, через чью голову перепрыгнет эта газель. Возвращаясь к нашему царю (из итерации первого порядка), мы видим, что он не желает убивать врача. Тогда визирь в ответ рассказывает историю (вторая итерация второго порядка) о визире, строившем козни против сына царя. Выслушав его историю, царь (из рассказа рыбака, итерация первого порядка) решает прислушаться к словам своего визиря и наказать врача. Последний горько плачет, но мирится со своей судьбой и даже дарит царю свои драгоценные книги и просит установить свою отрубленную голову на блюдо, чтобы она еще послужила царю. Когда отрубленная голова открывает глаза и велит царю открыть одну из книг, царь облизывает палец, перелистывая слипшиеся страницы, и умирает на месте – а все потому, что не следовало ему обижать мудреца-врача, заключает свой рассказ рыбак, уже замахиваясь сосудом с джинном, чтобы забросить его подальше в море. Конец второй фрактальной истории первого порядка.

О начале следующей (третьей) фрактальной истории первого порядка объявляет джинн: «О, рыбак, не поступай со мной так, как поступила Умама с Атикой!» - умоляет он. «Что же с ними случилось?» – заинтригован рыбак. Но ифрит отказывается рассказывать, пока он заключен в темнице, и ему так грустно и печально. Таким образом, третья итерация первого порядка оказывается вырожденной, и на этом исчерпана.

Рыбак же проникается к поэтически одаренному джинну добрыми чувствами и немедленно освобождает его, и тот навсегда уходит из нашего повествования, оставляя рыбака на берегу озера с чудесными рыбками с наказом не забрасывать сеть чаще, чем раз в день. Но что ж, ведь сказка, рассказываемая Шахразадой, не была сказкой о рыбаке и джинне, и с уходом джинна, жизнь рыбака и нулевая итерация еще продолжаются, хотя и связана с предыдущим повествованием тонкой сюжетной нитью, протянувшейся от рыбака к волшебным заколдованным рыбкам. Эти разноцветные рыбки, предложенные рыбаком царю, стали таинственным образом подгорать на сковороде, и царь в изумлении сам отправился в таинственному пруду за полчаса пути от дворца, чтобы узнать, в чем дело. А подивившись волшебству, царь снова отправился неизвестно куда, чтобы встретить хоть кого-нибудь, кто сумеет рассказать ему об этих рыбках. На третий день пути царь попадает в некий дворец, где встречает странного юношу, наполовину живого человека, наполовину камень. Юноша рассказывает ему свою историю (первая итерация ко второй половине нашей истории) о неверной жене-колдунье, изменявшей ему, сыну царя, с черным рабом, которого он почти, но, к сожалению, не до конца убил, и вот теперь злодейка обратила его наполовину в камень, бьет и унижает его, а сама продолжает прислуживать своему черному полутрупу. Конец первой итерации.

Царь (наш царь, из сказки о рыбаке и разноцветных рыбках) тут же вызывается помочь несчастному юноше, окончательно убивает черного раба, и закутавшись в его тряпки, заставляет колдунью расколдовать юношу и всех его подданных, жителей города, обращенных в рыбок, ибо это, конечно же, была та самая история о заколдованных разноцветных рыбках, которую царь так желал узнать. Добрые дела царь завершает убийством злодейки-колдуньи и заключением вечного союза с выздоровевшим юношей, царем расколдованной страны. Собрав караван подарков, они вместе отправляются в обратный путь в страну нашего царя. Обратная дорога занимает уже не полчаса, и не три дня, а целый год. Обнаружив, что в его отсутствие в стране был образцовый порядок, царь награждает своего верного везиря, а также рыбака (помните рыбака, с которого все началось?) и его детей. Все счастливы, конец нулевой итерации, или истории о рыбаке.

Итого, мы встречаемся здесь с историей, которая делится на две почти независимые истории – о злом джинне и о заколдованных рыбках. Внутри первой присутствуют одно вложение первого порядка – история джинна, другое вложение первого порядка – история о визире царя Дунана и враче Дубане, в которое включены два вложения второго порядка – о соколе, о злом визире, и вырожденное вложение первого порядка – о Умаме и Атике. Внутри второй истории находится единственное вложение первого порядка о злоключениях заколдованного юноши.





Рис.12. Схема сказки о рыбаке.


На протяжении следующих девятьсот девяноста двух ночей Шахразада рассказала царю Шахрияру еще много других фрактальных историй, которые все вместе объединяются в единый текст «Сказок тысячи и одной ночи».

Как мы видим, в сказке о рыбаке количество уровней вложенных историй ограничивается тремя, не слишком большое число по сравнению с бесконечностью. Автор «Сказок» при всей любви к сложным и завораживающим повествованиям не умножает количества вложенных историй, понимая, что это только запутает или отпугнет читателя. , а заскучавший слушатель Шахразаде смертельно опасен. И автор предпочитает набирать вариации увеличением количества рассказов. (Мы не будем здесь углубляться во фрактальную структуру «писатель-автор-повествователь-рассказчик-герой…-читатель», наше сообщение посвящено не мета-текстам, а собственно фрактальным произведениям).

Итак, хотя число вложенных уровней в «Сказках» уже позволяет сделать заключение о фрактальности произведения, структура «Сказок» не слишком сложна, и завораживающее кружево плетется количественным умножением сюжетов со сходными персонажами, обозначенными только именами и ролями – юный царь, мудрый или злобный везирь, джинн, волшебник, – за счет чего возникает еще и возможность отражения одной истории в другой.

Если в случае деревьев Луллия мы имели дело с мета-деревом, состоящим из шестнадцати деревьев, являющих частями друг друга, истории Шахразада – это скорее горизонтальный лес из сотен деревьев, на каждой из которых по два, три, четыре уровня ветвления – от ствола к веткам и цветам. Таким образом, весь текст обладает весьма сложной структурой, значительно превосходящей по сложности структуры рисунков 2-4.

Однако «Сказки» не ищут путей в высшее, пересказывая все те же волшебные истории, они не стремятся выйти из садов, гаремов и рынков, и красота «Сказок тысячи и одной ночи» более возбуждает, чем завораживает, она более пряная, чем пьянящая, и более дурманящая, чем раскрывающая сознание.


Другими примерами текстов с вложенными в них текстами является «готический» роман Яна Потоцкого «Рукопись, найденная в Сарагосе», романы «с выдвижными ящиками» Евгении Сюэ, или произведения Раймона Русселя, в которых внутренние сюжеты до шести раз «заключаются в скобки» (Berge Cl. Pour une analyse potentielle de la litterature combinatoire. // L’OULIPO: La litterature potentielle. Paris: Gallimard, 1973. P.57.).

В западной литературе существует интересное первое вложение «рассказа в рассказ», демонстрируемое В.Шекспиром. В III действии «Гамлета» актеры разыгрывают перед двором сцену, дублирующую основной сюжет – убийство короля и брак цареубийцы с королевой. Мимо этого вложения, разумеется, не мог пройти Т.Стоппард в пьесе «Розенкранц и Гильдернштерн мертвы», всей построенной на основе и поверх «Гамлета».

Т.Стоппард легко осуществляет вторую итерацию – в пьесу, разыгрываемую актерами, вставлен эпизод пантомимы на тот же сюжет. Интересно, что в одноименном фильме (автором сценария и режиссером его также был Т.Стоппард, что дает нам возможность делать отсылку к, вероятно, существующему сценарию как к литературному произведению), в этом фильме производится еще одна итерация, и на сцене появляется грубо вылепленные марионетки героев. Таким образом, трагическая история рассказывается в третий раз, на каждом уровне снижая стиль изложения, как теряет качество все уменьшающаяся копия.

Трех итераций, как мы видели, уже вполне достаточно, чтобы говорить о полноправном фрактальном произведении. Заметим, что ключевой момент, убийство короля, в пьесе Шекспира не представлено, и изначально существует только в виде копии, переложения заезжими актерами. А пересказывание его раз за разом, итерация за итерацией, все больше заостряет действие, усугубляя гнев нового короля и снимая неврозы у Гамлета.

Снижение качества копии при «увеличении масштаба» изображения является осознанным решением художника в поисках выхода из бесконечной цепи тавтологически повторяющихся повторений. Это решение должно, через какое-то количество чарующих итераций, снять вызванную им проблему и прервать ряд, ибо ни королевское спокойствие, ни гамлетовские комплексы не бесконечны.

Ряд рвется, рассказ в рассказе в рассказе в рассказе заканчивается, и история продолжается примерно там же, где прервалась. Из этого фрактального омута мы вынырнули.


Мы уже видели, что чары фрактальных литературных произведений часто лежат около волшебных снов. К структурным фракталам можно отнести такие произведения, в которых повествуется о снах, которые оказываются частью иного сна, а те – еще одного, так что всякое пробуждение приводит героя в новую сновидческую реальность. Это ощущение, вероятно, испытывали многие в собственной жизни, и многие писатели пытаются провести читателя коридорами вложенных снов в своих произведениях – среди них и Г.Майнринк в «Големе», и Достоевский в конце «Преступления и наказания», и С.Лем в одном из рассказов из серии «Приключений Ййона Тихого». Приведем здесь один поэтический пример, простой, но претендующий на всеохватность темы, стихотворение Э.А.По «Сон во сне» (перевод В.Брюсова):


В лоб тебя целую я,

И позволь мне, уходя,

Прошептать, печаль тая:

Ты была права вполне, -

Дни мои прошли во сне!

Упованье было сном;

Всё равно, во мгле иль днём,

В дымном призраке иль нет,

Но оно прошло, как бред.

Всё, что в мире зримо мне

Или мнится, – сон во сне.

Стою у бурных вод,

Кругом гроза растёт;

Хранит моя рука

Горсть зёрнышек песка.

Как мало! Как скользят

Меж пальцев все назад...

И я в слезах,— в слезах:

О боже! как в руках

Сжать золотистый прах?

Пусть будет хоть одно

Зерно сохранено!

Все ль то, что зримо мне

Иль мнится,— сон во сне?

ориг.1827-1849, пер.1924.


Структурно фрактальными являются и более сложные стихотворные циклы, состоящие из стихотворений твердых форм, как то венки сонетов. Если сонет – стихотворение из четырнадцати строк с заданным числом слогов в строке, строк в строке, схемой рифм и ритма, с небольшими различиями для традиционных французских, итальянских и английских сонетов, то венок сонетов представляет собой цикл из четырнадцати сонетов, связанных крайними строками – последняя строка первого сонета является первой строкой второго сонета венка, последняя строка второго сонета – первой строкой третьего сонета, и т.д., а все четырнадцать крайних строк образуют еще один, магистральный сонет, в котором и заключен общий замысел всего цикла.

В России венки сонетов писали Вяч.Иванов – «Cor ardens», М.Волошин – «Lunaria» и «Corona astralis», В.Брюсов – «Роковой ряд» и др.

Вот магистральные сонеты этих циклов:

М.Волошин. Corona astralis. Венок сонетов



В мирах любви неверные кометы,

Закрыт нам путь проверенных орбит!

Явь наших снов земля не истребит,

Полночных Солнц к себе нас манят светы.


Ах, не крещен в глубоких водах Леты

Наш горький дух, и память нас томит.

В нас тлеет боль внежизненных обид –

Изгнанники, скитальцы и поэты!


Тому, кто зряч, но светом дня ослеп,

Тому, кто жив и брошен в темный склеп,

Кому земля – священный край изгнанья,


Кто видит сны и помнит имена, –

Тому в любви не радость встреч дана,

А темные восторги расставанья!

1909


М.Волошин. Lunaria. Венок сонетов


Жемчужина небесной тишины,

Лампада снов, владычица зачатий,

Кристалл любви, алтарь ночных заклятий,

Царица вод, любовница волны.


С какой тоской из влажной глубины

К тебе растут сквозь мглу моих распятий,

К Диане бледной, к яростной Гекате

Змеиные, непрожитые сны.


И сладостен, и жутко-безотраден

Алмазный бред морщин твоих и впадин,

Твоих морей блестящая слюда —


Лик Ужаса в бесстрастности эфира,

Ты вопль тоски, застывший глыбой льда,

Ты жадный труп отвергнутого мира!

1913


В.Брюсов. Роковой ряд


Четырнадцать назвать мне было надо

Имен любимых, памятных, живых!

С какой, отравно ранящей, усладой,

Теперь, в мечтах я повторяю их!


Но боль былую память множить рада:

О, счастье мук, бесстрашных, молодых,

Навек закрепощенных в четкий стих!

Ты – слаще смерти! Ты – желанней яда!


Как будто призраков туманный строй,

В вечерних далях реет предо мной, –

И каждый образ для меня священен.


Вот близкие склоняются ко мне…

В смятеньи – думы, вся душа – в огне…

Но ты ль, венок сонетов, неизменен?

1
918

Рис.13. Схема венка сонетов (создана с подсказки схемы Л.Г.Портера из книги «Симметрия – владычица стихов: Очерк начал общей теории поэтических структур. М.: Языки славянской культуры, 2003).


У
сложним эту структуру – пусть теперь каждый сонет из венка сонетов будет магистральным для своего, второго порядка, венка сонетов, а все 14*14 + 14 + 1 = 211 сонетов образуют венок венков сонетов (рис.14). Эта конструкция настолько сложна, что она не имеет однозначного названия – различные исследователи именуют ее и венком в квадрате, и кружевом, и короной сонетов. На ней уже явно видна фрактальная природа такого цикла. И также очевидно направление усложнения – в сторону венка венков венков сонетов – он же венок в кубе, пирамида сонетов, диадема сонетов, состоящего из 143 + 142 + 141 + 140 = 2455 сонетов.

Рис.14. Схема венка венков сонетов.


Создать венок венков сонетов – чрезвычайно трудная задача. В.Шкловский выражал сомнение, что она может быть проведена без риска для психики автора. Однако таким стихотворным циклам нельзя отказать в наличии завораживающей красоты, настоятельно требующей полного в нее погружения и не дающего пустых обещаний относительно возвращения в реальный мир.

Создание фрактального произведения следующего уровня сложности, венка венков венков сонетов, представляется нам практически неосуществимым. И это еще одно подтверждение ограниченности человеческого духа, не способного справиться с задачей не то, что бесконечного, а хотя бы третьего уровня сложности.

Еще одна разновидность литературных фракталов, которые мы хотели бы представить на суд читателя – фракталы семантические, где о подобии части бесконечному и вечному целому только рассказывается. В таких произведениях писатель демонстрирует, что предметы, явления или люди бесконечно повторяются в цепи сходства-подобия. И уразумев сказанное, читатель получает и представление о беспредельной красоте сущего и беспредельный же экзистенциальный ужас.

К таким текстам отнесем рассказ Х.-Л.Борхеса «В кругу развалин» о неизвестном, возникшем неизвестно откуда у развалин храма Огня в неведомых джунглях, где «язык зенд не затронут греческим и редко встретишь проказу». Этот безымянный человек одержим желанием создать во сне человека, чтобы все, за исключением самого сновидца и бога Огня, считали бы его совершенно реальным. Все – это значит включая самого созданного. И когда дерзновенный замысел, над которым кудесник трудился тысячу и одну ночь, осуществляется, и создание оживает и отправляется к другой храм Огня вверх по реке, его создатель начинает тосковать и бояться – он не хочет, чтобы сын понял, что он – не человек, а только подделка, отражение чужого сна! Кудесник испытывает ужас: что может быть страшнее, чем знать, что ты – не настоящий, что ты – всего лишь чья-то выдумка. Вскоре кудесник осознает, и осознает с облегчением, что и сам он «лишь призрак, снящийся другому».

На крошечном отрезке цепи, минимальном возможном, чтобы показать подобие и перерождение, Борхес открывает целую бесконечность призрачных существ, порожденных одно за другим в течении неведомой, и тоже бесконечной, реки, в дурной бесконечности бледных копий без оригинала. Минимальная структура одного звена приводит к видению всей цепи, и эта цепь отвратительна, ибо есть бесконечное фрактальное умножение и повторение, а как сказано в другом рассказе Борхеса, «зеркала и совокупления отвратительны, ибо умножают количество людей». Никакого исхода, никаких разветвлений и бифуркаций, никакого развития и вариаций в цепи, один лишь экзистенциональный ужас, крик в одиночестве ночи и пустыни: «Кто я?», и стойкое принятие своей участи, я – тот, кто я есть, тот, кем я был создан, смирение, что паче гордыни.

Герой рассказа Х.Кортасара «Желтый цветок», напротив, предпринимает отчаянное действие, чтобы разорвать бесконечную цепь бессмысленных перерождений. Герой этот, рассказывающий повествователю свою историю, «совсем еще не старый человек, с высохшим лицом и глазами больного туберкулезом», встречает однажды в автобусе подростка и вдруг осознает, что этот мальчик, Люк, – это «еще раз родившийся он, смерти не существует, мы все – бессмертны». Люк повторяет его, он подобие, но не тождество, вывихнувший ключицу, там где старик вывихивал запястье, болевший корью, а не скарлатиной, потом безнадежно влюблявшийся, как и старик в свое время, получавший дорогой подарок и тут же терявший его, и все в той же последовательности, что и старик в его возрасте. И все, что у него было – это нищета, болезни, физические и душевные травмы, утраты и боль. И все, что будет у него в будущем, тоже известно: «унижения, жалкая рутина, безликие годы, неудачи, разъедающие душу, как моль – одежду, убежище в горьком одиночестве – в одном из бистро квартала». А за смертью прошедшего тягостный путь до конца будет рождение следующего Люка, и еще одного, все таких же униженных, несчастных неудачников. И старик, прерывая дурную бесконечность бессмысленных перерождений, убивает (или считает, что убивает) ребенка. Он уверен теперь, что тяготы его близятся к концу и никогда больше не повторятся, он разрезал нить и порвал цепь. Выйдя из порочного круга пустых и жалких перерождений, он счастлив, и вдруг он замечает на клумбе Люксембургского сада прекрасный желтый цветок, и уразумевает небытие. Небытие есть отсутствие цветка. И неожиданно, как пришло и откровение о другом, столь же бестолковом и несчастном «я», приходит понимание красоты и, напоследок, жизни, какой бы жалкой она ни была: «Весь вечер, до наступления ночи, я менял автобусы, и мысли мои были о цветке и Люке: среди пассажиров я искал кого-нибудь, похожего на Люка, кого-нибудь, похожего на меня или на Люка, кого-нибудь, кто мог бы быть другим я, кого-нибудь, чтобы смотреть на него, зная, что это – я, а затем позволить ему уйти, не сказав ни слова, почти защищая его, для того чтобы он мог продолжать жить своей бестолковой жизнью, своей дурацкой, неудавшейся жизнью, идущей к другой дурацкой и неудавшейся жизни, к другой, дурацкой и неудавшейся, к другой…

Расплатился в бистро я», – заключает автор.

Одно звено цепи демонстрирует бесконечную фрактальную структуру с вариациями, перерождения и повторения, сходства и подобия людей, звеньев в цепочке человеческого рода. И несчастия героя, унижения и утраты на одном звене цепи, вдруг, при взгляде сверху, сменяются пониманием радости, счастья бытия как такового, пронзительного счастья, видимого только на грани бытия. Слишком поздно, мальчик умер, а старик умирает от туберкулеза. Для героя рассказа – слишком поздно.


И последний вид литературных фракталов, который мы хотели бы представить вашему вниманию, можно было бы назвать нарративными фракталами, ибо они соотносятся не с умственными схемами, а с существующими или мнимыми визуальными произведениями.

Ряд картин известных художников представляют собой изображение множества картин внутри картины – барочные галереи, кабинеты или кунсткамеры, на которых изображаются другие картины или собрания картин, как на знаменитых «Менинах» Веласкеса или картинах Дж.-П.Паннини.

Литературное произведение, которое описывает визуальные фракталы или такие картины в картинах, мы будем называть нарративным фрактальным литературным произведением.

Мы рассмотрим здесь только одно литературное произведение, повествующее о художественной коллекции – «Кунсткамеру» Ж.Перека (Перек, Жорж. Кунсткамера. История одной картины. Пер. В.Кислова. Спб, Machina, 2001), структура которого настолько сложна, что для описания ее потребовалась бы отдельная большая работа. Скажем лишь, что оно посвящено многостороннему, подробному и повторяющемуся описанию некой коллекции картин, представленной на выставке. Среди картин этих мы замечаем и одну с названием «Кунсткамера», изображающую само помещение выставки с сотней представленных на ней картин, плотно развешенных по трем стенам. Заметим, что оригинал, предшествующий художественному творению, уже отсутствует – картина «Кунсткамера», чье название естественно повторяет название книги Перека, – это портрет хозяина галереи, рассматривающего свою коллекцию. За этим исчезнувшим оригиналом следует собственно картина, а дальше, внутри картины находятся, наряду с копиями всех картин выставки, и уменьшенная копия ее самой, а в нее – еще одна… «Все картины воспроизводятся снова, и так – несколько раз; при этом точность изображения сохраняется и на первом, и на втором, и на третьем уровне, – до тех пор, пока рассматриваемые произведения не превращаются в крохотные точки».

Невооруженным глазом зритель различает всего шесть уменьшающихся копий, но изучение последней в лупу якобы демонстрирует еще два вложенных изображения, последнее из которых было просто черточкой в полмиллиметра.

В отличие от Стоппарда, отказывающего уменьшающимся копиям в сохранении исходного качества, Перек категорично утверждает, что даже шестая, в несколько миллиметров копия, сохраняет детали оригинала.

Но копии Перека не воспроизводят оригинал тождественно, детали изображений варьируются или исчезают, чайник превращается в синий кофейник, боксер-победитель на одном уровне изображения в следующей копии лежит на ковре, лютнист превращается во флейтиста, пустынную площадь на следующем уровне заполняет карнавальная толпа, и пр.

Вскоре в результате несчастного случая исчезает и картина «Кунсткамера», что только подогревает интерес и к ней самой, и к коллекции в целом, состоящей из многих шедевров старых мастеров.

Мы, естественно, узнаем и о картинах, и об их истории, и о ценности, культурной и денежной, из текста Перека, и в отсутствии оригинальных изображений, обладаем только словесными описаниями картин.

Внутри текста включены и критические заметки, и интерпретации, также с вариациями: от трактовки «Кунсткамеры» как выражения глубокой горечи разочарованного автора, вынужденного бесконечно рефлексировать в бесконечно повторяющемся мире, до осуществления высшего внедрения и присвоения, «о проекции своих черт на Другого и о Похищении в прометеевском смысле слова».

И однако, многочисленные культурологические и историко-культурные исследования, все глубокомысленные фразы оборачиваются в конце концов смехом – всего лишь смехом и высшей формой человеческой деятельности – смехом, смехом, которым смеются перед лицом высшего, бесконечного и неизбежного не боги, а люди, ибо «Кунсткамера» оказывается грандиозной мистификацией. «…Картины, представленные как копии, как подражания, как повторения, и в самом деле выглядели как копии, подражания, повторения подлинных картин… Спешно предпринятая экспертиза сразу же показала, что картины из коллекции Раффке были, действительно, большей частью фальсифицированы, равно как большей частью фальсифицированы подробности этого вымышленного рассказа, задуманного ради одного лишь удовольствия, ради одного лишь трепета пред иллюзорностью».

Множественные варьирующиеся копии бесконечно схожи с оригиналом, которого нет и никогда не было, это – фальшивка, симулякр творения. Не расстраивайтесь, не плачьте о понапрасну израсходованном снобистком восхищении прекрасным или потерянных деньгах, вы восприняли происшедшее чересчур серьезно, а художник просто смеялся, и его смех создал бесконечные ряды и разрушил их, взошел к вершинам художественного мастерства и спустился в мир, к читателям.

И это лучшее из решений фрактальной литературы, которое нам известно.