Навчальна програма курсу за вибором «Основи прикладної математики» для учнів 10-11 класiв
| Вид материала | Диплом |
СодержаниеРазкладання функції в полином Жегалкіна Мета урока E, то доповненням I-III рівні |
- Програма курсу за вибором «Основи алгоритмізації та програмування» для організації, 361.72kb.
- Робоча навчальна програма курсу за вибором "Деонтологія в медицині", 223.13kb.
- Програма курсу за вибором "основи веб-дизайну" для основної школи, 194.57kb.
- Навчальна програма факультативного курсу Тема «Методи та прийоми пошуку розв’язання, 264.96kb.
- Програма курсу за вибором для учнів профільних класів суспільно-гуманітарного напряму, 721.59kb.
- Програма курсу за вибором для учнів 10-11 профільних класів суспільно-гуманітарного, 1151.86kb.
- Програма курсу за вибором "основи комп’ютерної безпеки " для основної школи, 119.72kb.
- Навчальна І робоча програма дисципліни за вибором студента "Наближені методи обчислень", 100.2kb.
- Робоча навчальна програма з вибіркової дисципліни «основи профілактики алкоголiзму, 578.51kb.
- Програма курсу за вибором "основи створення комп’ютерних презентацій" для основної, 163.05kb.
1 2
Разкладання функції в полином Жегалкіна
Додаток 4
Розробка конспекту уроку
з курсу за вибором
«Основи прикладної математики»
Т.1 (12год.) Множина, відображення, відношення.
Урок №4
Тема: Операції над множинами та їхні властивості. Об’єднання множин, перетин множин.
Мета уроку: ознайомити учнів із поняттям «операції над множинами», основними властивостями теоретико-
множинних операцій; надати знання щодо об’єднання та перетину множин; формувати вміння
знаходити об’єднання множин, їх перетин та різницю; формувати інтелектуальну й продуктивно
творчу компетентності; розвивати теоретичне мислення; виховувати пізнавальний інтерес до змісту
предмету.
Тип уроку: урок засвоєння нових знань
Жанр уроку: урок-лекція за моделлю прямого викладання
Перебіг уроку:
| № з/п | Назва етапу | Мета та дії вчителя |
| 1 | Орієнтація |
Мета урока: - ознайомити учнів із поняттям «операції над множинами», основними властивостями теоретико-множинних операцій;надати знання щодо об’єднання та перетину множин; формувати вміння знаходити об’єднання множин, їх перетин та різницю; формувати інтелектуальну й продуктивно творчу компетентност; розвивати теоретичне мислення; виховувати пізнавальний інтерес до змісту предмету.
|
| 2 | Подання нового матеріалу |
Для множин можна ввести ряд операцій (теоретико-множинних операцій), результатом виконання яких будуть також множини. За допомогою цих операцій можна конструювати із заданих множин нові множини. Нехай A і B деякі множини. а) Об’єднанням множин A і B (позначається AB ) називається множина тих елементів, які належать хоча б одній з множин A чи B. Символічно операція об’єднання множин записується так A B = { x | xA або xB} або xAB 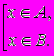 Приклад. {a,b,c} {a,c,d,e} = {a,b,c,d,e}. б) Перетином множин A і B (позначається AB ) називається множина, що складається з тих і тільки тих елементів, які належать множинам A і B одночасно. Тобто AB = { x | xA і xB} або xAB 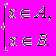 Приклад. {a,b,c}{a,c,d,e} = {a,c}, {a,b,c}{d,e} = . Кажуть, що множини A і B не перетинаються, якщо AB = . Операції об’єднання та перетину множин можуть бути поширені на випадок довільної сукупності множин {Ai | iІ}. Так об’єднання множин Ai (записується 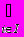 Ai ) складається з тих елементів, які належать хоча б одній з множин Ai даної сукупності. А перетин множин A (записується Ai ) складається з тих елементів, які належать хоча б одній з множин Ai даної сукупності. А перетин множин A (записується 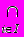 Ai) містить тільки ті елементи, які одночасно належать кожній з множин Ai. Ai) містить тільки ті елементи, які одночасно належать кожній з множин Ai.в) Різницею множин A і B (записується A\B ) називається множина тих елементів, які належать множині A і не належать множині B. Отже, A \ B = { x | xA і xB} або xA \ B 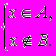 Приклад. {a,b,c} \ {a,d,c} = {b}, {a,c,d,e} \ {a,b,c} = {d,e}, {a,b} \ {a,b,c,d} = . г). Симетричною різницею множин A і B (записується AB, AB або AB ) називається множина, що складається з усіх елементів множини A, які не містяться в B, а також усіх елементів множини B, які не містяться в A. Тобто AB = { x | ( xA і xB ) або ( xB і xA )} або xAB 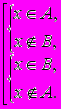 Приклад. {a,b,c}{a,c,d,e} = {b,d,e}, {a,b} {a,b} = . Введені теоретико-множинні операції можна проілюструвати діаграмою (рис.1.1). Тут множини A і B - це множини точок двох кругів. Тоді AB - складається з точок областей І, ІІ, ІІІ, AB - це область ІІ, A \ B - область І, B \ A - область ІІІ, AB - області І і ІІІ. 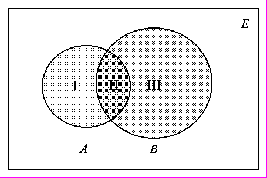 Рис. 1.1. д). У конкретній математичній теорії буває зручно вважати, що всі розглядувані множини є підмножинами деякої фіксованої множини, яку називають універсальною множиною або універсумом і позначають через E (або U). Наприклад, в елементарній алгебрі такою універсальною множиною можна вважати множину дійсних чисел R, у вищій алгебрі - множину комплексних чисел C, в арифметиці - множину цілих чисел Z, в традиційній планіметрії - множину всіх точок площини або множину всіх геометричних об’єктів, тобто множину множин точок на площині тощо. Якщо зафіксована універсальна множина E, то доповненням множини A (яке є підмножиною універсальної множини E ) - записується 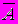 - називається множина всіх елементів універсальної множини, які не належать множині A. - називається множина всіх елементів універсальної множини, які не належать множині A.Тобто 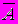 = { x | xE і xA } або x = { x | xE і xA } або x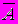 xA. xA.Неважко помітити, що 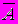 = E \ A. = E \ A.
|
| 3 | Структурована практика | Учитель разом із учнями розв’язує задачу. Задача. Маємо множину А={ 1,2,3} і множину В ={ 2,3,6}. Знайти об’єднання та претин множин. |
| 4 | Керована практика | Учні працюють самостійно, учитель забезпечує контроль і зворотній зв’язок. Для розв’язування пропонується наступна задача. Задача. Знайти перетин та об’єднання множин R і N. |
| 5 | Самостійна практика | Учні працюють самостійно без безпосереднього зворотного зв’язку з учителем. Задача. Дано: А={1,2,3,4,5,6,7,8,9 }і В={5,6,7,8,9,10,11,12,13}. Знайти: AB , A \ B. |
| 6 | Підсумок і завершення уроку | Повторюються основні поняття, учитель ще раз нагадує учням операції над множинами. Аналізуються навчальні цілі з позиції їх досягнення. |
| 7 | Домашнє завдання | Домашнє завдвння за рівнями складності: I-III рівні: Маємо множину А={ 0,2,4,6,8,10,12} і множину В ={0,1,3,5,7,9,11}. Знайти об’єднання та претин множин. IV рівень: Задача. На одній з кафедр університету працюють 13 осіб, причому кожен з них знає принаймні одну іноземну мову. 10 осіб знають англійську мову, 7 – німецьку, 6 – французьку. 5 знають англійську і німецьку мову, 4 – англійську і французьку, 3 – німецьку і французьку. а) Скільки осіб знають усі три мови? б) Скільки осіб знають рівно дві мови? в) Скільки осіб знають тільки англійську мову? |
