Geum.ru

Решение задач

Вид материалаРешение

Содержание


I. Введение
II. Основная часть
III. Заключение
Подобный материал:

Муниципальное общеобразовательное учреждение

«Лицей № 10» г.Перми


Проектная работа по математике

Загадки японских храмов


Выполнила:

Баландина Юлия,

ученица 10В класса

Руководитель:

Золотухина Л.В.,

учитель математики высшей категории


Пермь, 2010 год


Содержание


I. Введение…………………………………………………………………....3

II. Основная часть.
  1. История возникновения…………………………….……………………4
  2. Сангаку…………………………………………….……………………...9
  3. Решение задач…………………………………………………………....12

III. Заключение………………………………………………………………17

IV. Список литературы…………………………………………………...…18


^ I. Введение


Почему выбрана именно эта тема


В выборе моей проектной работы я основывалась на то, чтобы при выполнении ее я действительно заинтересовалась и увлеклась. И действительно, такая тема как «Загадки японских храмов» уже звучит интригующе.

Когда я начала только лишь знакомиться с выбранной темой, первое, на что я натолкнулась, это некоторые таблички под названием САНГАКУ. Меня поразили гениальные рисунки на этих дощечках, на которых изображались японские чертежи и загадки по геометрии. Гениальности японских математиков можно лишь только позавидовать, ведь их загадки популярны вот уже несколько сотен лет. Они имеют важное значение не только для японской, но и для мировой математики.

Темой проектной работы становится ознакомление и рассмотрение японских задач по геометрии.

Цель работы:

Для наиболее полного раскрытия темы и соответствия поставленной цели были поставлены следующие задачи:
  • Познакомиться с историей японской математики.
  • Познакомиться с биографией и достижениями крупнейшего представителя японской математики Секи Кова.
  • Изучить научную литературу, связанную с математическими задачами.
  • Разобраться в решении и японских задач по геометрии.
  • Перевести статьи о сангаку с английского на русский язык.
  • Показать связь математики с жизнью, архитектурой и строительство в Японии.



^ II. Основная часть

1. История возникновения.


Период Эдо - исторический период (1603—1868) Японии, время правления сёгунов из рода Токугава. Характеризуется как время установления диктатуры Токугава, одновременно с этим переход от средневековых междоусобиц даймё к полностью контролируемой стране. Так же характеризуется бурным ростом городов, развитием городской культуры, резким увеличением населения. После войн и усобиц наступило мирное время, в умах и сердцах людей произошёл, так называемый, переход "от возвышенного к земному".

В период Эдо произошло становление японского духа, появление национальной японской идеи, развитие экономики и чиновничьего аппарата. Период Эдо — золотой век литературы и японской поэзии, Мацуо Басё является наиболее ярким представителем поэзии как периода Эдо, так и японской поэзии в целом.

В результате политики практически весь период Эдо страна находилась за железным занавесом, не ведя торговли и не сообщаясь с другими странами (редкое исключение — Китай и Голландия). Католическое христианство жестоко подавлялось (восстание на Кюсю).

Так же в этот период произошло смещение политического влияния от военных домов (самурайское сословие) на торговые дома (купеческое сословие). По сути, страна совершила переход от феодального к капиталистическому режиму и само падение сёгуната характеризовалось политическими и экономическими, а не военными причинами. Одновременно с падением сёгуната Токугава произошло падение самой идеи сёгуната.

Если говорить о культуре периода Эдо, то можно сказать, что окончательное оформление традиционной японской культуры пришлось на 17 — 19 века. В течение второй половины 17 — начала 18 века культурно-научными центрами Японии были Киото и Осака, а с конца 18 века их роль взял на себя город Эдо. Культуру времён киотские-осацкого доминирования принято называть культурой Гэнроку, а культуру периода Эдо — культурой Кассей. Оба названия происходят от названий соответствующих девизов правления Императоров.

После возникновения и развития письменности искусство Японии пополнилось еще одним видом – каллиграфией. Только японцы с их врожденным эстетизмом и склонностью к созерцанию могли превратить письмо в живопись, а сам процесс рисования в дзенскую медитацию. Проверкой способностей каллиграфа считается умение изобразить дзен-буддистский символ энсо – окружность, бывающую как замкнутой, так и незамкнутой, символизирующую просветление и духовность. Только духовно продвинутый мастер может создать правильный энсо, и чтобы достигнуть этого приходиться тренироваться долгие дни и часы.

Культура Гэнроку характеризовалась появлением иллюстрированных рассказов укиё-дзоси, описывающие повседневную жизнь жителей городов. Танец кабуки трансформировался в театральное искусство. Кукольный театр нингё-дзюрури обогатился лирическими пьесами драматурга Тикамацу Мондзаэмона. Новое развитие получила поэзия в лице Мацуо Басе. В изобразительном искусстве активно работали художники школ Рин, Кано и Тоса. Одновременно появился новый жанр гравюр укиё-е, основоположником которого стал Хисикава Моронобу. Также имело место развитие точных и естественных наук, таких как математика и агрономия.


Крупнейший представитель японской математической школы того времени является японский математик Секи Кова (Seki Kowa 関孝和?) или Секи Такаказу (Seki Takakazu 関孝和) (родился 1637/1642? – 5 декабря, 1708) , создавшим новую алгебраическую систему записи и заложившим основы дальнейшего развития васан. Мотивируемый астрономическими вычислениями, он выполнил некоторые важные работы в области расчета и нахождения целого неопределенного уравнения, которые впоследствии развивали его преемники. Созданная его последователями математическая школа (Школа Seki) доминировала в Японской математике до конца эры Эдо.

Он жил в одно время с Готфридом Лейбницем и Исааком Ньютоном, хотя очевидно, что, в силу изоляционной политики Японии, не мог контактировать с ними. Он стал автором некоторых теорем и теорий, вскоре после этого открытых на Западе. Например, числа Бернулли (опубликовано в 1712), равнодействующей силы, детерминанта (первое открытие в 1683, завершенная теория опубликована позже в 1710) приписаны ему. Эти достижения удивляют, учитывая тот факт, что японская математика до появления ученого находилась в примитивной стадии, например, всестороннее введение в 13-м веке китайской алгебры было сделано позднее в 1671 Казуюки Савагучи (Kazuyuki Sawaguchi).

Однако по сей день не ясно, какие из приписанных ему достижений являются его собственным вкладом в науку, так как многие из них появляются только в описаниях или в соавторстве с его учениками. Также, не многое известно о его биографии. Местом его рождения может быть Фудзиока (Fujioka) в префектуре Гунма (Gunma), или Токио, и год рождения может быть любым между 1635 и 1643. Он родился в клане Учияма (Uchiyama), подданных Ко-шу хана (Ko-shu han), и позже был принят в семью Секи (Seki), к подданным Сёгуна. Будучи подданным Ко-шу хана, он занимался созданием достоверной карты территории своего господина. Также, он провел много лет за изучением китайского календаря 13-го столетия, для того чтобы заменить им менее точный календарь Японии, действовавший в то время.

На достижения Секи Кова имела влияние и китайская математика.

Математика Секи (и васан в целом) базируется на математических постулатах XIII-XV столетий. Среди них алгебра с числовым методом, многочленная интерполяция и их приложения, неопределенные интегральные уравнения. Работа Секи в той или иной мере была основана на них или имела к ним отношение.

Китайская алгебра открыла числовое решение (Метод Хорнера, восстановленный Хорнером в XIX столетии) произвольного алгебраического уравнения степени с действительными коэффициентами. Она приводила геометрические проблемы к алгебраическим, систематически используя теорему Пифагора.

Также, китайцы применяли многочленную интерполяцию. Мотивацией для этого открытия выступала возможность предсказывать движение небесных тел при помощи наблюдений такого рода. Этот метод также применялся для определения различных математических формул. Секи был знаком с этим методом, вероятнее всего, благодаря близкому изучению китайских календарей.

В 1674 г. Секи опубликовал трактат Хатсуби-Сампо(Hatsubi-Sampo 発微算法) с решениями всех 15 задач с помощью метода бушо-ху (bousho-hou). Он ввел иероглифы кандзи, чтобы представить неизвестные и переменные в уравнениях. Несмотря на возможность представить произвольные уравнения степени (он даже рассматривал 1458 ст.!) с негативными коэффициентами, не было никаких символов, соответствовавших круглым скобкам, равенству или делению. Например, уравнение вида ax + b могло также означать ax + b = 0. Позже, система была усовершенствована другими математиками, и, в конечном итоге, стала столь же мощной, как и европейская.

Однако, в своей книге, изданной в 1674 г., Секи дал уравнения с переменными после исключения, оставив за кадром все расчеты и свою новую систему алгебраических символов. Хуже того, в первом издании было несколько ошибок. Математик школы Хашимото (Hashimoto) критиковал его, сказав 'только 3 из 15 правильны'. В 1678 г. Танака Йошизане (Tanaka Yoshizane 田中 由真?), представитель школы Хашимото из Киото, в своем труде Сампо-меикаи (Sampo-meikai 算法明記) предложил новые решения 15 задач Савагуши, используя его версию множества переменных в алгебре, похожую на систему Секи. Чтобы ответить критике, в 1685 г. Такебе Кенко (Katahiro Takebe, 建部 賢弘?), один из учеников Секи, опубликовал в Хатсуби-Сампо Генкаи (Hatsubi-Sampo Genkai 発微算法諺解), заметки, в которых он подробно показал процесс исключения, использовав алгебраические символы.

Эффект введения такой системы символов не ограничивается алгеброй; с ее помощью математики того времени смогли выразить математические результаты в более общем и абстрактном виде.

Теперь, имея возможность выразить уравнение, они сосредоточились на изучении исключения переменных. В 1683 г. Секи выступил с теорией исключения, основанной на равнодействующей силе. Для определения результата он изобрел понятие детерминанта. Однако, в его рукописи, формула для матрицы 5×5 очевидно неправильна, равняясь всегда нулю. Все же в его более поздней публикации Таисеи-санкеи (大成算経Taisei-sankei), написанной в 1683-1710 годах, вместе с Такебе Кенко и его братьями, появляется более правильная и общая формула (Формула Лапласа).

Танака, независимо от них, также пришел к этой идее. Публикация появилась в его книге уже в 1678 г. некоторые из уравнений после исключения оставались такими же, как и результирующий вектор. В Сампо-Функаи (Sampo-Funkai 算法紛解 1690?), он явно описал результирующий вектор, и обратился к нескольким проблемам. В 1690, Изеки Томотоки (Izeki Tomotoki 井関 知辰?), и математики, не относящиеся к школе Hashimoto, работающие в Осаке, опубликовали Сампо-Хакки (Sampo-Hakki 算法発揮), в котором представили результирующий вектор и формулу Лапласа для детерминанта в случаи n×n.

Связи между этими работами не ясны. Но можно увидеть, что Секи развивал свою математику в жестокой конкуренции с математиками Осаки и Киото, который был культурным центром Японии.

В сравнении с Европейской математикой, первая рукопись Секи была столь же ранней, как и первый комментарий Лейбница на тему обработки массива в случае 3×3. Кроме того, в Европе, эта тема была забыта до тех пор, пока Габриель Крамер снова не поднял этот вопрос в 1750 г., руководствуясь теми же побуждениями, что и японские математики. Теорию исключения, которая эквивалентна японской теории, открыл вновь Безу в 1764 г. Так называемая формула Лапласа была принята только в 1750 г.

Во времена Секи, значительная часть проблем была решена, благодаря завершению теории исключения переменных. (Как вы помните, в Китайской традиционной математике геометрия почти сократилась до алгебры). На практике, конечно, вычисление не всегда можно было осуществить полностью в силу его огромной сложности. Все же, эта теория оказала существенное влияние на направление развития васан.

После того, как исключение переменных сделано, необходимо выяснить реальный корень единственной переменной в числовом уравнении. Метод Хорнера, завершенный в Китае, не был трансформирован в Японии. Так, Секи приходилось работать независимо от других ученых. (Благодаря этому, он иногда сопоставляется с методом Хорнера, который не совсем правилен.) Он также предложил усовершенствование метода Хорнера, сократив степень высшего порядка после некоторых повторений. Это, случается, так же как и в методе Ньютона-Рафсона (Newton-Raphson), но в абсолютно другой перспективе. Обратите внимание, ни он, ни его ученики никогда не выступали с идеей производной в точном значении.

Он также изучал свойства алгебраических уравнений c целью содействия числам. Самым выдающимся из них стало условие существования множества корней, основанных на дискриминанте (это теория также более ранняя, чем на Западе), которое является равнодействующей силой многочлена и его производной, а определение производной - o(h) превращается в f(x+h). Он также дал точную оценку числа реальных корней уравнения.


2. Сангаку.





Было в этой старой японской математике и что-то такое, что роднило её с японским искусством — живописью, поэзией, каллиграфией, театром, чайными церемониями, разбиением садов, изготовлением одежды и предметов быта. Одним из плодов этого математического искусства стали так называемые сангаку, «математические таблички».




Sangaku иллюстрируют решения загадок, используя традиционные японские геометрические методы, которые развивались независимо от Западных методов. Математики часто вешали их часто щедро украшенные таблетки в храмах и святыни как религиозные предложения. Посетителям храма было, таким образом, предложено подумать над ответом.

Любители математики из разных социальных классов — самураи, торговцы, ремесленники, крестьяне — открывали и доказывали разнообразные геометрические теоремы, от простых до очень сложных. Чертежи к теоремам вырезались на деревянных досках и красиво раскрашивались. Не все доски посвящены геометрическим задачам: на некоторых решались диофантовы уравнения или отыскивались объёмы криволинейных тел. На большинстве досок приводился только результат, а доказательство отсутствовало. Готовые доски вывешивались над входом в синтоистское святилище или буддистский храм в качестве приношения богам, а заодно — и вызова коллегам. (Здесь можно вспомнить о том, как шестнадцатилетний Блез Паскаль, получив свои замечательные результаты по проективной геометрии, издал афишку с их изложением и расклеивал её на улицах Парижа.)

Сангаку надписаны на языке по имени Кэнбун, который использовал китайские характеры и чрезвычайно китайскую грамматику, но включал диакритические знаки, чтобы указать японское значение. Кэнбун играл роль, подобную латыни на Западе, и его использование на Сангаку укажет, что, кто бы ни записывал проблемы, было высокообразованным.

Большинство предъявителей, фактически, кажется, было членами класса самурая.

Как пишут в предисловии к своей книге собиратели и исследователи задач японской храмовой геометрии Хидетоши Фукагава и Дэниел Педое, «чувство формы и восприятие природной красоты всегда отличали жителей Японии, так что неудивительно, что геометрия, притягательная своей красотой и неочевидностью задач и теорем, стала для практикующих это искусство людей не только развлечением, но и подходящим предметом для приношений богам». Японцы считают, что безымянных синтоистских божеств ками — восемь миллионов, и все они тайно странствуют по земле. Когда человеку открывается что-то прекрасное, это означает, что рядом с ним прошло незримое божество. (Приношение досок с доказанными теоремами в дар божеству напоминает известный рассказ о Пифагоре, принёсшим при открытии своей теоремы обильные жертвы богам.)

Многие из теорем сангаку по своим темам и стилю заметно отличаются от теорем, известных в геометрии Запада, а некоторые из них повторяют достижения европейской математики Нового времени. Очень много задач посвящено эллипсам и вписанным в ним окружностям, что связано с тем, что в Японии эллипс мыслился не как сечение конуса, что привычно для западной геометрии, но как сечение цилиндра. Японскими геометрами были открыты и доказаны многочисленные теоремы о цепях Штейнера, которые в европейской геометрии доказывались с помощью метода инверсии. Характерным было также использование пространственных образов при доказательстве планиметрических теорем. В частности, возможно, что в качестве аналога метода инверсии японские математики использовали стереографическую проекцию.

Вообще же метод открытия геометрических теорем, практиковавшийся японскими геометрами, основывался на интенсивной и продолжительной концентрации на рассматриваемом чертеже. Когда одного геометра спросили, как он получил свои замечательные теоремы об эллипсах, он ответил, что не размышлял ни над чем, кроме эллипсов, в течение последних десяти лет! Интересно, что когда японские геометры получили в свои руки и тайский перевод «Начал» Евклида, они были очень сильно удивлены. «Зачем, — сказали они, — доказывать такие очевидные факты, когда есть ещё столько красивых и сложных геометрических теорем?»

В большинстве сан гаку рассматриваются весьма прихотливые и изящные конструкции с окружностями, вписанными в квадраты, треугольники и более сложные фигуры, но есть и такие, где представлены эллипсы и сферы. Вот несколько примеров.

Сегодня, геометрия изучается в средней школе. Это идеальный способ развивать логическое мышление.


3. Решение задач


В качестве примера типичной теоремы храмовой геометрии рассмотрим одну задачу, связанную с эллипсом и вписанными в него окружностями. Решение этой задачи











методами высшей геометрии требует владения понятиями второй производной и кривизны кривой; однако она может быть решена и элементарными средствами.

Прежде чем сформулировать саму задачу, введём понятие об окружности кривизны эллипса в конечной точке его большой оси. Рассмотрим две окружности, касающихся друг друга внутренним образом. А затем начнём сжимать большую окружность по направлению, перпендикулярному к общей оси двух окружностей, превращая её в эллипс (рис. 1). До какого-то предельного момента эллипс будет охватывать меньшую окружность снаружи; но после этого момента часть дуги эллипса будет лежать внутри меньшей окружности. Эти два возможных состояния разделены пограничным эллипсом, выделенным на чертеже жирной линией. А малая окружность, всё ещё лежащая внутри пограничного эллипса, называется окружностью его кривизны в концевой точке большой оси.




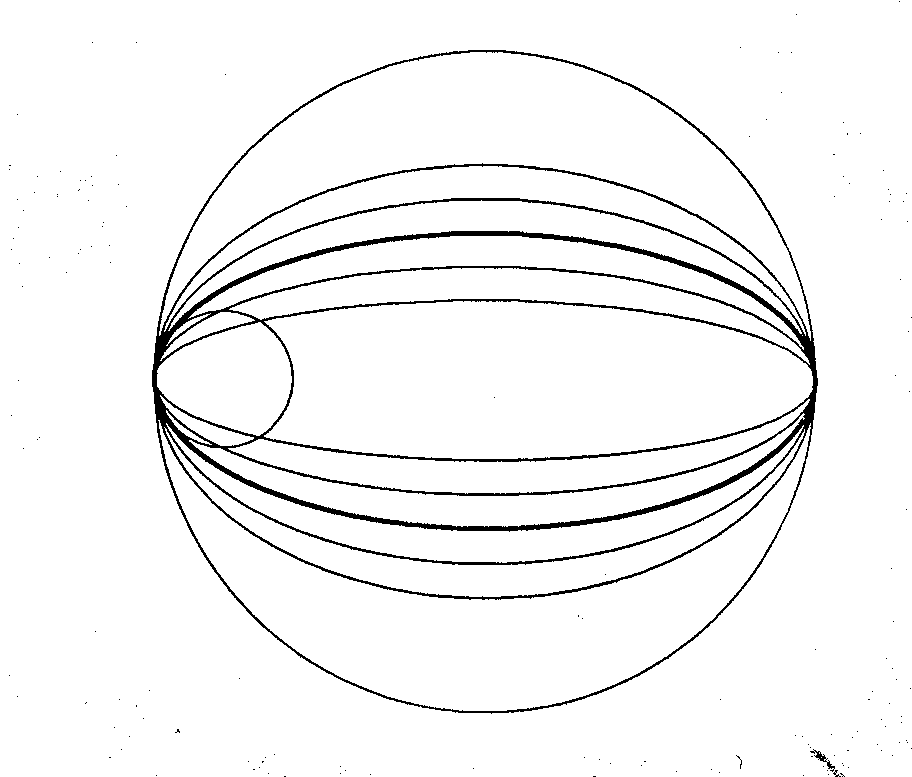
Рис. 1


Итак, пусть имеется эллипс, в который вписана цепь касания из n окружностей таким образом, что крайние окружности цепи являются окружностями кривизны эллипса в концах его большой оси (рис. 2). Требуется найти соотношение между осями эллипса и диаметрами окружностей.



Рис. 2

Решение задачи основано на представлении об эллипсе как о косом сечении цилиндрической трубы. Рассмотрим цилиндр с вписанными в него шарами, проницающими друг друга так, как показано на рис. 3, и рассечём этот цилиндр и шары косым плоским сечением, проекция которого выделена на чертеже жирной линией. Дальнейшее очевидно из чертежа. А именно, если на малой оси эллипса как на диаметре построить окружность и вписать в ней правильный многоугольник с 2n сторонами, то диаметры концевых окружностей цепи будут равны стороне этого многоугольника, диаметры следующих по порядку окружностей будут равны диагоналям, соединяющим вершины многоугольника, отдёлённые друг от друга 3 сторонами, 5 сторонами и т. д.




Рис. 3


Некоторые задачи сангаку.

1. ОкружностиO1(r1) и O2 (r2) касаются друг друга и прямой m. Окружность O3 (r3) касается O1 (r1), O2 (r2) и m (рис 4). Докажите, что

1 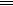1 + 1

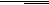
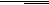
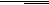r3  r1  r2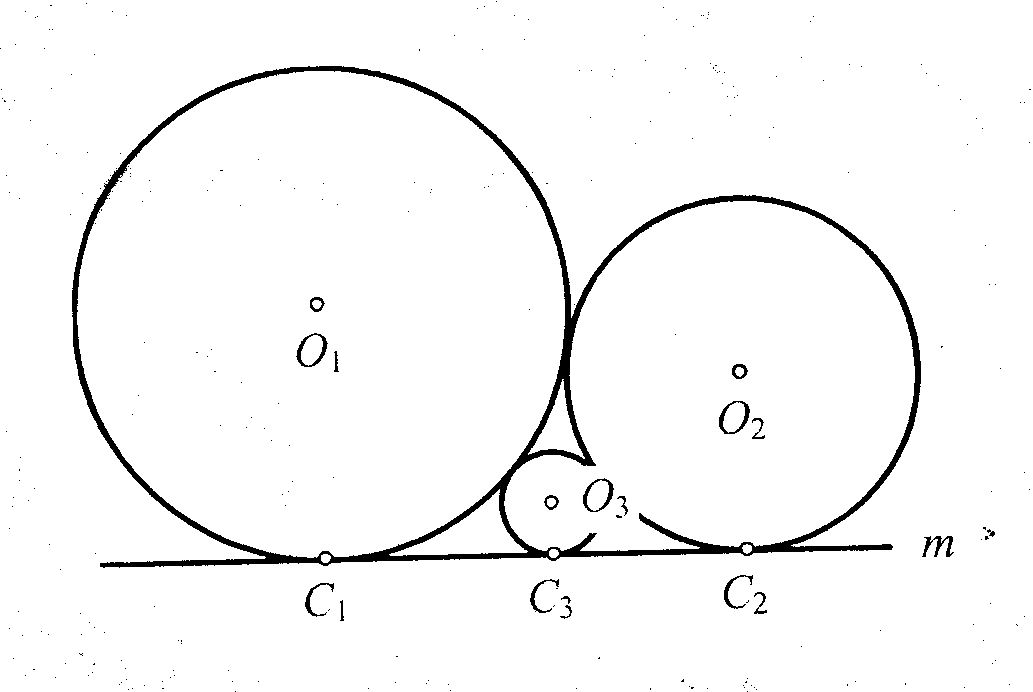




ЛЕММА. Пусть две окружности O1 (r1) и O2 (r2) касаются друг друга в точке A и касаются прямой m в точках B и C. При этом будет BC = 2r1r2

ДОКАЗАТЕЛЬСТВО. Точка A является точкой касания, поэтому она лежит на прямой O1 O2 . Проведём диаметры BD и CE; они будут параллельными как перпендикулярные к одной прямой BC. Соединим точку A с концами отрезков BD и CE. Треугольники DO1A и AO2C — равнобедренные. DO1A = AO2C как внутренние накрестлежащие. Отсюда O1AD =O2AC, и точки D, A, C лежат на одной прямой. Аналогично и точки B, A, E лежат на одной прямой. ACB =AEC, так как в сумме с ACE оба эти угла дают 90°. Поэтому прямоугольные треугольники DCB и BEC подобны. Из их подобия имеем 2r1:x = x:2r2, откуда x = 2r1r2




РЕШЕНИЕ. Поскольку C1C2 = C1C3 + C2C3, в силу леммы r1r2 =r1r3 + r2r3. Разделив все слагаемые на r1r2r3, получим

1 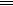1 + 1

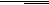
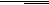
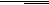r3  r1  r2


2. Параллельные прямые m1 и m2 касаются окружности O1(r1). Окружности O2(r2) и O3(r3) касаются друг друга и окружности O1(r1), при этом O2(r2) касается m1, а O3(r3) касается m3. Докажите, что r12 = 4r2r3 .





Рис. 6


КОММЕНТАРИЙ. С помощью теоремы Пифагора доказать это соотношение не слишком сложно. Но также можно придумать решение, опирающееся не на теорему Пифагора, а на соображения, связанные с подобием, как это было сделано в предыдущей задаче.


3. Во вписанном в окружность четырёхугольнике проведены диагонали, двояко рассекающие этот четырёхугольник на два треугольника. В каждый из четырёх получившихся треугольников вписана окружность. Докажите, что центры вписанных окружностей являются вершинами прямоугольника.




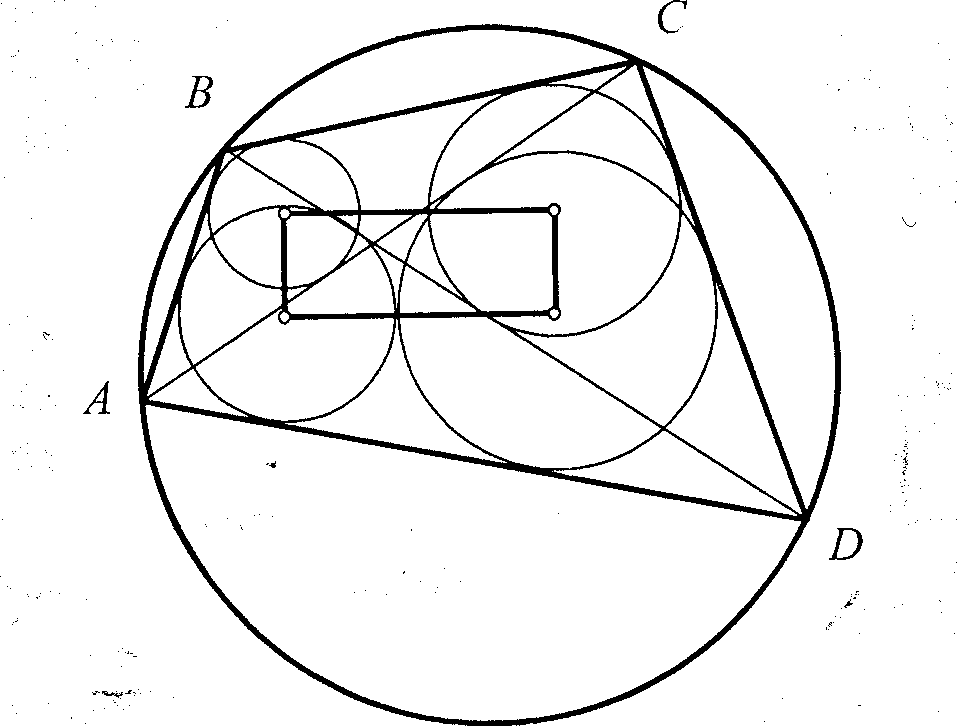
Рис. 7


ЛЕММА 1. Дуги, высекаемые на окружности парой вертикальных углов между двумя пересекающимися хордами, в сумме равны дуге, на которую опирается вписанный угол, равный углу между этими хордами.

ДОКАЗАТЕЛЬСТВО. Пусть хорды AB и CD, пересекающиеся в точке P, высекают на окружности дуги AD и CB. Проведём хорду CE, параллельную AB, здесь ECD = APD. Дуга AE равна дуге СB, поэтому дуга DE, на которую опирается вписанный угол ECD, равна сумме дуг AD и CB.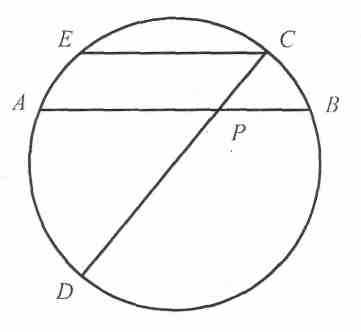




Рис. 8


  1. Вписанный в окружность многоугольник произвольным образом разбивается диагоналями на треугольники, и в каждый треугольник вписывается окружность. Докажите, что сумма радиусов всех вписанных окружностей будет одной и той же при любом порядке триангуляции (рис. 9).





Рис. 9


КОММЕНТАРИЙ. Если доказать это утверждение для четырёхугольника, его несложно будет обобщить и на случай многоугольника с произвольным числом углов. А доказательство для четырёхугольника можно получить как следствие предыдущей задачи.


^ III. Заключение


Сангаку – это уникальное достояние японской культуры. Эти дощечки с изображением задач, которые придумали японские математики, внесли огромный вклад в развитие истории математики в Японии. Сангаку, по структуре своей очень лаконичны и просты.

Данная проектная работа действительно заинтересовала меня. Я познакомилась с японской математикой и культурой. Рассмотрела одни из наиболее интересных задач и постаралась найти им доказательство. Также при выполнении своей проектной работы использовала статьи Принстонского университета и Колледжа Хьюстона, которые требовали тщательного перевода с английского на русский язык.

При рассматривании данной темы, я заметила взаимосвязь математических доказательств того периода и нашего времени, что задачи такого типа встречаются сейчас на ЕГЭ.

Во многих источниках говорится, что большинство открытий, не только географических, но и математических, были сделаны в Европе. Но после глубокого знакомства с историей математики Японии, можно смело сделать вывод, что развитие науки проходило также и на Востоке, и некоторые математические открытия впервые произошли именно там.


IV. Список литературы.

  1. ссылка скрыта
  2. ссылка скрыта
  3. FUKAGAWA H., PEDOE D. Japanese Temple Geometry Problems. Winnipeg: Charles Bab- bage Research Foundation, 1989.
  4. FUKAGAWA H., RIGBY J. F. Traditional Japanese Mathematics Problems from the 18th and 19th Centuries. Singapore: Science Culture Technology Press, 2002.
  5. ROTHMAN T. Japanese Temple Geometry. Scientific American, 278, # 5 1998, p. 85–91.