Geum.ru

Василя Сухомлинського (протокол №1 від 03. 02. 2009 року) Кіровоград 2009 ббк 74. 580. 044

Вид материалаДокументы

Содержание


Другій групі
Подобный материал:
1   ...   6   7   8   9   10   11   12   13   14

вчитель математики ліцею інформаційних технологі Олександрійської міської ради, спеціаліст вищої кваліфікаційної категорії, вчитель-методист, відмінник освіти України (стаж: 26 років).




Л.І.Халізова досконало володіє методикою викладання математики, творчо організовує навчально-виховний процес, впроваджує сучасні освітні технології, що допомагають їй урізноманітнити процес пізнання, зробити його цікавим, ефективним.

Для стилю роботи педагога характерні математична і педагогічна інтуїція, великий творчий потенціал. Вона – майстер імпровізації, нестандартних підходів до будь-якого виду діяльності. Її головна мета – навчити учнів учитися, проявляти творчість, критично осмислювати навколишній світ (від творчо-критичного аналізу тексту підручника, розв’язку задачі до вироблення власної думки з будь-якої проблеми, що постає перед людиною).

Творчо використовуючи ідеї В.О.Сухомлинського, Лариса Іванівна Халізова з 1990 р. працює над проблемою «Робота зі здібними та обдарованими учнями. Розвиток творчого мислення на уроці математики».

Одне з основних завдань, яке вона ставить перед собою, – допомогти учням в оволодінні засобами розумової діяльності, дати міцні знання з предмета, підготувати до вступу у вузи. Тому на кожному уроці старається, щоб всі діти були активними, щоб не механічно запам’ятовували готову інформацію, а заохочує думати, аналізувати і порівнювати, узагальнювати і класифікувати, робити висновки, формулювати правила і закони. Успішний розв’язок пізнавальних задач можливий лише за наявності в учнів певного запасу прийомів розумової діяльності.

Л.І.Халізова користується різними формами і методами викладу матеріалу. Перевагу надає лекційно-практичній роботі. Цю систему роботи варто використовувати під час вивчення таких тем, як «Розв’язання тригонометричних рівнянь, систем рівнянь», «Логарифми. Логарифмічна функція», «Об’єми многогранників», «Вектори в просторі» та інші.

Під час блочного вивчення теоретичного матеріалу звільняється багато часу на застосування отриманих знань, розв’язання різноманітних задач, вироблення в учнів самостійних умінь і навичок. Увага учнів постійно сконцентрована на матеріалі теми. Вони з кожним днем все з більшим інтересом беруть участь у роботі. Повторюється основний матеріал з попередніх тем, робляться узагальнення. Всі заняття математики в 10-11 класах спарені, що якраз добре сприяє лекційно-практичному методу навчання.

У ході розв’язку математичних задач, особливо нестандартних, можна формувати в учнів елементи творчого мислення. Саме тому більшу частину часу під час вивчення предмета вчитель відводить на розв’язування задач, вчить учнів думати, узагальнювати, аналізувати, розглядає різні способи розв’язку однієї задачі. На уроці створює атмосферу доброзичливості, взаємоповаги. Під час виконання вправ, особливо їх колективного розбору, всі учні можуть вільно, з місця висловлювати думки, висувати гіпотези, можуть обговорювати їх розв’язок з товаришами.

Вчитель вважає, що корисніше розв’язувати менше, але так, щоб всі думали, всі розбирались у задачі, відчули свої можливості і задоволення від самостійного розв’язку. Часто практикує розв’язання задач із збірника для вступників до вузів (на вибір) без попередньої підготовки учнів. Тоді апробує той чи інший метод розв’язку і тим самим активізує розумову діяльність вихованців, які разом з нею стараються знайти шлях до розв’язку.

Одним зі способів розвитку здібностей учнів є самостійна діяльність під час вивчення предмета. Особливо важливо навчити працювати самостійно старшокласників. Плануючи урок, Л.І.Халізова значну частину часу відводить на: самостійне вивчення нового матеріалу, самостійний розв’язок задачі, навчальну самостійну роботу (7-10 хв.), самостійну роботу контролюючого характеру (20-25 хв.). Під час проведення самостійних робіт (за допомогою тестів) організовує перевірку правильності виконання розв’язку задач самими учнями, використовуючи готові зразки, взаємоперевірку.

Працюючи над проблемою для учнів математичного профілю, вчитель підготувала методичні вказівки до вивчення окремих тем.
  1. Тригонометричні функції.
  2. Обернені тригонометричні функції.
  3. Тригонометричні рівняння з параметрами.
  4. Про появу сторонніх коренів рівняння.
  5. Втрата коренів рівняння.
  6. Рівняння площини.
  7. Довідковий матеріал із планіметрії.
  8. Довідковий матеріал із стереометрії.
  9. Розв’язування ірраціональних, логарифмічних нерівностей.

Л.І.Халізова вивчає і впроваджує сучасні технології навчання. Проводить факультативні заняття з розв’язання олімпіадних задач, індивідуальну роботу з обдарованими учнями. Постійно має призерів міських, регіональних та обласних олімпіад з математики. За останніх 5 років її вихованці були переможцями різних етапів Всеукраїнських олімпіад.

Протягом останніх двох років усі випускники Лариси Іванівни, ліцеїсти математично-інформаційного профілю, взяли участь в зовнішньому незалежному оцінювані й показали досить високі результати. Так, у 2006 році 96% учнів мали достатній і високий рівень досягнень. За результатами ЗНО всі випускники цього профілю стали студентами державної форми навчання престижних національних вузів міст Кіровограда, Києва, Дніпропетровська, Харкова.

З 1995 року Л.І.Халізова – викладач та методист центру довузівської підготовки Дніпропетровського національного технічного університету залізничного транспорту, Харківського національного університету радіоелектроніки, Харківського національного аерокосмічного університету.

Педагог бере активну участь у роботі шкільного та міського методичних об’єднань, вивчає, узагальнює, впроваджує передовий педагогічний досвід.

Л.І.Халізова проводить заняття у своєму кабінеті математики, у якому є все необхідне для забезпечення високої результативності кожного уроку (дидактичний роздатковий матеріал з усіх тем програми, тести, науково-методичні журнали, газети).

Лариса Іванівна має нестандартний творчий підхід до виховних функцій. Особистим прикладом утверджує повагу до загальнолюдських принципів моралі, справедливості, гуманізму, працелюбства. Користується повагою та авторитетом серед колег, батьків та учнів.

Навіть такий короткий екскурс у творчу лабораторію свідчить про високий рівень педагогічної майстерності вчителя. Результати роботи педагога – додаткове цьому підтвердження.


Хільченко Світлана Дмитрівна,

керівник гуртка з образотворчого мистецтва при спеціалізованому ЗНЗ І-ІІІ ступенів №3 м. Долинської, спеціаліст вищої кваліфікаційної категорії (стаж: 18 років).


Специфіка образотворчого мистецтва базується на емоційному світосприйнятті. Як зрозуміти, що дитина художньо здібна? Спеціальні здібності притаманні не всім. Наприклад, окомір необхідно розвивати, щоб навчитись співвідносити частини.

Як знайти художньо обдаровану дитину? Питання стосовно виявлення дитини із вродженими задатками до малювання досить проблематичне. Діти 6-9 років із задоволенням фантазують, не відчувають страху при перенесенні своїх фантазій на папір, картон, пластилін та інший матеріал. Це найкращий спосіб для них передати красу оточуючого світу, свої емоції. Їм подобається кожна власна робота, вони відчувають радість від створеного образу. Учні середньої ланки, вже починають боятися осуду однокласників, батьків, учителя. Старшокласники, у яких своєчасно не розвивали художні здібності, нерідко з роками взагалі втрачають уміння фантазувати, уявляти.

Наявність природних задатків ще не вирішує проблему вияву художніх здібностей. Необхідні відповідні заняття художньою діяльністю. Лише за такої умови можливий перехід задатків у здібності. Саме тому на педагога покладається відповідальна місія – якнайраніше виявляти й розвивати природні здібності учнів.

Слід зазначити, що для художника важливі якості зорового аналізатора (точне визначення пропорцій, кольору), гарна зорова пам’ять, розвинуте образне бачення, вміння уявляти, фантазувати. Педагогу необхідно вирізнити учнів, яким притаманні оригінальність, розвинений зоровий аналізатор, прагнення пошуку нового, гнучкість мислення, образність мислення, розвинута уява, фантазія, допитливість, прагнення до самоосвіти. За допомогою спеціальних додаткових завдань розвивати художні здібності цих дітей. Творче художнє мислення школярів необхідно підтримувати, створивши сприятливу атмосферу. При цьому вчитель є порадником і консультантом. Вважаю, що у співпраці з психологом легше виявляти художньо обдарованих дітей, розвивати та поглиблювати їхні знання й мистецькі уміння.

Поділюся деякими своїми напрацюваннями.

Досить часто застосовую тест «Фантазер». Роздаю всім учням у класі аркуші паперу, на яких фломастером зображена ламана лінія. Дітям пропонується повернути аркуш в будь-яку сторону і за 2 хвилини створити образ, який вони побачили. Результати завжди непередбачувані. Через деякий час цей тест проводжу знову. Це стимулює фантазію та творчість школярів, а для вчителя слугує способом виявлення учнів, які вміють бачити оригінальний образ в звичайній лінії.

Для виявлення та розвитку асоціативного мислення пропоную виконати творчі роботи з тем філософського спрямування: «Добро», «Зло», «Радість», «Успіх», «Щастя», «Біль», «Образа», «Дружба».

Велику увагу приділяю спостереженням. Наприклад, ставлю перед учнями завдання простежити, як зміниться природа за вихідні. Задаю запитання: «Що нового ви побачили?», «Якого кольору листя на деревах гармонує з осіннім небом; чому горобина така яскрава на тлі осінньої природи?» та ін. Переконана: якщо дитина вміє спостерігати за красою навколишнього світу, то вона зможе відтворити побачене на папері, мольберті тощо. З метою розвитку вміння спостерігати постійно проводжу екскурсії.

Залучаю школярів до участі в різноманітних конкурсах. Серед робіт учнів класу проводиться відбір на загальношкільний конкурс. Стало традицією до Дня відкритих дверей у школі проводити персональні виставки обдарованих учнів. Це стає святом не лише для юних художників, а й для вчителів, усіх учнів закладу.

Буває так, що дитина має здібності, добре розвинений окомір, фантазію, але не вдосконалює їх через почуття невпевненості у собі. Завдання педагога в такому випадку полягає у підтримці такого учня, підвищенні його самооцінки, формуванні мотивації до спеціального навчання. Це допоможе дитині знайти себе, врешті-решт реалізувати свій творчий потенціал.

Іноді складається така ситуація: визначивши, що дитина гарно малює, класний керівник змушує її постійно брати участь у багатьох конкурсах, звертаючись до її совісті. Цим самим нерідко відбивається бажання малювати. Вважаю це недопустимим явищем, адже дитяча творчість як квітка, яку необхідно захищати, підживлювати й підтримувати.

Складаючи програму гурткової роботи з образотворчого мистецтва, обов'язково враховую вікові особливості вихованців. При плануванні занять з дітьми 6-8 років перевагу надаю репродуктивно-творчим методам; з дітьми 9-15 років – проблемно-пошуковим, творчо спрямованим методам навчання. Треба пам’ятати, що кожна дитина – це непізнаний світ, величезна таємниця і завдання творчого вчителя спробувати відчинити двері до цієї таємниці.


Л.А. Ткаченко,
завідувач НМК математики КОІППО імені Василя Сухомлинського





Шверненко Ірина Євгенівна,

вчитель математики гімназії №9 Кіровоградської міської ради, спеціаліст вищої кваліфікаційної категорії, старший вчитель, переможець конкурсу «Учитель року – 2004» (стаж: 16 років).


Плануючи роботу з обдарованими учнями, І.Є.Шверненко виділяє три етапи, визначає мету і завдання кожного й наповнює їх відповідним змістом.

Цілі:

1 етапу: виявляти учнів, які мають природну обдарованість до точних наук; з високим рівнем навченості, мотивувати їх до вивчення точних наук; із яскраво вираженими організаційними, художньо-естетичними та іншими видами обдарованості; зацікавити їх можливостями вияву своїх обдарувань під час вивчення математики та участі в конкурсах математичного спрямування (учні 5-6 класів).

2 етапу: забезпечувати міцне засвоєння учнями програмового матеріалу на уроках математики, викликати стійкий інтерес до творчих робіт, розвивати творче мислення і уяву, формувати навички самоосвіти, мотивувати самовдосконалення успішною участю в конкурсах і олімпіадах (учні 7-9 класів).

3 етапу: підтримувати зацікавленість гімназистів у вияві своїх здібностей, створювати умови й надавати можливість практичного застосування набутих знань у позаурочній роботі та участі в олімпіадах різних рівнів (учні 9-11 класів).

На першому етапі важливе місце займають вправи та завдання з розвитку кмітливості, логічного мислення, різноманітні тести. Вчитель систематично використовує їх на уроках з метою надання учням можливостей виявляти свої здібності, досягати емоційного стану «Я можу!», викликати бажання працювати над самовдосконаленням. Уроки систематизації та корекції знань часто проходять у формі ділових ігор, тренінгів, змагань. І.Є.Шверненко вважає, що позитивний емоційний стан дітей на уроці у 5-6 класах відіграє вагому роль, оскільки сприяє народженню і зростанню авторитету знань у класному колективі, викликає бажання брати участь у конкурсах і олімпіадах.

Вчитель на цьому етапі постійно приділяє увагу вдосконаленню навичок усного рахунку, адже високий рівень швидкості розумових операцій є запорукою поглибленого вивчення учнями програмового матеріалу, що уможливлює їхню участь в олімпіадах.

Завдання другого етапу: навчити учнів класифікувати поняття, що вивчаються, розрізняти види вправ за темою, вміти використовувати стандартні алгоритми для їхнього розв’язання. Відпрацьовуючи ці навички, педагог поступово збільшує кількість нестандартних задач, широко використовує завдання випереджального характеру, обернені запитання до вправ, що вже розглядались. Ця робота продовжується й на третьому етапі.

Розвитку творчого мислення сприяють завдання на складання власних вправ і задач з теми, що вивчається на уроці. Після цього учні обмінюються завданнями й розв’язують їх самостійно. Обговорення правильності розв’язку та складності завдання відбувається колективно. Якщо завдання виконано неправильно, «автор» пояснює, як саме можна було знайти правильну відповідь. Пояснення власного ходу міркувань під час виконання складних завдань дає можливість вибудувати логічну послідовність думок і умовиводів, використання понять і правил, що вивчались, а це, в свою чергу, систематизує знання учнів. В кінці уроку виконуються вправи на рефлексію, що дають змогу кожному усвідомити особистий рівень навчальних досягнень. Результатом є впевненість учнів у власних силах («Я знаю!»), зацікавленість позапрограмовим матеріалом із предмета і здатність виконувати відповідні завдання.

На третьому етапі ефективними є уроки-семінари, на яких учні-доповідачі висвітлюють певні аспекти практичного застосування знань, а також питання, що не ввійшли до шкільної програми. Багатьох зацікавлює можливість розробити завдання і провести вікторини для молодших учнів. Це уможливлює повторення та систематизацію навчального матеріалу попередніх класів. До того ж, це шанс виявити організаційні та педагогічні здібності школярів.

Впровадження проектної технології стимулює творчий розвиток. Оскільки розподіл ролей відбувається за бажанням, кожен обирає собі завдання до снаги. Так, учень із академічною обдарованістю готує теоретичний матеріал, той, хто має хист до розв’язання складних математичних задач, підбирає цікаві завдання і пояснює їхні розв’язки, художньо обдарований гімназист придумує оформлення сайта, а знавець інформаційних технологій втілює ці задуми в програмі. Створюється ситуація, коли учень мусить взяти на себе якусь з цих ролей і виконати її, а це призводить до особистісного зростання і, водночас, є своєрідною підготовкою до участі в олімпіадах.

Учні Ірини Євгенівни беруть активну участь у роботі шкільного наукового товариства школярів «Обрій». Теми науково-дослідницьких робіт визначаються відповідно до віку учнів та їхньої особистої зацікавленості. Вони можуть виконуватися протягом декількох навчальних років. У перший рік роботи над темою учень цілеспрямовано знаходить і вивчає теоретичний матеріал із цієї проблеми, ознайомлюється з прикладами практичного застосування, що наводяться у різних підручниках та відповідних посібниках. Наступного року в межах опрацювання теми учень описує розв’язки олімпіадних та придуманих ними завдань. Кожен навчальний рік закінчується або захистом напрацювань або ж підсумковим захистом науково-дослідницьких робіт. Учитель небезпідставно вважає, що публічний захист своєї роботи сприяє виробленню навичок теоретичних виступів перед аудиторією, вмінню виділяти головне, цікаве, вести полеміку. Окрім того, довготривалий процес підготовки до захисту науково-пошукової роботи є ефективним засобом підготовки до олімпіад. Емоційний стан «Я досягаю вершин!» сприяє результативній участі вихованців Ірини Євгенівни у предметних олімпіадах та різноманітних математичних конкурсах (наприклад, «Кенгуру»), турнірах. Нерідко учні цього висококваліфікованого педагога запрошуються на навчання в заочні математичні школи та спеціалізовані школи-інтернати всеукраїнського рівня.

Слід зазначити, що І.Є.Шверненко ефективно розвиває латеральне мислення школярів, яке сприяє реалізації творчого потенціалу особистості на уроках і в позаурочній діяльності, зокрема під час проведення конкурсів і олімпіад. Вона ознайомилася з методикою формування латерального мислення школярів і на основі першоджерел розкриває деякі аспекти:

«Розмірковуючи над проблемою розвитку творчої складової особистості учня, слід зазначити, що ми більше приділяємо уваги розвитку логічного мислення школярів, аніж латеральному. Це поняття вперше використав Едвард Боно у 1967 році, розуміючи під ним «…специфічний процес обробки інформації, спрямований на зміну існуючої стереотипної моделі сприйняття навколишньої дійсності, групування вихідних елементів у більш незвичних сполученнях та створення альтернативних варіантів розв’язання певної проблеми» [1]. Латеральне мислення, зазначає учений, не замінює логічне мислення, воно його доповнює. Ця складова процесу мислення допомагає прийти до ефективного розв’язання проблеми, звільнитись від моделей-кліше, перебудувати стереотипні схеми. У латеральному мисленні є здатність змінювати сприйняття. Якщо у більшості випадків творчість потребує таланту для свого виявлення, то латеральне мислення доступне кожному, хто прагне створити нові ідеї.

Отже, для розв’язання різних проблем людина потребує як логічного, так і латерального мислення. Використання різних видів мислення залежить від того, яку мету вона ставить перед собою. Можна виділити три групи проблем:
  1. Проблеми, що потребують для свого розв’язання більшого обсягу інформації або кращих методів її обробки.
  2. Проблеми, для розв’язання яких потрібна не додаткова інформація, а лише перегрупування вже існуючої.
  3. Проблеми, що зводяться до відсутності проблеми. Людина не зосереджується на досягненні найкращого результату, тому що навіть не здогадується, що він можливий. Особистість повинна усвідомити, що проблема полягає в тому, що ситуацію можна і необхідно поліпшити.

Якщо для вирішення проблем першої групи достатньо логічного мислення, то для розв'язання двох інших типів проблем важливі широта і гнучкість мислення, його "нешаблонність", тобто необхідне латеральне мислення. Його мета – знаходження у хаосі нової плідної ідеї, яка має бути ефективною, дієвою, зосередженою на кінцевому результаті. Коли така ідея знайдена, слід перейти до її раціоналізації, логічної перевірки. Логічне мислення вдосконалює і обґрунтовує розв'язки, що з'явилися завдяки латеральному мисленню [3].

Методи для розвитку латерального мислення розроблені Е.Боно [2, 3]. Їх використання у навчальному процесі залежить від мети, яку ставить перед собою педагог на конкретному етапі своєї роботи.


«Плюс, мінус, цікаво». Прийом використовується для аналізу та розв'язання проблеми. Завдання: виявити всі позитивні, негативні та цікаві аспекти проблеми. Цікавими можуть бути аспекти, що не належать ні до позитивних, ні до негативних, чи такі, які можна розвинути у нову ідею.


«Розглядання всіх фактів». Метою цього прийому є складання переліку всіх факторів (умов, чинників), які необхідно враховувати при пошуках нової ідеї. Ефективність знайденого рішення оцінюється дотриманням цих умов.


«Погляд інших людей». Цей метод допомагає подивитися на проблему зі сторони. Завдання: скласти список осіб, яких стосується ця проблема. Кожен по черзі «ставить» себе на місце цих людей, щоб спробувати зрозуміти їх. Дуже важливо враховувати реальні погляди людей.

«Наслідки і результат». Ця вправа дає можливість серед нових ідей виділити таку, що є оптимальною за певних умов. Аналізуючи нові рішення, слід визначити, які наслідки вони матимуть (миттєві, короткострокові, середньострокові, довгострокові).


«Альтернативи, можливості, вибір». Цей метод спрямований на пошук альтернативних рішень. Досить часто ми навіть не усвідомлюємо, що існує вибір у вирішенні певних проблем, сприймаючи ситуацію як закономірну або складену історично. Генеруючи альтернативи, завжди можна від них відмовитись, якщо вони не кращі за нинішній спосіб виконання дій. Пошук альтернативи можна використовувати під час визначення проблеми (необхідно відшукати альтернативні причини виникнення проблеми) і під час її розв'язку (необхідно знайти якомога більше альтернативних способів вирішення проблеми).


«Мета, спрямування, завдання». Мета – це усвідомлений образ майбутнього результату. Приступаючи до вирішення проблеми, важливо запитати себе: «Яка мета моїх роздумів?», «Який результат я хочу отримати наприкінці?» Варто знайти декілька альтернативних формулювань мети й завдань.


«Метод випадкової стимуляції». На першому етапі роботи необхідно знайти випадкове слово (варіантів безліч: книга, журнал, подія, предмет чи образ, придуманий учасниками). На другому етапі необхідно пов'язати випадкове слово з проблемою, знайти і обґрунтувати новий варіант рішення.


«Провокаційна дія». Один із різновидів методу випадкової стимуляції. Являє собою зовнішній стимул, котрий сприяє появі нового розв'язання проблеми, завдяки поєднанню асоціацій, пов'язаних з темою, і асоціацій з іншої сфери, до якої ця проблема не належить.


«Шість капелюхів мислення». Цікавий і ефективний спосіб знаходження нових рішень. Ґрунтується на спробі розділити в часі такі дії, як збирання об'єктивних фактів (білий капелюх), вияв емоцій, почуттів та інтуїції (червоний капелюх), пошук позитивних сторін (жовтий капелюх), пошук недоліків (чорний капелюх), творчий пошук, генерування нових ідей, альтернативних підходів (зелений капелюх), аналіз усього процесу мислення, тобто рефлексія визначення мети, планування, висновків (синій капелюх). Капелюхи мають «одягати» всі учасники процесу пошуку нової ідеї.

Використання описаних методів розширює світогляд, сприяє усвідомленню відповідальності за прийняті рішення, підвищує загальний творчий потенціал людини. Дані методи можна адаптувати до аудиторії та завдань, що виносяться на розгляд. Вони є конкретними інструментами, за допомогою яких людина, в даному випадку учень, може створювати щось нове й продуктивне».

Слід зазначити, що на перший погляд, представлена методика немає ніякого відношення ні до математики, ні до проблеми підготовки учнів до участі в олімпіадах. Насправді ж, саме розвинуте латеральне мислення, як зазначає І.Є.Шверненко, допомагає її вихованцям досягати значних успіхів у навчанні, в тому числі в олімпіадах (14 учнів Ірини Євгенівни за останні 4 роки стали призерами олімпіад різних рівнів). Тому вчитель вважає цю методику одним із шляхів підготовки до олімпіад. Звичайно, потрібно глибоко її вивчити, щоб адаптувати до школи, уроків і позаурочної діяльності, використовуючи деякі елементи загальної методики, як це робить І.Є.Шверненко.

Література

1. Боно Е. Латеральное мышление. – СПб: Питер Паблишинг, 1997.

2. Боно Е. Нестандартное мышление /Пер. с англ. – Минск: ООО «Попурри», 2000.

3. Пивоварова О. Латеральне мислення і методи його розвитку. – Завуч. – 2006. – №33 (листопад).


Шигонова Ольга Петрівна,

вчитель фізики НВК «Загальноосвітня школа І-ІІІ ст. № 25, природничо-математичний ліцей» Кіровоградської міської ради, спеціаліст вищої кваліфікаційної категорії, вчитель-методист (стаж: 27 років).


Перед учителем фізики на сучасному етапі стоїть дуже складне завдання. Фізика як навчальний предмет стає все менш актуальною в нашому місті. Кіровоградські вузи відмовляються від вступного екзамену з фізики. Соціальний запит на знання фізики практично відсутній. В таких умовах надзвичайно важко сформувати і зберегти протягом декількох років навчання в школі стійкий інтерес до вивчення фізики.

У наш час учневі вже замало просто мати гарну оцінку з предмета. Величезна кількість різних телевізійних інтелектуальних ігор, конкурсів створює атмосферу, в якій дитині стає необхідним негайне визнання оточуючих. Створити атмосферу успіху і суспільного визнання - це одне з головних завдань в роботі з обдарованими дітьми. Учень повинен постійно відчувати, що його глибокі знання дають можливість вже зараз, а не тільки в далекому майбутньому, одержати визнання як однолітків, так і дорослих.

Це завдання можна розв'язати, залучивши дітей до участі в різного роду конкурсах та позакласних заходах.

Одним з таких конкурсів є Всеукраїнський фізичний конкурс «Левеня», в якому мої вихованці беруть участь з 2002 року. Підготовка до участі в конкурсі починається в жовтні, відразу після проведення шкільної олімпіади з фізики.

Заняття з підготовки до конкурсу проводяться один раз на два тижні. В основу роботи покладено розв'язування задач, які пропонувались на конкурсі «Левеня» в попередні роки, та завдань Всеукраїнської олімпіади з фізики. В залежності від рівня підготовки учні поділяються на дві групи. Одні з них повторюють теоретичний матеріал до наступного заняття та розв'язують завдання конкурсу Левеня» першого та другого рівня складності. Найбільш підготовлені діти розв'язують завдання третього рівня складності та завдання Всеукраїнської олімпіади з фізики.

Наприклад, під час повторення теми «Термодинаміка» учні 10 класу готують такі теоретичні питання:
  1. Визначення внутрішньої енергії та роботи ідеального газу.
  2. Перший та другий закони термодинаміки.
  3. Теплові машини.



Крім того учням першої групи пропонуються наступні завдання:

1. Який з графіків описує залежність внутрішньої енергії певної маси ідеального газу від:

а) температури;

б) молярної маси?


1 2 3 4


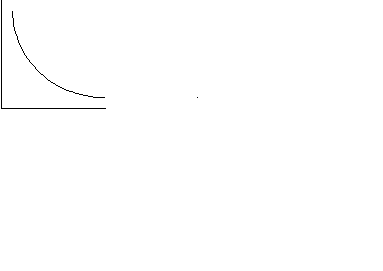
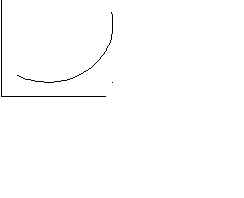
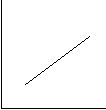
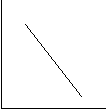u u u u


2. Під час яких процесів газ не виконує роботу?

а) Ізохорне нагрівання.

б) Ізобарне нагрівання.

в) Адіабатне нагрівання.

г) Ізохорне охолодження.

д) Ізобарне охолодження.





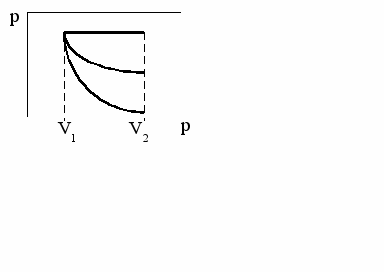
3. Нагрівник передав робочому тілу в k разів більше теплоти, ніж воно повернуло холодильнику. Обчислити ККД теплової машини.


4. Оборотний процес зміни стану ідеального газу здійснюють таким чином, що робота зовнішніх сил над газом в будь-який момент рівна зміні внутрішньої енергії газу. Який це процес?


5. Порівняйте роботу, що виконує газ при розширенні у трьох процесах:

1) ізобара;

2) ізохора;

3) адіабата.


Содержание